Design and Implementation of a MIMO Integral Resonant Control for Active Vibration Control of Pedestrian Structures
Abstract
1. Introduction
2. System Modeling and Control Structure
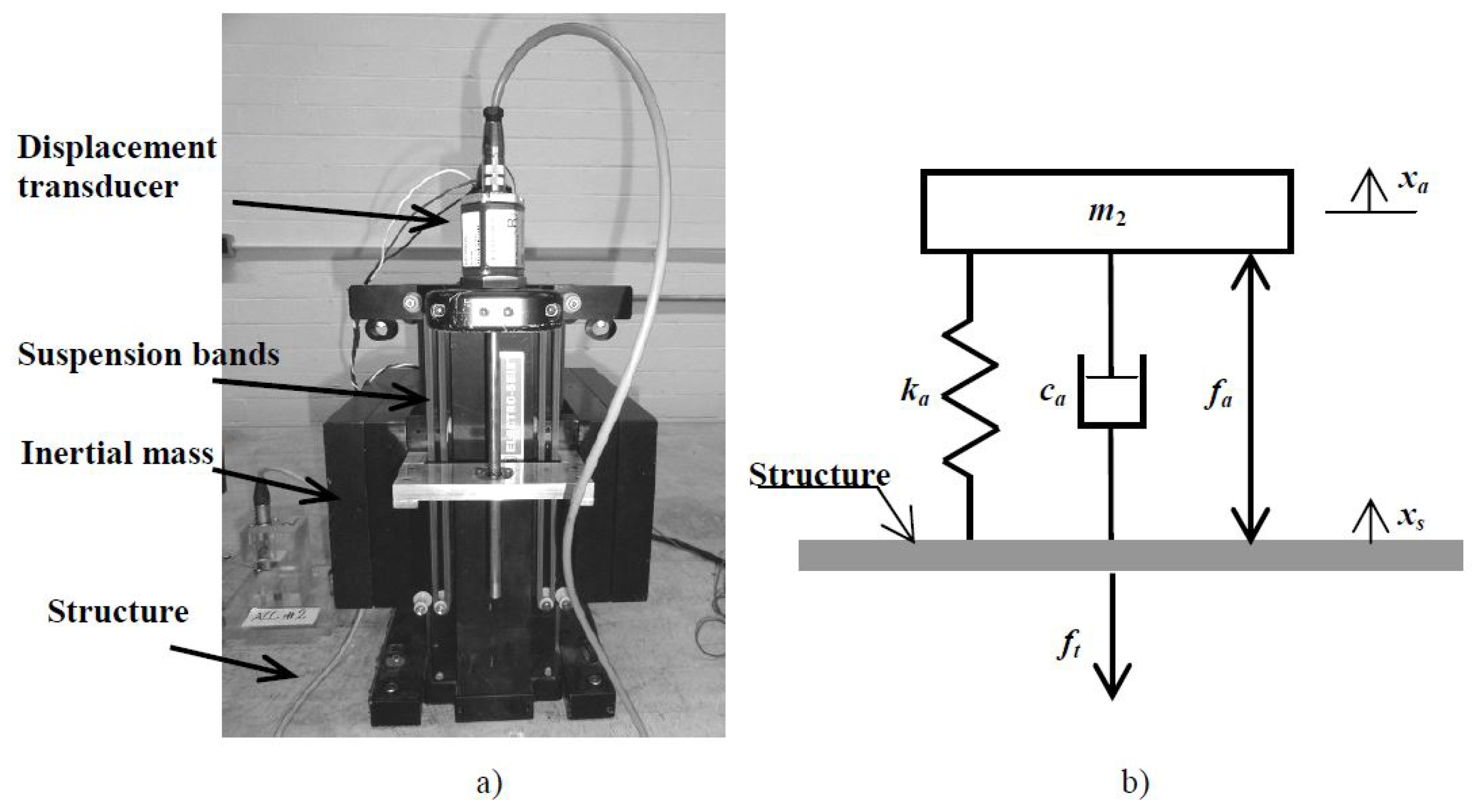
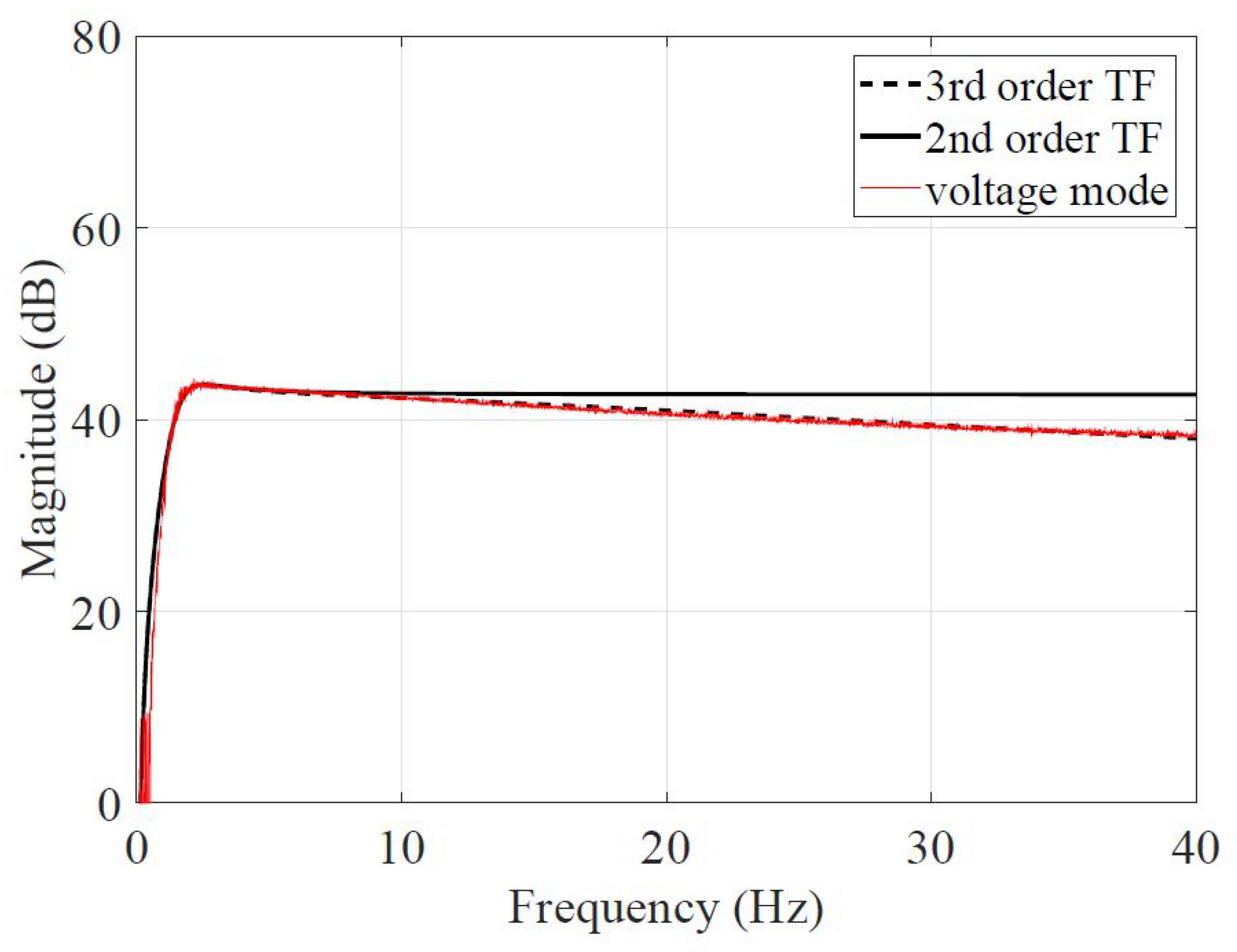
2.1. Parametric System Model
2.2. Proposed Control Scheme
3. Design Methodology Based on the Common Framework
- Identifications and finite-element (FE) model calibration;
- Define the performance index (PI);
- Define the strategy to find the optimal controller;
- Obtain the optimal controller.
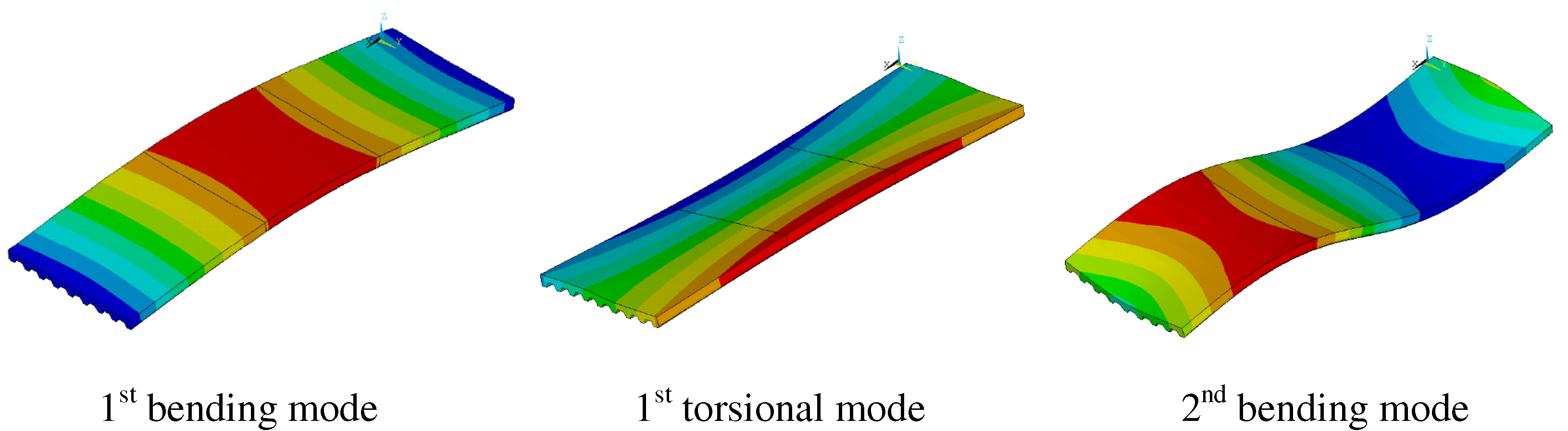
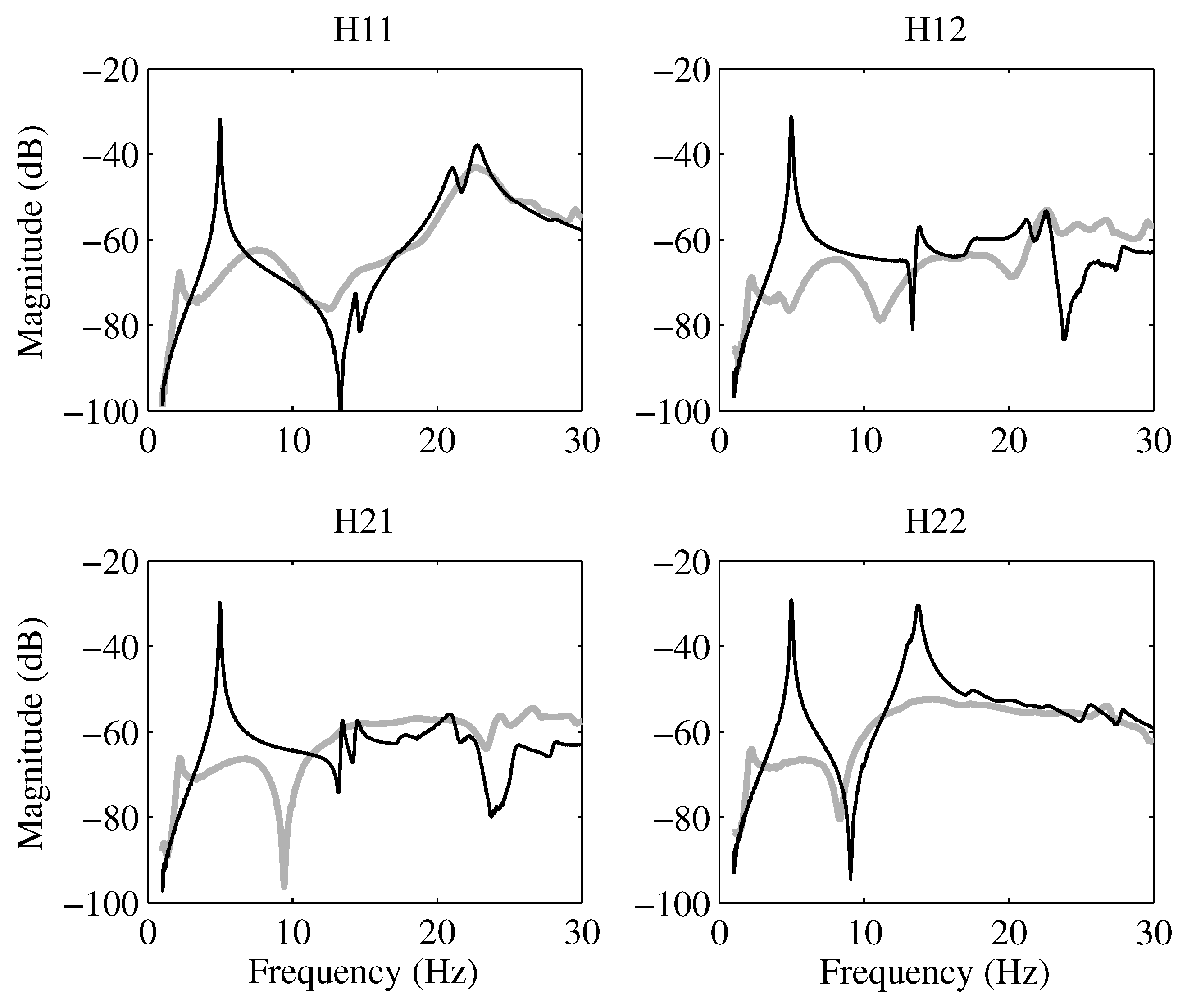
3.1. Identifications and FE Model Calibration
- N16: , , rad/s and ;
- N22: , , rad/s and .
- Natural frequencies (): rad/s, rad/s, rad/s, rad/s, , and rad/s.
- Damping ratios (): , , , , , and .
- Mode shape ():
- -
- Node N16: , , , , , and .
- -
- Node N22: , , , , , and .
3.2. Performance Index
3.3. Controller Optimization
- A variation of in the natural frequencies of the system was considered.
- The peak values of the FRFs associated with nodes N16 and N22 across the frequency range of 0 Hz to 15 Hz were obtained with the MATLAB function.
- In each optimization, the real part of the closest pole to the imaginary axis was calculated. If this value is greater than zero, the value of the magnitude is penalized.
- X = fminsearch (FUN, X0) was configured as follows: FUN is the magnitude obtained with , and the variable to optimize is X, being , , , and . The initial conditions were , which guaranteed the stability of the closed-loop system.
- ;
- .
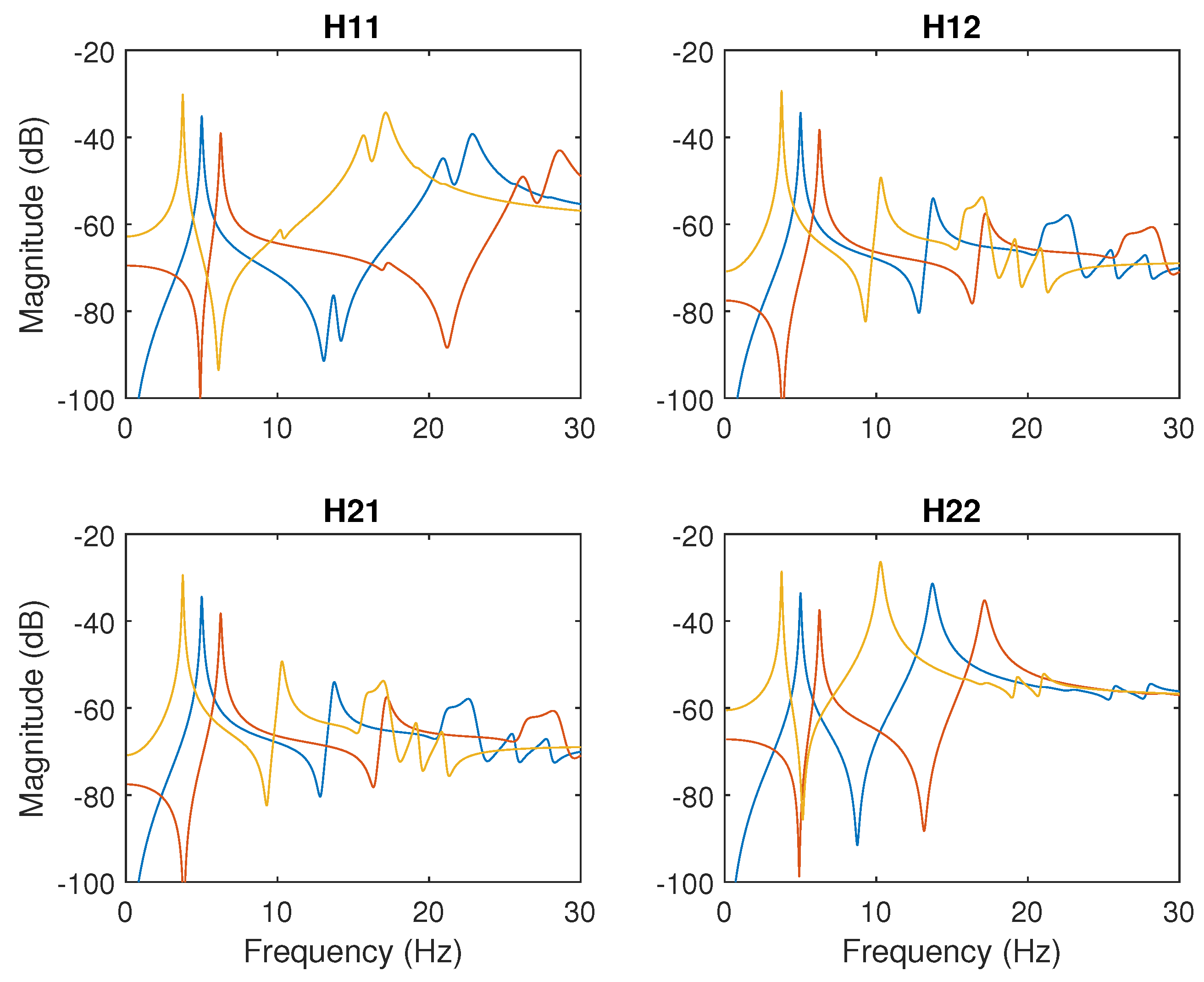
3.4. Robust Analysis: Simulation Results
4. Experimental Results
5. Conclusions
- The controller’s resilience against spillover effects, which has been tested in experiments by impact perturbation, which excites higher vibration modes.
- The robustness to system variations, which has been illustrated in the simulation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ebrahimpour, A.; Sack, R.L. A review of vibration serviceability criteria for floor structures. Comput. Struct. 2005, 83, 2488–2494. [Google Scholar] [CrossRef]
- Fanning, P.J.; Healy, P.; Pavic, A. Pedestrian Bridge Vibration Serviceability: A Case Study in Testing and Simulation. Adv. Struct. Eng. 2010, 13, 861–873. [Google Scholar] [CrossRef]
- Bouzari, N.; Van Engelen, N.; Cheng, S. Evaluation of Pedestrian-Induced In-Service Building Floor Performance Based on Short-Term Monitoring. J. Perform. Constr. Facil. 2023, 37, 04023045. [Google Scholar] [CrossRef]
- Wang, Z.; Song, L.; Cheng, Z.; Yang, H.; Wen, J.; Qi, M. Finite Element Model for Vibration Serviceability Evaluation of a Suspended Floor with and without Tuned Mass Dampers. Buildings 2023, 13, 309. [Google Scholar] [CrossRef]
- Avci, O.; Catbas, F.N. Editorial: Human-Induced Excitations and Vibrations Serviceability of Civil Engineering Structures. Front. Built Environ. 2022, 8, 846351. [Google Scholar] [CrossRef]
- Fujino, Y.; Siringoringo, D. Vibration Mechanisms and Controls of Long-Span Bridges: A Review. Struct. Eng. Int. 2013, 23, 248–268. [Google Scholar] [CrossRef]
- Chen, J.; Han, Z.; Xu, R. Effects of human-induced load models on tuned mass damper in reducing floor vibration. Adv. Struct. Eng. 2019, 22, 2449–2463. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Zhang, Q. Application of an Artificial Fish Swarm Algorithm in an Optimum Tuned Mass Damper Design for a Pedestrian Bridge. Appl. Sci. 2018, 8, 175. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 1: Assessment of dynamic behaviour. Eng. Struct. 2010, 32, 1069–1081. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W. Optimal Design and Application of a Multiple Tuned Mass Damper System for an In-Service Footbridge. Sustainability 2019, 11, 2801. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, Y. Dynamic Response Measurement and Finite Element Analysis of Large-Span Pedestrian Corridor. Buildings 2023, 13, 2857. [Google Scholar] [CrossRef]
- Li, J.; Liu, X. Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers. Appl. Sci. 2023, 13, 8263. [Google Scholar] [CrossRef]
- Wen, Q.; Hua, X.G.; Chen, Z.Q.; Yang, Y.; Niu, H.W. Control of Human-Induced Vibrations of a Curved Cable-Stayed Bridge: Design, Implementation, and Field Validation. J. Bridge Eng. 2016, 21, 04016028. [Google Scholar] [CrossRef]
- Zhou, L.; Wan, S. Vibration Control of Footbridges Based on Local Resonance Band Gaps. J. Struct. Eng. 2022, 148, 04022137. [Google Scholar] [CrossRef]
- Liu, K.; Shi, Q.; Liu, Y.; Liu, L.; Zhou, F. Investigation of an improved tuned liquid column gas damper for the vertical vibration control. Mech. Syst. Signal Process. 2023, 196, 110340. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Shi, W.; Zhou, Y. Semi-active control of walking-induced vibrations in bridges using adaptive tuned mass damper considering human-structure-interaction. Eng. Struct. 2021, 244, 112743. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Gao, H. Study on Adaptive-Passive and Semi-Active Eddy Current Tuned Mass Damper with Variable Damping. Sustainability 2018, 10, 99. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Zhou, Y.; Shi, W. Experimental study on adaptive-passive tuned mass damper with variable stiffness for vertical human-induced vibration control. Eng. Struct. 2023, 280, 115714. [Google Scholar] [CrossRef]
- Hudson, M.; Reynolds, P. Implementation considerations for active vibration control in the design of floor structures. Eng. Struct. 2012, 44, 334–358. [Google Scholar] [CrossRef]
- Wani, Z.R.; Tantray, M.; Noroozinejad Farsangi, E.; Nikitas, N.; Noori, M.; Samali, B.; Yang, T. A Critical Review on Control Strategies for Structural Vibration Control. Annu. Rev. Control. 2022, 54, 103–124. [Google Scholar] [CrossRef]
- Terrill, R.; Bäumer, R.; Van Nimmen, K.; Van den Broeck, P.; Starossek, U. Twin Rotor Damper for Human-Induced Vibrations of Footbridges. J. Struct. Eng. 2020, 146, 04020119. [Google Scholar] [CrossRef]
- Liu, X.; Schauer, T.; Goldack, A.; Schlaich, M. Multi-Modal Active Vibration Control of a Lightweight Stress-Ribbon Footbridge Based on Subspace Identification. IFAC-PapersOnLine 2017, 50, 7058–7063. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y.; Shi, W. Dynamic test, monitoring and active control of non-resonant running-induced vibration for floor structure. Structures 2024, 63, 106348. [Google Scholar] [CrossRef]
- Alujević, N.; Zhao, G.; Depraetere, B.; Sas, P.; Pluymers, B.; Desmet, W. Optimal vibration control using inertial actuators and a comparison with tuned mass dampers. J. Sound Vib. 2014, 333, 4073–4083. [Google Scholar] [CrossRef]
- Chesné, S.; Milhomem, A.; Collette, C. Enhanced Damping of Flexible Structures Using Force Feedback. J. Guid. Control. Dyn. 2016, 39, 1654–1658. [Google Scholar] [CrossRef]
- Ramírez-Senent, J.; Gallegos-Calderón, C.; García-Palacios, J.H.; Díaz, I.M. Active control of human-induced vibrations on lightweight structures via electrodynamic actuator dynamics inversion. J. Vib. Control. 2024, 30, 88–103. [Google Scholar] [CrossRef]
- Xue, K.; Igarashi, A.; Kachi, T. Independent modal space phase-lead velocity feedback control of floor vibration. Struct. Control. Health Monit. 2022, 29, e2954. [Google Scholar] [CrossRef]
- Ahmadi, M.W. Preventing stroke saturation of inertial actuators used for active vibration control of floor structures. Struct. Control. Health Monit. 2020, 27, e2546. [Google Scholar] [CrossRef]
- Hanagan, L.M.; Kulasekere, E.C.; Walgama, K.S.; Premaratne, K. Optimal Placement of Actuators and Sensors for Floor Vibration Control. J. Struct. Eng. 2000, 126, 1380–1387. [Google Scholar] [CrossRef]
- Pereira, E.; Díaz, I.M.; Hudson, E.J.; Reynolds, P. Optimal control-based methodology for active vibration control of pedestrian structures. Eng. Struct. 2014, 80, 153–162. [Google Scholar] [CrossRef]
- Nyawako, D.S.; Reynolds, P. Comparative studies of global and targeted control of walkway bridge resonant frequencies. J. Vib. Control. 2016, 24, 1670–1686. [Google Scholar] [CrossRef]
- Camacho-Gómez, C.; Wang, X.; Pereira, E.; Díaz, I.; Salcedo-Sanz, S. Active vibration control design using the Coral Reefs Optimization with Substrate Layer algorithm. Eng. Struct. 2018, 157, 14–26. [Google Scholar] [CrossRef]
- Zamani, A.A.; Etedali, S. Optimal fractional-order PID control design for time-delayed multi-input multi-output seismic-excited structural system. J. Vib. Control. 2021, 29, 802–819. [Google Scholar] [CrossRef]
- Díaz, I.M.; Pereira, E.; Reynolds, P. Integral resonant control scheme for cancelling human-induced vibrations in light-weight pedestrian structures. Struct. Control. Health Monit. 2010, 19, 55–69. [Google Scholar] [CrossRef]
- Wang, X.; Pereira, E.; García-Palacios, J.H.; Díaz, I.M. A general vibration control methodology for human-induced vibrations. Struct. Control. Health Monit. 2019, 26, e2406. [Google Scholar] [CrossRef]
- Bhikkaji, B.; Moheimani, S.O.R.; Petersen, I.R. A Negative Imaginary Approach to Modeling and Control of a Collocated Structure. IEEE/ASME Trans. Mechatronics 2012, 17, 717–727. [Google Scholar] [CrossRef]
- Gawronski, W.K. Advanced Structural Dynamics and Active Control of Structures; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Aphale, S.S.; Fleming, A.J.; Moheimani, S.O.R. Integral resonant control of collocated smart structures. Smart Mater. Struct. 2007, 16, 439–446. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S. Integral Resonant Controller for Suppressing Car’s Oscillations and Eliminating its Inherent Jump Phenomenon. Eur. J. Pure Appl. Math. 2023, 16, 2729–2750. [Google Scholar] [CrossRef]
- Loṕez-Romero, M.; Santos Peñas, M. A Positive Position Feedback controller for vibration control of wind turbines. Energy Rep. 2023, 9, 1342–1353. [Google Scholar] [CrossRef]
- Multiphysics, A. Release 2022 R2, Help System; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- McKelvey, T.; Akcay, H.; Ljung, L. Subspace-based multivariable system identification from frequency response data. IEEE Trans. Autom. Control. 1996, 41, 960–979. [Google Scholar] [CrossRef]
- ISO2631-1:1997; Mechanical Vibration and Shock. Evaluation of Human Exposure to Whole-Body Vibration Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1997.
- Patra, S.; Lanzon, A. Stability Analysis of Interconnected Systems With “Mixed” Negative-Imaginary and Small-Gain Properties. IEEE Trans. Autom. Control. 2011, 56, 1395–1400. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, E.; Wang, X.; Díaz, I.M.; Aphale, S.S. Design and Implementation of a MIMO Integral Resonant Control for Active Vibration Control of Pedestrian Structures. Appl. Sci. 2024, 14, 6784. https://doi.org/10.3390/app14156784
Pereira E, Wang X, Díaz IM, Aphale SS. Design and Implementation of a MIMO Integral Resonant Control for Active Vibration Control of Pedestrian Structures. Applied Sciences. 2024; 14(15):6784. https://doi.org/10.3390/app14156784
Chicago/Turabian StylePereira, Emiliano, Xidong Wang, Iván M. Díaz, and Sumeet S. Aphale. 2024. "Design and Implementation of a MIMO Integral Resonant Control for Active Vibration Control of Pedestrian Structures" Applied Sciences 14, no. 15: 6784. https://doi.org/10.3390/app14156784
APA StylePereira, E., Wang, X., Díaz, I. M., & Aphale, S. S. (2024). Design and Implementation of a MIMO Integral Resonant Control for Active Vibration Control of Pedestrian Structures. Applied Sciences, 14(15), 6784. https://doi.org/10.3390/app14156784






