Investigation of the Effect of Relative Density on the Dynamic Modulus and Damping Ratio for Coarse Grained Soil
Abstract
1. Introduction
2. Testing Apparatus and Program
2.1. Instruments and Equipment
2.2. Specimen Preparation Standard
2.3. Test Method
- Sample Preparation:
- 2.
- Saturation:
- 3.
- Consolidation:
- 4.
- Loading:
- 5.
- Sample Removal:
3. Interpretation of Experimental Results
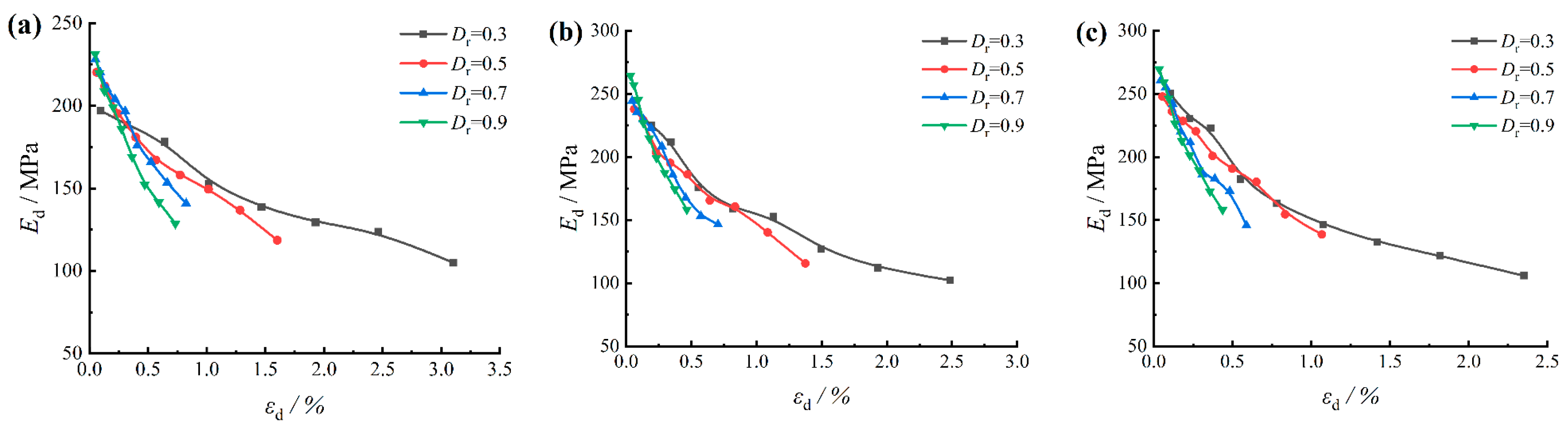
3.1. Relation of Dynamic Elastic Modulus and Dynamic Strain
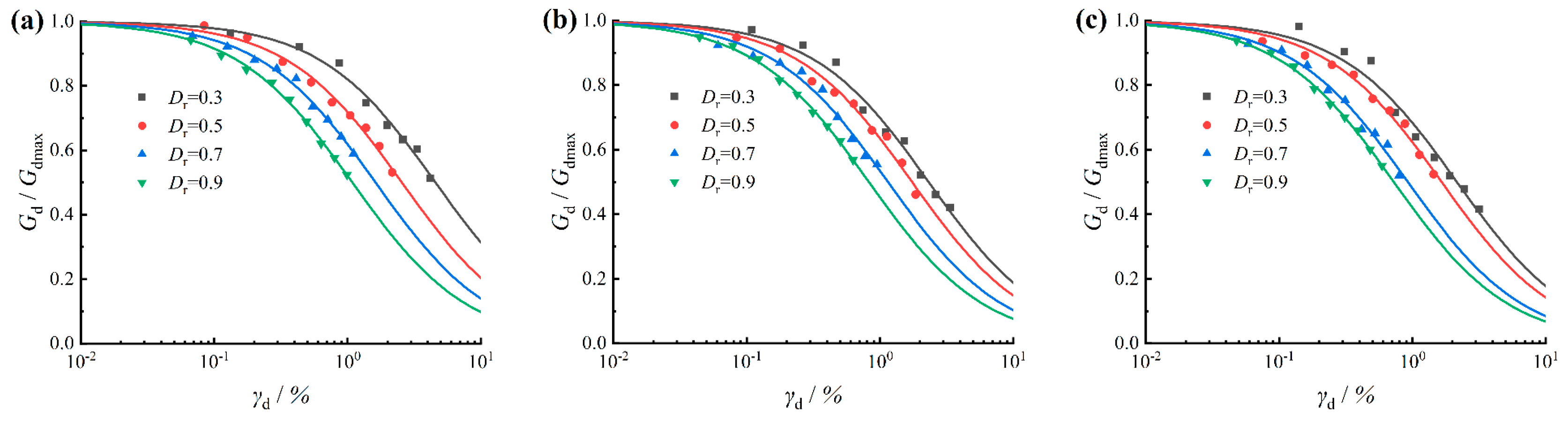
3.2. Relation of the Dynamic Shear Modulus Ratio and Dynamic Shear Strain
3.3. Relation of Dynamic Shear Strain and the Damping Ratio
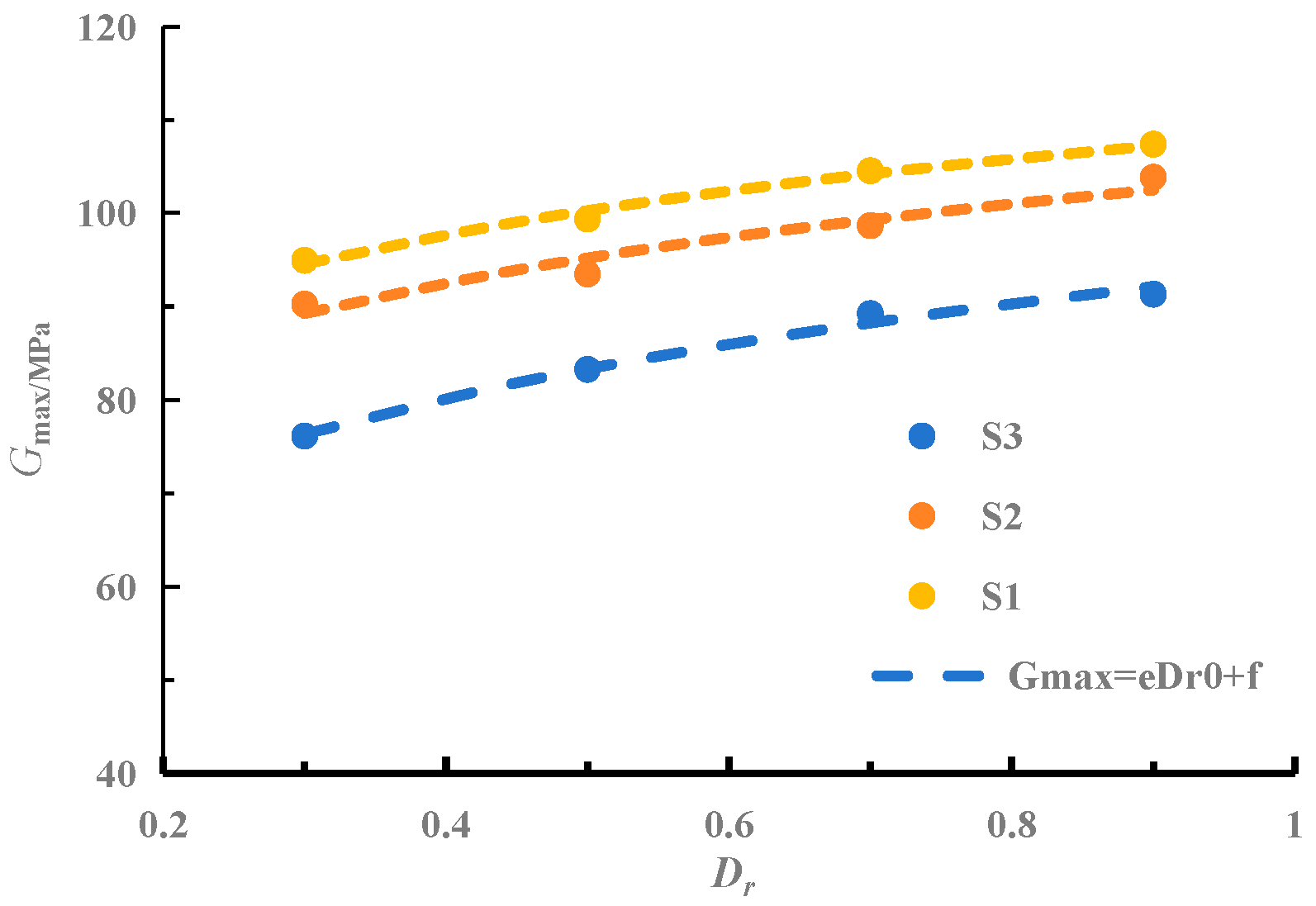
4. Influence of Relative Density on the Maximum Dynamic Shear Modulus
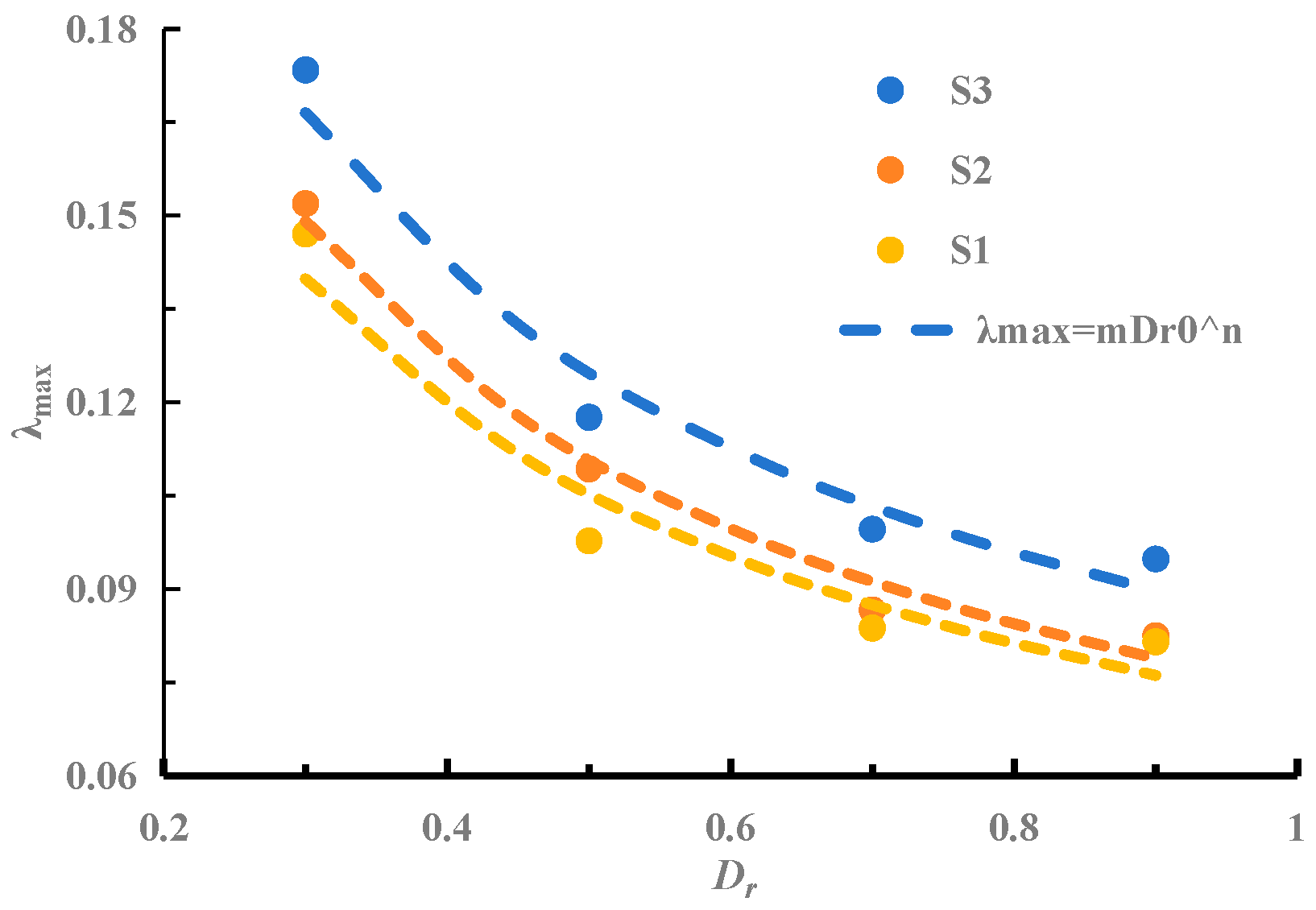
5. Influence of Relative Density on the Maximum Damping Ratio
6. Conclusions
- The dynamic elastic modulus of coarse-grained soil progressively diminishes with increasing dynamic strain. The attenuation rate of dynamic elastic modulus escalates with increasing relative density; the rate of decay of the coarse-grained soil’s normalized dynamic shear modulus with increasing dynamic shear strain also rises with an increase in relative density, with the attenuation trend becoming more distinct at higher relative density values. Additionally, the rate of increase in the damping ratio–dynamic shear strain relationship curve gradually decreases as relative density increases.
- The maximum dynamic shear modulus of coarse-grained soil increases with an increase in relative density. An empirical formula has been established to describe the relationship between the maximum dynamic shear modulus and relative density of coarse-grained soil.
- The maximum damping ratio of coarse-grained soil decreases progressively with increasing relative density. An empirical formula has been developed to delineate the relationship between the maximum damping ratio and relative density of coarse-grained soil.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Q. Engineering Properties and Application of Coarse-Grained Soil; Yellow River Conservancy Press: Zhengzhou, China, 1998. [Google Scholar]
- Xu, Z. Key Technologies and Geotechnical Problems in Contemporary High Rockfill Dam Construction. J. Geotech. Eng. 2011, 33, 34–40. [Google Scholar]
- Menq, F.Y.; Stokoe, K. Linear Dynamic Properties of Sandy and Gravelly Soils from Large-Scale Resonant Tests; A. A. Balkema: Lisse, The Netherlands, 2003. [Google Scholar]
- Sawangsuriya, A.; Bosscher, P.J.; Edil, T.B. Alternative Testing Techniques for Modulus of Pavement Bases and Subgrades. In Proceedings of the Great Lakes Geotechnical & Geoenvironmental Conference, Milwaukee, WI, USA, 13 May 2005. [Google Scholar]
- Kokusho, T. Cyclic Triaxial Test of Dynamic Soil Properties for Wide Strain Range. Soils Found. 1980, 20, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.K.; Reddy, K.R. Dynamic Moduli and Damping Ratios for Monterey No. 0 Sand by Resonant Column Tests. Soils Found. 1989, 29, 37–51. [Google Scholar]
- Li, Y.; Zhang, J.; Zhu, Z.; Wang, X.; Shi, X. Research on Dynamic Characteristics of Coarse-Grained Soil for Railway Subgrade under Graded Loading. J. Railw. Sci. Eng. 2019, 16, 620–628. [Google Scholar]
- Wang, J. Experimental Study on Dynamic Elastic Modulus and Damping Ratio of Coarse-Grained Soil. Master’s Thesis, Central South University, Changsha, China, 2013. [Google Scholar]
- Fang, E. Research on Dynamic Properties of Dam Building Materials. Thesis, Dalian University of Technology, Dalian, China, 2015. [Google Scholar]
- Du, C.; Xie, H.; Xiao, M.; He, C.R.; He, J.D. Experimental Study on Dynamic Properties of Dam Building Materials in Seismic Areas. J. Sichuan Univ. Eng. Sci. Ed. 2016, 48, 39–44. [Google Scholar]
- Matsui, T.; Bahr, M.A.; Abe, N. Estimation of Shear Characteristics Degradation and Stress-Strain Relationship of Saturated Clays after Cyclic Loading. Soils Found. 1992, 32, 161–172. [Google Scholar] [CrossRef]
- Yasuhara, K. Post-cyclic Degradation of Saturated Plasticity Silts. Cycl. Behav. Soils Liq. Phenom. 2004, 275–286. [Google Scholar]
- Zhou, W.; Leng, W.; Liu, W.; Nie, R.S.; Yang, Q.; Zhao, C.Y. Study on Dynamic Characteristics and Backbone Curve Model of Saturated Coarse-Grained Soil under Low Confining Pressure Cyclic Loading. Rock Soil Mech. 2016, 37, 415–423. [Google Scholar]
- Fu, H.; Han, H.; Ling, H. Experimental Study on the Influence of Density on Dynamic Properties of Coarse Particulate Materials. J. China Inst. Water Resour. Hydropower Res. 2014, 12, 437–441. [Google Scholar]
- Wang, B. Study on Static and Dynamic Properties of Saturated Round Gravel Soil in Nanning Metro Area. Ph.D. Thesis, Guangxi University, Nanning, China, 2018. [Google Scholar]
- Zhu, J.; Shi, J.; Luo, X.; Xu, J. Experimental Study on Stress-Strain-Strength Behavior of Sand with Different Densities. Chin. J. Geotech. Eng. 2016, 38, 336–341. [Google Scholar]
- Zhu, J.; Guo, W.L.; Xu, J.C.; Chu, F.Y. DEM Analysis on Impact of Gradation and Compactness on Coarse-Grained Soil in Tri-Axial Test. J. Chongqing Jiaotong Univ. 2017, 36, 70–74. [Google Scholar]
- Liu, X.; Zhang, J.; Liu, M. Exploration of Test Methods in GB/T 50123—2019 “Standards for Soil Test Methods”. Tianjin Constr. Sci. Technol. 2020, 30, 1–4. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear Modulus and Damping in Soils: Design Equations and Curves. Geotech. Spec. Publ. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Yang, P. Study on the Effect of Particle Grading and Compaction on the Dynamic Deformation Characteristics of Sand. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2021. [Google Scholar]
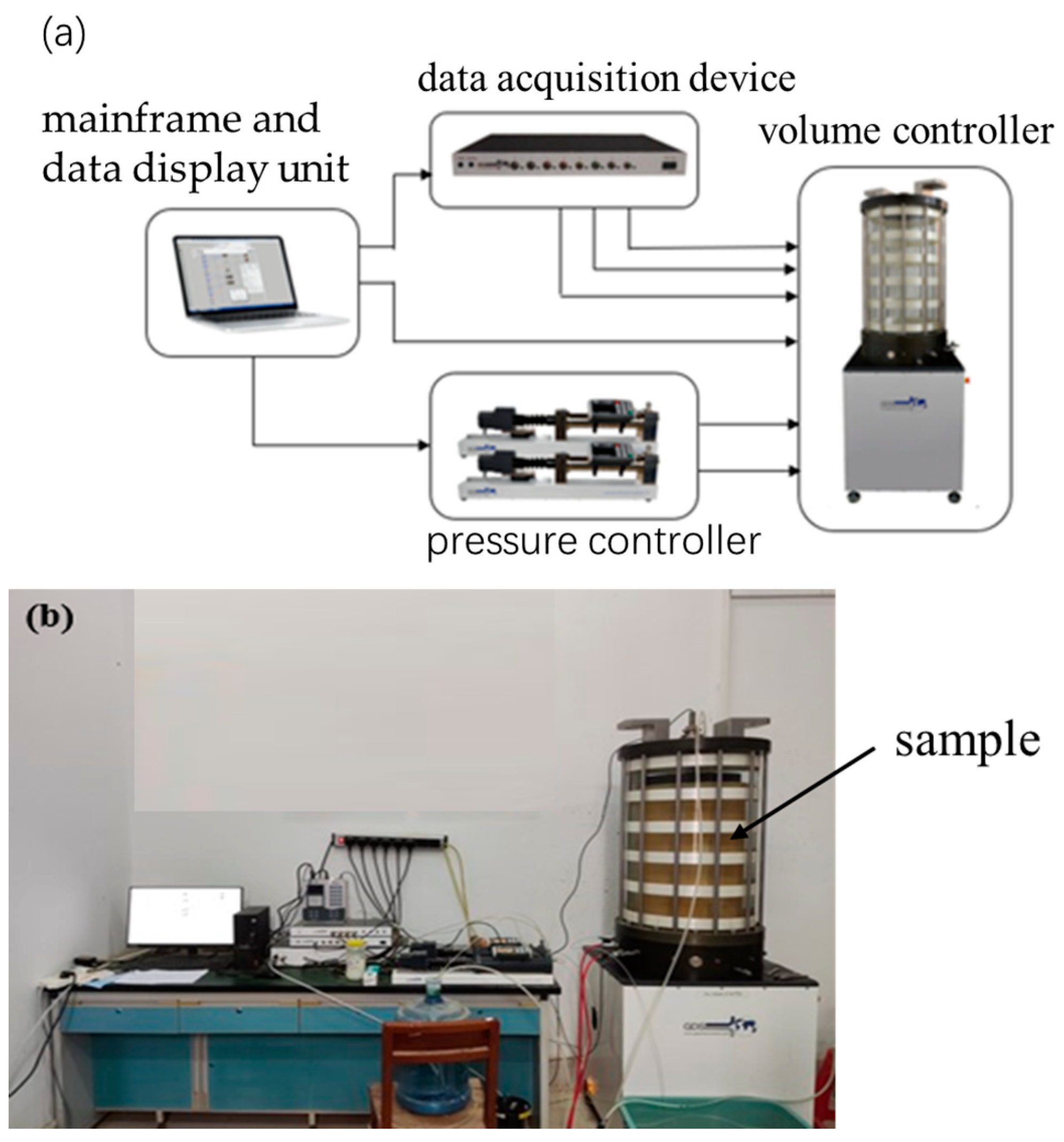

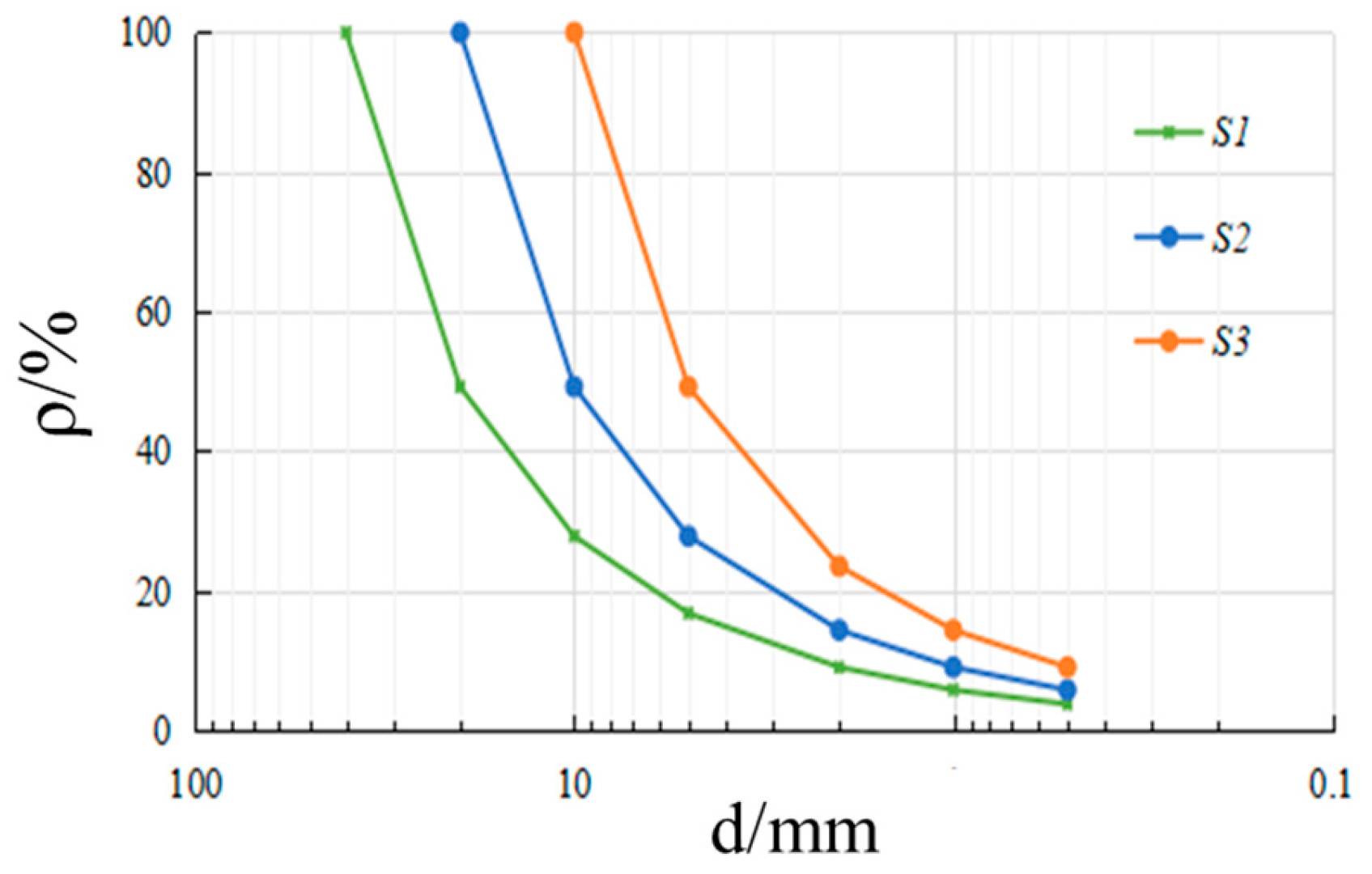


| Specimen Number | Maximum Particle Diameter/mm | Minimum Dry Density/(g∙cm−3) | Maximum Dry Density/(g∙cm−3) | Dry Density/(g∙cm−3) | |||
|---|---|---|---|---|---|---|---|
| Dr = 0.9 | Dr = 0.7 | Dr = 0.5 | Dr = 0.3 | ||||
| S1 | 40 | 1.884 | 2.244 | 2.202 | 2.122 | 2.048 | 1.979 |
| S2 | 20 | 1.844 | 2.174 | 2.136 | 2.063 | 1.995 | 1.932 |
| S3 | 10 | 1.798 | 2.1 | 2.065 | 1.999 | 1.937 | 1.879 |
| Specimen Number | Maximum Dynamic Shear Modulus | ||
|---|---|---|---|
| e | f | R2 | |
| S1 | 25.653 | 69.060 | 0.961 |
| S2 | 22.076 | 82.776 | 0.986 |
| S3 | 21.066 | 88.061 | 0.975 |
| Specimen Number | Maximum Damping Ratio | ||
|---|---|---|---|
| m | n | R2 | |
| S1 | 0.0072 | −0.554 | 0.9533 |
| S2 | 0.074 | −0.58 | 0.978 |
| S3 | 0.085 | −0.563 | 0.957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Cai, S.; Hu, R.; Wang, J.; Jiang, M.; Gong, J. Investigation of the Effect of Relative Density on the Dynamic Modulus and Damping Ratio for Coarse Grained Soil. Appl. Sci. 2024, 14, 6847. https://doi.org/10.3390/app14156847
Huang Z, Cai S, Hu R, Wang J, Jiang M, Gong J. Investigation of the Effect of Relative Density on the Dynamic Modulus and Damping Ratio for Coarse Grained Soil. Applied Sciences. 2024; 14(15):6847. https://doi.org/10.3390/app14156847
Chicago/Turabian StyleHuang, Ziying, Sen Cai, Rongfen Hu, Jianfeng Wang, Mingjie Jiang, and Jian Gong. 2024. "Investigation of the Effect of Relative Density on the Dynamic Modulus and Damping Ratio for Coarse Grained Soil" Applied Sciences 14, no. 15: 6847. https://doi.org/10.3390/app14156847
APA StyleHuang, Z., Cai, S., Hu, R., Wang, J., Jiang, M., & Gong, J. (2024). Investigation of the Effect of Relative Density on the Dynamic Modulus and Damping Ratio for Coarse Grained Soil. Applied Sciences, 14(15), 6847. https://doi.org/10.3390/app14156847







