A Meshless Method of Radial Basis Function-Finite Difference Approach to 3-Dimensional Numerical Simulation on Selective Laser Melting Process
Abstract
:1. Introduction
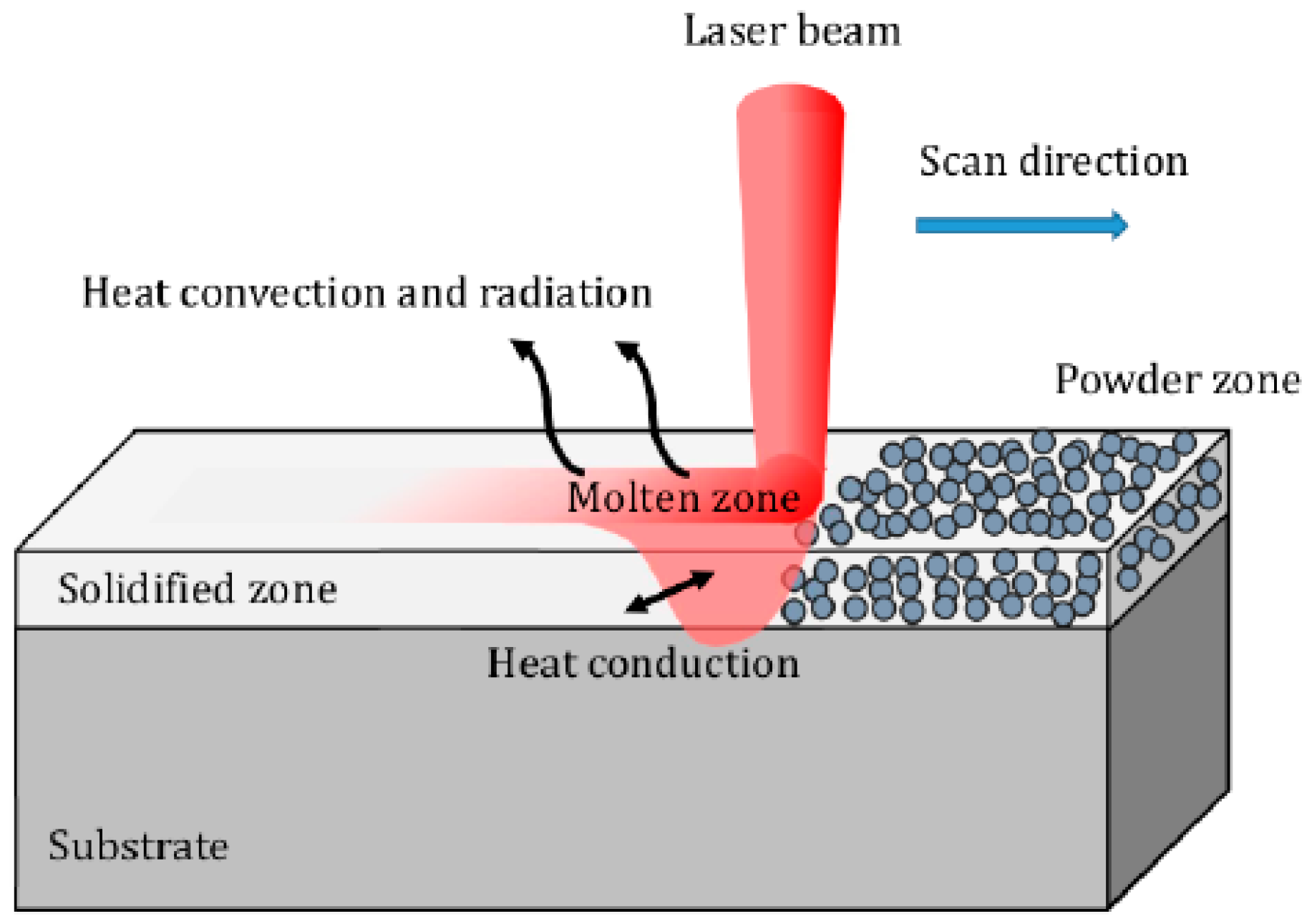
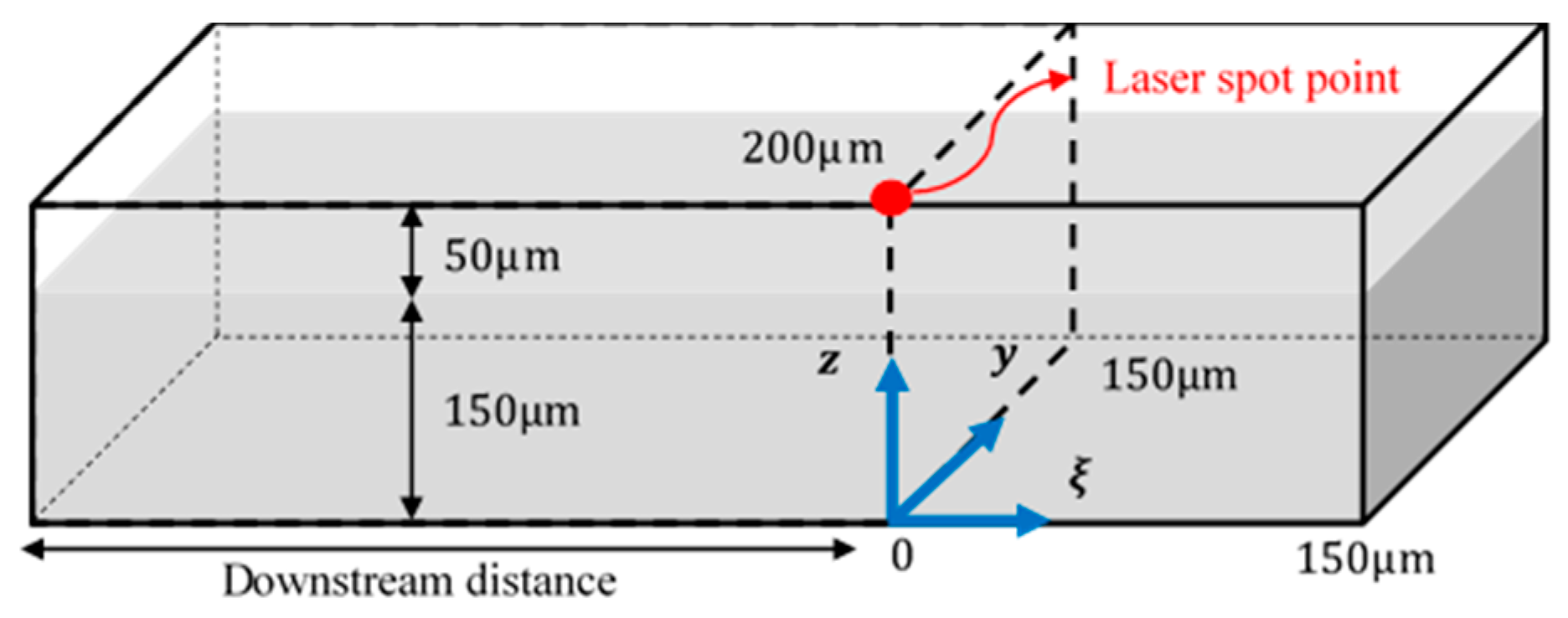
2. SLM Process Modeling in Moving Coordinate System
2.1. Assumptions
- The heat loss from the surface is by radiation and convection only.
- The energy equation of the molten pool is considered in the numerical analysis, but the fluid dynamics are not.
- The material properties are assumed to be temperature dependent. Phase transformation, such as melting and solidification, are discussed through modified thermal properties [1].
- Phenomena such as vaporization, surface tension effect, recoil pressure, and the Marangoni convection are not included in this study.
2.2. Governing Equations
2.3. Volumetric Heat Source Models
- Ray-tracing method heat source model (I)
- Double-ellipsoidal shape heat source model (II)
2.4. Initial and Boundary Conditions
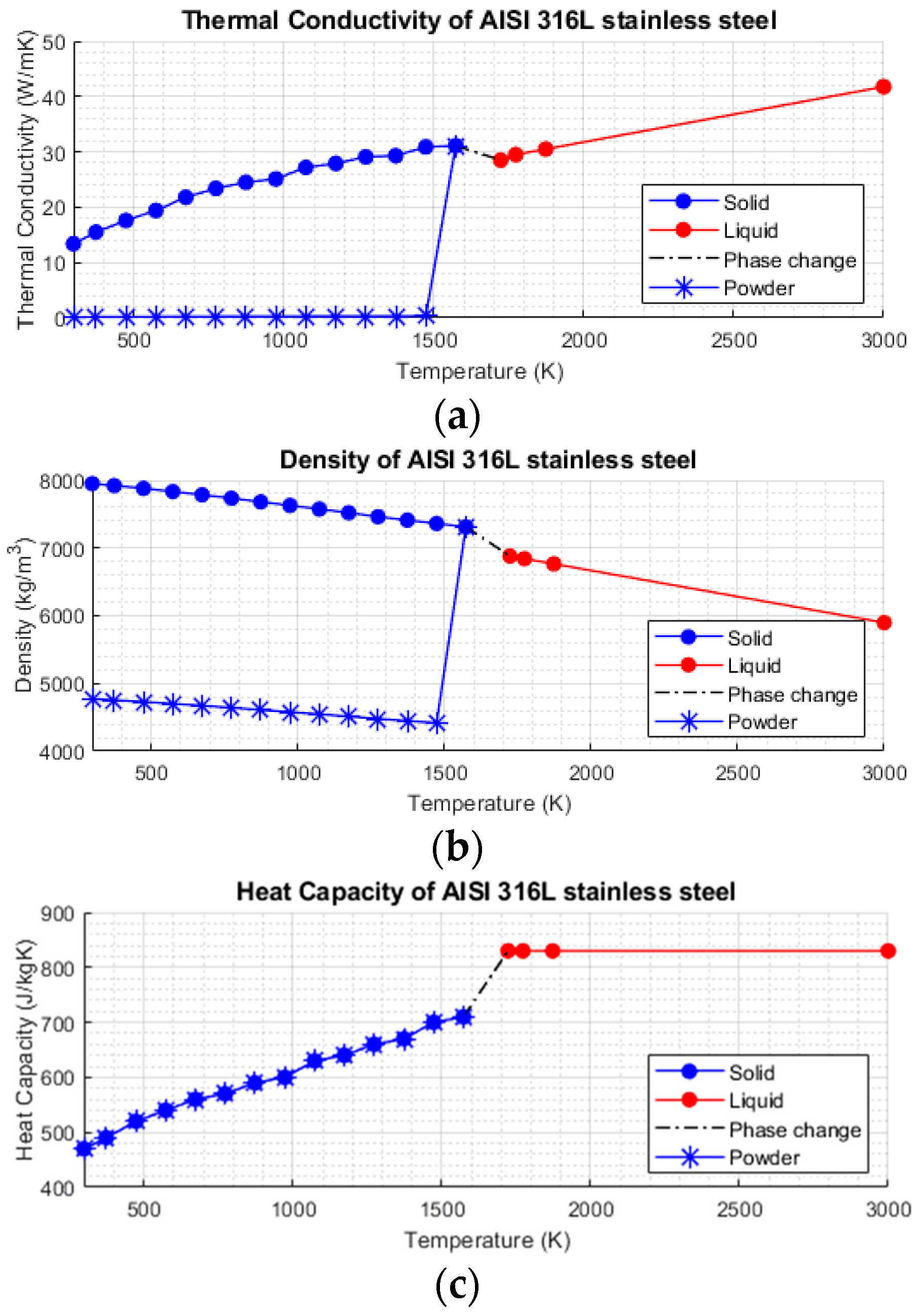
2.5. Material Properties
- Thermal conductivity
- Density
- Heat capacity
3. Methodology
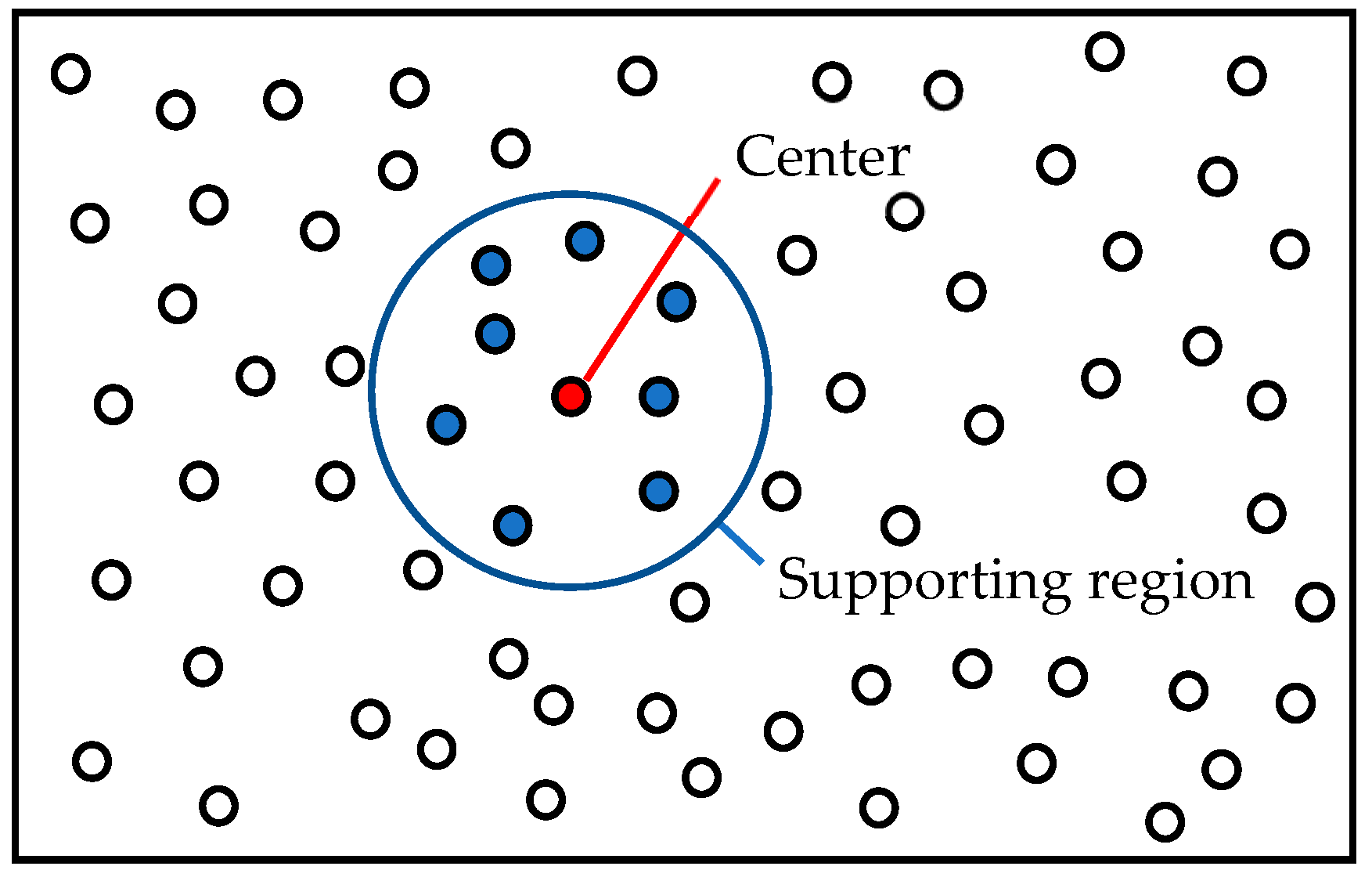
3.1. RBF-FD Approximations
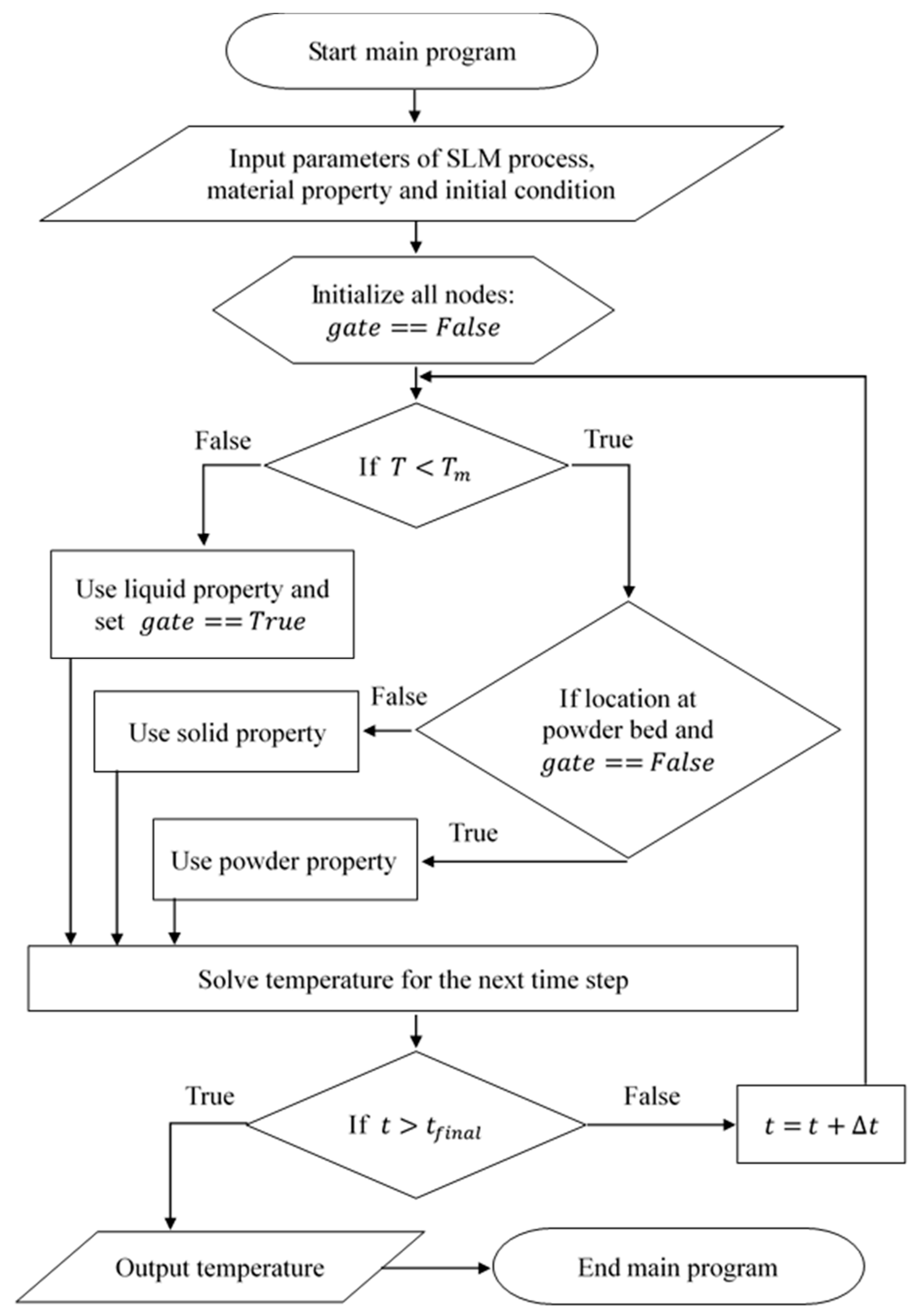
3.2. Flow Chart
- Handling complex geometries: The meshless method can efficiently handle complex-shaped domains without the need for mesh generation, which is often a time-consuming and challenging task in traditional methods like finite element methods (FEM) or finite volume methods (FVM).
- Computational efficiency: It provides a high level of computational efficiency, making it suitable for industrial applications that require fast and accurate simulations.
- Precision: The meshless method maintains a high level of precision in the simulations, even for three-dimensional problems, which is beneficial for predicting the thermal behavior and molten pool size in SLM processes.
- Flexibility: It is easily extendable to various types of problems, including those involving complex boundary conditions and material properties.
- Reduction in numerical artifacts: By avoiding the discretization of the domain into a mesh, the meshless method can reduce the numerical artifacts that may arise from mesh irregularities and improve the overall accuracy of the simulation results.
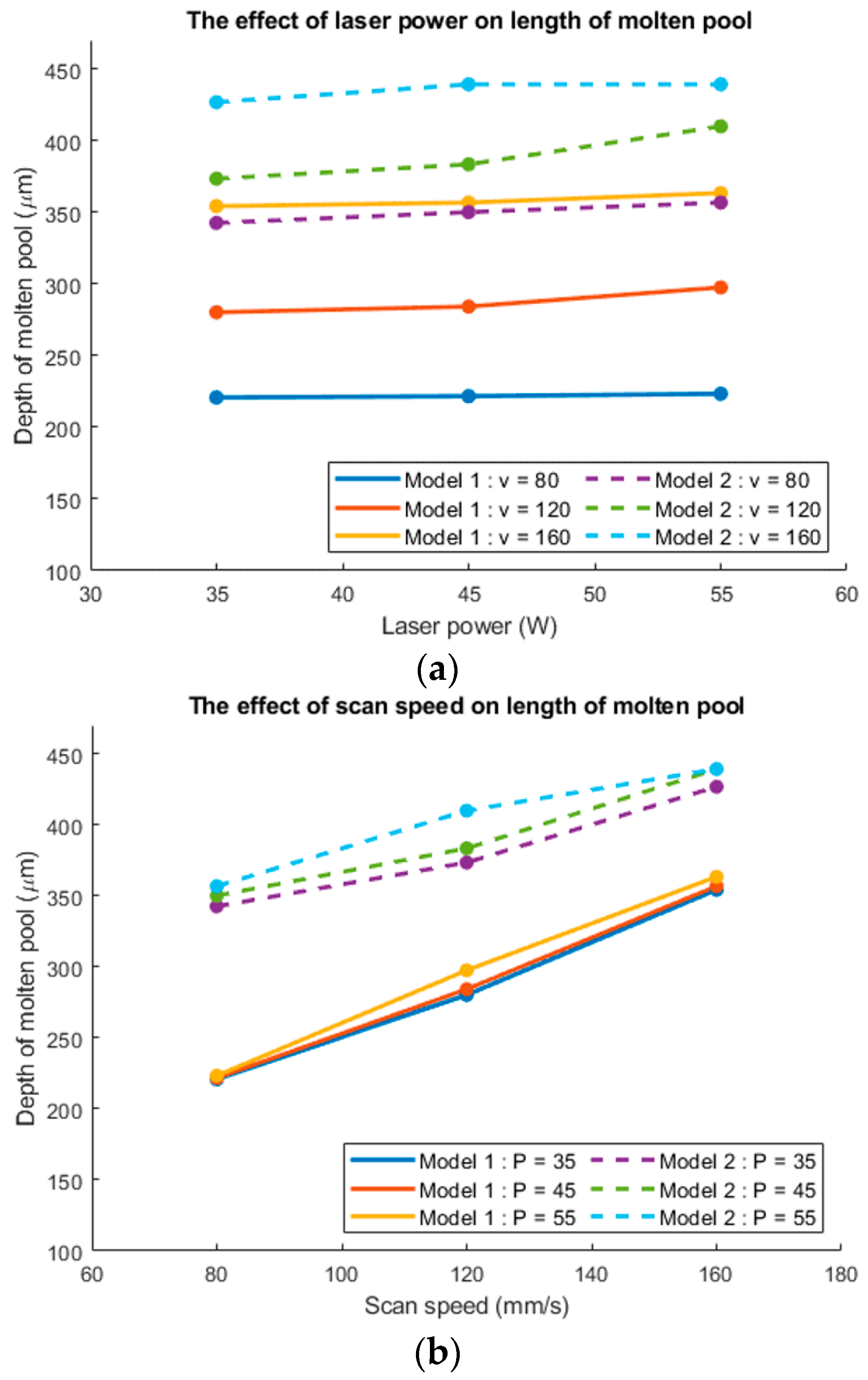
4. Results and Discussion
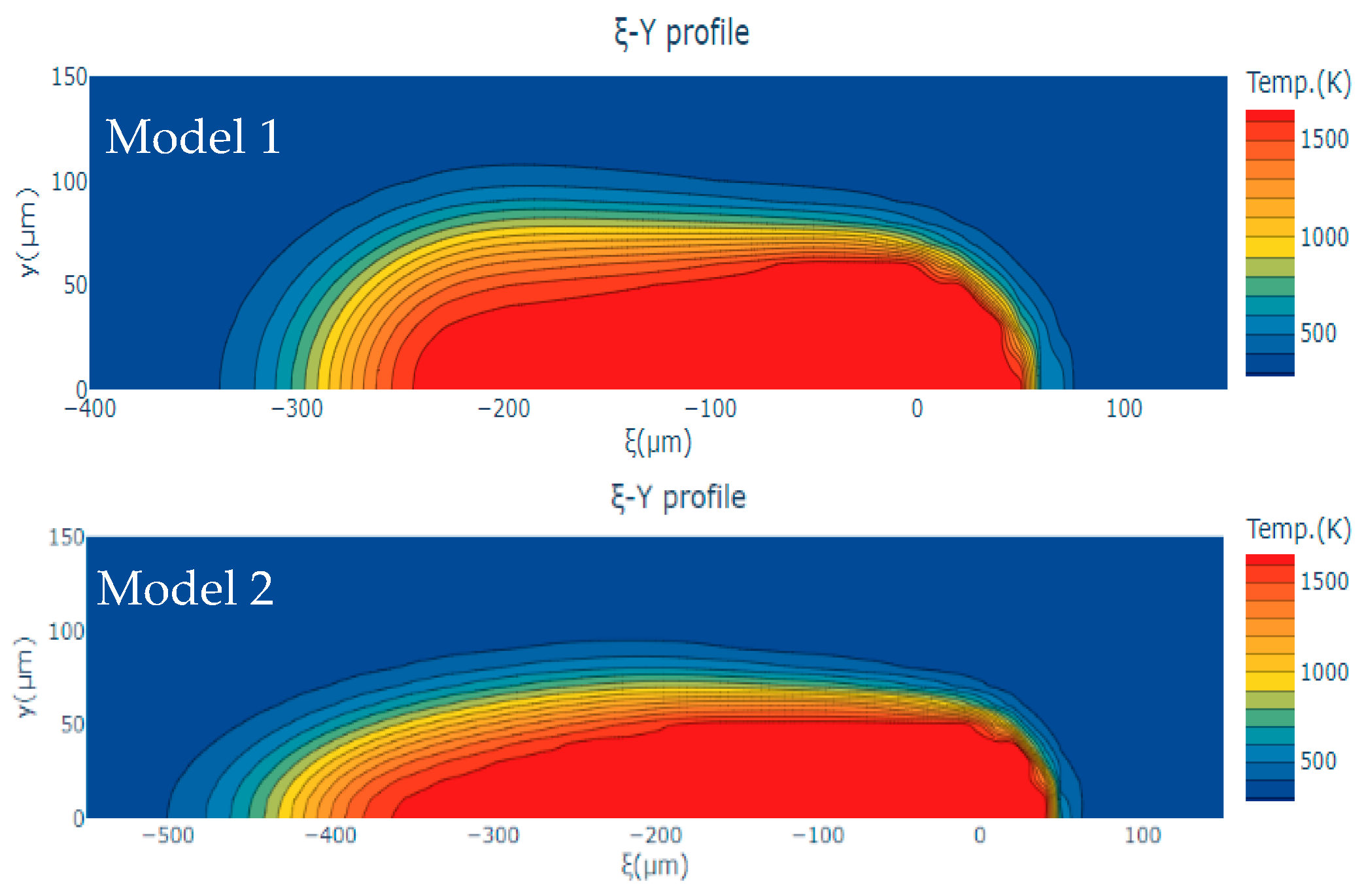
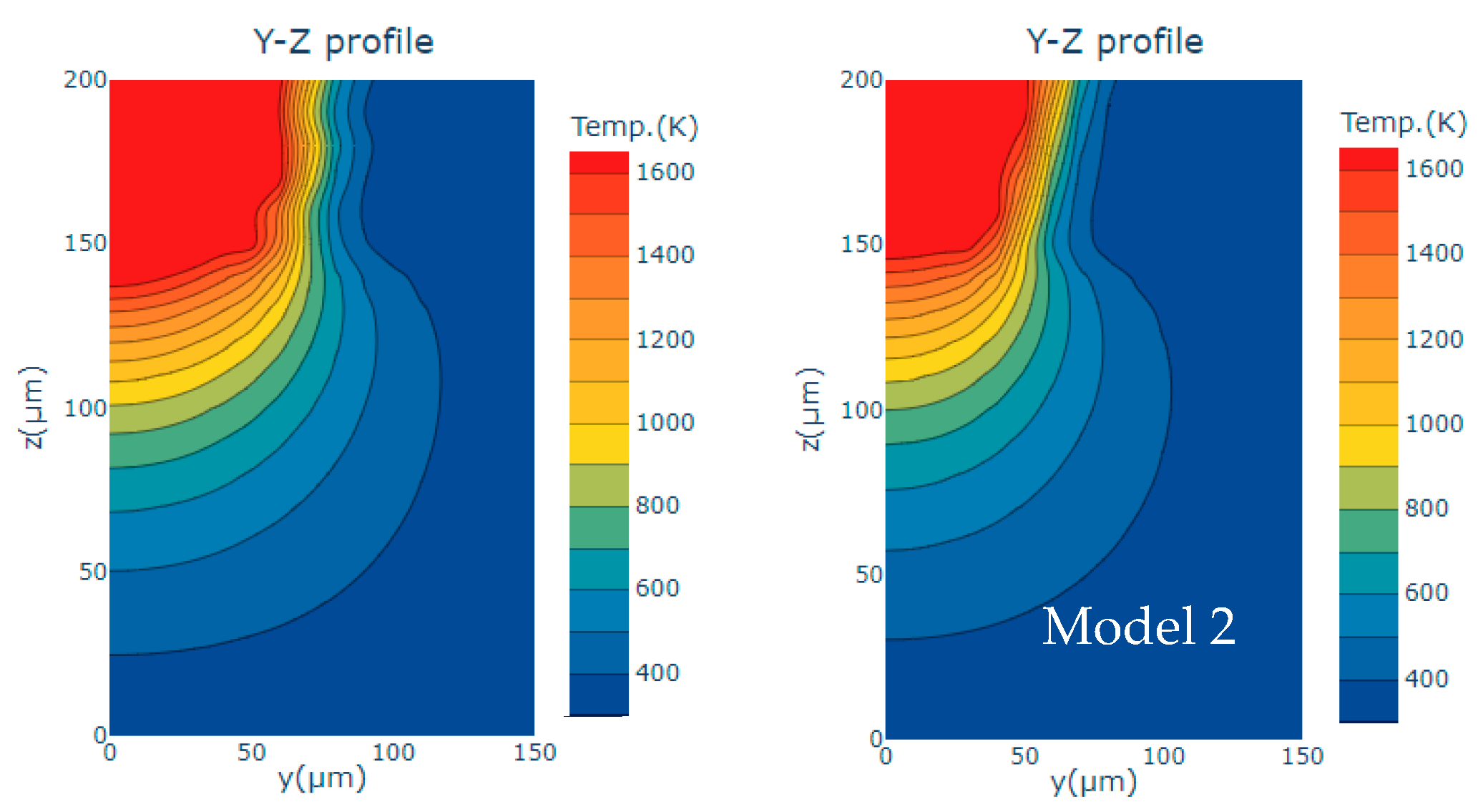
4.1. Model Validation
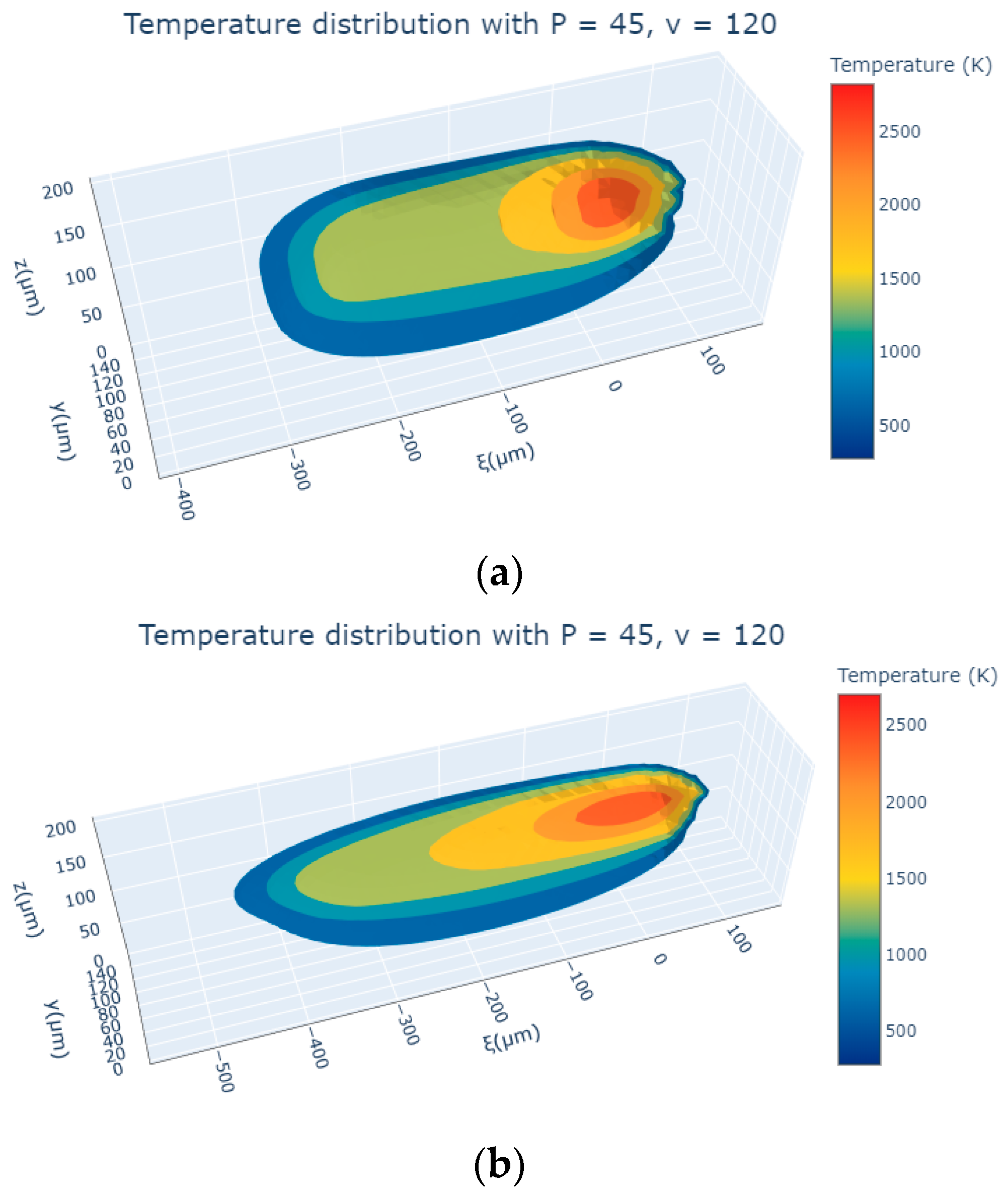
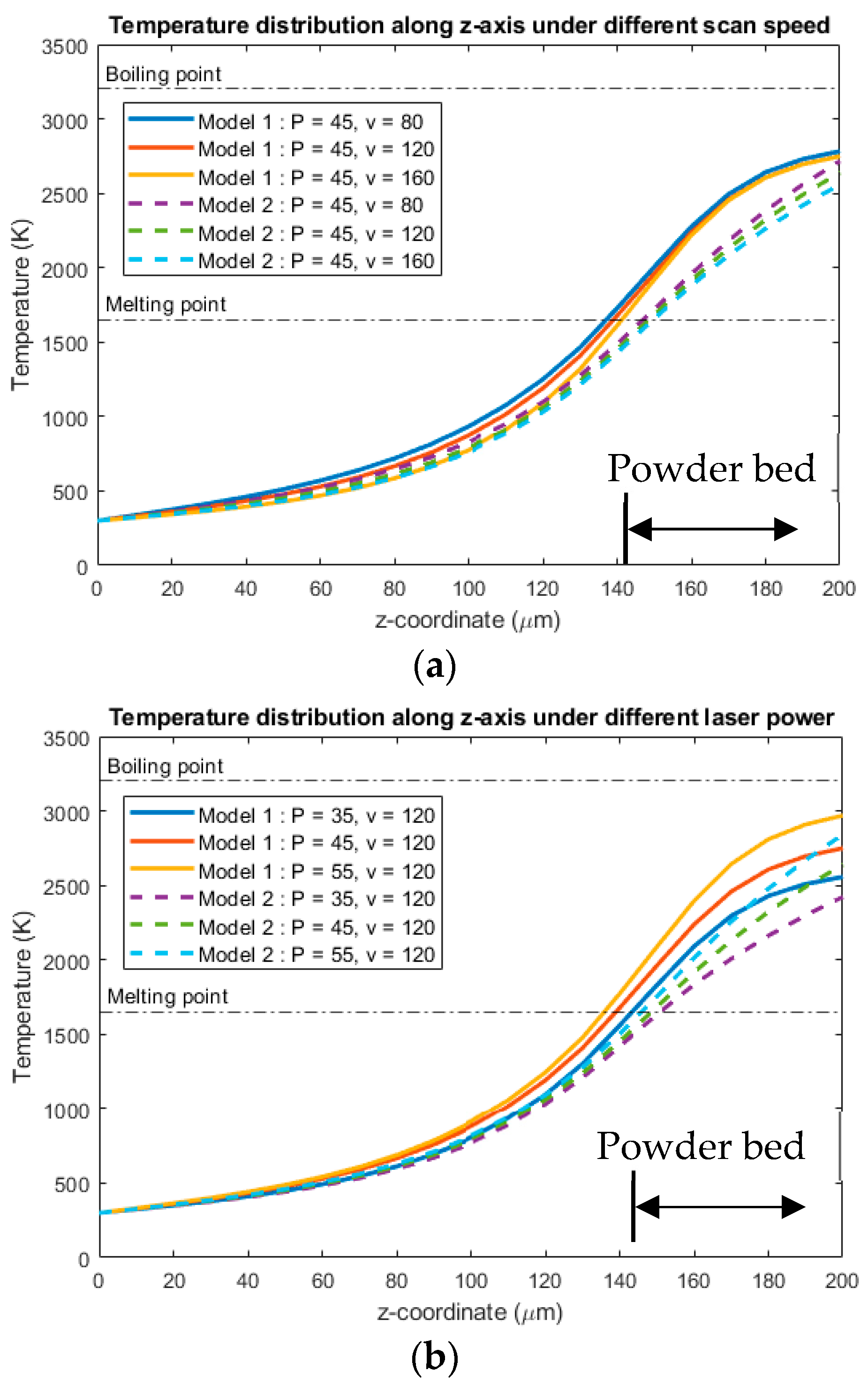
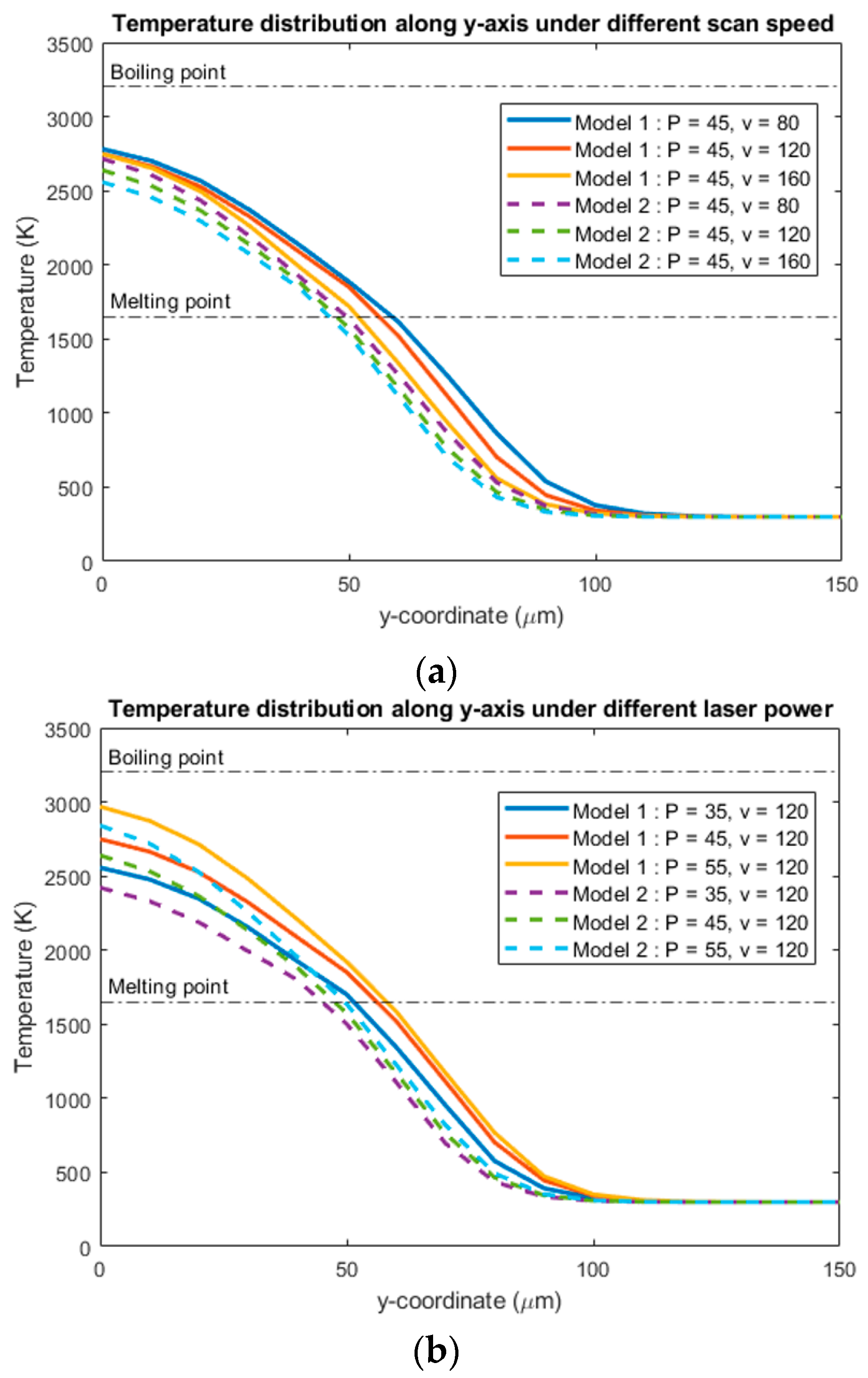
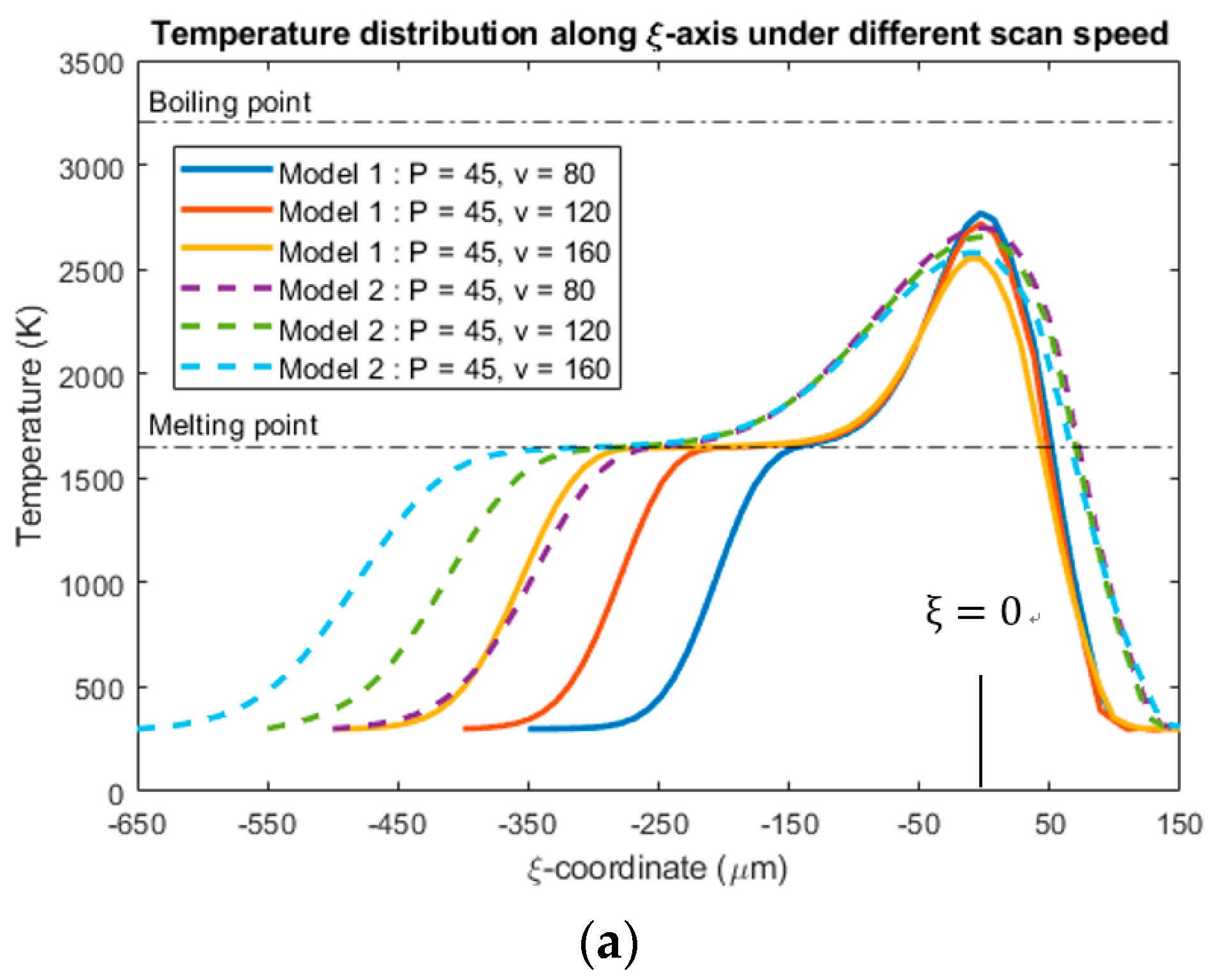
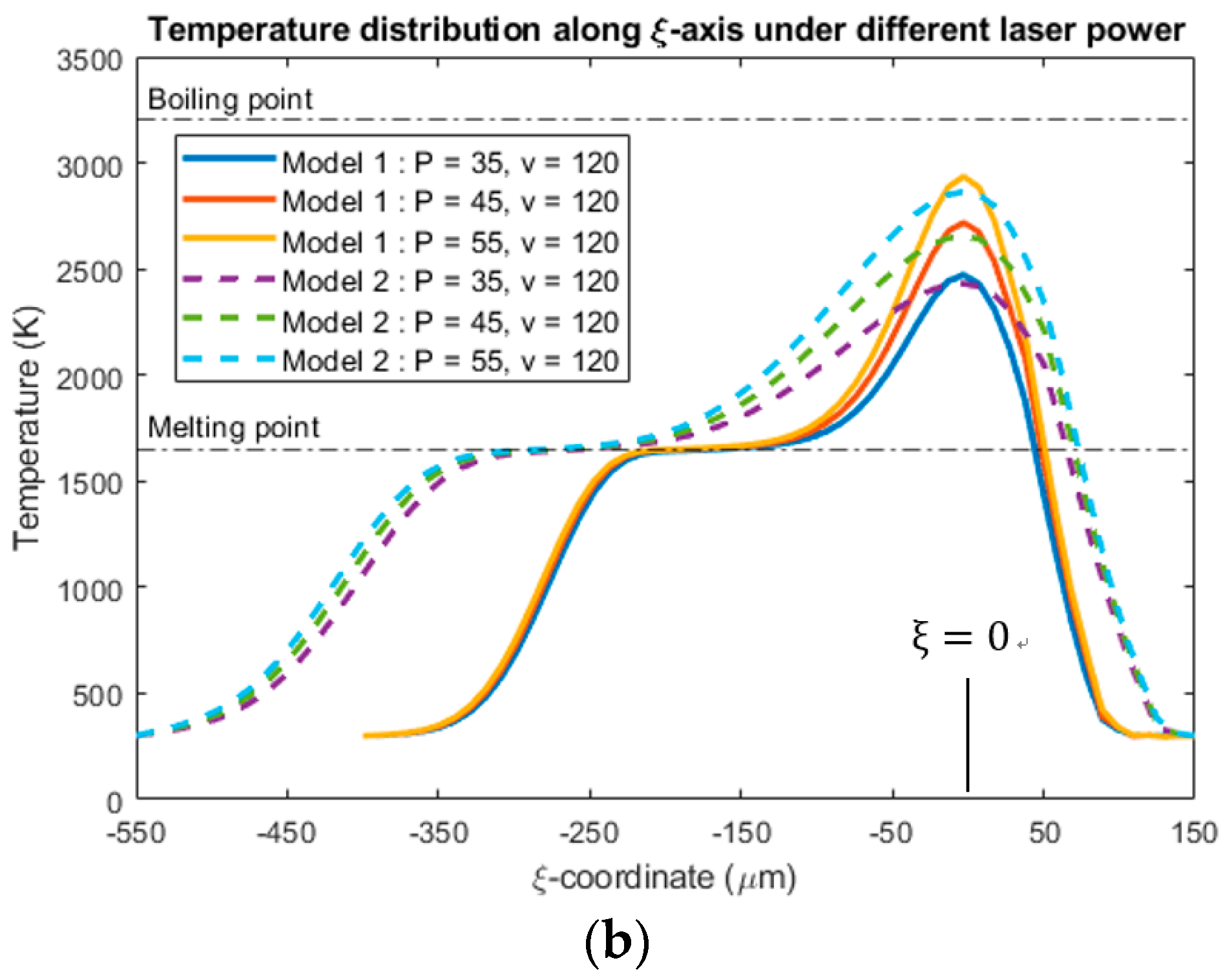
4.2. Temperature Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, Z.; Yin, M.; Dong, G.; Mei, X.; Yin, G. Modeling of the thermal physical process and study on the reliability of linear energy density for selective laser melting. Results Phys. 2018, 9, 939–946. [Google Scholar] [CrossRef]
- Duan, X.; Chen, X.; Zhu, K.; Long, T.; Huang, S.; Jerry, F.Y.H. The Thermo-Mechanical Coupling Effect in Selective Laser Melting of Aluminum Alloy Powder. Materials 2021, 14, 1673. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wu, S.; Fu, F.; Mai, S.; Yang, Y.; Liu, Y.; Song, C. Mechanisms and characteristics of spatter generation in SLM processing and its effect on the properties. Mater. Des. 2017, 117, 121–130. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Levy, G.; Klocke, F.; Childs, T.H.C. Consolidation phenomena in laser and powder-bed based layered manufacturing. CIRP Ann. 2007, 56, 730–759. [Google Scholar] [CrossRef]
- FVerhaeghe, F.; Craeghs, T.; Heulens, J.; Pandelaers, L. A pragmatic model for selective laser melting with evaporation. Acta Mater. 2009, 57, 6006–6012. [Google Scholar] [CrossRef]
- Boley, C.D.; Khairallah, S.A.; Rubenchik, A.M. Calculation of laser absorption by metal powders in additive manufacturing. Appl. Opt. 2015, 54, 2477–2482. [Google Scholar] [CrossRef] [PubMed]
- Badrossamay, M.; Childs, T.H.C. Further studies in selective laser melting of stainless and tool steel powders. Int. J. Mach. Tools Manuf. 2007, 47, 779–784. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Matsumoto, M.; Shiomi, M.; Osakada, K.; Abe, F. Finite element analysis of single layer forming on metallic powder bed in rapid prototyping by selective laser processing. Int. J. Mach. Tools Manuf. 2002, 42, 61–67. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Yadroitsev, I.; Bertrand, P.; Smurov, I. Model of radiation and heat transfer in laser-powder interaction zone at selective laser melting. J. Heat Transf. 2009, 131, 072101. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 1980–2015 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Dai, D.; Gu, D. Tailoring surface quality through mass and momentum transfer modeling using a volume of fluid method in selective laser melting of TiC/AlSi10Mg powder. Int. J. Mach. Tools Manuf. 2015, 88, 95–107. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef]
- Tran, H.-C.; Loa, Y.-L. Heat transfer simulations of selective laser melting process based on volumetric heat source with powder size consideration. J. Mater. Process. Technol. 2018, 255, 411–425. [Google Scholar] [CrossRef]
- Slama, M.B.; Chatti, S.; Hassine, N.; Kolsi, L. Numerical investigation of the melt pool geometry evolution during selective laser melting of 316L SS. Matériaux Tech. 2024, 112, 208. [Google Scholar] [CrossRef]
- Tolstykh, A.I.; Shirobokov, D.A. On using radial basis functions in a “finite difference mode” with applications to elasticity problems. Comput. Mech. 2003, 33, 68–79. [Google Scholar] [CrossRef]
- Shu, C. Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 2003, 192, 941–954. [Google Scholar] [CrossRef]
- Wright, G.B.; Fornberg, B. Scattered node compact finite difference-type formulas generated from radial basis functions. J. Comput. Phys. 2006, 212, 99–123. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Sundin, U. Global Radial Basis Function Collocation Methods for PDEs. Licentiate Thesis, Uppsala University, Uppsala, Sweden, 2019. [Google Scholar]
- Pooladi, F.; Larsson, E. Stabilized interpolation using radial basis functions augmented with selected radial polynomials. J. Comput. Appl. Math. 2024, 437, 115482. [Google Scholar] [CrossRef]
- Fornberg, B.; Larrson, E.; Flyer, N. Stable computations with Gaussian radial basis functions. Siam J. Sci. Comput. 2011, 33, 869–892. Available online: http://n2t.net/ark:/85065/d7zp47fz (accessed on 23 July 2024). [CrossRef]
- Bayona, V.; Flyer, N.; Fornberg, B. On the role of polynomials in RBF-FD approximations: III. Behavior near domain boundaries. J. Comput. Phys. 2019, 380, 378–399. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2021; Additive Manufacturing—General Principles—Terminology, Fundamentals and Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/74514.html (accessed on 23 July 2024).
- Hassine, N.; Chatti, S.; Kolsi, L. Tailoring grain structure including grain size distribution, morphology, and orientation via building parameters on 316L parts produced by laser powder bed fusion. Int. J. Adv. Manuf. Technol. 2024, 131, 4483–4498. [Google Scholar] [CrossRef]


| Type of RBFs | |
|---|---|
| Infinitely smooth RBFs | |
| Gaussian (GA) | |
| Inverse multiquadric (IMQ) | |
| Inverse quadratic (IQ) | |
| Multiquadric (MQ) | |
| Piecewise smooth RBFs | |
| Polyharmonic spline (PHS) including cubic, TPS | |
| Compact support | |
| Other hybrid RBFs | |
| Hybrid Gaussian-cubic | |
| Parameters | Values |
|---|---|
| Material | |
| Type | AISI 316L stainless steel [24] |
| Conditions | |
| Convective | |
| Emissivity ε | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-L.; Wu, C.-H.; Chen, C.-K. A Meshless Method of Radial Basis Function-Finite Difference Approach to 3-Dimensional Numerical Simulation on Selective Laser Melting Process. Appl. Sci. 2024, 14, 6850. https://doi.org/10.3390/app14156850
Chen C-L, Wu C-H, Chen C-K. A Meshless Method of Radial Basis Function-Finite Difference Approach to 3-Dimensional Numerical Simulation on Selective Laser Melting Process. Applied Sciences. 2024; 14(15):6850. https://doi.org/10.3390/app14156850
Chicago/Turabian StyleChen, Chieh-Li, Cheng-Hsuan Wu, and Cha’o-Kuang Chen. 2024. "A Meshless Method of Radial Basis Function-Finite Difference Approach to 3-Dimensional Numerical Simulation on Selective Laser Melting Process" Applied Sciences 14, no. 15: 6850. https://doi.org/10.3390/app14156850






