Parameter Estimation of Breakthrough Curve Models in the Adsorption Process of H2S and CO2 Using the Markov Chain Monte Carlo Method
Abstract
:1. Introduction
2. Analytical Models of Breakthrough Curves
2.1. Thomas Model
2.2. Yoon–Nelson Model
2.3. Adams–Bohart Model
2.4. Yan Model
3. Methodology
Markov Chain Monte Carlo (MCMC)
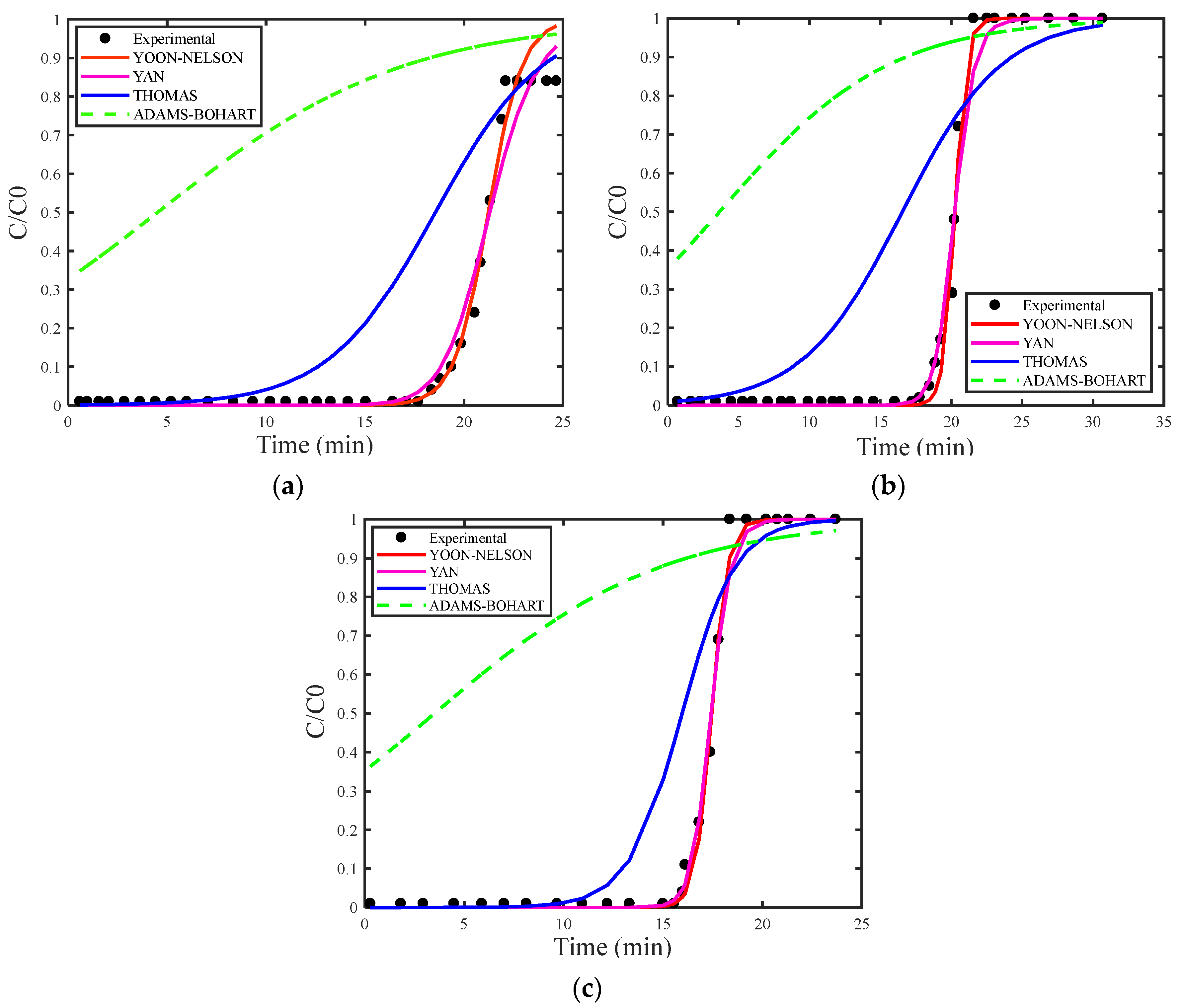
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baumann, R.; Libanio, G.; Iasco-Pereira, H.; Soares, F.V.; Pereira, K.C.; Neto, W.A.D. Indicadores Quantitativos da OCDE e o Brasil; Instituto de Pesquisa Econômica Aplicada (IPEA): Brasília, Brasil, 2023; Volume 5. [Google Scholar]
- Artaxo, P.E. O Estado da Qualidade do Ar no Brasil; Working Paper; WRI Brasil: São Paulo, Brazil, 2021; p. 32. [Google Scholar]
- Ghiat, I.; Al-Ansari, T. A review of carbon capture and utilisation as a CO2 abatement opportunity within the EWF nexus. J. CO2 Util. 2021, 45, 101432. [Google Scholar] [CrossRef]
- Majchrzak-Kucęba, I. CO2: A useful reactant. In The Carbon Chain in Carbon Dioxide Industrial Utilization Technologies: A Case Study; CRC Press: Boca Raton, FL, USA, 2022; pp. 17–35. [Google Scholar]
- Rehman, A.; Nazir, G.; Rhee, K.Y.; Park, S.J. Valorization of orange peel waste to tunable heteroatom-doped hydrochar-derived microporous carbons for selective CO2 adsorption and separation. Sci. Total Environ. 2022, 849, 157805. [Google Scholar] [CrossRef]
- Elgendy, K.; Elmehasseb, I.; Kandil, S. Efficient removal of common organic pollutants from water by Zn-doped TiO2 nanoparticles with different applications. Karbala Int. J. Mod. Sci. 2022, 8, 98–111. [Google Scholar] [CrossRef]
- Engenharia e Tecnologia de Processos Alimentares. In Adsorption and Ion Exchange; Zeki BERK: Istanbul, Turkey, 2009; pp. 279–294.
- Fujiwara, K.; Shibahara, M. Atomic-scale thermal manipulation with adsorbed atoms on a solid surface at a liquid-solid interface. Sci. Rep. 2019, 9, 13202. [Google Scholar] [CrossRef]
- Lee, S.Y.; Park, S.J. A review on solid adsorbents for carbon dioxide capture. J. Ind. Eng. Chem. 2015, 23, 1–11. [Google Scholar] [CrossRef]
- Juela, D.; Vera, M.; Cruzat, C.; Alvarez, X.; Vanegas, E. Mathematical modeling and numerical simulation of sulfamethoxazole adsorption onto sugarcane bagasse in a fixed-bed column. Chemosphere 2021, 280, 130687. [Google Scholar] [CrossRef]
- Páscoa, A.P.C. Modelação e Simulação Matemática da Adsorção em Leito Fixo. Aplicação à Adsorção de CO2 em Zeólito 4A. Master’s Thesis, Instituto Politécnico de Bragança, Bragança, Portugal, 2018. [Google Scholar]
- Qian, W.; Hu, M.; Su, Y.; Shan, S.; Zhang, Z.; Hu, L.; Lin, X. Insight into mass transfer during adsorption of geniposidic acid onto a fixed-bed column by numerical simulation considering influence of operating conditions on column adsorption performance. Sep. Purif. Technol. 2023, 319, 124021. [Google Scholar] [CrossRef]
- Lima, A.C.A. Adsorção de anions presente em efluente usando pó da casca de coco verde modificado. Master’s Thesis, Universidade Federal do Ceará, Fortaleza, Brazil, 2009. [Google Scholar]
- Galagali, N.; Marzouk, Y.M. Bayesian inference of chemical kinetic models from proposed reactions. Chem. Eng. Sci. 2015, 123, 170–190. [Google Scholar] [CrossRef]
- Orlande, H.R.B.; Colaço, M.J.; Cotta, C.P.; Guimarães, G.; Borges, V. Problemas Inversos em Transferencia de Calor; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014; p. 639. [Google Scholar]
- Gilks, W.R.; Roberts, G.O.; Sahu, S.K. Adaptive markov chain monte carlo through regeneration. J. Am. Stat. Assoc. 1998, 93, 1045–1054. [Google Scholar] [CrossRef]
- Mccabe, W.L.; Smith, J.C.; Harriot, P. Unit Operations of Chemical Engineering, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Oliveira, J.T.; Estumano, D.C.; Féris, L.A. Resolution methods for adsorption models, batch and continuous mode, and its impact on process implementation: An experimental and statistical comparison. J. Water Process Eng. 2024, 58, 104888. [Google Scholar] [CrossRef]
- Franco, M.A.E. Adsorção de Fármacos em Carvão Ativado: Processo em Batelada, Leito Fixo e Modelagem das Curvas de Ruptura. 2018. Ph.D. Thesis, Universidade Federal do Rio Grande Do Sul, Porto Alegre, Brazil, 2018. [Google Scholar]
- Nascimento, R.F.; Lima, A.C.A.; Vidal, C.B.; Melo, D.Q.; Raulino, G.S.C. Adsorção: Aspectos Teóricos e Aplicações Ambientais, 2nd ed.; Imprensa Universitária: Lisbon, Portugal, 2020. [Google Scholar]
- Tien, C. Introduction to Adsorption: Basics, Analysis and Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Thomas, H.C. Heterogeneous Ion Exchange in a Flowing System. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
- Yoon, Y.H.; Nelson, J.H. Application of Gas Adsorption Kinetics I. A Theoretical Model for Respirator Cartridge Service Life. Am. Ind. Hyg. Assoc. J. 1984, 53, 493–502. [Google Scholar] [CrossRef]
- Amador, I.C.B.; Nunes, K.G.P.; Franco, M.A.E.; Viegas, B.M.; Macêdo, E.N.; Féris, L.A.; Estumano, D.C. Application of Approximate Bayesian Computational technique to characterize the breakthrough of paracetamol adsorption in fixed-bed column. Int. Commun. Heat Mass Transfer. 2022, 132, 105917. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef]
- Chu, K.H. Breakthrough curve analysis by simplistic models of fixed bed adsorption: In defense of the century-old Bohart-Adams model. Chem. Eng. J. 2020, 380, 122513. [Google Scholar] [CrossRef]
- Yan, G.; Viraraghavan, T.; Chen, M. A new model for heavy metal removal in a biosorption column. Adsorpt. Sci. Technol. 2001, 19, 25–43. [Google Scholar] [CrossRef]
- Scheufele, F.B.; Silva, E.S.; Cazula, B.B.; Marins, D.S.; Sequinel, R.; Borba, C.E.; Patuzzo, G.S.; Lopez, T.F.M.; Alves, H.J. Mathematical modeling of low-pressure H2S adsorption by babassu biochar in fixed bed column. J. Environ. Chem. Eng. 2021, 9, 2213–3437. [Google Scholar] [CrossRef]
- Al Mesfer, M.K.; Amari, A.; Danish, M.; Al Alwan, B.A.; Shah, M. Simulation study of fixed-bed CO2 adsorption from CO2/N2 mixture using using activvated carbono. Chem. Eng. Commun. 2020, 208, 1358–1367. [Google Scholar] [CrossRef]
- Soeiro, W.F.; Moura, C.H.R.; Dias, C.S.; Rodrigues, E.C.; Da Costa, D.S.; Viegas, B.M.; Estumano, D.C. Mathematical Evaluation of Direct and Inverse Problem Applied in Breakthrough Models of Metal Adsorption. Appl. Sci. 2024, 14, 5035. [Google Scholar] [CrossRef]
- Dobbelaere, M.R.; Plehiers, P.P.; Van De Vijver, R.; Stevens, C.V.; Van Geem, K.M. Machine learning in chemical engineering: Strengths, weaknesses, opportunities, and threats. Engineering 2021, 7, 1201–1211. [Google Scholar] [CrossRef]
- Cardoso, A.C.; Dias, C.S.; Moura, C.H.R.D.; Ferreira, J.L.; Rodrigues, E.C.; Macêdo, E.N.; Estumano, D.C.; Viegas, B.M. Use of Bayesian Methods in the Process of Uranium Bioleaching by Acidithiobacillus ferrooxidans. Appl. Sci. 2023, 14, 109. [Google Scholar] [CrossRef]
- Tavares, R.; Santana, C.D.; Rodrigues, C.H.M.; Rodrigues, E.C.; Viegas, B.M.; Estumano, D.C. Parameter Estimation in Mass Balance Model Applied in Fixed Bed Adsorption Using the Markov Chain Monte Carlo Method. J. Heat Mass Transf. Res. 2022, 9, 219–232. [Google Scholar]
- Jurado-Davila, I.V.; Schneider, I.A.H.; Estumano, D.; Féris, L.A. Phosphate removal using dolomite modified with ultrasound: Mathematical and experimental analysis. J. Environ. Sci. Health 2023, 58, 469–482. [Google Scholar] [CrossRef]
- Giles, C.H.; Macewan, T.H.; Nakhwa, S.N.; Smith, D. Studies in adsorption, Part XI. A system of classification of solutions adsorption isotherms, and it’s uses in diagnosis os adsorption mechanisms and in measurement of specific areas of solids. J. Chem. Soc. 1960, 111, 10–1039. [Google Scholar]
- Meng, M.; Feng, Y.; Zhang, M.; Liu, Y.; Ji, Y.; Wang, J.; Yan, Y. Highly efficient adsorption of salicylic acid from aqueous solution by wollastonite-based imprinted adsorbent: A fixed-bed column study. Chem. Eng. J. 2013, 225, 331–339. [Google Scholar] [CrossRef]
- Jurado-Davila, V.; Oshiro, G.P.; Estumano, D.C.; Féris, L.A. Immobilization of Marbofloxacin for Water Treatment by Adsorption in Batch Scale and Fixed-Bed Column: Applying of Monte Carlo Bayesian Modeling. Ind. Eng. Chem. Res. 2024, 63, 9976–9987. [Google Scholar] [CrossRef]
- Aslam, Z.; Hussein, I.A.; Shawabkeh, R.A.; Parvez, M.A.; Ahmad, W.; Ihsanullah. Adsorption Kinetics and modeling of H2S by treated waste oil fly ash. J. Air Waste Manag. Assoc. 2019, 69, 246–257. [Google Scholar] [CrossRef]
- Saleh, A.M.; Mahdi, H.H.; Alias, A.B.; Abd Hadi, N.K.; Qarizada, D.; Jawad, A.H.; Saleh, N.M. Equilibrium and kinetic studies in adsorption of H2S using coconut shell activated carbon xerogel: Effect of mass adsorbent and temperature. Desalination Water Treat. 2024, 317, 100149. [Google Scholar] [CrossRef]
- Ligero, A.; Calero, M.; Martín-Lara, M.Á.; Blázquez, G.; Solís, R.R.; Pérez, A. Fixed-bed CO2 adsorption onto activated char from the pyrolysis of a non-recyclable plastic mixture from real urban residues. J. CO2 Util. 2023, 73, 102517. [Google Scholar] [CrossRef]
- Mrosso, R.; Mecha, A.C.; Kiplagat, J. Performance evaluation of calcined eggshell waste (Sorbent) for biogas upgrading: Adsorption isotherms, adsorption kinetics, and fixed bed studies. Environ. Chall. 2024, 16, 100961. [Google Scholar] [CrossRef]
- Carvalho, G.R. Breakthrough analysis of continuous fixed-bed dehydration of gas streams using 4A zeolite molecular sieve. Acta Sci. 2022, 45, e58764. [Google Scholar] [CrossRef]
- Moraes, S.C.G. Avaliação da Capacidade Adsortiva da Cinza do Bagaço de Cana-de-Açúcar para Remoção de H2S Oriundo da Gaseificação de Biomassas. Master’s Thesis, Universidade Federal de Pernambuco, Recife, Brazil, 2017. [Google Scholar]
- Tourzani, A.A.; Hormozi, F.; Asadollahzadeh, M.; Torkaman, R. Effective CO2 capture by using poly (acrylonitrile) nanofibers based on the radiation grafting procedure in fixed-bed adsorption column. Sci. Rep. 2023, 13, 6173. [Google Scholar] [CrossRef]




| Initial Concentration (mg/L) | H2S | CO2 | |||
|---|---|---|---|---|---|
| 1.327 | 2.577 | 18 | 29 | 35 | |
| Adsorbent mass (g) | 18.4052 | 18.3893 | 230 | ||
| Maximum adsorption capacity (mg/g) | 20.61 | 7.26165 | 10.43037 | 12.14676 | |
| Flow rate (L/min) | 1.8 | 5 | |||
| Models | Equations | Parameters | Assumptions | References |
|---|---|---|---|---|
| Thomas | —Initial concentration of adsorbate (mg/L); —Maximum adsorption ca-pacity (mg/g); t—Flow time (min); Q—Flow rate (L/min); W—Adsorbent mass (g); —Thomas velocity constant (L/min·mg). |
| [23] | |
| Yoon– Nelson | —Time required to reach 50% breakthrough (min); —Flow time (min); —Yoon–Nelson kinetic constant (1/min). |
| [24] | |
| Adams– Bohart | —Initial concentration of adsorbate (mg/L); N0—Maximum volumetric adsorption capacity (mg·L−1); v—Interstitial velocity (L/min·cm2); t—Flow time (min); H—Bed height (cm); kba—Adams–Bohart constant representing adsorption rate (L/min·mg). |
| [21,26] | |
| Yan | —Initial concentration of adsorbate W—Mass of adsorbent in the bed (g); —Feed flow rate of the column (L/min); — t—Flow time (min); —Yan model constant. |
| [28] |
| Models | Parameters |
|---|---|
| Thomas | PT = [kth qs] |
| Yoon–Nelson | PT = [] |
| Adams–Bohart | PT = [kba N0] |
| Yan | PT = [ay qs] |
| Models | Parameters | (qs, N0) Estimated (Present Work) | (qs, N0) Deterministic [29] | ||
|---|---|---|---|---|---|
| Thomas | C0 (mg/L) | 1.327 | 2.577 | 1.327 | 2.577 |
| qs (mg/g) | 18.9861 | 17.8316 | 20.61 | 20.61 | |
| kth (L/min·mg) | 0.0306 | 0.0204 | 0.0278 | 0.0168 | |
| R2 | 0.9937 | 0.9700 | 0.9746 | 0.9488 | |
| R2Adjusted | 0.9932 | 0.9673 | 0.9728 | 0.9443 | |
| BIC | 249.1613 | 1.0900 × 103 | 1.2473 × 103 | 1.9488 × 103 | |
| Yoon– Nelson | kyn (min) | - | - | 0.0412 | 0.0534 |
| τ (min) | - | - | 145.7883 | 69.9294 | |
| R2 | - | - | 0.9936 | 0.9698 | |
| R2Adjusted | - | - | 0.9732 | 0.9672 | |
| BIC | - | - | 251.3955 | 1.0958 × 103 | |
| Adams–Bohart | kba (105) | 3.0840 | 2.0333 | 2.4615 | 1.4473 |
| N0 (10−4) | 4.8053 | 4.5456 | 5.5729 | 5.5729 | |
| R2 | 0.9937 | 0.9701 | 0.9331 | 0.9293 | |
| R2Adjusted | 0.9932 | 0.9675 | 0.9284 | 0.9232 | |
| BIC | 249.2162 | 1.0845 × 103 | 3.6145 × 103 | 2.7708 × 103 | |
| Yan | qs | 18.5658 | 16.9291 | 20.61 | 20.61 |
| ay | 5.7419 | 3.3525 | 5.8802 | 3.3550 | |
| R2 | 0.9982 | 0.9899 | 0.9671 | 0.9479 | |
| R2Adjusted | 0.9981 | 0.9890 | 0.9648 | 0.9434 | |
| BIC | 11.2732 | 316.4672 | 1.6493 × 103 | 1.9835 × 103 | |
| Models | Parameters | (qs, N0) Estimated (Present Work) | (qs, N0) Deterministic [30] | ||||
|---|---|---|---|---|---|---|---|
| Thomas | C0 (mg/L) | 18 | 29 | 35 | 18 | 29 | 35 |
| qs (mg/g) | 8.3114 | 12.7682 | 13.2753 | 7.2617 | 10.43037 | 12.1468 | |
| kth (L/min·mg) | 0.0632 | 0.0801 | 0.0699 | 0.0205 | 0.0099 | 0.0213 | |
| R2 | 0.9811 | 0.9935 | 0.9955 | 0.6660 | 0.7059 | 0.8223 | |
| R2Adjusted | 0.9799 | 0.9934 | 0.9951 | 0.6451 | 0.6863 | 0.8062 | |
| BIC | 550.4370 | 274.7252 | 153.2467 | 1.6583 × 104 | 2.4228 × 104 | 1.0195 × 104 | |
| Yoon–Nelson | kyn (min) | - | - | - | 1.1780 | 2.4075 | 2.4467 |
| τ (min) | - | - | - | 21.2342 | 20.2541 | 17.4458 | |
| R2 | - | - | - | 0.9809 | 0.9939 | 0.9955 | |
| R2Adjusted | - | - | - | 0.9797 | 0.9935 | 0.9951 | |
| BIC | - | - | - | 557.1840 | 275.0701 | 153.3209 | |
| Adams– Bohart | kba | 6.4991 × 10−5 | 8.7282 × 10−5 | 7.0016 × 10−5 | 8.8822 × 10−6 | 5.7670 × 10−6 | 4.9604 × 10−6 |
| N0 (mg/L) | 18065 | 27771 | 28866 | 5954.6 | 8552.9034 | 9960.3 | |
| R2 | 0.9809 | 0.9940 | 0.9955 | 0.2020 | 0.3307 | 0.3665 | |
| R2Adjusted | 0.9797 | 0.9935 | 0.9951 | 0.1522 | 0.2861 | 0.3089 | |
| BIC | 557.3886 | 270.7467 | 153.3194 | 1.3121 × 105 | 1.1801 × 105 | 8.2006 × 104 | |
| Yan | qs | 9.5851 | 11.3468 | 13.0378 | 7.2617 | 10.4304 | 12.1468 |
| ay | 5.6501 | 5.0110 | 5.0643 | 7.4527 | 5.4479 | 5.4352 | |
| R2 | 0.9750 | 0.9891 | 0.9937 | 0.9749 | 0.9891 | 0.9937 | |
| R2Adjusted | 0.9734 | 0.9884 | 0.9932 | 0.9733 | 0.9884 | 0.9932 | |
| BIC | 763.9940 | 559.1430 | 236.2257 | 766.4743 | 559.1664 | 236.2271 | |
| Models | References | Qmax (mg/g) | Parameters | Operating Conditions | |
|---|---|---|---|---|---|
| Thomas | H2S | [39] | 8.5 | - | Adsorbent: residual oil fly ash W = 1 g; C0 = 100 ppm; Q = 0.4 L/min |
| [40] | 208.99 | Kth—0.001028 (L/min·mg) | Adsorbent: activated carbon xerogel from coconut shell W = 5 g; C0 = 25 ppm mol; Q = 2.5 L/min | ||
| CO2 | [41] | 22.9 | Kth—0.2329 (mL/mg·s) | Adsorbent: activated carbon W = 1 g; C0 = 10%; Q = 30 mL/min | |
| [42] | 16.257 (mL/min·mg) | Kth—9.12 × 10−6 (mL/min·mg) | Adsorbent: eggshell waste W = 25 g; C0 = 30.8%; Q = 0.03 m3/h | ||
| Yoon–Nelson | H2S | [40] | 208.99 | Kyn—0.0257 (min−1) | Adsorbent: activated carbon xerogel from coconut shell W = 5 g; C0 = 25 ppm mol; Q = 2.5 L/min |
| [39] | 8.5 | Kyn—0.1882 (min−1) τ—69.21 (min) | Adsorbent: residual oil fly ash W (g) = 1; C0 = 100 ppm; Q = 0.4 L/min | ||
| CO2 | [41] | 22.9 | Kyn—0.0434 (s−1) τ—73.8 (s) | Adsorbent: activated carbon W = 1 g; C0 = 10%; Q = 30 mL/min | |
| [43] | 126 | Kyn—4.24 (h−1) τ—2.37 (h) | Adsorbent: zeolite 4A W = 6.3 g; C0 = 20 mg/L; Q = 8 L/min | ||
| Adams–Bohart | H2S | [44] | - | kba—0.9595 N0—571.49 (mg/L·min) | Adsorbent: pure ash W = 3.4432 g; C0 = 500 mg/L; Q = 25 mL/min |
| [44] | 508.43 | kba—0.9595 N0—508.43 (mg/L·min) | Adsorbent: sol–gel method ash W = 1.9295 g; C0 = 500 mg/L; Q = 25 mL/min | ||
| CO2 | [42] | 16.257 (mL/min·mg) | kba—2.2 × 10−4 (L/mg·min) N0—28.15 (mg/L) | Adsorbent: eggshell waste W = 25 g; C0 = 30.8%; Q = 0.03 m3/h | |
| [41] | 2.9 | kba—0.2329 (mL/mg·s) N0—4515 (mg/L) | Adsorbent: activated carbon W = 1 g; C0 = 10%; Q = 30 mL/min | ||
| Yan | H2S | [44] | 502.35 | —1.14 | Adsorbent: hydrothermal process ashes W = 1.4843 g; C0 = 500 mg/L; Q = 25 mL/min |
| [44] | 571.49 | —10.58 | Adsorbent: pure ash W = 3.4432 g; C0 = 500 mg/L; Q = 25 mL/min | ||
| CO2 | [41] | 22.9 | —3.0939 | Adsorbent: activated carbon W = 1 g; C0 = 10%; Q = 30 mL/min | |
| [45] | 2.5 mmol/g | —19.27 | Adsorbent: modified polyacrylonitrile nanofibers C0 = 5%; Q = 100 mL/min | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, H.B.S.; Sousa, A.P.S.d.; Silva, W.B.d.; Costa, D.S.d.; Rodrigues, E.C.; Estumano, D.C. Parameter Estimation of Breakthrough Curve Models in the Adsorption Process of H2S and CO2 Using the Markov Chain Monte Carlo Method. Appl. Sci. 2024, 14, 6956. https://doi.org/10.3390/app14166956
Lima HBS, Sousa APSd, Silva WBd, Costa DSd, Rodrigues EC, Estumano DC. Parameter Estimation of Breakthrough Curve Models in the Adsorption Process of H2S and CO2 Using the Markov Chain Monte Carlo Method. Applied Sciences. 2024; 14(16):6956. https://doi.org/10.3390/app14166956
Chicago/Turabian StyleLima, Haianny Beatriz Saraiva, Ana Paula Souza de Sousa, Wellington Betencurte da Silva, Deibson Silva da Costa, Emerson Cardoso Rodrigues, and Diego Cardoso Estumano. 2024. "Parameter Estimation of Breakthrough Curve Models in the Adsorption Process of H2S and CO2 Using the Markov Chain Monte Carlo Method" Applied Sciences 14, no. 16: 6956. https://doi.org/10.3390/app14166956
APA StyleLima, H. B. S., Sousa, A. P. S. d., Silva, W. B. d., Costa, D. S. d., Rodrigues, E. C., & Estumano, D. C. (2024). Parameter Estimation of Breakthrough Curve Models in the Adsorption Process of H2S and CO2 Using the Markov Chain Monte Carlo Method. Applied Sciences, 14(16), 6956. https://doi.org/10.3390/app14166956






