Modern Dimensional Analysis Model Laws Used to Model Additive Manufacturing Processes

Featured Application

Additive Manufacturing (AM) represents new and very promising manufacturing processes. The results can be applied immediately in the manufacturing industry in order to obtain significant decreases of the costs in some specific domains.

Abstract

By means of its facilities, AM brings several advantages in comparison with the classical manufacturing technologies. Nowadays, there are a huge number of unexplored directions, which assure AM will become a very powerful manufacturing process in the next period, with an undoubted low cost and reduced material consumption, as well as optimal stiffness and competitiveness technology. Between the unexplored (or less-explored) directions, one has to mention the dimensional methods’ involvement in gaining an optimal, highly competitive final product. This means that instead of the real structural element, named the prototype, the engineers will perform high-accuracy tests on the attached reduced-scale models, whose experimental results are extended to the prototype by means of the deduced model law (ML). The authors, based on their previous theoretical research as well as experimental investigations, offer a new approach, which is less implemented in AM technologies. Based on the obtained results, these dimensional methods are very promising, especially the last one, the so-called Modern Dimensional Analysis (MDA), conceived by Thomas Szirtes and described in the following paper. Starting with the nowadays-applied dimensional methods’ critical analysis, the authors will present evidence for the advantages of MDA, especially on the polymer-based AM technology. They will prove that MDA represents a very promising, as well as easy approach, which through its implementation can offer a higher competitiveness for AM technologies. As an illustration of the advantages of MDA, the authors conceived several MDA approaches for a given structural element’s case (a cantilever beam, with an internal-ribbed structure loaded at its free end by means of a vertical concentrated load), which, through their high accuracy in experimental-validated MLs, offer very good accuracy in model–prototype correlation. The deviations between the effective measured values of the displacements on the prototypes and those predicted, based on the values of the measurements on the models assigned to the prototypes by the validated MLs, were 1.06, 1.60, and 2.35%, respectively. In the authors’ opinion, MDA can represent a starting point for conceiving a highly competitive product with an optimal filling, as well as the deposition of layers using AM technologies. Based on the authors’ best knowledge, up to this moment, it seems that this engineering area does not fully apply the advantages of MDA, only in few limited cases, analyzed in the following.

1. Introduction

Nowadays, AM represents a very promising way to obtain high-quality, cheap, low time consumption, and low pollution/waste products (unique components or spare parts, as well). Rapid Prototyping served to obtain the first complex products [1,2,3,4,5,6,7,8,9,10]. Later, the technology was applied not only for plastics, but also for plastic–metal, specifically only the metal parts [11,12,13,14,15,16,17,18,19,20,21].

Fuse Deposition Modeling (FDM), representing the authors’ main field of analysis/investigation, was one of the earlier technologies. It was followed by Power Bed Fusion processes, which were widely analyzed and applied [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Sheet Lamination processes, which followed them, gained a huge and efficient application [40,42,52,55,56,57,58,59,60,61]. Nowadays, Directed Energy Deposition, specifically Automated Fiber Placement techniques, are widely and successfully applied [62,63,64,65,66,67,68,69,70]. The accepted common casting technologies for metals, combined with AM, offer several facilities and advantages, both in obtaining the complex final products and in improving their initial manufacturing process from the point of view of cost, time, accuracy, and waste amount, as well as durability.

An efficient combination of the plastic and metal layers, mainly in the cases of the casting molds and cores manufactured using AM, offers new research directions. Taking into consideration the complexity of these final products, obtained using a combination of plastic and metal layers, there are several significant problems, such as their geometric accuracy, their obtained surface quality, their stiffness against the thermal loading, as well as their mechanical loading, their durability, and their dimensional stability. In order to solve these significant problems, dimensional methods were successfully introduced by specialists. These dimensional methods have demonstrated their effectiveness in solving complex problems related to the manufacture of these casting molds.

By applying these dimensional methods instead of testing the real structural element (here: the casting mold, specifically the core, i.e., the prototype), one can perform high-accuracy tests on an attached reduced-scale element, named the model [71,72,73,74,75,76]. It is known that performing experimental measurements on the real parts, that is, on the so-called prototypes, usually involves serious difficulties. Compared with this, on the attached model, made on a reduced scale, they become much simpler, safer, and repeatable, with significantly lower material and human expenses.

By adequately deducing the model law (ML), constituted strictly from the dimensionless variables, one can extend the obtained results from the model to the prototype, forecasting the prototype’s behaviors [77,78,79,80,81,82,83,84]. In the following, the authors briefly review the main dimensional methods, together with their advantages and limitations.

2. The Most Used Dimensional Methods

Starting with the indisputable advantages of the dimensional analysis, which will be briefly analyzed below, mathematicians and engineers have developed reliable and unambiguous correlations, determined between the behavior of the real part, i.e., the prototype, and the attached reduced-scale model. As mentioned above, due to the fact that the experimental investigations on the attached reduced-scale model become much simpler, safer, and repeatable, with significantly lower material and human expenses, one can conclude that the involvement of these dimensional methods in AM processes brings several advantages. In addition, as will be analyzed below, the deduced model laws (MLs) on simple parts (or structural elements) can be more easily extended to large and more complex structures, constituted from these simple parts.

Starting from the relatively simple cases with a reduced number of the involved dimensionless variables, where Geometric Analogy (GA) satisfies the imposed requirements, the Theory of Similarity (TS), particularly for very complex phenomenon using Classical Dimensional Analysis (CDA), can obtain useful results [85,86,87,88,89,90,91,92,93].

In the case of GA, the geometric similarity is compulsory; it supposes rigorous proportionality of lengths, as well as angular equality for the prototype and the attached model. One can define homologous points, lines, surfaces, and volumes; consequently, the attached model has a very limited flexibility with respect to the prototype.

The TS solves more complex phenomena, allowing both structural and functional similarity. In this case, the analyzed phenomena occur such that, at homologous times, in homologous points, each involved significant variable $\eta$ are described by a distinct (separate) constant ratio ${\mathrm{S}}_{\eta }=\mathrm{const}.$ of the values, where by definition, we have $S_{\eta }={\displaystyle \frac{{\eta }_2}{{\eta }_1}}$ corresponding to model (${\eta }_2$) and prototype (${\eta }_1$). One can mention the following, regarding the meaning of homologous time. Two processes assume homologous states (positions, configurations, etc.) at homologous times. The concept of homologous times does not ordinarily entail simultaneity, but rather the passing of time when two bodies/phenomenon occurred in similar positions, stress-states, deformations, shapes, etc. In this sense, perhaps the easier understandable values are their maximal, minimal, or zero values [94,95].

The $S_{\eta }$ dimensionless ratios are the so-called scale factors, which are always constant in time and space for the given phenomena; their number coincides with the involved variables’ number.

In principle, instead of some solutions of complicated equations, one can apply relatively simple correlation between a reduced numbers of ${\pi }_j , j=1\dots n$ dimensionless variables, which constitute the ML; at TS, they result by means of suitable grouping of the adequate terms of governing equations.

One has to mention that the involvement of the above-mentioned MLs assure a significant diminishing of the number of measurements.

For a large number of the dimensionless variables, CDA was applied, based on the well-known Buckingham’s $\pi$ theorem; taking into the consideration the very numerous references, the authors suggest only the followings ones [96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119].

At first sight, it seems that CDA offers a relatively easy manner for analysis of complex phenomena. Upon closer analysis, we notice its main disadvantages, based, among others, on its difficulties in deducing the demanded/requested ${\pi }_j , j=1\dots n$ dimensionless variables.

One has to mention that for obtaining these ${\pi }_j , j=1\dots n$ dimensionless variables, CDA offers three main modalities, namely from:

• the Buckingham’s $\pi$ theorem;
• the partial differential equations applied to fundamental differential relations of the analyzed phenomenon, when the initial variables, by suitable grouping, offer these dimensionless quantities;
• the complete, but at the same time the simplest, equation(s) which describe the phenomena, which will be transformed into dimensionless forms, finally offering the desired ${\pi }_j$ groups.

In the above-mentioned references, one can find their detailed analysis.

By a brief synthesis, one can summarize these shortcomings of CDA, namely:

• the protocol in obtaining the desired set of ${\pi }_j$ groups is rather chaotic, arbitrarily and strongly depending on the ingenuity and experience of the involved specialist;
• for the involved specialist, solid knowledge in the field of the analyzed phenomenon and higher mathematics are required as well;
• only rarely (occasionally) can the complete ML be obtained, mainly due to the fact that there are only a limited number of the involved mathematical relations related to the phenomena;
• for common engineers or specialists, involved in prototype–model correlation analysis, CDA does not represent an easy approach.

Based exactly on the above-mentioned reasons, for common engineers or specialists involved in prototype–model correlation analysis, CDA does not represent an easy, efficient, or user-friendly approach.

Compared to this, the methodology developed by Szirtes [94,95], hereafter named Modern Dimensional Analysis (MDA), offers an efficient, practical solution for all above-analyzed shortcomings.

As the authors will illustrate in the following Sections, the MDA represents a simple, unitary, and particularly accessible methodology, with the following main advantages:

• the involved specialist, instead of being a thorough connoisseur in the phenomenon as well as in higher mathematics, only has to identify the set of the involved variables, together with their dimensions, which have (or can present) a certain extent influence on the analyzed phenomena;
• it has a unitary, simple, and user-friendly protocol, which assures at once to automatically eliminate all insignificant/irrelevant variables;
• in all cases, MDA assures obtaining the complete set of the ${\pi }_j, j=1\dots n$ dimensionless variables, as well as the complete ML; this is practically impossible using the aforementioned methods, excepting some particular cases;
• this ML is very flexible, suitable for several particular cases, corresponding to simplified approaches of the phenomena;
• by a priori setting of the directly related variables to the conceived experimental investigations on model, hereafter named independent variables, MDA assures additional flexibility, which represents a significant advantage, non-existent in all the methods mentioned above; their a priori choice is possible both for the prototype and model;
• this set (of the independent variables) assures defining the most suitable model, which will offer for the involved model the most simple, lower-cost testing conditions, safety, as well as repeatable experimental investigations;
• the rest of the variables, hereafter named dependent variables, can be chosen priori only for the prototype; their magnitudes for the model are strictly obtained by applying a given (suitable) element of the ML;
• among the dependent variables there are also a small number of prototype variables, whose magnitude cannot be obtained more easily (with low cost or accessible experimental measurements) and whose determination is actually the purpose of this dimensional analysis; thus, these aforementioned prototype’s variables are obtained by applying the ML;
• furthermore, MDA removes the restriction of the geometric similarity of the model with the prototype, e.g., the shape of the cross-sections can be different at the model from the prototype; in this case, instead of choosing the cross-sectional dimensions as independent variables, one will substitute them by the $I_z$ second order moment of inertia of the cross-section;
• if the material is considered as an independent variable, chosen by means of $E$ Young modules, then one can accept different materials for the model, relative to the prototype;
• in the case of choosing the $E\cdot I_z$ flexural stiffness (rigidity) instead of the cross-sectional dimensions, than neither the shape of the cross-section, nor the type of material must be identical in the prototype and model; the single condition remaining is that their $S_{E\cdot I_z}$ scale factor must remain the same (to be constant), where this scale factor is defined as the ratio of the $E\cdot I_z$ flexural stiffnesses, that is, $S_{E\cdot I_z}={\displaystyle \frac{E_2\cdot I_{z,2}}{E_1\cdot I_{z,1}}}$, with the aforementioned indexing (2 for model, and 1 for prototype).

Of course, this evaluation can be continued, but only these aforementioned facilities underline the suitability of MDA in AM process optimization. In addition, readers can obtain additional information in applying the MDA facilities in different engineering applications from [94,95,120,121,122].

In Section 3, the authors offer an overview on the dimensional methods’ involvement in different aspects of Additive Manufacturing.

3. Most Used Dimensional Methods in Additive Manufacturing

From the rich literature that analyze the behaviors of the polymeric materials, as well as other studies related to their involvement in AM, one can find evidence in the following contributions [10,31,43,48,66,68,70,123,124,125,126,127,128].

In [49], the authors summarize the basic principle of AM technologies, as well as its developments not only in China, but around the world. They provide evidence for the evolution of AM technologies applicable for the foundry, among others direct preparation of the mold and cores without needing patterns as well as how to cast complex items in one attempt. The analyzed AM technologies mentioned include 3D printing, Selective Laser Sintering, Stereo-lithography, and Layered Extrusion Forming.

From the very large literature regarding the involvement of dimensional methods in AM, the most appropriate approach the authors found concerned the Szirtes’ theory [94,95], the so-called Dimensional Analysis Conceptual Modelling (DACM) Framework of Coatanéa [129,130,131,132,133,134,135,136], with several useful results. Coatanéa, in his PhD thesis [129], states a new and efficient approach, namely Conceptual modelling of life cycle design, later perfected as Conceptual Modelling and Simulation Framework for System Design [130,131,132,133,134,137,138,139,140,141].

In order to get a more efficient final product by AM, modelling and simulation are widely applied. In this process, the integration of different models has a great importance. Applying Coatanéa’s approach increases both the prediction capability of the involved parameters and the performances of the desired components by AM. In addition, this approach assures a systematic improving of the entire design of the manufacturing process. DACM offers useful causal graphs, helping designers in obtaining an efficient printing process; its efficiency is illustrated in Fused Filament Fabrication Powder Bed Fusion technology. Witherell in [119], as well as Williams in [140], offer similar efficient approaches.

Xie, in [116], based on CDA, introduced so-called dimensionless learning, which represents a two-level machine learning principle in order to identify relatively automatically the involved dimensionless quantities, as well as the corresponding MLs. This approach is efficient mainly when there are numerous variables and few governing equations. In [98], Lambert, by direct application of Buckingham’s $\pi$ theorem, modelled a flexible barrier, with its model manufactured by 3D printing technology. Dijkshoorn, in [88], based on a Finite Elements Analysis as well as a dimensional one, offered an improvement of 3D printed structure electrical conductivity, manufactured with FDM. The actual printed structures usually have anisotropic electrical properties, and their goal was to optimize these properties in order to assure isotropic electrical properties. These special electrical isotropic properties can offer different kinds of printed structures the opportunity to serve as new, and very high-sensitivity tensile and compressive sensors (pressure as well as force transducers) with large industrial applications. From the dimensional analysis point of view, by a particular grouping of the quantities from the analytical relations, the authors obtained useful results without applying Buckingham’s $\pi$ theorem. The authors defined several useful dimensionless quantities, such as inter-traxel resistance, aspect ratio (in order to provide evidence for the geometry effect), some anisotropy ratios (for the material effect evaluation), and a number of meanders and traxels (which are related to the print design, specifically for determining the entire path length).

In order to improve the classical AM by hybrid manufacturing, mainly for commercial carbon fiber-reinforced PLA and normal PLA filaments, Mertkan, in [124], described some useful results. There also offered a similarity study (prototype–model) of these products in order to optimize them. By a successful combination of the advantages of the AM and the Topology Optimization, Okoth, in [30], obtained promising improvements of a complex car part, namely an efficient material redistribution with respect to its maximal load-bearing capacity.

The original hybrid framework, obtained by combining a machine learning-assisted process modelling and an optimization, ensured efficient control of the melt pool geometry during the build process for Mondal in [28]. The theoretical results were validated by several accurate experimental investigations, mainly in prediction of the thermal distribution in a moving melt pool. These results are very significant in FDM processes. The influence of the most significant process parameters (the air gap, the printing orientation, the raster angle, the layer height, and the raster width) on the tensile strength of the components obtained by FDM were analyzed experimentally by Tura in [53]. In the study, they combined an adaptive neuro-fuzzy technique with an artificial neural network for predicting the system’s response. They found that the most significant effects on the tensile strength were the air gap, the raster width, and the raster angle.

Lim, in [100], performed accurate dimensionless analysis on the clad formation in metal deposition, proving that the process parameters influence their dimensions. These results serve as a starting point in improving standard pre-printing tool in the metal deposition process. For predicting the mechanical properties of different continuous fiber materials, manufactured with FDM, Polyzos, in [106], offers a multi-scale analytical methodology. Starting from the micro-scale and shifting up to the macro-scale elements, they determined the searched mechanical properties.

Mostafa, in the reference [103], offers an interesting implementation of TS for substituting by reduced scale-models’ experimental investigations the real-scale’s one, applied on common rectangular hollow cross-sectional structural elements manufactured by AM. The required material for the samples was selected using the printing time as the most significant parameter. By means of three-point bending tests, the results provided useful scaling curves in order to predict the real structural element for the ultimate load. The promising results, validated by accurate Finite Elements Analysis, offer a new approach for feasible and cost-effective modelling of these structural elements.

In [123], Mackay established a dimensionless approach between the dimensionless fiber feed velocity and the dimensionless temperature for polymer-based AM technology for three frequently used polymers: acrylonitrile butadiene styrene, poly(lactic acid) (PLA), and a PLA–polyhydroxybutyrate copolymer. The obtained dimensionless curves offer useful information for all sorts of analyzed polymers. The authors highlight the importance of establishing the thermal and rheological properties of the involved materials.

In [110], Rubenchik performed a simple thermal dimensional approach for the Selective Laser Melting (SLM) process. By identifying two important dimensionless variables, i.e., the ratio of dwell time and the normalized enthalpy, an adequate monitoring of the temperature distribution in the sample became possible. The melt pool width, length, and depth totally define these parameters; consequently, an adequate interpolation for the melt pool characteristics calculated in the spreadsheet model became possible. Similarly, Mugwagwa, in [142], analyzed the process parameters effect on the residual stresses, distortions, and porosity magnitudes in SLM. In [143], Du performed an accurate study on the pore formation mechanism in the Laser Power Bed Fusion process. Wang, in [65], identified four dimensionless variables (the melting and the vaporization efficiency, the welding parameter, and the track size parameter) based on dimensional analysis of the SLM process, which characterize the thermo-dynamical problems of this process.

Starting from the 3D printing difficulties and complexity, Simmons performed a useful dimensional analysis in [42]. It was proposed for the metal 3D printing, and universal as well as simply scaling laws for keyhole stability and porosity. The proposed scaling laws assure process optimization and defect elimination during printing, as well as a quantitative predictive framework. For the Laser Powder Bed Fusion process, a topological depression, named keyhole, appears frequently, which is difficult to predict and to understand. Its geometry influences the energy coupling mechanisms of the high-power laser with the material; thus, it produces unlikely melt pool dynamics, as well as solidification defects. It also can contribute to significant process instability, as well as structural defects, namely: porosity, spattering, balling effect, and unusual micro-structural phases. Their high-accuracy investigations with high-energy X-ray imaging in laser melting of bare plate, powder bed, and powder flow gave significant results.

In the case of the laser melting of austenitic stainless steel, based on in situ X-ray analysis, Miyagi deeply analyzed the effect of the process conditions on the keyhole behavior in [27]. Based on meticulous analysis, it was stated that the involved laser’s parameters significantly influence the keyhole formation and its parameters, such as keyhole depth and width, as well as the decrease of the keyhole depth together with the increasing of the laser power. In addition, the influence of the existence of shielding gas on the keyhole depth was also established. The diminishing of the laser power and the quality of the laser beam have significant influence on this effect due to the interaction between the laser beam and metal vapor. In the case of increasing of the laser transverse speed with respect to the keyhole forming speed, it was observed that a decrease of the keyhole inclination was related to an increase of its width as well as its opening. By increasing the defocus distance, a decreasing of the keyhole inclination was observed, specifically an increase of keyhole depth. Taking into consideration the above-mentioned process parameters, some useful dimensionless variables were proposed in order to improve the laser melting process results.

In [23,30], Krutis described a useful implementation of hybrid technologies on the aluminum casting topological optimization. With optical roughness measurement, they compared the surface qualities of the classical wax model versus the AM’s offered polymer part of polymethyl methacrylate (PMMA) using the binder jetting method, with PolyPor B used as a binder; the latter was determined to be much better. In addition, this polymer part significantly diminishes the thermal expansion, as was also analyzed with dimensional analysis. In the case of special alloys, in order to eliminate several manufacturing defects, the authors intended to propose some additional heat treatment methods, validated by rigorous experiments. For the study, in order to obtain an acceptable final surface, the model was treated using wax infiltration. Their further studies will be targeted on the evaluation of dimensional accuracy, surface quality, and internal defects in the manufactured metal casting, as well as some efficient heat treatments.

Similar useful research, including dimensional analysis, was performed by Kumar [25], providing evidence for the thermal treatment’s significance. The author offers useful information on the significance of post-AM double aging heat treatment (HT) of alloy IN718 (Inconel 718) obtained through a laser-based powder bed fusion process (L-PBF). The first, as-built samples were subjected for 1 hour to solution annealing at 980 °C, and later cooled in air. The L-PBF sample was subjected for 8 hours to double aging at 720 °C, followed by 2 h furnace cooling to 620 °C. Based on this heat treatment, were obtained improving of the manufacturing defects (pores and voids, micro-structural changes, and micro-hardness), confirmed by Micro-Computer Tomography examination. In addition, their hardness was increased with 35%. A rigorous study of the thermal loading effect was performed by dimensional analysis. A 3.084% volumetric shrinkage was observed at micron-scale due to the applied heat treatment.

It is well-known fact that the process parameters in AM technologies have a significant influence on the mechanical characteristics/parameters of the final product.

In order to improve these mechanical characteristics, Rivet, in [108], performed a useful dimensional analysis for a proposed three-level (cover, contour, and inner part) modelling, considered to be manufactured from three different materials, based on the deduced ML. The cover and contour zones required uni-axial tensile tests for their characterization, while the computational homogenization method was needed for the inner zones. By means of accurate bending tests, as well as corresponding computer simulations, the model was validated. Then, by applying the model law offered by the dimensional analysis, a useful correlation was established between the raw and 3D-printed materials characterizations, that is, their mechanical properties. In order to analyze the inter-layer adhesion, some Polycarbonate Acrylonitrile Butadiene Styrene (ABS/PC) samples, having well-known poor adhesion strength, were subjected to accurate tests. The number of demanded testing configurations were diminished by 2/3 through this new approach, which provides significant cost savings in obtaining a final high-competitive product.

Butt, in [4], compared two polymers (ABS and PLA) with two metal-infused thermoplastics (copper-enhanced PLA and aluminum-enhanced acrylonitrile styrene acrylate) through experimental investigations. The goal was to combine the advantages of the classical FFF method with the better mechanical properties of the metal-infused thermoplastics. Based on an accurate dimensional analysis, they evaluated the post-processing (i.e., annealing) effect on the mechanical properties. The obtained results were very promising in obtaining high-competitive final products.

In [14], Boyle et al. proposes a new bench-top powder melt extrusion 3D printer head for directly printing from powder-based materials rather than filament. Their experimental investigations, assisted by a dimensional analysis, offer a promising direction for improving the actual 3D printing systems.

A large number of mathematical modelling approaches have been synthesized in [21,28,30,32,41].

Because the present contribution focuses strictly on the involvement of dimensional methods in improving AM methods, these mathematical modelling results were not considered here.

The authors of this contribution have applied the advantages of MDA in different engineering fields over the last 20 years [144,145,146,147,148,149], starting from thermal problems and scaling up to structural engineering displacement forecasting. In recent years, their researches have been focused on the improvement of AM technologies by means of MDA [150,151,152,153,154,155,156,157,158].

In the next section, their own results are briefly analyzed, applying the advantages of MDA.

4. Modern Dimensional Analysis Involved in Additive Manufacturing

First, let us summarize the main steps of MDA, illustrated by the below-presented results:

• all the variables, together with their dimensions, that can influence the phenomena to a certain extent are selected;
• by taking into consideration the experimental requirement of as simple, repeatable, and less-expensive model as possible, the independent variables are selected; their dimensional exponents constitute the so-called Matrix A, a non-singular square one, i.e., $\det \left|A\right|\ne 0$;
• the rest of the variables (the dependent ones) constitute Matrix B, without any requirement; from matrix B, a number of variables can be neglected at any time in order to model a simpler case;
• completing these matrices with matrix $C=-{\left(A^{-1}\cdot B\right)}^T$ and an adequate unit matrix $D\equiv I_{n\mathrm{x}n}$ results in the so-called Dimensional Set (Table 1);

  Table 1. The Dimensional Set [94,95].

  Rows correspond to the remaining primary $k$ dimensions after defining matrix A	1.	B	A
  	2.
  	…
  	k.
  Rows correspond to n columns (dependent variables) that had matrix B; the number of the rows is the same as that of the ${\pi }_j$, resulting in dimensionless quantities	1.	$D\equiv I_{n\mathrm{x}n}$	$C=-{\left(A^{-1}\cdot B\right)}^T$
  	2.
  	…
  	n.

  Table 1. The Dimensional Set [94,95].

  Rows correspond to the remaining primary $k$ dimensions after defining matrix A	1.	B	A
  	2.
  	…
  	k.
  Rows correspond to n columns (dependent variables) that had matrix B; the number of the rows is the same as that of the ${\pi }_j$, resulting in dimensionless quantities	1.	$D\equiv I_{n\mathrm{x}n}$	$C=-{\left(A^{-1}\cdot B\right)}^T$
  	2.
  	…
  	n.

• Each line $j$, of matrices C–D, will offer by a simple calculus one element of the requested complete ML, corresponding to one of the ${\pi }_j$ dimensionless variable.

For illustration, let us consider 14 variables, where $\left(H_1, \dots , H_8\right)$ are the dependent variables, whose dimensional exponents form matrix B, and $\left(H_9, \dots , H_{14}\right)$ are the independent ones, whose dimensional exponents represent Matrix A.

In order to find the ${\pi }_5$ fifth dimensionless variable from the Dimensional Set, corresponding in fact to the dependent variable $H_5$, and which offers the adequate fifth line of the requested ML, at the level of ${\pi }_5$ (its line) one has only $H_5$ with non-zero exponent, i.e., “1” from dependent variables, and $\left(H_9, \dots , H_{14}\right)$ independent variables have $\left(a_5, b_5, \dots , f_5\right)$ exponents (

Table 2. Example of Dimensional Set with fourteen elements [122].

	$H_1$	$H_2$	$H_3$	$H_4$	$H_5$	$H_6$	$H_7$	$H_8$	$H_9$	$H_{10}$	$H_{11}$	$H_{12}$	$H_{13}$	$H_{14}$
$h_1$
$h_2$
$h_3$		Matrix B								Matrix A
$h_4$
$h_5$
$h_6$
${\pi }_1$	1	0	0	0	0	0	0	0	$a_1$	$b_1$	$c_1$	$d_1$	$e_1$	$f_1$
${\pi }_2$	0	1	0	0	0	0	0	0
${\pi }_3$	0	0	1	0	0	0	0	0
${\pi }_4$	0	0	0	1	0	0	0	0
${\pi }_5$	0	0	0	0	1	0	0	0	$a_5$	$b_5$	$c_5$	$d_5$	$e_5$	$f_5$
${\pi }_6$	0	0	0	0	0	1	0	0
${\pi }_7$	0	0	0	0	0	0	1	0
${\pi }_8$	0	0	0	0	0	0	0	1	$a_8$	$b_8$	$c_8$	$d_8$	$e_8$	$f_8$

).

Consequently, based on the unique protocol from Szirtes [94,95], the corresponding relation of ${\pi }_5$ will be:

$${\pi }_5={\left(H_5\right)}^1\cdot {\left(H_9\right)}^{a_5}\cdot {\left(H_{10}\right)}^{b_5}\cdot {\left(H_{11}\right)}^{c_5}\cdot {\left(H_{12}\right)}^{d_5}\cdot {\left(H_{13}\right)}^{e_5}\cdot {\left(H_{14}\right)}^{f_5}.$$

(1)

By equating to unity, and expressing the requested $H_5$ dependent variable, results in:

$$\begin{array}{l}{\pi }_5={\left(H_5\right)}^1\cdot {\left(H_9\right)}^{a_5}\cdot {\left(H_{10}\right)}^{b_5}\cdot {\left(H_{11}\right)}^{c_5}\cdot {\left(H_{12}\right)}^{d_5}\cdot {\left(H_{13}\right)}^{e_5}\cdot {\left(H_{14}\right)}^{f_5}=1 \Rightarrow \\ \Rightarrow H_5={\displaystyle \frac{1}{{\left(H_9\right)}^{a_5}\cdot {\left(H_{10}\right)}^{b_5}\cdot {\left(H_{11}\right)}^{c_5}\cdot {\left(H_{12}\right)}^{d_5}\cdot {\left(H_{13}\right)}^{e_5}\cdot {\left(H_{14}\right)}^{f_5}}} .\end{array}$$

(2)

Subsequently, replacing the $\left(H_5, H_9, \dots , H_{14}\right)$ involved variables with the related scale factors $\left(S_{H_n}\right)$, ultimately results in the desired expression (as an ordinary fraction) of the fifth element of the ML.

Taking into consideration the fact that some of the exponents $\left(a_5, b_5, \dots , f_5\right)$ are positive, others are negative, and some can be zero, so Equation (2) will be an ordinary fraction.

Useful remarks:

• One can observe that, for the requested ML, there are many complicated and sophisticated groupings of elements from the involved differential equations in order to obtain the required dimensionless variables and no requirement for deep connoisseurs in the analyzed phenomena;
• it must be emphasized that these elements of the ML do not represent actual physical laws, but only correlations between the variables related to the prototype and the model, which must be respected in everything;
• the unique protocol automatically eliminates the irrelevant variables (their columns in matrix C will contain only zeros);
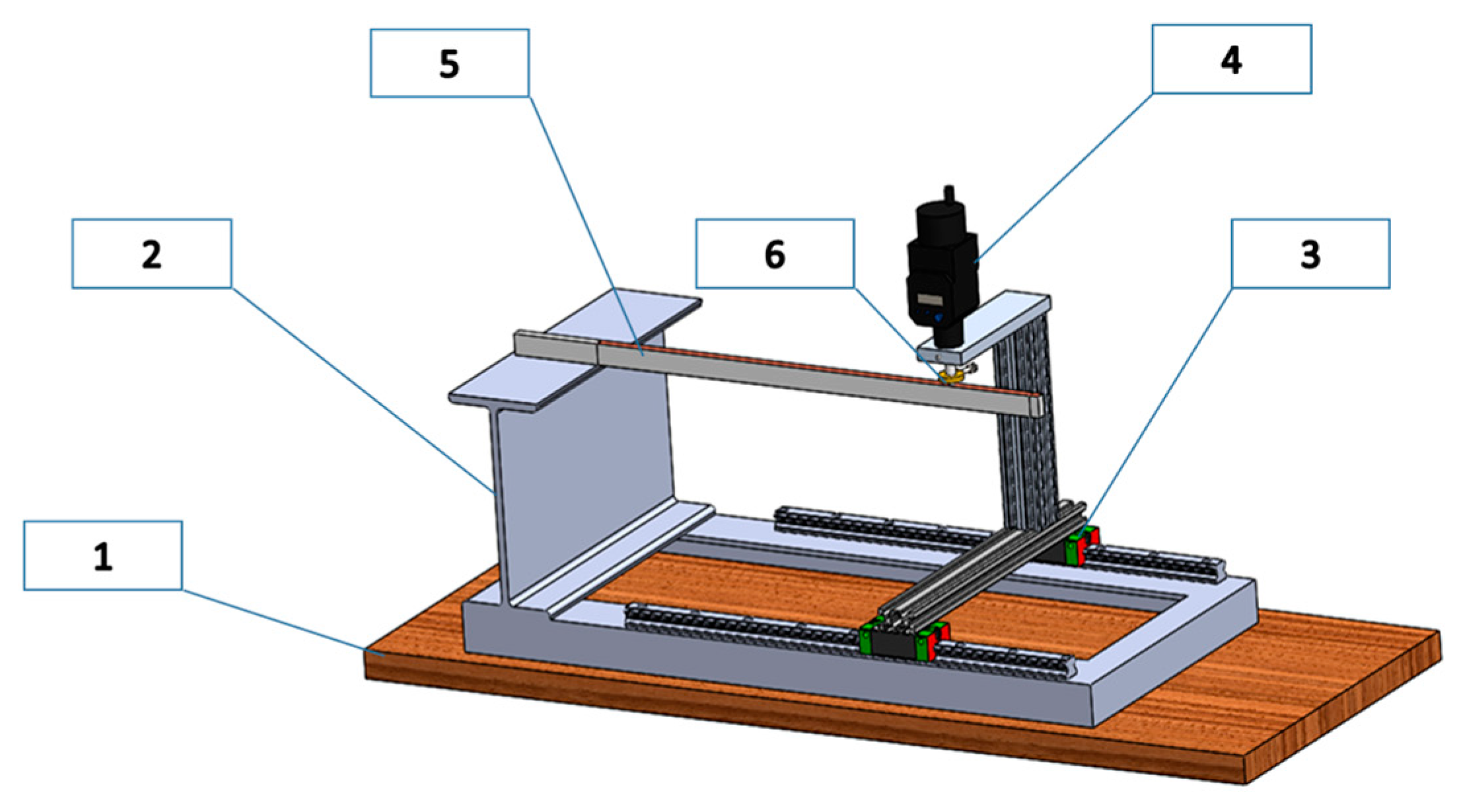
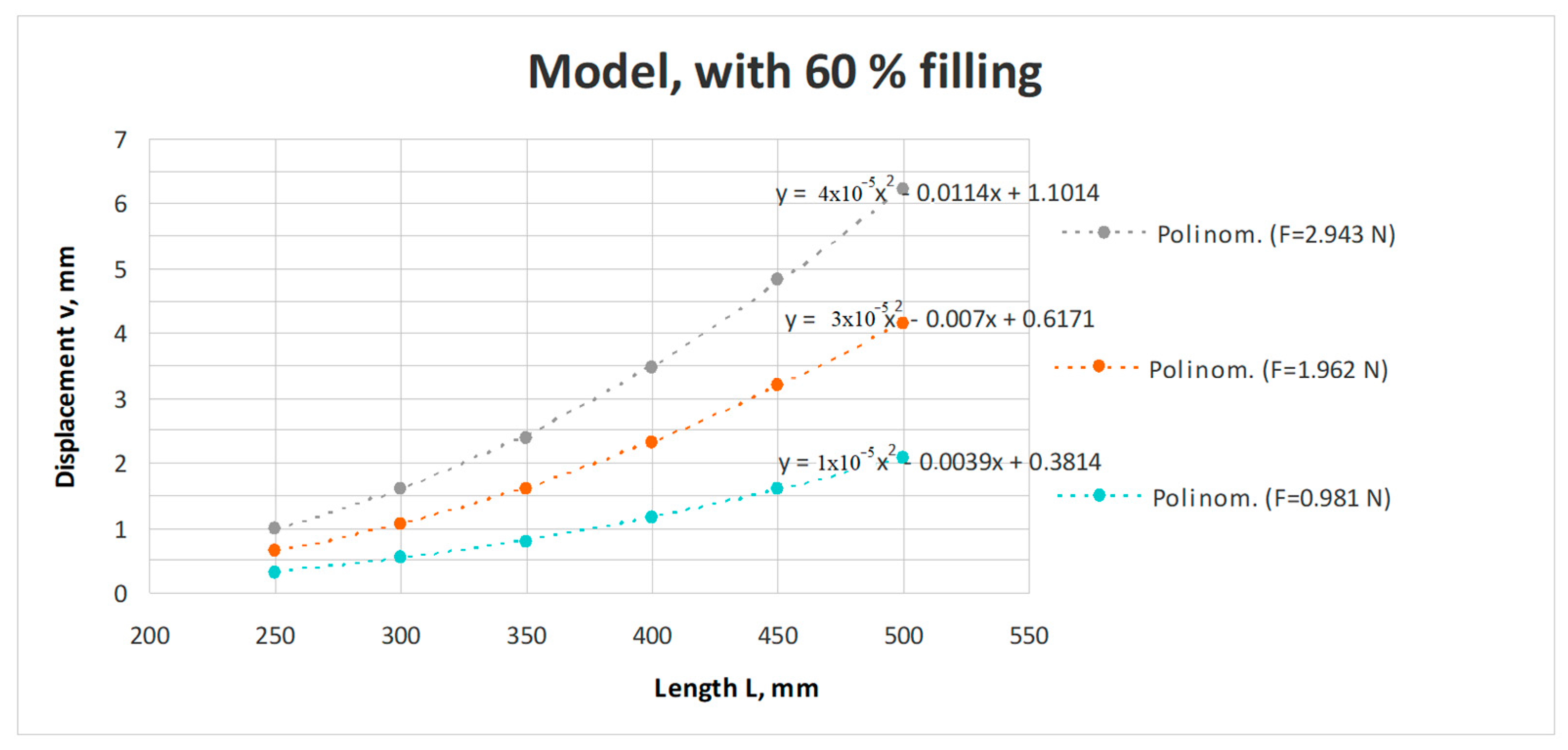
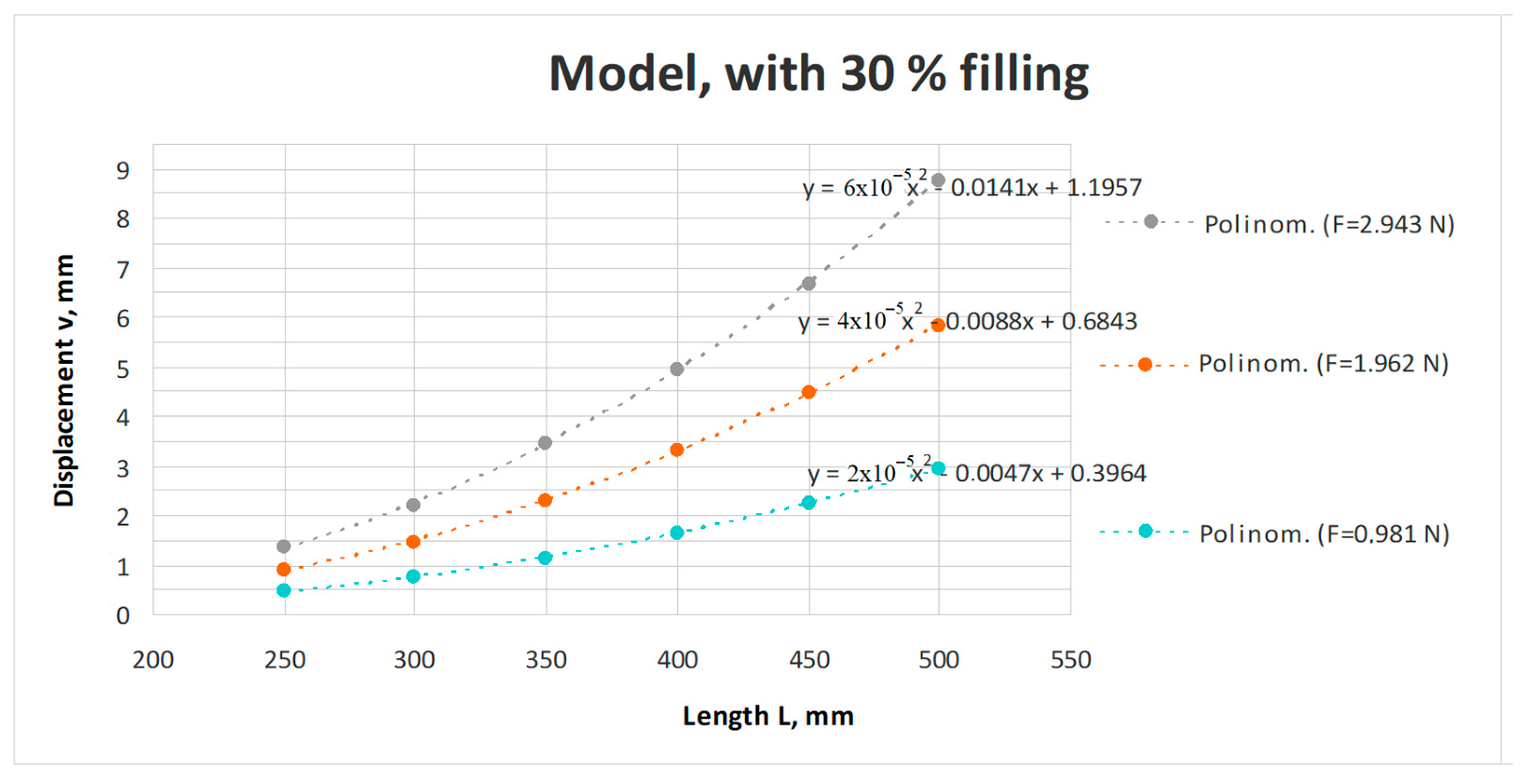
• based on experimental investigations (strictly on the attached model), it became possible to obtain the foresighted (anticipated) parameters for the prototype by means of the deduced ML;
• the deduced ML also represents a very flexible set of information, because one can ignore (eliminate) some elements, if we are looking for a simplified model–prototype correlation, without any changing in the expressions of the other elements of the ML; this also constitutes another distinctive advantage of the MDA, which is not proper to any of the above-mentioned dimensional methods;
• In addition, depending on the concrete conditions available, the strategy of the experimental investigations can be adapted to the new conditions, by reseating and reconsidering the sets of independent variables, relative to the dependent ones;
• The deduced ML for a given type of structural element (e.g., straight bars) can be extended without any difficulties to the real structure, taking into consideration their homologous points of time as well as loads for the demanded ${\eta }^{*}$ variable;

In this sense, in the initial Dimensional Set, deduced for the singular structural element, corresponding to one of the independent variable $\eta$ related to phenomenon from matrix A, one has to insert a new ${\eta }^{*}$ variable in matrix B; its corresponding ML element will be applied on each direction x, y, and z, resulting in the demanded ${\eta }_x^{*} ; {\eta }_y^{*} ; {\eta }_z^{*}$ variables of the real structure. They allow for obtaining the demanded variables’ variation at the level of these homologous points of the two structures (prototype, i.e., real structure, and model).

As an illustration of what was presented before, in this study the authors propose to develop, based on MDA, an adequate ML, suitable for different components, manufactured from usual plastic PLA (Polylactic Acid), involving a common Creality Ender-3 3D printer for the well-known Fused Deposition Modelling (FDM) Fused Filament Technology (FFT).

The main goal of the authors’ research was to obtain an optimal structure with maximal stiffness and at the same time having a minimal material consumption. This objective, reached by means a double-level ribbed cross-section, offered a good opportunity to involve the filling parameter in the ML as an independent variable. Consequently, it became possible to propose several useful filling modalities, both for the prototype and model.

Such a filling modality can be the well-known honeycomb structure, which assures a very good correlation between the strength and the consumed material; this modality results easily from the proposed cross-section. This independent variable of the filling degree assures not only a desired filling percentage of the nominal volume, but also a desired stiffness for the prototype, relative to the model.

In order to validate the deduced MLs, the authors conceived a simply structure, a simple cantilever beam with a reticular internal structure (Figure 1), having free length $L \left[\mathrm{m}\right]$, subjected to bending by mean a vertical concentrated force $F\left[\mathrm{N}\right]$ located at the free end of the beam, as shown in Figure 2. All dimensions are considered in $\left[\mathrm{m}\right]$. The dimensions $a\left[\mathrm{m}\right], b\left[\mathrm{m}\right], L\left[\mathrm{m}\right]$, the reference system $xGyz$, and the applied force $F\left[\mathrm{N}\right]$ are provided. Taking into account the very low rigidity of these bars, the case a < b was considered.

The possible influencing variables of the ${\mathrm{v}}_1 \left[\mathrm{m}\right]$ magnitude of the prototype’s vertical displacement at its free end are:

–

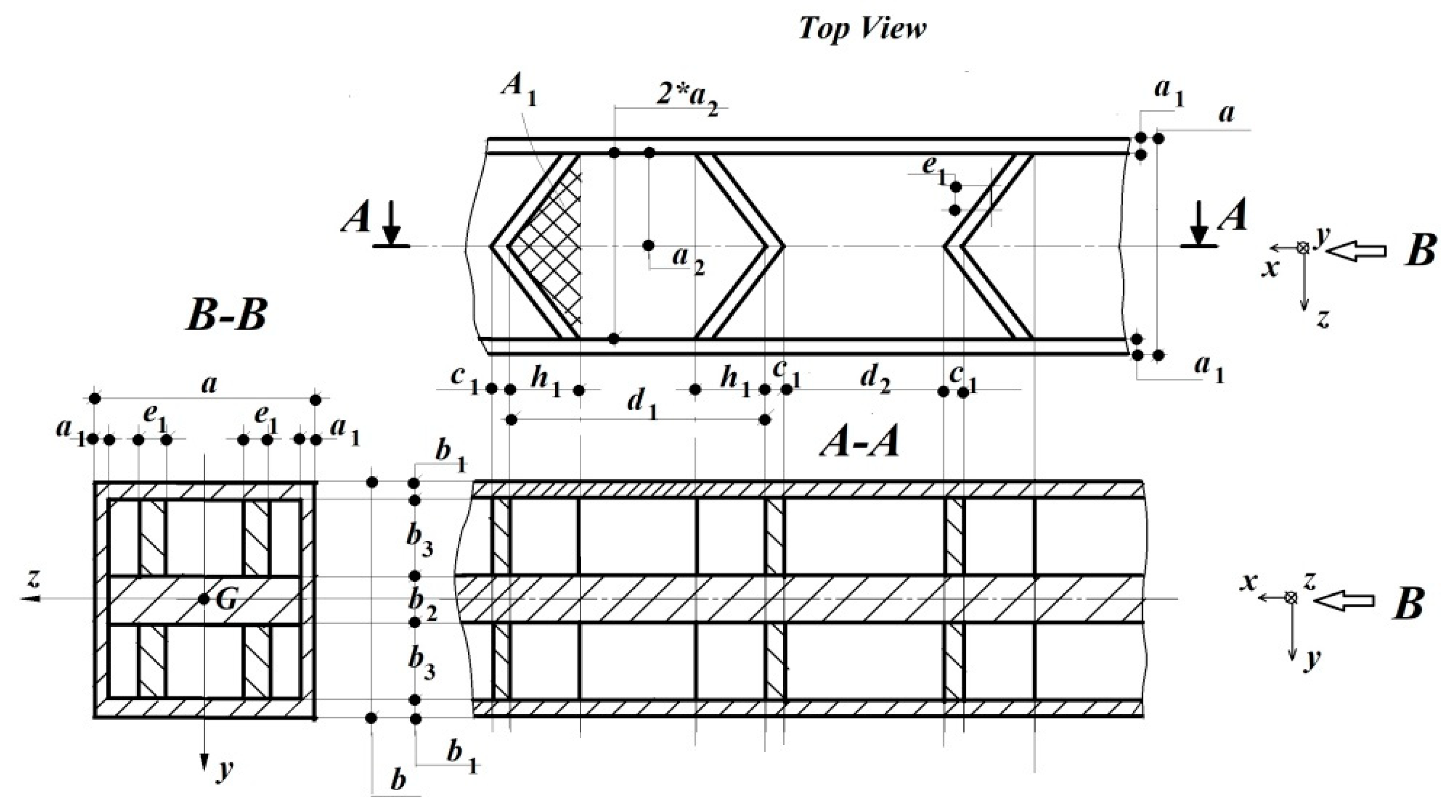
the beam’s dimensions $a \left[\mathrm{m}\right], b\left[\mathrm{m}\right], L\left[\mathrm{m}\right]$, as well as the $A_1\left[{\mathrm{m}}^2\right]$ area defined by the ribs;

–

the applied $F \left[\mathrm{N}\right]$ force;

–

the $E \left[\mathrm{N}/{\mathrm{m}}^2\right]$ Young modulus, which for PLA is $E=2.31\cdot {10}^9 {\displaystyle \frac{\mathrm{N}}{{\mathrm{m}}^2}}$;

–

the $V_{util} \left[{\mathrm{m}}^3\right]$ useful volume of the beam, that is related to the filling degree.

In addition, these variables, by their combination, as well as by their merging, offer several useful modalities for obtaining a more flexible model, associated to the given prototype, such as:

–

the $I_z \left[{\mathrm{m}}^4\right]$ second order moment of inertia, instead of the given $a \left[\mathrm{m}\right], b\left[\mathrm{m}\right]$ cross-sectional dimensions;

–

by fusion of the initial variables, a more flexible model can be obtained, e.g., instead of E and I_z, one can use their product $E\cdot I_z \left[\mathrm{N}\cdot {\mathrm{m}}^2\right]$, that is, the stiffness module; if necessary, the density $\rho \left[{\displaystyle \frac{\mathrm{kg}}{{\mathrm{m}}^3}}={\displaystyle \frac{\mathrm{N}\cdot s^2}{\mathrm{m}}}\cdot {\displaystyle \frac{1}{{\mathrm{m}}^3}}={\displaystyle \frac{\mathrm{N}\cdot s^2}{{\mathrm{m}}^4}}\right]$ or specific gravity $\gamma \left[{\displaystyle \frac{\mathrm{N}}{{\mathrm{m}}^3}}\right]$ can also be involved.

• On the other hand, in order to increase the number of dimensions and thus reduce the number of the ${\pi }_j$ dimensionless variables, the so-called dimension splitting can be applied, e.g., instead of length “m”, its components along $x, y, z$ (m_x, m_y, and m_z) can be used.
• By choosing $E \left[\mathrm{N}/{\mathrm{m}}^2\right]$ and $I_z \left[{\mathrm{m}}^4\right]$ as independent variables, there is evidence that that the remaining parameters $a^{**} \left[\mathrm{m}\right] \iff a_1, a_2, b_1, b_2, c_1, c_2, c_3$, can be divided into others, such as $a^{*} \left[\mathrm{m}\right] \iff a_1, a_2$; $b^{*} \left[\mathrm{m}\right] \iff b_1, b_2, b_3$; $c^{*} \left[\mathrm{m}\right] \iff c_1, c_2, c_3$ without affecting the final ML;
• In addition, for a correct merging of the initial sizes $a \left[\mathrm{m}\right], b\left[\mathrm{m}\right]$ in $I_z \left[{\mathrm{m}}^4\right]$, they (that is, $a$ and $b$) can no longer appear in other elements, as they are omitted in $a^{*}, b^{*}, c^{*}$;
• When we abstract from these $a^{*}, b^{*}, c^{*}$ internal dimensions, we obtain the solid cross-sectional beam; in this sense, we simply neglect these internal dimensions together with their corresponding elements of the deduced ML.

For the proposed experimental investigations on both model and prototype, two types of cross-sections were manufactured, having $a^{\prime }=18 \mathrm{mm}$; $b^{\prime }=30 \mathrm{mm}$; $a^{″}=10 \mathrm{mm}$; $b^{″}=20 \mathrm{mm}$, with lengths $L^{\prime }=768 \mathrm{mm}$; $L^{″}=590 \mathrm{mm}$, and with three different filling degrees (10%, 30% and 60%).

The protocol of the authors’ experimental investigations foresaw combining these six beams, considering even prototypes or models; the same high-accurate measurements were performed on all of them.

Taking into consideration the deduced MLs, where for the second analyzed version there are considered as independent variables $b$ and $L$, the authors a priori accepted such cross-sectional dimensions, which also fulfil the corresponding ML. The authors performed searching and repeated experimental investigation on these aforementioned beams with their own testing bench [120] (shown in the above-mentioned Figure 2).

This testing bench has the main advantage of allowing high-accuracy displacement measurements thanks to its electro-magnetic control of the sensor’s contact with the tested, non-metallic, cantilever beam (PLA). In order to obtain this, the authors glued a very thin copper band on the tested beam along the side where the sensor’s head touched the tested beam. When the sensor lightly touched this thin copper strip, the signal of the displacement sensor was recorded, without exerting a significant force on the cantilever beam subjected to test; consequently, the measurements results were not influenced by the sensor touching the tested beam.

The initially accepted protocol envisaged decreasing the length of the beam in steps of $50 \mathrm{mm}$, from the maximum value to the minimum one, the latter limited by the condition of the beam by the strength of the materials, i.e., $L_j \ge 10\cdot \max (a_j, b_j)$.

The tests were initiated from the maximal lengths of the beams in order not to include the pre-stressed areas from the realization of the fixed end (of the cantilever zone) of the previous beam.

When the ML required an intermediate length, interpolation was conducted, taking into account the exponential curve fitting laws mentioned for each experimentally obtained curve.

Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show these tests results, corresponding to the applied three forces $F_1=0.981 \mathrm{N} ; F_2=1.962 \mathrm{N} ; F_3=2.943 \mathrm{N} ,$ together with the adequate exponential curve fitting relations.

Based on these tests results, we analyzed three different MLs, together with their advantages as well as limitations. The first proposed and validated Dimensional Set was the following, having as independent variables the $\gamma$ specific gravity (“gamma”) and $E\cdot I_z$ bending stiffness (

Table 3. The first Dimensional Set.

				B				A
	v	a*	b*	c*	A1	F	L	Gamma	E*Iz
m	1	1	1	1	2	0	1	−3	2
N	0	0	0	0	0	1	0	1	1
π1	1	0	0	0	0	0	0	0.2	−0.2
π2	0	1	0	0	0	0	0	0.2	−0.2
π3	0	0	1	0	0	0	0	0.2	−0.2
π4	0	0	0	1	0	0	0	0.2	−0.2
π5	0	0	0	0	1	0	0	0.4	−0.4
π6	0	0	0	0	0	1	0	−0.4	−0.6
π7	0	0	0	0	0	0	1	0.2	−0.2

).

The above-mentioned matrixes A (blue), B (yellow), C (green), and D (pink) can be easily identified.

Based on the mentioned unique protocol of Szirtes, the demanded elements of ML were obtained as follows:

$$\mathrm{v}\cdot {\gamma }^{0.2}\cdot {\left(E\cdot I_z\right)}^{-0.2}=1 \Rightarrow S_{\mathrm{v}}={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.2}={\displaystyle \frac{{\mathrm{v}}_2}{{\mathrm{v}}_1}},$$

(3)

$$a*\cdot {\gamma }^{0.2}\cdot {\left(E\cdot I_z\right)}^{-0.2}=1 \Rightarrow S_{a*}={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.2}={\displaystyle \frac{a_2^{*}}{a_1^{*}}},$$

(4)

$$b*\cdot {\gamma }^{0.2}\cdot {\left(E\cdot I_z\right)}^{-0.2}=1 \Rightarrow S_{b*}={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.2}={\displaystyle \frac{b_2^{*}}{b_1^{*}}},$$

(5)

$$c*\cdot {\gamma }^{0.2}\cdot {\left(E\cdot I_z\right)}^{-0.2}=1 \Rightarrow S_{c*}={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.2}={\displaystyle \frac{c_2^{*}}{c_1^{*}}},$$

(6)

$$A_1\cdot {\gamma }^{0.4}\cdot {\left(E\cdot I_z\right)}^{-0.4}=1 \Rightarrow S_v={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.4}={\displaystyle \frac{A_{1,2}}{A_{1,1}}},$$

(7)

$$F\cdot {\gamma }^{-0.4}\cdot {\left(E\cdot I_z\right)}^{-0.6}=1 \Rightarrow S_F={\left(S_{\gamma }\right)}^{0.4}\cdot {\left(S_{E{I}_z}\right)}^{0.6}={\displaystyle \frac{F_2}{F_1}},$$

(8)

$$L\cdot {\gamma }^{0.2}\cdot {\left(E\cdot I_z\right)}^{-0.2}=1 \Rightarrow S_L={\left({\displaystyle \frac{S_{E{I}_z}}{S_{\gamma }}}\right)}^{0.2}={\displaystyle \frac{L_2}{L_1}},$$

(9)

By a priori selection, the prototype had:

$60\%$ filling percentage, ${\mathrm{L}}_1=0.5 \mathrm{m}$, ${\mathrm{b}}_1=0.03 \mathrm{m}$, ${\mathrm{a}}_1=0.018 \mathrm{m}$, ${\mathrm{F}}_1=2.943 \mathrm{N}$, ${\mathrm{E}}_1\cdot {\mathrm{I}}_{\mathrm{z},1}=116.5 \mathrm{N}\cdot {\mathrm{m}}^2$, ${\mathrm{\gamma }}_1=7806 \mathrm{N}/{\mathrm{m}}^3$.

In the same manner, the corresponding model had:

$30\%$ filling percentage, $E_2\cdot I_{z,2}=14.0 \mathrm{N}\cdot {\mathrm{m}}^2$; ${\gamma }_2=5986 \mathrm{N}/{\mathrm{m}}^3$.

Resulting:

$$S_{E\cdot I_z}={\displaystyle \frac{E_2\cdot I_{z,2}}{E_1\cdot I_{z,1}}}=0.12018 \mathrm{and} S_{\gamma }={\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}=0.76682.$$

From the mentioned ML result:

$$\begin{gathered} {\mathrm{S}}_{\mathrm{L}}={\displaystyle \frac{{\mathrm{L}}_2}{{\mathrm{L}}_1}}=0.6903 \Rightarrow {\mathrm{L}}_2={\mathrm{L}}_1\cdot {\mathrm{S}}_{\mathrm{L}}=0.345 \mathrm{m}; \\ {\mathrm{S}}_{\mathrm{F}}={\displaystyle \frac{{\mathrm{F}}_2}{{\mathrm{F}}_1}}=0.25222 \Rightarrow {\mathrm{F}}_2={\mathrm{F}}_1\cdot {\mathrm{S}}_{\mathrm{F}}=0.7423 \mathrm{N}; \\ {\mathrm{S}}_{\mathrm{v}}={\displaystyle \frac{{\mathrm{v}}_2}{{\mathrm{v}}_1}}=0.69029. \end{gathered}$$

By high-accuracy measurements on model, ${\mathrm{v}}_{2,meas}=0.97 \mathrm{mm}$ was obtained, resulting from ML for the prototype the predictable displacement in: ${\mathrm{v}}_{1MDA}={\displaystyle \frac{{\mathrm{v}}_{2,meas}}{{\mathrm{S}}_{\mathrm{v}}}}=1.405 \mathrm{mm}.$

In order to validate the ML, experimental investigations were similarly performed on the prototype, obtaining ${\mathrm{v}}_{1,meas}=1.42 \mathrm{mm}$, a deviation of $1.056 \%$.

In this case, by adapting $E\cdot I_z$ as independent variable, there is no restriction in choosing different materials for the prototype and model, as well as different cross-sectional shapes.

In addition, by means of $\gamma$, one can choose different filling degrees for prototype and model, which was happened in this case.

The second proposed and validated Dimensional Set, detailed in

Table 4. The second Dimensional Set.

	B						A
	v	a*	b*	c*	A1	a	b	L	F	E
mx	0	0	0	1	1	0	0	1	0	0
my	1	0	1	0	0	0	1	0	0	−1
mz	0	1	0	0	1	1	0	0	0	−1
N	0	0	0	0	0	0	0	0	1	1
π1	1	0	0	0	0	0	−1	0	0	0
π2	0	1	0	0	0	0	1	0	−1	1
π3	0	0	1	0	0	0	−1	0	0	0
π4	0	0	0	1	0	0	0	−1	0	0
π5	0	0	0	0	1	0	1	−1	−1	1
π6	0	0	0	0	0	1	1	0	−1	1

, had as independent variables $\left(b, L, F, E\right)$, with $a$ becoming a dependent variable.

In similar manner, the matrixes A, B, C, and D can be identified.

$$\mathrm{v}\cdot b^{-1}=1 \Rightarrow S_{\mathrm{v}}=S_b={\displaystyle \frac{b_2}{b_1}},$$

(10)

$$a*\cdot b\cdot F^{-1}\cdot E=1 \Rightarrow S_{a*}={\displaystyle \frac{S_F}{S_b\cdot S_E}}={\displaystyle \frac{a_2^{*}}{a_1^{*}}},$$

(11)

$$b*\cdot b^{-1}=1 \Rightarrow S_{b*}=S_b={\displaystyle \frac{b_2^{*}}{b_1^{*}}},$$

(12)

$$c*\cdot L^{-1}=1 \Rightarrow S_{c*}=S_L={\displaystyle \frac{c_2^{*}}{c_1^{*}}},$$

(13)

$$A_1\cdot b\cdot L^{-1}\cdot F^{-1}\cdot E=1 \Rightarrow S_{A_1}={\displaystyle \frac{S_L\cdot S_F}{S_b\cdot S_E}}={\displaystyle \frac{A_{1,2}}{A_{1,1}}},$$

(14)

$$a\cdot b\cdot F^{-1}\cdot E=1 \Rightarrow S_a={\displaystyle \frac{S_F}{S_b\cdot S_E}}={\displaystyle \frac{a_2}{a_1}} .,$$

(15)

For the prototype, by a priori selection, one has: $60\%$ filling percentage, $b_1=0.03 \mathrm{m}$, $L_1=0.45 \mathrm{m}$, $F_1=1.962 \mathrm{N}$, $E_1=2.31\cdot {10}^9 {\displaystyle \frac{\mathrm{N}}{{\mathrm{m}}^2}} ,$ respectively $a_1=0.018 \mathrm{m}$.

The corresponding model, by a priori selection, has:

$30\%$ filling percentage, ${\mathrm{b}}_2=0.02 \mathrm{m}$, ${\mathrm{L}}_2=0.25 \mathrm{m}$, ${\mathrm{F}}_2=0.981 \mathrm{N}$, ${\mathrm{E}}_2={\mathrm{E}}_1=2.31\cdot {10}^9 {\displaystyle \frac{\mathrm{N}}{{\mathrm{m}}^2}} .$

By unitary calculi, $S_b=0.66667$; $S_L=0.55556$; $S_F=0.5$; and $S_a=0.75$ are obtained. By applying the correspondent element of ML, i.e., (15), we obtain $a_2=0.0135 \mathrm{m}$. Performing accurate measuring on the model, we obtain ${\mathrm{v}}_{2,meas}=0.49 \mathrm{mm}$, resulting from ML for the prototype the predictable displacement in: ${\mathrm{v}}_{1MDA}={\displaystyle \frac{{\mathrm{v}}_{2,meas}}{{\mathrm{S}}_{\mathrm{v}}}}=0.7417 \mathrm{mm}.$

In order to validate the ML, experimental investigations on the prototype were similarly performed, obtaining ${\mathrm{v}}_{1,meas}=0.73 \mathrm{mm}$, a deviation of $1.603 \%$.

In this case, the geometric similarity is compulsory, because one of the cross-sectional dimensions is a dependent variable. The single advantage of this type of Dimensional Set consists of the free choice of material, otherwise this option is not recommended.

In the third proposed and validated Dimensional Set, detailed in Table 5, $\left(L, E\cdot I_z\right)$ are the independent variables, with $F$ becoming a dependent variable, which can be easily modified for a certain model attached/assigned to the given prototype.

Table 5. The third Dimensional Set.

				B				A
	v	a*	b*	c*	A1	F	Vutil	L	E*Iz
m	1	1	1	1	2	0	3	1	2
N	0	0	0	0	0	1	0	0	1
π1	1	0	0	0	0	0	0	−1	0
π2	0	1	0	0	0	0	0	−1	0
π3	0	0	1	0	0	0	0	−1	0
π4	0	0	0	1	0	0	0	−1	0
π5	0	0	0	0	1	0	0	−2	0
π6	0	0	0	0	0	1	0	2	−1
π7	0	0	0	0	0	0	1	−3	0

Table 5. The third Dimensional Set.

				B				A
	v	a*	b*	c*	A1	F	Vutil	L	E*Iz
m	1	1	1	1	2	0	3	1	2
N	0	0	0	0	0	1	0	0	1
π1	1	0	0	0	0	0	0	−1	0
π2	0	1	0	0	0	0	0	−1	0
π3	0	0	1	0	0	0	0	−1	0
π4	0	0	0	1	0	0	0	−1	0
π5	0	0	0	0	1	0	0	−2	0
π6	0	0	0	0	0	1	0	2	−1
π7	0	0	0	0	0	0	1	−3	0

$$v\cdot L^{-1}=1 \Rightarrow S_v=S_L={\displaystyle \frac{v_2}{v_1}},$$

(16)

$$a*\cdot L^{-1}=1 \Rightarrow S_{a*}=S_L={\displaystyle \frac{a_2^{*}}{a_1^{*}}},$$

(17)

$$b*\cdot L^{-1}=1 \Rightarrow S_{b*}=S_L={\displaystyle \frac{b_2^{*}}{b_1^{*}}},$$

(18)

$$c*\cdot L^{-1}=1 \Rightarrow S_{c*}=S_L={\displaystyle \frac{c_2^{*}}{c_1^{*}}},$$

(19)

$$A_1\cdot L^{-2}=1 \Rightarrow S_{A_1}={\left(S_L\right)}^2={\displaystyle \frac{A_{1,2}}{A_{1,1}}},$$

(20)

$$F\cdot L^2\cdot {\left(E\cdot I_z\right)}^{-1}=1 \Rightarrow S_F={\displaystyle \frac{S_{E{I}_z}}{{\left(S_L\right)}^2}}={\displaystyle \frac{F_2}{F_1}},$$

(21)

$$V_{util}\cdot L^{-3}=1 \Rightarrow S_{V_{util}}={\left(S_L\right)}^3={\displaystyle \frac{V_{util,2}}{V_{util,1}}},$$

(22)

By a priori selection, the prototype had: $60\%$ filling percentage, $L_1=0.4$ m, $E_1\cdot I_{z,1}=112.62$ N.m², $F_1=2.943$ N.

In the same manner, by a priori selection, the corresponding model had:

$$10\%\mathrm{filling} \mathrm{percentage}, E_2\cdot I_{z,2}=11.09 \mathrm{N}\cdot {\mathrm{m}}^2.$$

Performing the adequate calculi results in:

$$S_{E\cdot I_z}={\displaystyle \frac{E_2\cdot I_{z,2}}{E_1\cdot I_{z,1}}}=0.0985, S_{\mathrm{v}}=S_L=0.625 \mathrm{and} S_F={\displaystyle \frac{F_2}{F_1}}=0.25214.$$

From (21), we obtain: $S_F={\displaystyle \frac{F_2}{F_1}}=0.2521 \Rightarrow F_2=F_1\cdot S_F=0.7421 \mathrm{N}$;

By high-accuracy measurements on the model, ${\mathrm{v}}_{2,meas}=0.47 \mathrm{mm}$ is obtained, resulting from ML for the prototype the predictable displacement in:

$${\mathrm{v}}_{1MDA}={\displaystyle \frac{{\mathrm{v}}_{2,meas}}{{\mathrm{S}}_{\mathrm{v}}}}=0.7519 \mathrm{mm}.$$

In order to validate the ML, experimental investigations on the prototype were similarly performed, obtaining ${\mathrm{v}}_{1,meas}=0.77 \mathrm{mm}$, a deviation of $2.351 \%$.

In this case, by adapting $E\cdot I_z$ as independent variable, there is no restriction in choosing different materials for the prototype and model, as well as different cross-sectional shapes.

In addition, by means of $L$, different lengths for the model can be chosen in order to find the most suitable experimental correlation with the prototype.

5. Conclusions

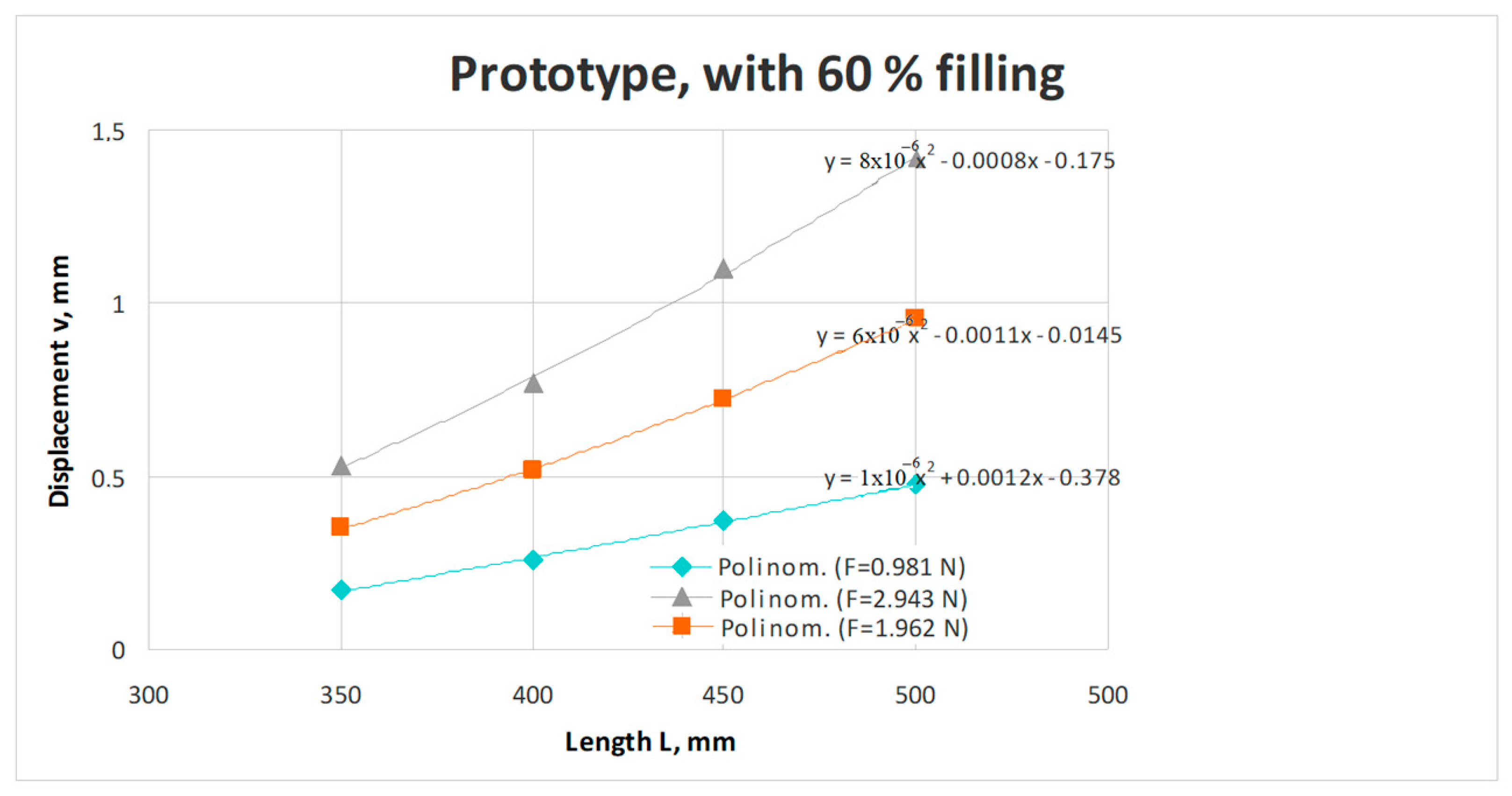
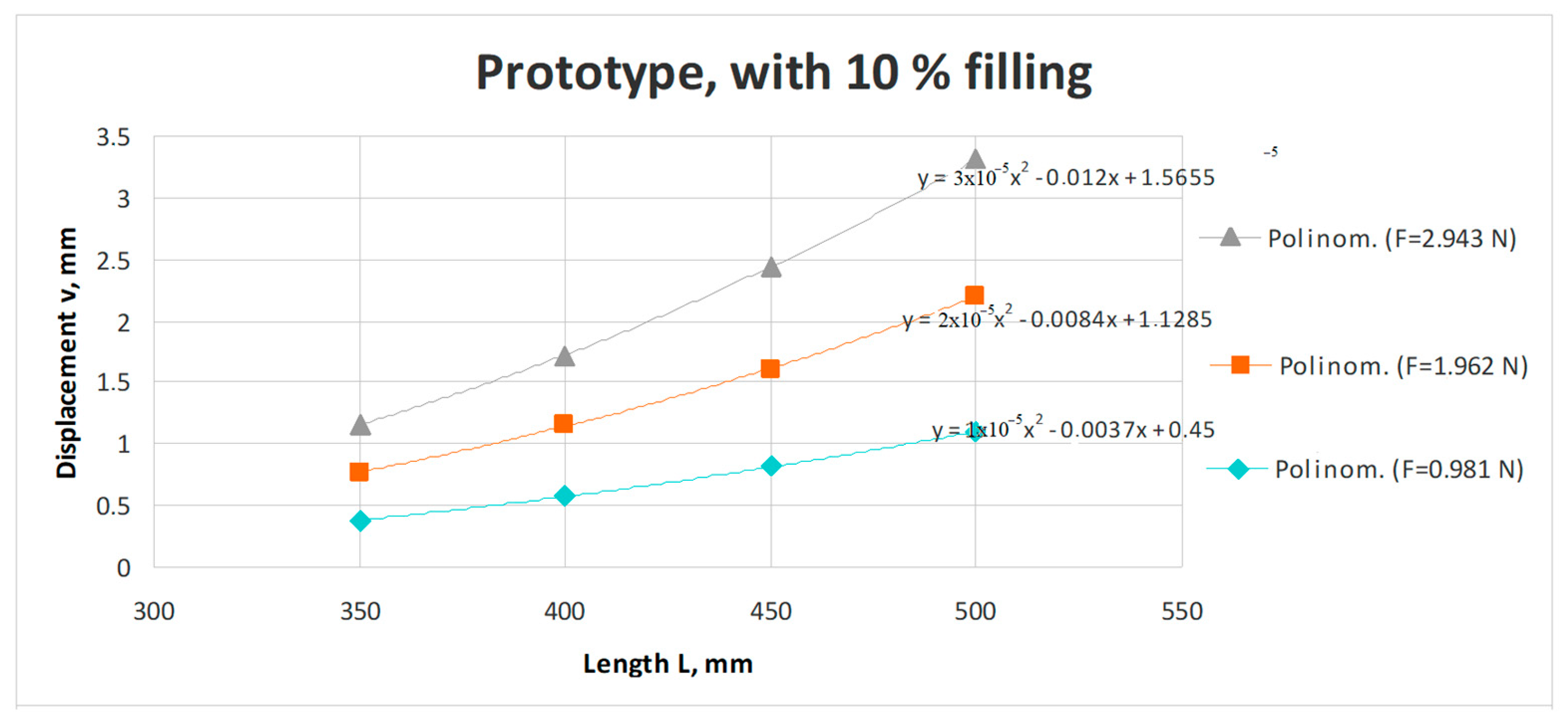
• The elaborated MLs, validated by meticulous experimental investigations, offer several useful correlations between the prototype’s (i.e., the final product) and the assigned reduced scale model’s geometrical parameters and mechanical behaviors;
• by performing experimental investigations on the assigned model, applying the ML, it was possible to predict the real-scale prototype’s response to the applied mechanical or thermal loading;
• the ML also assures the stiffness optimization of the final product by means of changing the geometry and orientation of the involved ribs, the filling percentage, and the usable material.
• one other kind of stiffness optimization is the well-known honeycomb cross-section, which can also be more easily modelled with the deduced MLs by substituting the involved new length variables instead of the used ones;
• all the above-analyzed MLs can be successfully applied both for solid cross-sectional beams manufactured from PLA, and metallic ones; metal beams have simpler and more flexible MLs, as verified in advance by the authors;
• The authors’ future goals consist of extending the research area on the optimization of mold-forms used in plastic material components fabrication, mainly for in demand spare parts.