Supervised Machine Learning Models for Mechanical Properties Prediction in Additively Manufactured Composites
Abstract
1. Introduction
1.1. Contributions
- A ML pipeline that estimates mechanical properties such as the strength and elasticity of AM composite materials reinforced with continuous fibers—carbon (CRTP), Kevlar (KvRTP), and fiberglass (FGRTP).
- A dataset was constructed from the peer-reviewed literature. It includes mechanical properties (elasticity and strength), materials for continuous fibers, and printing parameters. A robust analysis and the greater reliability of the ML models that have been tested enable the reproducibility and exploration of polymer-based AM technologies.
- In order to determine the most efficient ML models for predicting mechanical properties, this paper examines a variety of linear and nonlinear ML models. The performance analysis reveals their strengths and weaknesses when used within the AM context. As new algorithms are developed, they can be tested with the existing dataset. The modeling workflow used comprises k-fold cross-validation and Monte Carlo resampling, exploring different lightweight machine learning methods like Bayesian Ridge Regression (BAY), CatBoost Regression (CAT), Decision Tree Regression (DTR), k-nearest Neighbors (KNN), Lasso Regression (LAS), Random Forest Regression (RFR), Ridge Regression (RDG), and Support Vector Regression (SVR).
- The manuscript shows how decisive printing parameters are, such as deposition angles and fiber content, for the mechanical properties of Continuous Fiber Reinforced Polymer Matrix Compositess (CFRPCs). Therefore, the results can be used to optimize material properties without conducting extensive experimental campaigns. The identification of such parameters should lead to a more efficient design anddevelopment process.
1.2. Paper Organization
2. Technical Background
2.1. Models to Predict AM Composites’ Elasticity
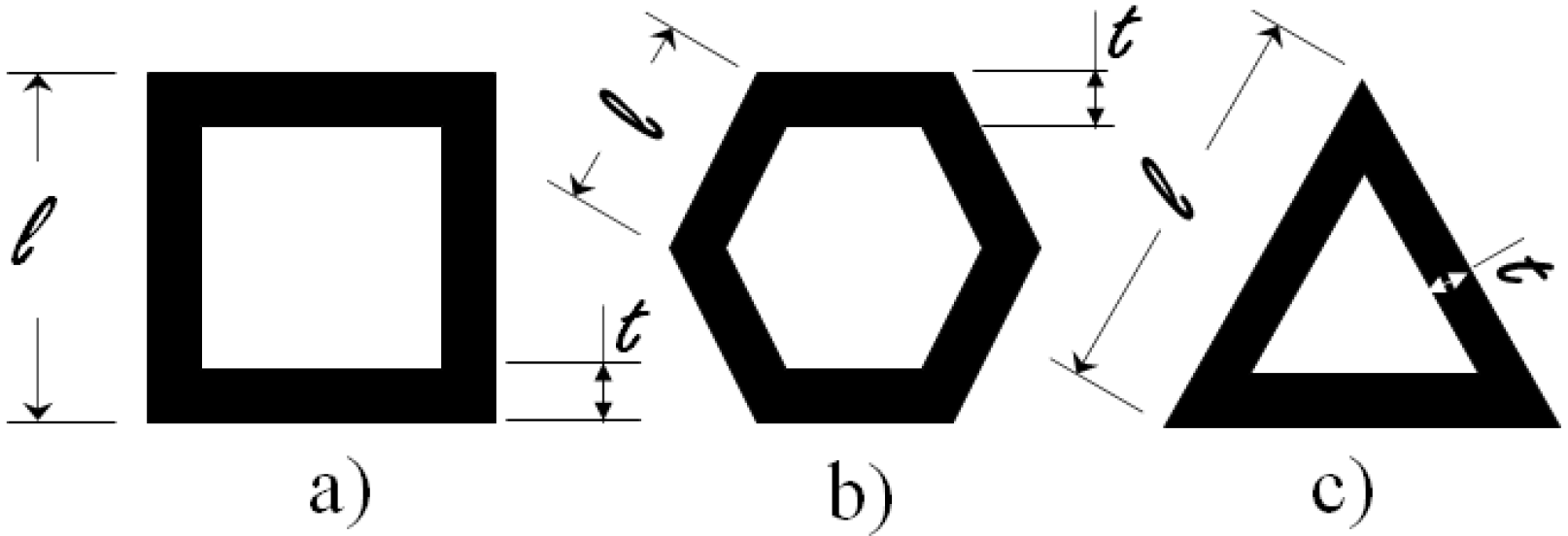
2.1.1. Square Lattice
2.1.2. Honeycomb or Hexagonal Lattice
2.1.3. Triangular Lattice
2.1.4. Solid Region
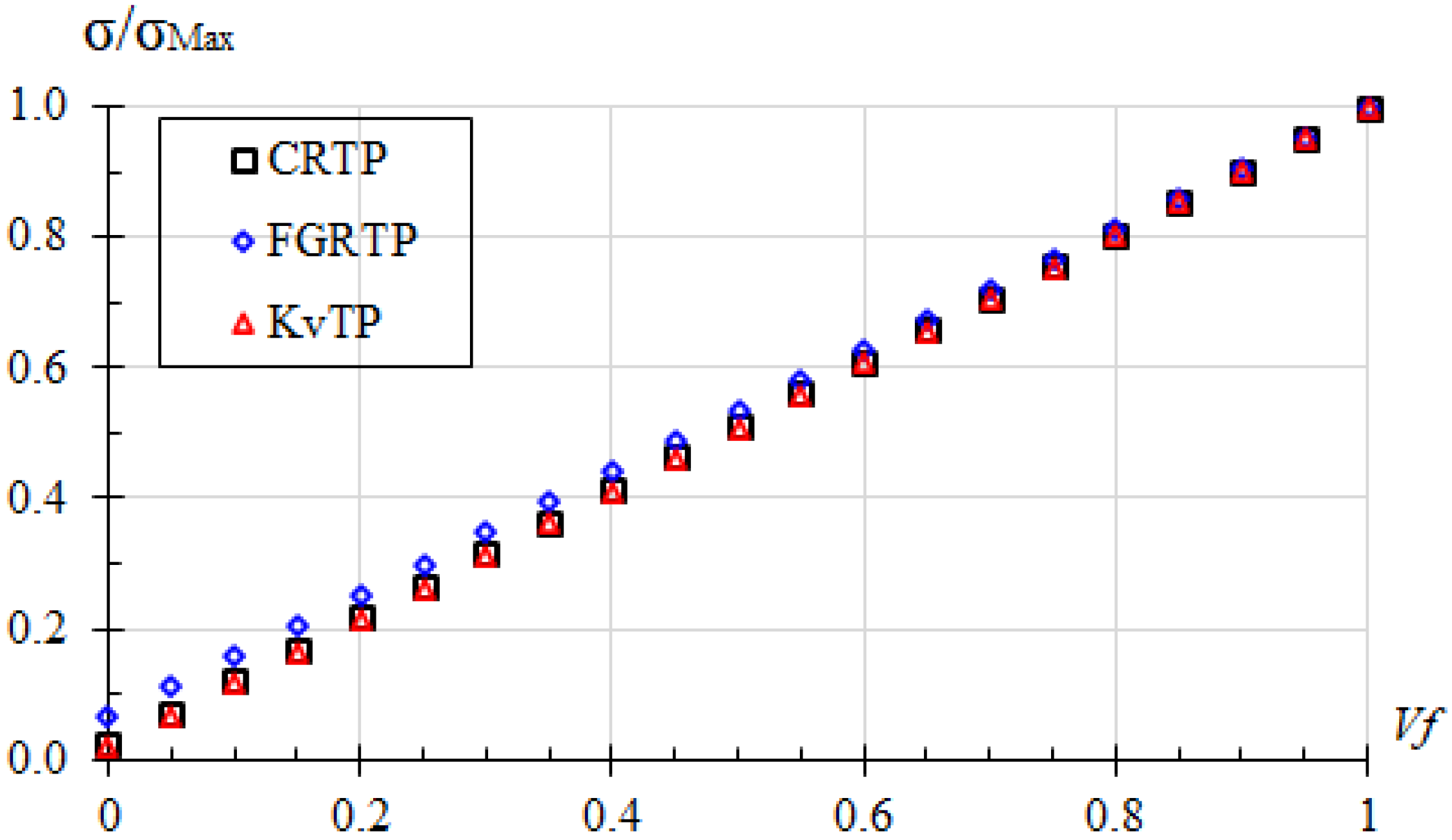
2.2. Models to Predict AM Composite Strength
2.3. Machine Learning Models
2.3.1. Linear Regression
2.3.2. CAT Boost Regression
2.3.3. K-Nearest Neighbors Regression
- Euclidean
- Manhattan
- Minkowski
3. Materials and Methods
3.1. Dataset
3.2. Machine Learning Pipeline
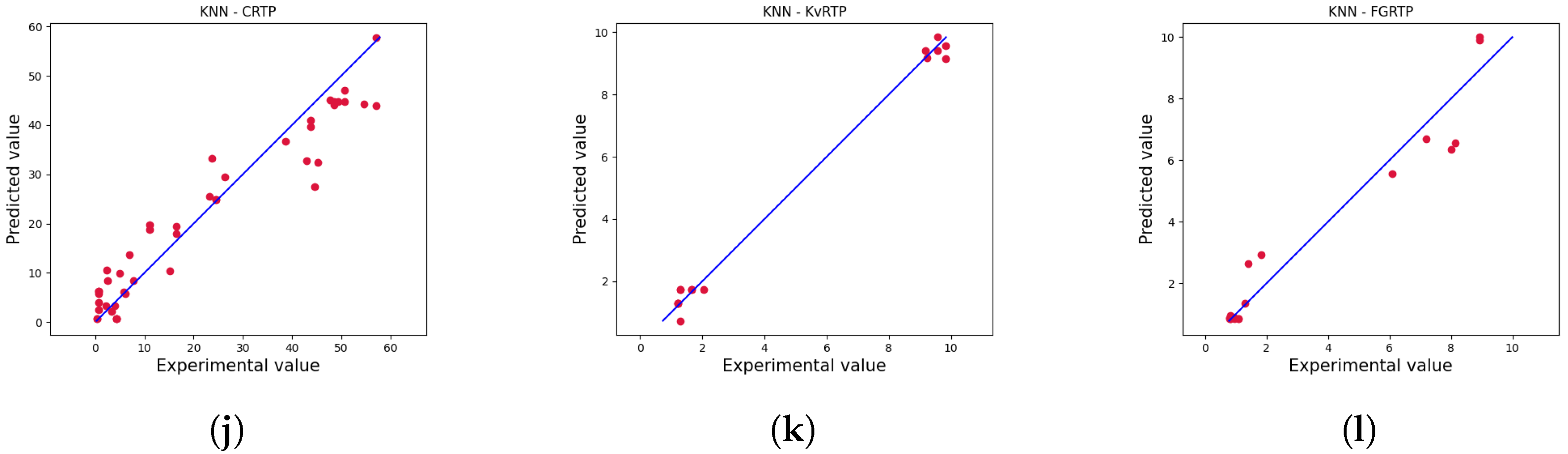
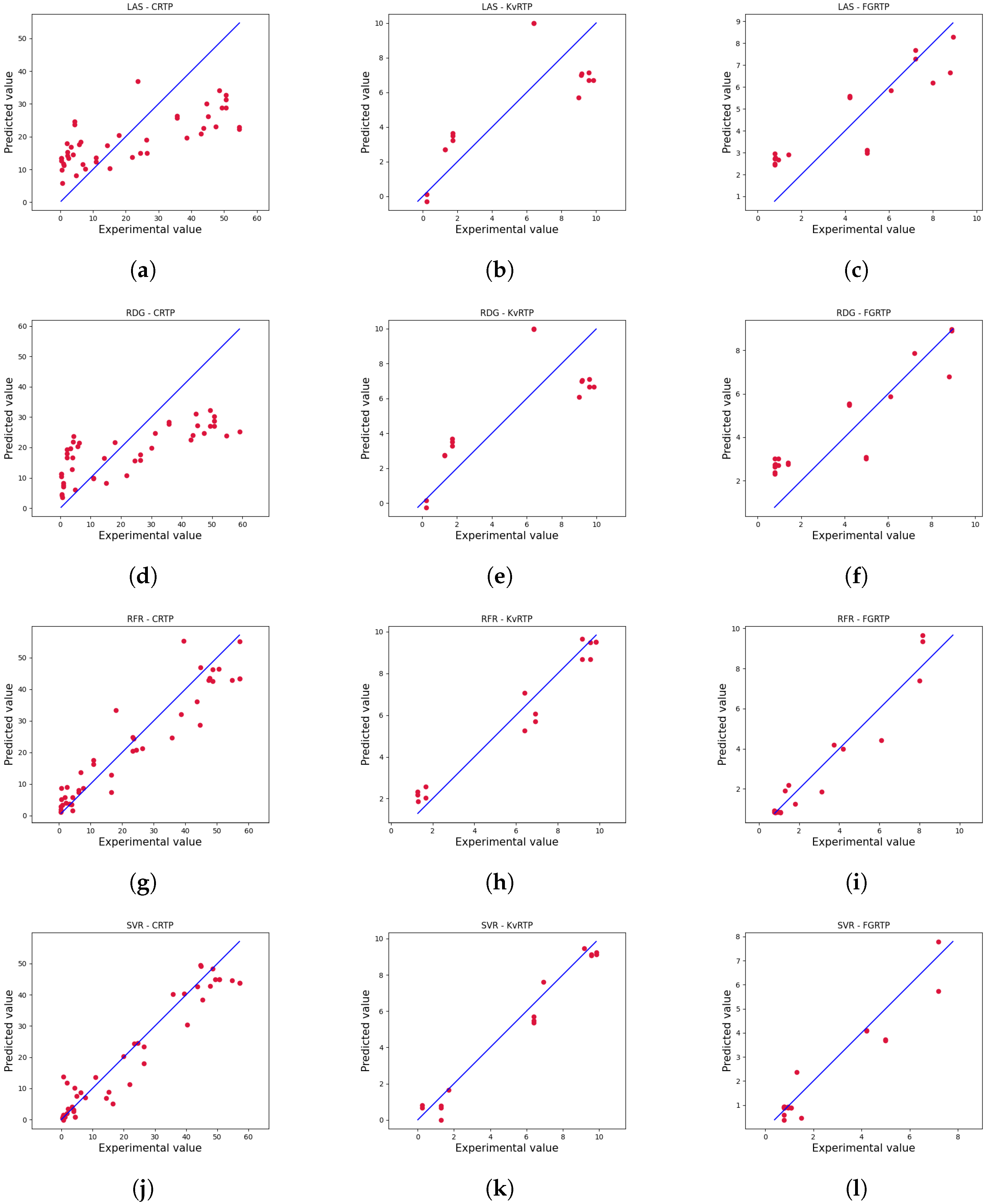
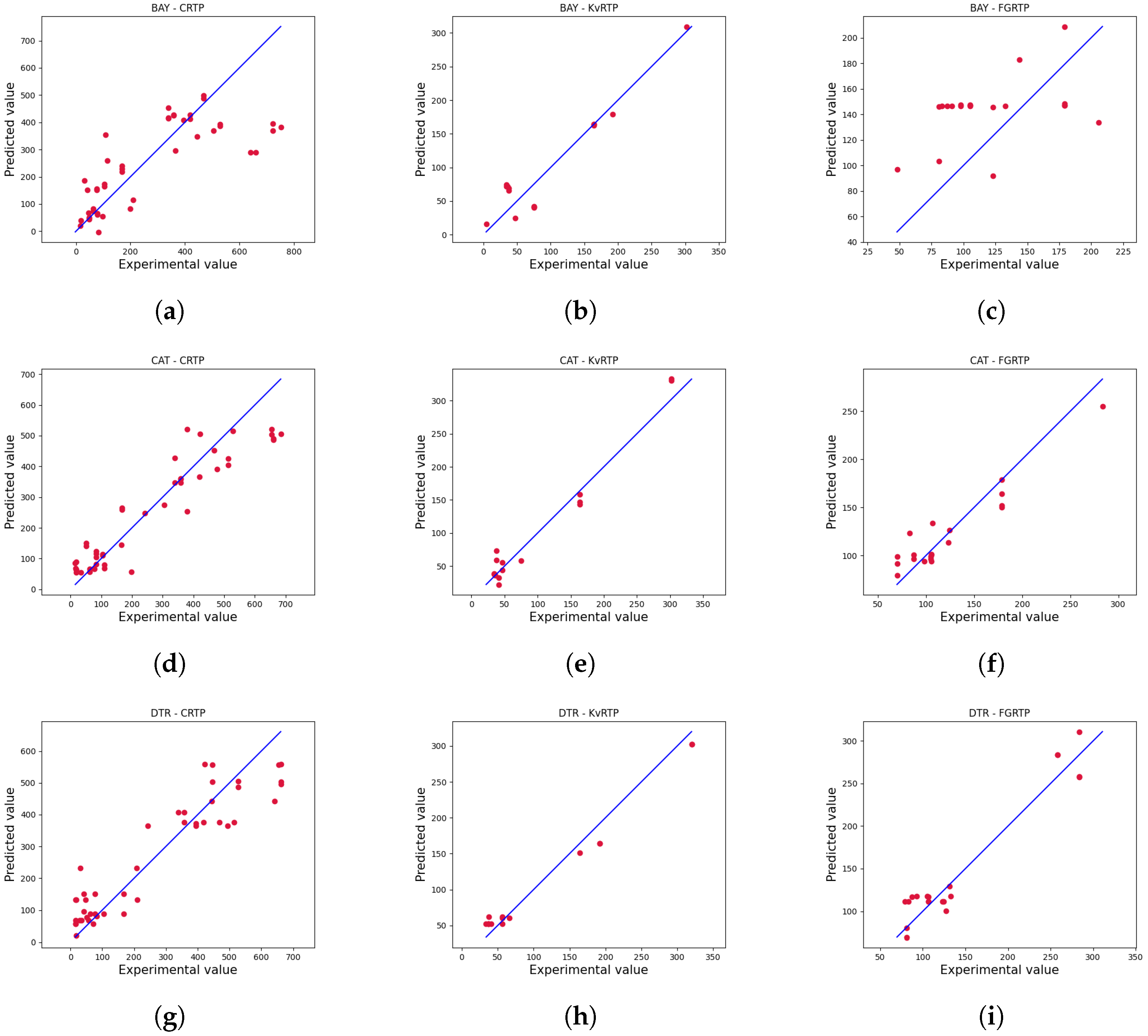
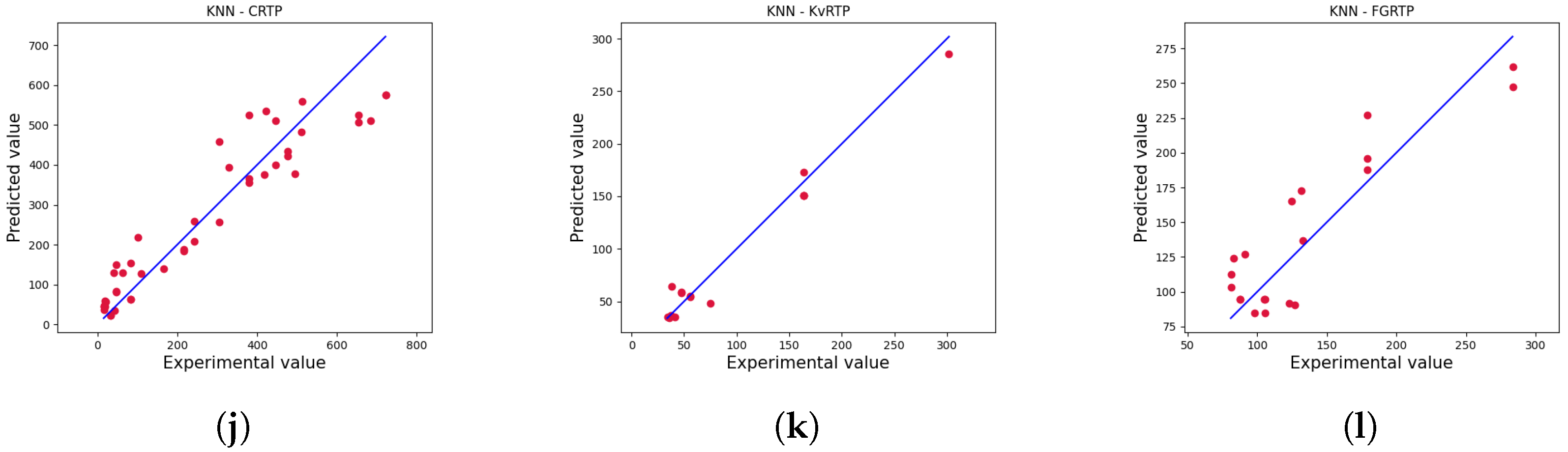
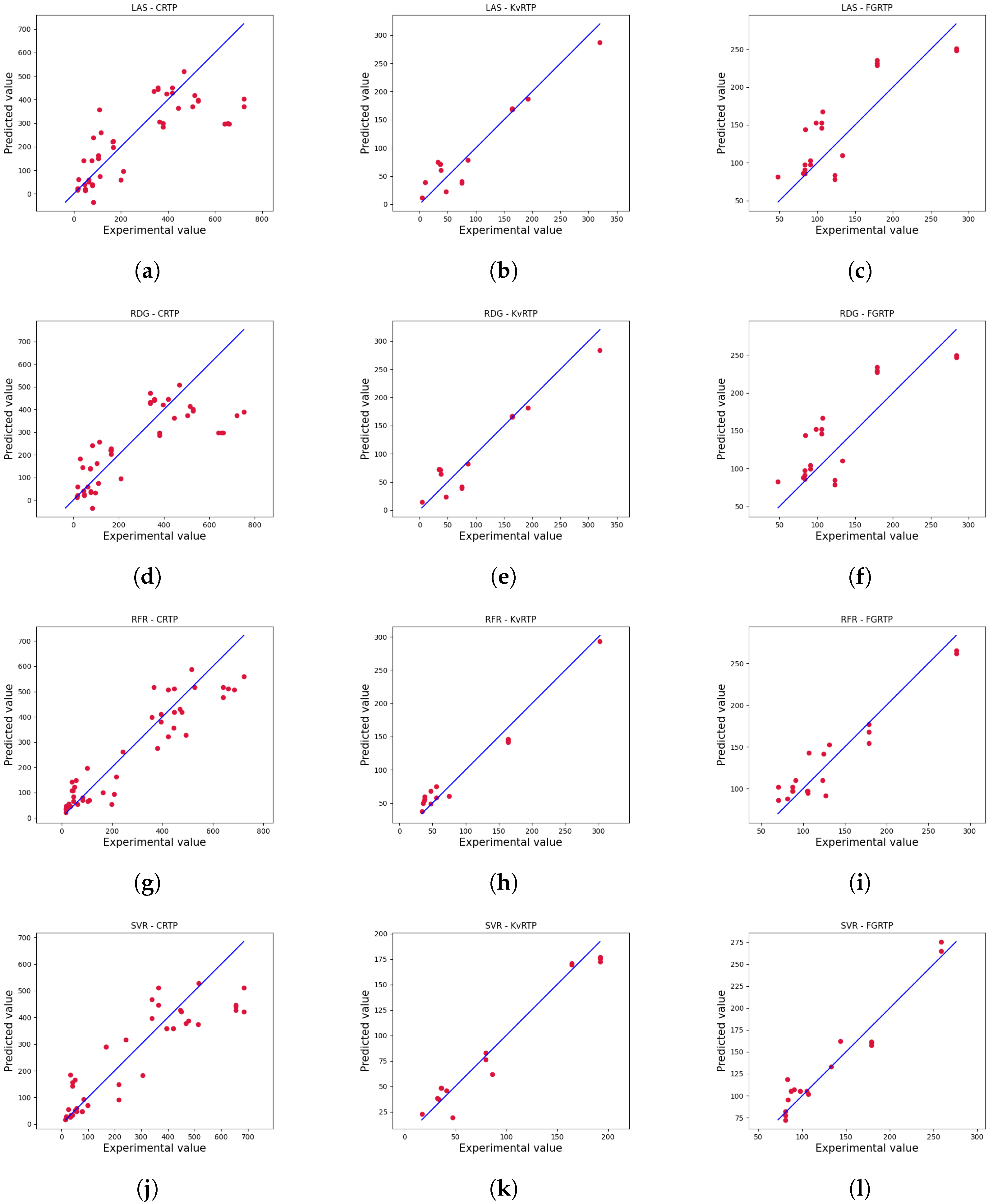
4. Results
4.1. Exploratory Analysis
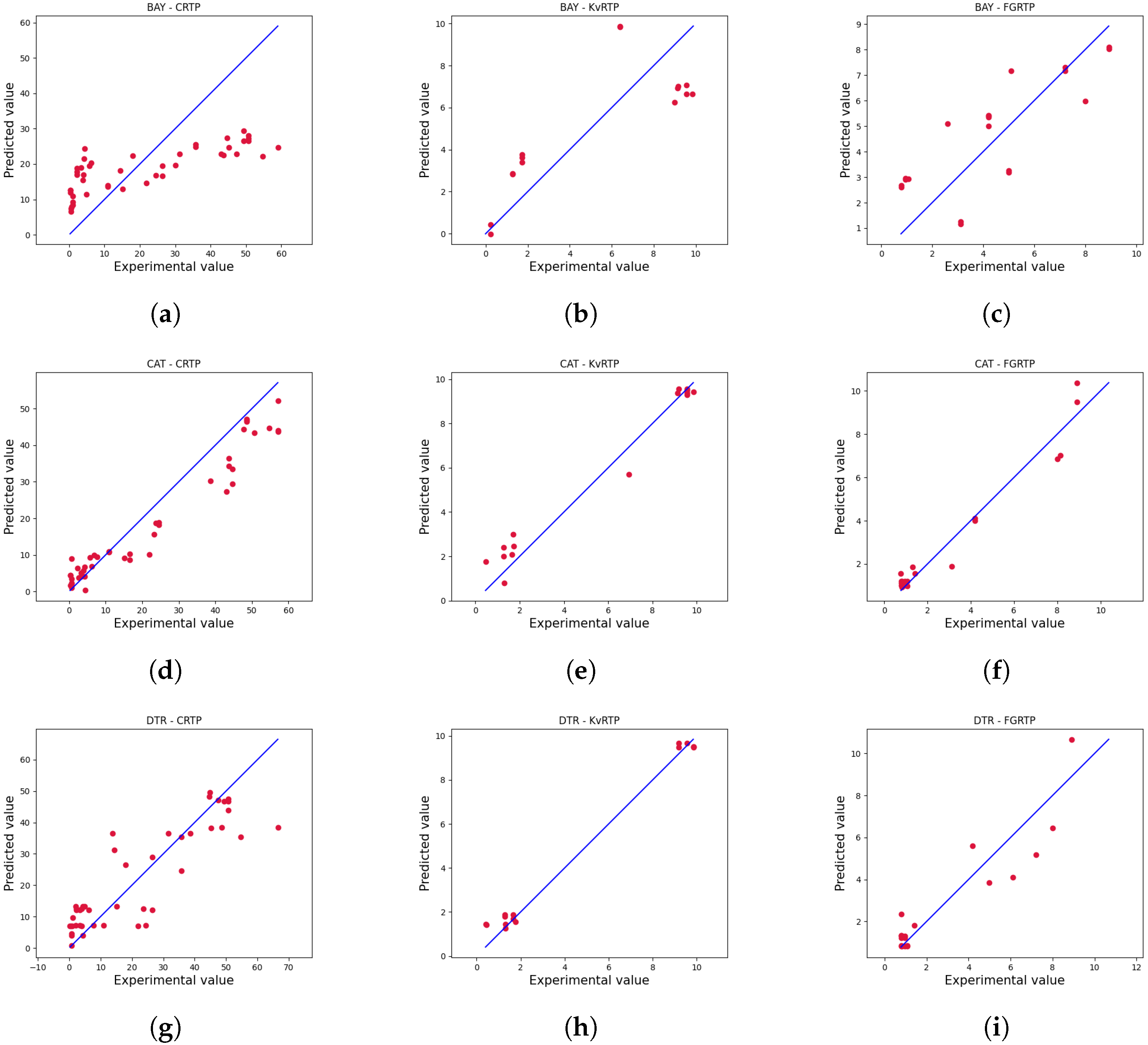
4.2. Numerical Results
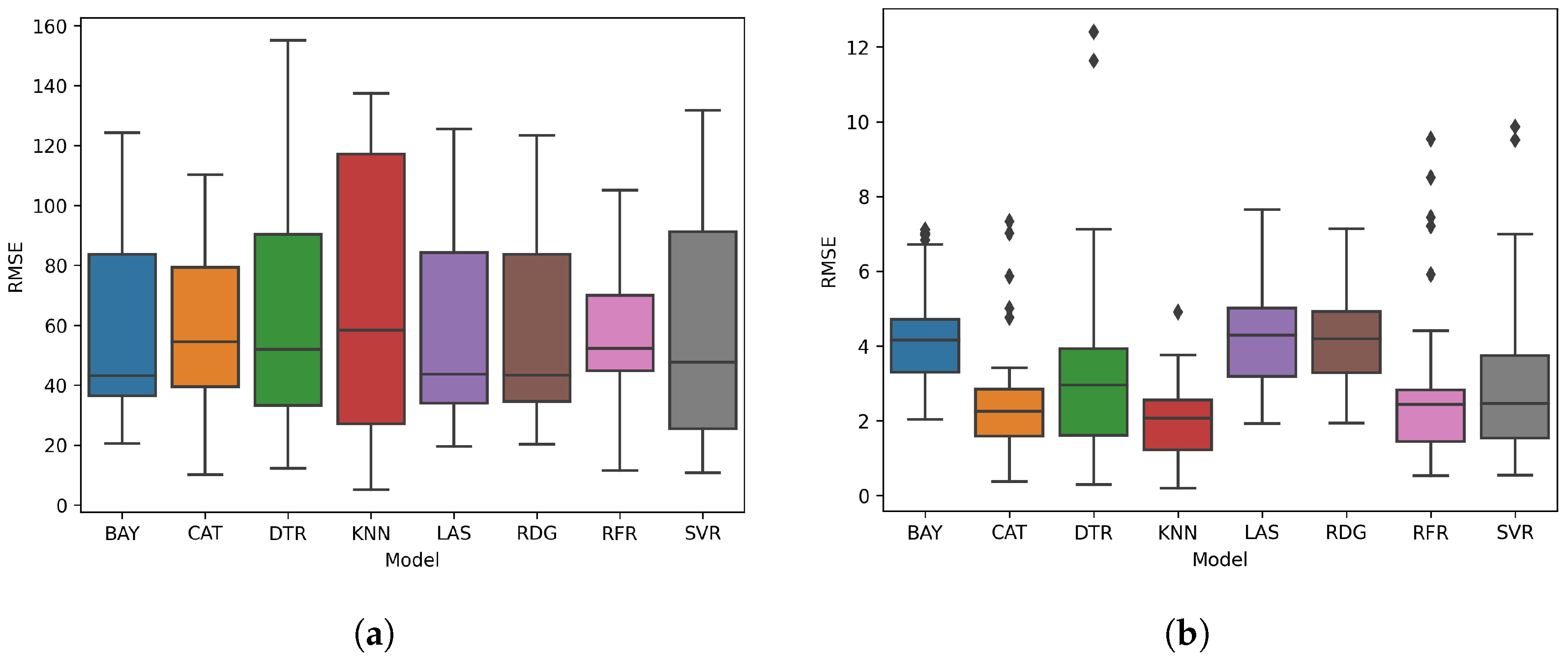
4.3. Computational Performance
4.4. Detailed Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chacón, J.; Caminero, M.A.; García-Plaza, E.; Núnez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Torries, B.; Shamsaei, N. Fatigue behavior and modeling of additively manufactured Ti-6Al-4V including interlayer time interval effects. Jom 2017, 69, 2698–2705. [Google Scholar] [CrossRef]
- Díaz, J.G.; Pertúz-Comas, A.D.; González-Estrada, O.A. Mechanical properties for long fibre reinforced fused deposition manufactured composites. Compos. Part B Eng. 2021, 211, 108657. [Google Scholar] [CrossRef]
- Mark, G.T.; Gozdz, A.S. Three Dimensional Printer with Composite Filament Fabrication. US Patent 10,099,427, 16 October 2018. [Google Scholar]
- Becerra, J.L.; Díaz-Rodríguez, J.G.; González-Estrada, O.A. Daño en partes de manufactura aditiva reforzadas por fibras continuas. Rev. UIS Ing. 2020, 19, 161–176. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, S.; Moridi, A.; Guagliano, M.; Ghidini, A.; Boniardi, M. The effect of nitriding, severe shot peening and their combination on the fatigue behavior and micro-structure of a low-alloy steel. Int. J. Fatigue 2014, 62, 67–76. [Google Scholar] [CrossRef]
- Parrado-Agudelo, J.Z.; Narváez-Tovar, C. Mechanical characterization of polylactic acid, polycaprolactone and Lay-Fomm 40 parts manufactured by fused deposition modeling, as a function of the printing parameters. Iteckne 2019, 16, 111–117. [Google Scholar] [CrossRef]
- Uribe-Lam, E.; Treviño-Quintanilla, C.D.; Cuan-Urquizo, E.; Olvera-Silva, O. Use of additive manufacturing for the fabrication of cellular and lattice materials: A review. Mater. Manuf. Process. 2020, 36, 257–280. [Google Scholar] [CrossRef]
- León-Becerra, J.S.; González-Estrada, O.A.; Pinto-Hernández, W. Mechanical characterization of additive manufacturing composite parts. Respuestas 2020, 25, 109–116. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-Based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.F.M. A critical review on 3D printed continuous fiber-reinforced composites: History, mechanism, materials and properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Díaz-Rodríguez, J.G.; Pertúz-Comas, A.D.; Ariza-González, C.J.; Garcia-López, D.D.; Pinto-Hernández, W. Monotonic crack propagation in a notched polymer matrix composite reinforced with continuous fiber and printed by material extrusion. Prog. Addit. Manuf. 2023, 8, 733–744. [Google Scholar] [CrossRef]
- Pertúz-Comas, A.D.; Díaz, J.G.; Meneses-Duran, O.J.; Niño-Álvarez, N.Y.; León-Becerra, J. Flexural Fatigue in a Polymer Matrix Composite Material Reinforced with Continuous Kevlar Fibers Fabricated by Additive Manufacturing. Polymers 2022, 14, 3586. [Google Scholar] [CrossRef] [PubMed]
- ASTM638; Standard Test Method for Tensile Properties of Plastics on Mechanical Properties, Defects and Treatments. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
- ASTM3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
- Dutra, T.A.; Ferreira, R.T.L.; Resende, H.B.; Guimarães, A. Mechanical characterization and asymptotic homogenization of 3D-printed continuous carbon fiber-reinforced thermoplastic. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 133. [Google Scholar] [CrossRef]
- Melenka, G.W.; Cheung, B.K.O.; Schofield, J.S.; Dawson, M.R.; Carey, J.P. Evaluation and prediction of the tensile properties of continuous fiber-reinforced 3D printed structures. Compos. Struct. 2016, 153, 866–875. [Google Scholar] [CrossRef]
- Ansari, A.A.; Kamil, M. Performance Study of 3D Printed Continuous Fiber-Reinforced Polymxer Composites Using Taguchi Method. J. Mater. Eng. Perform. 2022, 32, 9892–9906. [Google Scholar] [CrossRef]
- Lupone, F.; Padovano, E.; Venezia, C.; Badini, C. Experimental Characterization and Modeling of 3D Printed Continuous Carbon Fibers Composites with Different Fiber Orientation Produced by FFF Process. Polymers 2022, 14, 26. [Google Scholar] [CrossRef]
- Azarov, A.V.; Antonov, F.K.; Golubev, M.V.; Khaziev, A.R.; Ushanov, S.A. Composite 3D printing for the small size unmanned aerial vehicle structure. Compos. Part B Eng. 2019, 169, 157–163. [Google Scholar] [CrossRef]
- Swolfs, Y.; Pinho, S.T. 3D printed continuous fibre-reinforced composites: Bio-inspired microstructures for improving the translaminar fracture toughness. Compos. Sci. Technol. 2019, 182, 107731. [Google Scholar] [CrossRef]
- León-Becerra, J.; Hidalgo-Salazar, M.; González-Estrada, O.A. Progressive damage analysis of carbon fiber-reinforced additive manufacturing composites. Int. J. Adv. Manuf. Technol. 2023, 126, 2617–2631. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- León-Becerra, J.; González-Estrada, O.A.; Quiroga, J. Effect of Relative Density in In-Plane Mechanical Properties of Common 3D-Printed Polylactic Acid Lattice Structures. ACS Omega 2021, 6, 29830–29838. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using ANSYS, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Ten, J.S.J.; Yeong, W.Y. Progress and Opportunities for Machine Learning in Materials and Processes of Additive Manufacturing. Adv. Mater. 2024, 2310006. [Google Scholar] [CrossRef]
- Zhu, S.P.; Wang, L.; Luo, C.; Correia, J.A.F.O.; Jesus, A.M.P.D.; Berto, F. Physics-informed machine learning and its structural integrity applications: State of the art. Philos. Trans. R. Soc. A 2024, 381, 20220406. [Google Scholar] [CrossRef]
- Gaikwad, A.; Giera, B.; Guss, G.M.; Forien, J.B.; Matthews, M.J.; Rao, P. Heterogeneous sensing and scientific machine learning for quality assurance in laser powder bed fusion—A single-track study. Addit. Manuf. 2020, 36, 101659. [Google Scholar] [CrossRef]
- Tavares, T.B.; Finamor, F.P.; de Sousa Zorzi, J.C. Mechanical properties prediction of dual phase steels using machine learning. Rev. Tecnol. Em Metal. Mater. E Mineração 2022, 19, e2595. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Demir, K.; Gu, G.X. Machine Learning for Advanced Additive Manufacturing. Matter 2020, 3, 1541–1556. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Okafor, C.E.; Iweriolor, S.; Ani, O.I.; Ahmad, S.; Mehfuz, S.; Ekwueme, G.O.; Chukwumuanya, O.E.; Abonyi, S.E.; Ekengwu, I.E.; Chikelu, O.P. Advances in machine learning-aided design of reinforced polymer composite and hybrid material systems. Hybrid Adv. 2023, 2, 100026. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Gao, R.X. Deep learning-based tensile strength prediction in fused deposition modeling. Comput. Ind. 2019, 107, 11–21. [Google Scholar] [CrossRef]
- Leon-Becerra, J.; González-Estrada, O.A.; Sánchez-Acevedo, H. Comparison of Models to Predict Mechanical Properties of FR-AM Composites and a Fractographical Study. Polymers 2022, 14, 3546. [Google Scholar] [CrossRef]
- Rodríguez, J.F.; Thomas, J.P.; Renaud, J.E. Mechanical behavior of ABS fused deposition materials modeling. Rapid Prototyp. J. 2003, 9, 219–230. [Google Scholar] [CrossRef]
- Papon, E.A.; Haque, A. Tensile properties, void contents, dispersion and fracture behaviour of 3D printed carbon nanofiber reinforced composites. J. Reinf. Plast. Compos. 2018, 37, 381–395. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering—Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Kramer, O. K-Nearest Neighbors; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Blok, L.; Longana, M.; Yu, H.; Woods, B. An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Klift, F.V.D.; Koga, Y.; Todoroki, A.; Ueda, M.; Hirano, Y.; Matsuzaki, R. 3D Printing of Continuous Carbon Fibre Reinforced Thermo-Plastic (CFRTP) Tensile Test Specimens. Open J. Compos. Mater. 2016, 6, 18–27. [Google Scholar] [CrossRef]
- Dickson, A.N.; Ross, K.A.; Dowling, D.P. Additive manufacturing of woven carbon fibre polymer composites. Compos. Struct. 2018, 206, 637–643. [Google Scholar] [CrossRef]
- Justo, J.; Távara, L.; García-Guzmán, L.; París, F. Characterization of 3D printed long fibre reinforced composites. Compos. Struct. 2018, 185, 537–548. [Google Scholar] [CrossRef]
- Abadi, H.A.; Thai, H.T.; Paton-Cole, V.; Patel, V. Elastic properties of 3D printed fibre-reinforced structures. Compos. Struct. 2018, 193, 8–18. [Google Scholar] [CrossRef]
- Imeri, A.; Fidan, I.; Allen, M.; Wilson, D.A.; Canfield, S. Fatigue analysis of the fiber reinforced additively manufactured objects. Int. J. Adv. Manuf. Technol. 2018, 98, 2717–2724. [Google Scholar] [CrossRef]
- Mohammadizadeh, M.; Imeri, A.; Fidan, I.; Elkelany, M. 3D printed fiber reinforced polymer composites - Structural analysis. Compos. Part B Eng. 2019, 175, 107112. [Google Scholar] [CrossRef]
- Todoroki, A.; Oasada, T.; Mizutani, Y.; Suzuki, Y.; Ueda, M.; Matsuzaki, R.; Hirano, Y. Tensile property evaluations of 3D printed continuous carbon fiber reinforced thermoplastic composites. Adv. Compos. Mater. 2020, 29, 147–162. [Google Scholar] [CrossRef]
- Araya-Calvo, M.; López-Gómez, I.; Chamberlain-Simon, N.; León-Salazar, J.L.; Guillén-Girón, T.; Corrales-Cordero, J.S.; Sánchez-Brenes, O. Evaluation of compressive and flexural properties of continuous fiber fabrication additive manufacturing technology. Addit. Manuf. 2018, 22, 157–164. [Google Scholar] [CrossRef]
- González-Estrada, O.A.; Pertuz, A.; Quiroga Mendez, J.E. Evaluation of tensile properties and damage of continuous fibre reinforced 3D-printed parts. Key Eng. Mater. 2018, 774, 161–166. [Google Scholar] [CrossRef]
- Pertuz, A.D.; Díaz-Cardona, S.; González-Estrada, O.A. Static and fatigue behaviour of continuous fibre reinforced thermoplastic composites manufactured by fused deposition modelling technique. Int. J. Fatigue 2020, 130, 105275. [Google Scholar] [CrossRef]
- Podda, F. Modellazione, Produzione e Testing di Materiali Compositi a Fibra Lunga Realizzati Mediante Additive Manufacturing = Modelling, Production and Testing of Long Fibre Composites via Additive Manufacturing. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2018. [Google Scholar]
- Agarwal, K.; Kuchipudi, S.K.; Girard, B.; Houser, M. Mechanical properties of fiber reinforced polymer composites: A comparative study of conventional and additive manufacturing methods. J. Compos. Mater. 2018, 52, 3173–3181. [Google Scholar] [CrossRef]
- Mei, H.; Ali, Z.; Ali, I.; Cheng, L. Tailoring strength and modulus by 3D printing different continuous fibers and filled structures into composites. Adv. Compos. Hybrid Mater. 2019, 2, 312–319. [Google Scholar] [CrossRef]
- Naranjo-Lozada, J.; Ahuett-Garza, H.; Orta-Castañón, P.; Verbeeten, W.M.; Sáiz-González, D. Tensile properties and failure behavior of chopped and continuous carbon fiber composites produced by additive manufacturing. Addit. Manuf. 2019, 26, 227–241. [Google Scholar] [CrossRef]
- Pyl, L.; Kalteremidou, K.A.; Hemelrijck, D.V. Exploration of specimen geometry and tab configuration for tensile testing exploiting the potential of 3D printing freeform shape continuous carbon fibre-reinforced nylon matrix composites. Polym. Test. 2018, 71, 318–328. [Google Scholar] [CrossRef]
- Saeed, K.; McIlhagger, A.; Harkin-Jones, E.; McGarrigle, C.; Dixon, D.; Shar, M.A.; McMillan, A.; Archer, E. Characterization of continuous carbon fibre reinforced 3D printed polymer composites with varying fibre volume fractions. Compos. Struct. 2022, 282, 115033. [Google Scholar] [CrossRef]
- Tessarin, A.; Zaccariotto, M.; Galvanetto, U.; Stocchi, D. A multiscale numerical homogenization-based method for the prediction of elastic properties of components produced with the fused deposition modelling process. Results Eng. 2022, 14, 100409. [Google Scholar] [CrossRef]
- Lawrence, B.D.; Coatney, M.D.; Phillips, F.; Henry, T.C.; Nikishkov, Y.; Makeev, A. Evaluation of the mechanical properties and performance cost of additively manufactured continuous glass and carbon fiber composites. Int. J. Adv. Manuf. Technol. 2022, 120, 1135–1147. [Google Scholar] [CrossRef]
- Santos, J.D.; Fernández, A.; Ripoll, L.; Blanco, N. Experimental Characterization and Analysis of the In-Plane Elastic Properties and Interlaminar Fracture Toughness of a 3D-Printed Continuous Carbon Fiber-Reinforced Composite. Polymers 2022, 14, 506. [Google Scholar] [CrossRef] [PubMed]
- Heitkamp, T.; Girnth, S.; Kuschmitz, S.; Klawitter, G.; Waldt, N.; Vietor, T. Continuous Fiber-Reinforced Material Extrusion with Hybrid Composites of Carbon and Aramid Fibers. Appl. Sci. 2022, 12, 8830. [Google Scholar] [CrossRef]
- Bendine, K.; Gibhardt, D.; Fiedler, B.; Backs, A. Experimental characterization and mechanical behavior of 3D printed CFRP. Eur. J. Mech. A Solids 2022, 94, 104587. [Google Scholar] [CrossRef]
- Ojha, K.K.; Gugliani, G.; Francis, V. Tensile properties and failure behaviour of continuous kevlar fibre reinforced composites fabricated by additive manufacturing process. Adv. Mater. Process. Technol. 2022, 10, 142–156. [Google Scholar] [CrossRef]
- Ali, Z.; Yan, Y.; Mei, H.; Cheng, L.; Zhang, L. Effect of infill density, build direction and heat treatment on the tensile mechanical properties of 3D-printed carbon-fiber nylon composites. Compos. Struct. 2023, 304, 116370. [Google Scholar] [CrossRef]
- Xiang, J.; Cheng, P.; Wang, K.; Wu, Y.; Rao, Y.; Peng, Y. Interlaminar and translaminar fracture toughness of 3D-printed continuous fiber reinforced composites: A review and prospect. Polym. Compos. 2023, 45, 3883–3900. [Google Scholar] [CrossRef]
- Lee, G.W.; Kim, T.H.; Yun, J.H.; Kim, N.J.; Ahn, K.H.; Kang, M.S. Strength of Onyx-based composite 3D printing materials according to fiber reinforcement. Front. Mater. 2023, 10, 1183816. [Google Scholar] [CrossRef]
- Moreno-Núñez, B.; Abarca-Vidal, C.; Treviño-Quintanilla, C.; Sánchez-Santana, U.; Cuan-Urquizo, E.; Uribe-Lam, E. Experimental Analysis of Fiber Reinforcement Rings’ Effect on Tensile and Flexural Properties of Onyx™–Kevlar® Composites Manufactured by Continuous Fiber Reinforcement. Polymers 2023, 15, 1252. [Google Scholar] [CrossRef]
- Gljušćić, M.; Franulović, M.; Lanc, D.; Božić, Ž. Application of digital image correlation in behavior modelling of AM CFRTP composites. Eng. Fail. Anal. 2022, 136, 106133. [Google Scholar] [CrossRef]
- Ali, M. PyCaret: An Open Source, Low-Code Machine Learning Library in Python; PyCaret Version 1.0.0; 2020. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Ozer, D.J. Correlation and the coefficient of determination. Psychol. Bull. 1985, 97, 307. [Google Scholar] [CrossRef]
- Student. The probable error of a mean. In Biometrika; Oxford University Press: Oxford, UK, 1908; pp. 1–25. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]




| Material | E [GPa] | [MPa] | % |
|---|---|---|---|
| Nylon | 1.7 | 33.5 | 4.5 |
| Onyx | 1.4 | 36 | 33 |
| Standard | ASTM D638 [16] | ASTM D638 [16] | ASTM D638 [16] |
| Carbon | 60 | 800 | 1.5 |
| Fiberglass | 21 | 590 | 3.8 |
| Kevlar | 27 | 610 | 2.7 |
| Standard | ASTM D3039 [17] | ASTM D3039 [17] | ASTM D3039 [17] |
| Reference | Fiber Type | Fill Pattern | Fill Angle (°) | Fiber Angle (°) | Fiber Distrib. | Properties | |
|---|---|---|---|---|---|---|---|
| Blok [44] | C | T | NA | X | , , , G, | ||
| Dutra [18] | C | NA | NA | X | , , , , , , G, | ||
| Klift [45] | C | NA | 0 | NA | C | X | , |
| Melenka [19] | Kv | NA | 0 | NA | NA | , | |
| Dickson [46] | C, Kv, FG | NA | NA | NA | C | NA | , , , |
| Justo [47] | C, FG | NA | 0, 90 | NA | NA | , , , , | |
| Al-Abadi [48] | C, Kv, FG | NA | 0, 90 | C | NA | , | |
| Goh [13] | C, FG | NA | NA | 0, 90, | I | X | J, , |
| Fidan [49,50] | C, Kv, FG | NA | NA | NA | NA | NA | , , , |
| Todoroki [51] | C | NA | NA | NA | NA | , , | |
| Araya [52] | Kv | R, H | NA | I, C | NA | , , , | |
| González [53] | C, FG | T | 0 | C | NA | , | |
| Pertuz [54] | C, FG, Kv | T | NA | 0 | I | X | , , |
| Podda [55] | C | NA | NA | 0, 90 | NA | NA | , |
| Agarwal [56] | FG | H | NA | NA | NA | , , | |
| Mei [57] | C, FG, Kv | T, H, R | NA | 0 | C | NA | , |
| Naranjo [58] | C | T | NA | NA | NA | - | , |
| Pyl [59] | C | NA | NA | 0 | I | NA | , |
| Saeed [60] | C | S | 0 | I | X | , | |
| Tessarin [61] | C, Kv, HSHT | S | 0 | I | X | , | |
| Lawrence [62] | C, FG | S | 0 | 0 | I | X | , |
| Santos [63] | C, FG | S | 0 | 0 | I | X | , |
| Leon [36] | C | S | 0 | I | X | , | |
| Heitkamp [64] | C, Kv | S | 0 | 0 | I | X | , |
| Bendine [65] | C | S | 0 | 0 | I | X | , |
| Ojha [66] | Kv | S | 0 | 0 | I | X | , |
| Siddiqui [4] | C | S | 0 | 0 | I | X | , |
| Zeeshan Ali [67] | C | R | 0 | 0 | I | X | , |
| Xiang [68] | C | R | 0 | ±45 | C | X | , |
| Lee [69] | C, FG | S | 0 | ±45 | C | X | , |
| Moreno-Nuñez [70] | Kv | R | 0 | ±45 | C | X | , |
| Gljuscic [71] | C | S | 0 | 0 | I | X | , |
| Model | Mean | Std Dev | Min. | 1st Quartile | Median | 3rd Quartile | Max |
|---|---|---|---|---|---|---|---|
| BAY | 16.2405 | 3.2572 | 9.4879 | 14.0424 | 15.8779 | 18.3325 | 24.2133 |
| RDG | 16.2256 | 3.4534 | 9.0721 | 13.8824 | 16.0427 | 18.6324 | 25.0582 |
| LAS | 16.1670 | 3.2741 | 8.9366 | 14.1336 | 15.6067 | 18.0086 | 23.7556 |
| DTR | 14.8774 | 4.3100 | 7.6346 | 12.0422 | 14.4884 | 16.7512 | 27.0928 |
| SVR | 11.7524 | 5.0485 | 2.9113 | 7.6782 | 12.4260 | 15.4035 | 21.4587 |
| RFR | 9.8297 | 3.6813 | 3.6341 | 6.8087 | 8.6466 | 12.3373 | 19.6891 |
| KNN | 9.8020 | 4.1159 | 3.7364 | 6.6482 | 9.3383 | 11.9770 | 23.3197 |
| CAT | 9.4446 | 3.3558 | 3.0735 | 7.2028 | 8.8084 | 11.7664 | 18.1977 |
| Model | Mean | Std Dev | Min. | 1st Quartile | Median | 3rd Quartile | Max |
|---|---|---|---|---|---|---|---|
| BAY | 159.7859 | 24.6198 | 131.2626 | 143.6800 | 156.5881 | 166.6547 | 258.1069 |
| RDG | 159.4300 | 25.2739 | 128.5327 | 143.7674 | 155.4155 | 167.4714 | 258.7639 |
| LAS | 159.3340 | 25.2431 | 129.0285 | 143.4035 | 155.3209 | 166.2181 | 258.7624 |
| DTR | 152.2683 | 45.3625 | 76.5504 | 115.0226 | 150.2737 | 170.3594 | 289.0174 |
| SVR | 142.2886 | 43.2337 | 71.5865 | 115.0798 | 144.5133 | 164.2971 | 258.5963 |
| KNN | 121.4163 | 42.1382 | 53.4138 | 91.3910 | 111.6907 | 141.3862 | 251.2954 |
| CAT | 114.4038 | 32.6867 | 54.2600 | 91.3665 | 109.3586 | 139.4164 | 197.8857 |
| RFR | 113.1730 | 36.8256 | 52.8864 | 84.8905 | 107.1129 | 136.4452 | 209.2337 |
| Target | Model | Prediction Time (ms) | Model Size (kB) |
|---|---|---|---|
| E | BAY | 0.2464 ± 0.0655 | 1.8690 ± 0.0000 |
| E | RDG | 0.2571 ± 0.1237 | 1.0540 ± 0.0000 |
| E | LAS | 0.3108 ± 0.2160 | 1.1542 ± 0.0004 |
| E | DTR | 0.2475 ± 0.0485 | 2.6079 ± 0.0808 |
| E | SVR | 0.3114 ± 0.0791 | 9.8657 ± 0.3070 |
| E | RFR | 2.5034 ± 0.8491 | 323.2075 ± 107.4422 |
| E | KNN | 13.2900 ± 0.3737 | 12.1362 ± 0.0033 |
| E | CAT | 1.0333 ± 0.3281 | 213.9868 ± 114.2556 |
| BAY | 0.2542 ± 0.0797 | 1.8690 ± 0.0000 | |
| RDG | 0.2395 ± 0.0714 | 1.0540 ± 0.0000 | |
| LAS | 0.2494 ± 0.0535 | 1.1542 ± 0.0004 | |
| DTR | 0.2458 ± 0.0525 | 2.5439 ± 0.1393 | |
| SVR | 0.3184 ± 0.0753 | 10.5268 ± 0.0322 | |
| KNN | 13.3308 ± 0.3256 | 12.1356 ± 0.0024 | |
| CAT | 0.9430 ± 0.2397 | 198.7430 ± 102.1022 | |
| RFR | 2.8011 ± 0.9439 | 349.6818 ± 88.7123 |
| Fiber Type | Metric | SVR | DTR | RFR | CAT | KNN | RDG | LAS | BAY |
|---|---|---|---|---|---|---|---|---|---|
| r | 0.5835 | 0.6059 | 0.8062 | 0.8075 | 0.7972 | 0.3697 | 0.3473 | 0.3585 | |
| CRTP | 0.3404 | 0.3672 | 0.6500 | 0.6521 | 0.6355 | 0.1367 | 0.1206 | 0.1285 | |
| Student’s t-test | - | - | Ok | Ok | - | - | - | - | |
| r | −0.0075 | 0.0218 | 0.1100 | 0.1091 | −0.0849 | 0.0250 | −0.0119 | −0.0370 | |
| FGRTP | 0.0001 | 0.3672 | 0.6500 | 0.6521 | 0.6355 | 0.1367 | 0.1206 | 0.1285 | |
| Student’s t-test | - | - | Ok | Ok | - | - | - | - | |
| r | 0.5240 | 0.4342 | 0.5789 | 0.6695 | 0.7870 | 0.2731 | 0.2546 | 0.2715 | |
| KvRTP | 0.2746 | 0.1885 | 0.3351 | 0.4482 | 0.6193 | 0.0746 | 0.0648 | 0.0737 | |
| Student’s t-test | - | - | - | - | Ok | - | - | - |
| Fiber Type | Metric | SVR | DTR | RFR | CAT | KNN | RDG | LAS | BAY |
|---|---|---|---|---|---|---|---|---|---|
| r | 0.6819 | −0.0686 | −0.1237 | −0.0471 | -0.1073 | −0.0528 | −0.0528 | −0.0408 | |
| CRTP | 0.4649 | 0.0047 | 0.0153 | 0.0022 | 0.0115 | 0.0028 | 0.0028 | 0.0017 | |
| Student’s t-test | - | Ok | Ok | Ok | - | - | - | - | |
| r | 0.0846 | −0.0206 | 0.0897 | 0.0886 | −0.0013 | −0.0325 | -0.0212 | -0.0450 | |
| FGRTP | 0.0072 | 0.0004 | 0.0080 | 0.0078 | 0.0000 | 0.0011 | 0.0004 | 0.0020 | |
| Student’s t-test | - | - | - | - | - | - | - | - | |
| r | 0.8297 | 0.7266 | 0.8532 | 0.8146 | 0.7031 | 0.8235 | 0.8235 | 0.8215 | |
| KvRTP | 0.6884 | 0.5279 | 0.7279 | 0.6635 | 0.4944 | 0.6782 | 0.6782 | 0.6749 | |
| Student’s t-test | - | - | - | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prada Parra, D.; Ferreira, G.R.B.; Díaz, J.G.; Gheorghe de Castro Ribeiro, M.; Braga, A.M.B. Supervised Machine Learning Models for Mechanical Properties Prediction in Additively Manufactured Composites. Appl. Sci. 2024, 14, 7009. https://doi.org/10.3390/app14167009
Prada Parra D, Ferreira GRB, Díaz JG, Gheorghe de Castro Ribeiro M, Braga AMB. Supervised Machine Learning Models for Mechanical Properties Prediction in Additively Manufactured Composites. Applied Sciences. 2024; 14(16):7009. https://doi.org/10.3390/app14167009
Chicago/Turabian StylePrada Parra, Dario, Guilherme Rezende Bessa Ferreira, Jorge G. Díaz, Mateus Gheorghe de Castro Ribeiro, and Arthur Martins Barbosa Braga. 2024. "Supervised Machine Learning Models for Mechanical Properties Prediction in Additively Manufactured Composites" Applied Sciences 14, no. 16: 7009. https://doi.org/10.3390/app14167009
APA StylePrada Parra, D., Ferreira, G. R. B., Díaz, J. G., Gheorghe de Castro Ribeiro, M., & Braga, A. M. B. (2024). Supervised Machine Learning Models for Mechanical Properties Prediction in Additively Manufactured Composites. Applied Sciences, 14(16), 7009. https://doi.org/10.3390/app14167009







