A New Semi-Analytical Method for the Calculation of Multi-Crack Stress-Intensity Factors under Hydro-Mechanical Coupling
Abstract
:1. Introduction
2. New Extended Semi-Weight Function Method for Calculating SIFs under Hydro-Mechanical Coupling
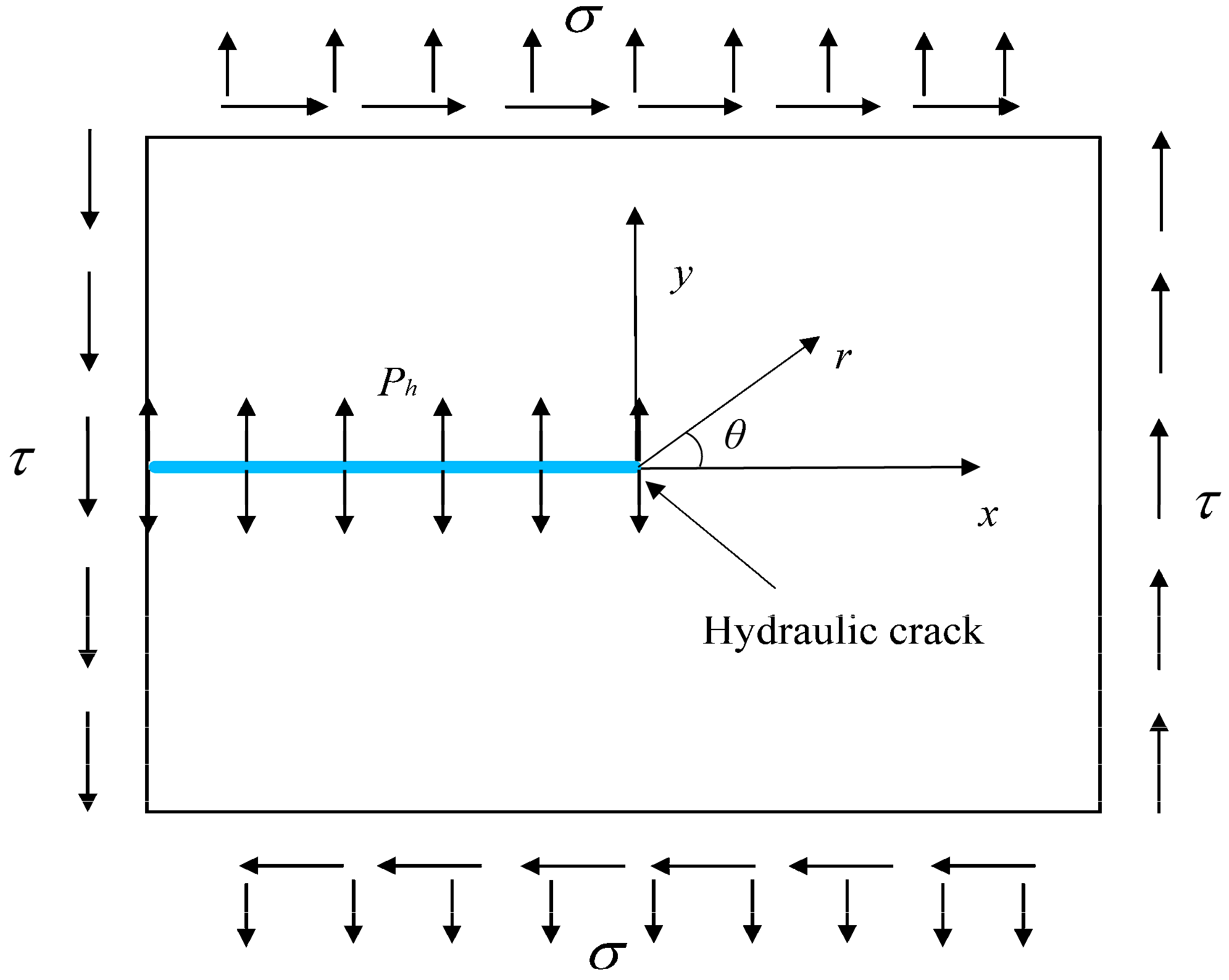
2.1. Derivation of New Stress Function for Hydro-Mechanical Coupling Cracks
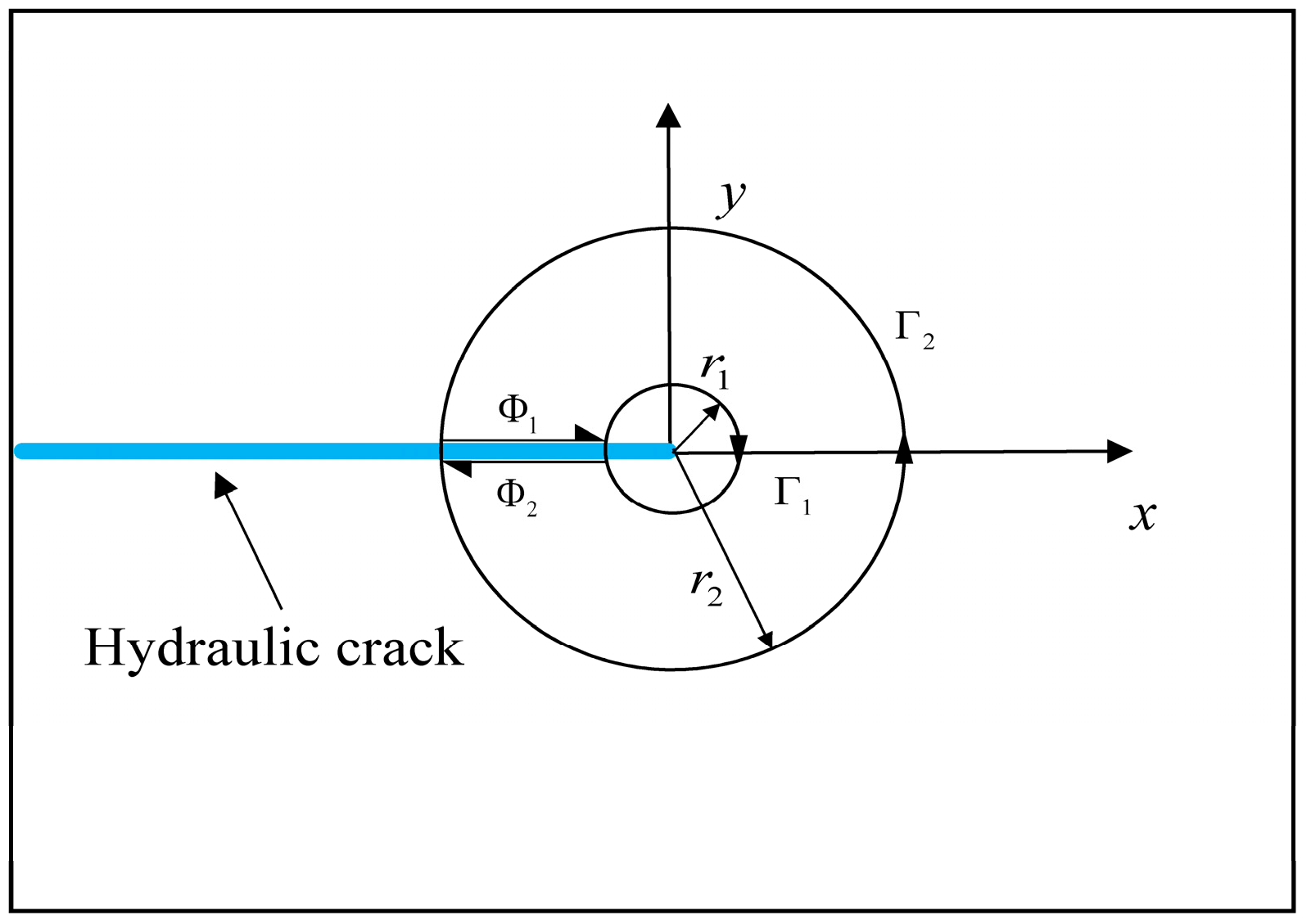
2.2. Determination of Weight Function and Semi-Weight Function for Hydro-Mechanical Coupling Crack
2.3. Calculation of Hydro-Mechanical Coupling Stress-Intensity Factors
3. Verification of the Extended Semi-Weight Function Method under Hydro-Mechanical Coupling
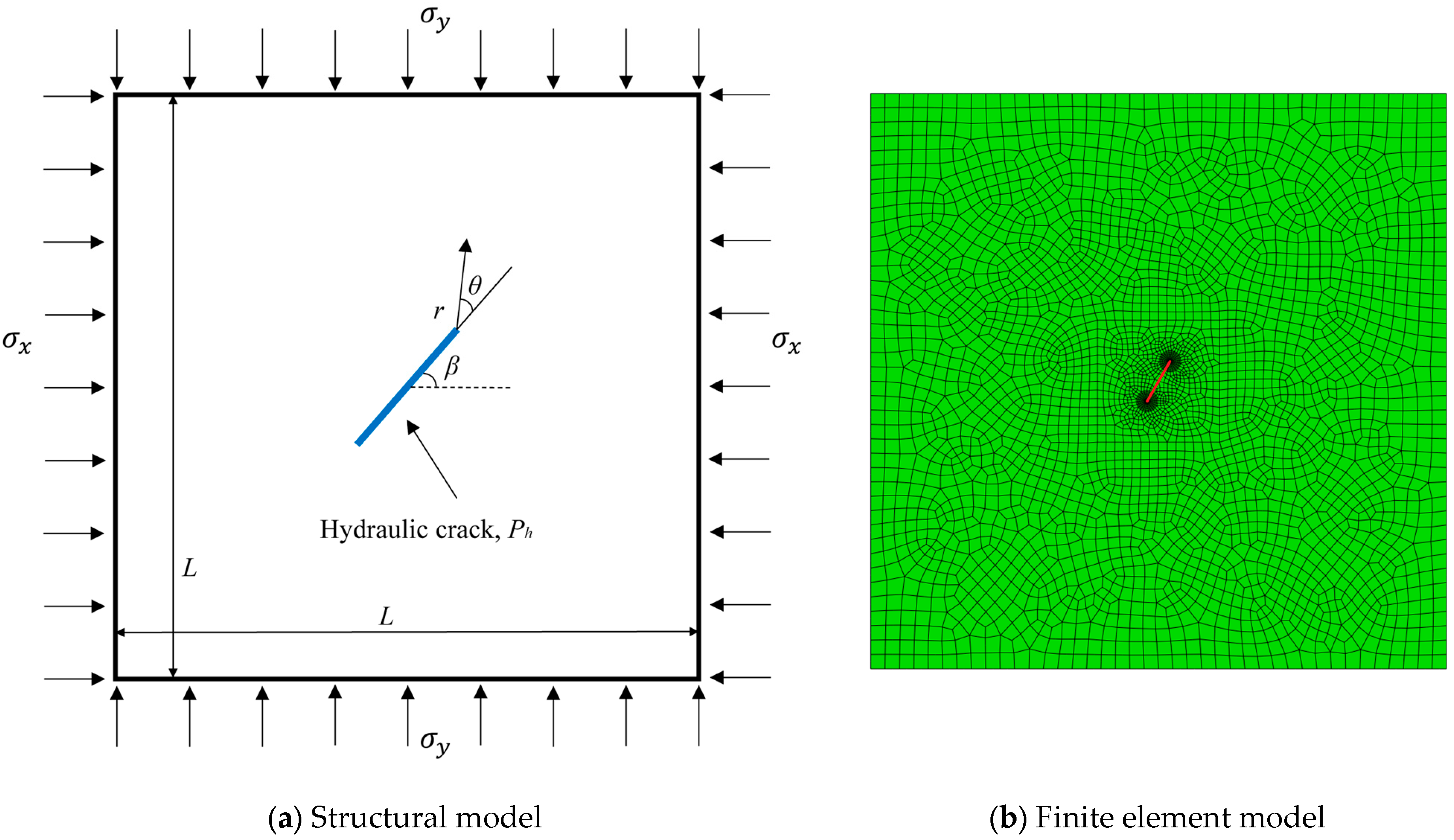
3.1. Example 1 (One Crack under Hydro-Mechanical Coupling)
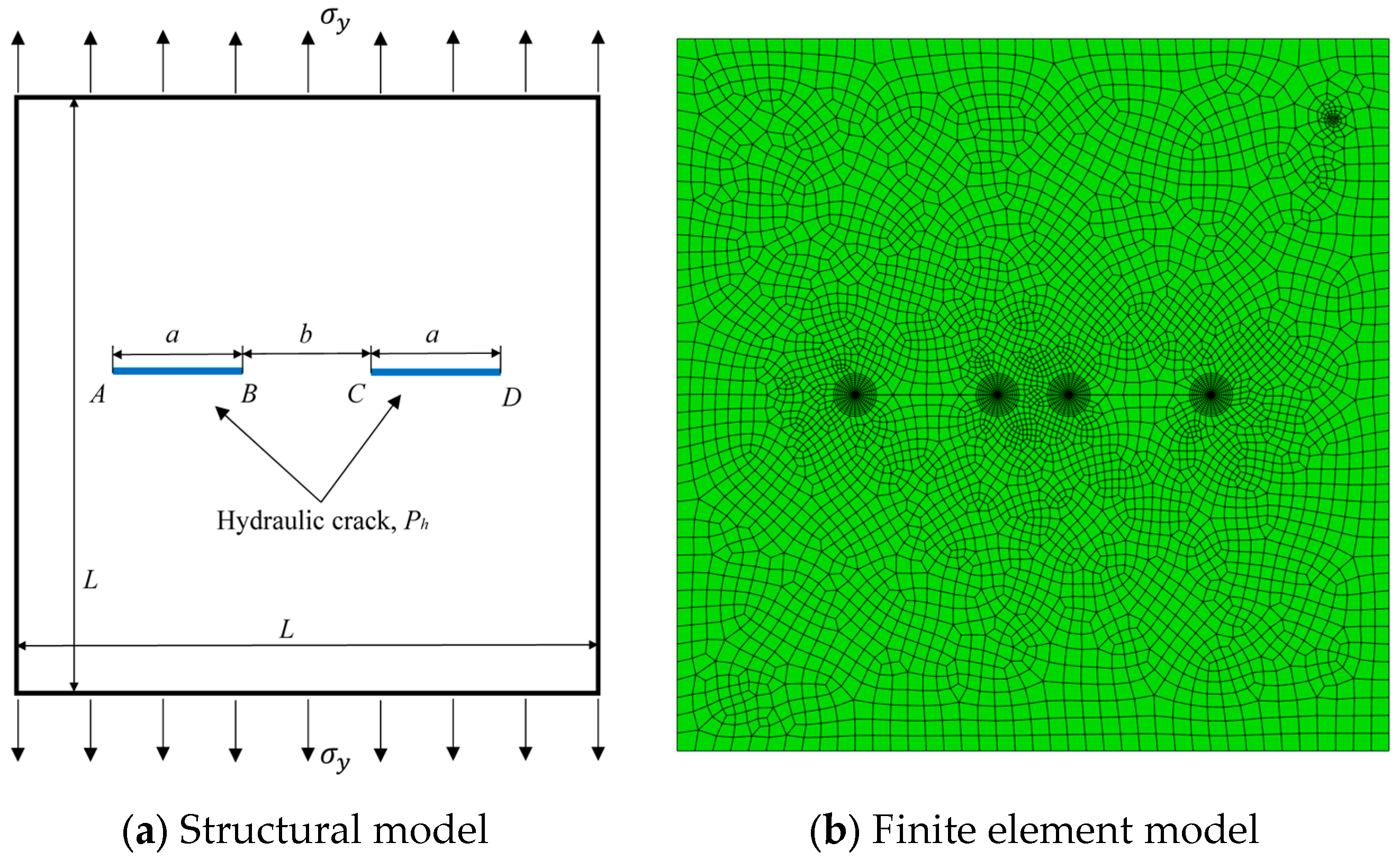
3.2. Example 2 (Arbitrary Multi-Cracks under Hydro-Mechanical Coupling)
4. Results and Discussion
4.1. Effect of Integral Paths
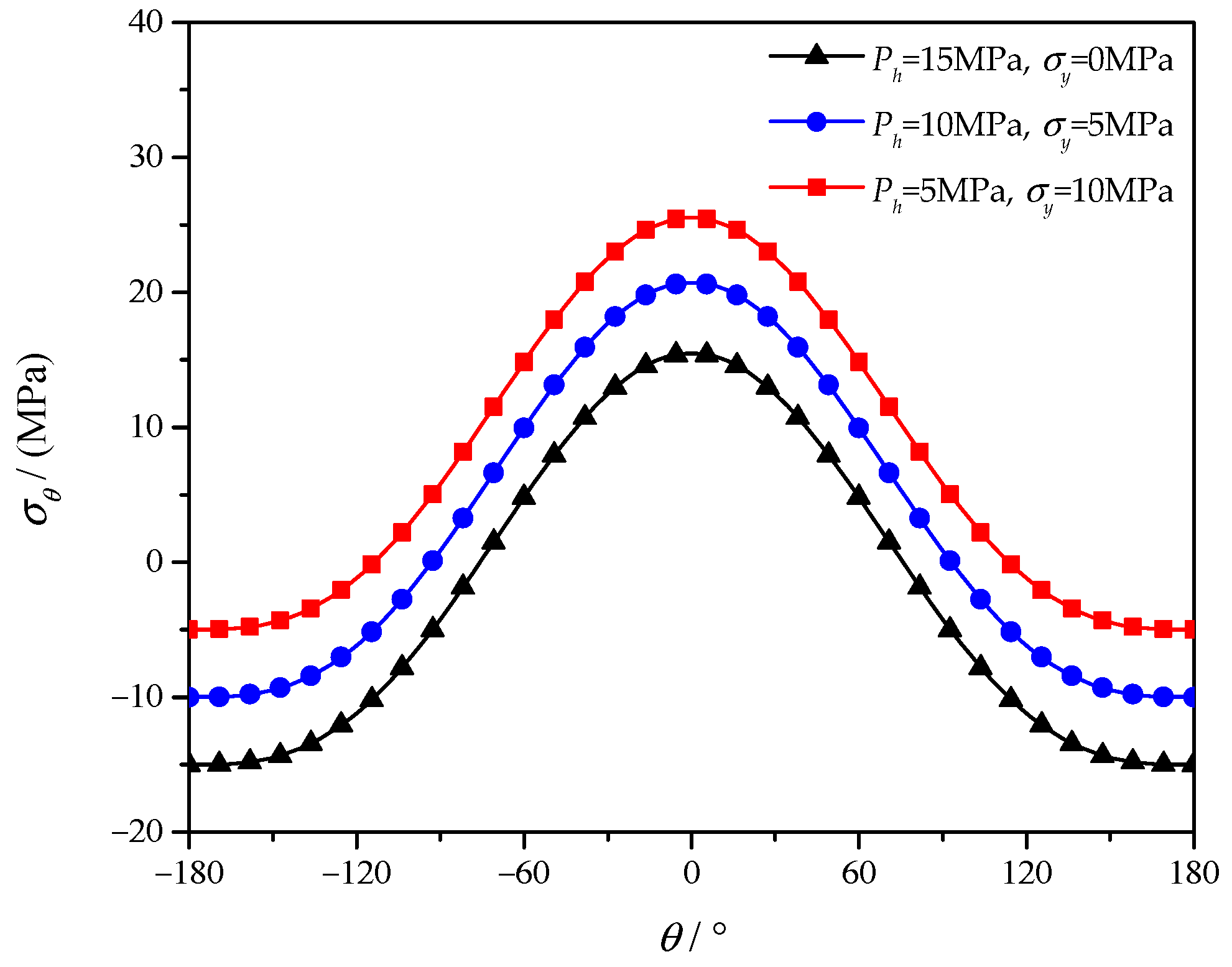
4.2. Effect of Loading Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Jia, J.S. Experimental study on the influence of hydraulic fracturing on high concrete gravity dams. Eng. Struct. 2017, 13, 2508–2517. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Su, K.; Wu, H.G. Hydro-mechanical interaction analysis of high pressure hydraulic tunnel. Tunn. Undergr. Space Technol 2015, 47, 28–34. [Google Scholar] [CrossRef]
- Yi, W.; Rao, Q.H.; Sun, D.L.; Shen, Q.Q.; Zhang, J. A new integral equation method for calculating interacting stress-intensity factors of multiple holed-cracked anisotropic rock under both far-field and arbitrary surface stresses. Int. J. Rock Mech. Min. Sci. 2021, 148, 104926. [Google Scholar] [CrossRef]
- Cheng, Y.X.; Zhang, Y.J.; Yu, Z.W.; Hu, Z.J. Investigation on reservoir stimulation characteristics in hot dry rock geothermal formations of china during hydraulic fracturing. Rock Mech. Rock Eng. 2021, 54, 3817–38452. [Google Scholar] [CrossRef]
- Cui, Z.D.; Liu, D.A.; Zeng, R.S.; Niu, J.R.; Wang, H.J.; Shi, X.S. Resistance of caprock to hydraulic fracturing due to CO2 injection into sand lens reservoirs. Eng. Geol. 2013, 164, 146–154. [Google Scholar] [CrossRef]
- Chen, W.H.; Chang, C.S. Analysis of multiple cracks in an infinite plate under arbitrary crack surface tractions. Arch. Appl. Mech. 1990, 60, 202–212. [Google Scholar] [CrossRef]
- Niu, J.; Wu, M.S. Analysis of Asymmetric Kinked Cracks of Arbitrary Size, Location and Orientation—Part I. Remote Compression. Int. J. Fract. 1998, 89, 19–57. [Google Scholar] [CrossRef]
- Rohde, L.; Kienzler, R.; Herrmann, G. On a new method for calculating stress-intensity factors of multiple edge cracks. Philos. Mag. 2005, 85, 4231–4244. [Google Scholar] [CrossRef]
- Wang, N.; Atluri, L.H. An implementation of the Schwartz-Neumann Alternating Method for collinear multiple cracks with mixed type of boundary conditions. Comput. Mech. 1995, 16, 266–271. [Google Scholar] [CrossRef]
- Hejazi, A.A.; Ayatollahi, M.; Bagheri, R.; Monfared, M.M. Dislocation technique to obtain the dynamic stress intensity factors for multiple cracks in a half-plane under impact load. Arch. Appl. Mech. 2014, 84, 95–107. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks: A simple method of analysis. Int. J. Solids Struct. Comput. Mech. 1987, 23, 23–43. [Google Scholar] [CrossRef]
- Gorbatikh, L.; Lomov, S.; Verpoest, I. On Stress Intensity Factors of Multiple Cracks at Small Distances in 2-D Problems. Int. J. Fract. 2007, 143, 377–384. [Google Scholar] [CrossRef]
- Sapora, A.; Spagnoli, A.; Susmel, L.; Cornetti, P. A simplified approach to hydraulic fracturing of rocks based on Finite Fracture Mechanics. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3029–3042. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Li, H. Simulation of hydraulic fracture utilizing numerical manifold method. Sci. China Technol. Sci. 2015, 58, 1542–1557. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Cao, P.; Wang, W.J.; Wan, W.; Chen, R. Wing crack model subjected to high hydraulic pressure and far field stresses and its numerical simulation. J. Cent. South Univ. 2012, 19, 578–585. [Google Scholar] [CrossRef]
- Wu, H.; Settgast, R.R.; Fu, P.; Morris, J.P. An Enhanced Virtual Crack Closure Technique for Stress Intensity Factor Calculation along Arbitrary Crack Fronts and the Application in Hydraulic Fracturing Simulation. Rock Mech. Rock Eng. 2021, 54, 2943–2957. [Google Scholar] [CrossRef]
- Cheng, L.; Luo, Z.; Yu, Y.; Zhao, L.Q.; Zhou, C.L. Study on the interaction mechanism between hydraulic fracture and natural karst cave with the extended finite element method. Eng. Fract. Mech. 2019, 222, 106680. [Google Scholar] [CrossRef]
- Yi, W.; Rao, Q.H.; Luo, S.; Shen, Q.Q.; Li, Z. A New Integral Equation Method for Calculating Interacting Stress Intensity Factor of Multiple Crack-hole Problem. Theor. Appl. Fract. Mech. 2020, 107, 102535. [Google Scholar] [CrossRef]
- Shen, Q.Q.; Rao, Q.H.; Sun, D.L.; Yi, W.; Huang, D.Y.; Li, Z. A new optimization method of double-crack distributions for improving network fracture conductivity of natural gas exploitation. Theor. Appl. Fract. Mech. 2022, 122, 103655. [Google Scholar] [CrossRef]
- Chang, J.H.; Wu, D.J. Calculation of mixed-mode stress intensity factors for a crack normal to a bimaterial interface using contour integrals. Eng. Fract. Mech. 2003, 70, 1675–1695. [Google Scholar] [CrossRef]
- Ševeček, O.; Kotoul, M.; Profant, T.; Hrstka, M. Crack kinking out of interface of two orthotropic materials under combined thermal/mechanical loading. Theor. Appl. Fract. Mech. 2020, 105, 102397. [Google Scholar] [CrossRef]
- Huang, D.Y.; Ma, Y.; Rao, Q.H.; Yi, W.; Shen, K. A new semi-analytic method for calculating the thermal–mechanical coupling stress intensity factor of interfacial crack. Theor. Appl. Fract. Mech. 2023, 128, 104156. [Google Scholar] [CrossRef]
- Karlsson, A.; Bäcklund, J. J-integral at loaded crack surfaces. Int. J. Fract. 1978, 14, R311–R318. [Google Scholar] [CrossRef]
- Song, H.; Rahman, S.S. An extended J-integral for evaluating fluid-driven cracks in hydraulic fracturing. J. Rock Mech. Geotech. Eng. 2018, 10, 832–843. [Google Scholar] [CrossRef]
- Huang, D.Y.; Rao, Q.H.; Ma, Y.; Yi, W.; Shen, Q.Q. A modified semi-weight function method for stress intensity factor calculation of a vertical crack terminating at the interface. Theor. Appl. Fract. Mech. 2021, 116, 103107. [Google Scholar] [CrossRef]
- Rice, J.R. Mathematical analysis in the mechanics of fracture. Fract. Adv. Treatise 1968, 2, 191–311. [Google Scholar]
- Bahrami, B.; Nejati, M.; Ayatollahi, M.R.; Driesner, T. Theory and experiment on true mode II fracturing of rocks. Eng. Fract. Mech. 2020, 240, 107314. [Google Scholar] [CrossRef]

| β | Analytical Method [26] | XFEM [17] | Present |
|---|---|---|---|
| 0° | 30.0773 | 30.0795 | 30.1446 |
| 20° | 27.7302 | 27.7338 | 27.9503 |
| 40° | 21.7938 | 21.7941 | 21.9319 |
| 60° | 15.0386 | 15.0398 | 15.1547 |
| 80° | 10.6345 | 10.6371 | 10.8092 |
| 90° | 10.0218 | 10.0265 | 10.1654 |
| No. | Dh (mm) | Dv (mm) | α (°) | β (°) |
|---|---|---|---|---|
| 1 | 10 | 40 | 85 | 5 |
| 2 | 10 | 40 | 50 | 5 |
| 3 | 10 | 30 | 85 | 5 |
| Point | A | B | C | D | |
|---|---|---|---|---|---|
| No.1 | |||||
| Shen [19] | K1 (MPa·mm0.5) | −59.76 | −60.83 | −43.09 | −41.95 |
| K2 (MPa·mm0.5) | −3.19 | −4.22 | 3.18 | −3.90 | |
| Present | K1 (MPa·mm0.5) | −60.24 | −61.51 | −43.7 | −42.13 |
| K2 (MPa·mm0.5) | −3.23 | −4.32 | 3.11 | −3.79 | |
| No.2 | |||||
| Shen [19] | K1 (MPa·mm0.5) | −57.21 | −58.38 | −54.82 | −48.94 |
| K2 (MPa·mm0.5) | −1.02 | −6.27 | 11.36 | 13.19 | |
| Present | K1 (MPa·mm0.5) | −58.17 | −58.99 | −55.25 | −49.73 |
| K2 (MPa·m0.5) | −0.97 | −6.07 | 11.48 | 13.30 | |
| No.3 | |||||
| Shen [19] | K1 (MPa·mm0.5) | −59.65 | −65.14 | −43.36 | −40.86 |
| K2 (MPa·mm0.5) | −1.35 | −3.39 | −1.43 | −9.82 | |
| Present | K1 (MPa·mm0.5) | −60.13 | −65.72 | −44.11 | −41.68 |
| K2 (MPa·mm0.5) | −1.27 | −3.28 | −1.27 | −9.55 | |
| b/6 | b/3 | b/2 | 2b/3 | 5b/6 | |
|---|---|---|---|---|---|
| Point A | 92.151 | 92.153 | 92.150 | 92.152 | 92.152 |
| Point B | 99.259 | 99.257 | 99.260 | 100.924 | 101.812 |
| Ph = 15 MPa σy = 0 MPa | Ph = 10 MPa σy = 5 MPa | Ph = 5 MPa σy = 10 MPa | |
|---|---|---|---|
| Point A | 92.151 | 92.151 | 92.150 |
| Point B | 99.301 | 99.259 | 99.224 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Huang, D.-y.; Zhang, L.; Li, C.; Qi, H. A New Semi-Analytical Method for the Calculation of Multi-Crack Stress-Intensity Factors under Hydro-Mechanical Coupling. Appl. Sci. 2024, 14, 7083. https://doi.org/10.3390/app14167083
Zhang L, Huang D-y, Zhang L, Li C, Qi H. A New Semi-Analytical Method for the Calculation of Multi-Crack Stress-Intensity Factors under Hydro-Mechanical Coupling. Applied Sciences. 2024; 14(16):7083. https://doi.org/10.3390/app14167083
Chicago/Turabian StyleZhang, Lan, Dian-yi Huang, Lei Zhang, Changmin Li, and He Qi. 2024. "A New Semi-Analytical Method for the Calculation of Multi-Crack Stress-Intensity Factors under Hydro-Mechanical Coupling" Applied Sciences 14, no. 16: 7083. https://doi.org/10.3390/app14167083




