Abstract
Tool holders are one of the most important structures in transferring machine tools and energy for manufacturing in CNC lathe. Power servo tool holders influence kinematic accuracy and machining accuracy and so are vital to the transposition system. Reliability evaluation is also critical to guaranteeing and maintaining the accuracy of the transposition system. The first four statistical moments are derived to depict the transmission error and system characteristics. Considering the Edgeworth expansion with higher terms, reliability and reliability-based sensitivity evaluations using moments are proposed to assess system accuracy. Compared with different methods, the proposed method can represent higher statistical characteristics, helping to avoid underestimations of system reliability. Also, results calculated with the proposed method for the transposition system are in agreement with the results from the Monte Carlo simulation with 107 samples. The relative error of failure probability is 4.32%. Considering the plus–minus sign and values of results, reliability-based sensitivity represents the effects of the parameters’ dispersions on system reliability. The reliability-based sensitivity indices can be utilized to optimize the system structure and to improve system accuracy, which can increase the system reliability from 98.34% to 99.99% in the transposition system of the power servo tool holder.
1. Introduction
The importance of CNC (Computer Numerical Control) machine tools cannot be overstated in today’s manufacturing industry. They represent the pinnacle of precision and efficiency, enabling manufacturers to produce complex parts and components with unprecedented accuracy and speed. CNC machine tools are essential for maintaining competitiveness in a globalized market, where demand for high-quality, cost-effective products is constantly rising. Based on different signals, researchers have analyzed different characteristics to enhance the transposition system’s performance. The cutting force signals and vibration signals have been investigated to design an intelligent tool holder. Also, the offline wear measurement of the face-milling cutter has been analyzed for the tool replacement [1]. Considering the dynamic responses of the transposition system in CNC, the vibration transmission path has been established, and the reliability indices have been analyzed with the degradation of stiffness in the servo turret [2]. The structure of the tool holder was designed by optimization, in which the required reliability index is used as the constraint and the detection accuracy is the highest as a target [3]. An integral smart toolholder with unique on-toolholder force sensing units [4] has been proposed to analyze the milling force and dynamic performance [5]. Also, a symmetric structure of tool servo was designed for a high tracking accuracy [6]. Considering the coupling effect between the servo axis dynamics and the cutting force, a dynamic surface generation model [7] was established for forming error and working precision. The effects of the misalignment of diaphragm coupling, caused by assembly, were analyzed, and the accuracy reliability of the motorized spindle was investigated [8]. The related proportional-integral controller and feed-forward compensation methods have been established for the system performance [9]. A systematic design of the power servo tool holder was analyzed with free force and motion functions based on computational science methods [10]. Vital to the transposition system, the power servo tool holder is one of the most imperative structures to transfer power and maintain precision for manufacturing. The accuracy is regarded as the vital index used to evaluate system performance in the transposition system of power servo tool holders.
Reliability analysis is a widely used tool used to measure a structure’s ability to fulfill safety and serviceability requirements, such as accuracy and strength. Based on the field failure data, a two-parameter exponential distribution is utilized for the description of the time between failures of the CNC system among different distributions [11]. A Bayesian network model is developed to conduct a comprehensive reliability analysis of the main drive systems of a heavy boring and milling machine tool [12], in which early failures of the main drive systems are considered. The relations of failure correlation among subsystems are integrated for the reliability evaluation of CNC [13]. Also, the failure mode and effects analysis have been investigated on the basis of cubic transformed functions of system responses [14]. Each subsystem of CNC is modeled by a different distribution based on collected data and the models are optimized by the modified gray correlation degree, which is called the similar slope and close median gray correlation method [15]. Methods of generating random data have been proposed for different models. The reliability evaluation algorithm based on the Monte Carlo simulation has been studied and the whole machine’s reliability of the CNC grinder can be evaluated with the proposed algorithm [16]. The phenomenon of the degradation of probe accuracy during measurements was investigated, and the most effective parameters were excavated for the degradation process [17]. Based on multiple non-correlated and correlated degradation data, a reliability assessment approach was investigated, focusing on a small data sample [18]. Also, considering the fault prediction and fault diagnosis, a health management system was established to evaluate the system reliability of power servo equipment [19]. According to geometric and vibration errors, a machining accuracy reliability evaluation method was investigated, based on the milling dynamics theory and the full-discretization method [20]. Considering the machining error out of tolerance, an evaluation method of accuracy reliability was proposed under different machining loads [21]. Accuracy reliability [22] and transmission error [23] are regarded as two of the most important indices to evaluate system performance. Both are influenced by the transposition system of the power servo tool holder. Qualitative and quantitative methods are utilized to investigate the reliability of the transposition system in power servo tool holders. Considering various factors, different indices and methods are analyzed for system accuracy reliability based on the use of quantitative methods.
The moment-based method for reliability evaluation attracts researchers’ attention. This method relies on the moment information of input variables rather than the probability distribution functions. The moment-based method can solve multi-dimensional reliability problems and improve the accuracy with low information [24]. The first two order moments of calculation error [25] can be estimated according to the statistical moment similarity for reliability analysis. The probability density function (PDF) of a performance function can be constructed from the perspective of the first four statistical moments [26,27]. Also, the fitting method is utilized for the descriptions of high moments in order to evaluate system reliability [28]. The properties of statistical moments of standard normal distribution parameters are utilized to improve the high-order statistical moment method for the stable and accurate calculation of structural reliability analysis with insufficient data [29]. The first four moments of random input variables are derived to improve the accuracy of the reliability prediction based on the statistical properties of the standard normal random variable [30]. The first three statistical moments and fault trees [31] are combined to optimize resource allocations for reliability improvement. An improved high-order moment-based saddle-point approximation method for reliability analysis is presented [32], and the reliability-based sensitivity [33] has been investigated to quantify the influences of different parameters in engineering. Also, the maximum entropy and different order moments [34] are utilized for the approximation of the reliability-based sensitivity index. The first four statistical moments can be utilized to evaluate system reliability with high-order characteristics and different performances. Also, based on statistical moments, reliability-based sensitivity can present the parameters’ influences and changing laws in engineering, which supports the need for system optimization and equipment upgrading.
Reliability evaluation and reliability-based sensitivity are investigated for the transposition system in the power servo tool holders of CNC. Based on statistical moments, the reliability method is proposed for accurately measuring system performance with random effects. Also, the reliability-based sensitivity with high-order moments is proposed to analyze the effects of different parameters in complex system analysis and design. This method is utilized to assess the system accuracy of the transposition system in the power servo tool holder. In Section 2, responses of the transposition system are investigated. The first four statistical moments are derived to depict the system characteristics in Section 3. Reliability and reliability-based sensitivity evaluation methods are proposed based on statistical moments in Section 4 and Section 5, respectively. Different methods are compared for their computational accuracy and rationality. Considering the manufacturing precision of the transposition system, reliability evaluation and reliability optimization are discussed in Section 6. The Conclusion is in Section 7.
2. Reponses of Transposition System in Tool Holder
The transposition system is the most important transmission structure of the power servo tool holder, as shown as Figure 1, which influences the positional accuracy of CNC machines. The transposition system is composed of gears; the main structure of SFW2512, made in China, is shown in Figure 2. The related parameters are listed in Table 1. Gear 1 is the input gear, and gear 4 is the output gear in the transposition system. Also, dual gear 2 and dual gear 3 are utilized to transfer power and extend torque. The transmission system in Figure 2 can determine the position precision of the transposition system, or even influence the movement of cutting tools in the power tool servo.
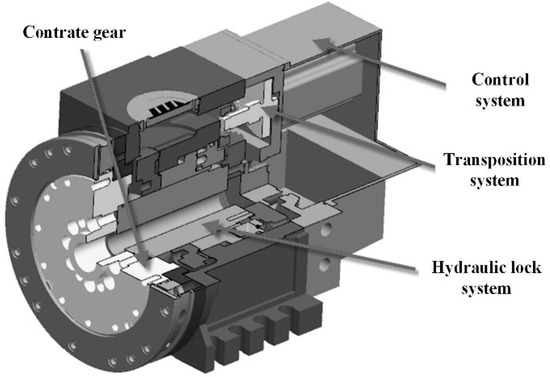
Figure 1.
Power tool servo SFW2512.
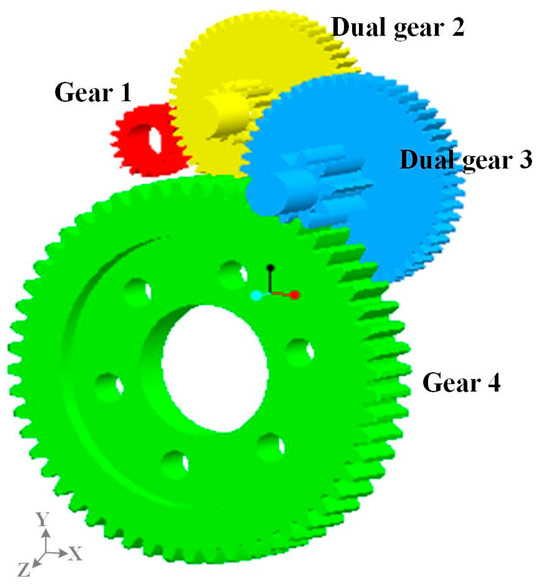
Figure 2.
Transposition system.

Table 1.
Basic parameters of transposition system.
In Figure 2, the basic parameters of the transposition system, such as the modulus and the coordinates of each gear center, are shown as listed in Table 1. The installation accuracy is an important factor for the transposition system, which is influenced by the mounting positions of the gears. Also, the transmission process is a cumulative process for the system. The rotational angle of gear 4 is affected by the rotational processes of gear 1, dual gear 2, and gear 4.
Transmission error can be used to evaluate the dynamic process of the transposition system power tool servo SFW2512 shown in Table 1. Depending on the rotational angle of gear 1, the transmission error can be defined as E = θ4 − (i12i23i34)θ1, where the parameters of θ4 and θ1 present rotational angles of gear 4 and gear 1, respectively. Parameters i12, i23, and i34 are the transmission ratios shown in Table 1. Based on the ADAMS simulation [35,36], the dynamic transmission error of the transposition system is shown in Figure 3.
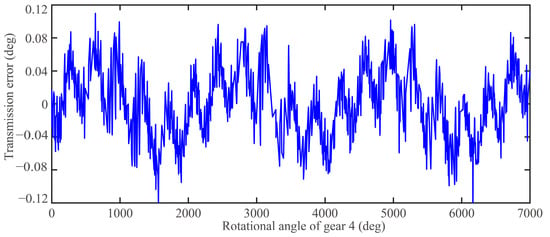
Figure 3.
Dynamic transmission error of transposition system.
In Figure 3, the transmission error is shown to vary across time based on the operation of the transposition system. However, the appearance of extreme responses can reduce the accuracy of the transposition system. Based on the transmission error, system reliability should be analyzed for the performance of the transposition system in the power tool servo.
3. System Statistical Moments
The performance function of the transposition system can be presented as function Z, Z = gX(X), and random variables can be depicted as X = [X1, X2, …, Xn]T. In the transposition system, the performance function can be represented as Z = gX(X) = ξ − E = ξ − [θ4 − (i12i23i34)θ1], in which ξ can be regarded as the threshold value. Random variables X can be regarded as X- and Y-coordinates of gear 1, 2, 3, and 4 in Table 1. Function Z can be established by a surrogate model, such as the response surface method [37,38]. Considering the computation and information quantity of function Z, the Taylor series up to the third term is taken to truncate the performance function. Hence, gX(X) at point x* can be indicated by
The last term o[ ] is the higher-order infinitesimal remainder, which can be ignored. The second degree of the Taylor series is considered. The symbol ∇gX () with x* = μ can be defined by
Also, the symbol ∇2gX () can be expressed as
The first four order center moments of X can be depicted as μx1, μx2, μx3, and μx4 in turn. The ζth center moment μxζ can be expressed as μxζ= [], ζ = 1,2,3,4, and n = 1, 2, 3, …. Based on Equation (1), the mean value μz1 of performance function Z can be expressed as
in which
Hence, the mean value μz1 of the transposition system can be presented by
The variance μz2 of the function Z can be expressed as . According to Equations (1) and (6), the variance μz2, the second center moment, can be expressed as
The third center moment μz3 of the performance function Z can be expressed as
Similarly, the fourth center moment μz4 of function Z is approximatively expressed as
Based on the statistical moments μxζ of random variables, the moment {μz1, μz2, μz3, μz4} can be computed from Equation (6) to Equation (9), which can be utilized to evaluate the system’s performance. The mean value and variance present the center location and the dispersion degree of responses, respectively. The third center moment can depict the skewed direction and degree, and the fourth center moment can present the asymmetry degree of g(X). Hence, different cases, normal and non-normal distributions, are considered for reliability evaluation. More information can be utilized to evaluate system performance based on statistical moments. The relationship between random variables and system responses can be established via the first four statistical moments of the transposition system.
4. Reliability Evaluation by Moments
These statistical moments can describe the distribution characteristics of system performance in engineering. The variation coefficient can be utilized to depict the dispersion degree of the mechanical property parameter, which is the ratio of standard deviation to the mean. In engineering, the variation coefficient is always assumed to be less than 5%. For a mechanical property parameter, the variation coefficient is always less than 0.05, which is utilized to express the uncertainty and randomness. Hence, parameter ε is defined as 0 < ε ≪ 1, and random variable X in the function Z = gX(X) can be represented by X = Xd + εXp and E(X) = μx1 = E(Xd) + εE(Xp) = Xd. Parameters Xd and εXp can be regarded as the main distribution and residual error, respectively. Also, other moments of X can be depicted by
in which (·)[β] = (·)[β−1]⊗(·) = (·)⊗(·)⊗…⊗(·) is the Kronecker operator, and ⊗ is regarded as the Kronecker product, (A)p×q⊗(B)s×t = [aijB]ps×qt. The relation, from Equation (10) to Equation (12), can be utilized to simplify the equations of high statistical moments in Section 3. Neglecting the terms εγ with γ ≥ 3, the covariance μz2, Equation (7), of the performance function Z can be expressed as
Also, the third center moments of the function Z can be expressed as
Considering the relation between and in Equation (9), partial items can be offset by each other. Hence, the fourth moment μz4 of the function Z can be approximated as
Hence, μz2, μz3, and μz4 can be simplified by Equations (13), (14), and (15) approximately and conveniently. The statistical moment μz1 can be calculated by Equation (6). Those equations can be utilized to evaluate the statistical characteristics of the system’s response. Considering the arbitrary distribution of system response Z, the Edgeworth series is considered to represent the cumulative distribution function F(Z) as follows:
where functions Φ() and φ() are the cumulative distribution function (CDF) and probability density function (PDF) of the normal distribution, respectively. Function Hj(Z) is the jth Hermite polynomial function. The recursion formula can be calculated using
Hence, the reliability index can be expressed as R(β) = [g(X) > 0] = 1−F(−β), and β = μz1(μz2)−1/2. The reliability index R(β) can be utilized to analyze the safety of system performance in engineering. According to the simplified statistical moments, the CDF of the system responses can be used for the reliability evaluation of the transposition system.
5. Reliability-Based Sensitivity Analysis
Based on the reliability evaluation method, reliability-based sensitivity is always used to investigate the relationship between random variables and system reliability. The changing rule of system parameters can be analyzed via the indices of reliability-based sensitivity. Based on Equation (16), the derivative of reliability index β, β = μz1(μz2)−1/2 is investigated to represent the reliability-based sensitivity as follows:
According to the formula of β, the derivative can be expressed as ∂β/∂μz1 = 1/(μz2)1/2. Also, the relationship between reliability index R and mean value μx1 can be expressed as
Introducing Equation (18) into Equation (19), the mean value reliability-based sensitivity can be achieved, which can evaluate the effects of the parameters in the transposition system of the power tool servo. Similarly, the derivative of β can be derived by ∂β/∂μz2 = −μz1/(2μz23/2). Considering the relationship in Equation (16), the derivative of R(β) can be calculated by
Based on the calculation law, the reliability-based sensitivity of covariance is expressed as
Based on Equation (13), Equation (21) can be rewritten as
Hence, the reliability-based sensitivity of covariance can be used to reflect the influence of the parameters’ dispersion degrees. Both the reliability-based sensitivity of the mean value and covariance can represent the relationship between system reliability and the parameters in the transposition system, which is beneficial for controlling and optimizing.
6. Reliability Analysis for Transposition System
6.1. Reliability Evaluation
According to the transposition system in Figure 2, coordinates (X1,Y1), (X2,Y2), (X3,Y3), and (X4,Y4), are the vital parameters for the gears’ center positions. Parameters X1, Y1, X2, Y2, X3, Y3, X4,, and Y4 can be regarded as eight independent random variables. The mean value μXi1 (i = 1, 2, …, 8) is listed in Table 1. Based on the mean values, the center distances of each gear are a1= 53.59 mm, a2 = 56.87 mm, and a3 = 95.50 mm, respectively. Considering the manufacturing precision, the limit deviation of each gear center is set as 0.21 mm, and the standard deviation (μXi2)0.5 of each coordinate can be set as 0.035 mm. Also, other statistical moments of the transposition system are listed in Table 2. Based on Table 1 and Table 2, the first four moments can be used for the description of the distribution range of each gear.

Table 2.
Moments of random variables in transposition system.
Considering the maximum allowed angle error ξ = 0.04° of Z = gX(X) = ξ − E, Equations (16) and (17) are utilized for the system reliability of the transposition mechanism in SFW2512. The reliability index can be calculated, β = 2.1393 and R = 0.983795, which is compared with the Monte Carlo simulation [39,40] with 107 samples. Comparing them with the FOSM (First-Order Second-Moment) and AFOSM (Advanced First-Order Second-Moment) methods, the results of the system reliability evaluation are listed in Table 3. The results calculated with the proposed method for the transposition system are in agreement with the results from the Monte Carlo simulation with 107 samples. The failure probability is an important factor in evaluating the calculation error. Based on Table 3, the probability values of the proposed method and the Monte Carlo simulation are Pf1 = 0.0162 and Pf2 = 0.0169. The relative error of failure probability is 4.32%. Regardless of the higher statistical characteristics, system reliability is underestimated.

Table 3.
Comparison of results of four methods.
Based on the Monte Carlo simulation, the values of the reliability index and the failure probability are shown in Figure 4. The value achieved by the Monte Carlo simulation approaches 0.9831 with the increasing of the sample size. However, a large number of samples is needed for the improvement of calculation accuracy. Results calculated using the proposed method are in agreement with results calculated through the Monte Carlo simulation with 107 and 108 samples. The calculated result is stable, based on a huge number of samples. The Monte Carlo simulation with 109 samples can also maintain the computational accuracy of the reliability index and the failure probability, costing extensive computational resources.
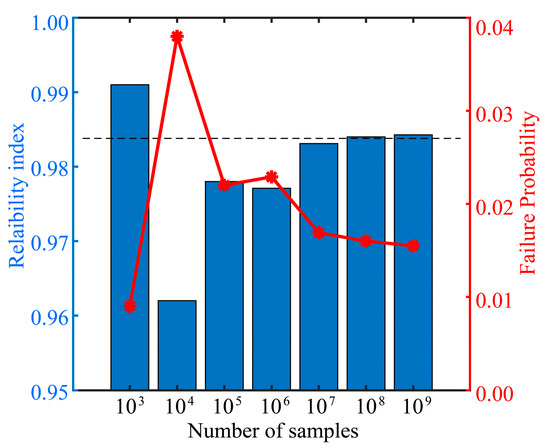
Figure 4.
Results between proposed method and Monte Carlo simulation with different samples.
Also, the reliability-based sensitivity indices of mean value and covariance are computed as shown in Table 3 and Equation (23), respectively. Compared with the Monte Carlo simulation, the indices of the reliability-based sensitivity are presented in Figure 5 and Figure 6, respectively.
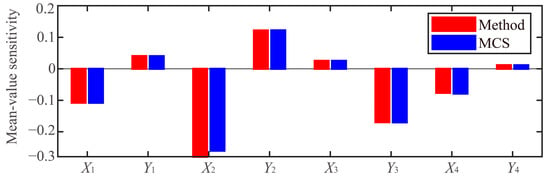
Figure 5.
Reliability-based sensitivity for random variables’ mean values.
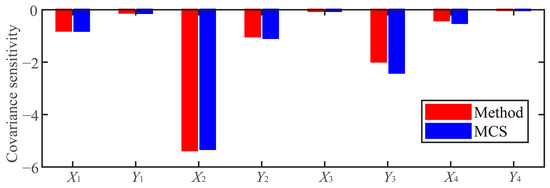
Figure 6.
Reliability-based sensitivity for random variables’ covariance.
In Figure 5, the parameters of dual gear 2 have greater impacts on system reliability than other gears in the transposition system of power tool servo SFW2512. Considering the plus or minus sign, the increases in mean values X1, Y2, X3, and Y4 can improve system reliability. However, the decreases in mean values Y1, X2, Y3, and X4 can reduce system reliability. In Figure 6, both the proposed method and the Monte Carlo simulation are considered to calculate the indices of the covariance reliability-based sensitivity, representing the effects of the parameters’ dispersions on system reliability. Considering the minus sign, the increases in each parameter can decrease system reliability, which makes it difficult to guarantee the system’s performance and accuracy. Also, the positions of dual gear 2 and dual gear 3 are more important than those of the other gears in the SFW2512.
6.2. Reliability Optimization
Based on the rules of reliability and reliability-based sensitivity, the mean values of the gears’ positions are regarded as design variables, (μX11, μX21, μX31, μX41, μX51, μX61, μX71, μX81). Also, the indices of the mean value reliability-based sensitivity are defined as the optimization object H(X), which can be written as
The constraint condition of the reliability index can be defined by R > Ru, Ru = 0.99. The scope of the design variables can be depicted as
The constraint conditions of center distances can be depicted as
in which parameter av = 0.5m(zv + zv + 1)cos20°/cosα’, v = 1, 2, 3, and α’ is the working pressure angle [41]. Based on Table 3, the initial optimization object H(X) is 0.3693. Considering the constraint conditions and scopes of the parameters, the optimization object H(X) can be reduced to 4.762 × 10−10. Table 4 shows the parameters after optimization, and the system reliability of the transposition system can be increased from 0.983795 to 0.999998.

Table 4.
Comparison of parameters after optimization.
According to the optimization model, the indices of the reliability-based sensitivity can be decreased, and the reliability index can be increased. The effects of the positions’ parameters can be reduced, which is beneficial for system performance. Considering the same standard deviation of each parameter, the reliability of the transposition system can also be enhanced in tool holders with the recommended values.
7. Conclusions
Reliability evaluation is the critical approach to guaranteeing and maintaining the accuracy of the transposition system in the power servo tool holder of CNC. Based on system responses, the first four statistical moments are derived to depict the system characteristics. Considering Kronecker operators and Edgeworth expansion, the reliability evaluation and reliability-based sensitivity by moments are proposed to present the system accuracy and performance. Also, results calculated with the proposed method for the transposition system are in agreement with the results from the Monte Carlo simulation with 107 samples. When compared with different methods, the proposed method can represent higher statistical characteristics, in order to prevent underestimations of system reliability. Considering the plus–minus sign, reliability-based sensitivity represents the effects of the parameters’ dispersions on system reliability. The sensitivity indices can be utilized to optimize the system structure and to improve system accuracy. Also, the positions of dual gear 2 and dual gear 3 are more important than those of the other gears in the transposition system of the power servo tool holder. Based on the first four statistical moments, reliability and reliability-based sensitivity can be evaluated. A complex system with a high variation coefficient can decrease the calculation accuracy, and this needs to be investigated further. The influence of the axis distance needs to be investigated in depth for reliability-based optimization. Also, the time-varying reliability and the parameters’ correlations can be analyzed based on the reliability evaluation method in the future.
Author Contributions
Methodology, D.Z.; Software, G.G.; Formal analysis, Y.G.; Resources, Q.M.; Supervision, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the Shanghai Scientific Research project (No. 22511103604) and the Fundamental Research Fund for the Central Universities (2232023D-17). Also, this project was supported by the Foundation of Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education (VCAME202104), which received support from Northeastern University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- An, Q.L.; Yang, J. A State-of-the-art Review on the Intelligent Tool Holders in Machining. Intell. Sustain. Manuf. 2024, 1, 10002. [Google Scholar] [CrossRef]
- Zhu, L.S.; Li, L.S. Research on Reliability for Servo Turret Based on Vibration Transmission Path System with Stiffness Degradation Model. Math. Probl. Eng. 2020, 2020, 3764546. [Google Scholar] [CrossRef]
- Wu, F.H.; Li, Y.X. The Design of Force Measuring Tool Holder System Based on Wireless Transmission. IEEE Access 2018, 6, 38556–38566. [Google Scholar] [CrossRef]
- Zhang, P.F.; Gao, D. A Novel Smart Toolholder with Embedded Force Sensors for Milling Operations. Mech. Syst. Signal Process 2022, 175, 109130. [Google Scholar] [CrossRef]
- Liu, J.F.; Luo, T.C. A Novel Fast Servo Tool Device with Double Piezoelectric Driving. Micromachines 2023, 14, 85. [Google Scholar] [CrossRef]
- Chen, Y.L.; Li, Z.W. Development of an Optimized Three-Axis Fast Tool Servo for Ultraprecision Cutting. IEEE/ASME Trans. Mech. 2022, 27, 3244–3254. [Google Scholar] [CrossRef]
- Huang, P.; Wu, X.Y. Deterioration of Form Accuracy Induced by Servo Dynamics Errors and Real-Time Compensation for Slow Tool Servo Diamond Turning of Complex-Shaped Optics. Int. J. Mach. Tools Manuf. 2020, 154, 103556. [Google Scholar] [CrossRef]
- Wang, L.P.; Zhu, B. Dynamic Performance Evaluation of Parallel Manipulators and Its Application in a 5-Axis Loading Device. Multibody Syst. Dyn. 2022, 56, 49–67. [Google Scholar] [CrossRef]
- Zhao, D.P.; Du, H.H. Development of a Novel Fast Tool Servo Using Topology Optimization. Int. J. Mech. Sci. 2023, 250, 108283. [Google Scholar] [CrossRef]
- Kriechenbauer, S.; Müller, P. Evolutionary Optimization of Deep-Drawing Processes on Servo Screw Presses with Freely Programmable Force and Motion Functions. Procedia CIRP 2021, 104, 1482–1487. [Google Scholar] [CrossRef]
- You, D.Z.; Pham, H. Reliability Analysis of the CNC System Based on Field Failure Data in Operating Environments. Qual. Reliab. Eng. Int. 2016, 32, 1955–1963. [Google Scholar] [CrossRef]
- Li, H.; Deng, Z.M. Reliability Analysis of the Main Drive System of a CNC Machine Tool Including Early Failures. Reliab. Eng. Syst. Saf. 2021, 215, 107846. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.M. A Reliability Allocation Method of CNC Lathes Based on Copula Failure Correlation Model. Chin. J. Mech. Eng. 2018, 111, 31. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, Y.P. Comprehensive Reliability Allocation Method for CNC Lathes Based on Cubic Transformed Functions of Failure Mode and Effects Analysis. Chin. J. Mech. Eng. 2015, 28, 315–324. [Google Scholar] [CrossRef]
- Liu, Y.J.; Peng, H. Reliability Modeling and Evaluation Method of CNC Grinding Machine Tool. Appl. Sci. 2019, 9, 14. [Google Scholar] [CrossRef]
- Zhang, K.Y.; Jia, Z.X. Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch. Appl. Sci. 2023, 13, 4951. [Google Scholar] [CrossRef]
- Rępalska, M.; Woźniak, A. Reliability of probes for CNC machine tools. Precis. Eng. 2024, 88, 767–776. [Google Scholar] [CrossRef]
- Duan, C.Q.; Deng, C. Reliability Assessment for CNC Equipment Based on Degradation Data. Int. J. Adv. Manuf. Technol. 2019, 100, 421–434. [Google Scholar] [CrossRef]
- Cheng, Q.; Cao, Y. A Health Management Technology Based on PHM for Diagnosis, Prediction of Machine Tool Servo System Failures. Appl. Sci. 2024, 14, 2656. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, Y.J. Machining Accuracy Reliability Evaluation of CNC Machine Tools Based on the Milling Stability Optimization. Int. J. Adv. Manuf. Technol. 2023, 124, 4057–4074. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhang, Y.J. Accuracy Reliability Analysis of CNC Machine Tools Considering Manufacturing Errors Degrees. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2024, 2383, 643–653. [Google Scholar] [CrossRef]
- Okwudire, C.E.; Lu, X. A Three-Tier Redundant Architecture for Safe and Reliable Cloud-Based CNC over Public Internet Networks. Robot. Comput. Manuf. 2020, 62, 101880. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.M. Investigation on the Multifactor Reliability Allocation Method for CNC Lathes Based on Modified Criticality and Objective Information. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1647–1656. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H. Moment-Based Evaluation of Structural Reliability. Reliab. Eng. Syst. Saf. 2019, 181, 38–45. [Google Scholar] [CrossRef]
- Wu, J.H.; Tian, P.P. Reliability Analysis of Industrial Robot Positional Errors Based on Statistical Moment Similarity Metrics. Appl. Math. Model. 2024, 131, 1–21. [Google Scholar] [CrossRef]
- Xu, J.; Kong, F. An Efficient Method For Statistical Moments and Reliability Assessment of Structures. Struct. Multidiscip. Optim. 2018, 58, 2019–2035. [Google Scholar] [CrossRef]
- Ding, C.; Xu, J. An Improved Adaptive Bivariate Dimension-Reduction Method for Efficient Statistical Moment and Reliability Evaluations. Mech. Syst. Signal Process. 2021, 149, 107309. [Google Scholar] [CrossRef]
- Low, Y.M. A New Distribution for Fitting Four Moments and Its Applications to Reliability Analysis. Struct. Saf. 2013, 42, 12–25. [Google Scholar] [CrossRef]
- Zhang, T.X.; He, D. An Improved High-Order Statistical Moment Method for Structural Reliability Analysis with Insufficient Data. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1050–1056. [Google Scholar] [CrossRef]
- Zhang, T.X. An Improved High-Moment Method for Reliability Analysis. Struct. Multidiscip. Optim. 2017, 56, 1225–1232. [Google Scholar] [CrossRef]
- Yılmaz, E.; Brian, J.G. Optimizing Resource Allocations to Improve System Reliability via the Propagation of Statistical Moments through Fault Trees. Reliab. Eng. Syst. Saf. 2023, 230, 108873. [Google Scholar] [CrossRef]
- Lu, H.; Cao, S. An Improved High Order Moment-Based Saddle-point Approximation Method for Reliability Analysis. Appl. Math. Model. 2020, 82, 836–847. [Google Scholar] [CrossRef]
- Zhou, D.; Pan, E.S. Dynamic Model-based Saddle-point Approximation for Reliability and Reliability-based Sensitivity Analysis. Reliab. Eng. Syst. Saf. 2020, 201, 106972. [Google Scholar] [CrossRef]
- Zhang, X.F.; Liu, J.K.; Yan, Y.; Pandey, M. An Effective Approach for Reliability-Based Sensitivity Analysis with the Principle of Maximum Entropy and Fractional Moments. Entropy 2019, 21, 649. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.L.; Xiao, Z.M.; Huan, L.R.; Fu, C. Simulation Analysis of Planetary Gears Train of Semi-Direct Drive Wind Turbine Based on ADAMS. Appl. Mech. Mater. 2015, 780–790, 311–315. [Google Scholar] [CrossRef]
- Lai, Q.; Yu, Q.; Dong, J. Dynamic Analysis of Rotary Tiller Gearbox Based on EDEM, ADAMS and ANSYS. J. Intell. Fuzzy Syst. 2019, 36, 1153–1160. [Google Scholar] [CrossRef]
- Zhou, D.; Pan, E.; Zhang, Y. Fractional polynomial function in stochastic response surface method for reliability analysis. J. Mech. Sci. Technol. 2021, 35, 121–131. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, X.; Zhang, Y. Reliability analysis on traction unit of shearer mechanism with response surface method. J. Mech. Sci. Technol. 2017, 31, 4679–4689. [Google Scholar] [CrossRef]
- Zhu, Z.F.; Du, X.P. Reliability Analysis with Monte Carlo Simulation and Dependent Kriging Predictions. ASME J. Mech. Des. 2016, 138, 121403. [Google Scholar] [CrossRef]
- Song, C.X.; Kawai, R. Monte Carlo and Variance Reduction Methods for Structural Reliability Analysis: A Comprehensive Review. Probab. Eng. Mech. 2023, 73, 103479. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: New York, NY, USA, 2004; pp. 23–56. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).