Analysis of the Transonic Buffet Characteristics of Stationary and Pitching OAT15A Airfoil
Abstract
:1. Introduction
2. Numerical Methods
2.1. Unsteady Aerodynamic Governing Equations
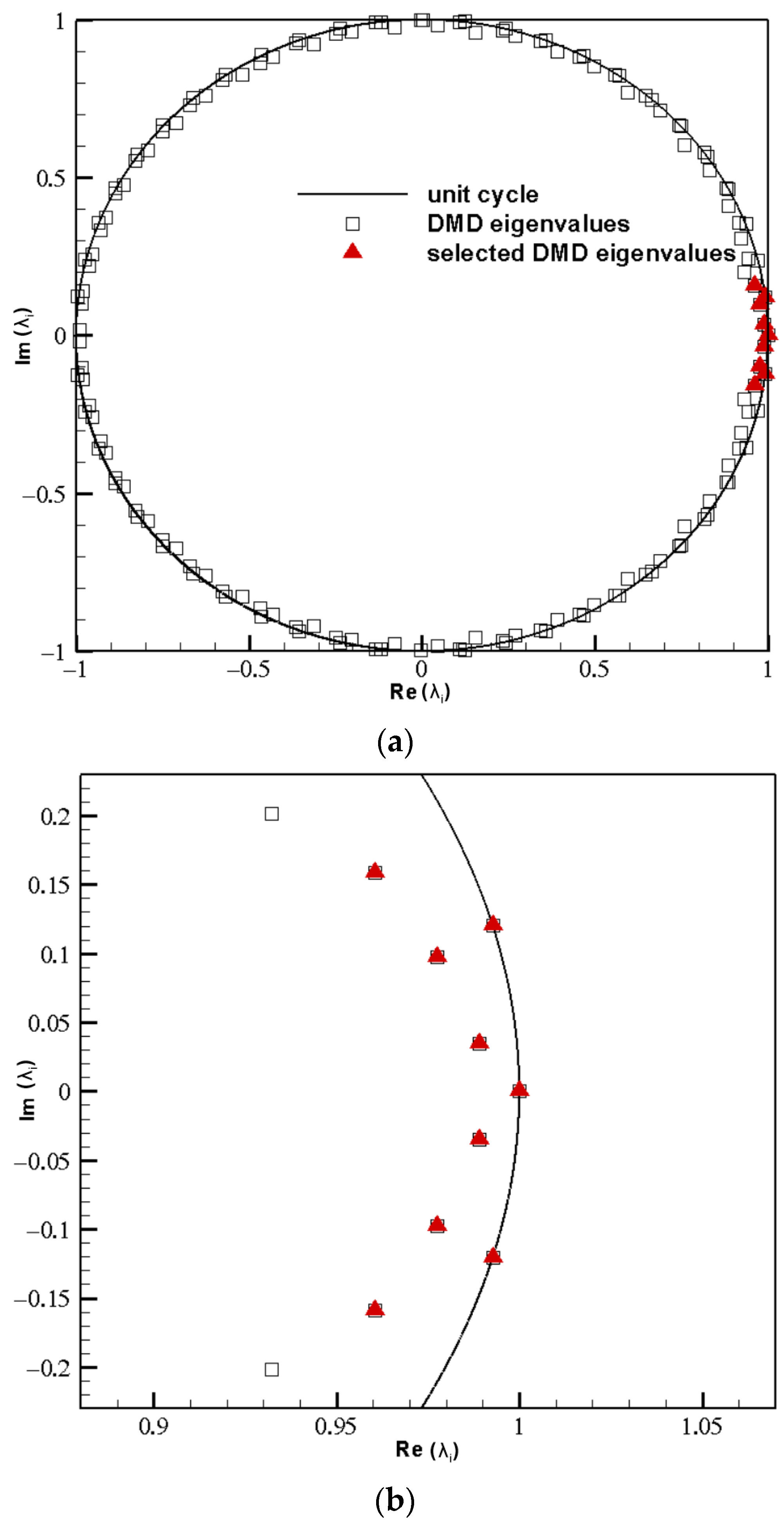
2.2. Dynamic Mode Decomposition
3. Numerical Example
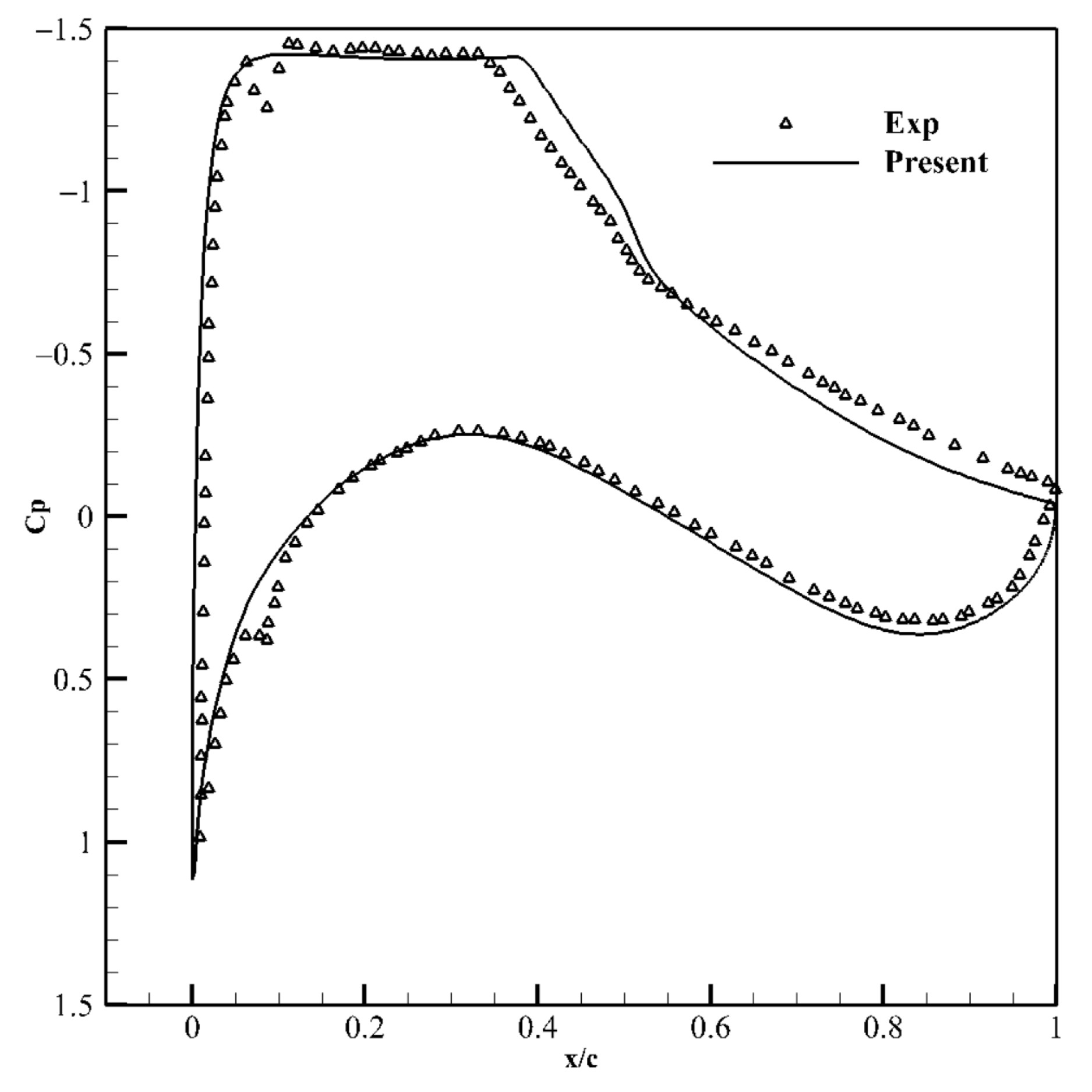
3.1. Validation of the CFD Method
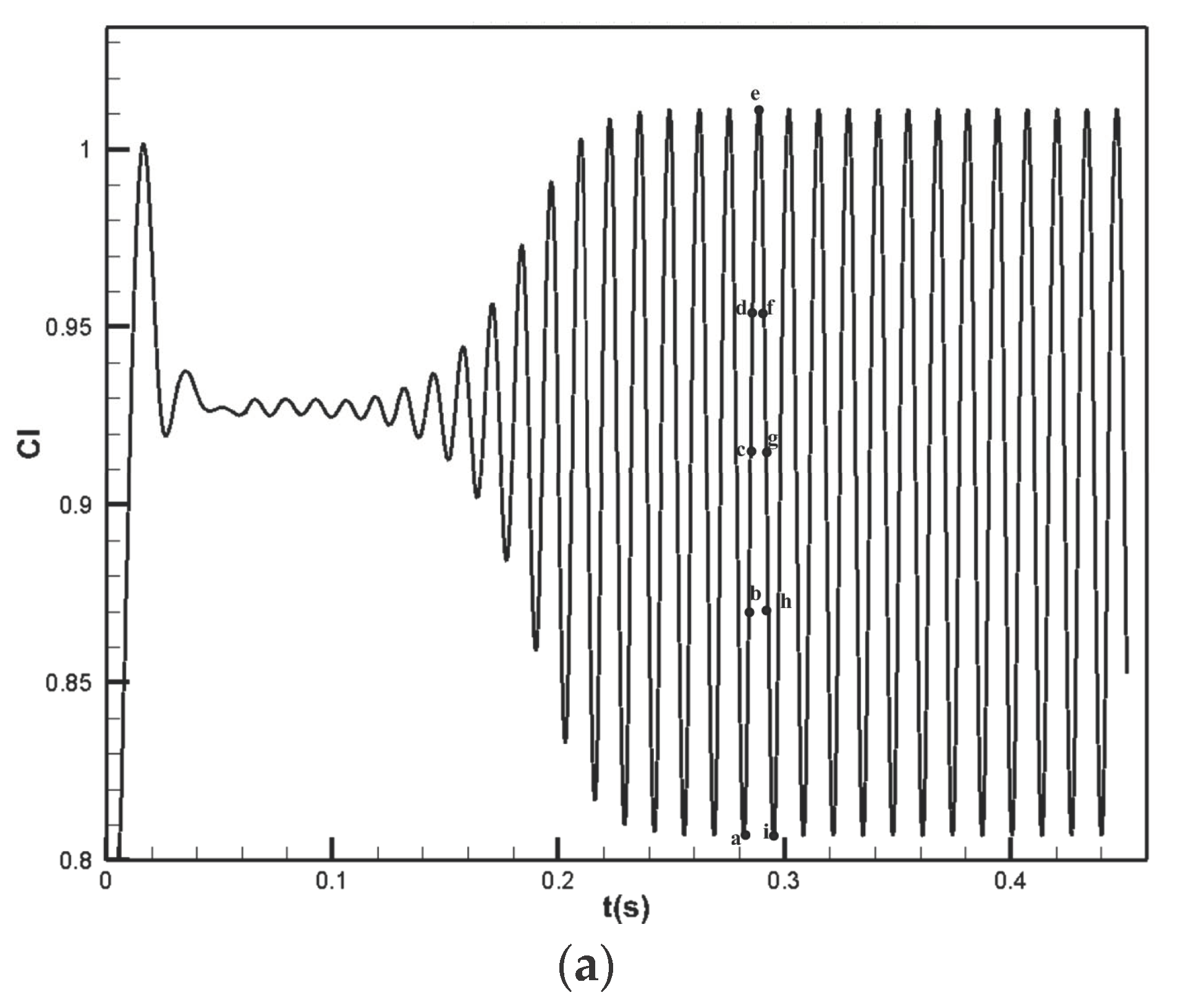
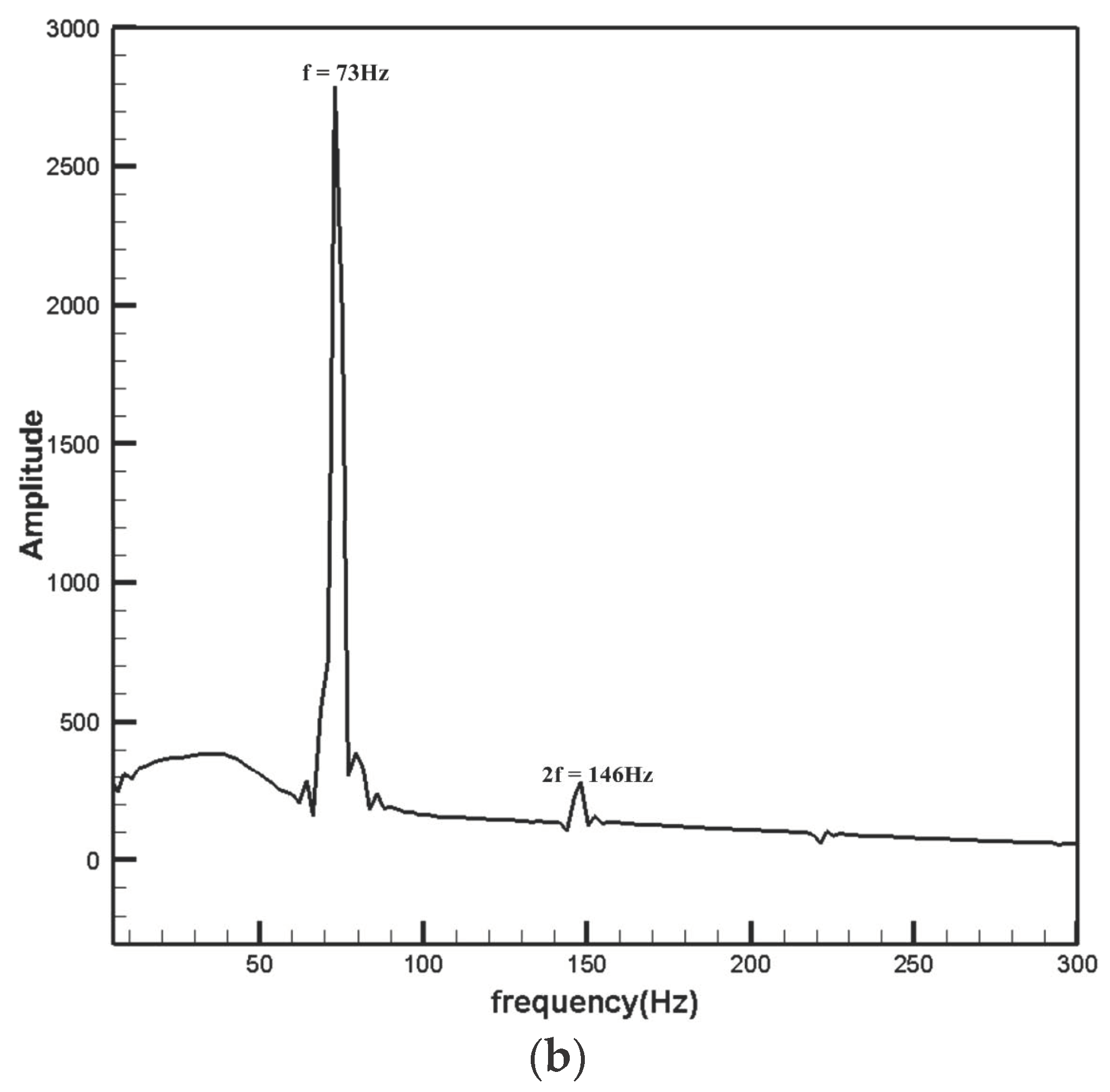
3.2. Flow Field Buffet Characteristics of the Fixed Airfoil
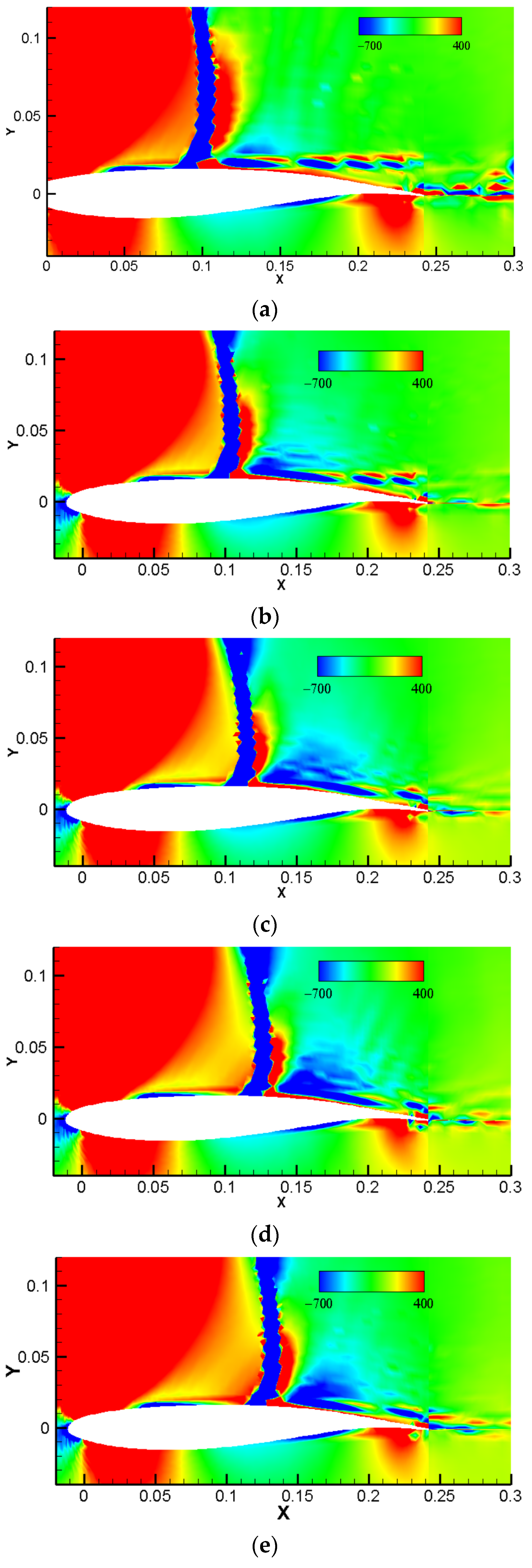
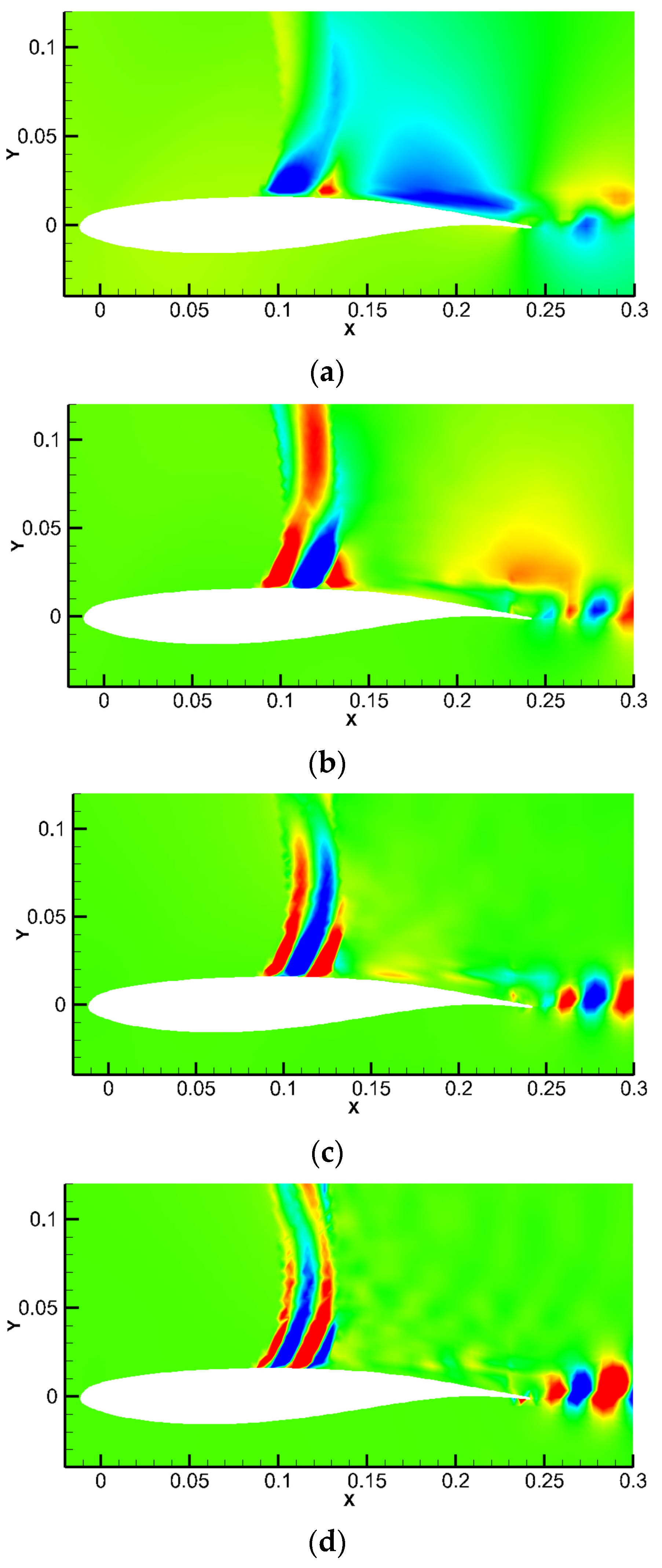
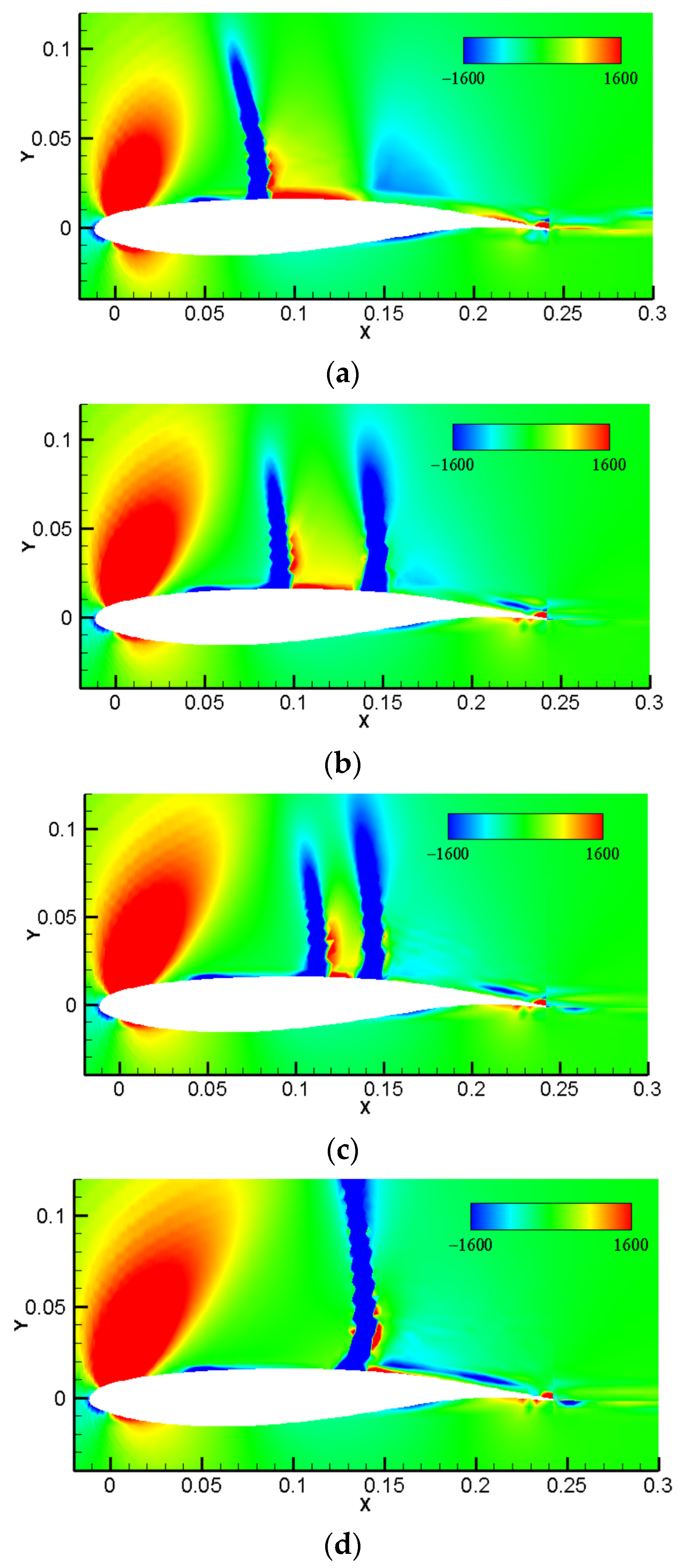
3.2.1. Instantaneous Flow Structure
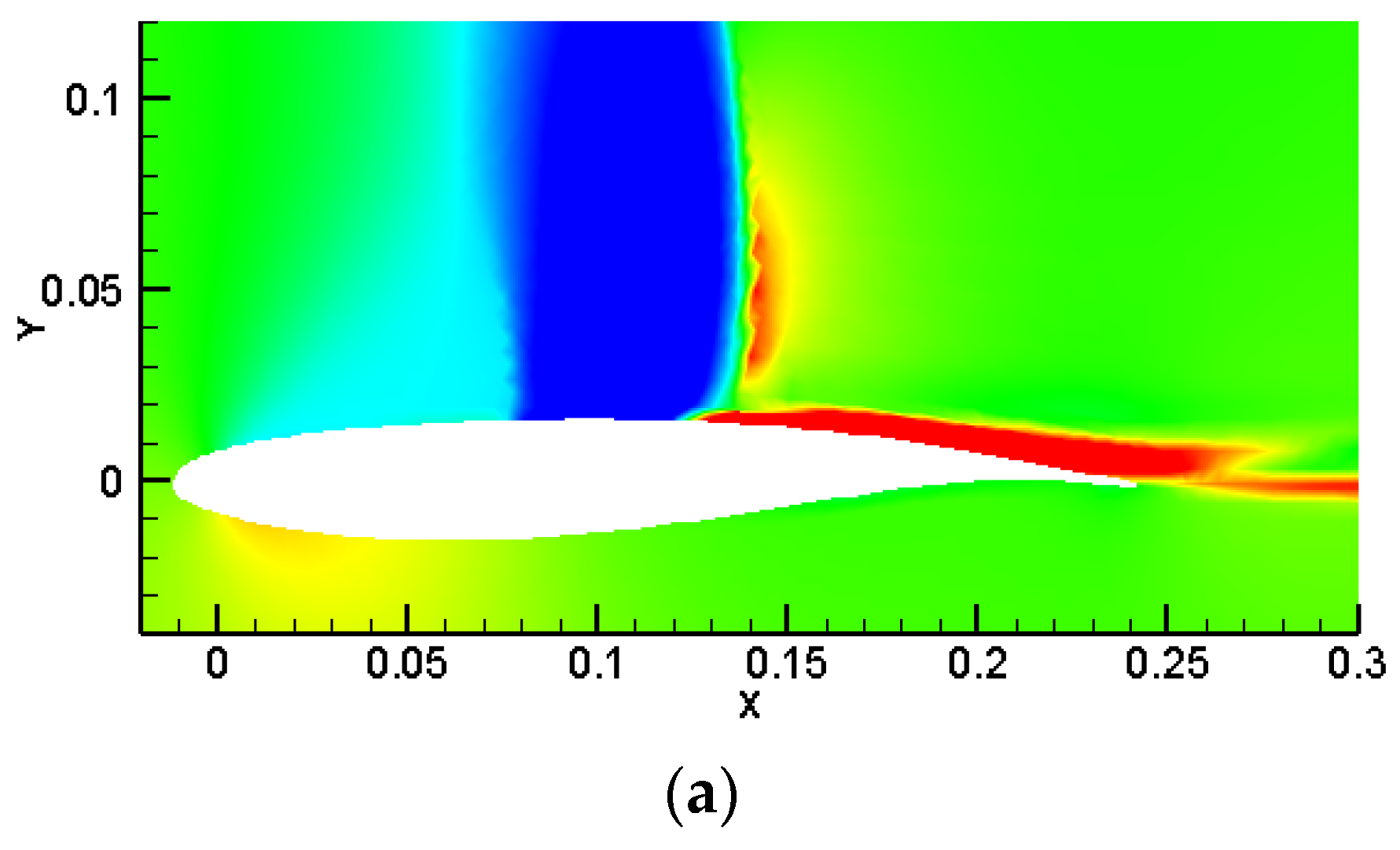
3.2.2. Fluidic Mode
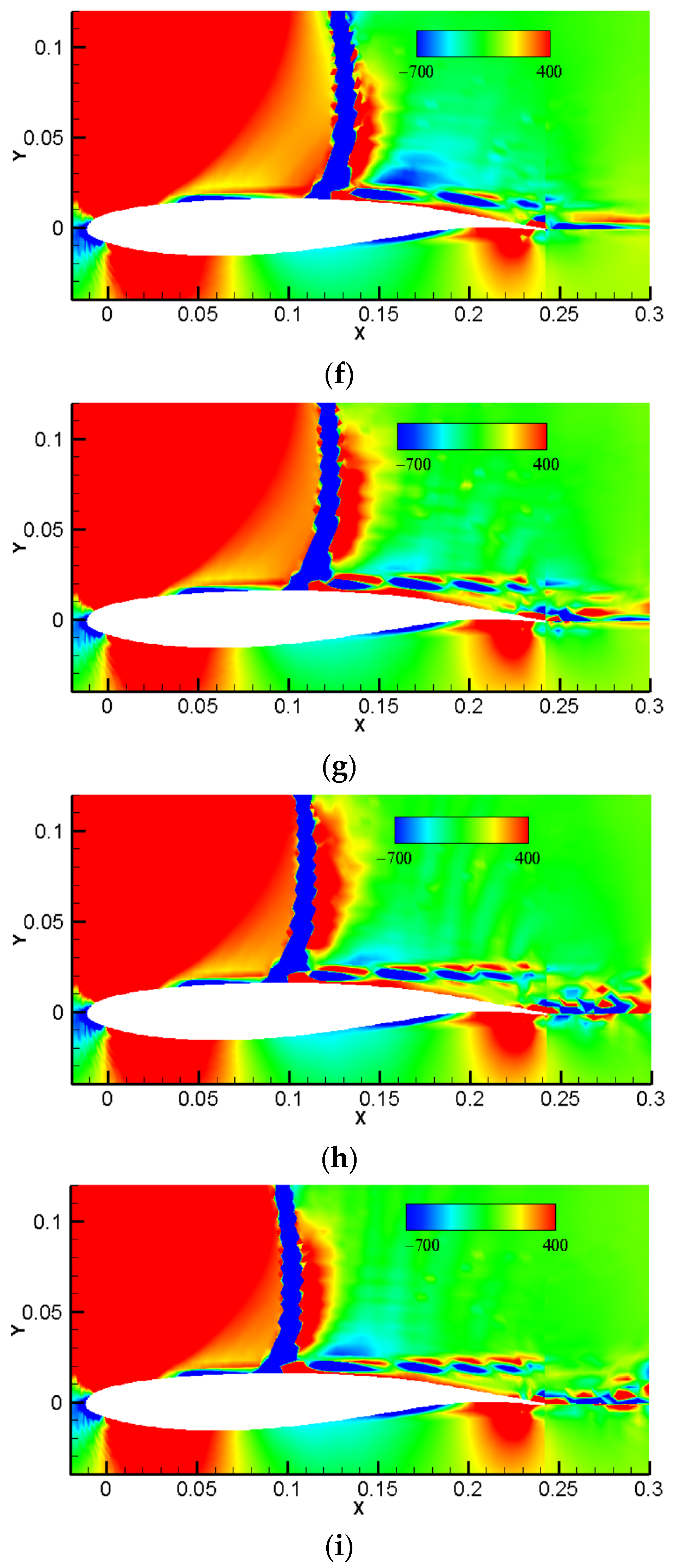
3.3. Flow Field Buffet Characteristics of Pitching Airfoils
3.3.1. Instantaneous Flow Structure
3.3.2. Fluidic Modes
4. Conclusions
- (1)
- When the airfoil is in pitching motion, the oscillation frequency has a significant effect on the flow characteristics. If the pitching frequency is close to the buffeting frequency of the flow, the aerodynamics may manifest as a harmonic vibration with only the pitching frequency of the structure as the fundamental frequency, and the frequency of the flow field disappears.
- (2)
- Velocity divergence snapshots show that for a given pitching motion, compared with the corresponding buffet characteristics of the stationary airfoil, the interaction of two shocks exists in the former, which leads to an increased range of shock motion. The wake shows obvious disordered motions compared with that of the latter, which results in a more complex unsteady shock behavior of the flow under elastic oscillation.
- (3)
- The DMD modes extracted by ordering the modes at different frequencies according to the modal energy criterion can obtain the principal modes, which reflectthe periodicity of the transonic shock oscillations, and facilitate the study of the dominant mode characteristics in the periodic flow.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dolling, D. Fifty years of shock-wave/boundary-layer interaction research: What next? AIAA J. 2001, 39, 517–1531. [Google Scholar] [CrossRef]
- Lee, B.H.K. Oscillatory shock motion caused by transonic shock boundary-layer interaction. AIAA J. 1990, 28, 942–944. [Google Scholar] [CrossRef]
- Lee, B.H.K. Self-sustained shock oscillations on airfoils at transonic speeds. Prog. Aerosp. Sci. 2001, 37, 147–196. [Google Scholar] [CrossRef]
- Xiao, Q.; Tsai, H.M.; Liu, F. Numerical study of transonic buffet on a supercritical airfoil. AIAA J. 2006, 44, 620–628. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidoy, D. Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 2007, 224, 924–940. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidoy, D.; Travin, A. Origin of transonic buffet on airfoils. J. Fluid Mech. 2009, 628, 357–369. [Google Scholar] [CrossRef]
- Jacquin, L.; Molton, P.; Deck, S.; Maury, B.; Soulevant, D. Experimental study of shock oscillation over a transonic supercritical profile. AIAA J. 2009, 47, 1985–1994. [Google Scholar] [CrossRef]
- Masini, L.; Timme, S.; Ciarella, A.; Peace, A. Influence of vane vortex generators on transonic wing buffet: Further analysis of the BUCOLIC experimental dataset. In Proceedings of the 52nd 3AF International Conference on Applied Aerodynamics, Lyon, France, 17–19 March 2017. [Google Scholar]
- Nitzsche, J. A numerical study on aerodynamic resonance in transonic separated flow. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Seattle, WA, USA, 22–24 June 2009. [Google Scholar]
- Gao, C.Q.; Zhang, W.W.; Ye, Z.Y. Study on the effects of elastic characteristics on transonic buffet onset. Eng. Mech. 2017, 34, 243–247. [Google Scholar]
- Zhang, W.W.; Gao, C.Q.; Ye, Z.Y. Research advances of wing/airfoil transonic buffet. Acta Aeronaut. Astronaut. Sin. 2015, 36, 1056–1075. [Google Scholar]
- Raveh, D.E. Numerical study of an oscillating airfoil in transonic buffeting flows. AIAA J. 2009, 47, 505–515. [Google Scholar] [CrossRef]
- Raveh, D.E.; Dowell, E.H. Frequency lock-in phenomenon for oscillating airfoils in buffeting flows. J. Fluids Struct. 2011, 27, 89–104. [Google Scholar] [CrossRef]
- Raveh, D.E.; Dowell, E.H. Aeroelastic responses of elastically suspended airfoil systems in transonic buffeting flows. AIAA J. 2014, 52, 926–934. [Google Scholar] [CrossRef]
- Gao, C.Q.; Zhang, W.W. Transonic aeroelasticity: A new perspective from the fluid mode. Prog. Aerosp. Sci. 2020, 113, 1–19. [Google Scholar] [CrossRef]
- Han, B.; Xu, M.; Chen, G.G.; Cai, T.X.; Wang, W.H.; Guan, S.X. Numerical investigation of transonic buffet on a prescribed-pitching OAT15A airfoil. AIP Adv. 2022, 12, 035301. [Google Scholar] [CrossRef]
- Nie, X.Y. Numerical analysis of geometrical nonlinear aeroelasticity with CFD/CSD method. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 243–253. [Google Scholar] [CrossRef]
- Kou, J.Q.; Zhang, W.W.; Gao, C.Q. Modal analysis of transonic buffet based on POD and DMD method. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2679–2689. [Google Scholar]
- Kou, J.Q.; Zhang, W.W. An improved criterion to select dominant modes from dynamic mode decomposition. Eur. J. Mech. B Fluids 2017, 62, 109–129. [Google Scholar] [CrossRef]
- Jovanovic, M.R.; Schmidp, J.; Nicholsj, W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Kou, J.Q.; Zhang, W.W. Dynamic mode decomposition with exogenous input for data-driven modeling of unsteady flows. Phys. Fluids 2019, 31, 057106. [Google Scholar] [CrossRef]
- Gao, C.Q.; Zhang, W.W.; Li, X.T.; Liu, Y.; Quan, J.; Ye, Z.; Jiang, Y. Mechanism of frequency lock-in transonic buffeting flow. J. Fluid Mech. 2017, 88, 528–561. [Google Scholar] [CrossRef]

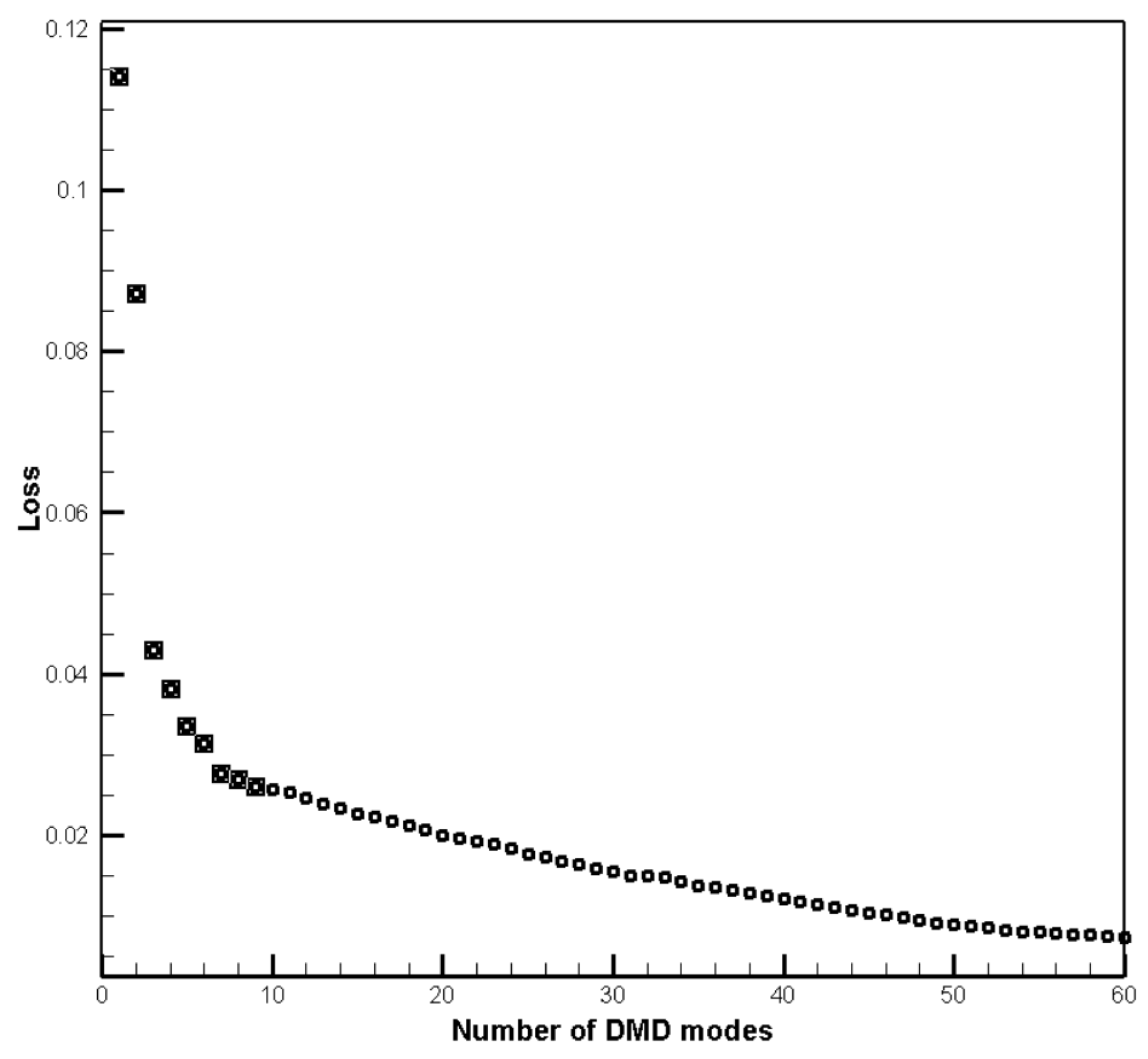





| Order | Growth Rate | Frequency (Hz) | Loss Function |
|---|---|---|---|
| 1 | 0 | 0 | 0.114 |
| 2–3 | 5.37 × 10−6 | 73.18 | 0.043 |
| 4–5 | −2.45 × 10−5 | 146.36 | 0.033 |
| 6–7 | 6.47 × 10−5 | 219.56 | 0.027 |
| 8–9 | 8.38 × 10−5 | 293.54 | 0.024 |
| Order | Growth Rate | Frequency (Hz) | Loss Function |
|---|---|---|---|
| 1 | 0 | 0 | 0.061 |
| 2–3 | −1.97 × 10−6 | 81.99 | 0.027 |
| 4–5 | −1.08 × 10−5 | 163.99 | 0.023 |
| 6–7 | −1.00 × 10−5 | 245.32 | 0.015 |
| 8–9 | 2.22 × 10−5 | 327.28 | 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, X.; Zheng, G.; Wei, L.; Huang, C.; Yang, G.; Ji, Z. Analysis of the Transonic Buffet Characteristics of Stationary and Pitching OAT15A Airfoil. Appl. Sci. 2024, 14, 7149. https://doi.org/10.3390/app14167149
Nie X, Zheng G, Wei L, Huang C, Yang G, Ji Z. Analysis of the Transonic Buffet Characteristics of Stationary and Pitching OAT15A Airfoil. Applied Sciences. 2024; 14(16):7149. https://doi.org/10.3390/app14167149
Chicago/Turabian StyleNie, Xueyuan, Guannan Zheng, Lianyi Wei, Chengde Huang, Guowei Yang, and Zhanling Ji. 2024. "Analysis of the Transonic Buffet Characteristics of Stationary and Pitching OAT15A Airfoil" Applied Sciences 14, no. 16: 7149. https://doi.org/10.3390/app14167149





