Abstract
This study revisits the freely vibrating problem of asymmetric L-shaped membranes using a three-segmented domain decomposition (3-SDD) strategy. Motivated by the need for more accurate and flexible methods, the 3-SDD strategy is compared with the previously proposed two-segmented domain decomposition (2-SDD) strategy. The region-matching technique is used to derive an alternative series solution, and the eigenvalues obtained are compared with those in existing research. The convergence behavior and sensitivity analyses reveal that the 3-SDD strategy offers improved accuracy and stability, particularly for higher truncation terms. Detailed comparisons of the first four eigenvalue squares show strong agreement between the 3-SDD and 2-SDD strategies, confirming the reliability of both methods. This research establishes a foundation for the vibration analysis of complex membrane structures, emphasizing the benefits of the 3-SDD approach for upcoming engineering applications and showcasing its potential for broader applicability in practical scenarios. The findings underscore the importance of utilizing multi-segmented decomposition strategies to enhance the accuracy and flexibility of free vibration analysis.
1. Introduction
Membranous structures are widely used in civil, mechanical, and biomedical applications owing to the advantages of easy folding, as well as being inflatable and lightweight [1]. In principle, one may view the natural vibration characteristics of membranes as exceptional cases of thin-plate vibrations. Nowadays, vibrating membranes are highly relevant to the design and fabrication of microelectromechanical systems (MEMSs) [2], sensors/transducers [3,4], nanoindenters [5], and atomic force microscopes [6]. In addition, membranes play a vital role in the development of space satellite technology, such as ultra-large membrane mirrors [7], solar sails [8], and gossamer spacecraft [9].
For simple geometric shapes such as rectangles, circles, ellipses, and triangles, the exact analytical solutions to the free vibration problems of elastic homogeneous membranes can be easily found in some engineering mathematics [10], vibration [11], or acoustics [12] reference books. However, when the geometric shape is slightly irregular or more complex, resorting to semi-analytical, mesh-free, or mesh-based numerical solutions (e.g., [13,14,15,16,17,18,19,20,21,22,23]) generally becomes necessary due to the relative difficulty of obtaining exact analytical solutions.
In past research related to the free vibration of membranes, the geometric configurations of membranes are diverse. The homogeneous “symmetric” L-shaped membrane is notably popular among these various shapes (e.g., [24,25,26,27]). The earliest related study dates back to the 1960s, with a semi-analytical solution provided by Fox et al. [28], whose solution is often used as a benchmark for comparing other numerical methods (e.g., [29,30,31,32,33]). Apart from the works of [28,34], most solutions are numerical (e.g., [35,36,37]). As for the “asymmetric” L-shaped membranes, there are even fewer studies, with the only recent semi-analytical series solution given by Xiong et al. [38]. Unfortunately, to the best of the authors’ knowledge, no exact analytical solutions are yet available for symmetric or asymmetric L-shaped membranes.
Pursuing enhanced performance and adaptability in MEMSs has led to significant advancements in device design. A critical focus in this arena is the development of piezoresistive pressure sensors with tunable operating frequencies, a feature vital for adapting to diverse applications and environmental conditions. The sensitivity of these sensors, primarily determined by the structure of the pressure-sensitive membrane, has been the subject of extensive research and optimization efforts. Traditional approaches have utilized composite membranes with center boss or island structures to increase stiffness [39]. At the same time, more recent innovations have explored the benefits of peninsula-structured membranes [40] and hollow stiffening structures [41]. Building upon these foundations, the L-shaped composite membrane [38] has emerged as a promising solution, offering a unique combination of geometric optimization and tunability.
This study revisits the issue of free vibration in asymmetric L-shaped membranes, previously explored by Xiong et al. [38]. The region-matching technique (RMT) remains the primary solution method used to derive a semi-analytical series solution. The RMT hinges on combining the domain decomposition method and the method of separation of variables (MSV), each leveraging its strengths. The former overcomes the inherent limitation of the MSV, which can only be applied when the geometric contours are comfortable with a separable coordinate system, while the latter uses eigenfunctions that satisfy most boundary conditions, ensuring convergent and stable computed results.
The present study introduces an advancement in the analysis of asymmetric L-shaped membranes through the application of a three-segmented domain decomposition (3-SDD) strategy, marking a notable departure from the two-segmented domain decomposition (2-SDD) strategy employed by Xiong et al. [38]. Such a 3-SDD strategy divides the entire computational domain into three rectangular subregions (see Figure 1a) instead of the two subregions used in the 2-SDD approach (see Figure 1b). While the primary distinction lies in the number of subregions, the implications of this difference are significant and wide-ranging.
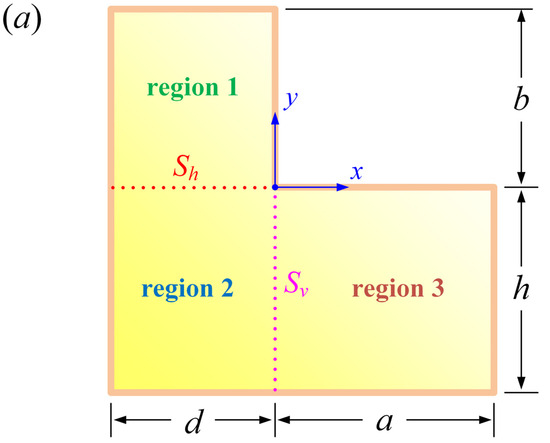
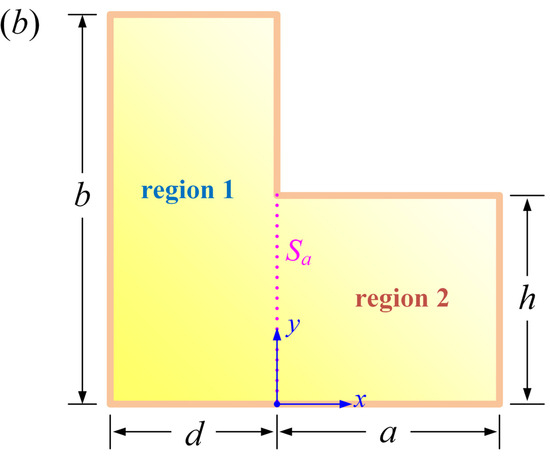
Figure 1.
Geometric layout of the asymmetric L-shaped membrane: (a) the 3-SDD strategy adopted in the present study; (b) the 2-SDD strategy employed by Xiong et al. [38].
Before delving into the complexities of multi-segmented composite L-shaped membranes, it is imperative to understand the fundamental building blocks first. The three-segmented L-shaped membrane represents the minimal unit that captures the essential characteristics of these more complex structures. While Xiong et al. [38] have previously investigated two-segmented L-shaped membranes, it is necessary to recognize that this configuration is merely a particular case of the three-segmented L-shaped membrane. The simplified models developed for two-segmented membranes are not fully applicable to the three-segmented case, highlighting the need for dedicated research in this area.
The actual superiority of the 3-SDD strategy becomes evident when dealing with L-shaped membranes featuring elongated horizontal and vertical arms characterized by high aspect ratios in the subregions. In such cases, the 3-SDD strategy necessitates the satisfaction of fewer boundary conditions than the 2-SDD strategy. The 3-SDD strategy captures the interactions between the membrane segments more faithfully, especially in regions where the membrane geometry changes abruptly, such as at the junction of the L-shape (i.e., region 2 in Figure 1a).
Consequently, the 3-SDD strategy is expected to yield more accurate computational results for asymmetric L-shaped membranes with slender arms than its 2-SDD counterpart. This enhanced accuracy is not merely a marginal improvement but represents a leap in our ability to model and predict the behavior of these sophisticated membrane structures. The improved precision is valuable in applications where even minor deviations in performance can have significant implications, such as in susceptible pressure sensors or precision MEMS devices [42].
From the perspective of advancing microfabrication techniques toward more flexible and tunable designs, the study of the 3-SDD strategy serves as a critical stepping stone. This research is necessary and pivotal in laying the groundwork for understanding multi-segmented composite L-shaped membranes. In the future, researchers can uncover fundamental principles governing more composite membrane structures (e.g., E-, I-, T-, and pi-shaped membrane-based sensors). The proposed 3-SDD strategy allows for a systematic exploration of how material properties, segment dimensions, and their interactions influence the overall performance and tunability of the device.
2. Formulations
Figure 1a illustrates an asymmetric L-shaped membrane initially stretched and clamped along its perimeter. The thin, elastic membrane is assumed to be homogeneous in material composition. The geometric configuration is defined by four parameters: a and b represent the lengths of the horizontal and vertical arms of the ‘L’ shape, respectively; d is the width of the vertical arm; and h is the height of the horizontal arm. The tension force per unit length is denoted as T. The mass per unit area is constant and represented by ρ. The concave corner of the membrane serves as the reference point for the Cartesian coordinate system (x, y).
Following the 3-SDD strategy, two auxiliary line boundaries, Sh and Sv, were introduced to segment the geometry of the problem into three distinct regions: three bounded areas designated as regions 1, 2, and 3 (see Figure 1a). Within these delineated regions, the membrane transverse deflections uj that remain small must conform to the governing Helmholtz equation, which is expressed as follows:
where is the Laplacian operator, is the wavenumber, and is the angular natural vibration frequency. The subscript j indicates the specific number. The time-harmonic factor is understood throughout this section.
The zero displacement boundary conditions on the edge of region 1 are as follows:
The clamped boundary conditions on the edge of region 2 are as follows:
The fixed boundary conditions on the edge of region 3 are as follows:
Using the MSV, the displacement fields in regions 1, 2, and 3 can be derived, respectively, as follows [43,44]:
with
where the expansion coefficients An, Bn, Cn, and Dn are undetermined. It should be noted that Equations (10)–(12) satisfy the governing Equation (1) and the majority of boundary conditions surrounding the membrane edge, except those on the Sh and Sv.
The displacement continuity conditions across Sh and Sv are, respectively, determined as follows:
Multiplying Equations (15) and (16) by a succession of sine functions, integrating over appropriate intervals, and utilizing the orthogonal property of sine functions leads to the following relations:
Next, consider the slope continuity conditions across Sh and Sv as follows:
Similarly, applying integration and the orthogonality of sine functions to Equations (19) and (20), eliminating the unknown coefficients Bn, and rearranging and truncating the summation indices after N terms produces a system of linear equations written in a matrix form as follows:
with
in which
and is the Kronecker delta function.
Given that Equation (21) represents a generalized matrix eigenvalue problem (a system of N equations with N + 1 unknowns), the eigenvalues (i.e., the natural frequencies of the membrane) can be evaluated using the determinant equation as follows:
Once the n-th eigenvalue has been identified, calculating the corresponding eigenmode (natural mode) becomes a relatively straightforward process. The desired precision determines the number of truncation terms (i.e., N).
3. Results
In this section, we discuss the dimensionless eigenvalues , which can be expressed as follows:
We considered a silicon nitride membrane sensor based on nitride materials commonly used for microfabricating flexible MEMS devices. The properties of this sensor include a density of 3100 kg/m3 and a biaxial prestress of 200 MPa. Regarding the dimensionless geometric parameters, we set the height of the membrane’s horizontal arm (h) to 250 μm, with other dimensions expressed as ratios to h, as detailed in Table 1.

Table 1.
Dimensionless parameters for selected cases of L-shaped membranes.
3.1. Convergence for the Symmetric Case
The data provided in Table 2 represent the square of the first ten eigenvalues for a symmetric L-shaped membrane, analyzed at different truncation indices N. The truncation indices used are 10, 60, 120, 1000, 1600, and 1800. Table 2 shows that the values converge rapidly for most eigenvalues as N increases. This can be observed because the values stabilize significantly as N approaches 1000. The first eigenvalue, , starts at 9.6558 for N = 10 and converges to 9.6397 for N > 1000. This indicates a minor deviation initially, which diminishes as N increases. The second eigenvalue, , exhibits minimal deviation across all truncation indices, indicating that it converges faster than others.

Table 2.
The square of the first ten eigenvalues versus truncation indices N for the symmetric case.
The fifth eigenvalue, , shows a noticeable change between N = 10 and N = 60, decreasing from 31.9521 to 31.9164. Further increases in N result in values that stabilize around 31.9127, indicating that higher-order eigenvalues may require a larger N for accurate convergence. Eigenvalues such as , , and also exhibit the trend of gradually stabilizing values as N increases. However, the changes are relatively small after N reaches 120.
3.2. Verification for the Symmetric Case
In this section, we provide a detailed verification of the first ten eigenvalue squares for symmetric L-shaped membranes by comparing our results with those reported in existing research. The comparison is shown in Table 3, which highlights the eigenvalue squares computed in the present study alongside those reported by Leung et al. [30], Still [31], Wu et al. [32], and Yuan and He [33].

Table 3.
Comparison of the first ten eigenvalue squares for symmetric cases with established results.
The results indicate a strong consistency with the results of [33], demonstrating that our computational approach yields accurate and reliable eigenvalues. Notably, the current values of all ten eigenvalues closely match those documented by Yuan and He [33], affirming the reliability of our methods.
The results from [30,32] generally align with our results, although slight discrepancies are noted. For example, the first eigenvalue in the study by Leung et al. [30] is 9.6814, slightly higher than our result of 9.6397. Such differences, though minor, may arise from variations in computational precision or the specific numerical methods used.
Higher-order eigenvalues also agree with the literature, although minor discrepancies are observed. These discrepancies highlight the sensitivity of higher-order modes to various numerical approaches and emphasize the importance of employing high-precision methods for accurate computations.
3.3. Convergence for the Asymmetric Case
This section examines the convergence behavior of the first ten eigenvalue squares for the asymmetric L-shaped membrane, as outlined in Table 4. The analysis spans truncation indices N of 20, 80, 160, 240, 420, and 520. The data indicate a clear convergence pattern as N increases, with eigenvalues stabilizing at higher truncation indices. Notably, and show rapid convergence, reaching stable values at lower N. For example, stabilizes at 12.5435 starting from N = 240, illustrating the efficient convergence for lower-order eigenvalues.

Table 4.
The square of the first ten eigenvalues versus truncation indices N for the asymmetric case.
Higher-order eigenvalues, such as , exhibit greater sensitivity, with values adjusting slightly even at N = 420. This heightened sensitivity underscores the need for a larger N to capture the complexity of higher-order modes accurately. For instance, changes from 84.7964 at N = 20 to 84.7864 at N = 520.
Overall, the convergence behavior is uniform across the eigenvalues, assuring the numerical stability and robustness of the method used. The consistent results for higher truncation indices validate the approach, demonstrating its capability to effectively handle the free vibration analysis of asymmetric L-shaped membranes. This detailed investigation into the convergence and sensitivity of eigenvalues highlights the importance of selecting appropriate truncation indices to ensure accurate and reliable computational results.
3.4. Verification for the Asymmetric Case
In this section, we present a detailed verification of the first ten eigenvalue squares for asymmetric L-shaped membranes by comparing our results with those given in [38]. The comparison shown in Table 5 demonstrates that our present 3-SDD results are in good agreement with the results of [38]. The eigenvalues calculated using the 3-SDD strategy closely align with those obtained through the 2-SDD strategy and Abaqus finite element (FE) software (version 2023), with minimal differences that fall within acceptable numerical tolerance levels. For example, the first eigenvalue matches almost exactly across all methods, demonstrating the high precision and reliability of our computations.

Table 5.
Comparison of the first ten eigenvalue squares for asymmetric cases with previous results.
Minor variations observed in higher-order eigenvalues, such as and , can be attributed to the inherent differences in numerical methods and the computational precision of the software used. These discrepancies do not significantly affect the overall accuracy of the results. Overall, such consistency confirms that the present 3-SDD strategy effectively handles asymmetric L-shaped membrane vibrations, offering a dependable alternative to existing methods.
The numerical differences between all three methods are minimal. The average relative difference between 3-SDD and Abaqus is less than 0.01% for all eigenvalues, while the difference between 2-SDD and Abaqus is typically less than 0.02%. The difference between 3-SDD and 2-SDD is minor, often around 0.001%.
The lack of significant differences between the 3-SDD and 2-SDD results in Table 5 can be attributed to the specific geometry of the L-shaped membrane used in this example. In this case, the L-shape’s horizontal and vertical arms have relatively low aspect ratios, meaning that neither arm is exceptionally slender. This geometric configuration does not fully leverage the advantages of the 3-SDD strategy over the 2-SDD strategy.
4. Discussion
This discussion aims to compare the performance of the 3-SDD strategy employed in this study with the 2-SDD strategy used by Xiong et al. [38]. The comparison focuses on the first four eigenvalue squares of asymmetric L-shaped membranes, as illustrated in Figure 2a–d. Several key points are discussed in subsequent sections.
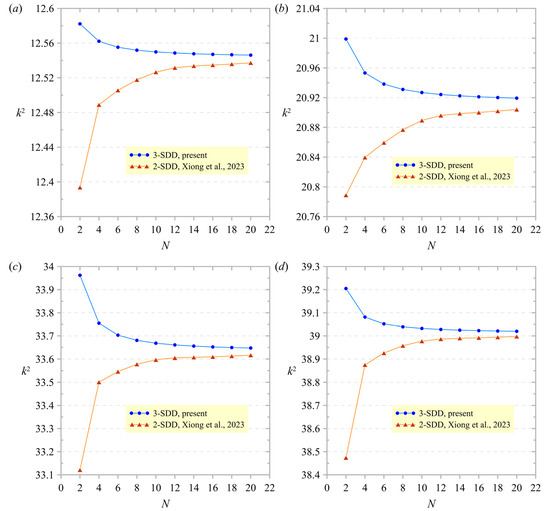
Figure 2.
Comparison of 3-SDD and 2-SDD strategies for the first four eigenvalue squares of asymmetric L-shaped membranes: (a) ; (b) ; (c) ; (d) [38].
4.1. Convergence Behavior
Our findings indicate that while both strategies tend to stabilize around N = 12, the path to stability and the reliability of results differ significantly between the two strategies. The 3-SDD strategy demonstrates rapid convergence, achieving near-stable results even at low N values (N = 4 to 6). As N increases, the relative error for 3-SDD quickly diminishes, showing a steep decline in the early stages (N = 2 to 6) and maintaining a consistently low error level. This is evident across all four eigenvalues, with the error reduction being particularly pronounced in the third and fourth eigenvalues shown in Figure 2c,d.
In contrast, the 2-SDD strategy exhibits slower convergence, with significant variations in results at lower N values. The relative error for 2-SDD starts much higher, especially for the third and fourth eigenvalues, and decreases more gradually as N increases. This is particularly noticeable in Figure 2c,d, where the 2-SDD strategy shows a more substantial initial error and a slower error reduction rate than 3-SDD.
The “cutoff” point of N = 12 affects the reliability of results differently for each method. For 3-SDD, this point serves more as a confirmation of stability than a critical threshold for result reliability. The relative error is minimal well before N = 12, indicating high reliability even at lower N values. For 2-SDD, however, the cutoff is more crucial. The relative error decreases significantly up to and beyond N = 12, especially for higher-order eigenvalues, suggesting that more terms are needed to achieve comparable accuracy to 3-SDD.
4.2. Numerical Stability
The numerical stability of both strategies is evident from the consistent convergence patterns observed across all four eigenvalues. The results of the 3-SDD strategy are very close to those obtained using the 2-SDD strategy, indicating that both methods are reliable for solving the free vibration problems of asymmetric L-shaped membranes.
4.3. Accuracy and Performance
The slight differences between the eigenvalue squares obtained from the 3-SDD and 2-SDD strategies are minimal, typically with a 1% or less relative error. This indicates that both methods are highly accurate.
The 3-SDD strategy, while slightly more complex due to the additional segment, does not show significant advantages over the 2-SDD strategy in terms of accuracy for the first four eigenvalues. However, the additional segment in the 3-SDD strategy could offer more flexibility for more complex geometries or higher-order modes.
4.4. Mode Shapes
The membranes’ eigenmodes reveal distinct spatial patterns at corresponding eigenvalues. Figure 3a–f display the first six eigenmodes for the asymmetric case. To distinguish between the two methods, a fluorescent green solid line represents the 3-SDD strategy, while an orange dotted line denotes the 2-SDD strategy. Each mode shape is normalized, with the peak displacement value set to unity and all other displacement values scaled accordingly. This normalization allows for direct comparisons between different modes and computational methods using the maximum transverse motion as the scaling factor.
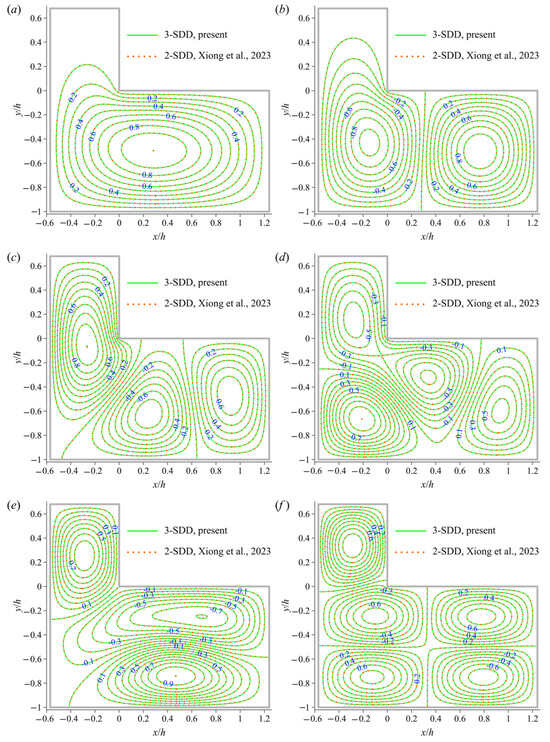
Figure 3.
Comparison of the first six eigenmode shapes for the asymmetric case: (a) 1st mode; (b) 2nd mode; (c) 3rd mode; (d) 4th mode (e) 5th mode; (f) 6th mode [38].
The comparison between the 3-SDD and 2-SDD strategies in Figure 3a–f demonstrates a high degree of concordance for each mode. The overlap of the two color lines indicates that both strategies produce virtually identical results for the current modes. This agreement is particularly evident in regions of maximum displacement and along the nodal lines, underscoring the robustness of both computational approaches in capturing the essential features of the membrane’s vibrational patterns.
The asymmetry in the membrane’s geometry is reflected in the slight eccentricity of the equal displacement contours. This asymmetry manifests as a subtle shift in the position of the maximum displacement point and a gentle distortion of the nodal lines compared to what would be expected in a perfectly symmetric case.
4.5. Eigenvalue Extraction from Sub-Squares
In analyzing L-shaped membrane vibrations, the domain decomposition method offers powerful strategies for eigenvalue extraction [45]. The 3-SDD and 2-SDD strategies enable the extraction of specific eigenvalues from the exact spectrum of rectangular or square membranes when the subregions’ side length ratios are rational. This extraction process, governed by the following relation [46], proves particularly effective for the symmetric case:
where represents the eigenvalue; m and n are positive integers denoting the mode numbers; and La and Lb are the length and width of the rectangular membrane, respectively.
The 3-SDD strategy, which divides the L-shaped membrane into three equal-sized square submembranes, allows for a straightforward correlation with the eigenvalues of a single square membrane. As seen in Table 3, the third eigenvalue ( = 19.7392) corresponds to the fundamental mode (m = 1, n = 1), while the eighth and ninth eigenvalues ( = = 49.3480) align with the second and third modes (m = 1, n = 2 and m = 2, n = 1), respectively.
In contrast, the 2-SDD strategy, which partitions the membrane into one rectangular and one square submembrane, necessitates a more intricate process. It requires computing eigenvalue spectra for both shapes and a meticulous cross-comparison to identify shared values. This method also demands the removal of certain eigenvalues from the rectangular submembrane’s spectrum, such as those corresponding to modes (m = 1, n = 1), (m = 3, n = 1), and (m = 1, n = 2).
While both strategies yield accurate results, the 3-SDD method offers a more direct and elegant solution for handling these “extra” eigenvalues, highlighting its computational efficiency in this particular scenario. Moreover, the 3-SDD strategy demonstrates superior capability in identifying repeated roots or degenerate modes (i.e., those with identical eigenvalues [45,47]). This advantage is particularly significant in nanomechanical mass spectrometry, where degenerate mechanical modes are standard in bi-axisymmetric resonators [48]. The 3-SDD strategy’s efficiency in this regard could lead to more precise calculations of analyte mass and adsorption positions, potentially improving these sensing devices’ overall performance and reliability.
Ultimately, while the choice between 3-SDD and 2-SDD strategies depends on specific problem characteristics and the desired balance between simplicity and versatility, the 3-SDD strategy’s advantages in handling degenerate modes position it as a promising tool for advancing the field of nanomechanical mass spectrometry and sensor design.
5. Potential Practical Applications
To understand performance sensitivity (S), we use the following relationship [49]:
where Δf is the fundamental frequency shift, and Δm is the change in mass. Analyzing the dimensionless parameters a/h and d/h within the context of fundamental frequency shift and performance sensitivity provides significant insights that are crucial for practical applications, such as membrane vibration-based sensors [50,51,52].
We modeled a scenario where particle adsorption (e.g., from gases or chemicals) causes a 1% increase in the membrane’s mass. This additional mass is represented as point-like particles uniformly distributed across the entire membrane surface. We set the membrane density to 750 kg/m3 for our analysis and applied a pre-stress of 0.1 MPa. Figure 4a,b illustrate the effects of varying geometric parameters on the asymmetric L-shaped membrane sensors, specifically showing the fundamental frequency shift and performance sensitivities, respectively. These results provide insights into how the sensor’s geometry influences its response to mass changes, which is crucial for gas and chemical detection applications.
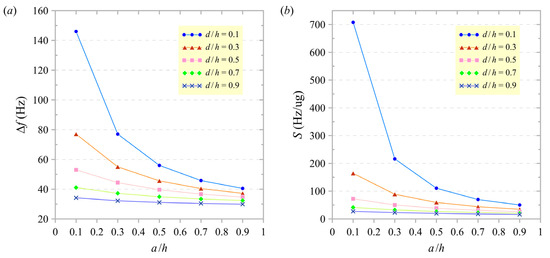
Figure 4.
(a) Fundamental frequency shift (Δf) and (b) performance sensitivity (S) versus dimensionless length of the horizontal arm (a/h) for various d/h ratios.
Figure 4a shows a clear trend: As a/h increases, Δf decreases for all values of d/h. This indicates that longer horizontal arms reduce the impact of asymmetry on the membrane’s vibrational characteristics. The rapid decrease in Δf for smaller values of d/h (e.g., d/h = 0.1) suggests high sensitivity to changes in a/h, stabilizing as a/h increases. For practical applications, structures requiring stable vibrational properties should opt for higher a/h and d/h values. For instance, in the design of sensors and actuators in MEMSs, achieving a stable fundamental frequency is critical for reliable performance. By adjusting a/h and d/h, engineers can fine-tune the vibrational properties to meet specific operational requirements.
Figure 4b displays a similar trend to the fundamental frequency shift. As a/h increases, S decreases, indicating reduced sensitivity to performance variations. The highest initial performance sensitivity is observed for d/h = 0.1, which decreases significantly with increasing a/h. For larger d/h values, the decrease in S is more gradual, demonstrating more excellent stability. In biomedical engineering, the design of implants and prosthetics [53] can be improved by understanding the vibrational properties of membrane-like structures. By adjusting a/h and d/h, the mechanical response of these devices can be tailored to better match the physiological conditions of the human body.
6. Conclusions
This study re-examined the free vibration problem concerning asymmetric L-shaped membranes using a 3-SDD strategy. Aimed at enhancing accuracy and flexibility, this approach was compared to the 2-SDD strategy previously proposed by Xiong et al. [38]. Utilizing the RMT for deriving an alternative series solution, our results, which were validated against established research, demonstrated improved accuracy and numerical stability with the 3-SDD strategy, especially at higher truncation terms. The good agreement between the first few eigenvalue squares from both strategies underscores the reliability of the 3-SDD strategy.
The 3-SDD strategy’s better performance in analyzing complex geometries opens opportunities for future research. It could advance MEMS design with intricate, space-optimized sensors and actuators, enhance nanomechanical mass spectrometry for single-molecule detection, and accelerate acoustic metamaterial development. Such a strategy also shows promise in the development of flexible electronics, biomedical implant design, quantum sensing optimization, and efficient energy harvesting devices. These diverse applications underscore the 3-SDD strategy’s potential to drive innovation across multiple technological fields, from nanotechnology to large-scale engineering.
Author Contributions
K.-H.C.: conceptualization, methodology, data curation, investigation, validation, visualization, writing—original draft preparation. W.-T.K.: conceptualization, investigation, supervision, project administration, funding acquisition, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support of the National Science and Technology Council, Taiwan (Project No. NSTC 112-2221-E-992-061).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
Special thanks are extended to the Office of Marine Science and Technology at the National Kaohsiung University of Science and Technology (Project No. 112A10) for their invaluable support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tamadapu, G.; DasGupta, A. In-plane surface modes of an elastic toroidal membrane. Int. J. Eng. Sci. 2012, 60, 25–36. [Google Scholar] [CrossRef]
- Batra, R.C.; Porfiri, M.; Spinello, D. Analysis of electrostatic MEMS using meshless local Petrov-Galerkin (MLPG) method. Eng. Anal. Bound. Elem. 2006, 30, 949–962. [Google Scholar] [CrossRef]
- Wan, K.T.; Guo, S.; Dillard, D.A. A theoretical and numerical study of a thin clamped circular film under an external load in the presence of a tensile residual stress. Thin Solid Film. 2003, 425, 150–162. [Google Scholar] [CrossRef]
- Komaragiri, U.; Begley, M.R.; Simmonds, J.G. The mechanical response of freestanding circular elastic films under point and pressure loads. J. Appl. Mech. 2005, 72, 203–212. [Google Scholar] [CrossRef]
- Maner, K.C.; Begley, M.R.; Oliver, W.C. Nanomechanical testing and circular freestanding polymer films with sub-micron thickness. Acta Mater. 2004, 52, 5451–5460. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Prorok, B.C.; Fischer, M. A methodology for determining mechanical properties of freestanding thin films and MEMS materials. J. Mech. Phys. Solids 2003, 51, 47–67. [Google Scholar] [CrossRef]
- Ruggiero, E.J.; Inman, D.J. Modeling and vibration control of an active membrane mirror. Smart. Mater. Struct. 2009, 18, 095027. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, Y.; Li, Y.; Liu, Y. Free vibration and buckling of a stripped solar sail. J. Spacecr. Rocket. 2019, 56, 1267–1272. [Google Scholar] [CrossRef]
- Jenkins, C.H.M. Gossamer Spacecraft: Membrane and Inflatable Structures Technology for Space Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Kreyszig, E.; Kreyszig, H.; Norminton, E.J. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Weaver, W. Vibration Problems in Engineering, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Morse, P.M. Theoretical Acoustics; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Heuer, R.; Irschik, H. A boundary element method for eigenvalue problems of polygonal membranes and plates. Acta Mech. 1987, 66, 9–20. [Google Scholar] [CrossRef]
- Kang, S.W.; Lee, J.M.; Kang, Y.J. Vibration analysis of arbitrarily shaped membranes using non-dimensional dynamic influence function. J. Sound Vib. 1999, 221, 117–132. [Google Scholar] [CrossRef]
- Karageorghis, A. The method of fundamental solutions for the calculation of the eigenvalues of the Helmholtz equation. Appl. Math. Lett. 2001, 14, 837–842. [Google Scholar] [CrossRef]
- Platte, R.B.; Driscoll, T.A. Computing eigenmodes of elliptic operators using radial basis functions. Comput. Math. Applic. 2004, 48, 561–576. [Google Scholar] [CrossRef]
- Betcke, T.; Trefethen, L.N. Reviving the method of particular solutions. SIAM Rev. 2005, 47, 469–491. [Google Scholar] [CrossRef]
- Buchanan, G.R.; Peddieson, J. A finite element in elliptic coordinates with application to membrane vibration. Thin-Walled Struct. 2005, 43, 1444–1454. [Google Scholar] [CrossRef]
- Houmat, A. Free vibration analysis of arbitrarily shaped membranes using the trigonometric p-version of the finite-element method. Thin-Walled Struct. 2006, 44, 943–951. [Google Scholar] [CrossRef]
- Houmat, A. A sector elliptic p-element applied to membrane vibrations. Thin-Walled Struct. 2009, 47, 172–177. [Google Scholar] [CrossRef]
- Amore, P.; Boyd, J.P.; Fernández, F.M.; Rösler, B. High order eigenvalues for the Helmholtz equation in complicated non-tensor domains through Richardson extrapolation of second order finite differences. J. Comput. Phys. 2016, 312, 252–271. [Google Scholar] [CrossRef]
- Alves, C.J.S.; Antunes, P.R.S. Determination of elastic resonance frequencies and eigenmodes using the method of fundamental solutions. Eng. Anal. Bound. Elem. 2019, 101, 330–342. [Google Scholar] [CrossRef]
- Ren, H.; Fan, W. An adaptive triangular element of absolute nodal coordinate formulation for thin plates and membranes. Thin-Walled Struct. 2023, 182, 110257. [Google Scholar] [CrossRef]
- Milsted, M.G.; Hutchinson, J.R. Use of trigonometric terms in the finite element method with application to vibrating membranes. J. Sound Vib. 1974, 32, 327–346. [Google Scholar] [CrossRef]
- Schiff, B. Finite element eigenvalues for the Laplacian over an L-shaped domain. J. Comput. Phys. 1988, 76, 233–242. [Google Scholar] [CrossRef]
- Amore, P. Solving the Helmholtz equation for membranes of arbitrary shape: Numerical results. J. Phys. A Math. Theor. 2008, 41, 265206. [Google Scholar] [CrossRef]
- Liu, X.; Oishi, S. Verified eigenvalue evaluation for the Laplacian over polygonal domains of arbitrary shape. SIAM J. Numer. Anal. 2013, 51, 1634–1654. [Google Scholar] [CrossRef]
- Fox, L.; Henrici, P.; Moler, C. Approximations and bounds for eigenvalues of elliptic operators. SIAM J. Numer. Anal. 1967, 4, 89–102. [Google Scholar] [CrossRef]
- Sideridis, A.B. A numerical solution of the membrane eigenvalue problem. Computing 1984, 32, 167–176. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Zhu, B.; Zheng, J.; Yang, H. A trapezoidal Fourier p-element for membrane vibrations. Thin-Walled Struct. 2003, 41, 479–491. [Google Scholar] [CrossRef]
- Still, G. Approximation theory methods for solving elliptic eigenvalue problems. Z. Angew. Math. Mech. 2003, 83, 468–478. [Google Scholar] [CrossRef]
- Wu, W.X.; Shu, C.; Wang, C.M. Vibration analysis of arbitrarily shaped membranes using local radial basis function-based differential quadrature method. J. Sound Vib. 2007, 306, 252–270. [Google Scholar] [CrossRef]
- Yuan, Q.; He, Z. Bounds to eigenvalues of the Laplacian on L-shaped domain by variational methods. J. Comput. Appl. Math. 2009, 233, 1803–1810. [Google Scholar] [CrossRef][Green Version]
- Jones, R.S. Computing ultra-precise eigenvalues of the Laplacian within polygons. Adv. Comput. Math. 2017, 43, 1325–1354. [Google Scholar] [CrossRef]
- Katsikadelis, J.T.; Sapountzakis, E.J. An approach to the vibration problem of homogeneous, non-homogeneous and composite membranes based on the boundary element method. Int. J. Numer. Meth. Eng. 1988, 26, 2439–2455. [Google Scholar] [CrossRef]
- Houmat, A. Hierarchical finite element analysis of the vibration of membranes. J. Sound Vib. 1997, 201, 465–472. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Viola, E. Generalized differential quadrature finite element method for vibration analysis of arbitrarily shaped membranes. Int. J. Mech. Sci. 2014, 79, 216–251. [Google Scholar] [CrossRef]
- Xiong, C.H.; He, L.G.; Chang, K.H.; Huang, C.W. Free vibration analysis of a tunable micro-fabrication device comprising asymmetric L-shaped membranes. Polymers 2023, 15, 2293. [Google Scholar] [CrossRef]
- Sandmaier, H.; Kuhl, K. A square-diaphragm piezoresistive pressure sensor with a rectangular central boss for low-pressure ranges. IEEE Trans. Electron Devices 1993, 40, 1754–1759. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, D. A high sensitivity and high linearity pressure sensor based on a peninsula-structured diaphragm for low-pressure ranges. Sens. Actuators A Phys. 2014, 216, 176–189. [Google Scholar] [CrossRef]
- Kinnell, P.K.; King, J.; Lester, M.; Craddock, R. A hollow stiffening structure for low-pressure sensors. Sens. Actuators A Phys. 2010, 160, 35–41. [Google Scholar] [CrossRef]
- Achouch, S.; Bousseta, R.; Regragui, F.; Gharbi, M. Conception and realization of a novel design for a capacitive pressure sensor with high sensitivity and linear response. Results Eng. 2022, 15, 100535. [Google Scholar] [CrossRef]
- Kang, S.W.; Lee, J.M. Free vibration analysis of composite rectangular membranes with an oblique interface. J. Sound Vib. 2002, 251, 505–517. [Google Scholar] [CrossRef]
- Kang, S.W. Free vibration analysis of composite rectangular membranes with a bent interface. J. Sound Vib. 2004, 272, 39–53. [Google Scholar] [CrossRef]
- Gottlieb, H.P.W. On vibrations of L-shaped regions. J. Sound Vib. 2001, 246, 387–388. [Google Scholar] [CrossRef][Green Version]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953; p. 1364. [Google Scholar]
- Kang, J.H.; Wei, B. Degenerate mode shapes for rectangular membranes and simply supported rectangular plates. J. Sound Vib. 2013, 332, 1633–1638. [Google Scholar] [CrossRef]
- Sanz-Jiménez, A.; Ruz, J.J.; Gil-Santos, E.; Malvar, O.; García-López, S.; Kosaka, P.M.; Cano, Á.; Calleja, M.; Tamayo, J. Square membrane resonators supporting degenerate modes of vibration for high-throughput mass spectrometry of single bacterial cells. ACS Sens. 2023, 8, 2060–2067. [Google Scholar] [CrossRef] [PubMed]
- Pang, W.; Zhao, H.; Kim, E.S.; Zhang, H.; Yu, H.; Hu, X. Piezoelectric microelectromechanical resonant sensors for chemical and biological detection. Lab Chip 2012, 12, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Hajjam, A.; Wilson, J.C.; Pourkamali, S. Individual air-borne particle mass measurement using high-frequency micromechan-ical resonators. IEEE Sens. J. 2011, 11, 2883–2890. [Google Scholar] [CrossRef]
- Choi, J.S.; Park, W.T. MEMS particle sensor based on resonant frequency shifting. Micro Nano Syst. Lett. 2020, 8, 1–6. [Google Scholar]
- Nazemi, H.; Antony Balasingam, J.; Swaminathan, S.; Ambrose, K.; Nathani, M.U.; Ahmadi, T.; Babu Lopez, Y.; Emadi, A. Mass sensors based on capacitive and piezoelectric micromachined ultrasonic transducers—CMUT and PMUT. Sensors 2020, 20, 2010. [Google Scholar] [CrossRef]
- Park, S.J.; Lee, H.B.; Kim, G.W. Eardrum-inspired soft viscoelastic diaphragms for CNN-Based speech recognition with audio visualization images. Sci. Rep. 2023, 13, 6414. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).