Research on an Evaluation Method of Snowdrift Hazard for Railway Subgrades
Abstract
:1. Introduction
2. Methods
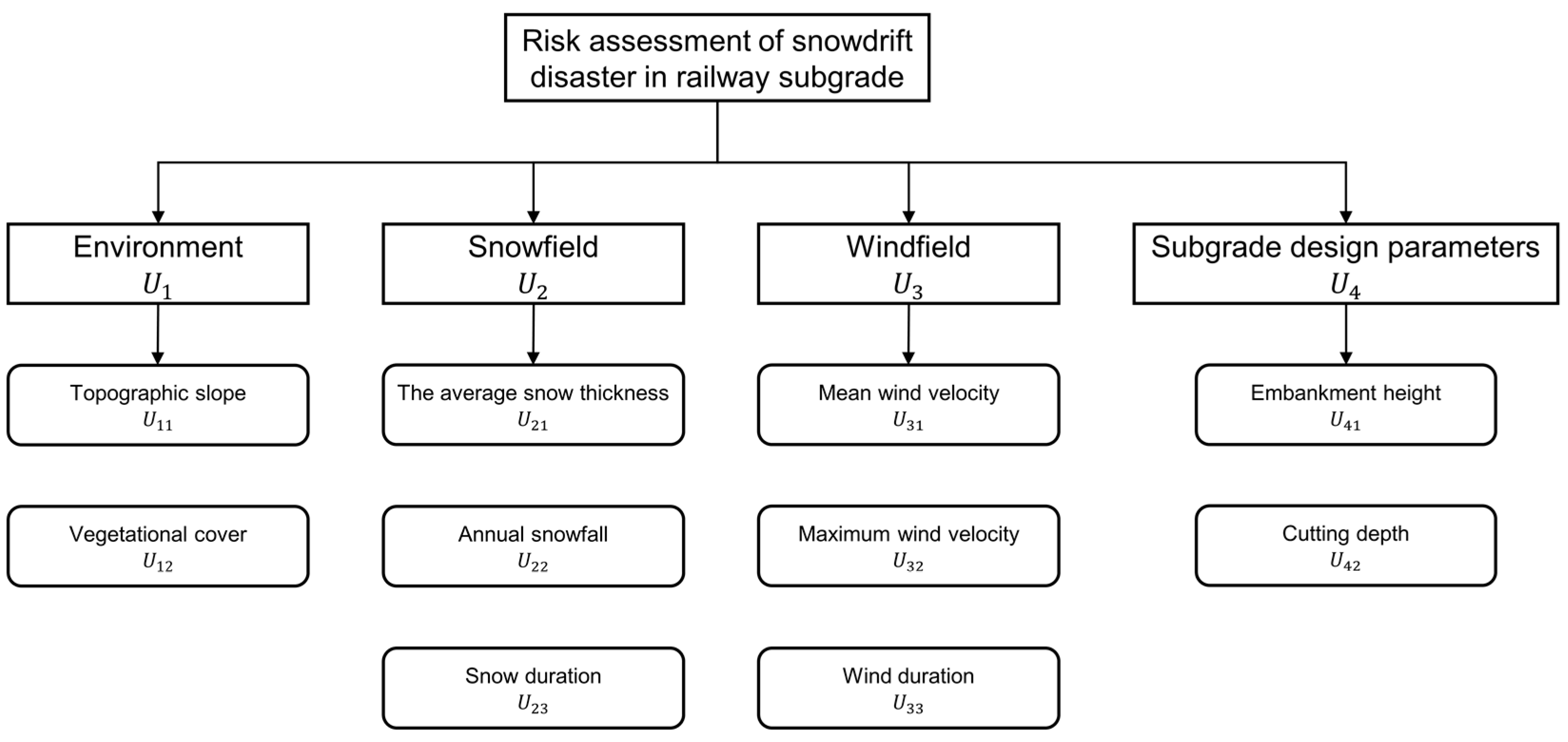
2.1. Factors
- Environment
- 2.
- Snowfield
- 3.
- Windfield
- 4.
- Subgrade design parameters
2.2. Analytic Hierarchy Process (AHP) Model
2.3. Establishment of the FCE Model
- Step 1: Establish the factor set, U.
- 2.
- Step 2: Establish the annotation set V
- 3.
- Step 3: Determine the weight vector W.
- (1)
- Normalize the column elements of the matrix
- (2)
- Sum the elements of each normalized column
- (3)
- Normalize the vector obtained from the previous step
- 4.
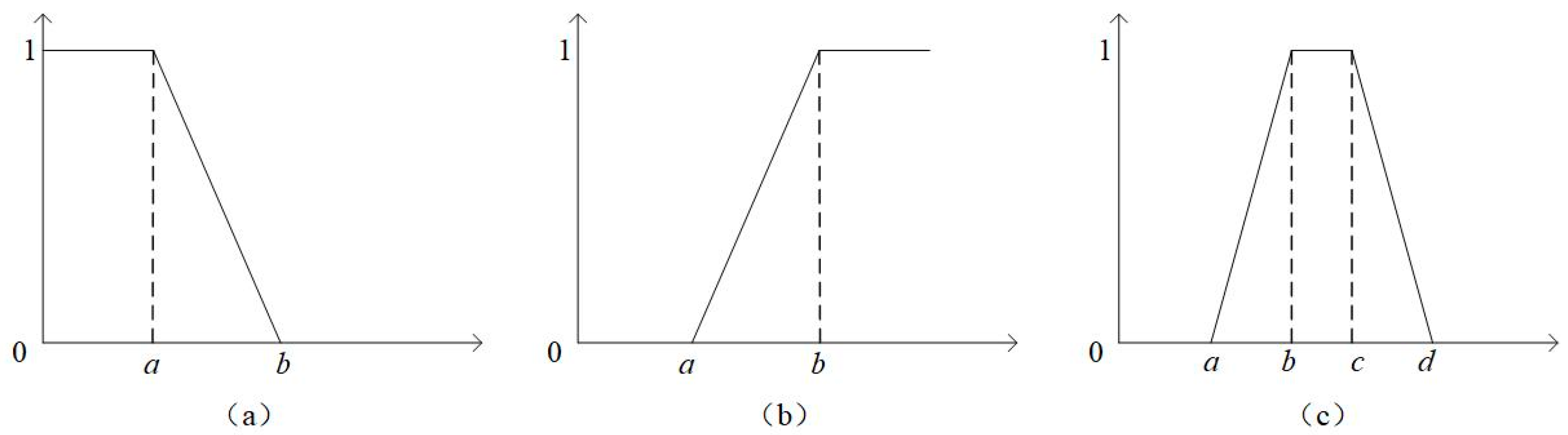
- Step 4: Calculate the single-factor membership degree
- (1)
- Ridge distribution.
- (2)
- Trapezoidal distribution.
- 5.
- Step 5: Establish the fuzzy comprehensive evaluation matrix
2.4. Determination of the Evaluation Weights
2.5. Validation of the Evaluation Results
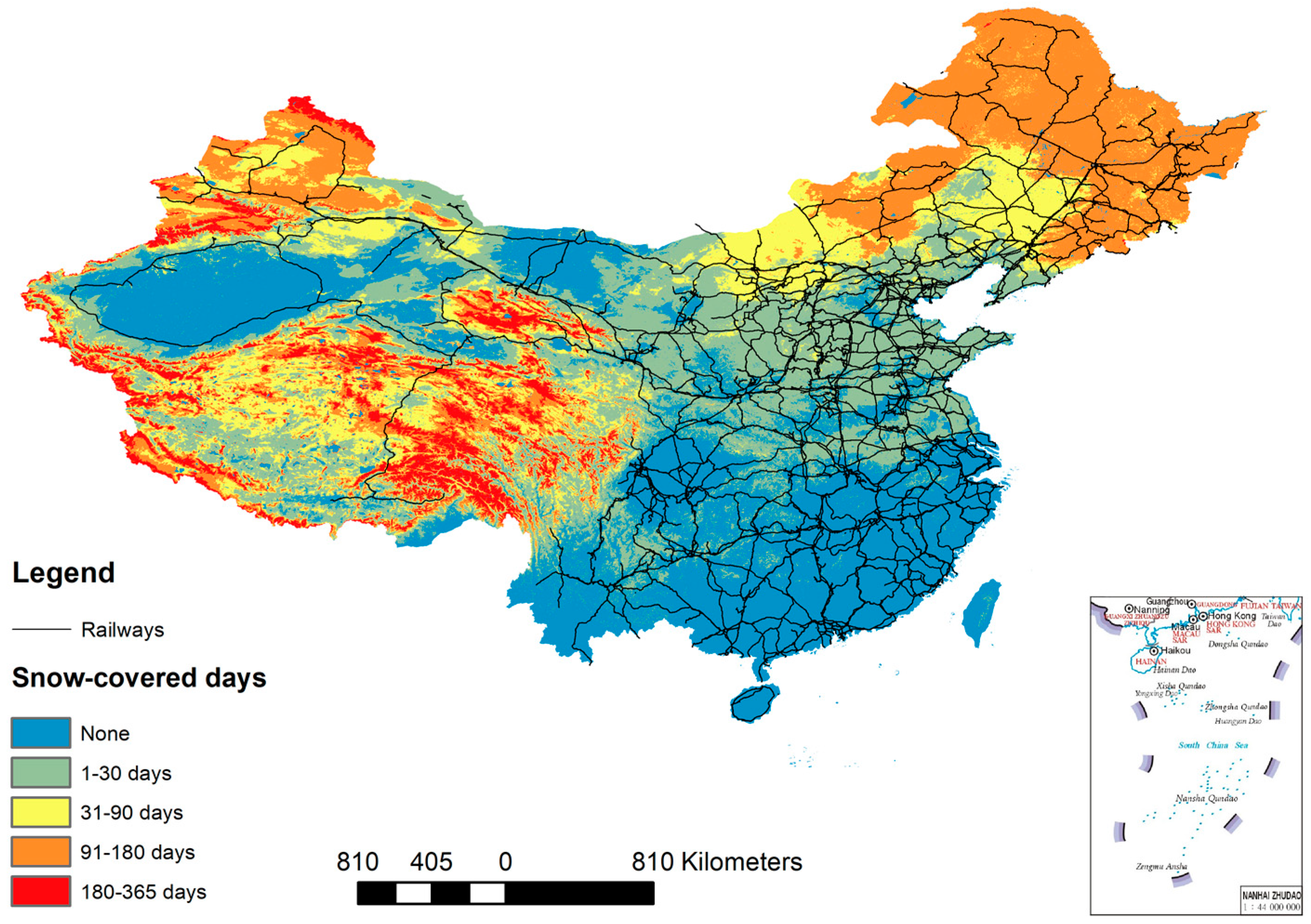
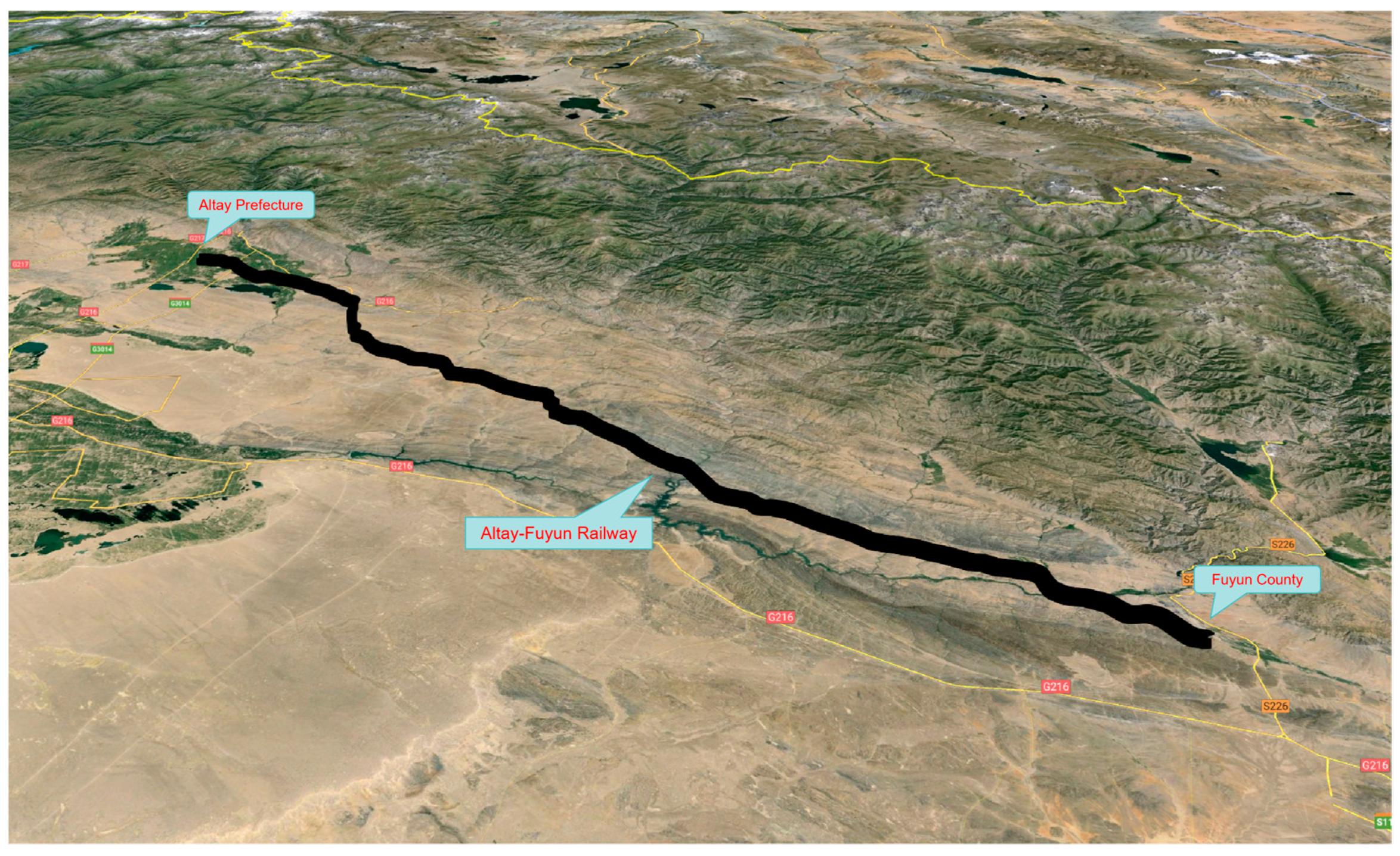
3. Project Overview and Results
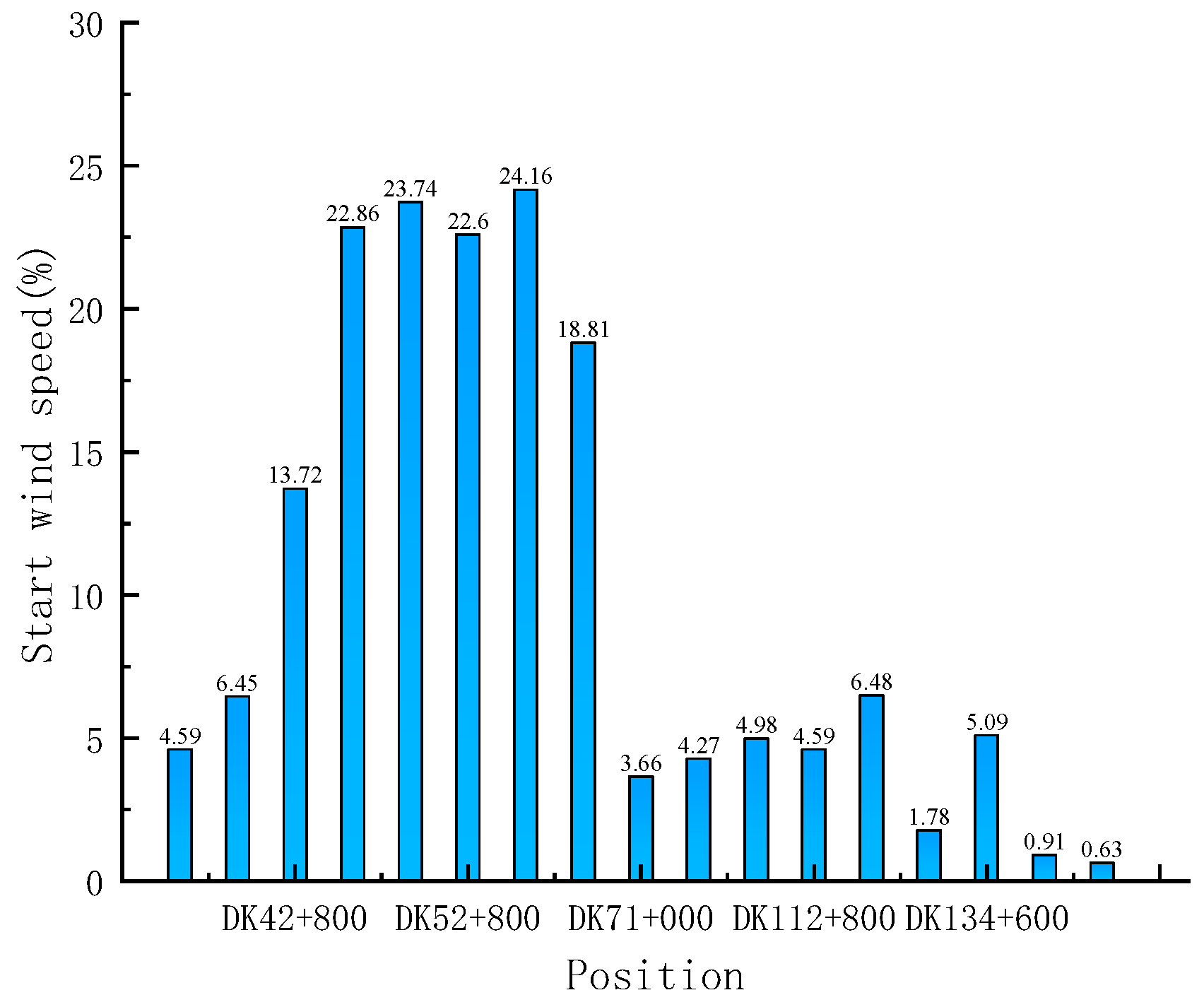
3.1. Wind Speed and Direction Characteristics
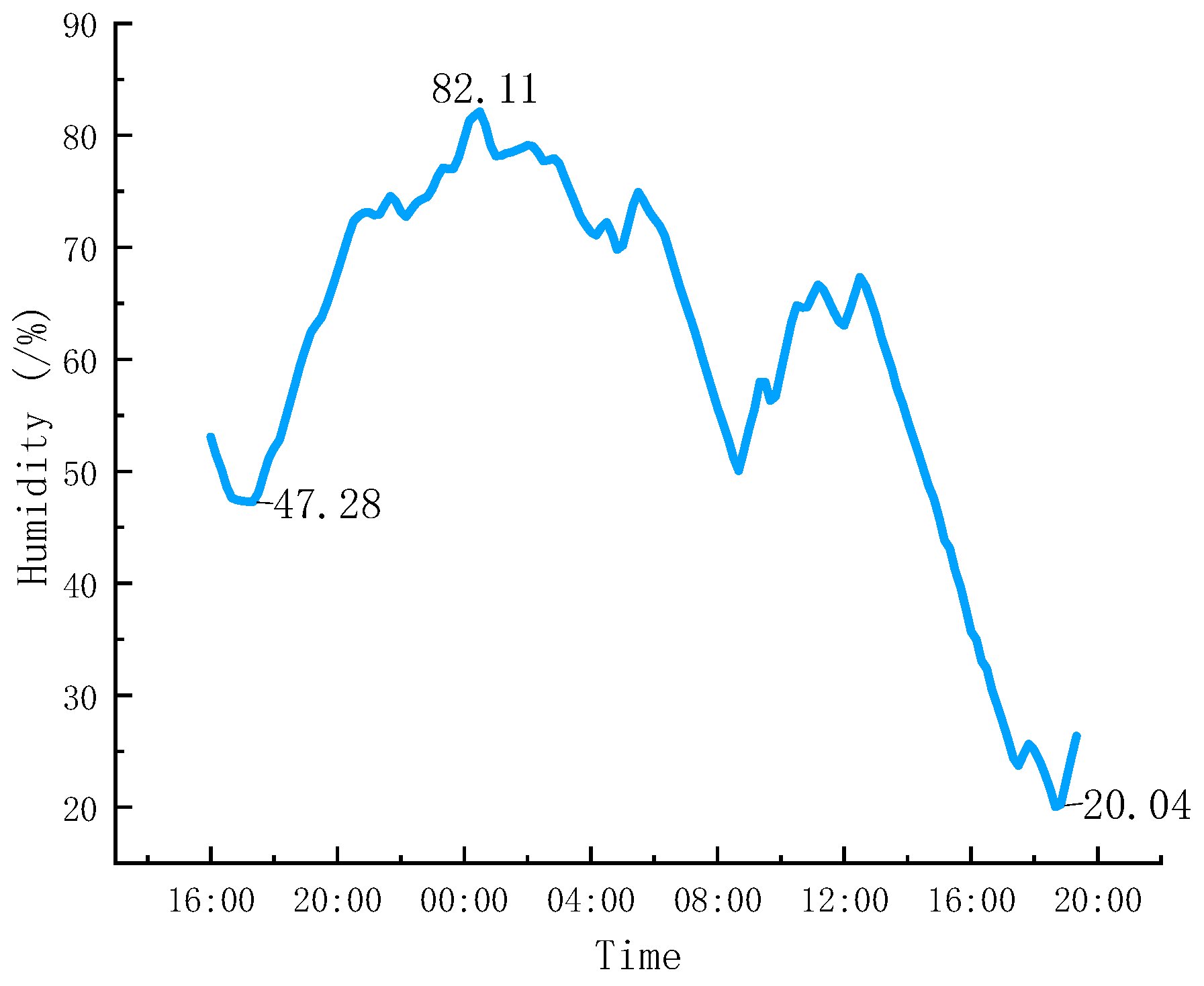
3.2. Snow Accumulation Characteristics
3.3. Risk Indicator Weights
- The judgment matrix for the first-level indicators is as follows:
- 2.
- The judgment matrix for the second-level indicators is as follows:
3.4. Risk Assessment Results
- DK27 + 600 Hazardous Fuzzy Judgment Set:where ; it is determined that the hazard level at DK27 + 900 is classified as Level III, indicating a moderate state of risk.
- 2.
- DK65 + 900 Hazardous Fuzzy Judgment Set:where ; it is determined that the hazard level at DK65 + 900 is classified as Level V, indicating a very high risk.
- 3.
- DK135 + 200 Hazardous Fuzzy Judgment Set:where ; it is determined that the hazard level at DK135 + 200 is classified as Level III, indicating a moderate state of risk.
- 4.
- DK198 + 200Hazardous Fuzzy Judgment Set:where ; it is determined that the hazard level at DK198 + 200 is classified as Level V, indicating a very high risk.
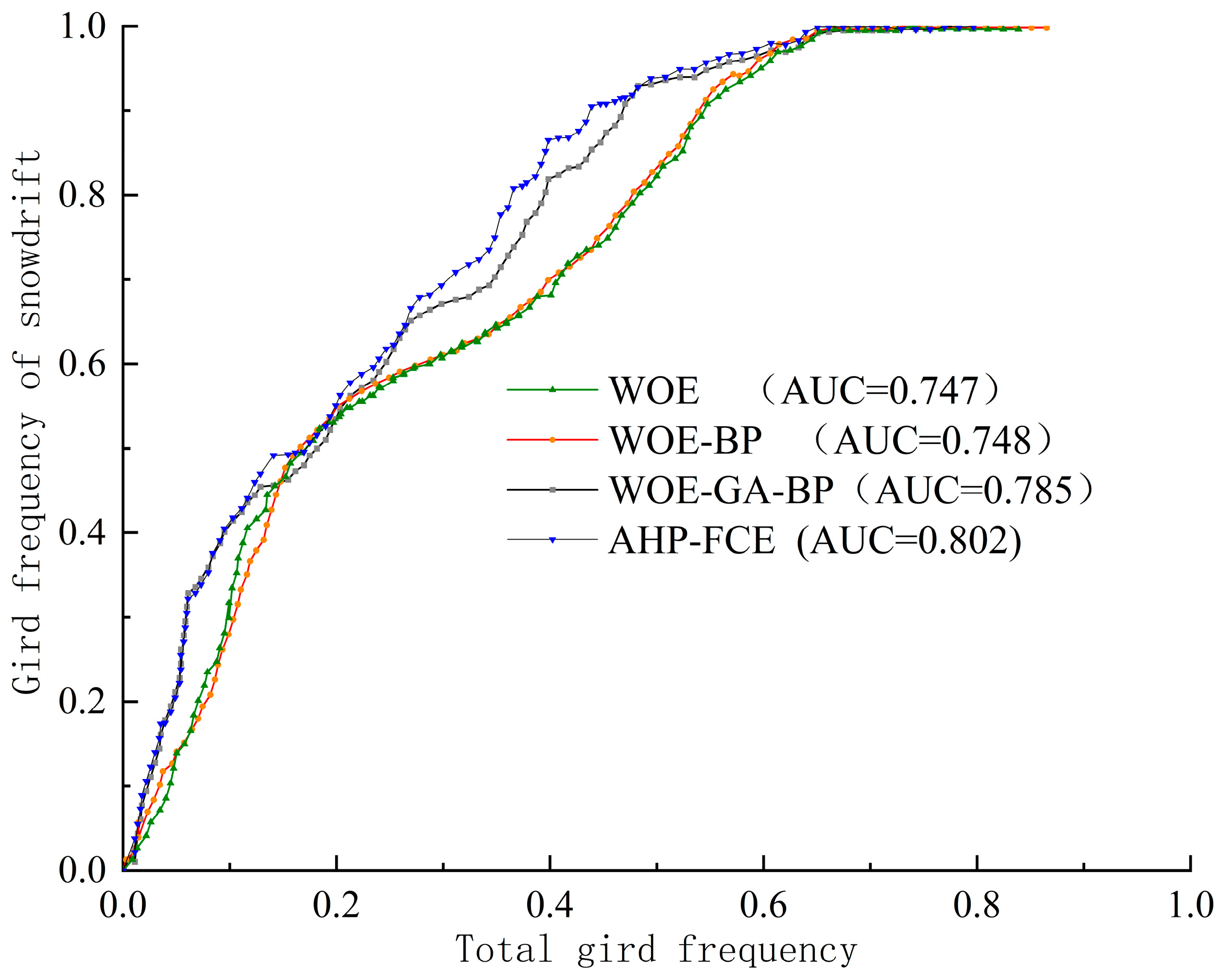
3.5. Accuracy Evaluation
4. Discussion
5. Conclusions
- Among the factors affecting the risk of snowdrift disasters on railway subgrades, four primary contributing metrics were selected: on-site environmental conditions, regional snowfield conditions, regional windfield conditions, and subgrade design parameters. Then, 11 underlying indicators were defined, and a “5-level” evaluation system for the risk of snowdrift disasters on railway subgrades was established. Through calculations, the risk levels of snowdrift disasters along the Afu Railway line were determined.
- In the weight distribution of the snowdrift disaster risk on railway subgrades, it was found that among the first-level metrics, regional snowfield conditions and subgrade design parameters have a significant impact on the risk of snowdrift disasters, with weights of 26.81% and 40.53%, respectively. Among the secondary indicators, the depth of cuttings and average snow depth have a considerable impact on the risk of snowdrift disasters to the railway subgrade, with weights of 29.04% and 15.09%, respectively.
- During the evaluation process, individual indicator evaluation values from typical work points were substituted into the corresponding membership functions to obtain the membership degree values for the indicators at these work points. Subsequently, through fuzzy calculations and normalization processing, the hazard degree of each typical work point was determined. Moreover, by fixing the relevant parameters within the region according to regional characteristics and only considering changes in the form of the subgrade structure, the calculations were simplified.
- The scientific and systematic hazard assessment method developed in this research offers foundational data and theoretical support for future studies. It provides relevant departments with a scientific basis for formulating effective countermeasures, ultimately enhancing the safety and reliability of railway operations. Additionally this assessment method serves as a valuable guide for the risk evaluation of snowdrift disasters on railways, informing the design of railway subgrades and the development of disaster prevention and mitigation strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Zhang, Z. Wind blown snow zoning in China. J. Mt. Sci. 1999, 17, 312–317. [Google Scholar]
- Yu, X.; Liu, M.; Wang, J.; Liu, Q.; Bu, J. Statistical characteristics of the spatial distribution of wind and snow in the Xinjiang Uygur Autonomous Region. Nat. Hazards 2022, 111, 1977–2009. [Google Scholar] [CrossRef]
- Ding, Y.; Sun, Q.; Zhu, Q. A dynamic snow accumulation simulation approach for forecasting snow distribution over regional-scale terrain. Trans. GIS 2022, 26, 1421–1443. [Google Scholar] [CrossRef]
- Wang, Z. Researches on Snow Cover, Snow-drifts and Avalanches in China. J. Glaciol. Geocryol. 1988, 10, 273–278. [Google Scholar]
- Tachiiri, K.; Shinoda, M.; Klinkenberg, B.; Morinaga, Y. Assessing Mongolian snow disaster risk using livestock and satellite data. J. Arid. Environ. 2008, 72, 2251–2263. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.J.; Yu, I.; Jeong, S.; Chung, G. Snow disaster risk index in the Ulsan Metropolitan City. J. Korean Soc. Hazard Mitig. 2014, 14, 97–106. [Google Scholar] [CrossRef]
- Marković, M.; Lukić, S.; Baumgertel, A. Sensitivity analysis of roads to snowdrifts in the autonomous province Vojvodina area, republic of Serbia. Environ. Eng. Manag. J. 2023, 22, 779–790. [Google Scholar] [CrossRef]
- Liao, X.; Huang, K.; Song, D.; Wen, H.; Ling, S.; Wu, X. Distribution characteristics of snow and evaluation of snowdrift susceptibility along the Xinku section of Yining-Aksu Railway in China. Cold Reg. Sci. Technol. 2024, 217, 104020. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Özger, M. An integrated framework for the comprehensive evaluation of low impact development strategies. J. Environ. Manag. 2021, 294, 113023. [Google Scholar] [CrossRef]
- Wang, X.; Lv, S.; Quan, J. The evolution of cooperation in the Prisoner’s Dilemma and the Snowdrift game based on Particle Swarm Optimization. Phys. A Stat. Mech. Appl. 2017, 482, 286–295. [Google Scholar] [CrossRef]
- Li, S.; Feng, X.; Zuo, W. Research on fuzzy comprehensive evaluation for regional dangerousdegree of snow disaster in Nagqu of Tibet. J. Nat. Disasters 2001, 1, 86–91. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Q.; Liang, T.; Guo, Z.; Chai, Q. Establishment of snow disaster remote sensing monitoring and damage estimation systems in Altai pastoral region of Xinjiang. Chin. J. Appl. Ecol. 2006, 17, 215–220. [Google Scholar] [CrossRef]
- Han, S.; Guo, W.; Ke, C.; Zhao, J.; Ma, D. Comprehensive assessment of snow disaster risk in Northeast China. High-Tech Commun. 2020, 30, 91–100. [Google Scholar]
- Wu, P.; Chen, F.; Liu, J.; Ma, L.; Liu, L.; Hu, Z. Evaluation of highway wind and snow blowing risk based on fuzzy comprehensive evaluation method. J. Saf. Environ. 2017, 17, 2273–2276. [Google Scholar] [CrossRef]
- Wang, R.; Wei, J.; Liu, J.; Yan, Z.; Liu, Q. Blowing snow characteristics and risk assessment of the Yiwu-Mulei section of Beijing-Xinjiang Expressway. J. Glaciol. Geocryol. 2023, 45, 1314–1326. [Google Scholar]
- Li, P.; Bai, M.; Li, J.; Qiu, S.; Wei, Z. Analysis of the influence of snow fences on snow redistribution under snow-drifting in railway cuttings. Cold Reg. Sci. Technol. 2022, 196, 103520. [Google Scholar] [CrossRef]
- He, B.; Bai, M.; Liu, B.; Li, P.; Qiu, S.; Li, X.; Ding, L. Evaluation of Drifting Snow Susceptibility Based on GIS and GA-BP Algorithms. ISPRS Int. J. Geo-Inf. 2022, 11, 142. [Google Scholar] [CrossRef]
- Gao, W.D.; Liu, M.Z.; Wei, W.S.; Xu, G. The occurrence and mitigation of drifting snow and avalanche hazard in the mountains along the Jinghe-Yining railway, Tianshan, China. J. Mt. Sci. 2005, 23, 43–52. [Google Scholar] [CrossRef]
- Qiu, S.; Bai, M.; Jiang, H.; Li, P.; Wei, Z.; Li, X. Field Measurements and Numerical Simulation of Snowdrift on Railway Subgrade. J. Test. Eval. 2022, 50, 2988–3000. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Sun, Y. Evaluation of wind and snow blowing characteristics and their hazard zones in Keta Railway. Subgrade Work. 2022, 1, 25–30. [Google Scholar] [CrossRef]
- Zhou, Z.; Jiala; Xiao, T. Study on a grade evaluation method for snow disaster in Tibet. J. Glaciol. Geocryol. 2016, 38, 1560–1567. [Google Scholar]
- Li, T.; Sun, Y.; Chen, X.; Yu, H. Hazard assessment of snow disaster in Hebei province based on GIS. Henan Sci. 2018, 36, 1099–1104. [Google Scholar]
- Wang, X.; Lu, X.; Ma, Y.; Wang, X. Study on snow disaster assessment method and snow disaster regionalization in Xinjiang. J. Glaciol. Geocryol. 2019, 41, 836–844. [Google Scholar]
- Zhang, X.; Luo, H.; Zeng, X.; Zhou, C.; Shu, Z.; Li, H.; Fei, Z.; Liu, G. Research on regional economic development and natural disaster risk assessment under the goal of carbon peak and carbon neutrality: A case study in Chengdu-Chongqing economic circle. Land Use Policy 2024, 143, 107206. [Google Scholar] [CrossRef]
- Zhang, W.; He, J.; Chen, A.; Wu, X.; Shen, Y. Observations of Drifting Snow Using FlowCapt Sensors in the Southern Altai Mountains, Central Asia. Water 2022, 14, 845. [Google Scholar] [CrossRef]
- Ohara, N.; Kavvas, M.L. Field observations and numerical model experiments for the snowmelt process at a field site. Adv. Water Resour. 2006, 29, 194–211. [Google Scholar] [CrossRef]
- Zhong, C.; Yang, Q.; Liang, J.; Ma, H. Fuzzy comprehensive evaluation with AHP and entropy methods and health risk assessment of groundwater in Yinchuan Basin, northwest China. Environ. Res. 2022, 204, 111956. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Liu, Y.; Ma, D.; Li, M.; Xiang, B. Comparison of GA-BP and PSO-BP neural network models with initial BP model for rainfall-induced landslides risk assessment in regional scale: A case study in Sichuan, China. Nat. Hazards 2020, 100, 173–204. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, Q.; Yin, Z.; Zhang, B.; Liu, M.; Zhang, G.; Fan, F. Experiments on snowdrifts around two adjacent cube models based on a combined snow-wind facility. Cold Reg. Sci. Technol. 2022, 198, 103536. [Google Scholar] [CrossRef]
- Rafique, A.; Dasti, M.Y.S.; Ullah, B.; Awwad, F.A.; Ismail, E.A.A.; Saqib, Z.A. Snow Avalanche Hazard Mapping Using a GIS-Based AHP Approach: A Case of Glaciers in Northern Pakistan from 2012 to 2022. Remote Sens. 2023, 15, 5375. [Google Scholar] [CrossRef]
- Saigger, M.; Sauter, T.; Schmid, C.; Collier, E.; Goger, B.; Kaser, G.; Prinz, R.; Voordendag, A.; Mölg, T. A drifting and blowing snow scheme in the weather research and forecasting model. J. Adv. Model. Earth Syst. 2024, 16, e2023MS004007. [Google Scholar] [CrossRef]
- Xie, Z.; Hu, Z.; Ma, Y.; Sun, G.; Gu, L.; Liu, S.; Wang, Y.; Zheng, H.; Ma, W. Modeling Blowing Snow over the Tibetan Plateau with the Community Land Model: Method and Preliminary evaluation. J. Geophys. Res. Atmos. 2019, 124, 9332–9355. [Google Scholar] [CrossRef]
- Foglietta, C.; Panzieri, S. CISIApro Critical Infrastructures Modeling Technique for an Effective Decision Making Support. Cyber-Phys. Threat. Intell. Crit. Infrastruct. Secur. 2020, 385–396. [Google Scholar] [CrossRef]
- Atrigna, M.; Buonanno, A.; Carli, R.; Cavone, G.; Scarabaggio, P.; Valenti, M.; Graditi, G.; Dotoli, M. A Machine Learning Approach to Fault Prediction of Power Distribution Grids Under Heatwaves. IEEE Trans. Ind. Appl. 2023, 59, 4835–4845. [Google Scholar] [CrossRef]
- Cavone, G.; van den Boom, T.; Blenkers, L.; Dotoli, M.; Seatzu, C.; De Schutter, B. An MPC-Based Rescheduling Algorithm for Disruptions and Disturbances in Large-Scale Railway Networks. IEEE Trans. Autom. Sci. Eng. 2022, 19, 99–112. [Google Scholar] [CrossRef]



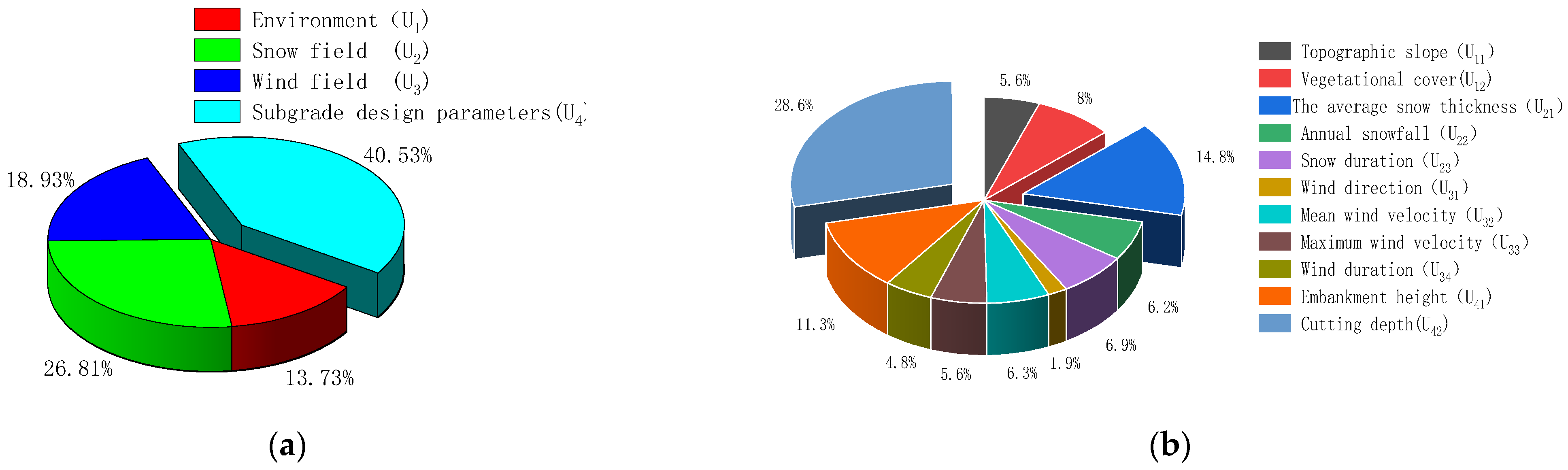
| Primary Indicators | Secondary Indicators | Risk Assessment Criteria | ||||
|---|---|---|---|---|---|---|
| Level I | Level II | Level III | Level IV | Level V | ||
| Environment (U1) | Topographic slope (U11) | Flat | Gentle hill | Average hill | Steep hill | Mountainous area |
| Vegetational cover (U12) | Dense | Moderate | Medium | Thin | No vegetation | |
| Snowfield (U2) | The average snow thickness/cm (U21) | H < 10 | 10 ≤ H < 20 | 20 ≤ H < 30 | 30 ≤ H < 40 | H ≥ 40 |
| Annual snowfall/mm (U22) | a < 200 | 200 ≤ a < 400 | 400 ≤ a < 800 | 800 ≤ a < 1200 | a ≥ 1200 | |
| Snow duration/h (U23) | T < 6 | 6 ≤ T < 12 | 12 ≤ T < 18 | 18 ≤ T < 24 | T ≥ 24 | |
| Windfield (U3) | Wind direction (U31) | Parallel with the line | Angle to the line | Angle to the line | Angle to the line | Angle to the line |
| Mean wind velocity/m/s (U32) | V < 1 | 1 ≤ V < 2 | 2 ≤ V < 3 | 3 ≤ V < 4 | V ≥ 4 | |
| Maximum wind velocity/m/s (U33) | Vm < 3 | 3 ≤ Vm < 5 | 5 ≤ Vm < 7 | 7 ≤ Vm < 9 | Vm ≥ 9 | |
| Wind duration/h (U34) | T < 6 | 6 ≤ T < 12 | 12 ≤ T < 18 | 18 ≤ T < 24 | T ≥ 24 | |
| Subgrade design parameters (U4) | Embankment height/m (U41) | h ≥ 5 | 4 ≤ h < 5 | 3 ≤ h < 4 | 2 ≤ h < 3 | h < 2 |
| Cutting depth/m (U42) | h ≥ 8 | 7 ≤ h < 8 | 5 ≤ h < 7 | 3 ≤ h < 5 | h < 3 | |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| V | Effectiveness of the Maximum Membership Principle |
|---|---|
| +∞ | Complete response |
| [1,+∞) | Very effective |
| [0.5,1) | Effective |
| [0,0.5) | Low efficiency |
| 0 | Completely invalid |
| Time | New Snow Density/(g·cm−3) |
|---|---|
| 13 November 2017 | 0.133 |
| 15 December 2018 | 0.143 |
| 26 February 2019 | 0.146 |
| 21 December 2019 | 0.151 |
| 19 November 2020 | 0.138 |
| 21 January 2021 | 0.136 |
| Level | The First Level | The Second Level | |||
|---|---|---|---|---|---|
| Pu | Pu1 | Pu2 | Pu3 | Pu4 | |
| CR | 0.008 | 0 | 0 | 0 | 0.052 |
| Evaluating Indicator | Index Evaluation Value | ||||
|---|---|---|---|---|---|
| DK27 + 600 | DK65 + 900 | DK135 + 200 | DK198 + 200 | ||
| Qualitative indicators | Topographic slope (U11) | 55 | 55 | 55 | 55 |
| Vegetational cover (U12) | 0 | 0 | 0 | 0 | |
| Wind direction (U31) | 75 | 80 | 65 | 85 | |
| The average snow thickness (U21) | 25 | 50 | 65 | 45 | |
| Quantitative indicators | Annual snowfall (U22) | 1148 | 1148 | 1148 | 1148 |
| Snow duration (U23) | 14.6 | 16.2 | 14.2 | 9.4 | |
| Mean wind velocity (U32) | 2.1 | 1.7 | 2.5 | 3.2 | |
| Maximum wind velocity (U33) | 8.7 | 7.5 | 10.2 | 13.5 | |
| Wind duration (U34) | 2.4 | 5.2 | 3.4 | 7.2 | |
| Embankment height (U41) | 3.1 | 0 | 0 | 1.4 | |
| Cutting depth (U42) | 0 | 1.5 | 5.8 | 0 | |
| Index | Index Membership | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Topographic slope (U11) | 0 | 0 | 1 | 0 | 0 |
| Vegetational cover (U12) | 0 | 0 | 0 | 0 | 1 |
| Wind direction (U31) | 0 | 0 | 1 | 0 | 0 |
| The average snow thickness (U21) | 0 | 0 | 0 | 1 | 0 |
| Annual snowfall (U22) | 0 | 0 | 0.5027 | 0.4972 | 0 |
| Snow duration (U23) | 0 | 1 | 0 | 0 | 0 |
| Mean wind velocity (U32) | 0 | 0.4966 | 0.5034 | 0 | 0 |
| Maximum wind velocity (U33) | 0 | 0 | 0 | 0.4931 | 0.5068 |
| Wind duration (U34) | 1 | 0 | 0 | 0 | 0 |
| Embankment height (U41) | 0 | 0 | 0.5034 | 0.4965 | 0 |
| Cutting depth (U42) | 0 | 0 | 0 | 0 | 0 |
| Index | Index Membership | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Topographic slope (U11) | 0 | 0 | 1 | 0 | 0 |
| Vegetational cover (U12) | 0 | 0 | 0 | 0 | 1 |
| Wind direction (U31) | 0 | 0 | 0 | 0 | 1 |
| The average snow thickness (U21) | 0 | 0 | 0 | 1 | 0 |
| Annual snowfall (U22) | 0 | 0 | 0.4918 | 0.5082 | 0 |
| Snow duration (U23) | 0 | 1 | 0 | 0 | 0 |
| Mean wind velocity (U32) | 0 | 0.5102 | 0.4897 | 0 | 0 |
| Maximum wind velocity (U33) | 0 | 0 | 0.4886 | 0.5114 | 0 |
| Wind duration (U34) | 0.5109 | 0.4891 | 0 | 0 | 0 |
| Embankment height (U41) | 0 | 0 | 0 | 0 | 0 |
| Cutting depth (U42) | 0 | 0 | 0 | 0 | 1 |
| Index | Index Membership | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Topographic slope (U11) | 0 | 0 | 1 | 0 | 0 |
| Vegetational cover (U12) | 0 | 0 | 0 | 0 | 1 |
| Wind direction (U31) | 0 | 0 | 0 | 0 | 1 |
| The average snow thickness (U21) | 0 | 0 | 0 | 1 | 0 |
| Annual snowfall (U22) | 0 | 0 | 0.5055 | 0.4945 | 0 |
| Snow duration (U23) | 0 | 0 | 0 | 1 | 0 |
| Mean wind velocity (U32) | 0 | 0 | 1 | 0 | 0 |
| Maximum wind velocity (U33) | 0 | 0 | 0 | 0 | 1 |
| Wind duration (U34) | 1 | 0 | 0 | 0 | 0 |
| Embankment height (U41) | 0 | 0 | 0 | 0 | 0 |
| Cutting depth (U42) | 0 | 0 | 1 | 0 | 0 |
| Index | Index Membership | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| Topographic slope (U11) | 0 | 0 | 1 | 0 | 0 |
| Vegetational cover (U12) | 0 | 0 | 0 | 0 | 1 |
| Wind direction (U31) | 0 | 0 | 0 | 0 | 1 |
| The average snow thickness (U21) | 0 | 0 | 0 | 1 | 0 |
| Annual snowfall (U22) | 0 | 0 | 0 | 1 | 0 |
| Snow duration (U23) | 0 | 0.4958 | 0.5041 | 0 | 0 |
| Mean wind velocity (U32) | 0 | 0 | 0.4931 | 0.5069 | 0 |
| Maximum wind velocity (U33) | 0 | 0 | 0 | 0 | 1 |
| Wind duration (U34) | 1 | 0 | 0 | 0 | 0 |
| Embankment height (U41) | 0 | 0 | 0 | 0 | 1 |
| Cutting depth (U42) | 0 | 0 | 0 | 0 | 0 |
| Position | Maximum Membership | The Second Largest Membership Degree | n | α | Effectiveness |
|---|---|---|---|---|---|
| DK27 + 600 | 0.3749 | 0.1740 | 5 | 0.63 | Effective |
| DK65 + 900 | 0.4772 | 0.1507 | 5 | 1.15 | Very effective |
| DK135 + 200 | 0.4349 | 0.261 | 5 | 0.56 | Effective |
| DK198 + 200 | 0.402 | 0.157 | 5 | 0.80 | Effective |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Bai, M.; Lin, D.; Zhang, Y.; Xia, H.; Fan, J.; Zhou, W.; Tang, Z. Research on an Evaluation Method of Snowdrift Hazard for Railway Subgrades. Appl. Sci. 2024, 14, 7247. https://doi.org/10.3390/app14167247
Qiu S, Bai M, Lin D, Zhang Y, Xia H, Fan J, Zhou W, Tang Z. Research on an Evaluation Method of Snowdrift Hazard for Railway Subgrades. Applied Sciences. 2024; 14(16):7247. https://doi.org/10.3390/app14167247
Chicago/Turabian StyleQiu, Shumao, Mingzhou Bai, Daming Lin, Yufang Zhang, Haoying Xia, Jiawei Fan, Wenjiao Zhou, and Zhenyu Tang. 2024. "Research on an Evaluation Method of Snowdrift Hazard for Railway Subgrades" Applied Sciences 14, no. 16: 7247. https://doi.org/10.3390/app14167247
APA StyleQiu, S., Bai, M., Lin, D., Zhang, Y., Xia, H., Fan, J., Zhou, W., & Tang, Z. (2024). Research on an Evaluation Method of Snowdrift Hazard for Railway Subgrades. Applied Sciences, 14(16), 7247. https://doi.org/10.3390/app14167247






