A Mathematical Model for Conical Hopper Mass Efficiency
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model of Granular Material Discharge from the Conical Hopper—Assessments
- —frictional force [N];
- —force normal to the hopper walls [N];
- —coefficient of friction of material sliding along the hopper walls [–];
- —diameter of the hopper outlet [m];
- —height of the considered elementary volume [m];
- —pressure of the material acting on the hopper walls [Pa].
- —weight of the elemental volume [N];
- —density of the granular material [];
- —acceleration of gravity [].
- —packing angle of the material inside the hopper [°];
- —pressure acting on the upper surface of the elemental volume [Pa].
- —downward acceleration of the elemental volume []
- x—distance from the origin to the cross-section [m].
- —height of the elemental volume (EV) of the granular material [m];
- —cross-sectional area, varying with the displacement of the EV [m2].
- —diameter at the upper part of the hopper [m];
- —diameter at the lower part of the hopper [m];
- —hopper height [m];
- —inclination angle of the cone generatrix [°].
- —acceleration of the material in elemental volume [];
- —increase in the cross-sectional area of the elementary volume [m2];
- —weight of the elementary volume of the material [N];
- —angle of repose for the considered material [°];
- —angle of the given material’s external friction (material-to-vessel) [°].
- —the simplifying coefficient [].
- —a solution to the homogenous Equation (21);
- —a partial solution of the non-homogeneous Equation (19).
- B—constant;
- K(z)—a coefficient determined by Formula (15);
- z—the integration variable.
- —the height of the whole cone [m].
- , [m];
- , [m];
- , [Pa];
- —density of the material, [];
- pa—atmospheric pressure, [Pa].
2.2. Mathematical Model of Granular Material Discharge from the Conical Hopper—Simulation
3. Results
4. Discussion
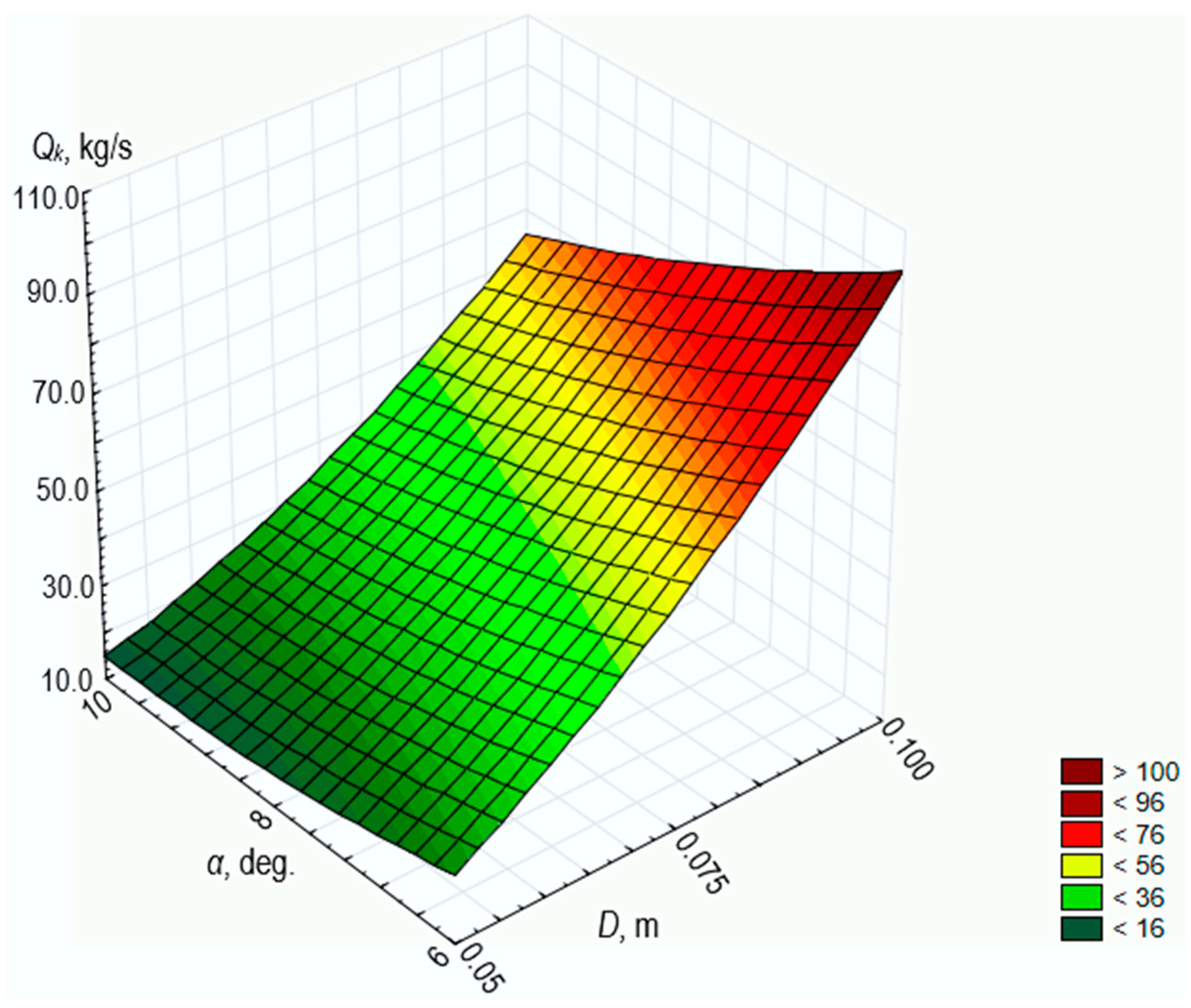
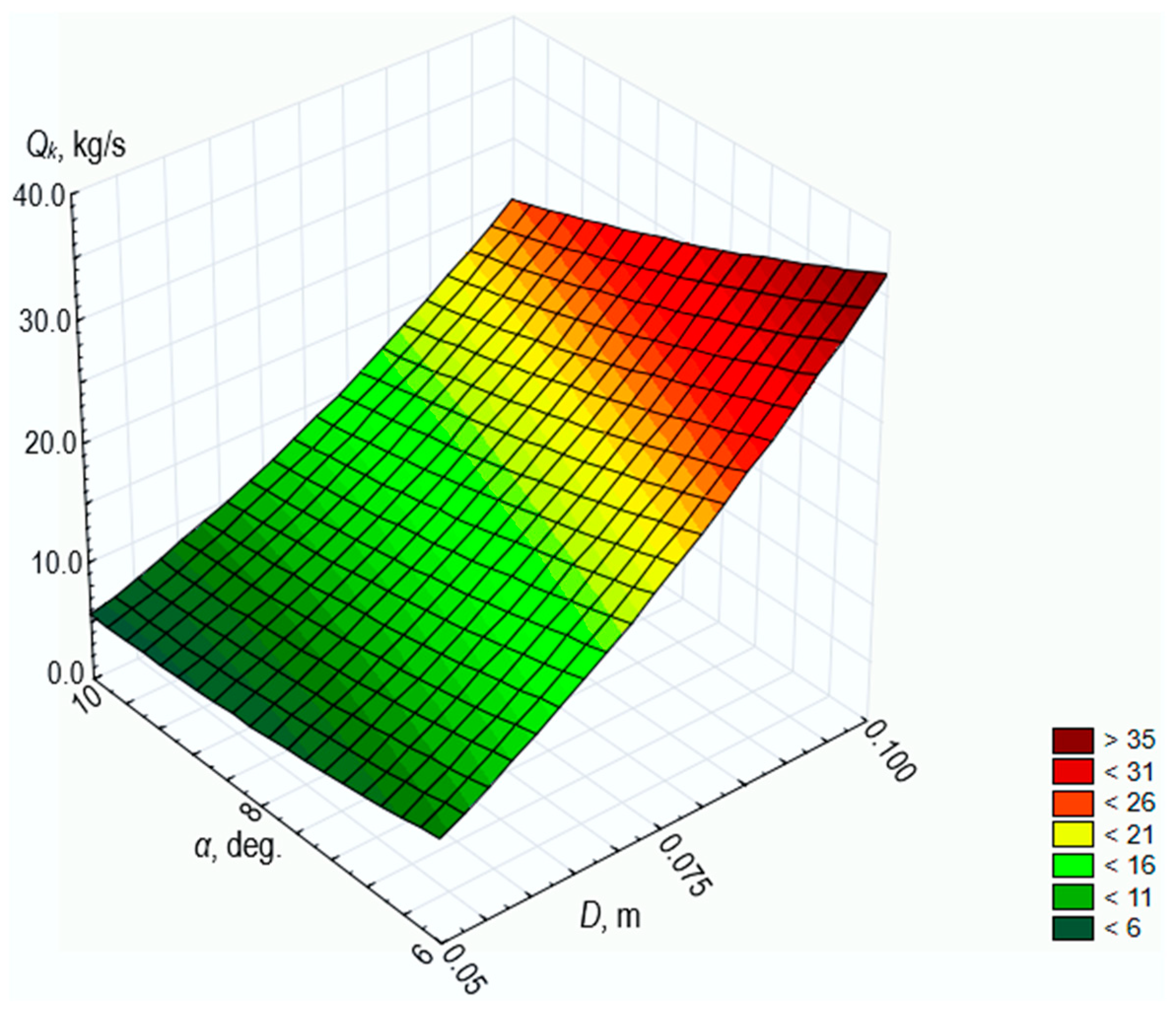
- The results of the experimental studies are consistent with the results of the theoretical modeling.
- The difference between the experimental data and the theoretical modeling results does not exceed 5%.
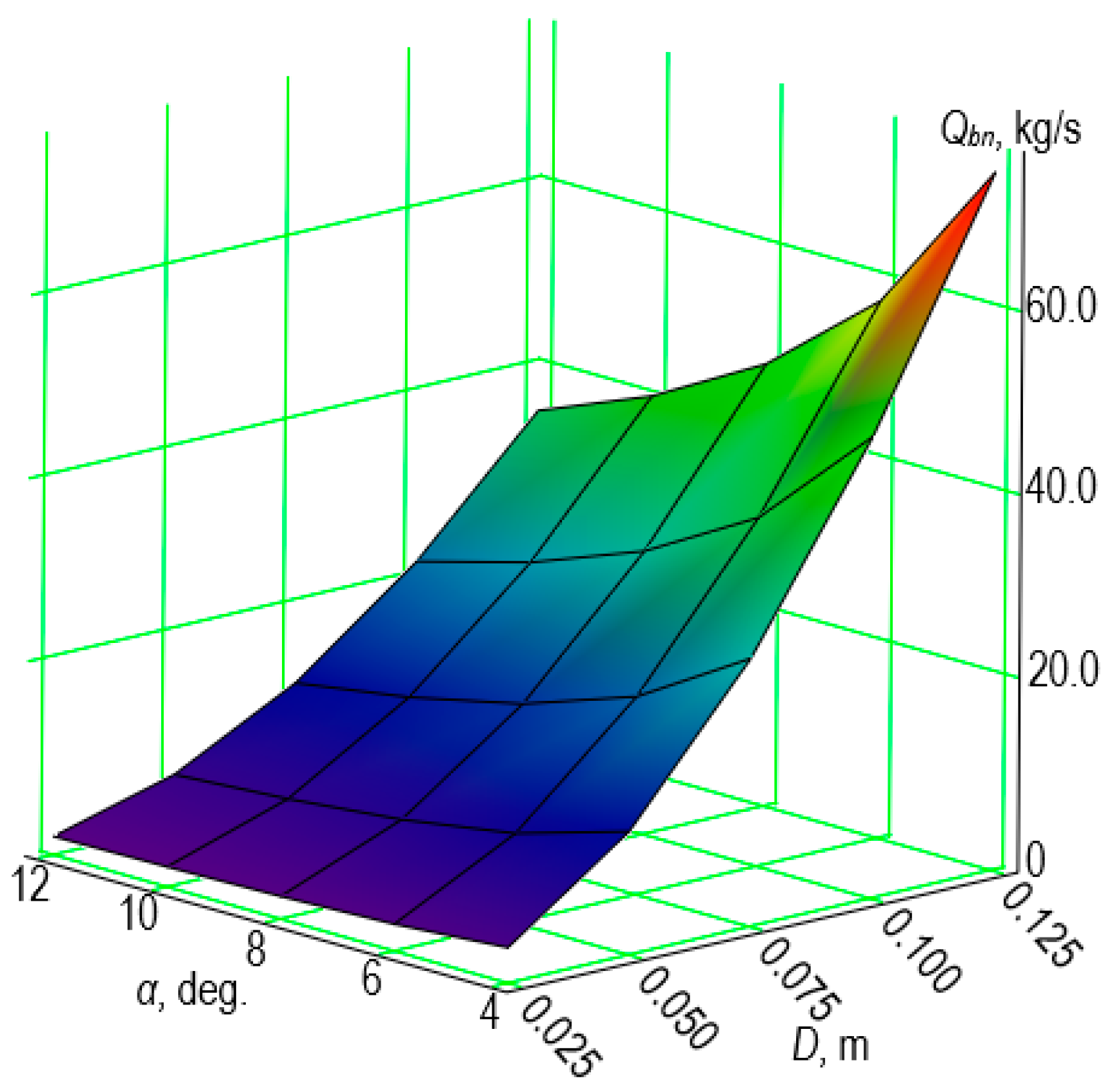
- For D = 0.05 m and α = 4°, Qk = 12.36 kg/s;
- For D = 0.05 m and α = 12°, Qk = 4.56 kg/s;
- For D = 0.10 m and α = 4°, Qk = 49.33 kg/s;
- For D = 0.10 m and α = 12°, Qk = 21.67 kg/s.
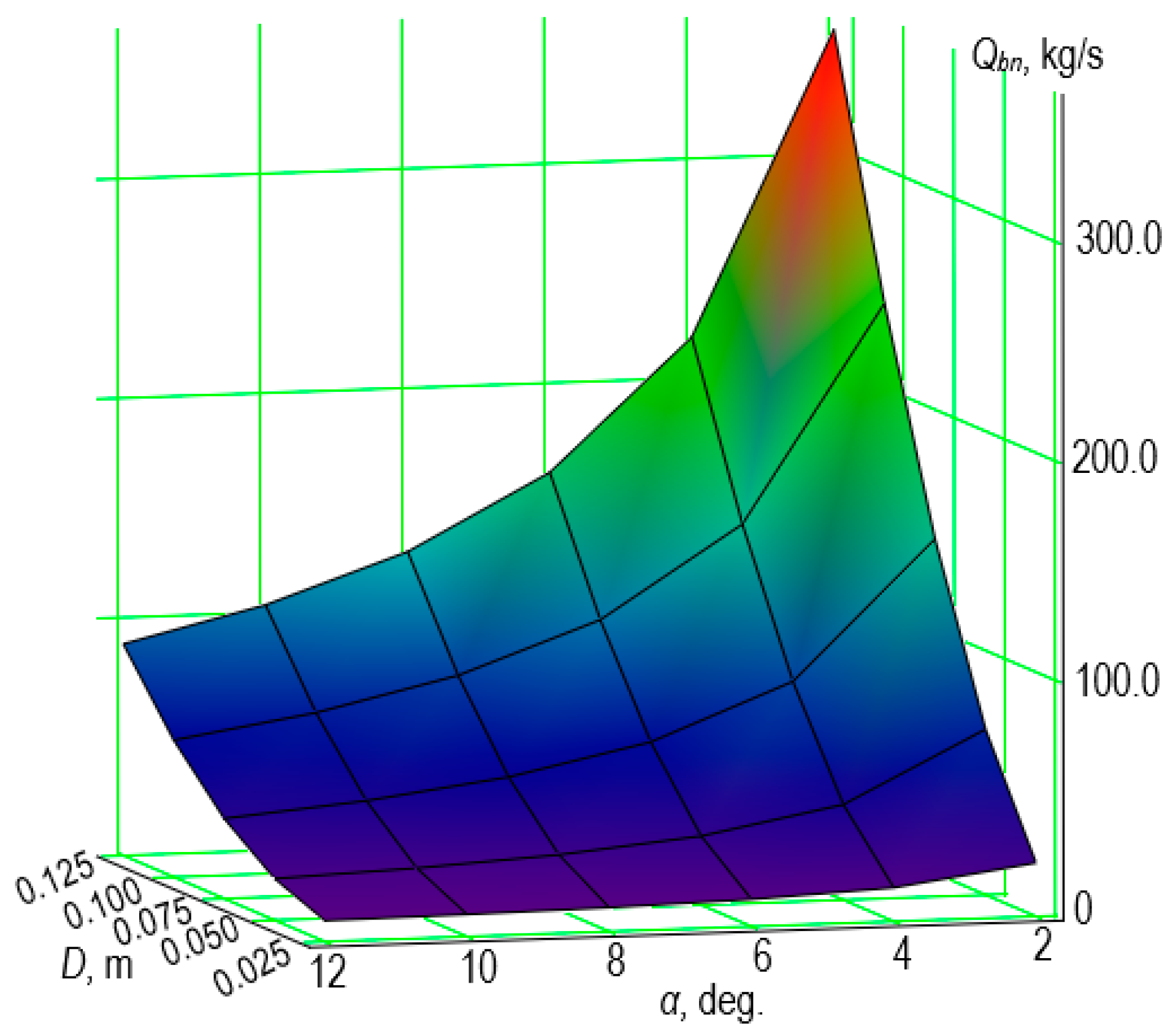
- For D = 0.05 m and α = 4°, Qk = 36.15 kg/s;
- For D = 0.05 m and α = 12°, Qk = 11.59 kg/s;
- For D = 0.10 m and α = 4°, Qk = 144.3 kg/s;
- For D = 0.10 m and α = 12°, Qk = 55.08 kg/s.
5. Conclusions
- the density of the bulk material;
- the angle of particle packing in the overall mass;
- the external friction angle of the material;
- the internal friction angle of the material (angle of repose);
- the coefficient of sliding friction of the bulk material against the hopper walls.
- the generatrix angle of the hopper cone;
- the height of the hopper;
- the diameter of the discharge orifice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chou, C.S.; Tzeng, C.Y.; Smid, J.; Kuo, J.T.; Hsiau, S.S. Experimental study of moving granular bed: Wall stress measurement. In Proceedings of the 14th ASCE Engineering Mechanics Division Conference, Austin, TX, USA, 21–24 May 2000. [Google Scholar]
- Longhi, E.; Easwar, N.; Menon, N. Large force fluctuations in a flowing granular medium. Phys. Rev. Lett. 2002, 89, 045501. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.F.; Rotter, J.M.; Ooi, J.Y.; Zhong, Z. Correlation between flow pattern and wall pressures in a full scale silo. Eng. Struct. 2006, 29, 2308–2320. [Google Scholar] [CrossRef]
- González-Montellano, C.; Gallego, E.; Ramírez-Gómez, Á.; Ayuga, F. Three dimensional discrete element models for simulating the filling and emptying of silos: Analysis of numerical results. Comput. Chem. Eng. 2012, 40, 22–32. [Google Scholar]
- Magalhães, F.G.; Atman, A.P.; Moreira, J.G.; Herrmann, H.J. Analysis of the velocity field of granular hopper flow. Granul. Matter 2016, 18, 33. [Google Scholar]
- Zuriguel, I.; Parisi, D.R.; Hidalgo, R.C.; Lozano, C.; Janda, A.; Gago, P.A.; Peralta, J.P.; Ferrer, L.M.; Pugnaloni, L.A.; Clément, E.; et al. Clogging transition of many-particle systems flowing through bottlenecks. Sci. Rep. 2014, 4, 7324. [Google Scholar]
- Cleary, P.W.; Sawley, M.L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Appl. Math. Model. 2002, 26, 89–111. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, A. A numerical study of the stress distribution in hopper flow. China Particuol. 2003, 1, 57–63. [Google Scholar] [CrossRef]
- Landry, J.W.; Grest, G.S.; Plimpton, S.J. Discrete element simulations of stress distributions in silos: Crossover from two to three dimensions. Powder Technol. 2004, 139, 233–239. [Google Scholar] [CrossRef]
- Masson, S.; Martinez, J. Effect of particle mechanical properties on silo flow and stresses from distinct element simulations. Powder Technol. 2000, 109, 164–178. [Google Scholar] [CrossRef]
- Goda, T.J.; Ebert, F. Three-dimensional discrete element simulations in hoppers and silos. Powder Technol. 2005, 158, 58–68. [Google Scholar] [CrossRef]
- Yang, S.C.; Hsiau, S.S. The simulation and experimental study of granular materials discharged from a silo with the placement of inserts. Powder Technol. 2001, 120, 244–255. [Google Scholar] [CrossRef]
- Hirshfeld, D.; Rapaport, D.C. Granular flow from a silo: Discrete-particle simulations in three dimensions. Eur. Phys. J. E 2001, 4, 193–199. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Cogné, C.; Guessasma, M.; Bellenger, E.; Fortin, J. Discrete modeling of granular flow with thermal transfer: Application to the discharge of silos. Applied Thermal. Engineering 2009, 29, 1846–1853. [Google Scholar] [CrossRef]
- Parisi, D.R.; Masson, S.; Martinez, J. Partitioned distinct element method simulation of granular flow within industrial silos. J. Eng. Mech. 2004, 130, 71–779. [Google Scholar] [CrossRef]
- Sykut, J.; Molenda, M.; Horabik, J. DEM simulation of the packing structure and wall load in a 2-dimensional silo. Granul. Matter 2008, 10, 273–278. [Google Scholar] [CrossRef]
- Rogovskii, I.L.; Shymko, L.S.; Voinash, S.A.; Sokolova, V.A.; Rzhavtsev, A.A.; Andronov, A.V. Mathematical modeling of grain mictures in optimatization tasks of the dump bunker’s kinematic parameters. IOP Conf. Ser. Earth Environ. Sci. Chem. Ecol. Oil Gas Eng. 2020, 548, 062055. [Google Scholar] [CrossRef]
- Kobyłka, R.; Wiacek, J.; Parafiniuk, P.; Horabik, J.; Banda, M.; Stasiak, M.; Molenda, M. Discharge Flow of Spherical Particles from a Cylindrical Bin: Experiment and DEM Simulations. Processes 2021, 9, 1860. [Google Scholar] [CrossRef]
- Gella, D.; Maza, D.; Zuriguel, I. Role of particle size in the kinematic properties of silo flow. Phys. Rev. E 2017, 95, 052904. [Google Scholar] [CrossRef]
- Danczyk, M.; Meaclem, T.; Mehdizad, M.; Clarke, D.; Galvosas, P.; Fullard, L.; Holland, D. Influence of contact parameters on Discrete Element method (DEM) simulations of flow from hopper: Comparison with magnetic resonance imaging (MRI) measurements. Powder Technol. 2020, 372, 671–684. [Google Scholar] [CrossRef]
- Parafiniuk, P.; Molenda, M.; Horabik, J. Discharge of rapeseeds from a model silo: Physical testing and discrete element method simulations. Comput. Electron. Agric. 2013, 97, 40–46. [Google Scholar]
- Wang, X.W.; Yang, Z.J.; Shu, X.F.; Feng, J.L. The static contact statuses between granular materials and flat-bottomed steel silos. Powder Technol. 2013, 235, 1053–1059. [Google Scholar]
- Kobylka, R.; Molenda, M.; Horabik, J. Loads on grain silo insert discs, cones, and cylinders: Experiment and DEM analysis. Powder Technol. 2019, 343, 521–532. [Google Scholar]
- Guo, J.; Roberts, A.W.; Prigge, J.D. Experimental investigation of wall pressure and arching behavior under surcharge pressure in mass- flow hoppers. Powder Technol. 2014, 258, 272–284. [Google Scholar]
- Sun, W.W.; Zhu, J.P.; Zhang, X.D.; Wang, C.C.; Wang, L.; Feng, J. Multi-Scale experimental study on filling and discharge of squat silos with aboveground conveying channels. J. Stored Prod. Res. 2020, 88, 101679. [Google Scholar]
- Wang, X.W.; Li, B.; Xie, J.C.; Xia, R. Discharge flow and dynamic stress of coal particles in rectangular silos with pyramidal hopper. Int. J. Coal Prep. Util. 2020, 40, 513–523. [Google Scholar]
- An, H.Q.; Wang, X.; Fang, X.H.; Liu, Z.; Liang, C. Wall normal stress characteristics in an experimental coal silo. Powder Technol. 2021, 377, 657–665. [Google Scholar]
- Wu, Y.P.; Liu, M.Y.; Xie, P.S.; Wang, H.W.; Hu, B.S. Three-Dimensional physical similarity simulation experiments for a transparent shaft coal pocket wall in coal mines. ACS Omega 2022, 7, 16442–16453. [Google Scholar]
- Wang, P.J.; Zhu, L.; Zhu, X.L. Flow pattern and normal pressure distribution in flat bottom silo discharged using wall outlet. Powder Technol. 2016, 295, 104–114. [Google Scholar]
- Bembenek, M.; Buczak, M.; Baiul, K. Modelling of the Fine-Grained Materials Briquetting Process in a Roller Press with the Discrete Element Method. Materials 2020, 15, 4901. [Google Scholar] [CrossRef]
- Karwat, B.; Machnik, R.; Niedźwiedzki, J.; Nogaj, M.; Rubacha, P.; Stańczyk, E. Calibration of bulk material model in Discrete Element Method on example of perlite D18-DN. Eksploat. I Niezawodn.—Maint. Reliab. 2019, 21, 351–357. [Google Scholar]
- Baiul, K.; Vashchenko, S.; Khudyakov, A.; Bembenek, M.; Zinchenko, A.; Krot, P.; Solodka, N. A Novel Approach to the Screw Feeder Design to Improve the Reliability of Briquetting Process in the Roller Press. Eksploat. I Niezawodn.—Maint. Reliab. 2023, 25, 67967. [Google Scholar] [CrossRef]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A. DEM Calibration Approach: Design of experiment. J. Phys. Conf. Ser. 2018, 1015, 032017. [Google Scholar]
- Hlosta, J.; Jezerská, L.; Rozbroj, J.; Žurovec, D.; Nečas, J.; Zegzulka, J. DEM Investigation of the Influence of Particulate Properties and Operating Conditions on the Mixing Process in Rotary Drums: Part 1—Determination of the DEM Parameters and Calibration Process. Processes 2020, 8, 222. [Google Scholar] [CrossRef]
- Wang, X.; Yi, J.; Zhou, Z.; Yang, C. Optimal Speed Control for a Semi-Autogenous Mill Based on Discrete Element Method. Processes 2020, 8, 233. [Google Scholar] [CrossRef]
- Dmytriv, V.; Bembenek, M.; Banha, V.; Dmytriv, I.; Dzienniak, D.; Nurkusheva, S. Modeling of the Efficiency of the Centrifugal Conical Disk Dispenser of Bulk Materials. Materials 2024, 17, 1815. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Horodetskyy, I.M.; Horodniak, R.V.; Dmytriv, T.V. Method of theory of dimensions in experimental research of systems and processes. INMATEH—Agric. Eng. 2021, 65, 233–240. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Horodetskyy, I.M.; Yatsunskyi, P.P. Adaptive cyber-physical system of the milk production process. INMATEH—Agric. Eng. 2020, 61, 199–208. [Google Scholar] [CrossRef]


| Feature | Buckwheat | Coal |
|---|---|---|
| Density, ρ [] | 560 | 900 |
| Particle packing angle, β [°] | 56 | 35 |
| External friction angle, φ [°] | 15 | 25 |
| Internal friction angle, ψ [°] | 17 | 34 |
| Material-wall friction coefficient [-] | 0.47 | 0.47 |
| Cone angle, α [°], step: 2° | 4–12 | 2–12 |
| Hopper height, [m] | 0.5 | 0.5 |
| Hopper orifice diameter, [m], step: 0.025 m | 0.025–0.125 | 0.025–0.125 |
| Factors | Designation | Unit | Levels of Factors | Variation Interval | ||
|---|---|---|---|---|---|---|
| Upper | Null | Lower | ||||
| Code Values | ||||||
| +1 | 0 | −1 | ||||
| Hopper orifice diameter, D | x1 | m | 1.0 | 0.075 | 0.050 | 0.025 |
| Hopper cone generatrix angle, α | x2 | deg. | 10 | 8 | 6 | 2 |
| Experiment No. | x1 | x2 | x1·x2 | y1 (QK), Buckwheat, kg/s | y2 (QK), Coal, kg/s | ||
|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | 0.3333 | 0.3333 | 25.0 | 65.3 |
| 2 | 0 | +1 | 0 | −0.6667 | 0.3333 | 13.4 | 35.0 |
| 3 | −1 | +1 | −1 | 0.3333 | 0.3333 | 5.4 | 14.0 |
| 4 | +1 | −1 | −1 | 0.3333 | 0.3333 | 37.0 | 103.0 |
| 5 | 0 | −1 | 0 | −0.6667 | 0.3333 | 20.5 | 57.0 |
| 6 | −1 | −1 | +1 | 0.3333 | 0.3333 | 8.6 | 24.0 |
| 7 | +1 | 0 | 0 | 0.3333 | −0.6667 | 29.8 | 80.0 |
| 8 | 0 | 0 | 0 | −0.6667 | −0.6667 | 16.2 | 43.0 |
| 9 | −1 | 0 | 0 | 0.3333 | −0.6667 | 6.6 | 18.0 |
| ∑ | 6 | 6 | 4 | - | - | - | - |
| Coefficient of the Regression Equation | Coded Coefficient | Real Coefficient |
|---|---|---|
| b0 | 43.222 | 3.557 |
| b1 | 32.0 | 1039.99 |
| b2 | −11.667 | −6.0 |
| b12 | −7.0 | −140.0 |
| b11 | 5.667 | 9066.72 |
| b22 | 2.667 | 0.667 |
| Coefficient of the Regression Equation | Coded Coefficient | Real Coefficient |
|---|---|---|
| b0 | 16.178 | −0.123 |
| b1 | 11.867 | 338.676 |
| b2 | −3.717 | −1.692 |
| b12 | −2.2 | −44.0 |
| b11 | 2.033 | 3253.28 |
| b22 | 0.783 | 0.196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bembenek, M.; Dmytriv, V.; Banha, V.; Horodniak, R.; Pawlik, J. A Mathematical Model for Conical Hopper Mass Efficiency. Appl. Sci. 2024, 14, 7373. https://doi.org/10.3390/app14167373
Bembenek M, Dmytriv V, Banha V, Horodniak R, Pawlik J. A Mathematical Model for Conical Hopper Mass Efficiency. Applied Sciences. 2024; 14(16):7373. https://doi.org/10.3390/app14167373
Chicago/Turabian StyleBembenek, Michał, Vasyl Dmytriv, Vasyl Banha, Roman Horodniak, and Jan Pawlik. 2024. "A Mathematical Model for Conical Hopper Mass Efficiency" Applied Sciences 14, no. 16: 7373. https://doi.org/10.3390/app14167373





