Abstract
The main purpose of this study is to examine the behavior of certain industrial systems under the conditions of product warranty policy. Given this policy, we are interested in considering all the parameters of the system in order to study them and show their impact on the proposed system. In order to increase the efficiency of the system and activate the product warranty policy, the system will undergo a preliminary examination for any system failure occurrence to determine the reasons that led to the failure. After completing the initial inspection, the mechanic will decide whether it is a user-caused failure or a manufacturing defect to determine whether or not the repair of the broken appliance is covered by the manufacturer’s contractual warranty policy. All times in the system are assumed as a negative exponential distribution. The expressions for some measures of system effectiveness such as reliability, mean time to system failure (MTSF), and availability are derived using the supplementary variable technique and Laplace transform. Sensitivity analysis and a relative sensitivity are then carried out in order to recognize how each system parameter affects performance measures. Finally, some numerical examples are designed and performed to show how the change of each system parameter affects system performance.
1. Introduction
In contract law, a warranty is a product manufacturer’s or service provider’s documented guarantee of quality to the customer; in other words, the warranty is a certificate issued by a manufacturer about the condition of its product. It also refers to the agreements and cases where repairs or replacements are made if the product does not work as well as originally described or intended.
Nowadays, the various industrial systems are becoming more complicated day by day, so manufacturing experts are constantly striving to produce a product with high reliability and low cost. To achieve this, a significant amount of money is spent every year worldwide to reduce failure rates in industrial systems. In addition, developments in the industry are constantly focused on identifying defects that affect the operational efficiency of the product over time. However, failure is an inescapable reality associated with equipment manufacturing. These failures may be due to several reasons, including human error, manufacturing defects, or weather conditions surrounding the system. Strategic planning of the equipment industry plays an important role in improving the reliability and validity of systems.
In the past, some researchers have stated that it is inevitable and necessary to prepare the repair process before repairing failed units in the system without considering the conditions for ensuring product quality, e.g., refs. [1,2,3,4,5,6,7,8] analyzed some industrial systems and examined the benefits that arise for these systems when the failed unit is prepared before the repair process. As a follow-up to the aforementioned studies, M.A.W. Mahmoud et al. [9] studied a two-unit cold standby system with a single repairer performing inspection, replacement, preparation, and repair. L. R. Goel et al. (1995) [10] proposed a cold standby system with two units and preparation time for repairing a failed unit and assumed that the joint distribution of the failure and repair times of each unit is assumed to be a bivariate exponential distribution. Singh and Srinivasu (1987) [11] analyzed a model for a two-unit standby system, assuming that a failed unit is first prepared before it goes into repair. Both the preparation and the repair of the defective unit are performed by a single repairperson. R. Gupta and Ram Krishan (1999) [12] presented a comparison between two random models A and B that had a fixed preparation time to run the spare units and the repaired units. A.K. Mogha and A.K. Gupta (2002) [13] discussed the behavior of a cold standby system with two identical units and three different cases for the active unit (normal, partial, and complete failure). They also assumed that some preparations had to be made for the failed unit before it could be repaired and is sent for repair after completion of preparation. Regardless of the previous literature, most researchers have also focused on performing an inspection of the repaired unit to verify whether the repair is good or whether the unit needs to be repaired again [14,15,16,17,18,19,20]. Kalantari and Johari [21] investigated the soil properties of three real wells at a depth of 22.5 m using field and laboratory tests and then determined indicators for the distribution and reliability of firm service under different failure modes for both static and seismic cases. Some researchers have recently published several articles in which they emphasized the importance of the link between reliability theory and the free warranty policy. For example, in 2011, Ahmed F. Attia et al. [22] examined the preventive maintenance policies of the multistate system and the cost of these policies on manufacturers and buyers. In 2013, Kadyan and Ramniwas [23] discussed the cost of a single-unit system under the conditions of the free warranty policy for repair. In August of the same year, Ramniwas et al. [24] presented the effects of preventive maintenance in the presence of a warranty policy on a single-unit repairable system. Ram et al. [25] in 2015, introduced the concept of preventive maintenance beyond warranty in two reliability models for a single-unit system. Providing a free system warranty for a given operating period is one of the most effective means to ensure the reliability of the system. In 2016, the same authors [26] calculated the mean time to system failure and profit function of a single-unit system with inspection of unit beyond warranty. Ram Niwas and M.S. Kadyan (2015) [27] developed the previously proposed system in 2013 in which they examined the concept of preventive maintenance during the warranty period and assumed that there is a repair force that repairs and replaces the defective device within the warranty period. In 2018, Niwas and Garg [28] presented a single-unit industrial system operating under the cost-free guarantee policy. Here, the system goes to rest after a random period of time. After a complete break, the system resumes its work with full efficiency. In the same year, more precisely in September, Ram Niwas [29] presented a model for maintenance scheduling based on the concepts of the failure-free warranty policy. Pardeep and Amit [30] emphasized that systems that rest after a certain period of operation have a longer life and fewer failures. Finally, in 2022, Mohamed and Hussien [31] introduced the idea of linking the administrative delay time for repairing a failed unit with the free warranty policy for a single-unit repairable system.
Many of the authors who have addressed the free warranty policy mentioned above have assumed that a completely failed unit is immediately taken to a repair shop for maintenance. However, we think this is not realistic in many cases, as the failed unit requires some preparation time before repair can begin. Example: When a car breaks down, the mechanic gathers some materials, including the defective parts, before starting to repair the fault that caused the car to fail.
It is clear that the above studies have only dealt with the analysis of systems without considering the product warranty strategy with the need for preparation before repairing the failed device. Therefore, this article focuses on presenting the product warranty policy with the product repair plan in terms of pre-repair preparation and post-repair inspection to ensure that they obtain a product with high operating efficiency.
The residuum of this article is organized as follows. Section 2 contains the system assumptions, state-specification and notations. Section 3 presents the mathematical model of this system to derive metrics for the reliability of the system, such as the reliability function, mean time to system failure, and steady state availability, using the Markov process. In Section 4, sensitivity and relative sensitivity analyses of the system parameters are obtained. Numerical examples illustrating the behavior of the system are shown in Section 5. Conclusions are summarized in the final section.
2. Description of the System
The system in question has a single active unit with a single repairer who performs detection of the causes of failure, preparation for repair, repair of the failed unit, and post-repair inspection to ensure that the failed unit is repaired or re-repaired again, so we assume the following:
| 1. | The system has single active unit to work. |
| 2. | A single repairman is available for inspection of the causes of failure, repair preparation, repair of the failed unit, and post-repair inspection. |
| 3. | Inspection time, preparation for repair time, repair time, and re-repair time are independent and perfect. |
| 4. | After the failure of the active unit (within the warranty period), the unit goes for inspection to determine whether or not this failure was caused by the user. |
| 5. | After the discovery of the defect by the inspection and the determination of whether the unit is still subject to the warranty of the company or if the repair is at the expense of the user, the preparation of the repair begins, and after the completion of the repair preparation, the repair is started directly. |
| 6. | After the repair (within the warranty period/after the warranty period has expired), the unit will be inspected to determine whether the repair is satisfactory or not. If the repaired unit is not satisfactory, it will be sent for re-repair. |
| 7. | The manufacturer will cover the cost of repairing the defective unit during the warranty period, provided that the user is not the one who causes the malfunction of the unit. |
| 8. | The distribution of all times in this system follows negative exponential distribution . The selection of all system times for this distribution is due to the following reasons: The exponential distribution is a simple distribution with only one parameter and is commonly used to model reliability data. The exponential distribution is actually a special case of the Weibull distribution with ß = 1. The exponential distribution provides a good model for the phase of a product or item’s life when it is just as likely to fail at any time, regardless of whether it is brand new, a year old, or several years old. The exponential distribution is frequently used to model electronic components that usually do not wear out until long after the expected life of the product in which they are installed. Examples include components of high-quality integrated circuits, such as diodes, transistors, resistors, and capacitors. |
| 9. | The system works like new after repair or re-repair. |
State-Specification.
To study the behavioral changes of this system at any virtual time t, we can describe the system states as follows:
| S0/S8 | the unit is active during/within the warranty period/after the warranty period has expired; |
| S1 | the failed unit under inspection, to determine whether or not the system is under warranty; |
| S2/S6 | the failed unit under preparation for repair during/within the warranty period/after the warranty period has expired; |
| S3/S7 | the failed unit under repair during/within the warranty period/after the warranty period has expired; |
| S4/S9 | the unit under inspection after repair, to determine whether the repair is satisfactory or not (during/within the warranty period/after the warranty period has expired); |
| S5/S10 | the unit under re-repair after inspection during/within the warranty period/after the warranty period has expired. |
With these symbols, the possible states of the system under study are as follows:
| Unit in normal mode and operative under warranty period/post-warranty period. | |
| Unit in failure mode and inspection to determine whether this unit is still under warranty or not. | |
| Unit in failure mode and preparation to repair under warranty period/post-warranty period. | |
| Unit in failure mode and repair under warranty period/post-warranty period. | |
| Failed unit under inspection under warranty period/post-warranty period. | |
| Failed unit under re-repair under warranty period/post-warranty period. |
Possible states of the system are as follows:
Up states:
Down states:
Possible states and transitions are shown in Figure 1.
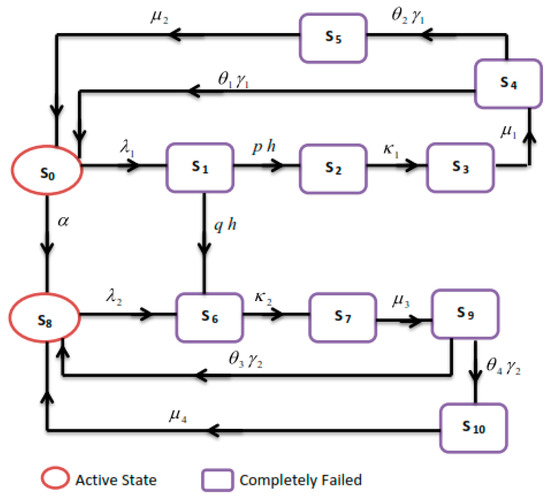
Figure 1.
State-transition diagram of the system.
3. Analysis of the System
3.1. Reliability
The system reliability is the probability that the system will perform adequately for a given time period (0, t). To derive system measures, we use the Markov process for the live states, i.e., S0 and S1. We first infer the reliability function according to the proposed equations.
The initial conditions are as follows:
We apply the Laplace transformation of Equations (1) and (2) and also use the initial condition, and we obtain
From Equation (4), we obtain
By substituting Equation (6) into Equation (5), we obtain
From the two Equations (6) and (7), we obtain the Laplace transformation formula for the reliability of the system as follows:
If we use the inverse Laplace transform for Equation (8), we obtain the reliability function as follows:
3.2. Mean Time to System Failure (MTSF)
The mean time to system failure (MTSF) is the average time a unit can run before it fails. You can also think of (MTSF) as the average life span of a unit. We can calculate the mean time to failure (MTSF) by using Equation (9) as follows:
Hence, the mean time to failure (MTSF) of the system is
3.3. System Availability
There are various definitions of availability but all involve the probability that a system will function as desired when it is needed. First, we can describe the states of this system in the form differential equations as follows:
The initial conditions are
If we perform the Laplace transformation of all the previous equations, we obtain the following equations:
We also note the following:
From Equations (24)–(34), we obtain
where
From Equations (36)–(46), we conclude that the Laplace transform formula for the availability is as follows:
It follows that the steady-state availability of the system is
4. Sensitivity and Relative Sensitivity Analysis
This part of the article is limited to the calculation of sensitivity analyses and relative sensitivity analyses for MTSF and with respect to the system parameter .
Where .
4.1. Sensitivity and Relative Sensitivity Analysis for Reliability Function
In this subsection, we first compute a sensitivity analysis for the changes that occur in the reliability function for all system parameters that depend on it.
By differentiating Equation (9) with respect to parameter , we obtain
Second, through our sensitivity analysis calculations in Equation (49), we can also calculate the relative sensitivity as shown below.
4.2. Sensitivity and Relative Sensitivity Analysis for Mean Time to System Failure
We can also determine the sensitivity analysis of mean time to system failure based on the parameters that affect it.
By differentiating Equation (11) with respect to parameter , we obtain
The relative sensitivity of the mean time to system failure can be represented as follows:
5. Numerical Results
In this section, we perform the numerical analysis. First, we conduct numerical examples to investigate how the system reliability, , the mean time to system failure, MTSF, and steady-state availability, , are affected by changing each system parameter. Subsequently, sensitivity and relative sensitivity analyses are computed for system reliability, , and the mean time to system failure, MTSF.
5.1. Numerical Results for , MTSF, and
In this part of this section, we use numerical examples to study how , MTSF, and are affected by changing various system parameters. The numerical results for are offered first. We fix and for each value of and t, where the parameter takes the values 0.1, 0.4, and 0.8 and the time t ranges from 1 to 10 with a constant step of 1; we obtain Table 1. Table 2 explains the changes that occur in the reliability of the system when takes the values 0.1, 0.5, and 0.8, respectively, and the time from 1 to 10, fixing the other parameters that affect the reliability function. Finally, in Table 3, we examine the effect of the warranty expiration rate on the reliability of the system , where the warranty expiration rate takes the values 0.1, 0.5, and 0.9, the time changes from 1 to 10, and the other system parameters remain unchanged. From all these considerations on the study of the effects of system parameters on system reliability, the following conclusions can be drawn:

Table 1.
Variation of reliability values for different values of “t” at .

Table 2.
Variation of reliability values for different values of “t” at .

Table 3.
Variation of reliability values for different values of “t” at .
Table 1: the influence of parameter and t on is shown as follows.
- (1)
- In the first column of this table, the value of decreases when , and t varies from 1 to 10.
- (2)
- In the second column of same table, the value of decreases when , and t varies from 1 to 10.
- (3)
- Finally, in the third column, we show that the value of decreases when , and t varies from 1 to 10.
From (1), (2) and (3) we can conclude that the reliability of the system decreases when both and t increases and .
Table 2 shows the effect of system parameter and t on as follows.
- (1)
- In the first column of this table, we notice that the value of decreases when , and t varies from 1 to 10.
- (2)
- In the second column shows that the value of decreases when , and t varies from 1 to 10.
- (3)
- In the third column, we show that the value of decreases when , and t varies from 1 to 10.
From the previous three points, we conclude that the value of decreases when , and t varies from 1 to 10.
From the previous three points, we conclude that the value of decreases when the value of increases, and the value of t varies from 1 to 10 with constant values and .
Table 3 also illustrates the effect of when it has the values of and t varies from 1 to 10 on when and . Therefore, we note that the reliability of the system of the system decreases when both and t increases, and and take the constant values of 0.5 and 0.6, respectively.
Second, we examine the effect of the system parameters , , and on the mean to system failure, which can be seen in Figure 2 and Figure 3. The variations of the mean time to system failure are summarized as follows: Figure 2 shows that the mean time to failure of the system in the interval increases when the parameter decreases from 0.9 to 0.4 to 0.2 at . In the same figure, the mean time to system failure in the interval increases by increasing the value of parameter from 0.2 to 0.4 to 0.9 at . Figure 3 shows that the rate of warranty expiration increases from 0.2 to 0.9 in interval , leading to an increase in the mean time to failure of the MTSF system when . In contrast, in interval , when the rate of warranty expiration decreases from 0.2 to 0.9, the mean time to failure of the MTSF increases in this interval.
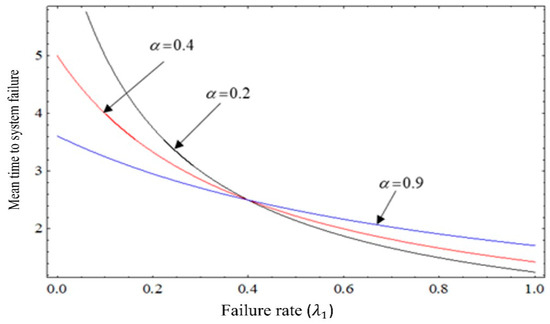
Figure 2.
Mean time to system failure versus failure rate and rate of completion of warranty .
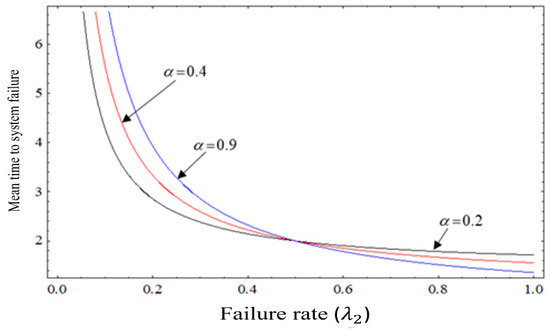
Figure 3.
Mean time to system failure versus failure rate and rate of completion of warranty .
Finally, we track the change in steady state availability with the parameters that affect it through Table 4 and Table 5 as follows:

Table 4.
The steady-state availability for different values of at .

Table 5.
The steady-state availability for different values of at .
Table 4 explains the generation of steady state availability values when the out-of-warranty unit failure rate changes from 0.1 to 0.9 for three different cases of repair rates. As we note, steady state availability decreases with increasing values of in the following cases: , , and . Comparing the three states of repair rates with the steady state availability results in the same table; we find that the highest steady state availability values can be obtained when . Table 5 shows the variety of steady-state availability values with increasing values of the preparation rate before repair of the failed unit and different repair rates (, , ); we can observe the following:
- (1)
- The higher the preparation rate before repairing the failed unit , the higher the steady state availability values.
- (2)
- The steady state availability value increases when and starts to decrease gradually in the following cases: and , respectively.
5.2. Numerical Results for Sensitivity Analysis and Relative Sensitivity Analysis
In this subsection, numerical results are presented for both sensitivity and relative sensitivity analyses. First, sensitivity and relative sensitivity analyses of the MTSF with various parameters are carried out. Table 6 and Table 7 show that the signs of the sensitivity of MTSF (, ) with and are negative; indicating that increasing these parameters worsens MTSF. However, in Table 8, the sensitivity of the MTSF () to parameter b is positive, indicating that the MTSF is improved by incremental changes in this parameter. In addition, the absolute values in these tables can be used to determine the order of the effects of the individual parameters on the MTSF. It can be seen that the order of sensitivity to MTSF is as follows: (i) when and (ii) when . The arranged relative sensitivity of MTSF () is as follows: (i) when , (ii) when , and (iii) when .

Table 6.
Sensitivity and relative sensitivity analysis of MTSF for different values of .

Table 7.
Sensitivity and relative sensitivity analysis of MTSF for different values of .

Table 8.
Sensitivity and relative sensitivity analysis of MTSF for different values of .
Finally, we perform a sensitivity analysis of resulting from various parameters; the results are shown in Figure 4. Figure 4 shows that the parameter has a significant influence on . While the parameter also has a clear effect on , it comes second only to the effect of the parameter on . Finally, we find that parameter has a weak effect on because it approaches the horizontal axis. Moreover, the signs of the sensitivity values for are negative for the parameters , , and , indicating that increasing the values of these parameters worsens the reliability of the system.
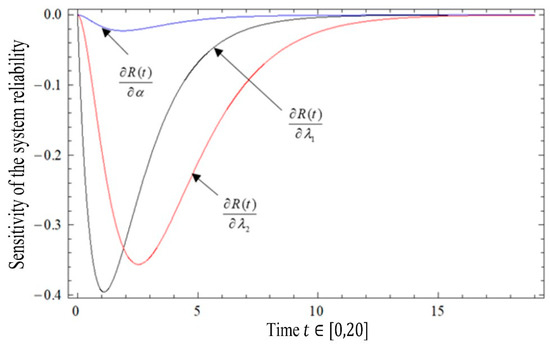
Figure 4.
Sensitivity analysis with different parameters.
6. Conclusions
This study discusses the reliability and sensitivity analyses of a system with a single unit with a preparation time for repair under product warranty policy conditions. Using the state-transition rate diagram of the system, the Laplace transform of the probability of each state was derived, and reliability measures of the system were successfully obtained. Sensitivity and relative sensitivity analyses of two system measures were also derived. Finally, some numerical results were extracted to draw the following conclusions:
- (1)
- The values presented in Table 1, Table 2 and Table 3 show that the reliability function () of the system decreases with the increase of the failure rate (), (), and the rate of termination of the warranty () in relation to time (t) and with constant values of other parameters. It is also analyzed that there are no sudden jumps in the values of the reliability function and that the system remains reliable over a long period of time.
- (2)
- (i)
- Table 4 shows that the steady-state availability decreases with the increase of the failure rate () in all cases of rates of repair (, , ) and for fixed values of other parameters.
- (ii)
- Table 5 shows that the steady-state availability increases with the increase of the preparation of repair rate () in all cases of rates of repair (, , ).
- (3)
- (i)
- Figure 2 shows that the mean time to system failure MTSF increases when the rate of termination of the warranty () decreases in the interval and conversely MTSF increases when the rate of termination of the warranty () increases in the interval .
- (ii)
- Figure 3 also shows that the mean time to system failure MTSF increases when the rate of termination of the warranty () increases in the interval , and conversely, MTSF increases when the rate of termination of the warranty () decreases in the interval .
According to Figure 4, only and have significant sensitivities for . Finally, the sensitivity and relative sensitivity of the MTSF to the system parameters are arranged as follows:
- (i)
- when
- (ii)
- when
From prior relationships, it can be observed that the parameters and are the most important parameters that affect both performance metrics; therefore, it is necessary to monitor their values.
Author Contributions
Conceptualization, M.S.E.-S.; Methodology, Z.M.H.; Software, M.S.E.-S.; Formal analysis, Z.M.H.; Investigation, Z.M.H. and M.S.E.-S.; Writing—original draft, Z.M.H.; Writing—review & editing, M.S.E.-S.; Supervision, M.S.E.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained with the article.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| Constant rate of expiry of the warranty period. | |
| Constant failure rate of active unit (within the warranty period/after the warranty period has expired). | |
| Constant inspection rate of the failed unit to determine whether or not the system is under warranty | |
| Constant preparation of repair rate (within the warranty period/after the warranty period has expired). | |
| Constant repair rate of the unit (within the warranty period/after the warranty period has expired). | |
| Constant inspection rate of the failed unit to determine whether the repair is satisfactory or not (within the warranty period/after the warranty period has expired). | |
| Constant re-repair rate of the unit (within the warranty period/after the warranty period has expired). | |
| Probability that warranty is completed/not completed. | |
| Probability that the repair is satisfactory after inspection (within the warranty period/after the warranty period has expired). | |
| Probability that the repair is not satisfactory after inspection (within the warranty period/post-warranty period. | |
| the probability at time “t” that the system is in good state within the warranty period/post-warranty period. | |
| the probability at time “t” that the system inspection state to determine the system is under warranty or not. | |
| the probability at time “t” that the system is in a preparation state to repair in the warranty period/post-warranty period. | |
| the probability at time “t” that the system is in a failed state and getting the repairman available within the warranty period/post-warranty period. | |
| the probability at time “t” that the system is in an inspection state to determine whether the repair is satisfactory or not within the warranty period/post-warranty period. | |
| the probability at time “t” that the system is under post repair state within the warranty period/post-warranty period. |
References
- Mwanga, Y.A.; Jouber, J.W.; Yadavalli, V.S.S. A complex three-unit parallel system with preparation time for repair. S. Afr. J. Ind. Eng. 2009, 20, 59–68. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Botha, M.; Bekker, A. Asymptotic confidence limits for the steady state availability of a two-unit parallel system with ‘preparation time’ for the repair facility. Asia Pac. J. Oper. Res. 2002, 19, 249–256. [Google Scholar]
- Yadavalli, V.S.S.; Botha, M.; Bekker, A. Confidence limits for the steady state availability of a system with ‘rest period’ for the repair facility. Electron. Model. 2002, 24, 99–103. [Google Scholar]
- Yadavalli, V.S.S.; Claasen, S.J.; Udayabaskaran, S.; Geetha, S. An Intermittently Used System with Preparation Time for the Repair Facility. Int. J. Reliab. Qual. Saf. Eng. 2004, 11, 379–386. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Van Wyk, E. Two Unit Warm Standby Systems with ‘Preparation Time’ For the Repair. In Proceedings of the CIE42, Cape Town, South Africa, 16–18 July 2012; pp. 51–57. [Google Scholar]
- Butani, N.L. Generalized availability measures for reparable systems with preparation time for repair. Microelectron. Reliab. 1991, 31, 43–46. [Google Scholar] [CrossRef]
- Subramanian, R.; Sarma, Y.V.S. A redundant system with non-instantaneous switchover and “preparation time” for the repair facility. Microelectron. Reliab. 1981, 21, 593–596. [Google Scholar] [CrossRef]
- Singh, H.R.; Singh, S.K.; Shukla, S. Cost analysis of a two unit cold standby system with preparation time for repair. Microelectron. Reliab. 1989, 29, 729–732. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; Mohie El-Din, M.M.; Moshref, M.E. Reliability analysis of a two-unit cold standby system with inspection, replacement, proviso of rest, two types of repair and preparation time. Microelectron. Reliab. 1995, 35, 1063–1072. [Google Scholar] [CrossRef]
- Goel, L.R.; Gupta, R.; Tyagi, P.K. Analysis of a two unit standby system with preparation time and correlated failures and repairs. Microelectron. Reliab. 1995, 35, 1163–1165. [Google Scholar] [CrossRef]
- Singh, S.K.; Srinivasu, B. Stochastic analysis of a two unit cold standby system with preparation time for repair. Microelectron. Reliab. 1987, 27, 55–60. [Google Scholar] [CrossRef]
- Gupta, R.; Krishan, R. On profit comparison of two stochastic models each pertaining to two unit standby system with fixed preparation time and hyper exponential repair time distribution. Int. J. Syst. Sci. 1999, 30, 1309–1317. [Google Scholar] [CrossRef]
- Mogha, A.K.; Gupta, A.K. A two priority unit warm standby system model with preparation for repair. Aligarh J Stat. 2002, 22, 73–90. [Google Scholar]
- Mahmoud, M.A.W.; Rashad, A.M.; Hussien, Z.M. Stochastic Analysis of a Repairable Cold Standby System Attacked by Poisson Shocks Considering Inspection and Post Repair. Int. J. Comput. Appl. 2015, 132, 33–40. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, B.; Ravi, V. Study of Reliability Measures of A Two Unit System with Inspection and On-Line/Off-Line Repairs Using the Regenerative Point Technique. Int. J. Oper. Res. 2021, 18, 57–77. [Google Scholar]
- Barak, M.S.; Yadav, D.; Barak, S.K. Stochastic analysis of two-unit redundant system with priority to inspection over repair. Life Cycle Reliab. Saf. Eng. 2018, 7, 71–79. [Google Scholar] [CrossRef]
- Kakkar, M.K.; Bhatti, J.; Gupta, G.; Sharma, K.D. Reliability analysis of a three unit redundant system under the inspection of a unit with correlated failure and repair times. AIP Conf. Proc. 2022, 2357, 100025. [Google Scholar]
- EL-Sherbeny, M.S.; Mahmoud, M.A.W.; Hussien, Z.M. Reliability analysis of a two-unit cold standby system with arbitrary distributions and change in units. Life Cycle Reliab. Saf. Eng. 2020, 9, 261–272. [Google Scholar] [CrossRef]
- Gupta, R.; Kumar, S.; Agrawal, D.C. A two unit parallel system with inspection repair and post repair. J. Math. Sci. 2006, 1, 189–200. [Google Scholar]
- Malik, S.C.; Bhardwaj, R.K.; Grewal, A.S. Probabilistic Analysis of a System of Two Non-identical Parallel Units with Priority to Repair Subject to Inspection. J. Reliab. Stat. Stud. 2010, 3, 1–11. [Google Scholar]
- Kalantari, A.R.; Johari, A. System Reliability Analysis for Seismic Stability of the Soldier Pile Wall Using the Conditional Random Finite-Element Method. Int. J. Geomechanics. 2022, 22, 04022159. [Google Scholar] [CrossRef]
- Attia, A.F.; Elela, E.D.A.; Hosham, H.A. The Optimal warranty and preventive maintenance policy for the four-state system. Appl. Math. 2011, 2011, 407457. [Google Scholar] [CrossRef]
- Kadyan, M.S.; Ramniwas, R. Cost benefit analysis of a single-unit system with warranty for repair. Appl. Math. Comput. 2013, 223, 346–353. [Google Scholar] [CrossRef]
- Ramniwas, R.; Kadyan, M.S.; Kumar, J. Stochastic modeling of a Single-Unit Repairable System with Preventive Maintenance under Warranty. Int. J. Comput. Appl. 2013, 75, 36–41. [Google Scholar] [CrossRef]
- Ramniwas, R.; Kadyan, M.S.; Kumar, J. Probabilistic analysis of two reliability models of a single-unit system with Preventive maintenance beyond warranty and degradation. Eksploat. I Niezawodn. Maint. Reliab. 2015, 17, 535–543. [Google Scholar]
- Ramniwas, R.; Kadyan, M.S.; Kumar, J. MTSF (mean time to system failure) and profit analysis of a single-unit system with inspection for feasibility of repair beyond warranty. Int. J. Syst. Assur. Eng. Manag. 2016, 7 (Suppl. S1), 198–204. [Google Scholar]
- Niwas, R.; Kadyan, M.S. Reliability modeling of a maintained system with warranty and degradation. J. Reliab. Stat. Stud. 2015, 8, 63–75. [Google Scholar]
- Niwas, R.; Garg, H. An approach for analyzing the reliability and profit of an industrial system based on the cost free warranty policy. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 265. [Google Scholar] [CrossRef]
- Niwas, R. Reliability Analysis of a maintenance scheduling model under failure free warranty policy. J. Reliab. Theory Appl. 2018, 13, 49–65. [Google Scholar]
- Kumar, P.; Kumar, A. Reliability Analysis of an industrial system under cost-free warranty and system rest policy. J. KONBiN 2019, 49, 377–395. [Google Scholar] [CrossRef]
- El-Sherbeny, M.S.; Hussien, Z.M. Reliability and sensitivity analysis of a repairable system with warranty and administrative delay in repair. J. Math. 2021, 2021, 9424215. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).