A Novel Approach to Energy Management with Power Quality Enhancement in Hydrogen Based Microgrids through Numerical Simulation
Abstract
:1. Introduction
- The proposed research design offers notable returns over traditional microgrid design approaches, including the following: Emphasizing the significance of proposed design and energy management optimization in MG systems involves developing a comprehensive cost-driven approach to optimize DERs. This approach considers the integration of hydrogen () storage and electrolyzer within a grid-tied operation mode.
- The problem formulation integrates economic and environmental considerations, particularly focusing on the utilization of an electrolyzer for hydrogen () production to FCs. The analysis explores the ideal scale for various resources in the energy system operation, emphasizing the potential for greater financial returns through increased integration of RESs.
- Rule-based fuzzy logic consistently outperforms traditional hydrogen-based microgrid design methods in terms of availability, present cost, power efficacy, and power quality enhancement.
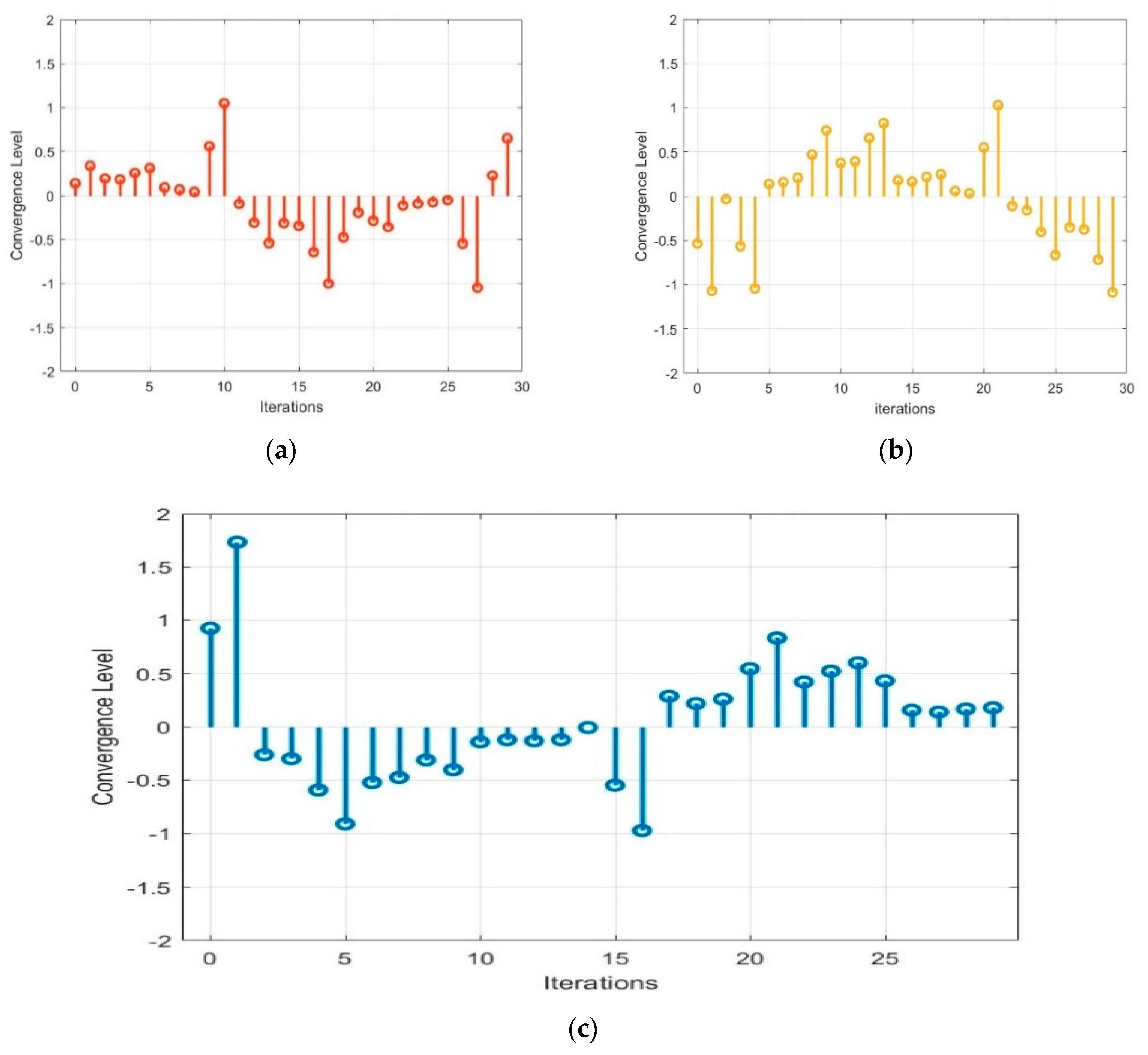
- In the context of hydrogen-based microgrid context, the PSO method revolutionized the construction of MG architecture, streamlining the initial design phase and elevating system performance. Economic competence for the hydrogen-based microgrid is enhanced by proper energy management. PSO converges power within the constraints and improves the power quality, ultimately with the expected lowest cost.
- The obtained outcomes show that the proposed method is vigorous and beats the other traditional techniques in terms of faster performance, lowest costs, inferior level of harmonics, improved battery state of charge (SoC), more FC load power, and increased overall efficacy.
2. System Model
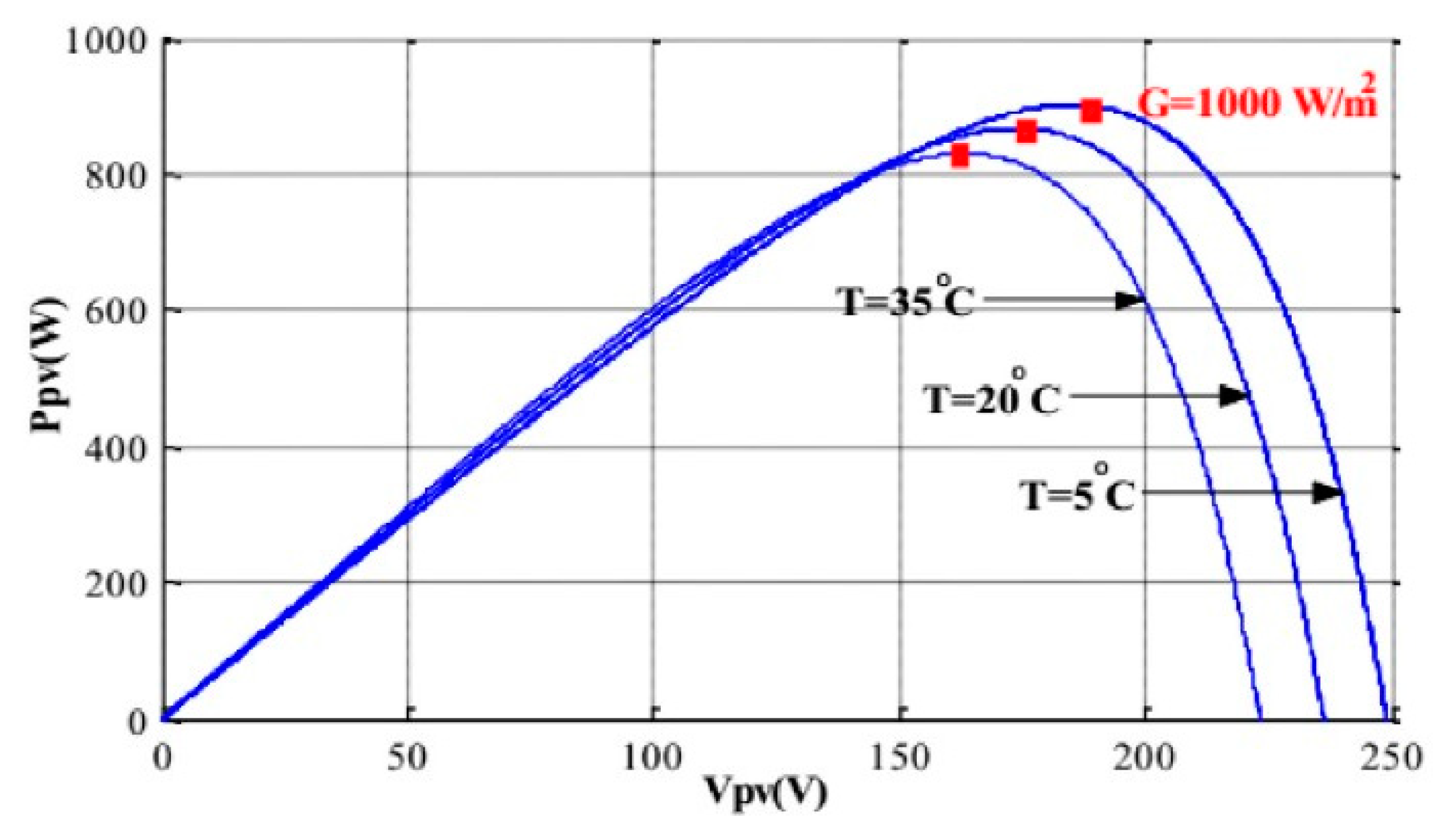
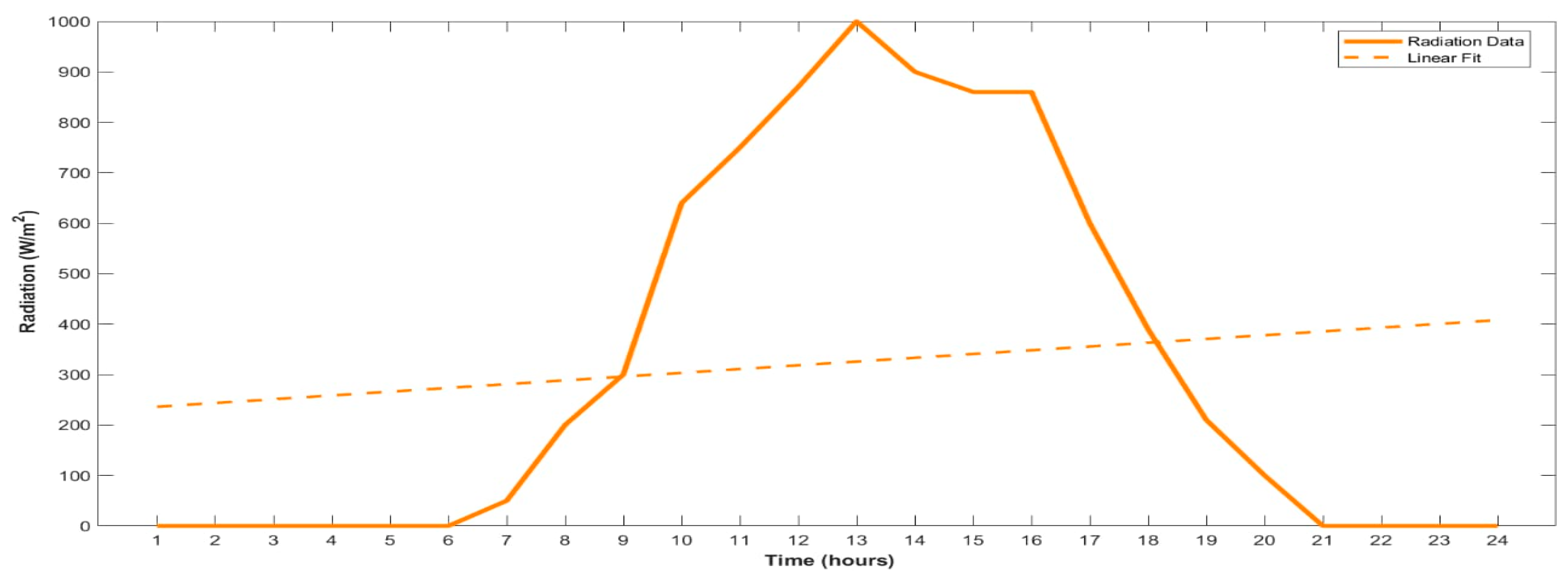
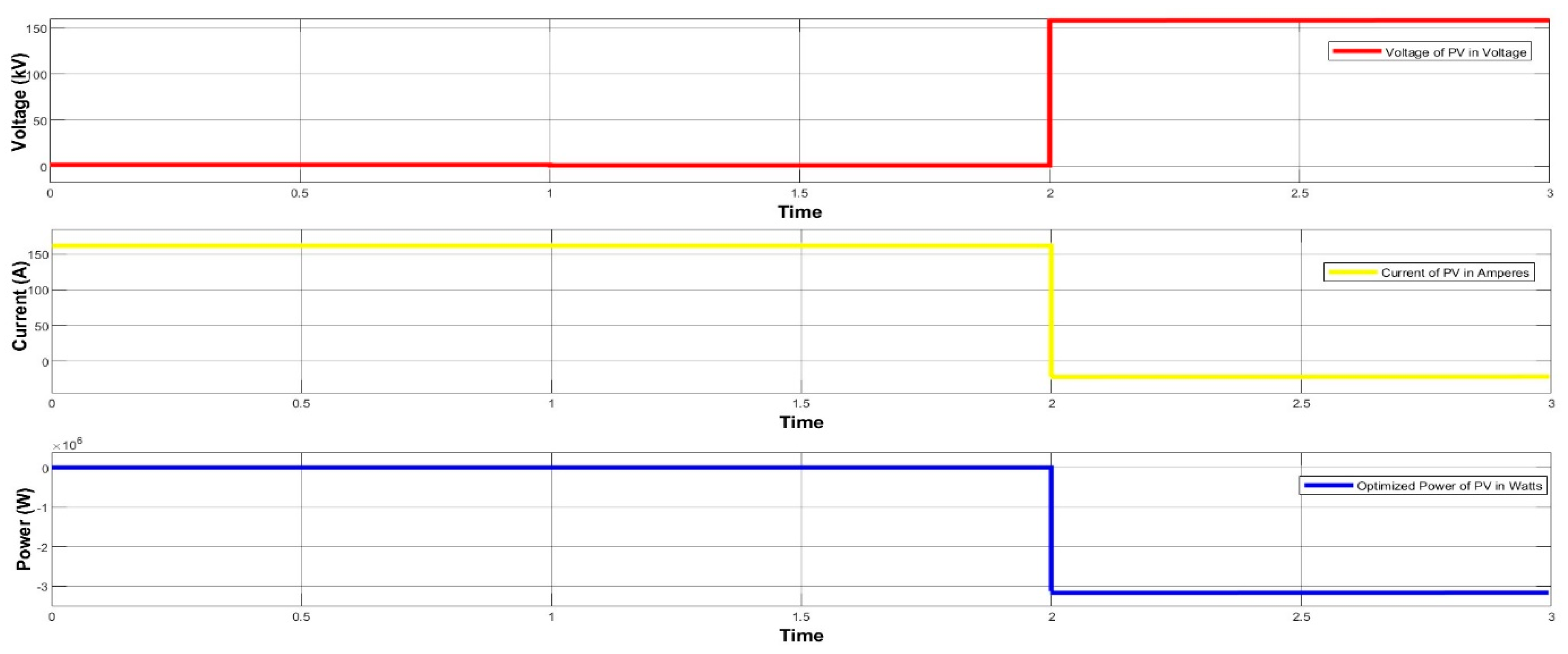
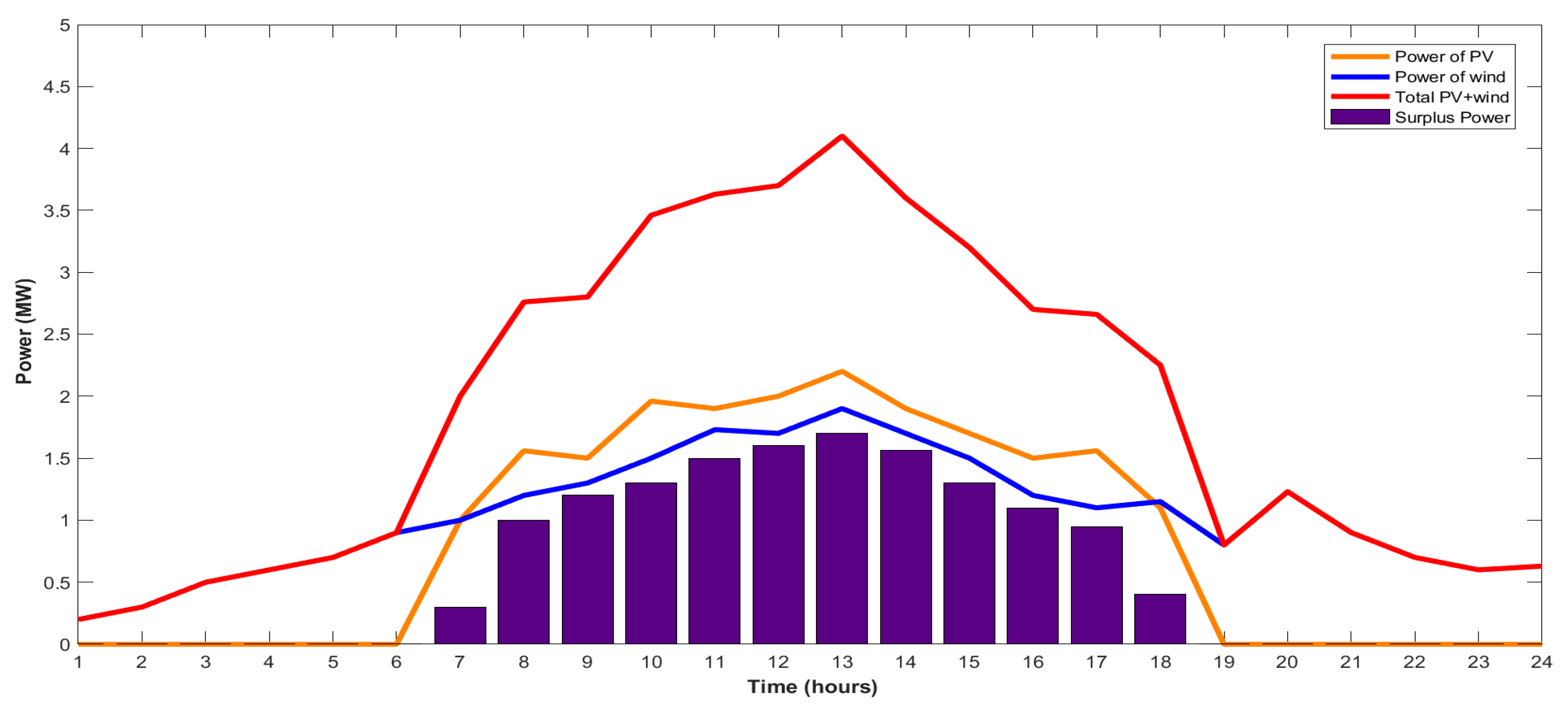
2.1. PV Power Management
2.2. Wind Power Management
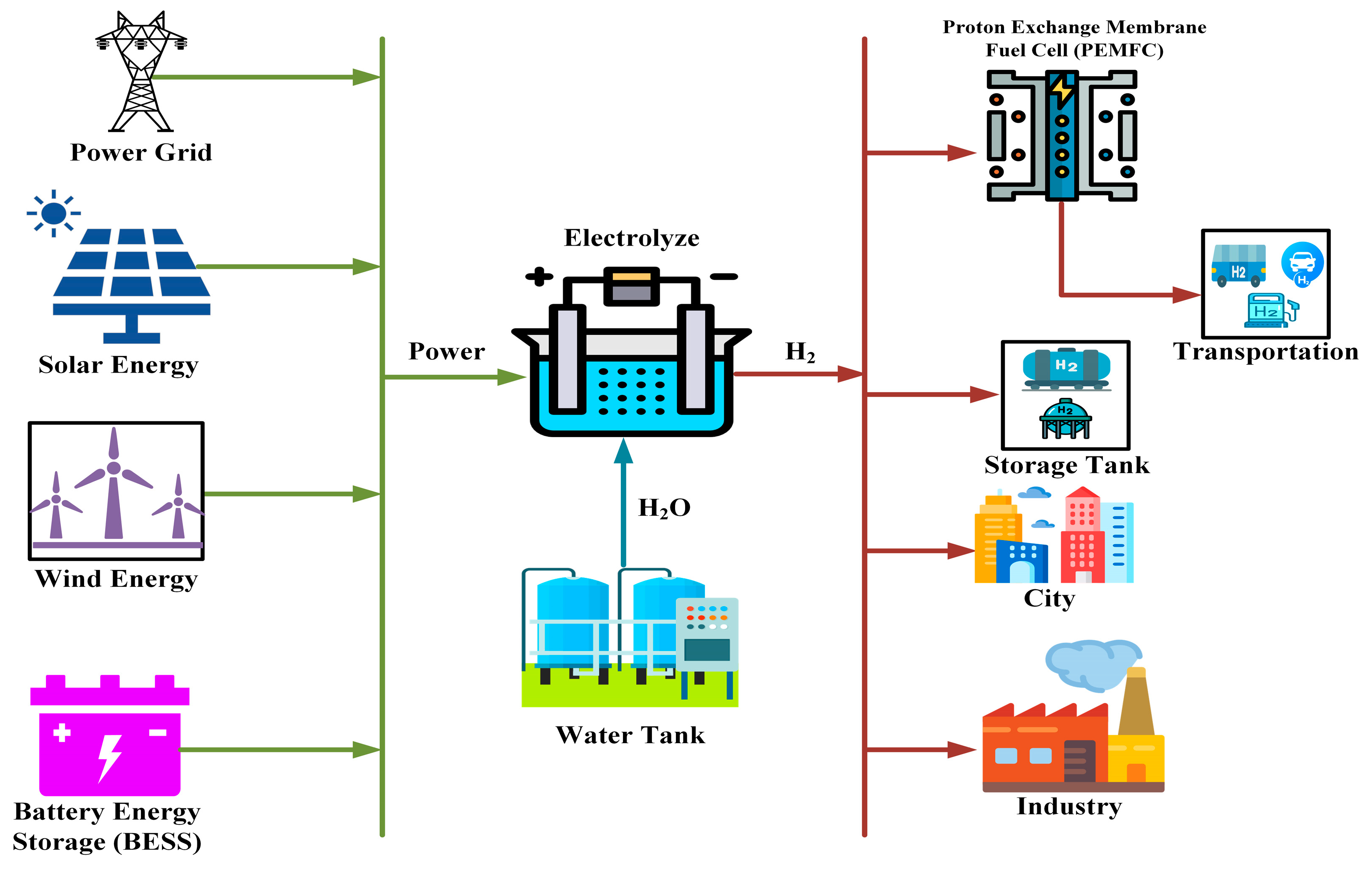
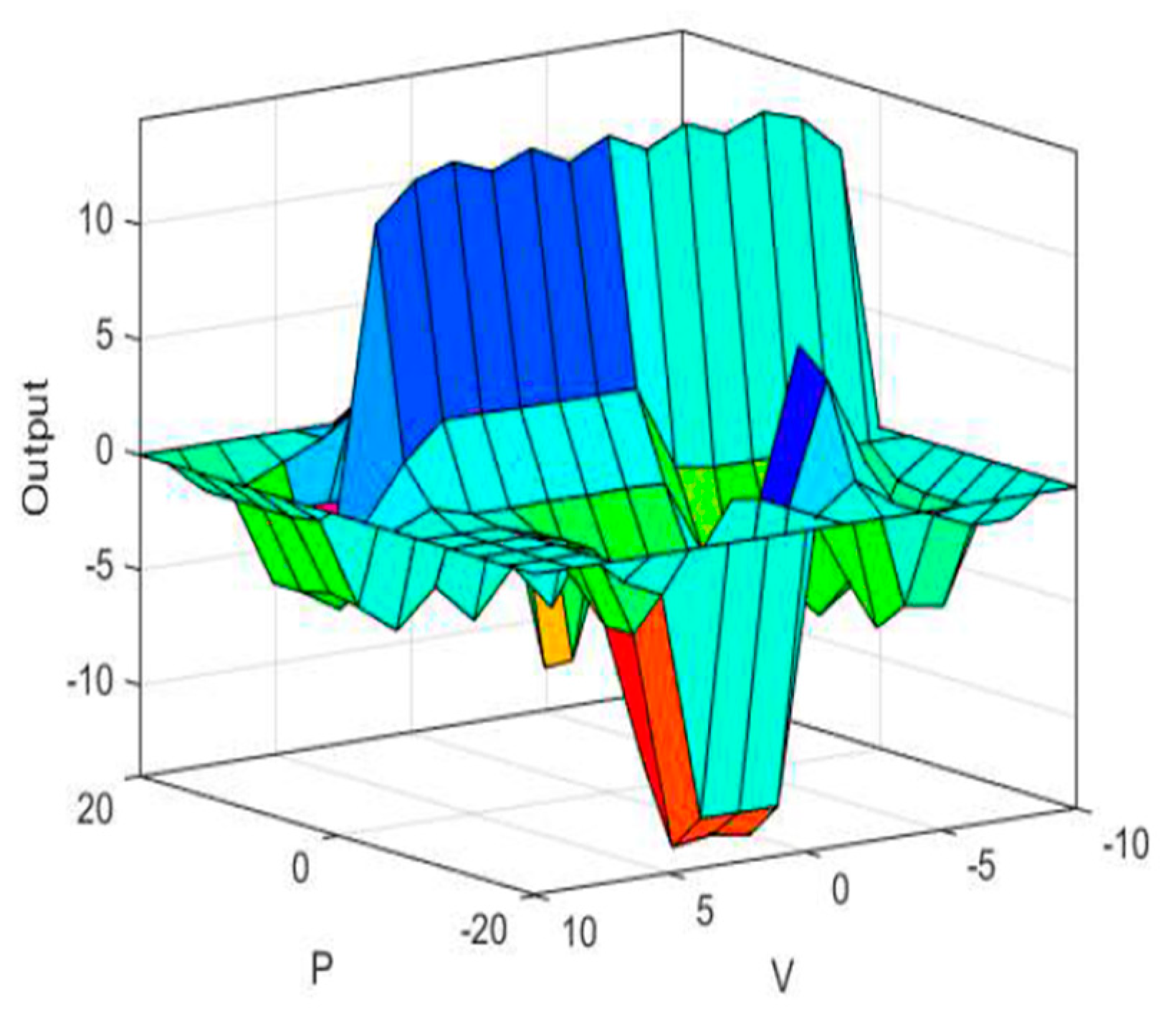
2.3. Hydrogen Power Management
2.4. Grid Integration
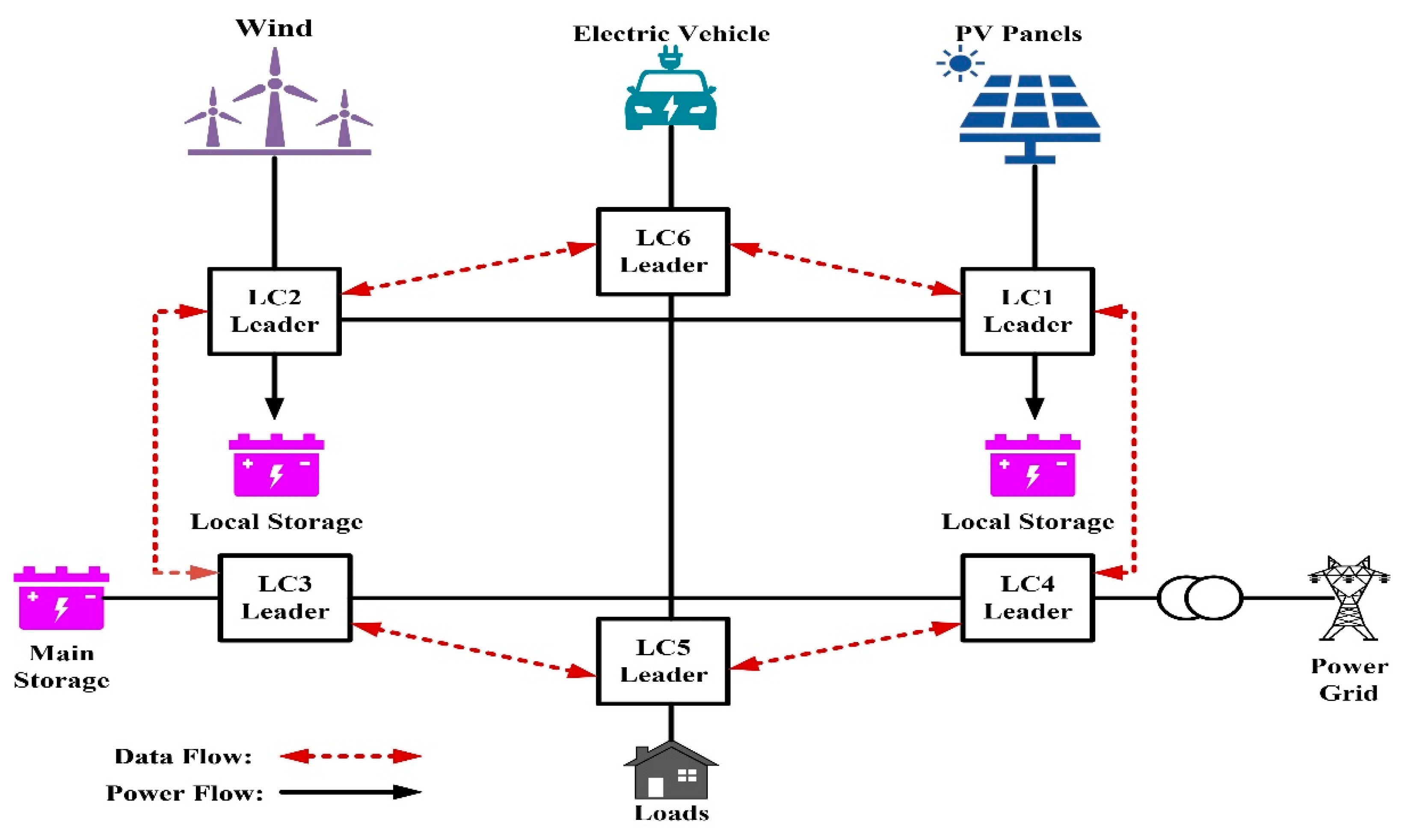
3. Energy Management System
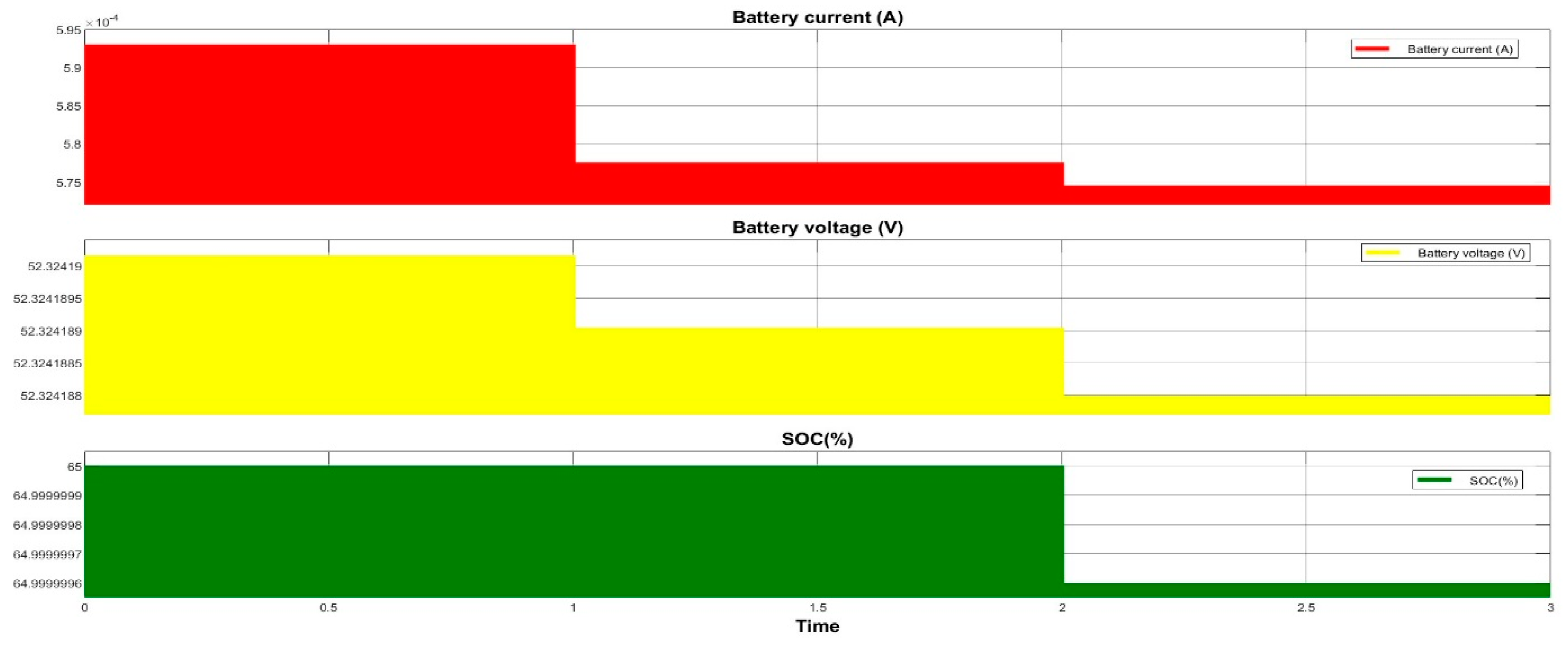
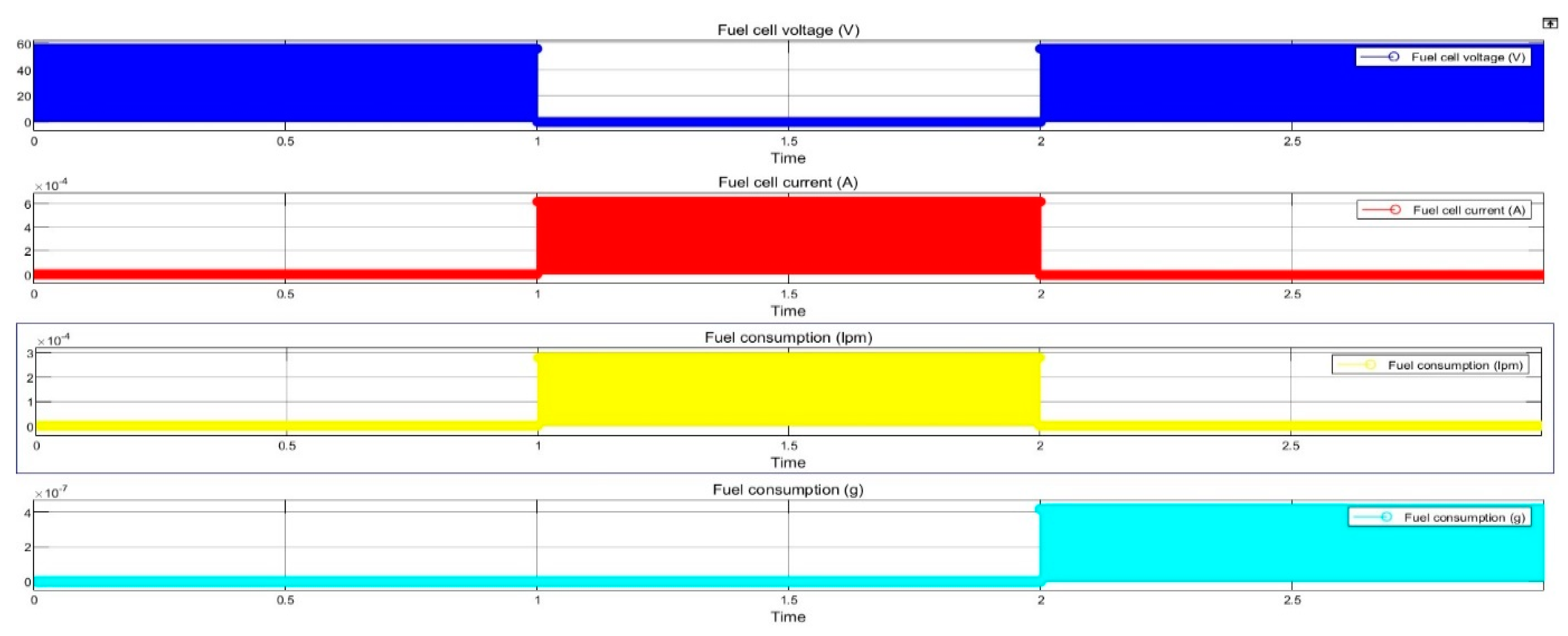
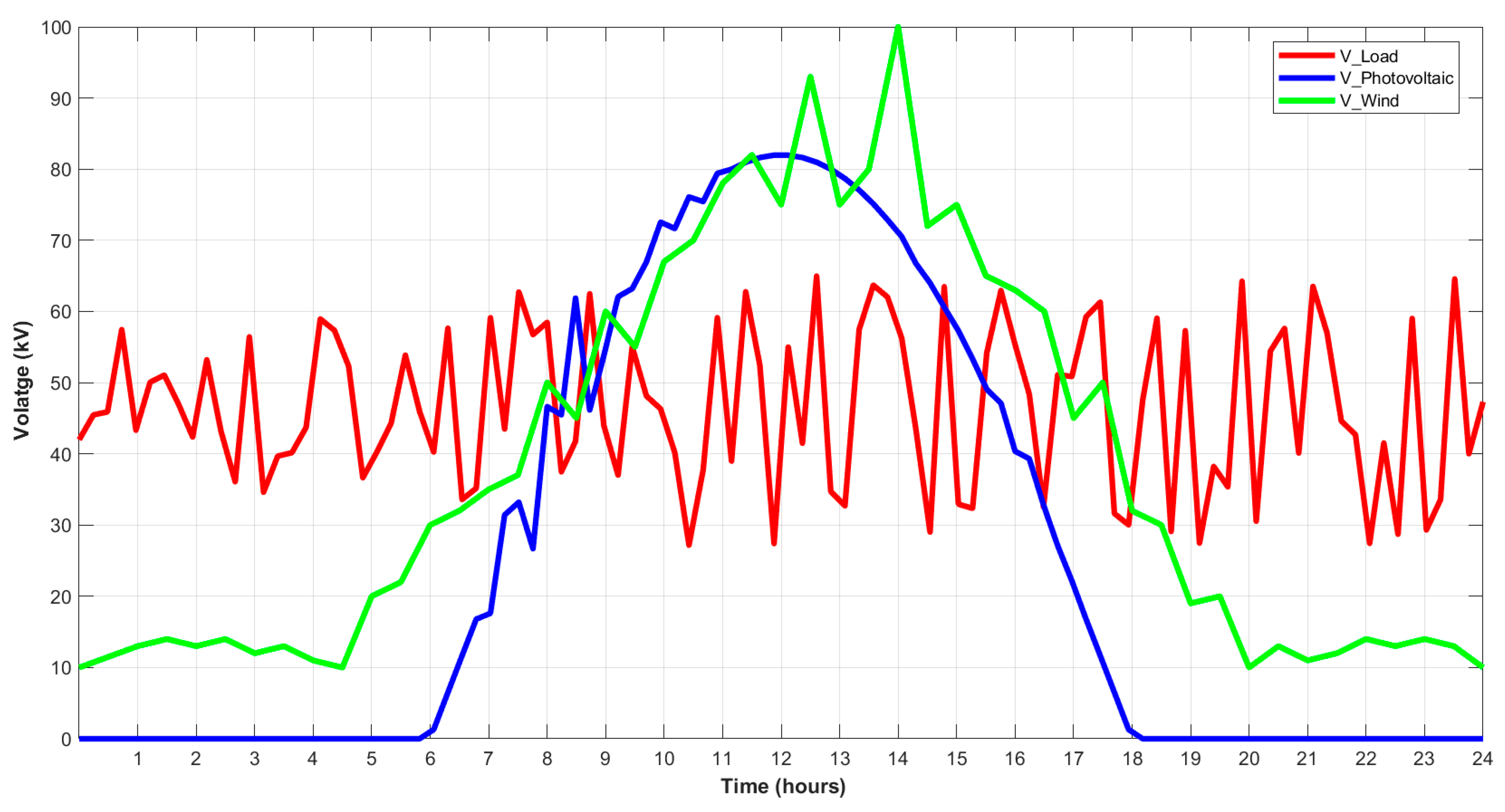
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |||
| HBESS | Hydrogen-Based Energy Storage Systems | NSRDB | National Solar Radiation Database |
| HMGs | Hybrid Microgrids | NOCT | Nominal Operating Cell Temperature |
| FCs | Fuel Cells | WT | Wind Turbine |
| RESs | Renewable Energy Resources | HT | Hydrogen Tank |
| EMS | Energy Management System | Hydrogen (kg) | |
| DERs | Distributed Energy Resources | Carbon dioxide (kg) | |
| ESS | Energy Storage systems | PSO | Particle Swarm Optimization |
| SoC | State of Charge | MPPT | Maximum Power Point Tracking |
| IMES | Integrated Management System | NP-Cost | Net Present Cost ($) |
| PEMFC | Proton Exchange Membrane Fuel cell | NP- | Net present cost of solar ($) |
| BESS | Battery Energy Storage System | NP- | Net present cost of wind ($) |
| PV | Photovoltaic | NP- | Net present cost of fuel cell ($) |
| Parameters and variables | |||
| I | Solar Irradiation () | Flow rate values oxygen () | |
| Ambient temperature (°C) | Hydrogen-based electrolyzer flow rates () | ||
| Cell temperature (°C) | Hydrogen-based fuel cell flow rates () | ||
| Area of solar () | Electrolyzer cell flow rates of oxygen () | ||
| Temperature coefficient () | Fuel cell flow rates of oxygen () | ||
| Output power of a solar panel (kW) | Minimum hydrogen energy () | ||
| Number of cells | Maximum hydrogen energy () | ||
| and | Wind velocities (m/s) | Precise carbon emission (kg/kWh) | |
| Reference height (m) | Emission penalty ($/kg) | ||
| Output power of wind turbine (kW) | Power generated from solar (kW) | ||
| Cut-in velocity () | Power generated from wind (kW) | ||
| Cut-off speed () | Power generated from fuel cells (kW) | ||
| Volume of hydrogen () | Hydrogen quantity by electrolyzers (kg) | ||
| . | Volume of oxygen () | Hydrogen quantity by fuel cells (kg) | |
| Flow rate values of hydrogen () | , | Efficiencies of corresponding inverters (%) | |
| Efficiency of electrolyzer (%) | |||
References
- Gugulothu, R.; Nagu, B.; Pullaguram, D. Energy management strategy for standalone DC microgrid system with photovoltaic/fuel cell/battery storage. J. Energy Storage 2023, 57, 106274. [Google Scholar] [CrossRef]
- SaberiKamarposhti, M.; Kamyab, H.; Krishnan, S.; Yusuf, M.; Rezania, S.; Chelliapan, S.; Khorami, M. A comprehensive review of AI-enhanced smart grid integration for hydrogen energy: Advances, challenges, and future prospects. Int. J. Hydrogen Energy 2024, 67, 1009–1025. [Google Scholar] [CrossRef]
- Zhong, X.; Zhong, W.; Liu, Y.; Yang, C.; Xie, S. Optimal energy management for multi-energy multi-microgrid networks considering carbon emission limitations. Energy 2022, 246, 123428. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, Y.; Guo, X.; Li, Z.; Song, X.; Blaabjerg, F. Overview of US patents for energy management of renewable energy systems with hydrogen. Int. J. Hydrogen Energy 2023, 48, 9574–9591. [Google Scholar] [CrossRef]
- Van, L.P.; Chi, K.D.; Duc, T.N. Review of hydrogen technologies based microgrid: Energy management systems, challenges and future recommendations. Int. J. Hydrogen Energy 2023, 48, 14127–14148. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, X.; Lin, D.; Calvin, M.M.; Morgan, J.C.; Qin, R.; Wang, C. Energy management of multiple microgrids based on a system of systems architecture. IEEE Trans. Power Syst. 2018, 33, 6410–6421. [Google Scholar] [CrossRef]
- Talaat, M.; Elkholy, M.H.; Alblawi, A.; Said, T. Artificial intelligence applications for microgrids integration and management of hybrid renewable energy sources. Artif. Intell. Rev. 2023, 56, 10557–10611. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A Review of Microgrid Energy Management and Control Strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Khan, T.; Yu, M.; Waseem, M. Review on recent optimization strategies for hybrid renewable energy system with hydrogen technologies: State of the art, trends and future directions. Int. J. Hydrogen Energy 2022, 47, 25155–25201. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chatterjee, D.; Goswami, S.K. A fuzzy based improved power sharing methodology for islanded microgrid with hybrid sources. Electr. Power Syst. Res. 2023, 217, 109069. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Tooryan, F.; Collins, E.R.; Jin, S.; Ramezani, B. Design and optimum energy management of a hybrid renewable energy system based on efficient various hydrogen production. Int. J. Hydrogen Energy 2020, 45, 30113–30128. [Google Scholar] [CrossRef]
- Jiang, J.J.; Wei, W.X.; Shao, W.L.; Liang, Y.F.; Qu, Y.Y. Research on Large-Scale Bi-Level Particle Swarm Optimization Algorithm. IEEE Access 2021, 9, 56364–56375. [Google Scholar] [CrossRef]
- Tajjour, S.; Chandel, S.S. A comprehensive review on sustainable energy management systems for optimal operation of future-generation of solar microgrids. Sustain. Energy Technol. Assess. 2023, 58, 103377. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Yousif, M.; Ai, Q.; Gao, Y.; Wattoo, W.A.; Jiang, Z.; Hao, R. Application of particle swarm optimization to a scheduling strategy for microgrids coupled with natural gas networks. Energies 2018, 11, 3499. [Google Scholar] [CrossRef]
- Modu, B.; Abdullah, M.P.; Bukar, A.L.; Hamza, M.F. A systematic review of hybrid renewable energy systems with hydrogen storage: Sizing, optimization, and energy management strategy. Int. J. Hydrogen Energy 2023, 48, 38354–38373. [Google Scholar] [CrossRef]
- Alvarez, J.A.M.; Zurbriggen, I.G.; Paz, F.; Ordonez, M. Microgrids Multiobjective Design Optimization for Critical Loads. IEEE Trans. Smart Grid 2023, 14, 17–28. [Google Scholar] [CrossRef]
- Vivas, F.J.; De las Heras, A.; Segura, F.; Andújar, J.M. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Petrollese, M.; Valverde, L.; Cocco, D.; Cau, G.; Guerra, J. Real-time integration of optimal generation scheduling with MPC for the energy management of a renewable hydrogen-based microgrid. Appl. Energy 2016, 166, 96–106. [Google Scholar] [CrossRef]
- Aribowo, W.; Ghith, E.S.; Rahmadian, R.; Widyartono, M.; Wardani, A.L.; Prapanca, A.; Nur Vidia Laksmi, B. Sand cat swarm optimization for controlling PID in DC motor. Telkomnika (Telecommun. Comput. Electron. Control) 2024, 22, 462–470. [Google Scholar] [CrossRef]
- Elkholy, M.H.; Senjyu, T.; Metwally, H.; Farahat, M.; Irshad, A.S.; Hemeida, A.M.; Lotfy, M.E. A resilient and intelligent multi-objective energy management for a hydrogen-battery hybrid energy storage system based on MFO technique. Renew. Energy 2024, 222, 119768. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, Y.; Fang, J.; Alkhayyat, A. An optimal methodology for optimal controlling of a PEMFC connected to the grid based on amended penguin optimization algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102401. [Google Scholar] [CrossRef]
- Elkholy, M.H.; Senjyu, T.; Elymany, M.; Gamil, M.M.; Talaat, M.; Masrur, H.; Ueda, S.; Lotfy, M.E. Optimal resilient operation and sustainable power management within an autonomous residential microgrid using African vultures optimization algorithm. Renew. Energy 2024, 224, 120247. [Google Scholar] [CrossRef]
- Elmetwaly, A.H.; ElDesouky, A.A.; Omar, A.I.; Saad, M.A. Operation control, energy management, and power quality enhancement for a cluster of isolated microgrids. Ain Shams Eng. J. 2022, 13, 101737. [Google Scholar] [CrossRef]
- Ren, K.; Liu, J.; Wu, Z.; Liu, X.; Nie, Y.; Xu, H. A data-driven DRL-based home energy management system optimization framework considering uncertain household parameters. Appl. Energy 2024, 355, 122258. [Google Scholar] [CrossRef]
- Raghav, L.P.; Kumar, R.S.; Raju, D.K.; Singh, A.R. Optimal Energy Management of Microgrids Using Quantum Teaching Learning Based Algorithm. IEEE Trans. Smart Grid 2021, 12, 4834–4842. [Google Scholar] [CrossRef]
- Knosala, K.; Kotzur, L.; Röben, F.T.; Stenzel, P.; Blum, L.; Robinius, M.; Stolten, D. Hybrid Hydrogen Home Storage for Decentralized Energy Autonomy. Int. J. Hydrogen Energy 2021, 46, 21748–21763. [Google Scholar] [CrossRef]
- Hilairet, M.; Ghanes, M.; Béthoux, O.; Tanasa, V.; Barbot, J.P.; Normand-Cyrot, D. A passivity-based controller for coordination of converters in a fuel cell system. Control Eng. Pract. 2013, 21, 1097–1109. [Google Scholar] [CrossRef]
- Diéguez, P.M.; Ursúa, A.; Sanchis, P.; Sopena, C.; Guelbenzu, E.; Gandía, L.M. Thermal performance of a commercial alkaline water electrolyzer: Experimental study and mathematical modeling. Int. J. Hydrogen Energy 2008, 33, 7338–7354. [Google Scholar] [CrossRef]
- K/bidi, F.; Damour, C.; Grondin, D.; Hilairet, M.; Benne, M. Multistage power and energy management strategy for hybrid microgrid with photovoltaic production and hydrogen storage. Appl. Energy 2022, 323, 119549. [Google Scholar] [CrossRef]
- Li, B.; Miao, H.; Li, J. Multiple hydrogen-based hybrid storage systems operation for microgrids: A combined TOPSIS and model predictive control methodology. Appl. Energy 2021, 283, 116303. [Google Scholar] [CrossRef]
- Zarate-Perez, E.; Santos-Mejía, C.; Sebastián, R. Reliability of autonomous solar-wind microgrids with battery energy storage system applied in the residential sector. Energy Rep. 2023, 9, 172–183. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. Experimental validation of performance and degradation study of canal-top photovoltaic system. Appl. Energy 2019, 243, 102–118. [Google Scholar] [CrossRef]
- Alimi, O.A.; Meyer, E.L.; Olayiwola, O.I. Solar Photovoltaic Modules’ Performance Reliability and Degradation Analysis—A Review. Energies 2022, 15, 5964. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Solar Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind. Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef]
- Hannan, M.A.; Al-Shetwi, A.Q.; Mollik, M.S.; Ker, P.J.; Mannan, M.; Mansor, M.; Al-Masri, H.M.K.; Mahlia, T.M.I. Wind Energy Conversions, Controls, and Applications: A Review for Sustainable Technologies and Directions. Sustainability 2023, 15, 3986. [Google Scholar] [CrossRef]
- Valverde, L.; Rosa, F.; Bordons, C. Design, planning and management of a hydrogen-based microgrid. IEEE Trans. Industr Inform. 2013, 9, 1398–1404. [Google Scholar] [CrossRef]
- Fragiacomo, P.; Genovese, M. Developing a mathematical tool for hydrogen production, compression and storage. Int. J. Hydrogen Energy 2020, 45, 17685–17701. [Google Scholar] [CrossRef]
- Zhu, J.R.; Jin, Y.; Zhu, W.; Lee, D.-K.; Bohlooli, N. Multi-objective planning of micro-grid system considering renewable energy and hydrogen storage systems with demand response. Int. J. Hydrogen Energy 2023, 48, 15626–15645. [Google Scholar] [CrossRef]
- Olivares, D.E.; Cañizares, C.A.; Kazerani, M. A Centralized Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Ramadhani, F.; Hussain, M.A.; Mokhlis, H.; Illias, H.A. Two-stage fuzzy-logic-based for optimal energy management strategy for SOFC/PV/TEG hybrid polygeneration system with electric charging and hydrogen fueling stations. J. Renew. Sustain. Energy 2021, 13, 024301. [Google Scholar] [CrossRef]
- Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Mekhilef, S.; Stojcevski, A. Role of optimization techniques in microgrid energy management systems—A review. Energy Strat. Rev. 2022, 43, 100899. [Google Scholar] [CrossRef]
- Efberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Musa, H. A Review of Particle Swarm Optimization (PSO) Algorithms for Optimal Distributed Generation Placement. Int. J. Energy Power Eng. 2015, 4, 232. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, W.; Du, J.; Liu, H. A Multiobjective Optimal Operation of a Stand-Alone Microgrid Using SAPSO Algorithm. J. Electr. Comput. Eng. 2020, 2020, 6042105. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Jalilian, A. Optimal sizing and location of renewable energy based DG units in distribution systems considering load growth. Int. J. Electr. Power Energy Syst. 2018, 101, 356–370. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Singh, N.J. Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm. Int. J. Hydrogen Energy 2020, 45, 10070–10088. [Google Scholar] [CrossRef]
- Mohammadi, M.; Ghasempour, R.; Astaraei, F.R.; Ahmadi, E.; Aligholian, A.; Toopshekan, A. Optimal planning of renewable energy resource for a residential house considering economic and reliability criteria. Int. J. Electr. Power Energy Syst. 2018, 96, 261–273. [Google Scholar] [CrossRef]
- Onori, S.; Serrao, L.; Rizzoni, G. Adaptive Equivalent Consumption Minimization Strategy for Hybrid Electric Vehicles. 2010. Available online: https://api.semanticscholar.org/CorpusID:12583370 (accessed on 25 January 2011).
- Paladini, V.; Donateo, T.; de Risi, A.; Laforgia, D. Super-capacitors fuel-cell hybrid electric vehicle optimization and control strategy development. Energy Convers. Manag. 2007, 48, 3001–3008. [Google Scholar] [CrossRef]



| Ref. | EMS Strategy | Contribution | Constraints |
|---|---|---|---|
| [22] | Moth-Flame Optimization (MFO) | An Integrated Management System (IMES) has been devised to oversee energy management. Achieved 1.287% reduction in the operational cost. Accomplished its objectives within an impressive time frame of under 150 min. | Taking power and cost under consideration while taking much time about to more than 150 min. |
| [23] | Amended Penguin Optimization Algorithm (APOA) | This research focuses on reducing steady-state error and improvement in power quality. Addressing Sag and Swell situations are discussed for enhancement of systems efficiency. | Power balancing only. |
| [24] | African Vulture’s Optimization Algorithm (AVO) | Techno-economic goals have been addressed comprehensively. Assessing daily operational expenses, including operational costs. BESS performance improved by using AVO. | Battery performance and operational cost. |
| [25] | Marine Predator Algorithm (MPA) | Introduces a centralized control system designed to manage large-scale distributed energy resources. To improve the microgrid performance, an adaptive dynamic voltage restorer (ADVR) with PID based on MPA has been utilized. This research includes a comparative analysis with two other distinct methods. | Power maintenance condition is under consideration. |
| [26] | SAC and XGBoost | A methodology has been devised that leverages the SAC algorithm as the decision-making tool for Home Energy Management Systems (HEMS). The comprehensive evaluation included an assessment of internal system factors as well as external environmental aspects. | Charging and discharging of electric vehicles, battery constraints and operational appliances limitations. |
| [27] | Quantum Teaching Learning-Based Optimization (QTLBO) | A daily optimal scheduling framework has been developed and implemented. Reduced the standard deviation in stochastic scenarios to a minimum value. | Power balancing and considering only global values for different sources. |
| [28] | Mixed Integer Linear Programming (MILP) | This study introduces an approach for storage systems, offering a new perspective on energy storage solutions. A techno-economic approach primarily focuses on future homes as self-sufficient entities. | Balancing of power and storage only. |
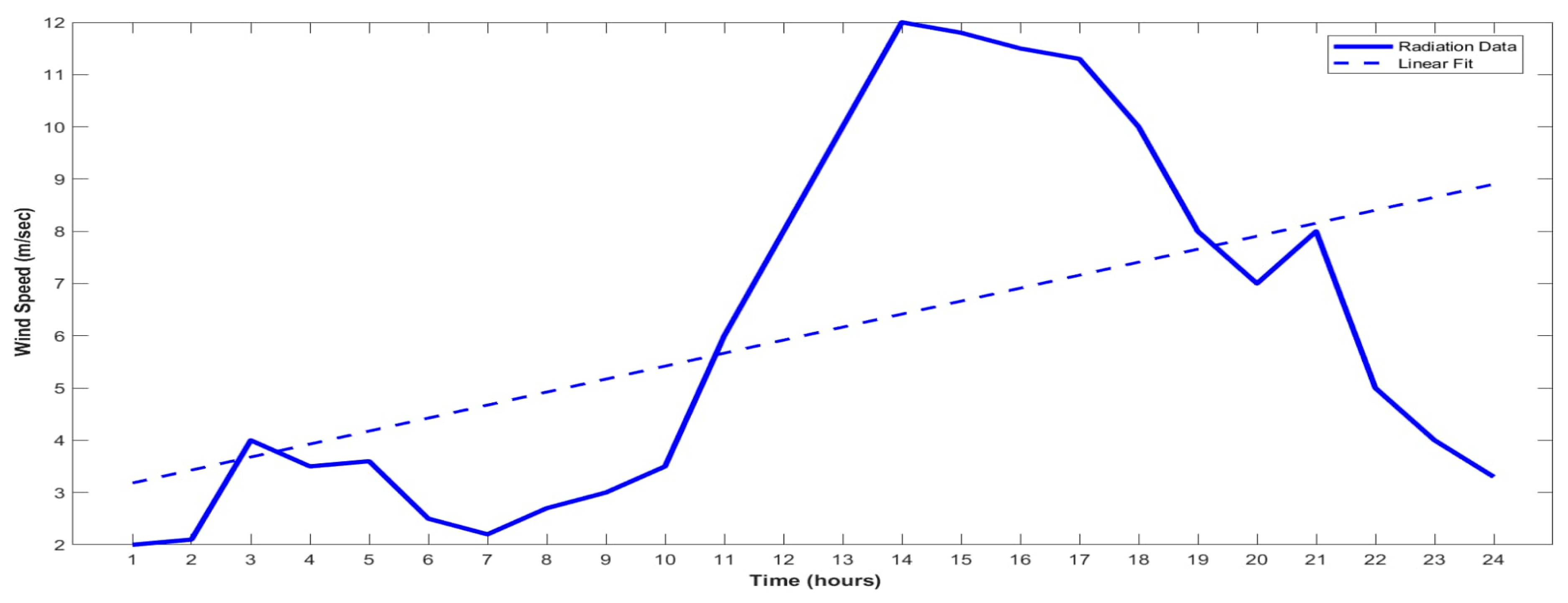
| Wind Speed (m/s) | Electrical Load (p.u.) | |
|---|---|---|
| 422 | 6.45 | 0.6211 |
| Unit Type | Solar Panel ($/kW) | Wind System ($/kW) | FCs ($/kW) | Electrolyzer ($/kW) |
|---|---|---|---|---|
| Capital Cost | 1000 | 950 | 600 | 150 |
| Solar Panel (kW) | Wind System (kW) | FCs (kW) | Electrolyzer (kW) | Cost (T $) |
|---|---|---|---|---|
| 700 | 670 | 900 | 440 | 25 |
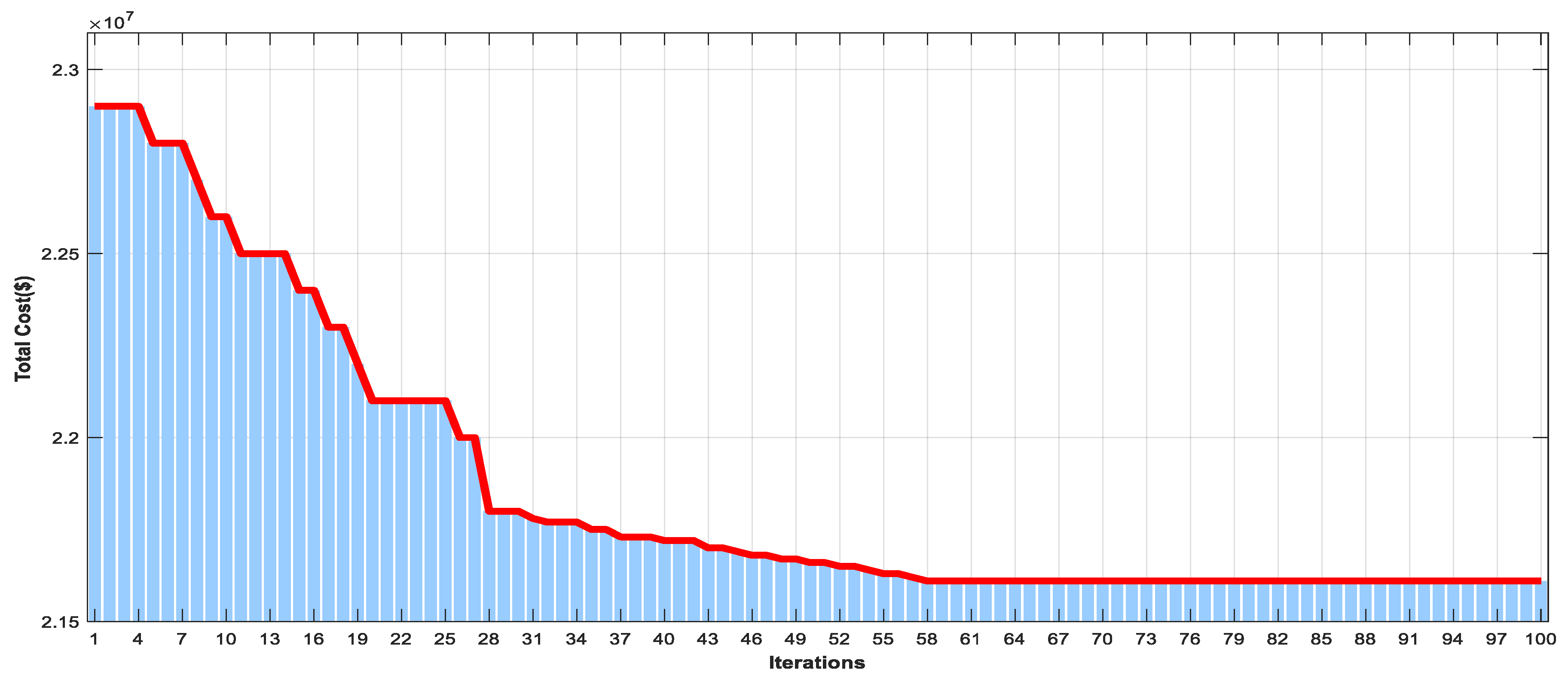
| Solar Panel ($/kW) | Wind System ($/kW) | FCs ($/kW) | Electrolyzer ($/kW) | Total Cost after Assessment $ | Time or Total Number of Iterations | Voltage Convergence | Power Quality Improvement | |
|---|---|---|---|---|---|---|---|---|
| Ref. [8] | 360 | 200 | 150 | - | - | 3500 s | No | No |
| Ref. [51] | 5 | 5 | 5 | 30 | - | 1408 s | No | No |
| Ref. [52] | 60 | - | 2 | 45 | - | - | No | No |
| Ref. [12] | 770 | 900 | 907 | 439 | to | 200 iterations | No | No |
| In this research | 700 | 670 | 900 | 440 | to | 100 iterations | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qamar, H.G.M.; Guo, X.; Ghith, E.; Tlija, M. A Novel Approach to Energy Management with Power Quality Enhancement in Hydrogen Based Microgrids through Numerical Simulation. Appl. Sci. 2024, 14, 7607. https://doi.org/10.3390/app14177607
Qamar HGM, Guo X, Ghith E, Tlija M. A Novel Approach to Energy Management with Power Quality Enhancement in Hydrogen Based Microgrids through Numerical Simulation. Applied Sciences. 2024; 14(17):7607. https://doi.org/10.3390/app14177607
Chicago/Turabian StyleQamar, Hafiz Ghulam Murtza, Xiaoqiang Guo, Ehab Ghith, and Mehdi Tlija. 2024. "A Novel Approach to Energy Management with Power Quality Enhancement in Hydrogen Based Microgrids through Numerical Simulation" Applied Sciences 14, no. 17: 7607. https://doi.org/10.3390/app14177607
APA StyleQamar, H. G. M., Guo, X., Ghith, E., & Tlija, M. (2024). A Novel Approach to Energy Management with Power Quality Enhancement in Hydrogen Based Microgrids through Numerical Simulation. Applied Sciences, 14(17), 7607. https://doi.org/10.3390/app14177607










