Abstract
With the widespread application of infrared technology in military, security, medical, and other fields, the demand for high-definition infrared images has been increasing. However, the complexity of the noise introduced during the imaging process and high acquisition costs limit the scope of research on super-resolution algorithms for infrared images, particularly when compared to the visible light domain. Furthermore, the lack of high-quality infrared image datasets poses challenges in algorithm design and evaluation. To address these challenges, this paper proposes an optimized super-resolution algorithm for infrared images. Firstly, we construct an infrared image super-resolution dataset, which serves as a robust foundation for algorithm design and rigorous evaluation. Secondly, in the degradation process, we introduce a gate mechanism and random shuffle to enrich the degradation space and more comprehensively simulate the real-world degradation of infrared images. We train an RRDBNet super-resolution generator integrating the aforementioned degradation model. Additionally, we incorporate spatially correlative loss to leverage spatial–structural information, thereby enhancing detail preservation and reconstruction in the super-resolution algorithm. Through experiments and evaluations, our method achieved considerable performance improvements in the infrared image super-resolution task. Compared to traditional methods, our method was able to better restore the details and clarity of infrared images.
1. Introduction
With the rapid development of computer vision and digital image processing, super-resolution technology has garnered significant interest and served as an important image enhancement method. Such technology aims to reconstructing high-resolution images from their low-resolution counterparts, improving the quality and clarity of the images. It holds significant importance across diverse areas of image processing, such as surveillance video enhancement, remote monitoring, and medical image analysis [,,,,]. On the other hand, infrared images, as a special type of image, are extensively utilized and valued in military, security, and medical fields. Their unique physical properties and information content offer enhanced thermal and concealed insights, critical for applications such as target recognition, night vision, and thermal imaging. Owing to their unique physical properties and information sources, infrared images offer a wealth of concealed and thermal data, thereby playing a pivotal role in areas such as target recognition, night vision, and thermal imaging [,,,]. However, low-resolution infrared images lack detail, which limits their effectiveness in practical applications. Therefore, developing effective methods to enhance the resolution of infrared images is imperative for recovering lost details and improving their utility in critical applications.
Compared to visible light images, infrared images usually have fewer textures and less detail. This poses a challenge in accurately reconstructing the missing details in infrared super-resolution tasks. Currently, most super-resolution datasets [,,,] focus on the visible light domain. The degradation processes of infrared images are more varied than, and are distinct from, those affecting visible light images. Classical degradation models for visible light images, which include blur, downsampling, noise, and JPEG compression [,], are relatively straightforward and fail to accurately simulate the complex degradation processes of infrared images. Practical degradation processes [,] are more complex but relatively singular, often overlooking the potential for simpler degradation scenarios. This implies that direct application of these models to infrared images may not adequately address degradation issues, thereby impacting super-resolution performance.
Infrared images typically exhibit less structural clarity compared to visible light images, because of increased blurriness and discontinuity. Consequently, models must accurately capture and reconstruct the structural information in infrared images. Deep-learning-based image super-resolution networks encompass convolutional neural networks, deep residual networks, and generative adversarial networks. The commonly employed loss functions in the super-resolution domain, including pixel-level loss [,,] and perceptual loss [,], fail to differentiate between structural and appearance attributes. Furthermore, applying RGB three-channel super-resolution models, originally designed for visible light images, to infrared image processing can lead to substantial redundant computation, and such redundant computations do not yield additional useful information pertinent to infrared images.
To address these issues, this paper proposes a deep-learning-based super-resolution method for infrared images. In order to effectively tackle the limitations and challenges associated with infrared image processing, several key strategies were adopted. First, we constructed a large-scale dataset dedicated to infrared image super-resolution research, which contains scene-rich high-resolution infrared image samples. This dataset provided ample data support and served as a solid foundation for our study. It enabled us to train and evaluate our method on diverse and realistic datasets. Second, for the common degradation factors in infrared images, such as noise and blur, we enhanced the degradation process to accurately restore the intricate details and textures present in infrared images. In the design of the loss function, we introduced a new spatially correlative loss [] function to improve the spatial consistency and retention of detail between the generated image and the real image. The incorporation of this innovative loss function into our method significantly improved the visual quality and realism of the generated images.
The main contributions of this paper are as follows:
- We constructed a high-quality super-resolution dataset for the infrared image super-resolution task.
- We enrich the degradation process by adding a gate mechanism and random shuffle strategy to the degradation process.
- We introduce a spatially correlative loss function to improve the model’s ability to retain structural texture.
2. Related Works
Infrared image super-resolution algorithms aim to construct real and reliable high-resolution infrared images from low-resolution ones for visual analysis in the real world. Real and reliable means that the super-resolved images should perform well in detail recovery, denoising, deblurring, artifact removal, and subjective perceptual quality.
2.1. Traditional Algorithms
Traditional image super-resolution algorithms rely on the statistical information of the image and fixed pixel information to generate high-resolution images. These methods include statistical-based [], edge-based [,], patch-based [,], prediction-based [,], and sparse representation techniques []. Although these methods have been widely applied in practice, it is worth noting that they cannot eliminate issues such as noise, blurring, and visual artifacts.
2.2. Deep Learning Methods
Advances in deep neural network technology and enhanced computing power have led to deep-learning-based image super-resolution algorithms that surpass the traditional methods in terms of both objective metrics and subjective perception. Initially, these methods primarily employed convolutional neural networks for end-to-end mapping on artificially paired data, exemplified by the SRCNN [] model, which pioneered the use of neural networks in the super-resolution task. Subsequently, researchers have made further improvements to network model design, proposing network architectures such as FSRCNN [], ESPCNN [], VDSR [], SRResNet [], RDN [], SRDenseNet [], DRCN [], DRRN [], RCAN [], etc. These designs incorporated ideas including aspects of network depth, feature dimensions, residual information, dense stacking, and recursive structures, and effectively improved the super-resolution performance. In practice, task-based designs that rely on network training often yield more significant performance improvements. Constraints based solely on pixel loss in end-to-end mapping can result in images that appear blurry and overly smooth. However, generative models based on generative adversarial networks (GANs) [] can mitigate this limitation. Through adversarial training between a generator and a discriminator, GAN-based models can progressively acquire the ability to generate realistic details.
The SRGAN [] model was the first to introduce GAN networks into the super-resolution task and proposed perceptual loss, which effectively addressed the issue of the low perceptual quality in reconstructed images, thereby enhancing the realism of the generated images. The ESRGAN model [] introduced the RRDBNet generator network structure. However, the exclusive focus on the classic degradation process restricts its applicability in real-world scenarios. In comparison to the kernel-based degradation estimation in RealSR [], Real-ESRGAN [] introduced higher-order degradation processes that more accurately reflect real-world conditions. Subsequently, the BSRGAN [] model and GD model [] independently proposed the shuffle strategy and a gate mechanism to diversify the degradation space. However, these operations merely capture non-combinations within the degradation space and fail to establish a unified baseline degradation model.
In the quest to enhance image details, researchers initially concentrated on optimizing the discriminator’s role. The SRGAN [] model employs a discriminator that directly assesses the authenticity of generated images, whereas the ESRGAN [] model refines the discriminator to gauge relative realism rather than absolute values. Real-ESRGAN [] further employs a U-Net [] structure to discriminate the realism of images at the pixel level, effectively improving the model’s generalization and performance. The AESRGAN [] model adopts a multi-scale U-Net discriminator to further sharpen details. However, in infrared super-resolution tasks that prioritize texture restoration, noise interference can exacerbate artifacts. Therefore, it is necessary to further constrain texture and structural information through loss functions, ensuring that the generative model converges effectively within the degradation space and demonstrates generalization in real-world scenarios.
2.3. Open-Source Infrared Datasets
High-quality datasets are crucial for deep neural network-based super-resolution algorithms. The diversity of images is essential for learning generalized representations, which in turn significantly enhances the model’s generalization capabilities. In the realm of visible light image algorithms, a plethora of high-quality open-source datasets are readily accessible. For example, commonly used datasets like DPED [] and DF2K [,] provide unified training and evaluation benchmarks for algorithms. However, in the field of infrared images, the availability of datasets is limited, with examples including [,,] or datasets derived from self-taken images []. However, the quality of these images varies significantly, and there is a notable lack of scene diversity. For instance, images extracted from the same video often exhibit considerable similarities, thereby diminishing the diversity of the dataset. Additionally, the majority of infrared images obtained via web crawlers, which typically have very low resolutions, are not conducive to algorithm development.
Therefore, we constructed a multi-scene infrared super-resolution image dataset []. This dataset contains a total of 7224 images across nine distinct scenes, including seascape images, animal images, industrial scenes, urban landscapes, natural landscapes, indoor images, portraits, surveillance perspectives, and vehicle perspectives, as shown in Figure 1. The majority of images have resolutions of (1280 × 1024, 1920 × 1080), with a minority of (640 × 512), providing rich details and texture information with high resolution and quality. This dataset facilitates the development of more powerful and accurate super-resolution algorithms using real-world high-quality infrared image data, thus promoting the application of infrared super-resolution technology across diverse fields.

Figure 1.
Multiple-scene image samples. Our dataset encompasses a diverse range of scenes, including seascapes, animal imagery, industrial environments, urban landscapes, natural landscapes, indoor settings, portraits, surveillance perspectives, and viewpoints featuring vehicles.
3. Method
This article builds upon the foundation of the Real-ESRGAN [] model and proposes improvements to it.
3.1. Degradation Model
3.1.1. Prior Research
Blind super-resolution (Blind SR) represents a complex ill-posed inverse problem, positing that high-resolution (HR) images suffer from various forms of degradation. Typically, classic degradation models [,] are used to synthesize low-resolution inputs:
where represents the degradation process. In general, the high-resolution image is convolved with a blur kernel , followed by a downsampling operation with a scale factor and the addition of noise . Finally, the process concludes with the application of a commonly used JPEG compression, resulting in a low-resolution image .
Traditional degradation models, although simple and mathematically convenient, often fall short in representing the spectrum of degradation present in actual low-resolution (LR) images. LR images may be affected by degradation such as blurring, downsampling, and various levels of noise with different orders. Therefore, a random shuffle strategy [] is proposed to address this issue.
The degraded sequence is shuffled randomly, where denotes performing a downsampling operation with scale factor s randomly selected from the set . In particular, sequences of and can be inserted into other degradations.
To obtain more realistic degradation, ref. [] enhanced the classic degradation model by extending it to high-order degradation processes. Classical degradation models, which can be considered as first-order modeling, only contain a limited number of degradations. In real-world scenarios, the degradation is varied and often involves multiple steps. These complex degradation processes cannot be adequately captured by a classic degradation model. Instead, a more sophisticated high-order degradation model is needed, which incorporates n repetitive degradation processes. Each degradation process within the model is described using a classical degradation model, as demonstrated:
High-order degradation uses the same procedure but with varying hyperparameters. The term “higher-order” in this context refers to the execution time of the operation. The key aspect is the repeated execution of the operation with different parameters.
While a random shuffle strategy and high-order degradation model are effective in managing complex degradation scenarios by encompassing all basic degradation types, they often overlook important extreme cases prevalent in the real world. These extreme cases involve combinations of different subsets of basic degradation types. In order to tackle this issue, ref. [] introduced a degradation model that utilizes a gate mechanism to select the basic degradation types that should be randomly incorporated into the degradation process:
where represents the gated degradation process, and denotes the basic degradation type. is the gate controller that determines whether a specific degradation type should be included in the degradation process, given by
where represents the input high-resolution (HR) image. When all gates are turned on, the gated degradation model becomes the same as the complex degradation model, while when all gates are shut off, it is equivalent to the traditional non-blind SR model. By manipulating the gate controller, a variety of combinations of basic degradation types can be generated, resulting in a model that covers non-blind SR, classic blind SR, and practical blind SR.
3.1.2. The Proposed Degradation Model
The proposed degradation model aims to reduce computational complexity, while enriching the degradation space. In the degradation process, a gate mechanism and random shuffle strategy are introduced into the second-order degradation model of Real-ESRGAN. Additionally, based on the characteristics of the experimental data and infrared devices, JPEG compression was not performed. This decision was made because the experimental data were stored in a single-channel format, while JPEG compression was primarily used for compressing color information in RGB images. Moreover, in practical scenarios, infrared devices can always export in lossless BMP format, thereby minimizing the need for JPEG compression of their images. Consequently, JPEG compression was excluded from the degradation process. The architecture of the proposed degradation model is illustrated in Figure 2.
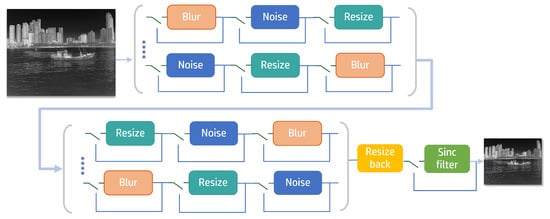
Figure 2.
The proposed degradation model integrates a gate mechanism and a random shuffle strategy based on second-order degradation. The degradation model performs second-order degradation, applying the shuffle strategy at each stage, while incorporating a gate controller into each degradation operation.
The high-resolution (HR) image undergoes a two-stage degradation process to obtain the low-resolution (LR) image. In Equation (5), and represent the first-order and second-order degradation processes, respectively. The LR image can be obtained by
In each round of degradation, we perform a random shuffling of the degradation sequence . We use to represent the basic degradation, where n represents the corresponding sequence. Here, in Equation (6), denotes the input image, and represents the output image.
For example, for a specific shuffling order , the proposed degradation model processes the image as follows:
Step 1: Resize-,
Step 2: Blur-,
Step 3: Noise-,
Each order generates a random list , which determines whether is executed. If the value is 0, the corresponding degradation process is not performed. If the is 1, the degradation process is executed. To ensure the complexity of degradation, in our experiments the random list was not all filled with 0 s, meaning that at least one degradation process was performed.
The blur degradation uses both isotropic and anisotropic Gaussian noise. The noise degradation applies Gaussian noise and Poisson noise. For the resize degradation, the image is randomly resized using area, bilinear, and bicubic interpolation.
By combining a gate mechanism and random shuffle strategy, the proposed degradation model can flexibly handle different basic degradation types and generate diverse degradation patterns. Such a strategy can better simulate diverse degradation situations in the real world and improve the adaptability and robustness of the model.
3.2. Network Structure
We adopted the same generator, RRDBNet, as the Real-ESRGAN [] model, as well as a U-Net discriminator with skip connections. RRDBNet is a deep neural network architecture designed for image super-resolution tasks. It is based on the RRDB structure, standing for residual-in-residual dense blocks, that is formed by cascading three residual dense blocks (RDB) with an additional residual connection added. Our implementation of RRDBNet integrates 23 RRDBs to formulate a robust and efficacious model tailored for augmenting the resolution of images. The complete network structure of Inf-OSRGAN is shown in Figure 3.
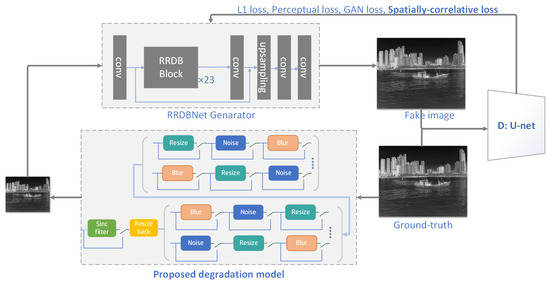
Figure 3.
The complete network architecture of Inf-OSRGAN includes a generator based on RRDBNet and a discriminator utilizing U-Net. The degradation process employs our proposed model, and during the training phase, a combination of L1 loss, perceptual loss, and spatially correlative loss was utilized.
3.3. Spatially Correlative Loss
To maintain the accuracy and perceptual quality of the reconstructed images within the degradation space described in Section 3.1, we introduced a spatially correlative loss function, namely F-LSeSim [], that constrains the reconstruction outcomes by calculating the correlation between feature maps, paying more attention to maintaining the structural consistency and detail information to improve the accuracy and realism of the generated images.
F-LSeSim is designed for image-to-image (I2I) translation tasks requiring strict constraints on the structural consistency before and after image translation. FSeSim [] employs pre-trained networks like VGG16 [] to extract features, and then constructs spatial correlation maps at the patch level [,,], encouraging structural consistency in the corresponding regions. Building upon this, LSeSim [] discards the use of pre-trained networks and optimizes a new feature extraction network specifically for each task through self-supervised learning. This enables the network to provide more accurate spatial correlation maps for a specific task.
F-LSeSim
We introduced the constraint concept of F-LSeSim into the super-resolution task. The computation process is detailed as follows:
We generate contrastive maps at the patch level, following PatchNCE [].
Let denote the spatially correlative map associated with the “query” patch in the ground-truth image. is a positive sample at the same location as the query region in the generated image . is negative samples.
The query patches are positively matched with patches located at identical positions in the generated image and negatively matched with patches taken from different positions within in or from other images. A total of negative patches are utilized. The LSeSim contrast loss is given Equation (7):
In Equation (7), denotes the cosine similarity of the two spatially correlated patches and act as the temperature parameter. To minimize the loss, LSeSim promotes the closeness of corresponding patches that share similar structures, even if they have very different visual appearances, maintaining the structural coherence of the images. The loss in Equation (7) is exclusively employed to optimize the structural representation network.
FSeSim generates spatially correlative maps by calculating the self-similarity between features extracted from LSeSim. These maps elucidate the spatial relationships among various structures within the images, rather than their visual appearance.
Let x be the generated image and be the corresponding ground-truth image, respectively. Using LSeSim, we can extract features from the two input images, denoted as and . For each query point in the image, the self-similarity between this feature and the features of other points in the image is computed, creating what is known as a spatially correlative map, formally represented as Equation (8):
where represents the feature of a particular query point , and the corresponding features contained within a patch composed of points are included in . By combining self-similarity maps of multiple query points , a spatially correlative map of the entire image is formed, where stands for the number of sampled patches. These maps show the spatial relationships between different regions in the image. Subsequently, a comparison is made between several structural similarity maps, focusing on the ground-truth and generated image x, as Equation (9) shows below:
In this equation, the spatially correlative map corresponding to the ground-truth images is signified by . Two different forms of are considered: the distance and the cosine distance . The distance promotes the spatial similarity across all points within a patch that is uniform, emphasizing the similarity in magnitude. Meanwhile, the cosine distance supports pattern correlation, irrespective of magnitude differences, focusing more on the overall pattern rather than specific magnitudes. In the generator, the spatially correlative loss is consistently defined by the loss in Equation (9).
By incorporating spatially correlative loss, we can constrain the reconstruction outcomes by calculating the correlation between features. This method emphasizes maintaining the structural consistency and capturing fine details of the image, thereby improving the accuracy and realism of the reconstructed image.
4. Experiments
4.1. Experiment Setup
4.1.1. Implementation Details
To demonstrate the advantages of the proposed model, we trained six 4× super-resolution networks using the widely used Real-ESRGAN generator, namely RRDBNet, and executed comparative experiments on diverse datasets. To reduce redundant computations and adapt to infrared images, we modified the input and output channels to be single-channel and used LR/HR synthetic pairs generated by the proposed degradation model for training. Firstly, we trained the first-stage model, Inf-OSRNet, using loss with a learning rate of . Then, we trained a Inf-OSRGAN model, which combined loss, perceptual loss, GAN loss, and spatially correlative loss with weights and a learning rate of . Both stages of training were iterated 100,000 times, using the Adam optimizer.
4.1.2. Degradation Details
During the two-stage training process, we employed the degradation process described in Section 3.1, which incorporated a shuffle strategy and gate mechanism into the second-order degradation process of Real-ESRGAN, excluding JPEG compression. The second-order degradation process involves three primary operations: blur, noise, and resize, which can be combined in six different sequences due to the shuffle strategy. The gate mechanism was employed to selectively execute these operations, ensuring a controlled application of degradation processes in the pipeline. For the blur operation, three types of kernels were utilized: Gaussian kernels with a probability of 0.7, generalized Gaussian kernels with a probability of 0.15, and plateau-shaped kernels with a probability of 0.15. The Gaussian kernels had a size range of 7 to 21 and a standard deviation varying from 0.2 to 3 for first-order degradation and 0.2 to 1.5 for second-order degradation. The generalized Gaussian kernels featured a shape parameter ranging from 0.5 to 4, while the plateau-shaped kernels had a value between 1 and 2. The noise operation consisted of Gaussian noise and Poisson noise, each with a probability of 0.5. The standard deviation for Gaussian noise ranged from 1 to 30 for the first-order and 1 to 25 for the second-order degradation. Poisson noise scaled from 0.05 to 3 in the first order and 0.05 to 2.5 in the second order. Resizing operations considered area, bilinear, and bicubic interpolation methods, applicable for both upsampling and downsampling, with a scaling range of 0.15 to 1.5. After completing the degradation process in the two stages, all images had to be resized to one-quarter of the size of the high-resolution (HR) images. Subsequently, the images underwent processing through a sinc filter, which was applied in a random manner.
4.1.3. Datasets
We adopted 6498 images from the training set of the infrared super-resolution dataset [] mentioned in Section 2.3 for the experiment. We downsampled HR images to obtain several images with different scales and generated multi-scale versions with different scale factors (0.75, 0.5, 1/3). When evaluating our model, we used high-resolution images from the infrared super-resolution test set mentioned in Section 2.3 and other low-resolution images from open-source infrared datasets [,].
4.1.4. Evaluation Metrics
We evaluated different models using mean peak signal to noise ratio (PSNR), structural similarity (SSIM), and Fréchet inception distance (FID).
PSNR evaluates the quality of reconstructed images by quantifying the difference between the original and the reconstructed signal by calculating the ratio of the maximum possible power of a signal to the power of the noise, determining the ratio of the maximum possible power of a signal to the noise power. A higher PSNR value signifies that the reconstructed image closely resembles the original, indicating better quality. PSNR is usually measured in decibels (dB), calculated as in Equation (10):
where is the maximum possible pixel value of the image and is the mean squared error.
SSIM, examining the similarity of two images, takes into account their structural information, luminescence, and contrast. The SSIM index, which varies from −1 to 1, has a value of 1 when images perfectly match. The SSIM index can be broken down into three components: luminance (L), contrast (C), and structure (S), with the overall formula given by Equation (11):
where and are the mean luminance of images and ; and are the variances of the respective images; and is the covariance between the two images. and are constants used for stability in the calculations.
FID gauges the resemblance between two image sets by computing the distance between their feature representations, with lower FID values suggesting a closer resemblance between the actual and generated images. The calculation of FID involves the following steps. We extracted features from real and generated images, then calculated the mean and covariance of the features for both sets, including the mean and covariance of the real image features , and the mean and covariance of the generated image features . The FID is calculated as in Equation (12):
where Tr denotes the trace operator.
4.1.5. Training Curves
We present the training loss curve in Figure 4, where the horizontal axis represents the number of training iterations and the vertical axis represents the loss value. It can be observed from the graph that the loss value exhibited a consistent downward trend as the training progressed. This indicates that our algorithm gradually optimized the model parameters, resulting in an improved alignment between the predicted values and the ground truth. The decreasing trend of the loss curve reflects the learning capacity and optimization effectiveness of our model, providing strong support for our research.
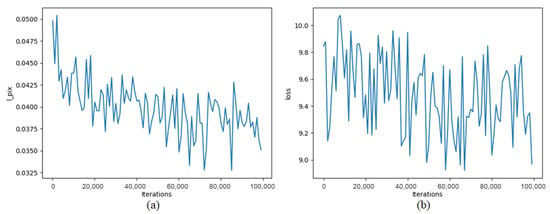
Figure 4.
Relationship between iterations and loss. (a) This panel depicts the relationship between the training iterations and loss for Inf-OSRNet. During this phase, there was a notable trend of fluctuating decline in the loss as the iterations progressed. (b) The relationship between the training iterations of Inf-OSRGAN and loss. In this phase, while the loss decreased with increasing iterations, the trend was less pronounced.
We include the PSNR (peak signal-to-noise ratio) curve in Figure 5, where the horizontal axis represents the training iterations and the vertical axis represents the PSNR value.
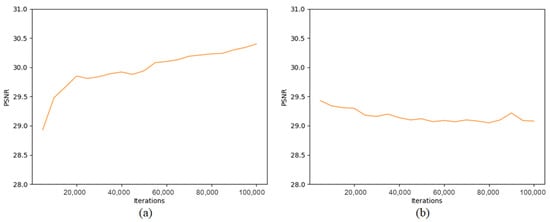
Figure 5.
Relationship between iterations and PSNR. (a) This panel depicts the relationship between the training iterations and PSNR for Inf-OSRNet. During this phase, as the number of iterations increased, the PSNR exhibited a trend of rapid initial growth followed by a slower increase. (b) This panel illustrates the relationship between the training iterations and PSNR for Inf-OSRGAN. In this phase, the PSNR demonstrated a decreasing trend as iterations increased.
In the first stage of training, we observed a consistent increase in the PSNR as the training progressed. This indicates that our algorithm successfully improved the quality of the reconstructed images at the pixel level, resulting in higher PSNR values. However, in the second stage of optimization, the objective was not solely focused on pixel-level accuracy. Instead, it aimed to enhance the visual quality of the images. As a result, we noticed a slight decrease in the PSNR values. This can be attributed to the fact that the optimization process prioritized perceptual aspects, such as enhancing texture details and reducing artifacts, rather than solely maximizing the PSNR metric. Despite the decrease in PSNR, it is important to note that the visual quality of the images significantly improved.
4.2. Comparisons with Prior Works
We compared our proposed Inf-OSRGAN model with several state-of-the-art super-resolution models, including RCAN [], SRGAN [], RealSR [], and Real-ESRGAN []. We utilized low-resolution (LR) images obtained by downscaling the images from the test set by a factor of four. The experiments were conducted on a Linux (Ubuntu 20.04 LTS) system with an NVIDIA RTX A6000 GPU (Nvidia, Santa Clara, CA, USA). Table 1 presents a comparison of our method with prior works in terms of runtime and number of parameters.

Table 1.
The various models along with their corresponding number of parameters and the time taken to process a single image. All models were tested on a Linux (Ubuntu 20.04 LTS) server equipped with an NVIDIA RTX A6000 GPU.
While our approach, along with Real-ESRGAN (our baseline), exhibited a larger model size and slightly longer runtime, it compensated for this with superior visual quality. As illustrated in Figure 6, our method outperformed prior works in both overall aesthetic appeal and detail restoration, demonstrating a marked improvement in the fidelity of the images produced. Notably, Real-ESRGAN also exhibited better visual results compared to the other existing methods.

Figure 6.
This figure presents a side-by-side comparison of our proposed model, Inf-OSRGAN, against several established methods: RCAN, SRGAN, RealSR, and Real-ESRGAN. In the first group of images, particular attention is drawn to the bridge pier. In the second group, the focus shifts to the textures of the pillars on the ship and the fabric.
The primary focus of our optimization efforts was to enhance the super-resolution performance and visual quality, rather than to prioritize processing speed. The decision to sacrifice some processing time in favor of significant improvements in visual outcomes is a worthwhile trade-off. This strategy aligns with our goal of delivering high-quality images that meet the demands of various applications where visual fidelity is of utmost importance. By prioritizing these aspects, we are confident that the benefits of enhanced visual performance substantially outweigh the costs associated with increased processing time.
4.3. Ablation Studies
To illustrate the efficacy of our proposed degradation and spatially correlative loss function, this chapter presents ablation studies conducted on the baseline network of Real-ESRGAN. In the ablation studies, spatially correlative loss was first embedded into the baseline network without modifying the degradation process. For the degradation component, a gate mechanism and random shuffle strategy were individually integrated into the baseline network for separate evaluations, and then the degradation methods of the gate mechanism and random shuffle strategy were jointly embedded into the baseline network. Finally, both the spatially correlative loss and our degradation were embedded into the baseline network, resulting in the Inf-OSRGAN model.
The experimental results are shown in Figure 7, with the best results highlighted with stars. The ablation studies followed the same experimental settings as the main experiment.
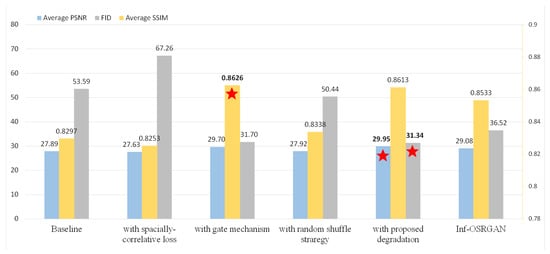
Figure 7.
Quantitative results of the ablation studies. The best results are highlighted with stars. The left vertical axis represents the average PSNR and FID values, while the average SSIM is indicated using the right vertical axis.
It can be observed in Figure 7 that, compared to the baseline, the proposed Inf-OSRGAN led to an improvement, particularly in the degradation. Specifically, when only the random shuffle was added, the PSNR increased from 27.89 to 27.92. When only the gate mechanism was added, the PSNR increased from 27.89 to 29.70. When both the gate mechanism and random shuffle were added, the PSNR improved to 29.95. The optimization of metrics could also be observed in terms of SSIM and FID.
Low-resolution (LR) images were obtained through interpolation from the original images. When there was a rich degradation space, the super-resolution algorithms could recover more high-frequency details and textures from the low-resolution inputs, thereby improving the image quality. The improvement in super-resolution effect could be reflected through the metrics considering pixel-level, feature distribution, brightness, and contrast. Therefore, these metrics could effectively evaluate the improvement in super-resolution algorithms resulting from a rich degradation space.
Upon the integration of the spatially correlative loss function, there was a marginal reduction in PSNR, FID, and SSIM values. The introduction of spatially correlative loss in super-resolution tasks enhances the structural integrity of the reconstructed images, leading to a more uniform and visually cleaner output. Since the optimization goal of spatially correlative loss is not entirely consistent with traditional metrics, they may decrease. Spatially correlative loss prioritizes the optimization of image structure rather than pixel-level similarity. This approach aids in preserving the structural consistency of the image, emphasizing enhancing details and textures. Consequently, it yields a clearer and more visible image structure but also tends to smooth out the noise signal.
The traditional metrics primarily focus on the pixel-level similarity and statistical features of an image, rather than maintaining the structural consistency. Therefore, when introducing spatially correlative loss, the reconstructed image’s structure may be more pronounced, but a decrease in comparison with traditional metrics may be observed. This does not imply a decline in the actual visual quality and enhancement of details. In fact, enhancing spatial consistency can improve the structure and details of an image, leading to improved perceptual quality. Spatially correlative loss can effectively handle texture details and high-frequency information. Super-resolution tasks often involve the recovery of textures and edges. Traditional loss functions may struggle to capture these intricate patterns and tend to amplify artifacts of the generated images. In contrast, spatially correlative loss incorporates spatial information, enabling the network to better preserve and reconstruct these high-frequency components. This leads to sharper and more accurate representations of the underlying structures in the super-resolved images.
4.4. Visual Results
4.4.1. Results on Our Datasets
Metrics like PSNR and SSIM can be used to quantify the variances between high-resolution images and their reconstructed counterparts. However, these metrics only offer a partial assessment and cannot fully represent real perception. Due to the high sensitivity and subjectivity of human vision regarding image quality, sole reliance on objective metrics falls short in providing a comprehensive evaluation of visual quality. Visual comparison, however, can account for perceptual attributes such as details, textures, clarity, and naturalness.
Figure 8 displays the results of the super-resolution model on high-resolution images (1280 × 1024) from the test set proposed in Section 2.3, with the bicubic upsampled LR images used as references.

Figure 8.
Visual comparisons of ablation studies in blind SR on our high-resolution datasets. On the left is the complete image. The groups on the right show the enlarged portions of the red-framed areas using various methods.
Compared to the baseline, after employing our degradation, the model was better able to enhance details and preserve more textures. Concurrently, it risked over-emphasizing non-existent details, thereby introducing supplementary noise and artifacts. The buildings depicted in the final set of images serve as a case in point.
Incorporation of spatially correlative loss accentuates the structural integrity of an image, yielding a more uniform visual outcome. However, this approach risks over-smoothing, which can result in the attenuation of subtle textures and the distortion of intricate details, as exemplified by the trunk images in the sixth set. Conversely, the absence of spatially correlative loss can lead to an increase in artifacts and a less pronounced structural clarity in the generated images. The proposed Inf-OSRGAN combines both approaches, effectively reducing noise, while preserving sharp edges and rich details, thus achieving a more realistic visual effect.
4.4.2. Results on Other Datasets
Figure 9 shows the results of the previous methods applied to low-resolution infrared images (256 × 192, 384 × 288) from other publicly available datasets [,,,,], an infrared security target identification dataset and an infrared image denoising dataset.

Figure 9.
Visual comparisons of ablation studies in blind SR on other publicly available low-resolution datasets. On the left is the complete image. The groups on the right show enlarged portions of the red-framed areas using various methods.
By processing these low-resolution data, our model was able to reconstruct detailed textures, thereby enhancing their clarity and naturalness. Additionally, the model effectively suppressed noise and artifacts, enhancing the visual quality of the images. For the sixth set of images, the result of the baseline exhibited a lack of clarity in the main structures, with fine hair strands appearing indistinct. When our degradation model was integrated, the hair textures became more pronounced, but this came at the cost of introducing artifacts that cluttered the image. The application of the spatially correlative loss function improved the clarity of the main structures but resulted in an over-smoothing of weaker textures. The Inf-OSRGN model successfully emphasized the main structures while maintaining the hair textures and did not suffer from the issue of artifacts.
This set of low-resolution experimental data differed significantly from the test set mentioned earlier in terms of resolution and capture devices. This demonstrates the strong generalization capability of the Inf-OSRGAN model when applied to diverse datasets.
4.5. Discussion
Our model has a few limitations that are worth mentioning. Firstly, due to the diverse range of degradation modes present in infrared images, the convergence of our model requires a longer training time. This is because the model needs to learn and adapt to various degradation patterns, which leads to a more complex optimization process. Additionally, our model does not specifically simulate certain degradation models unique to infrared images, such as blind pixels or elemental stripes. These degradation modes tend to result in overcompensation, leading to worse results. This limitation arises from the fact that the training data and the designed loss function may not fully capture the complexities associated with these specific degradation modes.
It is important to acknowledge that these limitations suggest potential areas for future research and improvement. Future work could focus on developing more robust models that can handle a wider variety of degradation modes and specifically address the challenges posed by unique infrared degradation patterns. By addressing these limitations, we can further enhance the performance and applicability of our proposed model. Additionally, we plan to explore the applicability of the optimization techniques proposed in this paper to other super-resolution models. By applying these optimization methods to different models, we aim to assess their effectiveness and potential for improving the performance of various super-resolution approaches. Furthermore, we intend to investigate the transferability of these optimization strategies across different domains, such as medical imaging, satellite imagery, or low-light photography. This will involve conducting a series of experiments to evaluate how well these techniques perform when applied to datasets specific to these domains, which often present unique challenges, such as the varying anatomical structures in medical images. By evaluating the performance of the proposed techniques in these diverse domains, we will gain insights into their adaptability and potential for wider adoption. In addition, if there is sufficient demand, we may develop a software interface for the Inf-OSRGAN model, to enhance the user experience and accessibility.
5. Conclusions
To overcome the constraints of current infrared image super-resolution algorithms, this paper proposed an optimized method for super-resolution in the infrared image domain. Firstly, we constructed a high-quality infrared image dataset enriched with detailed textures, serving as the basis for evaluating infrared image super-resolution models. In terms of degradation, we incorporated a gate mechanism and random shuffle strategy to encompass a broad spectrum of realistic degradation encountered in real-world situations. Furthermore, in the training process of the Inf-OSRGAN network, we integrated a spatially correlative loss function to measure feature correlations, to ensure the preservation of structural consistency and detailed information, thereby enhancing both the accuracy and perceptual fidelity of the reconstructed images.
We validated the proposed method on the constructed high-resolution test set and various publicly available low-resolution infrared image datasets. Our method achieved outstanding performance on both the high-resolution test set and a diverse array of publicly available datasets. The experimental results demonstrated the superior capabilities of our method for detail restoration, with a particular emphasis on the recovery of nuanced textures. Specifically, these experiments substantiated the method’s reliability and practicality, showing its versatility across various scenes and scenarios, as well as its robust generalization across images of varying resolutions. The findings of this study offer a potent approach to infrared image enhancement.
Author Contributions
Conceptualization, Z.X. and C.K.; methodology, Z.X.; software, J.G. and X.W.; validation, Z.X., J.G., X.W. and C.K.; formal analysis, Z.X., J.G. and X.W.; investigation, C.K.; resources, Z.X.; data curation, Z.X.; writing—original draft preparation, J.G. and X.W.; writing—review and editing, Z.X. and C.K.; supervision, C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shandong Provincial Natural Science Foundation, grant number ZR2022QF101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hazra, D.; Byun, Y.C. Upsampling real-time, low-resolution CCTV videos using generative adversarial networks. Electronics 2020, 9, 1312. [Google Scholar] [CrossRef]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Task-driven super resolution: Object detection in low-resolution images. In Proceedings of the Neural Information Processing: 28th International Conference, ICONIP 2021, Sanur, Bali, Indonesia, 8–12 December 2021; Proceedings, Part V 28. Springer: Berlin/Heidelberg, Germany, 2021; pp. 387–395. [Google Scholar]
- Ku, B.; Kim, K.; Jeong, J. Real-Time ISR-YOLOv4 Based Small Object Detection for Safe Shop Floor in Smart Factories. Electronics 2022, 11, 2348. [Google Scholar] [CrossRef]
- Maity, S.; Abdel-Mottaleb, M.; Asfour, S.S. Multimodal Low Resolution Face and Frontal Gait Recognition from Surveillance Video. Electronics 2021, 10, 1013. [Google Scholar] [CrossRef]
- Qin, B.; Li, D. Identifying Facemask-Wearing Condition Using Image Super-Resolution with Classification Network to Prevent COVID-19. Sensors 2020, 20, 5236. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Zhong, F.; Li, Q.; Weng, J.; Li, J.; Lu, H.; Wu, H.; Liu, S.; Wang, J.; Deng, K.; et al. Infrared Photodetection from 2D/3D van der Waals Heterostructures. Nanomaterials 2023, 13, 1169. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Moreno, A.; Puig, D. Breast Cancer Detection in Thermal Infrared Images Using Representation Learning and Texture Analysis Methods. Electronics 2019, 8, 100. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Li, J. Real-Time Ground Vehicle Detection in Aerial Infrared Imagery Based on Convolutional Neural Network. Electronics 2018, 7, 78. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared thermography for temperature measurement and non-destructive testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R.N. Challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HA, USA, 21–26 July 2017; pp. 21–26. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 114–125. [Google Scholar]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 606–615. [Google Scholar]
- Ignatov, A.; Kobyshev, N.; Timofte, R.; Vanhoey, K.; Van Gool, L. Dslr-quality photos on mobile devices with deep convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3277–3285. [Google Scholar]
- Agustsson, E.; Timofte, R. NTIRE 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, San Francisco, CA, USA, 18–20 June 1996; pp. 126–135. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “Zero-shot” super-resolution using deep internal learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 3118–3126. [Google Scholar]
- Zhang, K.; Liang, J.; Van Gool, L.; Timofte, R. Designing a practical degradation model for deep blind image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4791–4800. [Google Scholar]
- Zhang, W.; Shi, G.; Liu, Y.; Dong, C.; Wu, X.M. A closer look at blind super-resolution: Degradation models, baselines, and performance upper bounds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 527–536. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 15–17 June 1993; pp. 1125–1134. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Wang, W.; Webb, R. Learning from simulated and unsupervised images through adversarial training. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 15–17 June 1993; pp. 2107–2116. [Google Scholar]
- Chen, Q.; Koltun, V. Photographic image synthesis with cascaded refinement networks. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 1511–1520. [Google Scholar]
- Dosovitskiy, A.; Brox, T. Generating images with perceptual similarity metrics based on deep networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; Volume 29. [Google Scholar]
- Johnson, J.; Alahi, A.; Li, F. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Zheng, C.; Cham, T.J.; Cai, J. The spatially-correlative loss for various image translation tasks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16407–16417. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar]
- Freedman, G.; Fattal, R. Image and video upscaling from local self-examples. ACM Trans. Graph. (Tog) 2011, 30, 12. [Google Scholar] [CrossRef]
- Sun, J.; Xu, Z.; Shum, H.Y. Image super-resolution using gradient profile prior. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. 275–282. [Google Scholar]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech, Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part IV 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 1874–1883. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 1646–1654. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 4681–4690. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 2472–2481. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 4799–4807. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 3147–3155. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 286–301. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Ji, X.; Cao, Y.; Tai, Y.; Wang, C.; Li, J.; Huang, F. Real-world super-resolution via kernel estimation and noise injection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Vancouver, BC, Canada, 17–24 June 2023; pp. 466–467. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference On computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1905–1914. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Wei, Z.; Huang, Y.; Chen, Y.; Zheng, C.; Gao, J. A-ESRGAN: Training real-world blind super-resolution with attention U-Net Discriminators. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Jakarta, Indonesia, 15–19 November 2023; Springer: Berlin/Heidelberg, Germany, 2015; pp. 16–27. [Google Scholar]
- He, Z.; Cao, Y.; Dong, Y.; Yang, J.; Cao, Y.; Tisse, C.L. Single-image-based nonuniformity correction of uncooled long-wave infrared detectors: A deep-learning approach. Appl. Opt. 2018, 57, D155–D164. [Google Scholar] [CrossRef] [PubMed]
- St-Charles, P.L.; Bilodeau, G.A.; Bergevin, R. Mutual foreground segmentation with multispectral stereo pairs. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Paris, France, 2–6 October 2023; pp. 375–384. [Google Scholar]
- Xu, Z.; Zhuang, J.; Liu, Q.; Zhou, J.; Peng, S. Benchmarking a large-scale FIR dataset for on-road pedestrian detection. Infrared Phys. Technol. 2019, 96, 199–208. [Google Scholar] [CrossRef]
- Gao, C.; Du, Y.; Liu, J.; Lv, J.; Yang, L.; Meng, D.; Hauptmann, A.G. Infar dataset: Infrared action recognition at different times. Neurocomputing 2016, 212, 36–47. [Google Scholar] [CrossRef]
- High Resolution Multi Scene Infrared Database. Available online: https://github.com/Gaojjjie/Inf-OSRGAN (accessed on 13 August 2024).
- Elad, M.; Feuer, A. Restoration of a single superresolution image from several blurred, noisy, and undersampled measured images. IEEE Trans. Image Process. 1997, 6, 1646–1658. [Google Scholar] [CrossRef]
- Liu, C.; Sun, D. On Bayesian adaptive video super resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 346–360. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. arXiv 2018, arXiv:1808.06670. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 1597–1607. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9729–9738. [Google Scholar]
- Park, T.; Efros, A.A.; Zhang, R.; Zhu, J.Y. Contrastive learning for unpaired image-to-image translation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 319–345. [Google Scholar]
- Infrared Security Database. Available online: http://openai.raytrontek.com/apply/Infrared_security.html/ (accessed on 30 March 2024).
- Infrared Image Denoising Database. Available online: http://openai.raytrontek.com/apply/E_Image_noise_reduction.html/ (accessed on 30 March 2024).
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 391–407. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4401–4410. [Google Scholar]
- Abrahamyan, L.; Truong, A.M.; Philips, W.; Deligiannis, N. Gradient variance loss for structure-enhanced image super-resolution. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 7–13 May 2022; pp. 3219–3223. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).