Solving Arithmetic Word Problems by Synergizing Large Language Model and Scene-Aware Syntax–Semantics Method
Abstract
1. Introduction
- It proposes a novel algorithm that leverages the LLM to divide the problem into multiple scenes, thereby enhancing the relation-flow approach in relation extraction and reasoning, achieving high accuracy and reliability in solving AWPs.
- It proposes a COS prompting method, which constructs prompts through a retrieval-augmented strategy, enabling the LLM to accurately generate scenes from an AWP while avoiding the errors caused by direct solving.
- It proposes a Scene-Aware method, which combines scene types with syntax–semantics to extract both explicit and implicit relations, thereby enhancing the efficiency and accuracy of relation acquisition.
2. Related Work
2.1. Usage of LLM in Solving AWPs
2.2. Advance in Relation-Flow Approach
2.3. Progress of Symbolic Solver
3. Methodology
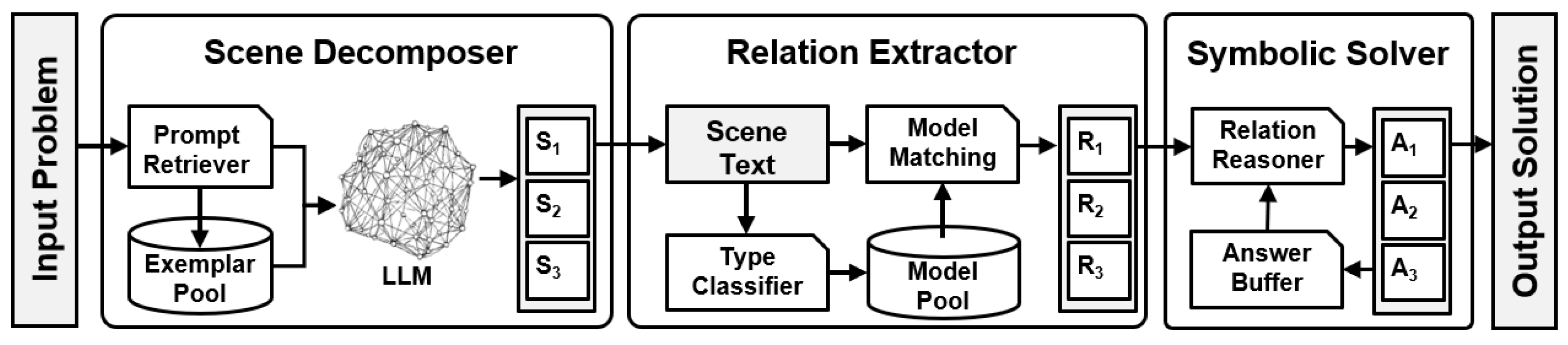
3.1. The Pipeline of Proposed Algorithm
- Scene Decomposer: The first component uses the COS prompting method to decompose the input problem into a list of scenes, each represented as a text closure. This method is detailed in Section 3.2.1 and constitutes one of the primary contributions of our algorithm.
- Relation Extractor: The second component uses the Scene-Aware method to extract a relation set from each scene, producing a list of relation sets. This method is another major contribution and is discussed in Section 3.3.1.
- Symbolic Solver: The third component derives the final solution by reasoning through the list of relation sets. This component primarily enhances the symbolic solver proposed by [17], adapting it for use in our context.
| Algorithm 1: The algorithm for solving AWPs. |
Input: A problem text T Output: A solution A
|
3.2. Scene Decomposer
3.2.1. COS Prompting Method
3.2.2. Implementation of COS Prompting Method
| Procedure 1: Scene Decomposer using COS Prompting |
|
3.3. Relation Extractor
3.3.1. Scene-Aware Method
3.3.2. Implementation of Scene-Aware Method
| Procedure 2: Relation extractor using Scene-Aware S2 method. |
 |
3.4. Symbolic Solver
| Procedure 3: Symbolic Solver |
 |
4. Experiments
4.1. Experimental Settings
4.1.1. Datasets
4.1.2. Baselines
- YuAlg: A relation-flow algorithm presented [17] in 2023. This algorithm is the most advanced algorithm in the relation-flow approach for solving AWPs so far. It synergizes the method for extracting explicit relations and a neural miner for extracting implicit relations. It develops a symbolic solver to reason the relation set.
- ZhangAlg: A Sequence-to-Sequence (Seq2Seq) algorithm presented in [19] in 2020. It constructs a graph encoder with a tree decoder to generate an arithmetic expression for a problem text. It achieved the highest solving accuracy without the use of a pre-trained model.
- JieAlg: A Seq2Seq algorithm presented in [28] in 2022. It uses BERT as the pre-trained encoder and proposes a deductive reasoner to construct target expression iteratively. It achieves SOTA performance on Math23k and MAWPS.
- YasuAlg: An LLM-based algorithm presented in [32] in 2023. It proposes an analogy-based prompting method, prompting the LLM to first recall relevant exemplars before solving the initial problem. This method significantly improves the performance of LLMs on mathematical reasoning tasks.
- LiuAlg: An LLM-based algorithm presented in [14] in 2023. It introduces an XOT method, which integrates a problem-solving framework by prompting LLM with diverse reasoning thoughts. This method achieves SOTA performance on the GSM8K dataset under the same LLM settings.
4.2. Experimental Results
- PROP achieves an average accuracy of 90.4% on Chinese datasets and 90.3% on English datasets, outperforming the best Seq2Seq-based algorithm (JieAlg) by 6% and 10.9%, and outperforming the best LLM-based algorithm (LiuAlg) by 1.1% and 0.7%. The differences between the Chinese and English versions are mainly due to translation errors, which are reflected in the performance of all algorithms.
- PROP (90.4%) achieved an improvement of 31.9% and 34.6% on the Chinese and English datasets, respectively, compared to YuAlg (58.5%), despite both using a relation-flow approach to solve AWPs. This significant improvement indicates that PROP’s relation-flow approach, empowered by LLM, has a broader solvable range for AWPs.
- PROP (90.3%) outperformed YasuAlg (86.1%) and LiuAlg (89.6%) on the English dataset by 4.2% and 0.7%, respectively. This demonstrates that symbolic reasoning based on relation sets effectively reduces errors compared to LLM directly reasoning based on natural language or invoking code interpreters.
4.3. Case Study
5. Final Remarks
5.1. Discussion of Experiment Results
5.2. Conclusions and Future Work
5.3. Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWP | Arithmetic Word Problem |
| NLP | Natural Language Processing |
| LLM | Large Language Model |
| Syntax-Semantic | |
| SOTA | State-Of-The-Art |
| COT | Chain-Of-Thought |
| COS | Chain-Of-Scene |
| POS | Part-Of-Speech |
| QRAN | Quantity-to-Relation Attention Network |
| Seq2Seq | Sequence-to-Sequence |
References
- Zhang, D.; Wang, L.; Zhang, L.; Dai, B.T.; Shen, H.T. The Gap of Semantic Parsing: A Survey on Automatic Math Word Problem Solvers. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2287–2305. [Google Scholar] [CrossRef] [PubMed]
- Bobrow, D.G. Natural Language Input for a Computer Problem Solving System; Massachusetts Institute of Technology: Cambridge, MA, USA, 1964. [Google Scholar]
- Kintsch, W.; Greeno, J.G. Understanding and solving word arithmetic problems. Psychol. Rev. 1985, 92, 109–129. [Google Scholar] [CrossRef] [PubMed]
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman, F.L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Anadkat, S.; et al. GPT-4 Technical Report. arXiv 2023, arXiv:2303.08774. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Xia, F.; Chi, E.; Le, Q.V.; Zhou, D. Chain-of-thought prompting elicits reasoning in large language models. Adv. Neural Inf. Process. Syst. 2022, 35, 24824–24837. [Google Scholar]
- Zhou, A.; Wang, K.; Lu, Z.; Shi, W.; Luo, S.; Qin, Z.; Lu, S.; Jia, A.; Song, L.; Zhan, M.; et al. Solving Challenging Math Word Problems Using GPT-4 Code Interpreter with Code-based Self-Verification. In Proceedings of the Twelfth International Conference on Learning Representations, ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Lu, Y.; Pian, Y.; Chen, P.; Meng, Q.; Cao, Y. RadarMath: An Intelligent Tutoring System for Math Education. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 19–21 May 2021; Volume 35, pp. 16087–16090. [Google Scholar] [CrossRef]
- Mousavinasab, E.; Zarifsanaiey, N.; Kalhori, S.R.N.; Rakhshan, M.; Keikha, L.; Saeedi, M.G. Intelligent Tutoring Systems: A Systematic Review Of Characteristics, Applications, And Evaluation Methods. Interact. Learn. Environ. 2021, 29, 142–163. [Google Scholar] [CrossRef]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. Adv. Neural Inf. Process. Syst. 2022, 35, 27730–27744. [Google Scholar]
- Zong, M.; Krishnamachari, B. Solving math word problems concerning systems of equations with gpt-3. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 15972–15979. [Google Scholar] [CrossRef]
- Zong, M.; Krishnamachari, B. Solving math word problems concerning systems of equations with GPT models. Mach. Learn. Appl. 2023, 14, 100506. [Google Scholar] [CrossRef]
- Wang, X.; Wei, J.; Schuurmans, D.; Le, Q.V.; Chi, E.H.; Narang, S.; Chowdhery, A.; Zhou, D. Self-Consistency Improves Chain of Thought Reasoning in Language Models. In Proceedings of the Eleventh International Conference on Learning Representations, ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Liu, T.; Guo, Q.; Yang, Y.; Hu, X.; Zhang, Y.; Qiu, X.; Zhang, Z. Plan, Verify and Switch: Integrated Reasoning with Diverse X-of-Thoughts. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing (EMNLP), Singapore, 6–10 December 2023; pp. 2807–2822. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X.; Mishra, S.; Zheng, H.S.; Yu, A.W.; Song, X.; Zhou, D. Large Language Models Cannot Self-Correct Reasoning Yet. In Proceedings of the Twelfth International Conference on Learning Representations, ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Huang, L.; Yu, X.; Niu, L.; Feng, Z. Solving Algebraic Problems with Geometry Diagrams Using Syntax-Semantics Diagram Understanding. Comput. Mater. Contin. 2023, 77, 517–539. [Google Scholar] [CrossRef]
- Yu, X.; Lyu, X.; Peng, R.; Shen, J. Solving arithmetic word problems by synergizing syntax-semantics extractor for explicit relations and neural network miner for implicit relations. Complex Intell. Syst. 2023, 9, 697–717. [Google Scholar] [CrossRef]
- Yu, X.; Sun, H.; Sun, C. A relation-centric algorithm for solving text-diagram function problems. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 8972–8984. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Y.; Ma, Y.; Cheng, X.; Tan, Z.; Nong, Q.; Lu, W. Multi-View Reasoning: Consistent Contrastive Learning for Math Word Problem. In Proceedings of the Findings of the Association for Computational Linguistics, EMNLP, Abu Dhabi, United Arab Emirates, 7–11 December 2022; Association for Computational Linguistics: Stroudsburg, PA, USA, 2022; pp. 1103–1116. [Google Scholar] [CrossRef]
- Roberts, A.; Raffel, C.; Shazeer, N. How Much Knowledge Can You Pack Into the Parameters of a Language Model? In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 5418–5426. [Google Scholar] [CrossRef]
- Kauf, C.; Ivanova, A.A.; Rambelli, G.; Chersoni, E.; She, J.S.; Chowdhury, Z.; Fedorenko, E.; Lenci, A. Event knowledge in large language models: The gap between the impossible and the unlikely. Cogn. Sci. 2023, 47, e13386. [Google Scholar] [CrossRef] [PubMed]
- Cobbe, K.; Kosaraju, V.; Bavarian, M.; Chen, M.; Jun, H.; Kaiser, L.; Plappert, M.; Tworek, J.; Hilton, J.; Nakano, R.; et al. Training verifiers to solve math word problems. arXiv 2021, arXiv:2110.14168. [Google Scholar] [CrossRef]
- Chen, W.; Ma, X.; Wang, X.; Cohen, W.W. Program of Thoughts Prompting: Disentangling Computation from Reasoning for Numerical Reasoning Tasks. arXiv 2023, arXiv:2211.12588. [Google Scholar] [CrossRef]
- Zhou, D.; Schärli, N.; Hou, L.; Wei, J.; Scales, N.; Wang, X.; Schuurmans, D.; Cui, C.; Bousquet, O.; Le, Q.V.; et al. Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. In Proceedings of the Eleventh International Conference on Learning Representations, ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Shridhar, K.; Stolfo, A.; Sachan, M. Distilling Reasoning Capabilities into Smaller Language Models. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2023, Toronto, ON, Canada, 9–14 July 2023; Association for Computational Linguistics: Stroudsburg, PA, USA, 2023; pp. 7059–7073. [Google Scholar] [CrossRef]
- Yu, X.; Gan, W.; Wang, M. Understanding explicit arithmetic word problems and explicit plane geometry problems using syntax-semantics models. In Proceedings of the 2017 International Conference on Asian Language Processing (IALP), Singapore, 5–7 December 2017; pp. 247–251. [Google Scholar] [CrossRef]
- Jian, P.; Sun, C.; Yu, X.; He, B.; Xia, M. An End-to-end Algorithm for Solving Circuit Problems. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1940004:1–1940004:21. [Google Scholar] [CrossRef]
- Jie, Z.; Li, J.; Lu, W. Learning to Reason Deductively: Math Word Problem Solving as Complex Relation Extraction. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Dublin, Ireland, 22–27 May 2022; Association for Computational Linguistics: Stroudsburg, PA, USA, 2022; Volume 1, pp. 5944–5955. [Google Scholar] [CrossRef]
- Kushman, N.; Artzi, Y.; Zettlemoyer, L.; Barzilay, R. Learning to automatically solve algebra word problems. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Long Papers), ACL, Baltimore, MD, USA, 23–24 June 2014; Association for Computer Linguistics: Stroudsburg, PA, USA, 2014; Volume 1, pp. 271–281. [Google Scholar] [CrossRef]
- Qin, J.; Liang, X.; Hong, Y.; Tang, J.; Lin, L. Neural-Symbolic Solver for Math Word Problems with Auxiliary Tasks. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Virtual, 1–6 August 2021; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; Volume 1, pp. 5870–5881. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, J.; Wang, L.; Qin, W.; Lan, Y.; Shao, J.; Zhang, X. MWP-BERT: Numeracy-Augmented Pre-training for Math Word Problem Solving. In Proceedings of the Findings of the Association for Computational Linguistics: NAACL, 2022. Association for Computational Linguistics, Seattle, WA, USA, 10–15 July 2022; pp. 997–1009. [Google Scholar] [CrossRef]
- Yasunaga, M.; Chen, X.; Li, Y.; Pasupat, P.; Leskovec, J.; Liang, P.; Chi, E.H.; Zhou, D. Large Language Models as Analogical Reasoners. In Proceedings of the Twelfth International Conference on Learning Representations, ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Mitra, A.; Baral, C. Learning To Use Formulas To Solve Simple Arithmetic Problems. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Long Papers), ACL, Berlin, Germany, 7–12 August 2016; Association for Computer Linguistics: Stroudsburg, PA, USA, 2016; Volume 1, pp. 2144–2153. [Google Scholar] [CrossRef]
- Roy, S.; Roth, D. Mapping to Declarative Knowledge for Word Problem Solving. Trans. Assoc. Comput. Linguist. 2018, 6, 159–172. [Google Scholar] [CrossRef]
- Che, W.; Feng, Y.; Qin, L.; Liu, T. N-LTP: An Open-source Neural Language Technology Platform for Chinese. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Virtual, 7–11 November 2021; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 42–49. [Google Scholar] [CrossRef]
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Shi, S. Deep Neural Solver for Math Word Problems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing (EMNLP), Copenhagen, Denmark, 9–11 September 2017; Association for Computational Linguistics: Stroudsburg, PA, USA, 2017; pp. 845–854. [Google Scholar] [CrossRef]
- Koncel-Kedziorski, R.; Roy, S.; Amini, A.; Kushman, N.; Hajishirzi, H. MAWPS: A Math Word Problem Repository. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; Association for Computational Linguistics: Stroudsburg, PA, USA, 2016; pp. 1152–1157. [Google Scholar] [CrossRef]
- Mishra, S.; Finlayson, M.; Lu, P.; Tang, L.; Welleck, S.; Baral, C.; Rajpurohit, T.; Tafjord, O.; Sabharwal, A.; Clark, P.; et al. LILA: A Unified Benchmark for Mathematical Reasoning. In Proceedings of the Findings of the Association for Computational Linguistics, EMNLP, Abu Dhabi, United Arab Emirates, 7–11 December 2022; Association for Computational Linguistics: Stroudsburg, PA, USA, 2022; pp. 5807–5832. [Google Scholar] [CrossRef]

| Name | Year | Approach | LLM | Symbolic Solver |
|---|---|---|---|---|
| ZhangAlg [31] | 2022 | Sequence-to-Sequence | No | No |
| JieAlg [28] | 2022 | Sequence-to-Sequence | No | No |
| YuAlg [17] | 2023 | Relation-Flow | No | Yes |
| LiuAlg [14] | 2023 | Prompting-LLM | Yes | No |
| YasuAlg [32] | 2024 | Prompting-LLM | Yes | No |
| Our Work | 2024 | Prompting-LLM + Relation-Flow | Yes | Yes |
| Scene Type | Model Structure | Matched Sentence | Explicit Relations |
|---|---|---|---|
| General | n m q a = n; b = m; c = q a = b * c | Ming had 15 stamps | Ming = 15 × stamp |
| General | n m [more than] n a = n; b = m; c = n a = b + c | Pens are 5 more than eraser | Pen = 4 + Eraser |
| General | n [of] n m [times] n a = n; b = n; c = m; d = n a (b) = c * a (d) | The price of durian is 5 times that of apple | Price (durian) = 5 × Price (apple) |
| Change | n m q [left] a = n; b = m; c = q Left (a) = b * c | The match is still 2 cm left. | Left (match) = 2 × cm |
| Rate and Journal | n [average] m q [per] q a = n; b = m; c = q; d = q Rate (a) = b * (c/d) | The factory binds an average of 90 books per day | Rate (factory) = 90 × (book/day) |
| Discount | n [at] m [discount] a = n; b = m Discount (a) = b | A product is sold at a 10% discount | Discount (product) = 10% |
| Solution | n [made of] n n [ratio of] q a = n; b = n; c = n; d = q Solution (a), Solute (b)/Solvent (c) = d | An alcohol is made of ethanol and water in a mass ratio of 1:5. | Solution(alcohol), Solute (ethanol) ÷ Solvent (water) = 1:5 |
| Dataset | Size | AvgLen | AvgOp | Source | Language |
|---|---|---|---|---|---|
| PBE [17] | 3262 | 33.76 | 2.95 | textbook, exam | CN |
| Math23a [37] | 20,160 | 27.68 | 2.70 | web | CN |
| APECa [31] | 15,245 | 29.32 | 2.82 | textbook, web | CN |
| AGG [34] | 1492 | 26.96 | 1.30 | web, exam | EN |
| MAWPS [38] | 1987 | 30.28 | 1.47 | web | EN |
| GSM8K [34] | 1319 | 42.25 | 3.29 | web | EN |
| Algorithms Tested on Chinese Version | Algorithms Tested on English Version | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| YuAlg | ZhangAlg | JieAlg | LiuAlg | PROP | YuAlg | JieAlg | YasuAlg | LiuAlg | PROP | ||
| Dataset | # | % | % | % | % | % | % | % | % | % | % |
| PBE | 3262 | 55.2 | 49.2 | 52.8 | 85.2 | 89.5 | 54.0 | 49.0 | 75.7 | 82.8 | 88.2 |
| Math23a | 20,160 | 60.0 | 77.8 | 87.8 | 90.1 | 91.2 | 58.2 | 84.3 | 88.0 | 90.2 | 91.0 |
| APECa | 15,245 | 58.1 | 72.6 | 81.9 | 89.4 | 90.0 | 52.3 | 80.5 | 85.5 | 89.9 | 89.6 |
| AGG | 1492 | 54.2 | 66.7 | 73.4 | 86.2 | 88.2 | 55.3 | 72.5 | 85.1 | 90.4 | 90.9 |
| MAWPS | 1987 | 69.7 | 84.3 | 91.5 | 94.6 | 94.2 | 71.2 | 92.0 | 94.4 | 95.3 | 95.7 |
| GSM8K | 1492 | 35.0 | 38.5 | 43.7 | 81.3 | 83.2 | 37.8 | 46.5 | 77.8 | 83.2 | 84.5 |
| Avg | 43,465 | 58.5 | 72.6 | 81.4 | 89.3 | 90.4 | 55.7 | 79.1 | 86.1 | 89.6 | 90.3 |
| Dataset | LiuAlggpt | PROPgpt | LiuAlgqwen | PROPqwen |
|---|---|---|---|---|
| PBE | 85.2 | 89.5 | 88.9 | 90.3 |
| AGG | 86.2 | 88.2 | 94.8 | 95.1 |
| GSM8K | 81.3 | 83.2 | 91.3 | 93.6 |
| Avg | 84.6 | 87.8 | 90.9 | 92.2 |
| AWP case 1 | Ming has 15 stamps, and Li has 5 stamps less than Ming. How many stamps does Li have? |
| Output | ZhangAlg: Equation: ‘15−5’, Answer: 10 Correct LiuAlg: 1. Let Ming have xx stamps; 2. According to the question, Ming has 15 stamps, that is, x = 15; 3. The question also mentions that Li has 5 fewer stamps than Ming. Therefore, the number of stamps Li has can be expressed as x − 5; 4. Now let’s substitute the number of stamps Ming has x = 15; 5. The number of stamps Li has is: x − 5 = 15 − 5 = 10; 6. Therefore, Li has 10 stamps; Correct PROP: 1. {Type: General, Relation Set: {Ming = 15 * stamps, Li = Ming − 5 * stamps}, Answer: {Li = 10 * stamps}; Final Answer: Li has 10 stamps. Correct |
| AWP case 2 | There are 15 kg of apples, 20 kg of bananas, and 20 kg of rice in the store. Divide all the fruits equally into 5 boxes. How many kg of fruits should be put in each box? |
| Output | ZhangAlg: Equation: ‘(15 + 20 + 20)/5’, Answer: 11 Incorrect LiuAlg: 1. Calculate the total number of kg of fruit: 15 kg of apples, 20 kg of bananas, total fruit = apples + bananas = 15 + 20 = 35 kg; 2. Determine the number of boxes and the average amount of fruit in each box: the number of boxes is 5 boxes, the average amount of fruit in each box = total amount of fruit/number of boxes; 3. Calculate how many kg of fruit should be put in each box: the amount of fruit that should be put in each box = total amount of fruit/number of boxes, the amount of fruit that should be put in each box = 35/5 = 7 kg. 4. Therefore, each box should have 7 kg of fruit, so that all the fruit can be divided equally into 5 boxes. Correct PROP: 1. {Type: Part-Whole, Relation Set:{apples = 15 * kg, bananas = 20 * kg}, Answer: {fruits = 35 * kg}; 2. {Type: Rate, Relation Set: {Total (fruits) = 35 * kg, Amount (fruits) = 5 * boxes}, Answer: {Rate (fruits) = 7 * (kg/box)}; Final Answer: 7 kg in each box. Correct |
| AWP case 3 | There are 36 students in the morning, of which girls account for (5/9) of the total number of students. Later, a few boys came. Now girls account for (2/5) of the total number of students. Later, how many boys came? |
| Output | ZhangAlg: Equation: ‘36 * (5/9)/(1 − (2/5)) − 36’, Answer: −2.666 Incorrect LiuAlg: 1. Let the total number of people in the morning be N; 2. Initially, girls account for (5/9) of the total number of people in the morning, so the number of girls is (5/9) * N; 3. Later, several boys came, making girls account for (2/5) of the total number of people, so the number of girls is still (5/9) * N, and the total number is N + x, where x is the number of new boys; 4. According to the proportional relationship given in the question, we can establish the following equation: (5/9) * N/N = (2/5); 5. This is because in the second state, the number of girls is still (5/9) * N, and the total number becomes N + x; 6. Solving this equation, we can get: (5/9) = (5/2), which is obviously inconsistent, so we need to re-examine the problem. Incorrect PROP: 1. {Type: General, Relation Set: {students (morning) = 36, girls = students (morning) * (5/9)}, Answer: {girls = 20}; 2. {Type: General, Relation Set: {girls = 20, girls = students (now) * (2/5)}, Answer: {students (now) = 50}; 3. {Type: Change, Relation Set: {students (morning) = 36, students (now) = 50}, Answer: {Came (boys) = 14}; Final Answer: 14 boys came. Correct |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, R.; Huang, L.; Yu, X. Solving Arithmetic Word Problems by Synergizing Large Language Model and Scene-Aware Syntax–Semantics Method. Appl. Sci. 2024, 14, 8184. https://doi.org/10.3390/app14188184
Peng R, Huang L, Yu X. Solving Arithmetic Word Problems by Synergizing Large Language Model and Scene-Aware Syntax–Semantics Method. Applied Sciences. 2024; 14(18):8184. https://doi.org/10.3390/app14188184
Chicago/Turabian StylePeng, Rao, Litian Huang, and Xinguo Yu. 2024. "Solving Arithmetic Word Problems by Synergizing Large Language Model and Scene-Aware Syntax–Semantics Method" Applied Sciences 14, no. 18: 8184. https://doi.org/10.3390/app14188184
APA StylePeng, R., Huang, L., & Yu, X. (2024). Solving Arithmetic Word Problems by Synergizing Large Language Model and Scene-Aware Syntax–Semantics Method. Applied Sciences, 14(18), 8184. https://doi.org/10.3390/app14188184






