Numerical Modeling of Scholte Wave in Acoustic-Elastic Coupled TTI Anisotropic Media
Abstract
:1. Introduction
2. Wave Equations
2.1. Acoustic-Elastic Coupled Equation
2.2. Bond Transformation
3. Staggered-Grid Finite Difference
Stability Condition
4. Numerical Experiments
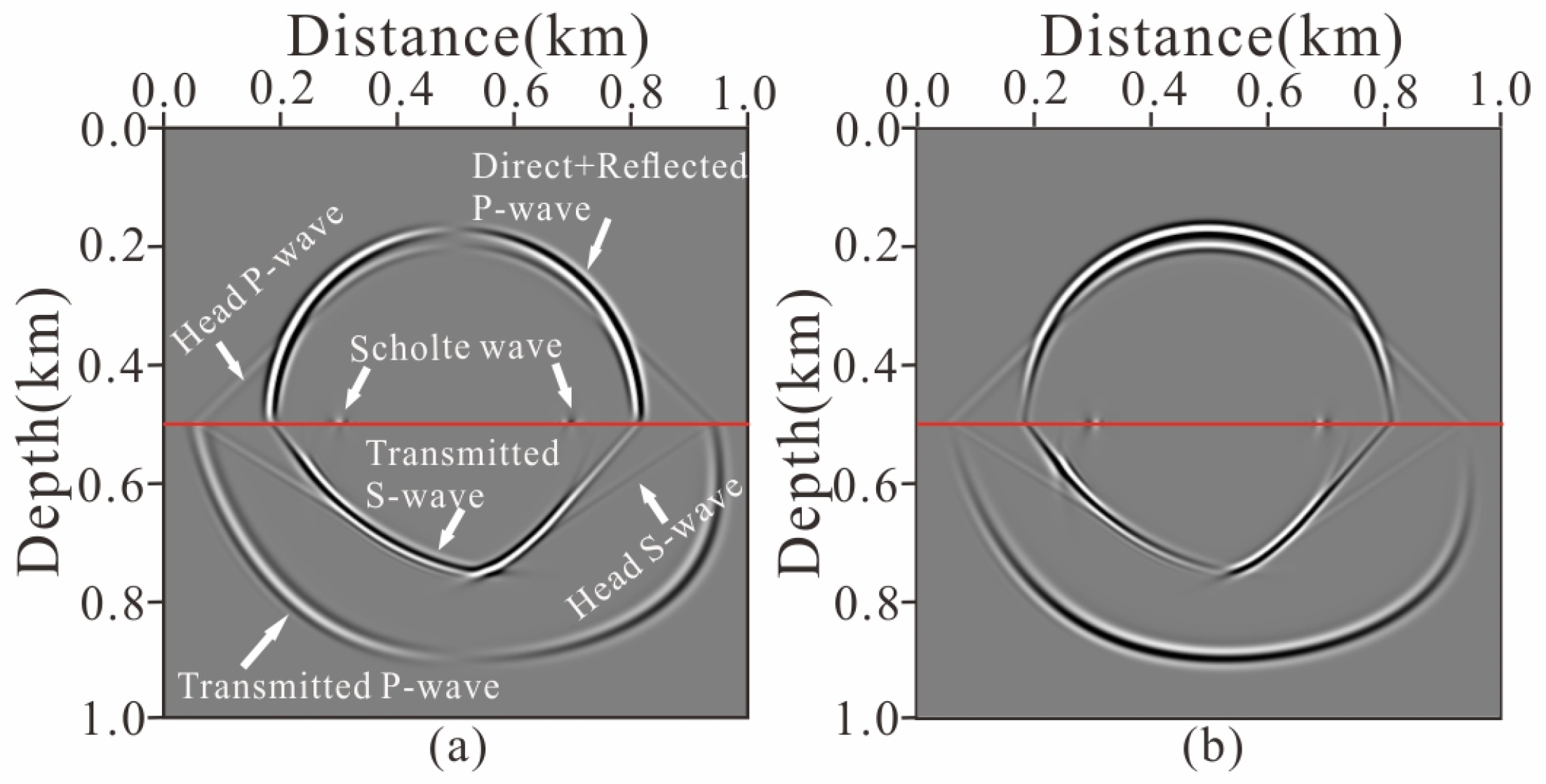
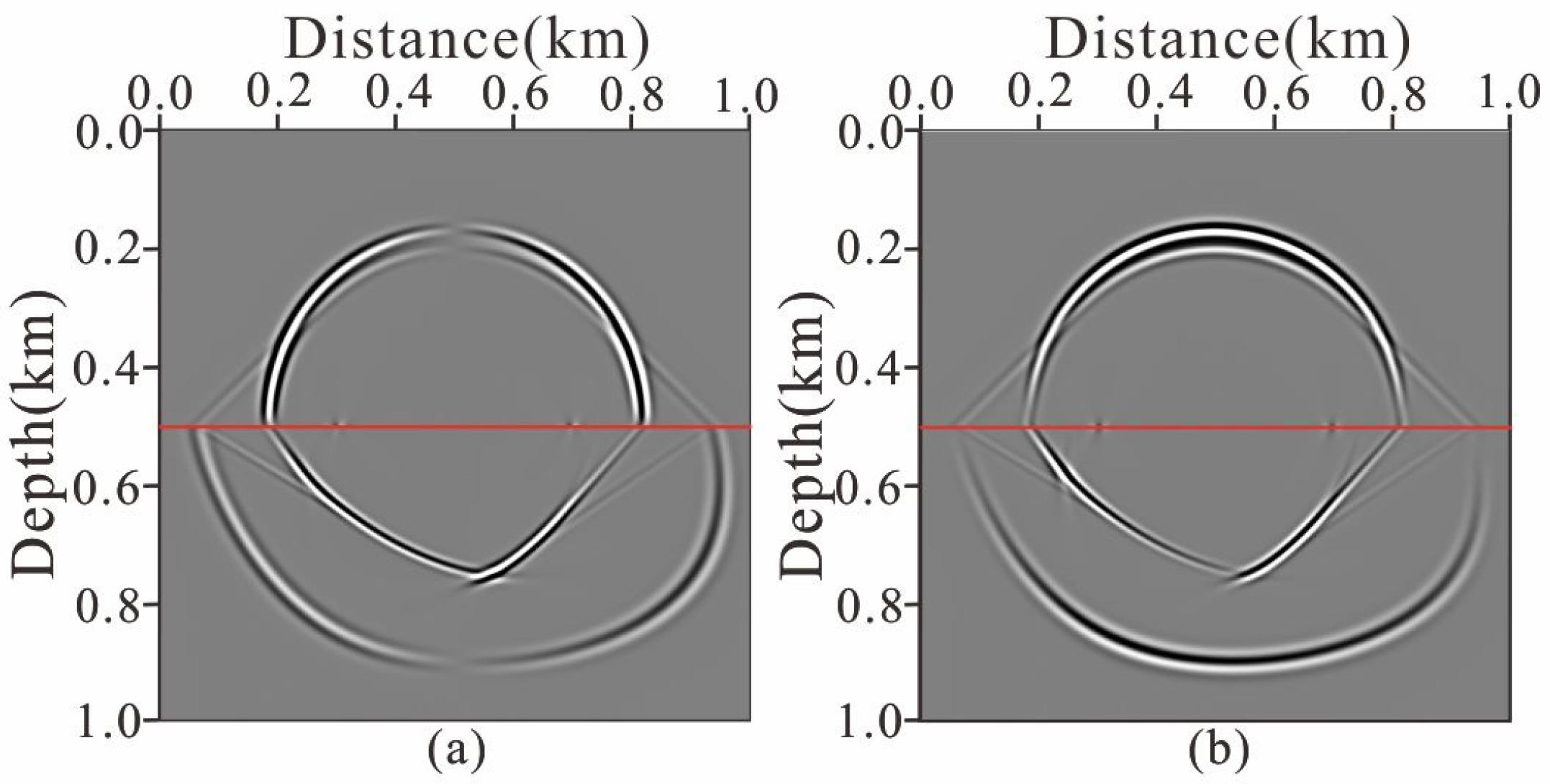
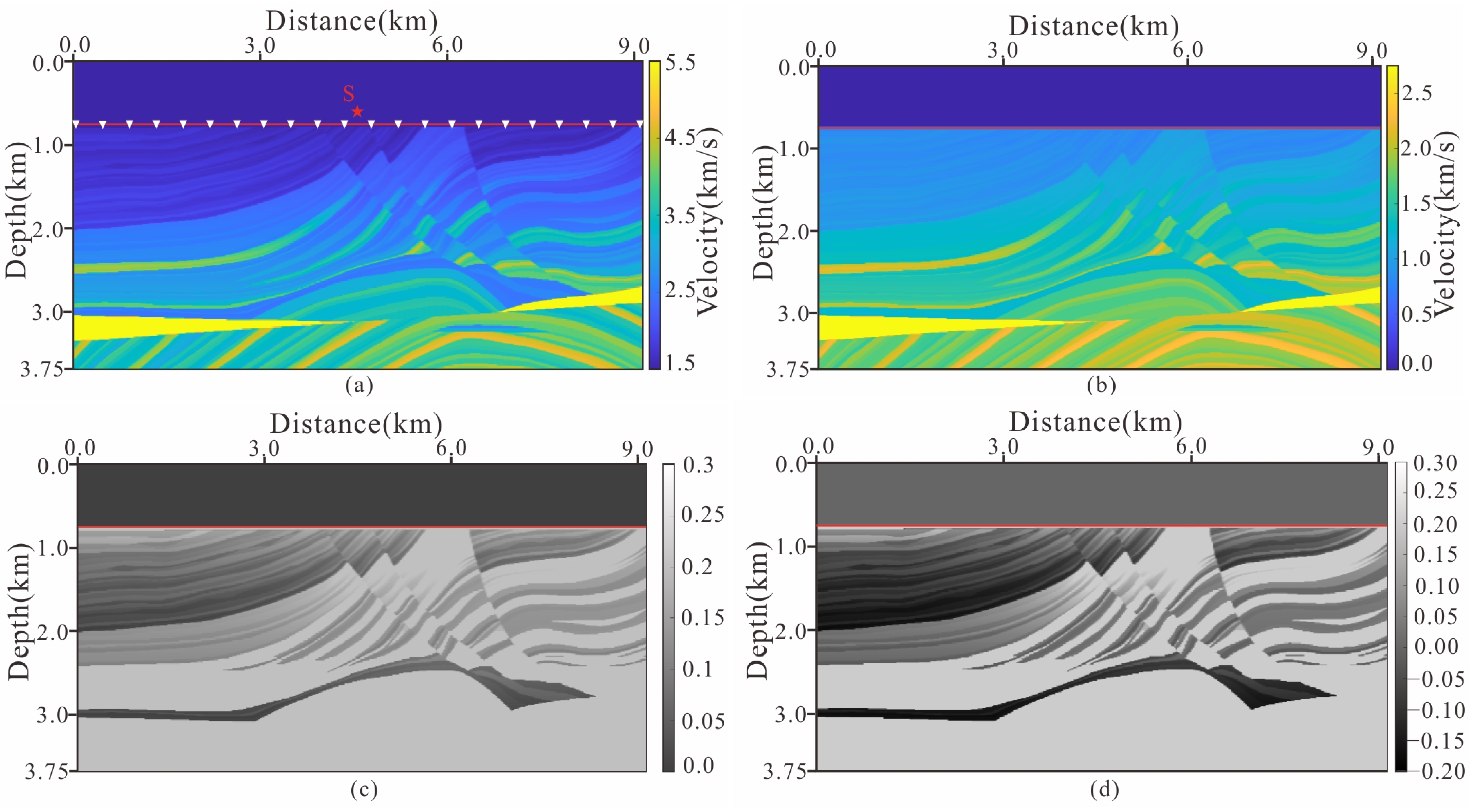
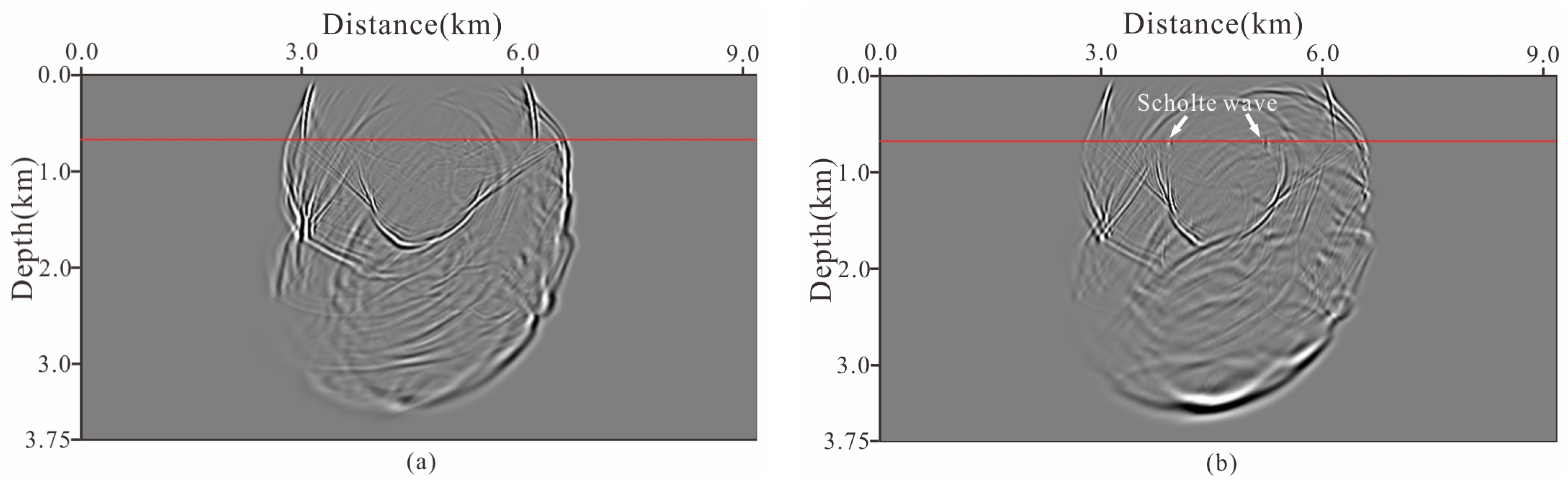
4.1. 2D Two-Layer Acoustic-Elastic Coupled Model
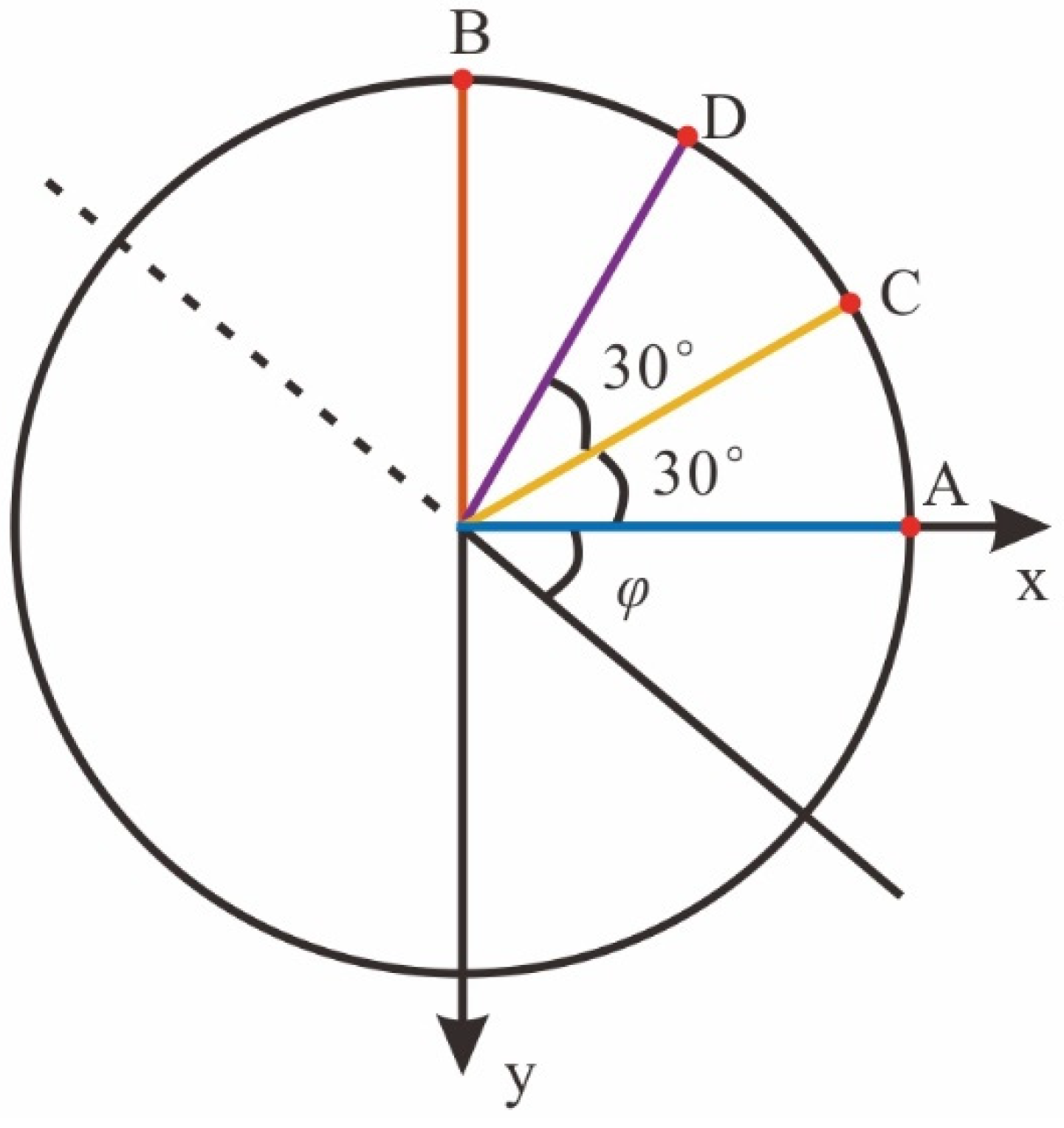
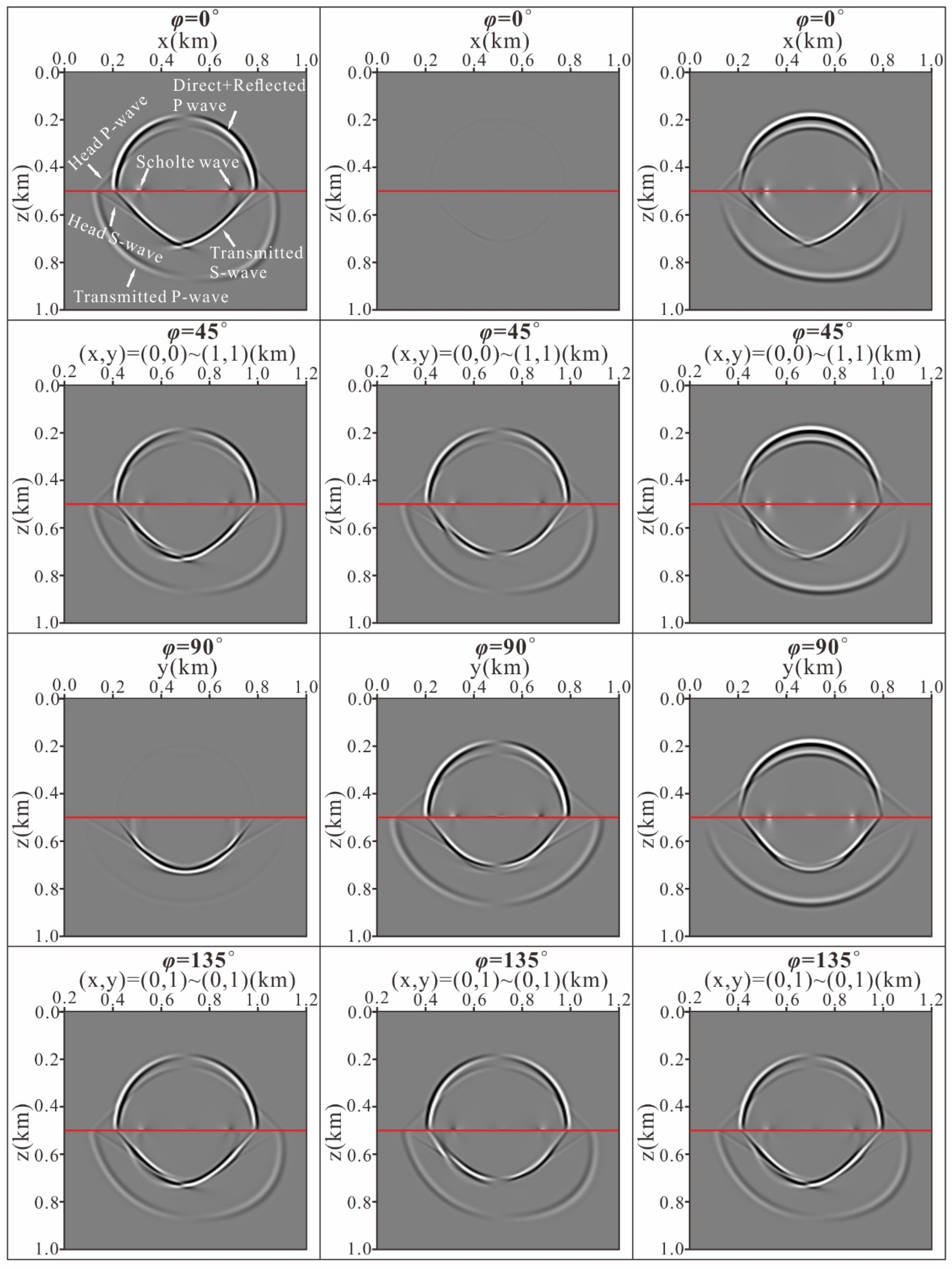
4.2. 3D Two-Layer Acoustic-Elastic Coupled Model
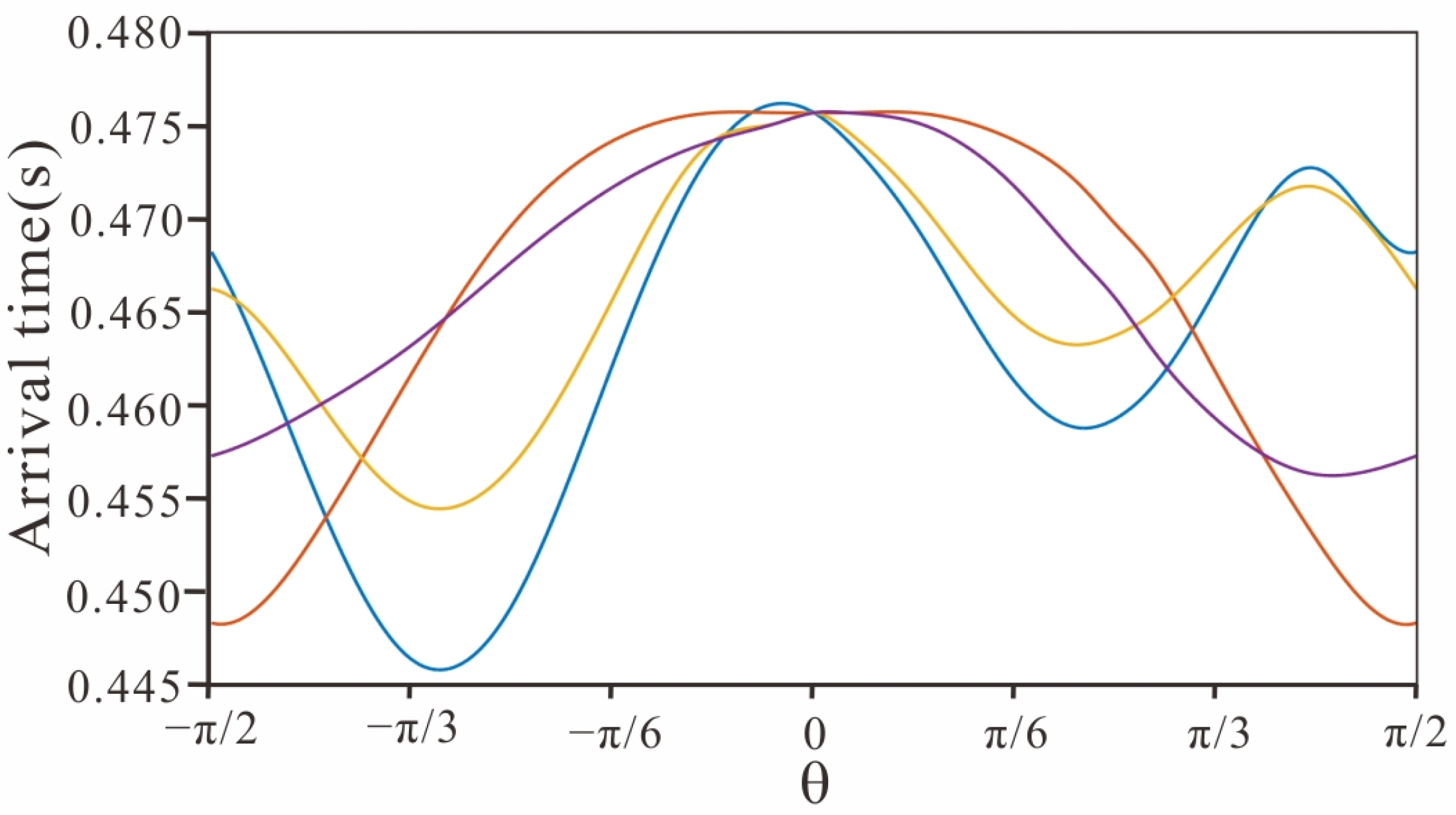
4.3. Inhomogeneous Acoustic-Elastic Coupled Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Thomsen Parameter
- acoustic-elastic coupled equation in a 3D TTI media
Appendix B
References
- Miele, R.; Barreto, B.V.; Yamada, P.; Varella, L.E.S.; Pimentel, A.L.; Costa, J.F.; Azevedo, L. Geostatistical seismic rock physics AVA inversion with data-driven elastic properties update. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4506915. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, H.; Yan, W.; Gao, J. A unified numerical scheme for coupled multiphysics model. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8228–8240. [Google Scholar] [CrossRef]
- Carcione, J.M.; Helle, H.B. The physics and simulation of wave propagation at the ocean bottom. Geophysics 2004, 69, 825–839. [Google Scholar] [CrossRef]
- Shukla, K.; Carcione, J.M.; Hesthaven, J.S.; L’heureux, E. Waves at a fluid-solid interface: Explicit versus implicit formulation of boundary conditions using a discontinuous Galerkin method. J. Acoust. Soc. Am. 2020, 147, 3136–3150. [Google Scholar] [CrossRef]
- Kovářík, K.; Mužík, J. The Modified Local Boundary Knots Method for Solution of the Two-Dimensional Advection–Diffusion Equation. Mathematics 2022, 10, 3855. [Google Scholar] [CrossRef]
- Kovářík, K.; Mužík, J.; Gago, F.; Sitányiová, D. Modified local singular boundary method for solution of two-dimensional diffusion equation. Eng. Anal. Bound. Elem. 2022, 143, 525–534. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Zhang, J.; Geng, J.; You, Q.; Hu, Y.; Liu, Y.; Hao, T.; Yao, Z. Separating Scholte Wave and Body Wave in OBN Data Using Wave-Equation Migration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5914213. [Google Scholar] [CrossRef]
- Zhan, G.; Pestana, R.C.; Stoffa, P.L. Decoupled equations for reverse time migration in tilted transversely isotropic media. Geophysics 2012, 77, T37–T45. [Google Scholar] [CrossRef]
- Zdraveva, O.; Ogunsakin, A.; Hootman, B.; Kristiansen, P.; Quadt, E. Improved imaging of deepwater reservoir by TTI model building and optimized use of OBN data: 85th SEG Annual International Meeting. In Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2015; pp. 5198–5201. [Google Scholar] [CrossRef]
- Qu, Y.; Li, J.; Li, Y.; Li, Z. Joint acoustic and decoupled-elastic least-squares reverse time migration for simultaneously using water-land dual-detector data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5909511. [Google Scholar] [CrossRef]
- Lan, T.; Zong, Z.; Jia, W. Reservoir hydrocarbon identification method based on pre-stack seismic frequency-dependent anisotropic inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5915413. [Google Scholar] [CrossRef]
- Cagniard, L.; Flinn, E.A.; Hewitt Dix, C.; Mayer, W.G. Reflection and refraction of progressive seismic waves. Phys. Today 1963, 16, 64. [Google Scholar] [CrossRef]
- Carbajal-Romero, M.; Flores-Mendez, E.; Flores-Guzmán, N.; Núñez-Farfán, J.; Olivera-Villaseñor, E.; Sánchez-Sesma, F.J. Scholte waves on fluid-solid interfaces by means of an integral formulation. Geofís. Int. 2013, 52, 21–30. [Google Scholar] [CrossRef]
- van Vossen, R.; Robertsson, J.O.; Chapman, C.H. Finite-difference modeling of wave propagation in a fluid-solid configuration. Geophysics 2002, 67, 618–624. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, J.; Wang, Z.; Huang, H.; Hu, J.; Guo, C.a. Improving Scholte-Wave vibration signal recognition based on polarization characteristics in coastal waters. J. Coast. Res. 2020, 36, 382–392. [Google Scholar] [CrossRef]
- Xin, X.; Yong-Ge, W.; Zhen-Yue, L.; Shu-Zhong, S. Scholte wave dispersion and particle motion mode in ocean and ocean crust. Appl. Geophys. 2022, 19, 132–142. [Google Scholar] [CrossRef]
- Wang, W.; Mokhtari, A.A.; Srivastava, A.; Amirkhizi, A.V. Angle-dependent phononic dynamics for data-driven source localization. J. Acoust. Soc. Am. 2023, 154, 2904–2916. [Google Scholar] [CrossRef] [PubMed]
- Auld, B. Rayleigh wave propagation. In Rayleigh-Wave Theory and Application, Proceedings of the International Symposium Organised by the Rank Prize Funds at the Royal Institution, London, UK, 15–17 July 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 12–27. [Google Scholar]
- Carcione, J.M.; Bagaini, C.; Ba, J.; Wang, E.; Vesnaver, A. Waves at fluid–solid interfaces: Explicit versus implicit formulation of the boundary condition. Geophys. J. Int. 2018, 215, 37–48. [Google Scholar] [CrossRef]
- Glorieux, C.; Van de Rostyne, K.; Gusev, V.; Gao, W.; Lauriks, W.; Thoen, J. Nonlinearity of acoustic waves at solid–liquid interfaces. J. Acoust. Soc. Am. 2002, 111, 95–103. [Google Scholar] [CrossRef]
- Glorieux, C.; Van de Rostyne, K.; Nelson, K.; Gao, W.; Lauriks, W.; Thoen, J. On the character of acoustic waves at the interface between hard and soft solids and liquids. J. Acoust. Soc. Am. 2001, 110, 1299–1306. [Google Scholar] [CrossRef]
- Padilla, F.; de Billy, M.; Quentin, G. Theoretical and experimental studies of surface waves on solid–fluid interfaces when the value of the fluid sound velocity is located between the shear and the longitudinal ones in the solid. J. Acoust. Soc. Am. 1999, 106, 666–673. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Lim, S.-C.; Min, D.-J.; Kwon, B.-D.; Park, M. 2D time-domain acoustic-elastic coupled modeling: A cell-based finite-difference method. Geosci. J. 2009, 13, 407–414. [Google Scholar] [CrossRef]
- Bernth, H.; Chapman, C. A comparison of the dispersion relations for anisotropic elastodynamic finite-difference grids. Geophysics 2011, 76, WA43–WA50. [Google Scholar] [CrossRef]
- Cao, J.; Brossier, R.; Górszczyk, A.; Métivier, L.; Virieux, J. 3-D multiparameter full-waveform inversion for ocean-bottom seismic data using an efficient fluid–solid coupled spectral-element solver. Geophys. J. Int. 2022, 229, 671–703. [Google Scholar] [CrossRef]
- Di Bartolo, L.; Manhisse, R.R.; Dors, C. Efficient acoustic-elastic FD coupling method for anisotropic media. J. Appl. Geophys. 2020, 174, 103934. [Google Scholar] [CrossRef]
- Qu, Y.; Huang, J.; Li, Z.; Li, J. A hybrid grid method in an auxiliary coordinate system for irregular fluid-solid interface modeling. Geophys. J. Int. 2016, 208, 1540–1556. [Google Scholar] [CrossRef]
- Li, Q.; Wu, G.; Jia, Z.; Duan, P. Full-waveform inversion in acoustic-elastic coupled media with irregular seafloor based on the generalized finite-difference method. Geophysics 2023, 88, T83–T100. [Google Scholar] [CrossRef]
- Sethi, H.; Shragge, J.; Tsvankin, I. Tensorial elastodynamics for coupled acoustic/elastic anisotropic media: Incorporating bathymetry. Geophys. J. Int. 2022, 228, 999–1014. [Google Scholar] [CrossRef]
- Fornberg, B. The pseudospectral method; accurate representation of interfaces in elastic wave calculations. Geophysics 1988, 53, 625–637. [Google Scholar] [CrossRef]
- Komatitsch, D.; Barnes, C.; Tromp, J. Wave propagation near a fluid-solid interface: A spectral-element approach. Geophysics 2000, 65, 623–631. [Google Scholar] [CrossRef]
- Sun, M.; Jin, S.; Yu, P. Elastic least-squares reverse-time migration based on a modified acoustic-elastic coupled equation for OBS four-component data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9772–9782. [Google Scholar] [CrossRef]
- Yu, P.; Geng, J.; Li, X.; Wang, C. Acoustic-elastic coupled equation for ocean bottom seismic data elastic reverse time migration. Geophysics 2016, 81, S333–S345. [Google Scholar] [CrossRef]
- Yu, P.; Geng, J.; Wang, C. Separating quasi-P-wave in transversely isotropic media with a vertical symmetry axis by synthesized pressure applied to ocean-bottom seismic data elastic reverse time migration. Geophysics 2016, 81, C295–C307. [Google Scholar] [CrossRef]
- Yu, P.; Geng, J. Acoustic-elastic coupled equations in vertical transverse isotropic media for pseudoacoustic-wave reverse time migration of ocean-bottom 4C seismic data. Geophysics 2019, 84, S317–S327. [Google Scholar] [CrossRef]
- Han, L.; Huang, X.; Hao, Q.; Greenhalgh, S.; Liu, X. Incorporating the nearly constant Q models into 3-D poro-viscoelastic anisotropic wave modeling. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4501811. [Google Scholar] [CrossRef]
- He, X.; Yang, D.; Huang, J.; Huang, X. Modeling 3-D Elastic Wave Propagation in TI Media Using Discontinuous Galerkin Method on Tetrahedral Meshes. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5904514. [Google Scholar] [CrossRef]
- Mathewson, J.; Bachrach, R.; Ortin, M.; Decker, M.; Kainkaryam, S.; Cegna, A.; Paramo, P.; Vincent, K.; Kommedal, J. Offshore Trinidad tilted orthorhombic imaging of full-azimuth OBC data. In Proceedings of the SEG International Exposition and Annual Meeting, New Orleans, LA, USA, 18–23 October 2015; p. SEG–2015-5848590. [Google Scholar]
- Xie, Y.; Zhou, B.; Zhou, J.; Hu, J.; Xu, L.; Wu, X.; Lin, N.; Loh, F.C.; Liu, L.; Wang, Z. Orthorhombic full-waveform inversion for imaging the Luda field using wide-azimuth ocean-bottom-cable data. Lead. Edge 2017, 36, 75–80. [Google Scholar] [CrossRef]
- Raymer, D.; Kendall, J.; Pedlar, D.; Kendall, R.; Mueller, M.; Beaudoin, G. The significance of salt anisotropy in seismic imaging. In Proceedings of the SEG International Exposition and Annual Meeting, Online, 11–16 October 2000; p. SEG–2000-0562. [Google Scholar]
- Hao, Q.; Stovas, A. The offset-midpoint travel-time pyramid for P-wave in 2D transversely isotropic media with a tilted symmetry axis. Geophys. Prospect. 2015, 63, 587–596. [Google Scholar] [CrossRef]
- Zeighami, F.; Quqa, S.; De Ponti, J.M.; Ayyash, N.; Marzani, A.; Palermo, A. Elastic metasurfaces for Scholte–Stoneley wave control. Philos. Trans. A 2024, 382, 20230365. [Google Scholar] [CrossRef]
- DONG, L.G.; MA, Z.T.; CAO, J.Z. Stability of the staggered-grid high-order difference method for first-order elastic wave equation. Chin. J. Geophys. 2000, 43, 904–913. [Google Scholar]
- Igel, H.; Mora, P.; Riollet, B. Anisotropic wave propagation through finite-difference grids. Geophysics 1995, 60, 1203–1216. [Google Scholar] [CrossRef]
- Koene, E.F.; Robertsson, J.O.; Broggini, F.; Andersson, F. Eliminating time dispersion from seismic wave modeling. Geophys. J. Int. 2018, 213, 169–180. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, W.; Nashed, Z.; Li, X.; Liang, G.; Yang, C. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics 2014, 79, T277–T285. [Google Scholar] [CrossRef]
- Komatitsch, D.; Vilotte, J.-P. The spectral element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. Seismol. Soc. Am. 1998, 88, 368–392. [Google Scholar] [CrossRef]








| Method | Time (s) | Memory (G) |
|---|---|---|
| FD | 418.26 | 0.24 |
| SEM | 3769.98 | 1.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, D. Numerical Modeling of Scholte Wave in Acoustic-Elastic Coupled TTI Anisotropic Media. Appl. Sci. 2024, 14, 8302. https://doi.org/10.3390/app14188302
Chen Y, Wang D. Numerical Modeling of Scholte Wave in Acoustic-Elastic Coupled TTI Anisotropic Media. Applied Sciences. 2024; 14(18):8302. https://doi.org/10.3390/app14188302
Chicago/Turabian StyleChen, Yifei, and Deli Wang. 2024. "Numerical Modeling of Scholte Wave in Acoustic-Elastic Coupled TTI Anisotropic Media" Applied Sciences 14, no. 18: 8302. https://doi.org/10.3390/app14188302





