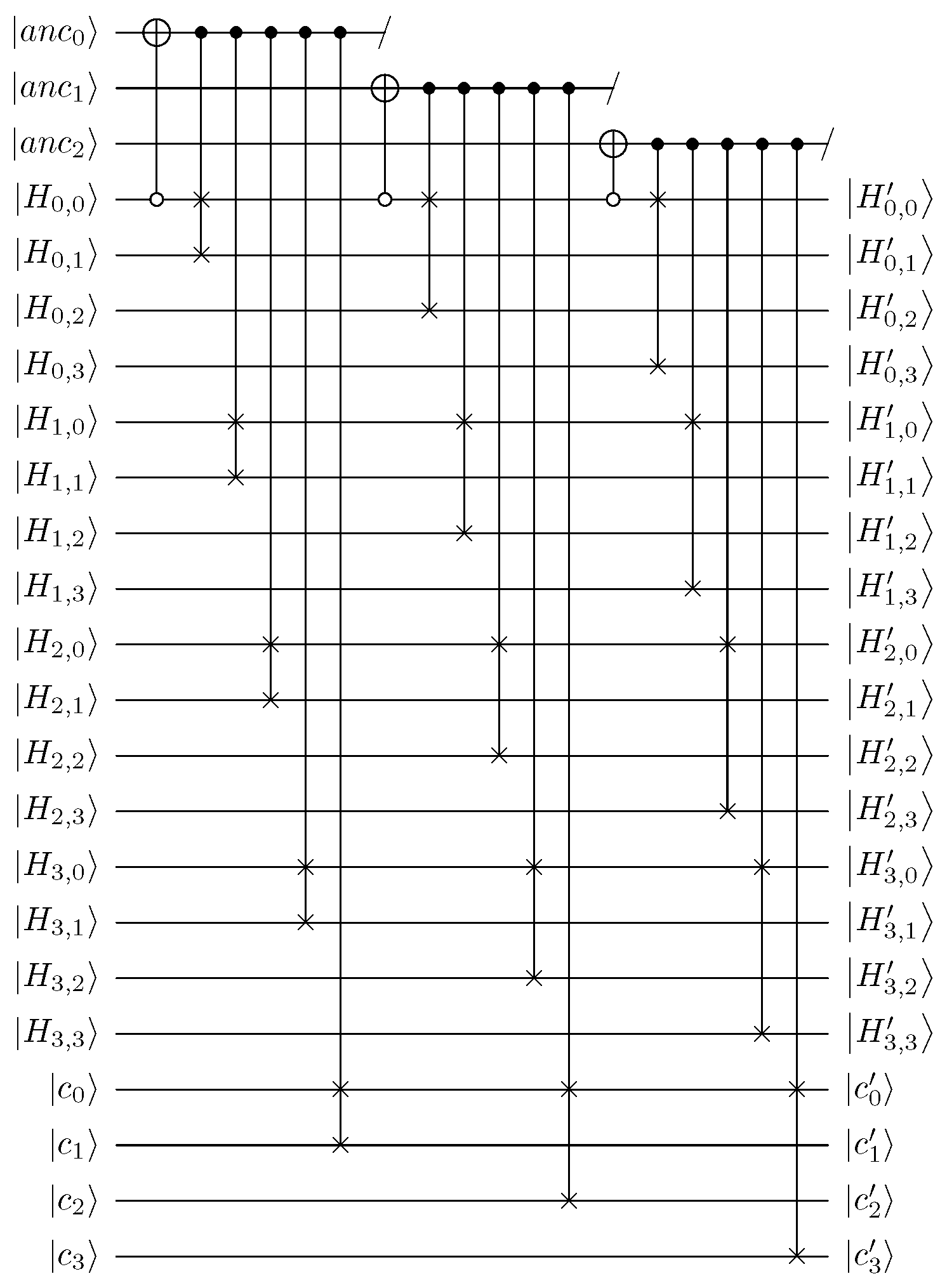Abstract
Quantum computers have the capacity to solve certain complex problems more efficiently than classical computers. To fully leverage these quantum advantages, adapting classical arithmetic for quantum systems in a circuit level is essential. In this paper, we introduce a depth-optimized quantum circuit of Gauss–Jordan elimination for matrices in binary. This quantum circuit is a crucial module for accelerating Information Set Decoding (ISD) using Grover’s algorithm. ISD is a cryptographic technique used in analyzing code-based cryptographic algorithms. When combined with Grover’s search, it achieves a square root reduction in complexity. The proposed method emphasizes the potential for parallelization in the quantum circuit implementation of Gauss–Jordan elimination. We allocate additional ancilla qubits to enable parallel operations within the target matrix and further reuse these ancilla qubits to minimize overhead from our additional allocation. The proposed quantum circuit for Gauss–Jordan elimination achieves the lowest Toffoli depth compared to the-state-of-art previous works.
1. Introduction
Shor [1] presented a quantum algorithm for attacking the ECC and RSA cryptosystems, which are based on the discrete logarithm and factoring problems. In Shor’s paper [1], he demonstrated the potential to solve these problems faster (exponentially) than traditional classical algorithms. As a result, there is a necessity for cryptographic algorithms that can withstand both quantum and classical computing attacks. To address this, the National Institute of Standards and Technology (NIST) hosted the Post-Quantum Cryptography (PQC) standardization (https://csrc.nist.gov/projects/post-quantum-cryptography (accessed on 19 September 2024)) in 2016.
Error-correcting codes, originally conceived as a method for identifying and correcting corrupted information in communication channels, were formalized by Shannon [2]. There is growing interest in using them at the core of asymmetric cryptosystems. NIST considered code-based cryptographic algorithms as a potential alternative, advancing all code-based cryptographic methods to the fourth round of its competition (https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4 (accessed on 19 September 2024)). NIST specifically announced that one or more of the three code-based candidates—Classic McEliece [3], BIKE [4], and HQC [5]—are likely to be standardized as an alternative to lattice-based cryptographic techniques.
As such, accurately assessing the computational complexity of potential quantum computer attacks on code-based cryptographic algorithms is essential for optimizing their parameters. The security of these algorithms fundamentally depends on the difficulty of solving the Syndrome Decoding Problem (SDP), which involves finding a solution to a system of linear equations with a predetermined number of non-zero components.
The most well-known classical algorithm for solving the SDP, Information Set Decoding (ISD), still runs in exponential time. One of the prominent studies theorizing the potential speedup of ISD attacks using quantum computers was [6], which demonstrated a significant reduction in computational requirements when Grover’s algorithm [7] is applied. However, the work did not provide specific quantum circuits for ISD. As far as we know, the first quantum circuit implementation for ISD was presented in [8]. Very recently, the authors of [8] extended and improved their work in [9].
Various modules are needed to construct a complete quantum circuit for ISD, including input preparation, Hamming-weight checking, and Gaussian elimination. Among these, Gaussian elimination is particularly crucial because it requires significant quantum resources but can be optimized through various designs and implementations. In this context, this work present a depth-optimized quantum circuit of Gauss–Jordan elimination in ISD.
Contributions
In summary, our work involves the following:
- Quantum Circuit of Gauss–Jordan Elimination in ISD. We present the implementation of quantum circuit of Gauss–Jordan elimination, which is one of the crucial modules in ISD.
- Depth-Optimized Quantum Circuit Implementation. Our focus is on minimizing both the Toffoli depth and the overall depth in our implementation of the quantum circuit for Gauss–Jordan elimination. To achieve this while keeping the number of qubits reasonable, we employ several methods, including duplicating pivot elements, designing parallel swap and elimination steps in Gauss–Jordan elimination, and using reverse operations to initialize qubits (i.e., set to s 0⟩), in order to reuse and reduce the qubit count.
- Concrete Estimates of Required Quantum Cost. Using the quantum programming tool ProjectQ [10] (https://github.com/ProjectQ-Framework/ProjectQ (accessed on 19 September 2024)), we verify our quantum circuit implementation and analyze the needed quantum resources in detail. By decomposing high-level quantum gates (specifically Toffoli gates in this work), we estimate the number of Clifford and T gates needed.
2. Preliminaries
2.1. Syndrome Decoding Problem (SDP)
Code-based cryptographic algorithms derive their security from the difficulty of the Syndrome Decoding Problem (SDP), which is known to be NP-hard.
In SDP, a secret vector is challenging to recover from the syndrome (ciphertext) , even when the parity-check matrix (which is public) is known. It is essential to recognize that the vector e has a specific low Hamming-weight t in SDP.
2.2. Information Set Decoding (ISD)
Information Set Decoding (ISD) is a well-known algorithm for tackling the Syndrome Decoding Problem. Essentially, ISD utilizes a brute-force strategy that systematically narrows the search space. The process is as follows: An information set S is chosen (randomly) from a matrix H. If S is invertible, the Hamming-weight is assessed by multiplying the inverse of S (i.e., by the syndrome c. If the Hamming-weight of the resulting vector equals t, the secret vector e can be recovered. If not, the process is repeated from the start. Prange first proposed the basic ISD algorithm [11], and subsequently, various variants of the ISD algorithm have been introduced [12,13,14].
In ISD, Gauss–Jordan elimination is employed to find the inverse of an information set S; thus, it can compute (if S is invertible). This process involves transforming the matrix into an identity matrix through a series of row operations. What we aim to compute using Gaussian elimination is , which can be achieved without explicitly calculating . By applying the row operations used in Gauss–Jordan elimination to c, we compute a vector that corresponds to . Thus, instead of constructing explicitly, we apply the same operations to c to compute the desired result.
2.3. Gauss–Jordan Elimination
Gauss–Jordan elimination is a technique in linear algebra used for solving linear equation systems, determining the rank of a matrix, and calculating the inverse of an invertible matrix. It involves transforming a given matrix into its reduced row echelon form using a sequence of row operations. Algorithm 1 describes the process of Gauss–Jordan elimination. Note that the operations performed between rows are also applied to the vector c.
The process begins with forward elimination, transforming the matrix into an upper triangular form by ensuring that all elements below the main diagonal are zero. This transformation is achieved through row operations, including swapping rows, multiplying a row by a non-zero scalar, and adding or subtracting multiples of one row to another. The key step is to identify pivot elements, which are the leading non-zero entries in each row, and use these to eliminate the entries below them.
| Algorithm 1: Gauss–Jordan Elimination |
| Input:
A matrix H of size , a vector c of size n Output: Transformed matrix H and updated vector c
|
2.4. Grover’s Algorithm
The Grover algorithm is a quantum search algorithm that reduces complexity compared to classical computers by a square root. Exhaustive search on quantum computers has a complexity of . On the other hand, quantum search using the Grover algorithm reduces the complexity to . The process of Grover’s search is summarized as follows:
At first, the database of search targets is prepared in a quantum superposition state using Hadamard (H) gates. Applying n Hadamard gates to n qubits yields the following superposition state:
The primary element, the Grover oracle, includes the quantum circuit used for querying. The Grover oracle answers the solution by inverting the sign of the solution state of the query as follows:
The amplitude of the solution provided by the Grover oracle is enhanced using the diffusion operator. The Grover algorithm repeatedly applies the oracle and the diffusion operator times to sufficiently increase the amplitude of the solution. Finally, it recovers the solution with a high amplitude (probability) by measuring the qubits.
2.5. Parallelization of Grover’s Algorithm
Exhaustive search using Grover’s algorithm is significantly ahead of the current capabilities in quantum computing. While Grover’s algorithm theoretically reduces complexity by the square root, executing the attack requires managing an extremely high circuit depth. In practical attack scenarios, Grover’s algorithm may be operated in parallel by dividing it into smaller instances to mitigate the lengthy sequential computations (as discussed on page 46 of [15]).
For this limitation, NIST has introduced a parameter called MAXDEPTH (≤), which sets a maximum on the required circuit depth for quantum algorithms. Thus, if Grover’s algorithm exceeds the MAXDEPTH limit, a parallel strategy for Grover’s algorithm should be considered. Parallelization of Grover’s algorithm can be designed into inner and outer methods (for details, see [16]).
However, the performance of Grover’s algorithm parallelization is poor. To reduce the depth D of Grover’s algorithm by a factor of S (to satisfy the MAXDEPTH, where ), instances must be operated in parallel [16,17,18]. Typically, the product of the depth D and the qubit count M is adopted as a primary metric for determining the efficiency of a quantum circuit. For Grover’s parallelization, this metric D−M is redefined as due to the poor parallelization performance (). Consequently, reducing the depth becomes more effective in minimizing the depth2-qubit count product −M when the parallelization of Grover’s algorithm is considered.
2.6. Quantum Gates
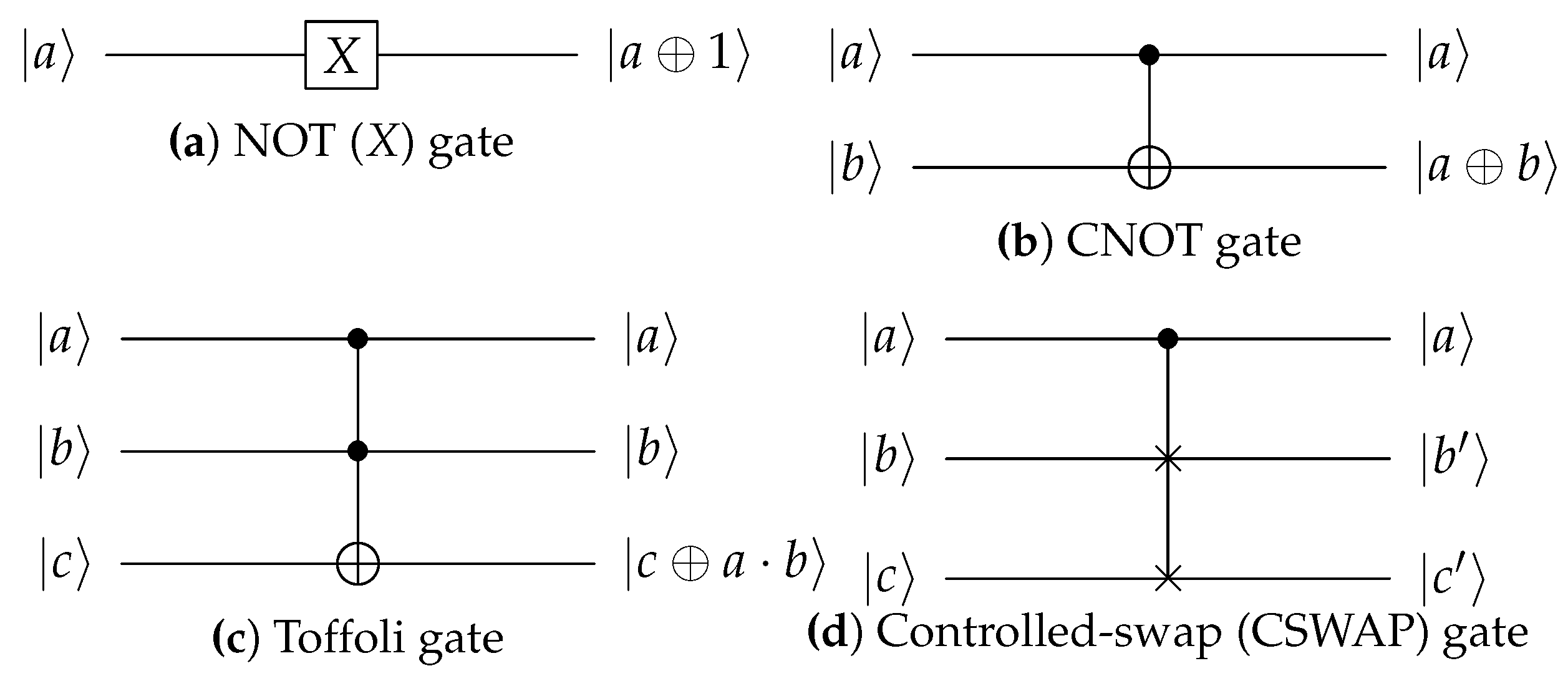
In quantum computing, quantum gates in Figure A1 are frequently employed to perform arithmetic operations in quantum circuits. These include the NOT (X), CNOT, Toffoli, and controlled-swap (CSWAP) gates. The X gate changes the state of a qubit, serving as a quantum equivalent of the NOT operation (i.e., X (a) = ). The CNOT gate operates on a pair of qubits, where the sate of target qubit is altered based on the state of control qubit. If the control qubit is set to 1, the state of target qubit is inverted; if the control qubit is 0, there are no changes in the target qubit (i.e., CNOT () = ()). This gate effectively performs an XOR operation between the control and target qubits. The Toffoli gate operates with three qubits: two serving as control qubits and one as the target qubit. The target qubit’s state is flipped only if both control qubits are 1 (i.e., Toffoli () = ()). This gate XOR is the result of the AND operation of the control qubit to the target qubit. Thus, Toffoli gates can be used for AND operations in quantum circuits. The controlled-swap (CSWAP) gate exchanges the states of two qubits depending on a control qubit, acting as the quantum equivalent of a conditional swap operation (i.e., CSWAP if and if ).
These quantum gates allow cryptographic algorithms to be implemented in quantum computing by replacing classical NOT, XOR, AND, and swap (including branch) operations. To optimize quantum circuits, minimizing the number of Toffoli gates is essential. The Toffoli gate has a high cost to implement because it requires a combination of a T gate (which affects the depth of T) and a Clifford gate. Several decomposition methods for the Toffoli gate are available, and the total depth represents the depth after the Toffoli gate is decomposed. In this work, following one of the methods presented in [19], we use a decomposition method involving seven T gates and eight Clifford gates with a T depth of four and a total depth of eight for a single Toffoli gate.
3. Parallel Implementation for Quantum Circuit of Gauss–Jordan Elimination
This section presents the quantum circuit implementation of Gauss–Jordan elimination. In our implementation, we focus on the fact that there are many opportunities for parallelization in Gauss–Jordan elimination. It is important to note that our method is specialized for ISD and not intended for generic use. Recall that the matrix of the information set is the input for Gauss–Jordan elimination in ISD, and the operations performed to transform the matrix into the identity matrix are applied to the syndrome vector. Simply put, our goal is to obtain the final syndrome vector depending on the input matrix of the input matrix. Thanks to this specialization, several operations can be omitted in our Gauss–Jordan elimination for ISD compared to the generic approach.
Further, our quantum circuit is designed to minimize the depth by exploring possible parallelization points in Gauss–Jordan elimination for ISD. To achieve parallelization, we allocate a sufficient number of ancilla qubits. However, as discussed earlier (in Section 2.5), reducing the depth rather than the number of qubits is recommended for optimizing Grover’s algorithm due to its poor parallelization performance.
3.1. Obstacles to the Parallelization of Gauss–Jordan Elimination
In this section, we analyze the obstacles to the parallelization of the Gauss–Jordan elimination quantum circuit. In the swap stage in Gauss–Jordan elimination, swap operations between rows are performed depending on the pivot (in quantum implementation, these conditional operations must be designed to be reversible). If the pivot is
and the element in the target row is , an actual swap operation between the rows (one containing the pivot and the other being the target row) is executed. In Gauss–Jordan elimination, the pivot is checked repeatedly many times. However, this implies a sequential flow that increases the circuit depth by iteratively checking pivots and elements. Figure 1 shows the case of sequential flow in the swap operation. For a comprehensive understanding, throughout Section 3, we represent a matrix H (size ) and a syndrome c (size 4) as follows, and our method is described based on the following arrangement:
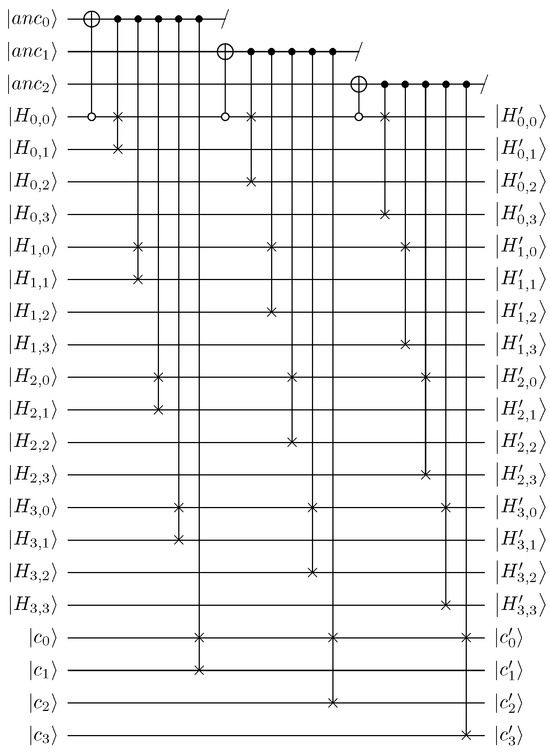
Figure 1.
Sequential quantum circuit implementation of the swap stage (where is the pivot).
Depending on the pivot , swap gates between the rows are performed (the pivot is copied to the ancilla qubit ). However, subsequent swap gates for the remaining elements of the rows (i.e., CSWAP (, , ), CSWAP (, , ), and CSWAP (, , )) must wait until the current pivot operation (CSWAP (, , )) is completed. This sequential flow also occurs in the elimination stage (not only in the swap stage).
3.2. Parallel Implementation of Swap: Copying Pivot
To achieve the parallelism, we copy the pivot, which acts as a control qubit, to avoid the sequential flow where subsequent operations wait for the pivot. Figure 2 shows our parallel quantum circuit implementation of the swap stage in Gauss–Jordan elimination. We recommend that readers cross-check our implementation details with Figure 2, Figure 3 and Figure 4, as well as the matrix representation and arrangement in Equation (4).
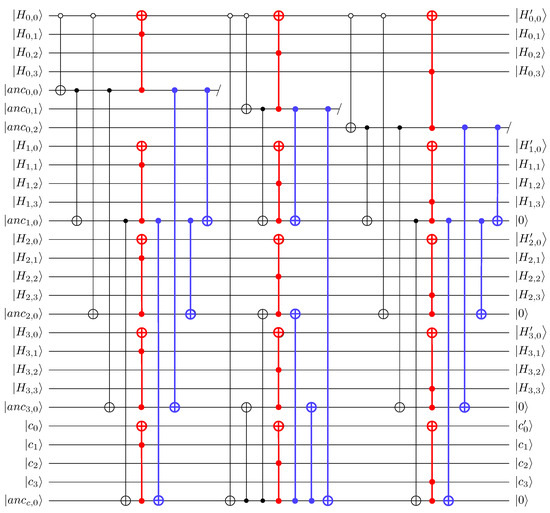
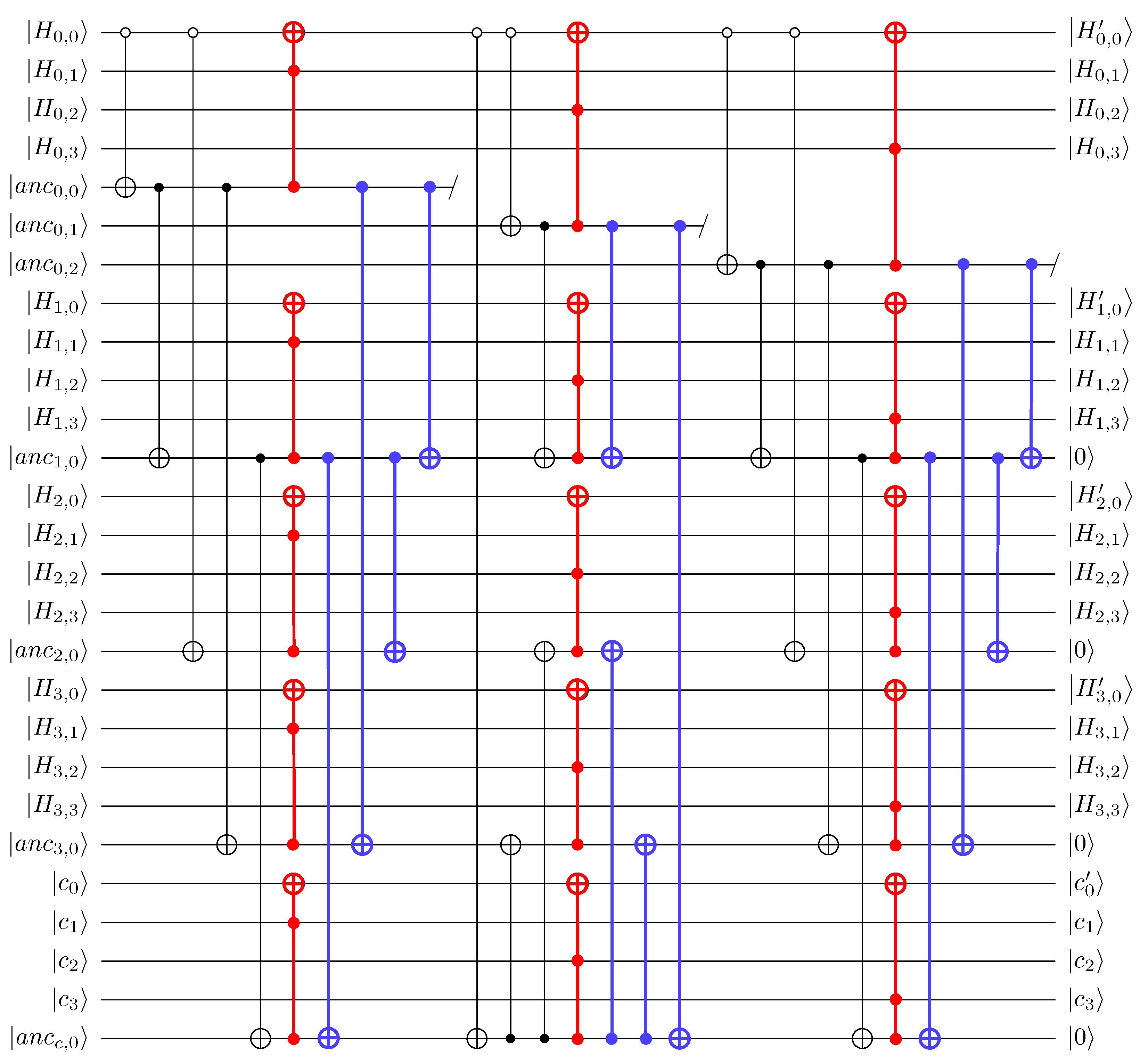
Figure 2.
Quantum circuit implementation of the swap stage (where is the pivot).
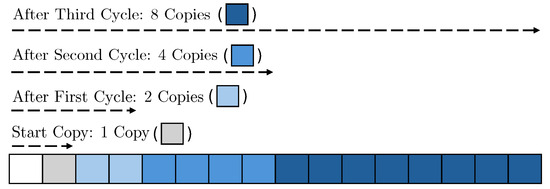
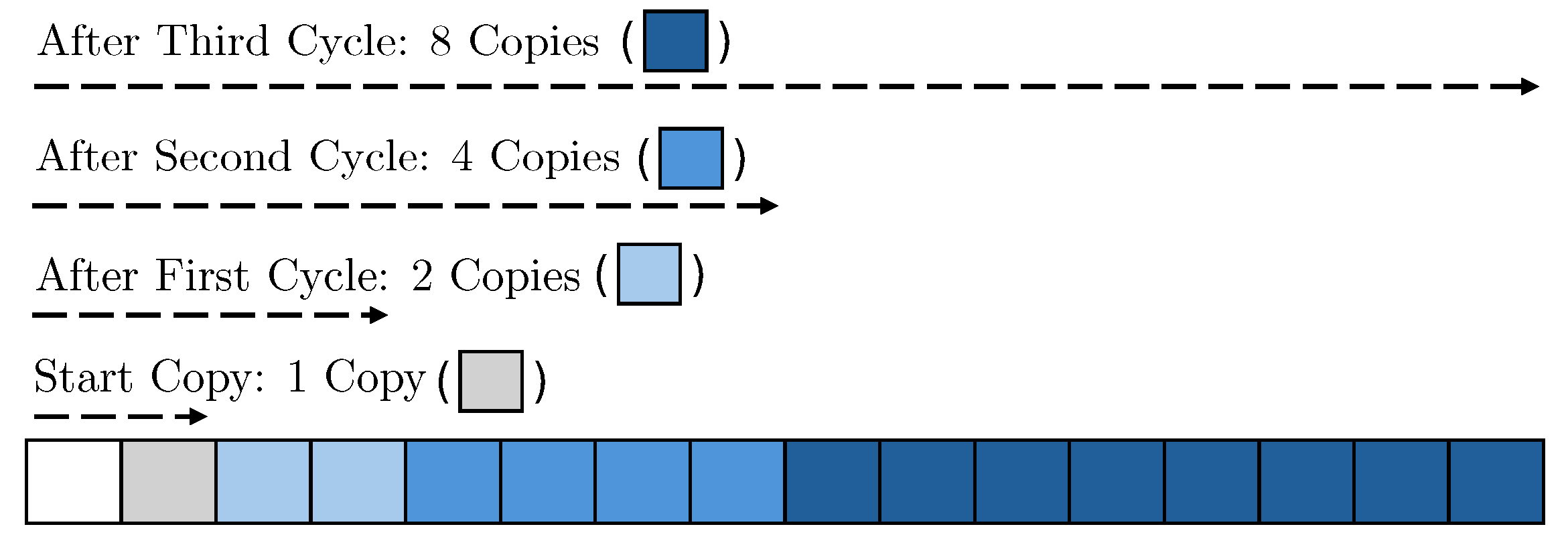
Figure 3.
Exponential copy.
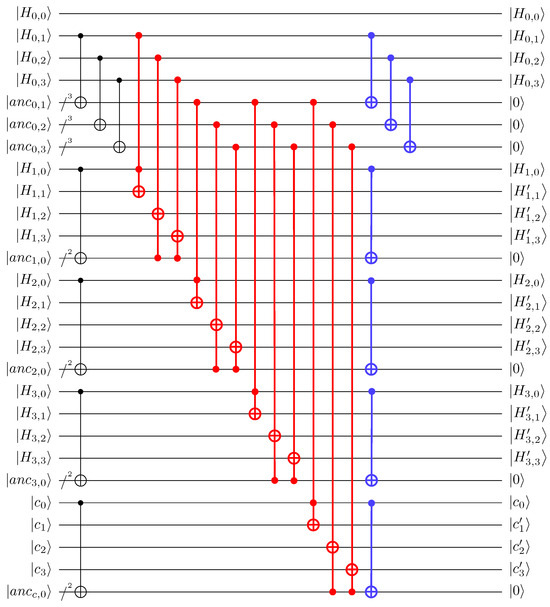
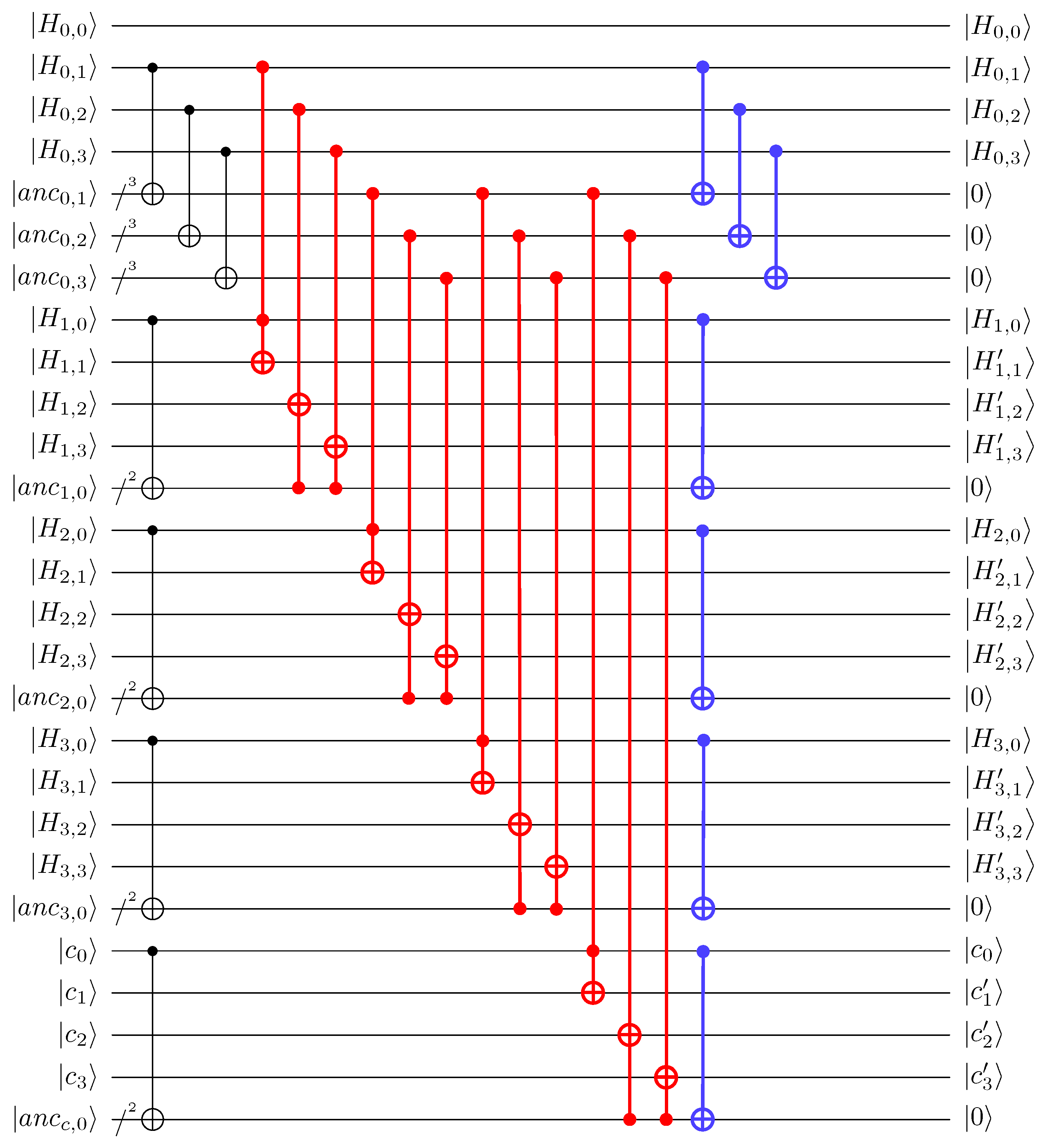
Figure 4.
Quantum circuit implementation of the elimination stage (where is the pivot); red and blue lines have no dependency.
Firstly, we copy the pivot to perform controlled-swap operations (between the row containing the pivot and the target row) simultaneously. Specifically, for the pivot (where i denotes the step of Gaussian elimination, ), we copy the pivot times. As illustrated in Figure 2, using the copied pivots (i.e., ), controlled-swap gates (in red) between the first and second rows (where is the pivot) are performed in parallel.
3.2.1. Replacing Controlled-Swap Gates with Toffoli Gates
We use Toffoli gates instead of controlled-swap gates. As far as we know, this optimization method was first presented in [9]. We briefly review this method. Let the (pivot of ) be . If controlled-swap gates are used, the swap between the first row and the second row is performed as follows (where is ):
In contrast, if Toffoli gates are used, the first row changes to
through the following linear operation (where is ):
Both methods successfully change the pivot () to
(assuming H is invertible). However, as described in [9] (see Section 3.2), replacing controlled-swap gates with Toffoli gates is more efficient in terms of quantum resources (controlled swap gate can implemented using one Toffoli gate and two CNOT gates). Further, using Toffoli gates between rows has the advantage of parallelization compared to using controlled-swap gates. The controlled-swap gates in Figure 1 cannot be performed in parallel (i.e., subsequent operations must wait for previous operations to complete). However, if the controlled-swap gates in Figure 1 are replaced with Toffoli gates, many of these Toffoli gates can be executed simultaneously.
3.2.2. Exponential Copy
For copying the pivot, we use the previous copies for the next stage, as shown in Figure 3. As implied by the name of the method, each cycle exponentially increases the number of copies. The method of exponential copying is efficient not only in classical implementation but also in quantum implementation; so, we adopt it. As a result, the depth of CNOT gates required for copying is reduced.
3.2.3. Reuse Technique
In the copy task, additional ancilla qubits were allocated to store the copies of the pivot, which increases the total number of qubits. To address this overhead, we initialize and reuse the ancilla qubits after the execution of Toffoli gates. By performing the reverse operation (reversing the previous operation is often adopted in quantum implementations to reduce qubit count) of exponential copy (shown in blue in Figure 2), the ancilla qubits are initialized to a clean state (i.e., ), except for the first copies (, shown in gray in Figure 3). In subsequent copy tasks, we can efficiently reuse these initialized ancilla qubits.
3.3. Parallel Implementation of Elimination
The methods presented earlier (Copying Pivot, Section 3.2; Exponential Copy, Section 3.2.2; Reuse Technique, Section 3.2.3) are also applied to the parallel implementation of the elimination stage. Compared to the parallel implementation of the swap stage, more ancilla qubits for copying are allocated in the parallel implementation of the elimination stage. Figure 4 shows the parallel implementation of the elimination stage in Gauss–Jordan elimination.
Recall that in the swap stage, to perform Toffoli gates between the and rows, the previous Toffoli gates between the and rows must be completed. In contrast, in the elimination stage, there is no dependency between all of the rows since the targets of the change are the elements, not the pivot. Thus, in the elimination stage, we do not need to change the pivot as in the swap stage.
If we sufficiently copy elements used for the Toffoli gates, high parallelism can be achieved. In the elimination stage, elimination operations (i.e., changing
to ) are performed between rows based on the elements (, , for , except for the pivot) in the column containing the pivot. As we performed in the swap stage, we copy each element with reduced repetitions. In Figure 4, each of , and contains three qubits but is illustrated as a single line for simplicity. In the same context, each of and contains two qubits . Unlike in the swap stage, we can omit the actual operations on the i-th column (i.e., ) in Gaussian elimination, reducing the number of copies by 1. In [9] (Section 3.2), the authors proposed this optimization method, called Avoid Clearing Pivot Column. Additionally, we can utilize the elements of the i-th column as control qubits, further reducing the number of copies by 1.
As mentioned before, we can achieve more parallelism in the elimination stage compared to the swap stage. Recall that in the swap stage, swap operations are only possible between two rows, but in the elimination stage, elimination operations can be performed on all of the rows. To achieve high parallelism, we also copy the elements of the row containing the pivot (i.e., , , , ()). Conceptually, the matrix is copied at once (although, strictly speaking, not all elements in the matrix) in the elimination stage, whereas in the swap stage, only the pivot is copied. Finally, using the copied elements, all of the Toffoli gates in the elimination stage (shown in red in Figure 4) is executed simultaneously (i.e., Toffoli depth one). After the Toffoli gate operations, the reuse technique (described in Section 3.2.3) is used to initialize ancilla qubits (shown in blue in Figure 4) and to reuse them in the subsequent elimination stages (i.e., the i-th stage where ). In contrast to the swap stage, all of the ancilla qubits are initialized to
. Finally, Algorithm 2 summarizes our parallel implementation of the Gauss–Jordan elimination quantum circuit.
| Algorithm 2: Quantum Implementation of Gauss–Jordan Elimination |
| Input:
A matrix H of size , a vector c of size n (the n-th column of H) Output: Updated vector c
|
4. Performance and Evaluation
This section evaluates the performance of our parallel implementation of the quantum circuit for Gauss–Jordan elimination. We used the quantum programming tool ProjectQ to verify and evaluate the required quantum resources for our implementation. Table 1 shows the estimated quantum resources based on the matrix size n. As mentioned in Section 2.6, for the decomposition of Toffoli gates, we use one of the methods presented in [19], which involves seven T gates and eight Clifford gates with a T depth of four and a total depth of eight for each Toffoli gate.

Table 1.
Quantum resources required for quantum Gauss–Jordan elimination; # indicates the number of circuits.
In Table 1, we could not report specific quantum resources of the quantum circuit presented in [9] because they did not provide details on decomposed resources (such as Clifford and T gates, or full depth). However, it is intuitively clear that our method uses significantly more qubits compared to [9], but provides a much lower Toffoli depth. We report conservative estimates of Toffoli depth. It appears that unexpected, non-trivial parallelization of Toffoli gates occurs in the quantum circuit. Thus, the actual Toffoli depth is likely lower than the reported result in Table 1.
Our quantum circuit for Gauss–Jordan elimination is designed for quantum Information Set Decoding using Grover’s algorithm. Since the parallelization performance of Grover’s algorithm is poor (see Section 2.5), minimizing depth is more effective than reducing qubit count. In this context, our depth-optimized quantum circuit for Gauss–Jordan elimination proves to be effective for quantum Information Set Decoding.
5. Conclusions
This paper introduced a parallel implementation of the quantum circuit for Gauss–Jordan elimination, a crucial component in quantum Information Set Decoding (ISD). To improve the efficiency of Grover’s search through enhanced parallelization, our implementation reduces circuit depth, but keeps the number of qubits manageable. We achieved this by employing several optimization techniques, including pivot and element copying, exponential copying, and the reuse of ancilla qubits. Nevertheless, we believe that there is still room for optimizing the required quantum resources (such as gate count, qubit count, and depth) for Gauss–Jordan elimination using additional techniques based on our architecture.
We also estimated the quantum resources required for Gauss–Jordan elimination based on matrix sizes using our method. Although making strict comparisons with previous works is challenging, our results suggest that our implementation achieves the lowest Toffoli depth to date.
Given the potential threats posed by quantum computers, analyzing the post-quantum security of cryptographic systems is essential for ensuring security. In this context, our future work will focus on evaluating the post-quantum security of code-based ciphers by developing a complete quantum circuit for ISD. Optimizing other components of quantum ISD to reduce their depth will be important for developing a more effective quantum circuit for ISD.
Additionally, the quantum circuits presented in this work are still significantly large for successful operation on real hardware in the Noisy Intermediate-Scale Quantum (NISQ) era. In this limitation, exploring solutions such as quantum circuit recompilation and error correction [20,21,22,23] would be valuable for future work.
Author Contributions
Software, K.J.; Investigation, Y.O.; Writing—original draft, K.J.; Writing—review & editing, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute for Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (<Q|Crypton>, No.2019-0-00033, Study on Quantum Security Evaluation of Cryptography based on Computational Quantum Complexity, 100%).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
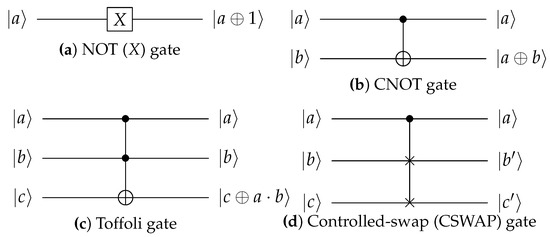
Figure A1.
Common Quantum gates.
Figure A1.
Common Quantum gates.
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the Proceedings 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; IEEE: New York, NY, USA, 1994; pp. 124–134. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM Sigmob. Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Chou, T.; Lange, T.; von Maurich, I.; Misoczki, R.; Niederhagen, R.; Persichetti, E.; Peters, C.; Schwabe, P.; Sendrier, N.; et al. Classic McEliece: Conservative Code-Based Cryptography. 2017. Available online: https://classic.mceliece.org/nist/mceliece-20190331.pdf (accessed on 24 December 2021).
- Aragon, N.; Barreto, P.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Gaborit, P.; Ghosh, S.; Gueron, S.; Güneysu, T.; et al. BIKE: Bit Flipping Key Encapsulation. 2022. Available online: https://hal.science/hal-01671903/document (accessed on 19 September 2024).
- Melchor, C.A.; Aragon, N.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Gaborit, P.; Persichetti, E.; Zémor, G.; Bourges, I. Hamming quasi-cyclic (HQC). NIST PQC Round 2018, 2, 13. [Google Scholar]
- Bernstein, D.J. Grover vs. mceliece. In Proceedings of the Post-Quantum Cryptography: Third International Workshop, PQCrypto 2010, Darmstadt, Germany, 25–28 May 2010; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2010; pp. 73–80. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Perriello, S.; Barenghi, A.; Pelosi, G. A complete quantum circuit to solve the information set decoding problem. In Proceedings of the 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 17–22 October 2021; IEEE: New York, NY, USA, 2021; pp. 366–377. [Google Scholar]
- Perriello, S.; Barenghi, A.; Pelosi, G. Improving the efficiency of quantum circuits for information set decoding. ACM Trans. Quantum Comput. 2023, 4, 1–40. [Google Scholar] [CrossRef]
- Steiger, D.S.; Häner, T.; Troyer, M. ProjectQ: An open source software framework for quantum computing. Quantum 2018, 2, 49. [Google Scholar] [CrossRef]
- Prange, E. The use of information sets in decoding cyclic codes. IRE Trans. Inf. Theory 1962, 8, 5–9. [Google Scholar] [CrossRef]
- Becker, A.; Joux, A.; May, A.; Meurer, A. Decoding random binary linear codes in 2n/20: How 1 + 1 = 0 improves information set decoding. In Proceedings of the Advances in Cryptology–EUROCRYPT 2012: 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Proceedings 31. Springer: Berlin/Heidelberg, Germany, 2012; pp. 520–536. [Google Scholar]
- Stern, J. A new identification scheme based on syndrome decoding. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 22–26 August 1993; Springer: Berlin/Heidelberg, Germany, 1993; pp. 13–21. [Google Scholar]
- Peters, C. Information-set decoding for linear codes over F q. In Proceedings of the Post-Quantum Cryptography: Third International Workshop, PQCrypto 2010, Darmstadt, Germany, 25–28 May 2010; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2010; pp. 81–94. [Google Scholar]
- NIST. Stateless Hash-Based Digital Signature Standar. 2023. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.205.ipd.pdf (accessed on 19 September 2024).
- Kim, P.; Han, D.; Jeong, K.C. Time–space complexity of quantum search algorithms in symmetric cryptanalysis: Applying to AES and SHA-2. Quantum Inf. Process. 2018, 17, 339. [Google Scholar] [CrossRef]
- Jaques, S.; Naehrig, M.; Roetteler, M.; Virdia, F. Implementing Grover Oracles for Quantum Key Search on AES and LowMC. In Proceedings of the Advances in Cryptology-EUROCRYPT 2020-39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Proceedings, Part II. Canteaut, A., Ishai, Y., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2020; Volume 12106, pp. 280–310. [Google Scholar] [CrossRef]
- Sarah, D.; Peter, C. On the Practical Cost of Grover for AES Key Recovery 2024. Available online: https://csrc.nist.gov/csrc/media/Events/2024/fifth-pqc-standardization-conference/documents/papers/on-practical-cost-of-grover.pdf (accessed on 19 September 2024).
- Amy, M.; Maslov, D.; Mosca, M.; Roetteler, M.; Roetteler, M. A Meet-in-the-Middle Algorithm for Fast Synthesis of Depth-Optimal Quantum Circuits. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 818–830. [Google Scholar] [CrossRef]
- Sun, S.N.; Motta, M.; Tazhigulov, R.N.; Tan, A.T.; Chan, G.K.L.; Minnich, A.J. Quantum computation of finite-temperature static and dynamical properties of spin systems using quantum imaginary time evolution. PRX Quantum 2021, 2, 010317. [Google Scholar] [CrossRef]
- Yuan, X.; Endo, S.; Zhao, Q.; Li, Y.; Benjamin, S.C. Theory of variational quantum simulation. Quantum 2019, 3, 191. [Google Scholar] [CrossRef]
- Chen, T.; Shen, R.; Lee, C.H.; Yang, B. High-fidelity realization of the AKLT state on a NISQ-era quantum processor. Scipost Phys. 2023, 15, 170. [Google Scholar] [CrossRef]
- Jones, T.; Benjamin, S.C. Robust quantum compilation and circuit optimisation via energy minimisation. Quantum 2022, 6, 628. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).