Multi-Layer Objective Model and Progressive Optimization Mechanism for Multi-Satellite Imaging Mission Planning in Large-Scale Target Scenarios
Abstract
1. Introduction
- Addressing the MSIMPLTS problem requires considering multiple optimization objectives, such as the target task benefit, task allocation rate, and response time. Most of the current studies use single-objective optimization models to achieve the optimal solution by setting the weights of different objectives. However, conflict or mutual constraints between the optimization objectives make it difficult to obtain high-quality task-planning solutions. In this context, designing optimization models that can take into account the interactions and constraints between the objectives is a new challenge in solving the MSIMPLTS problem.
- Existing research on the MSIMPLTS problem mainly focuses on the study of the sequence of satellite-target mission assignments, ignoring the feature that the same satellite resource can observe multiple targets at the same time. This leads to difficulties such as overlapping observation time windows, conflicting planning programs, and low utilization of satellite resources. Therefore, constructing a more reasonable mission planning method is a major objective for MSIMPLTS work.
- Large-scale target task requirements lead to a significant increase in the problem decision dimension and a larger solution space. The current MSIMPLTS-solving algorithms mostly focus on improving the ratio of feasible solutions, which leads to problems such as the mission planning scheme easily falling into local optimums or converging prematurely. Going forward, designing reasonable solution algorithms that effectively balance the solution efficiency and solution quality is also another challenge for MSIMPLTS studies.
- In terms of constructing a task planning model, we propose the MSIMPLTS based on Multi-layer Objective Optimization (MSIMPLTS-MLOO). The model is structured by setting up three layers: the superstructure, mesostructure, and understructure, with each layer focusing on a different optimization objective. These, respectively, optimize the task benefit, task completion, and response time functions. At each level, a resource selection diversity approach is used, which helps to better balance the interactions and constraints between the optimization objectives.
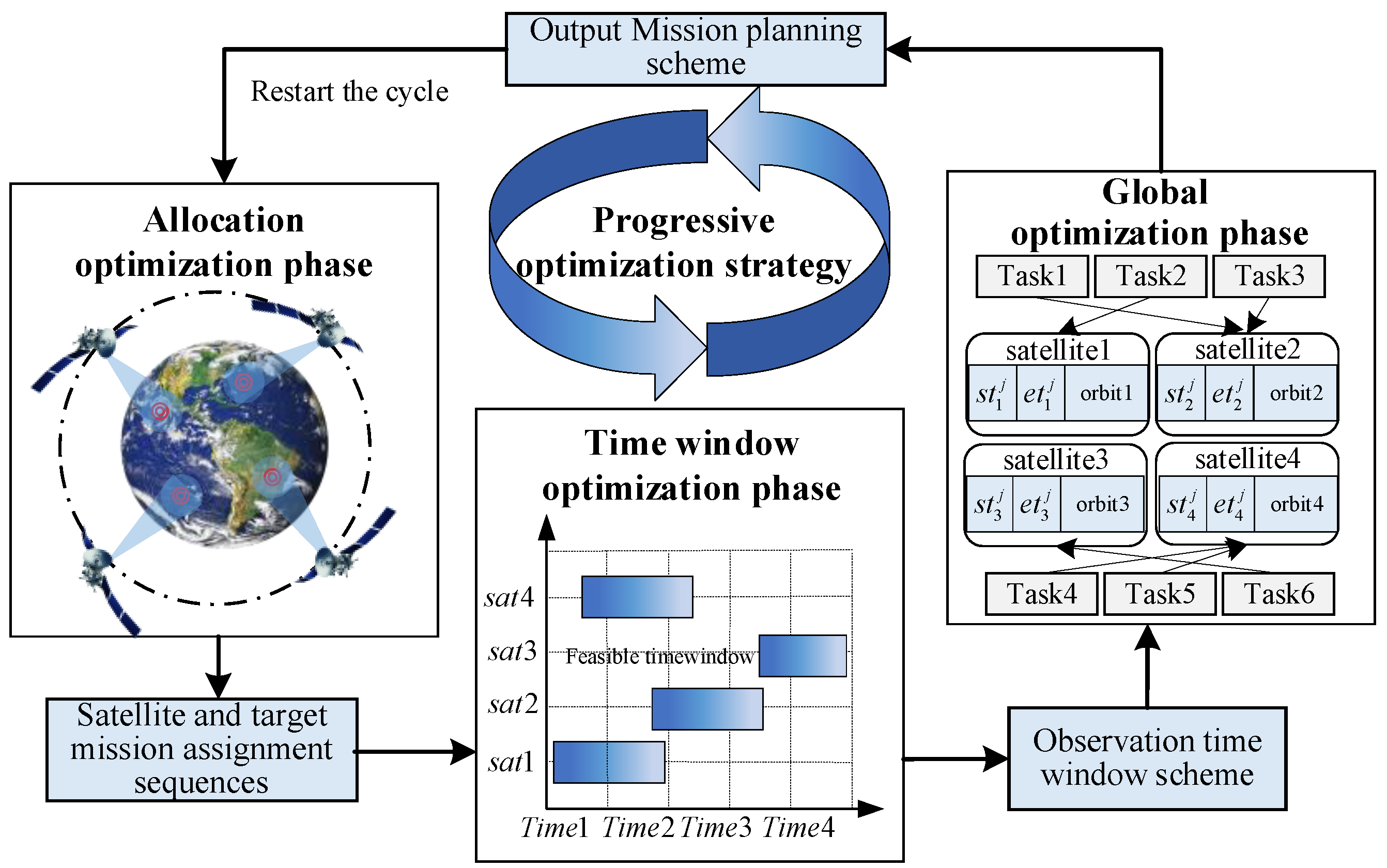
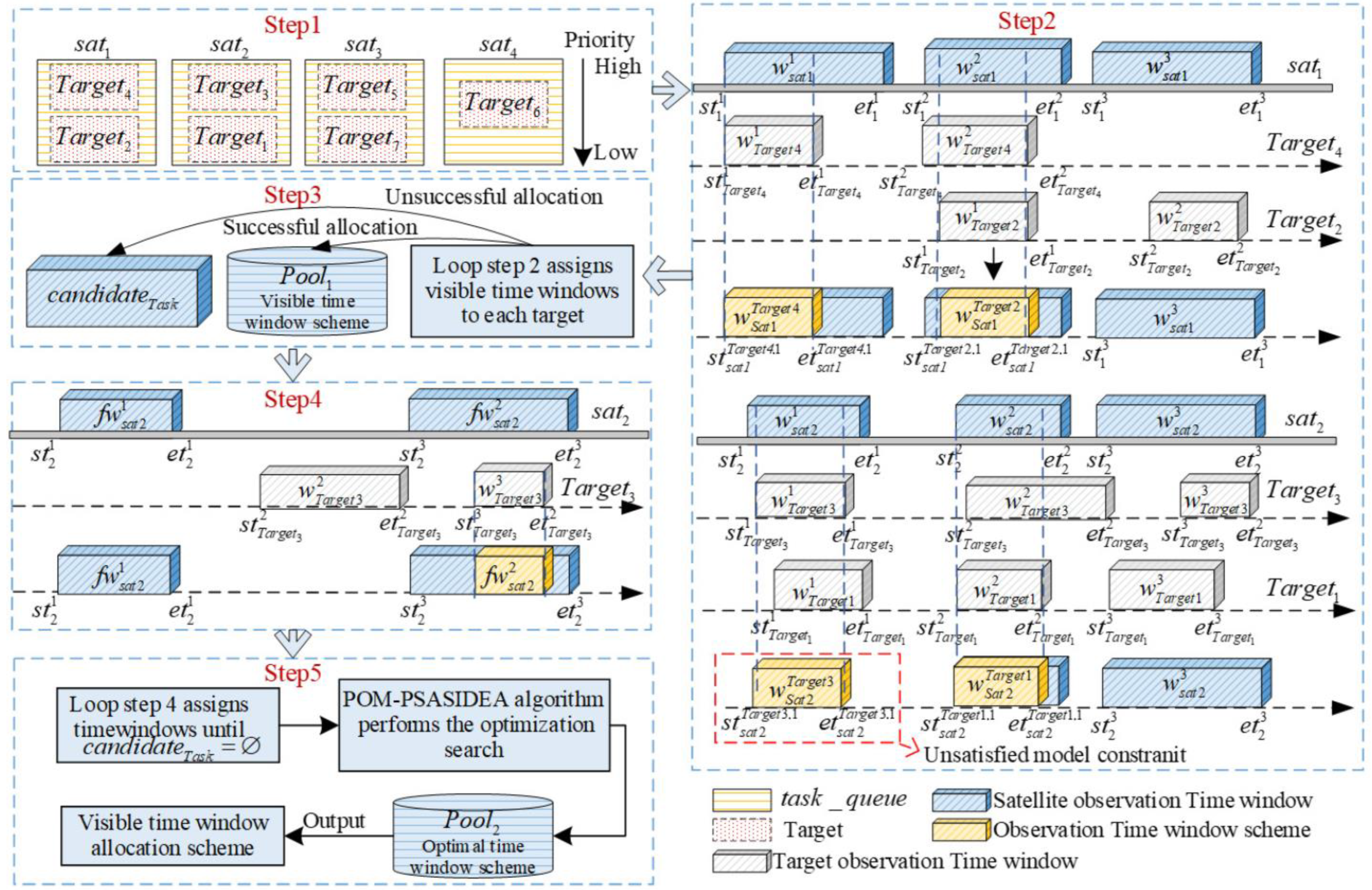
- In terms of the mission planning methodology, we propose a progressive optimization mechanism. Firstly, an initial task planning scheme is generated in the allocation optimization phase, which contains the allocation sequences of satellites and target tasks. Secondly, in the time window optimization phase, an execution time window is assigned to each target task based on the planning scheme in the allocation optimization phase. Finally, the planning results of the previous two phases are combined in the global optimization phase to generate the final mission planning scheme. Through stage-by-stage incremental decision-making, conflicts between planning schemes can be reduced, and the utilization rate of satellite resources can be effectively improved.
- In terms of constructing the mission planning algorithm, a population size adaptive strategy for an improved differential evolution algorithm is proposed to address the problem that multiple satellites are prone to falling into the local optimal solution under the large-scale target mission scenario, as well as for solving the difficulty of different constraints faced by the three-layer structure of the MSIMPLTS-MLOO model. The algorithm dynamically adjusts the population size according to the evolution of the population to adapt to the needs for model solving and thus improve the solving efficiency and quality of the mission planning scheme.
2. Related Works
2.1. MSIMP Basic Mission Scenarios
2.2. Motivation
3. Model Construction
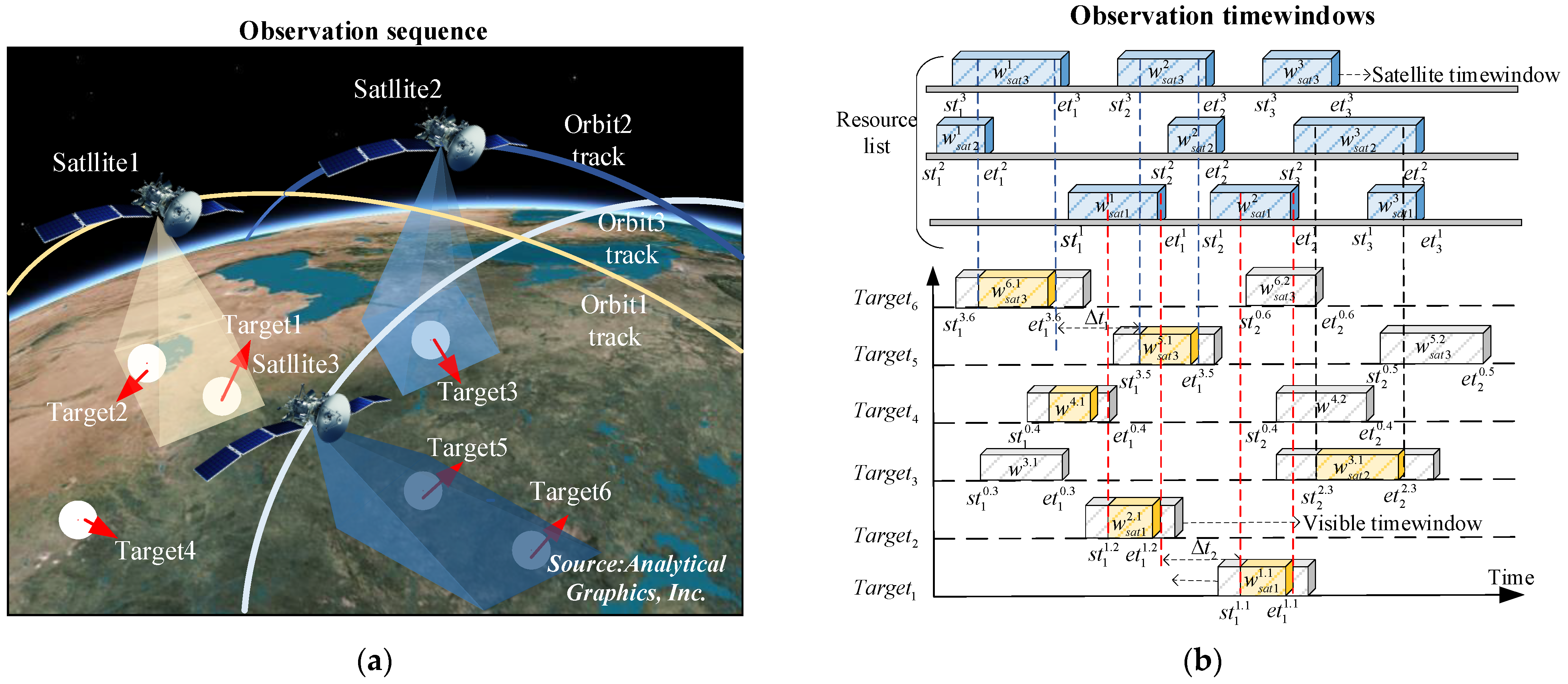
3.1. Problem Description
- Satellite resource in which denotes the number of satellites, denotes satellite , denotes the maximum side-swing angle of the load carried by satellite , denotes the observation field-of-view angle of satellite , denotes the longest start-up time of satellite , denotes the shortest start-up time of satellite , the satellite resource set executable orbits are , denotes the orbital parameters where satellite is located, denotes the number of executable orbits, and denotes the observation resolution of the payload carried by satellite .
- Target task , where denotes the number of target tasks, denotes the -th target task, and denote the latitude and longitude of the target task, denotes the task priority of the target task , denotes the duration of the target task , and denotes the resolution requirement of the target task .
- The set of visible time windows of the target mission ,, where denotes the visible time window of the target , and and denote the start and end times of the visible time window of the target mission, respectively.
- The set of visible time windows of the satellite , , where and denote the start and end times of the visible time window of satellite , respectively.
- The observation time window of the satellite for the target mission , , where and denote the start and end times of the observation time window of satellite for the target , respectively.
3.2. Establish Model Objective Functions and Constraints
3.2.1. Superstructure of the MSIMPLTS-MLOO Model
- Satellite power-on time constraints: Satellite power-on time is limited by task requirements and the satellite’s status. The satellite activation time constraint is set to ensure that observation tasks are carried out during the satellite start-up hours’ active time.where and denote the shortest and longest power-on times of satellite , respectively. and denote the end and start observation times of the satellite for the target task , respectively.
- Maximum number of satellite observation constraints: In the task mission model, satellite capacity is defined by the maximum number of observation tasks each satellite can perform within a unit of time. This ensures that each satellite operates within its capacity when executing observation tasks. If the assigned tasks exceed the satellite’s observation capacity, a penalty function is applied.where denotes the number of current observation missions, denotes the maximum number of observations within the capacity of the satellite, denotes the penalty function, and denotes the weighting coefficients.
- Target mission uniqueness constraints: Target mission uniqueness means that each target task can only be completed by one satellite, preventing the same task from being redundantly executed by multiple satellites, which could lead to resource waste and task conflicts.
3.2.2. Mesostructure of the MSIMPLTS-MLOO Model
- Side-swing angle conversion time constraint: The side-swing angle conversion time refers to the time required for a satellite to adjust its observation angle while in orbit to perform different tasks. This constraint ensures that there is sufficient time between consecutive tasks.where denotes the satellite side-swing angle conversion time.
- Task urgency constraints: Task urgency indicates the level of urgency for a target task within the designated task planning period. This constraint requires the model to prioritize urgent tasks, ensuring that high-priority tasks are not delayed due to the execution of other tasks.where denotes the prescribed time for the target task , and denotes the number of visible time windows for the target task .
- Task visible time window constraint: Task visible time window refers to the time interval during which a target task is visible to satellite resources. This constraint ensures that task assignments adhere to visibility conditions, guaranteeing that the tasks are executed correctly during the satellite’s visibility period.where and denote the start and end of the visible time window of the target mission , respectively, and and denote the start and end of the observation time window of the satellite for the target mission, respectively.
3.2.3. Understructure of the MSIMPLTS-MLOO Model
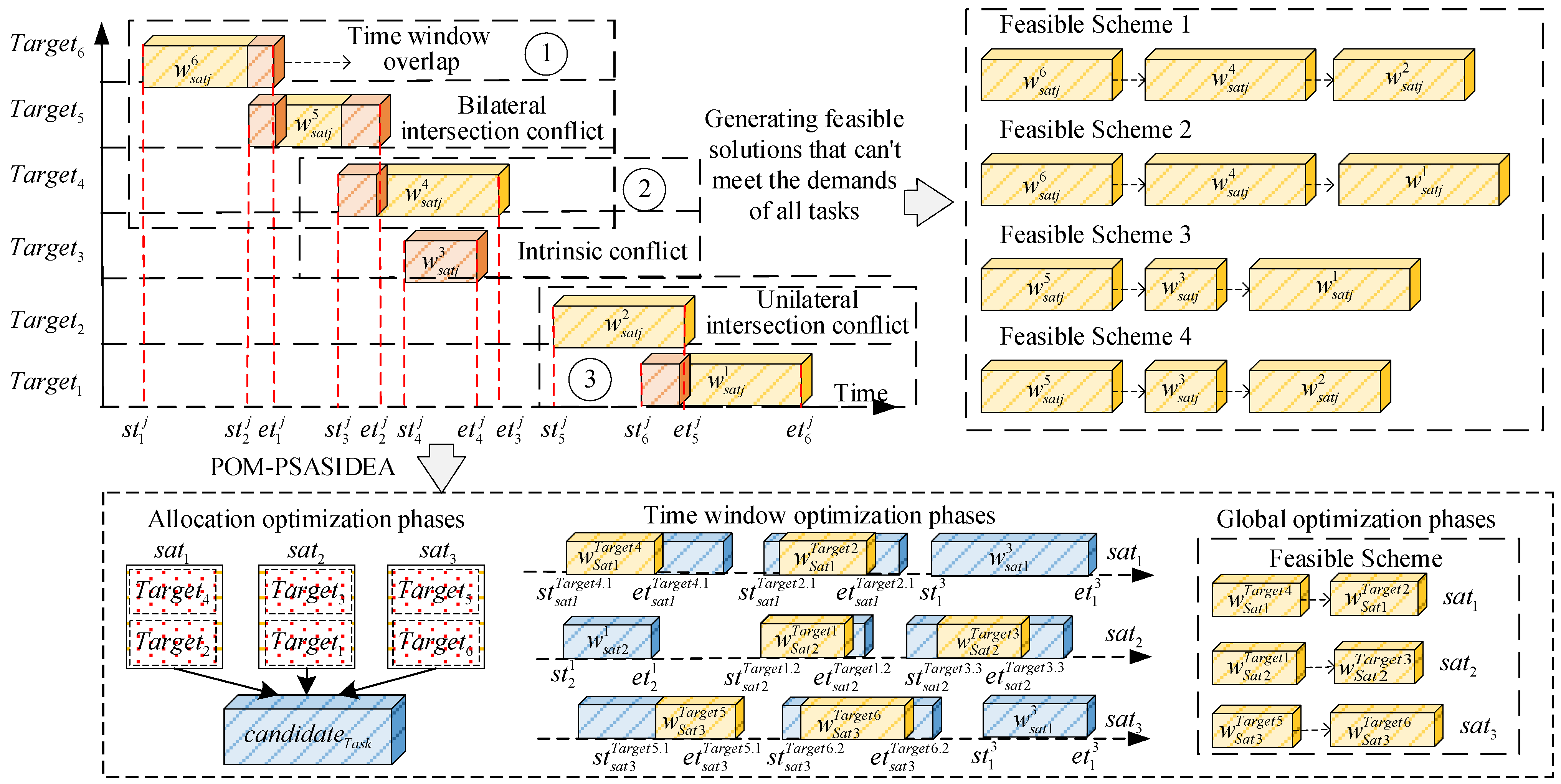
- Neighboring task observation time window constraints: When the observation time windows of neighboring missions overlap, the satellite is unable to perform more than one mission at the same time. To avoid resource conflicts, the constraint ensures that there is no overlap in the time windows of neighboring missions on satellite resources in the same time frame.where and denote the shortest and longest on-time of the satellite, respectively.
- Observation duration constraints: Observation duration refers to the total time a satellite spends performing all assigned target tasks. This constraint ensures that task allocation remains within the satellite’s capacity and that the satellite’s observation time does not exceed the maximum operating time for a single orbital pass.where indicates the maximum operating time of the satellite on a single orbital lap.
- Task execution order constraint: In cases where there is a precedence relationship between tasks, this constraint requires that a given task must be performed before another task , meaning the start time of the task must be earlier than the end time of the task .In summary, the total objective function of the MSIMPLTS-MLOO model can be expressed as a weighted sum of the objective functions from the superstructure, mesostructure, and understructure, reflecting the overall goal of multi-layer optimization. The mathematical expression for the MSIMPLTS-MLOO model’s objective function is shown in Equation (13):where, , , and , respectively, are the proportional scaling factors of task benefit, task allocation rate, and task response time. Satellite controllers can adaptively adjust the weights according to the preference demand. This work does not consider the preference situation in the experiment, so the proportionality factor is set to . The weighted solution of the optimization objective can transform the multi-objective problem into a single-objective problem.
4. Design of the POM-PSASIDEA Algorithm
| Algorithm 1. The framework of POM-PSASIDEA |
| Input: (Parameters of the satellites , Parameters of the target task , Population size ); |
| Output: MSIMPLTS optimal scheme.; 1 According to the Equations (1)–(13) build MSIMPLTS—MLOO model; 2/* Allocation optimization phase */ 3 ; /* initial scheme*/ 4 ; 5 ; 6 /* Time window optimization phase*/ 7 ; 8 ; 9 ; 10 /*Global optimization phase */ 11 ; 12 ; 13 ; 14 end |
4.1. Progressive Optimization Mechanism
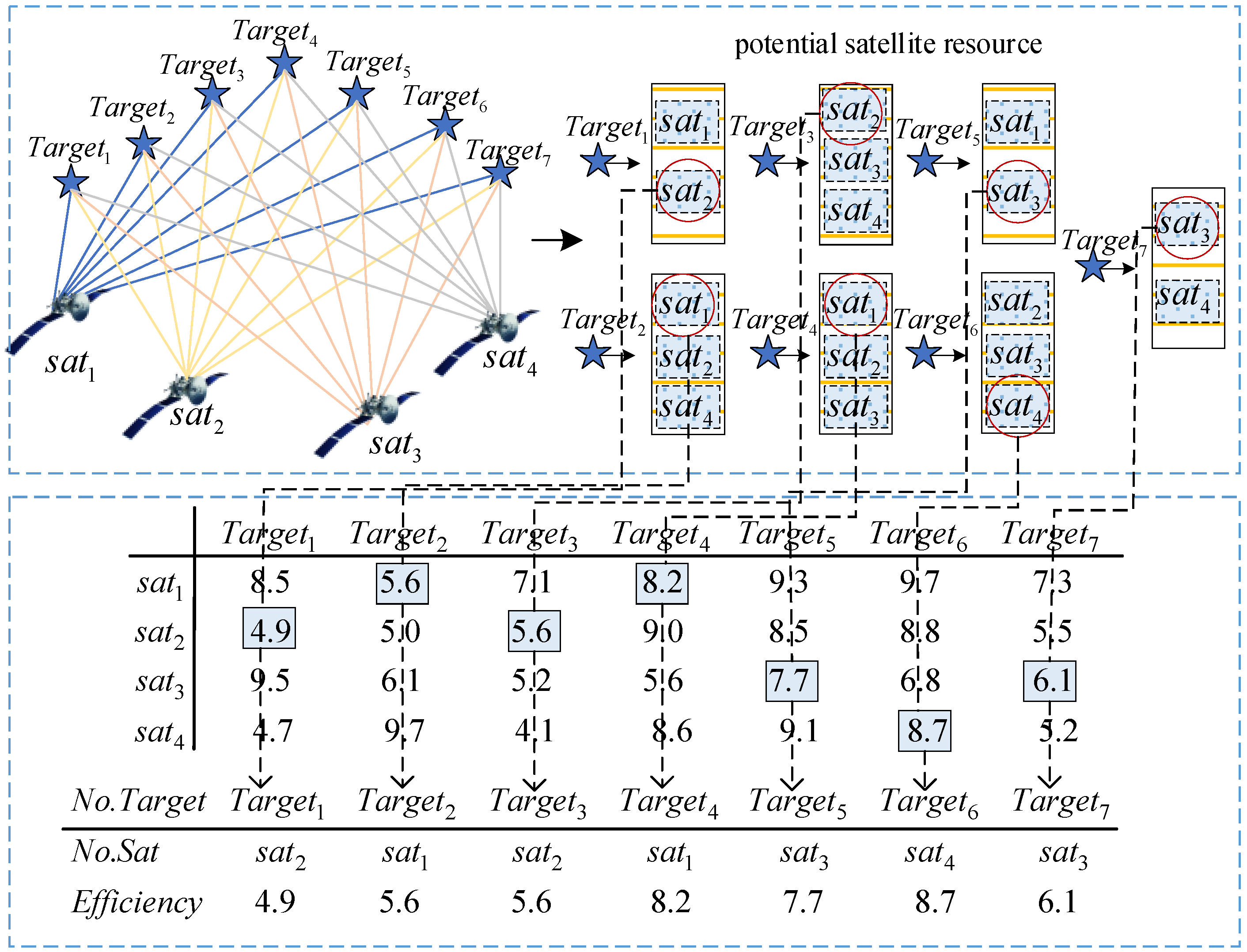
4.1.1. Allocation Optimization Phase
| Algorithm 2. Allocation optimization phase |
| Input: (Parameters of the satellites , Parameters of the target task , Population size ); |
| Output: AllocationPlan 1 ,;/* initial Task benefit repository and potential satellite resources */ 2 ;/* calculate Task benefit repository 3 ;/* obtain potential satellite resource sets*/ 4 while 5 for target = 1: 6 ; 7 ;/* Traverse Task benefit repository obtain corresponding Efficiency*/ 8 ; 9 end 10 ; 11 ; 12 ; 13 end |
4.1.2. Time Window Optimization Phase
| Algorithm 3. Time window optimization phase |
| Input: AllocationPlan, Parameters of the satellites , Parameters of the target task Output: |
| 1 for j = 1: 2 3 ; 4 for i = 1:length() 5 ; 6 if allocated satisfy the mesostructure of MSIMPLTS-MLOO model constraint 7 ; 8 else 9 ; 10 end 11 end 12 end 13 for = 1:length() 14 ~any( (:, 1) visible_windows(i, 1) &(:, 1) visible_windows(i, 2)); 15 ; 16 if Adjacent but not overlapping 17 end 18 ,; 19 for 20 21 ; 22 ; 23 end 24 ; |
4.1.3. Global Optimization Phase
| Algorithm 4. Global optimization phase |
| Input: , , Parameters of the satellites , Parameters of the target task , Population size Output: MSIMPLTS optimal scheme: |
| 1 ;/* Integration Scheme */ 2 while 3 Traverse the integration scheme in 4 if 5 ; 6 ; 7 else 8 ; 9 end 10 ; 11 ; 12 for 13 if ~any( (:, 1)(i, 1) &(:, 1) (i, 2)) 14 if allocated satisfy the understructure of MSIMPLTS-MLOO model constraint 15 ; 16 end 17 end 18 end 19 ; 20 ; 21 ; 22 end 23 ; 24 ; 25 end 26 ; |
4.2. Population Size Adaptive Strategy for the Improved Differential Evolution Algorithm
| Algorithm 5. Population size adaptive strategy for the improved differential evolution algorithm |
| Input: , , Parameters of the satellites , Parameters of the target task , Population size Output: MSIMPLTS optimal scheme: |
| 1 /* Initialization parameter*/ 2 ; 3 ; /*Initial population*/ 4 while 5 ; 6 ; /*update population*/ 7 ;/*update optimal fitness*/ 8 if 9 Calculate Population individual similarity by using Equation (15); 10 Calculate individual diversity between populations by using Equation (16); 11 if 12 ; 13 else 14 ; 15 end 16 else 17 Calculate population evolution rate by using Equation (17); 18 if The population evolution rate stagnated more than generations 19 20 else 21 ; 22 end 23 end 24 ; 25 end 26 ; |
5. Experimental Results and Analysis
5.1. Subsection Experimental Setting
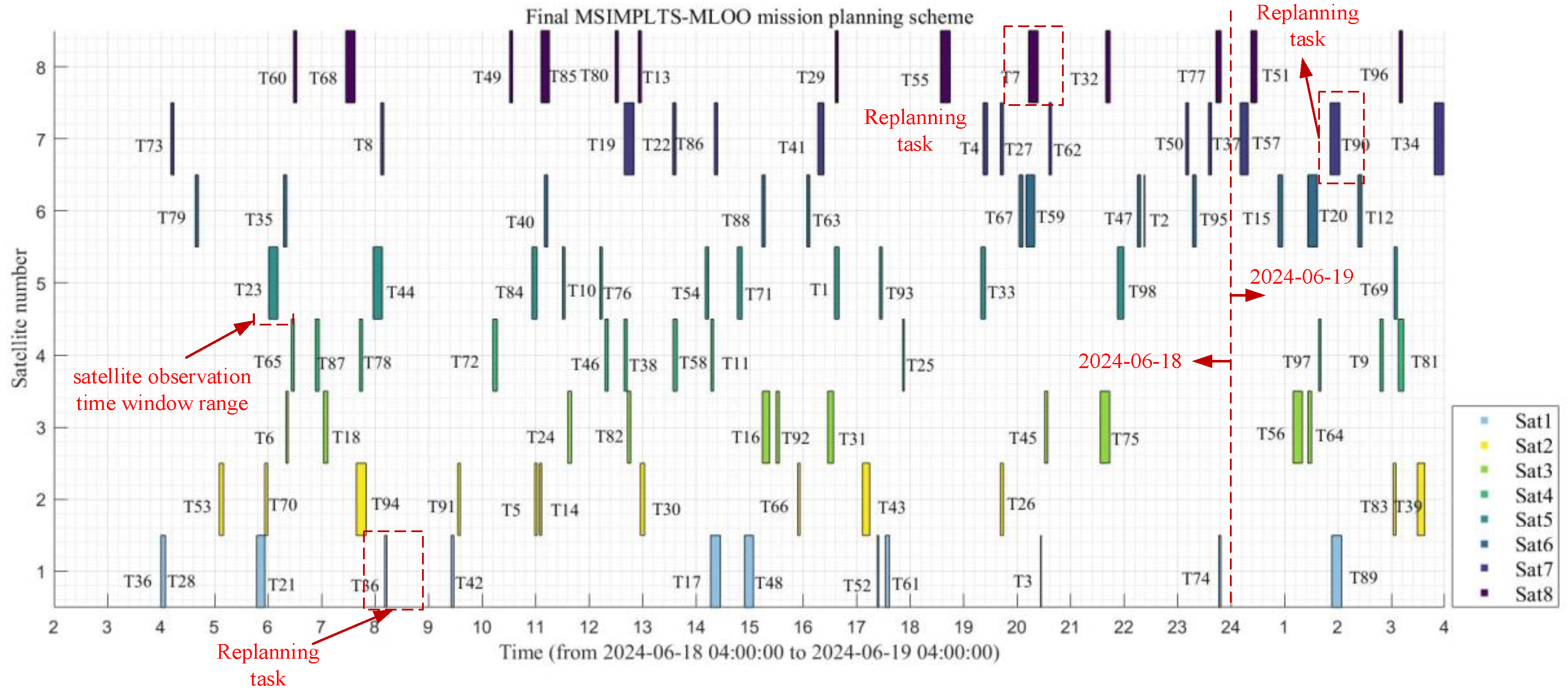
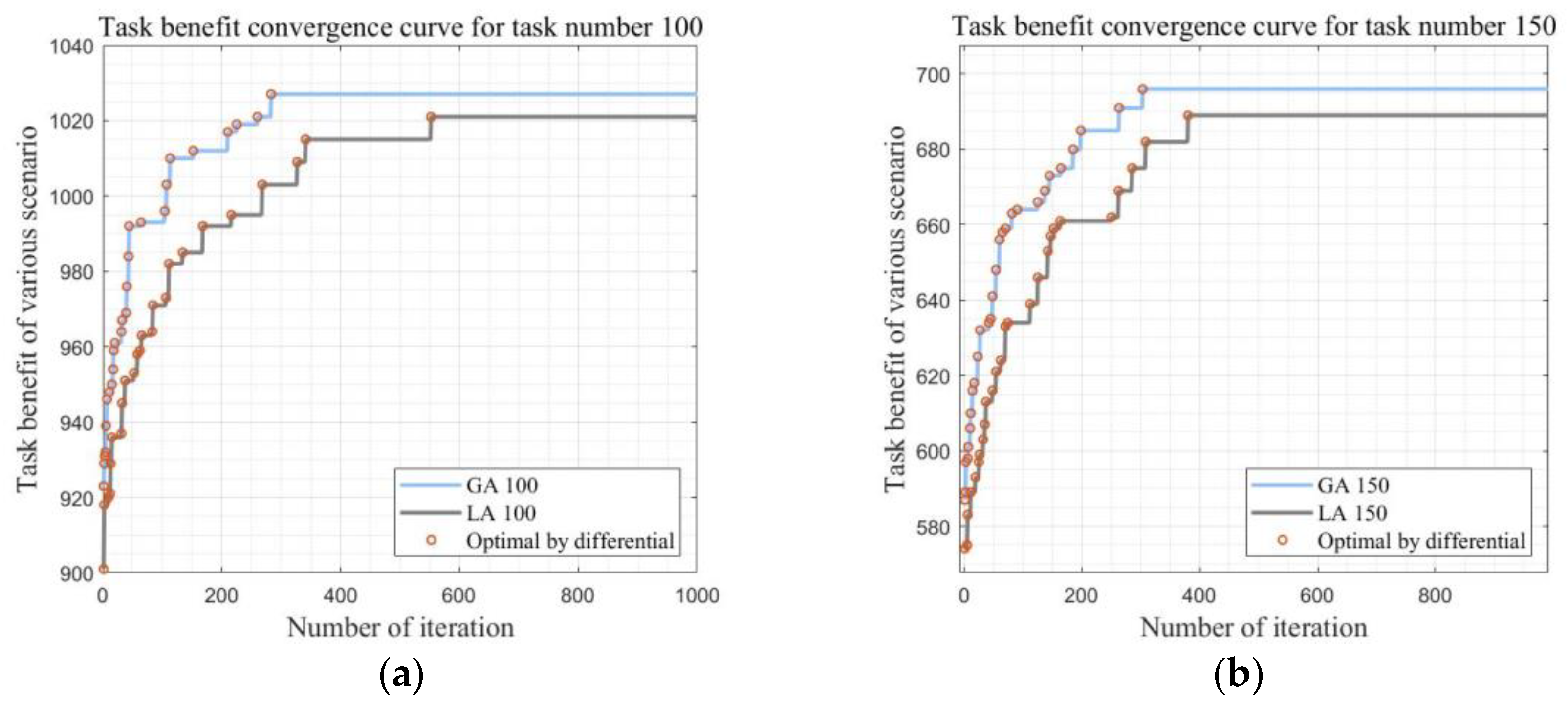
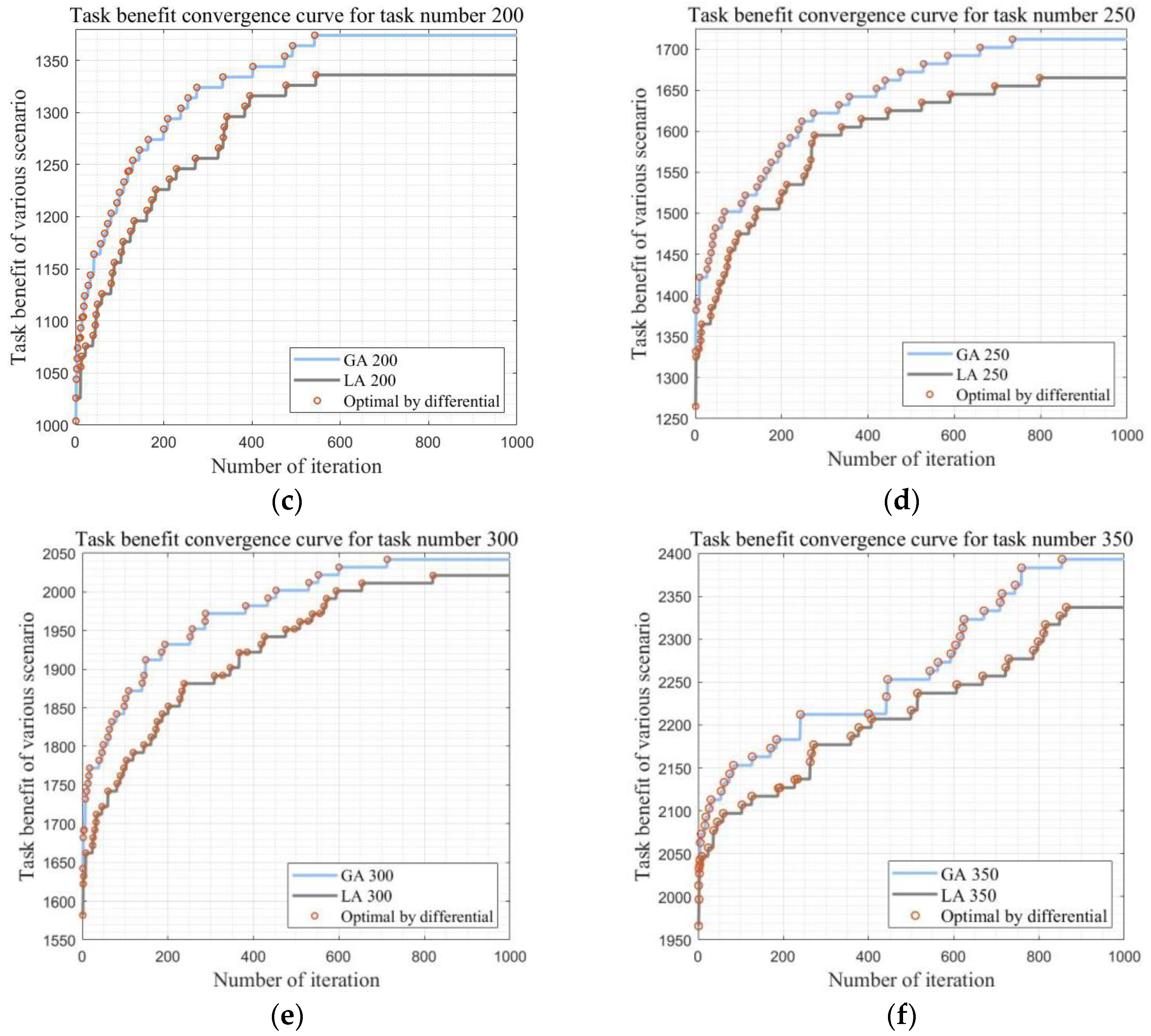
5.2. Experiment 1: POM-PSASIDEA Algorithm Resolves MSIMPLTS Effectiveness
5.3. Experiment 2: POM-PSASIDEA Algorithm Resolves MSIMPLTS Scalability
5.4. Experiment 3: POM-PSASIDEA Algorithm Performance Analysis
6. Discussion
6.1. Discussion of the Current Research
- Scalability of MSIMPLTS based on Multi-layer Objective Optimization
- 2.
- Effectiveness of the progressive optimization mechanism
- 3.
- Superiority of the population size adaptive strategy for an improved differential evolution algorithm
6.2. Limitation Analysis and Future Research Direction
- Limitations of responsiveness in dynamic environments
- 2.
- Intelligent adaptive adjustment capability limitations
- 3.
- Event-driven integration with MSIMPLTS
- 4.
- Data-driven and big data analysis combined with MSIMPLTS
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| MSIMP | Multi-Satellite Imaging Mission Planning |
|---|---|
| MSIMPLTS | Multi-Satellite Imaging Mission Planning in Large-scale Target Scenarios |
| MSIMPLTS-MLOO | Multi-Satellite Imaging Mission Planning in Large-scale Target Scenarios based on Multi-layer Objective Optimization |
| POM-PSASIDEA | Progressive optimization mechanism-population size adaptive strategy for improved differential evolution algorithm |
| POM | Progressive optimization mechanism |
| AOP | Allocation Optimization Phase |
| TOP | Time window Optimization Phase |
| GOP | Global Optimization Phase |
| DE | Differential Evolution |
| UTCG | Universal Time Coordinated, Gregorian |
| AGDE-MPP | Adaptive Guided Differential Evolution algorithm on Mutation, Parameter, and Population |
| A-MPMO | Adaptive strategy with a multi-population multi-objective algorithm |
| APSDE | Adaptive Parameter and strategy with Differential Evolution algorithm |
| ADECSA | Adaptive Clonal Selection Algorithm with Multiple Differential Evolution Strategies |
| SLPS-ADE | Sawtooth-Linear Population Size based Adaptive Differential Evolution |
Appendix B
| Algorithm Name | Description | Applicable Scenarios |
|---|---|---|
| AGDE-MPP | Uses a new mutation scheme, parameter adaptation, and non-linear population size reduction strategy to achieve high-precision and fast convergence in task planning. | Suitable for large-scale target mission scenarios, especially when high precision and fast convergence are required. |
| A-MPMO | Divides the population into multiple sub-populations to expand the search space, with adaptive selection for each sub-population to improve task planning adaptability. | Best for scenarios requiring a broader search space, particularly in multi-objective optimization for task planning. |
| APSDE | Optimizes through accompanying populations, mutation strategies, and control parameters to enhance task planning diversity. | Suitable for complex task planning scenarios, particularly effective in maintaining population diversity and avoiding premature convergence. |
| ADECSA | Introduces an adaptive mutation strategy library based on historical optimal solutions and adjusts the population adaptively, solving the issue of local optima in task planning. | Effective in large-scale task planning scenarios, especially where tasks tend to get stuck in local optima. |
| SLPS-ADE | Uses an external archive to store disadvantageous vectors and adaptively adds vectors from the archive to the new population generation, improving task allocation efficiency. | Ideal for scenarios requiring efficient resource allocation, particularly when high task allocation efficiency is needed. |
References
- Fan, H.; Yang, Z.; Zhang, X.; Wu, S.; Long, J.; Liu, L. A Novel Multi-Satellite and Multi-Task Scheduling Method Based on Task Network Graph Aggregation. Expert Syst. Appl. 2022, 205, 117565. [Google Scholar] [CrossRef]
- Wei, L.; Xing, L.; Wan, Q.; Song, Y.; Chen, Y. A Multi-Objective Memetic Approach for Time-Dependent Agile Earth Observation Satellite Scheduling Problem. Comput. Ind. Eng. 2021, 159, 107530. [Google Scholar] [CrossRef]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A Reinforcement Learning-Based Genetic Algorithm for Electromagnetic Detection Satellite Scheduling Problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Wei, L.; Chen, M.; Xing, L.; Wan, Q.; Song, Y.; Chen, Y.; Chen, Y. Knowledge-Transfer Based Genetic Programming Algorithm for Multi-Objective Dynamic Agile Earth Observation Satellite Scheduling Problem. Swarm Evol. Comput. 2024, 85, 101460. [Google Scholar] [CrossRef]
- Huang, W.; Wang, H.; Yi, D.; Wang, S.; Zhang, B.; Cui, J. A Multiple Agile Satellite Staring Observation Mission Planning Method for Dense Regions. Remote Sens. 2023, 15, 5317. [Google Scholar] [CrossRef]
- Yan, B.; Wang, Y.; Xia, W.; Hu, X.; Ma, H.; Jin, P. An Improved Method for Satellite Emergency Mission Scheduling Scheme Group Decision-Making Incorporating PSO and MULTIMOORA. J. Intell. Fuzzy Syst. 2022, 42, 3837–3853. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, X.; Zhang, G.; Lu, Z. Multi-Objective Multi-Satellite Imaging Mission Planning Algorithm for Regional Mapping Based on Deep Reinforcement Learning. Remote Sens. 2023, 15, 3932. [Google Scholar] [CrossRef]
- Kandepi, R.; Saini, H.; George, R.K.; Konduri, S.; Karidhal, R. Agile Earth Observation Satellite Constellations Scheduling for Large Area Target Imaging Using Heuristic Search. Acta Astronaut. 2024, 219, 670–677. [Google Scholar] [CrossRef]
- Kocaman, S.; Seiz, G. Contribution of Photogrammetry for Geometric Quality Assessment of Satellite Data for Global Climate Monitoring. Remote Sens. 2023, 15, 4575. [Google Scholar] [CrossRef]
- Tran, T.-N.-D.; Le, M.-H.; Zhang, R.; Nguyen, B.Q.; Bolten, J.D.; Lakshmi, V. Robustness of Gridded Precipitation Products for Vietnam Basins Using the Comprehensive Assessment Framework of Rainfall. Atmos. Res. 2023, 293, 106923. [Google Scholar] [CrossRef]
- Tran, T.-N.-D.; Lakshmi, V. Enhancing Human Resilience against Climate Change: Assessment of Hydroclimatic Extremes and Sea Level Rise Impacts on the Eastern Shore of Virginia, United States. Sci. Total Environ. 2024, 947, 174289. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.-N.-D.; Nguyen, B.Q.; Grodzka-Łukaszewska, M.; Sinicyn, G.; Lakshmi, V. The Role of Reservoirs under the Impacts of Climate Change on the Srepok River Basin, Central Highlands of Vietnam. Front. Environ. Sci. 2023, 11, 174289. [Google Scholar] [CrossRef]
- Nguyen, B.Q.; Van Binh, D.; Tran, T.-N.-D.; Kantoush, S.A.; Sumi, T. Response of Streamflow and Sediment Variability to Cascade Dam Development and Climate Change in the Sai Gon Dong Nai River Basin. Clim. Dyn. 2024, 11, 174289. [Google Scholar] [CrossRef]
- Tran, T.-N.-D.; Tapas, M.R.; Do, S.K.; Etheridge, R.; Lakshmi, V. Investigating the Impacts of Climate Change on Hydroclimatic Extremes in the Tar-Pamlico River Basin, North Carolina. J. Environ. Manag. 2024, 363, 121375. [Google Scholar] [CrossRef]
- Qu, Q.; Liu, K.; Li, X.; Zhou, Y.; Lu, J. Satellite Observation and Data-Transmission Scheduling Using Imitation Learning Based on Mixed Integer Linear Programming. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1989–2001. [Google Scholar] [CrossRef]
- Yu, Y.; Hou, Q.; Zhang, J.; Zhang, W. Mission Scheduling Optimization of Multi-Optical Satellites for Multi-Aerial Targets Staring Surveillance. J. Franklin Inst. 2020, 357, 8657–8677. [Google Scholar] [CrossRef]
- Lin, Z.; Ni, Z.; Kuang, L.; Jiang, C.; Huang, Z. Satellite-Terrestrial Coordinated Multi-Satellite Beam Hopping Scheduling Based on Multi-Agent Deep Reinforcement Learning. IEEE Trans. Wirel. Commun. 2024, 23, 10091–10103. [Google Scholar] [CrossRef]
- Wu, G.; Xiang, Z.; Wang, Y.; Gu, Y.; Pedrycz, W. Improved Adaptive Large Neighborhood Search Algorithm Based on the Two-Stage Framework for Scheduling Multiple Super-Agile Satellites. IEEE Trans. Aerosp. Electron. Syst. 2024, 178, 1–17. [Google Scholar] [CrossRef]
- Ren, L.; Ning, X.; Wang, Z. A Competitive Markov Decision Process Model and a Recursive Reinforcement-Learning Algorithm for Fairness Scheduling of Agile Satellites. Comput. Ind. Eng. 2022, 169, 108242. [Google Scholar] [CrossRef]
- Feng, X.; Li, Y.; Xu, M. Multi-Satellite Cooperative Scheduling Method for Large-Scale Tasks Based on Hybrid Graph Neural Network and Metaheuristic Algorithm. Adv. Eng. Inform. 2024, 60, 102362. [Google Scholar] [CrossRef]
- Linares, L.; Vazquez, R.; Perea, F.; Galán-Vioque, J. A Mixed Integer Linear Programming Model for Resolution of the Antenna-Satellite Scheduling Problem. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 463–473. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Bai, X.; Li, S. Real-Time Satellite Constellation Scheduling for Event-Triggered Cooperative Tracking of Space Objects. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2169–2182. [Google Scholar] [CrossRef]
- Li, C.; Xu, W.; Xu, L.; Wang, Y. An Approach to Multi-Satellite TT&C Resource Scheduling Based on Multi-Agent Technology and Comprehensive Weighted Priority Determination Method. J. Phys. Conf. Ser. 2021, 1812, 012001. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, X.; Ma, H.; Xia, W. Learning Multi-Satellite Scheduling Policy with Heterogeneous Graph Neural Network. Adv. Space Res. 2024, 73, 2921–2938. [Google Scholar] [CrossRef]
- He, Y.; Xing, L.; Chen, Y.; Pedrycz, W.; Wang, L.; Wu, G. A Generic Markov Decision Process Model and Reinforcement Learning Method for Scheduling Agile Earth Observation Satellites. IEEE Trans. Syst. Man. Cybern. Syst. 2022, 52, 1463–1474. [Google Scholar] [CrossRef]
- Zhibo, E.; Shi, R.; Gan, L.; Baoyin, H.; Li, J. Multi-Satellites Imaging Scheduling Using Individual Reconfiguration Based Integer Coding Genetic Algorithm. Acta Astronaut. 2021, 178, 645–657. [Google Scholar] [CrossRef]
- Gu, Y.; Han, C.; Chen, Y.; Liu, S.; Wang, X. Large Region Targets Observation Scheduling by Multiple Satellites Using Resampling Particle Swarm Optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 52, 1800–1815. [Google Scholar] [CrossRef]
- Tian, M.; Ma, G.; Huang, P.; Cheng, B.; Li, W. Optimizing Satellite Ground Station Facilities Scheduling for RSGS: A Novel Model and Algorithm. Int. J. Digit. Earth 2023, 16, 3949–3972. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Song, Y.; He, L.; Lu, F.; Du, Y.; Yan, J.; Chen, Y.; Xing, L.; Ou, J. Frequent Pattern-Based Parallel Search Approach for Time-Dependent Agile Earth Observation Satellite Scheduling. Inf. Sci. 2023, 636, 118924. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, L.; Peng, G.; Yao, F.; Chen, C. A Large-Scale Multiobjective Satellite Data Transmission Scheduling Algorithm Based on SVM+NSGA-II. Swarm Evol. Comput. 2019, 50, 100560. [Google Scholar] [CrossRef]
- Wang, J.; Demeulemeester, E.; Hu, X.; Qiu, D.; Liu, J. Exact and Heuristic Scheduling Algorithms for Multiple Earth Observation Satellites Under Uncertainties of Clouds. IEEE Syst. J. 2019, 13, 3556–3567. [Google Scholar] [CrossRef]
- Ou, J.; Xing, L.; Yao, F.; Li, M.; Lv, J.; He, Y.; Song, Y.; Wu, J.; Zhang, G. Deep Reinforcement Learning Method for Satellite Range Scheduling Problem. Swarm Evol. Comput. 2023, 77, 101233. [Google Scholar] [CrossRef]
- Chang, Z.; Chen, Y.; Yang, W.; Zhou, Z. Mission Planning Problem for Optical Video Satellite Imaging with Variable Image Duration: A Greedy Algorithm Based on Heuristic Knowledge. Adv. Space Res. 2020, 66, 2597–2609. [Google Scholar] [CrossRef]
- Ayana, S.E.; Kim, H.-D. Optimal Scheduling of Imaging Missions for Multiple Satellites Using Linear Programming Model. Int. J. Aeronaut. Space Sci. 2023, 24, 559–569. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, J.; He, R.; Ou, J. An Efficient Local Search Heuristic for Earth Observation Satellite Integrated Scheduling. Appl. Sci. 2020, 10, 5616. [Google Scholar] [CrossRef]
- Wang, T.; Luo, Q.; Zhou, L.; Wu, G. Space Division and Adaptive Selection Strategy Based Differential Evolution Algorithm for Multi-Objective Satellite Range Scheduling Problem. Swarm Evol. Comput. 2023, 83, 101396. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Lu, J.; Chen, C.; Wu, G. Scheduling Multiple Agile Earth Observation Satellites with an Edge Computing Framework and a Constructive Heuristic Algorithm. J. Syst. Archit. 2019, 95, 55–66. [Google Scholar] [CrossRef]
- Wei, L.; Chen, Y.; Chen, M.; Chen, Y. Deep Reinforcement Learning and Parameter Transfer Based Approach for the Multi-Objective Agile Earth Observation Satellite Scheduling Problem. Appl. Soft Comput. 2021, 110, 107607. [Google Scholar] [CrossRef]
- Chatterjee, A.; Tharmarasa, R. Multi-Stage Optimization Framework of Satellite Scheduling for Large Areas of Interest. Adv. Space Res. 2024, 73, 2024–2039. [Google Scholar] [CrossRef]
- Song, Y.; Ou, J.; Wu, J.; Wu, Y.; Xing, L.; Chen, Y. A Cluster-Based Genetic Optimization Method for Satellite Range Scheduling System. Swarm Evol. Comput. 2023, 79, 101316. [Google Scholar] [CrossRef]
- Han, C.; Gu, Y.; Wu, G.; Wang, X. Simulated Annealing-Based Heuristic for Multiple Agile Satellites Scheduling Under Cloud Coverage Uncertainty. IEEE Trans. Syst. Man. Cybern. Syst. 2023, 53, 2863–2874. [Google Scholar] [CrossRef]
- Zhang, S.X.; Hu, X.R.; Zheng, S.Y. Differential Evolution with Evolutionary Scale Adaptation. Swarm Evol. Comput. 2024, 85, 101481. [Google Scholar] [CrossRef]
- Lin, X.; Meng, Z. An Adaptative Differential Evolution with Enhanced Diversity and Restart Mechanism. Expert Syst. Appl. 2024, 249, 123634. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.; Qu, Y. An Adaptive Differential Evolution Algorithm with Population Size Reduction Strategy for Unconstrained Optimization Problem. Appl. Soft Comput. 2023, 138, 110209. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, L.; Cui, Z.; Qin, A.K. An Adaptive Strategy Based Multi-Population Multi-Objective Optimization Algorithm. Inf. Sci. 2024, 138, 120913. [Google Scholar] [CrossRef]
- Wang, M.; Ma, Y.; Wang, P. Parameter and Strategy Adaptive Differential Evolution Algorithm Based on Accompanying Evolution. Inf. Sci. 2022, 607, 1136–1157. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Liu, X.; Yao, J. An Adaptive Clonal Selection Algorithm with Multiple Differential Evolution Strategies. Inf. Sci. 2022, 604, 142–169. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, M.; Zhang, H.; Hong, Z. Improved Differential Evolution Algorithm Based on the Sawtooth-Linear Population Size Adaptive Method. Inf. Sci. 2022, 608, 1045–1071. [Google Scholar] [CrossRef]
| No. Sat | /(km) | /(°) | /(°) | /(°) | /(°) | /(°) | /(°) | /(s) | (°) | /(°/s) | /(m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sat1 | 6871 | 0.013 | 98.54 | 179 | 94.764 | 109.153 | 6 | 400 | 30 | 0.2 | 2 |
| Sat2 | 6871 | 0.021 | 97.42 | 159 | 97.034 | 122.516 | 6 | 400 | 30 | 0.2 | 2 |
| Sat3 | 6871 | 0.016 | 90.32 | 139 | 90.972 | 162.317 | 6 | 400 | 30 | 0.2 | 2 |
| Sat4 | 6871 | 0.014 | 98.50 | 119 | 92.612 | 119.562 | 6 | 450 | 30 | 0.3 | 2 |
| Sat5 | 6871 | 0.037 | 97.90 | 99 | 92.860 | 157.373 | 7 | 450 | 35 | 0.3 | 2 |
| Sat6 | 6871 | 0.028 | 96.31 | 79 | 92.172 | 188.254 | 7 | 450 | 35 | 0.3 | 1.5 |
| Sat7 | 6871 | 0.055 | 97.44 | 59 | 97.629 | 172.768 | 8 | 500 | 35 | 0.3 | 1.5 |
| Sat8 | 6871 | 0.051 | 90.65 | 29 | 93.795 | 103.553 | 8 | 500 | 35 | 0.4 | 1.5 |
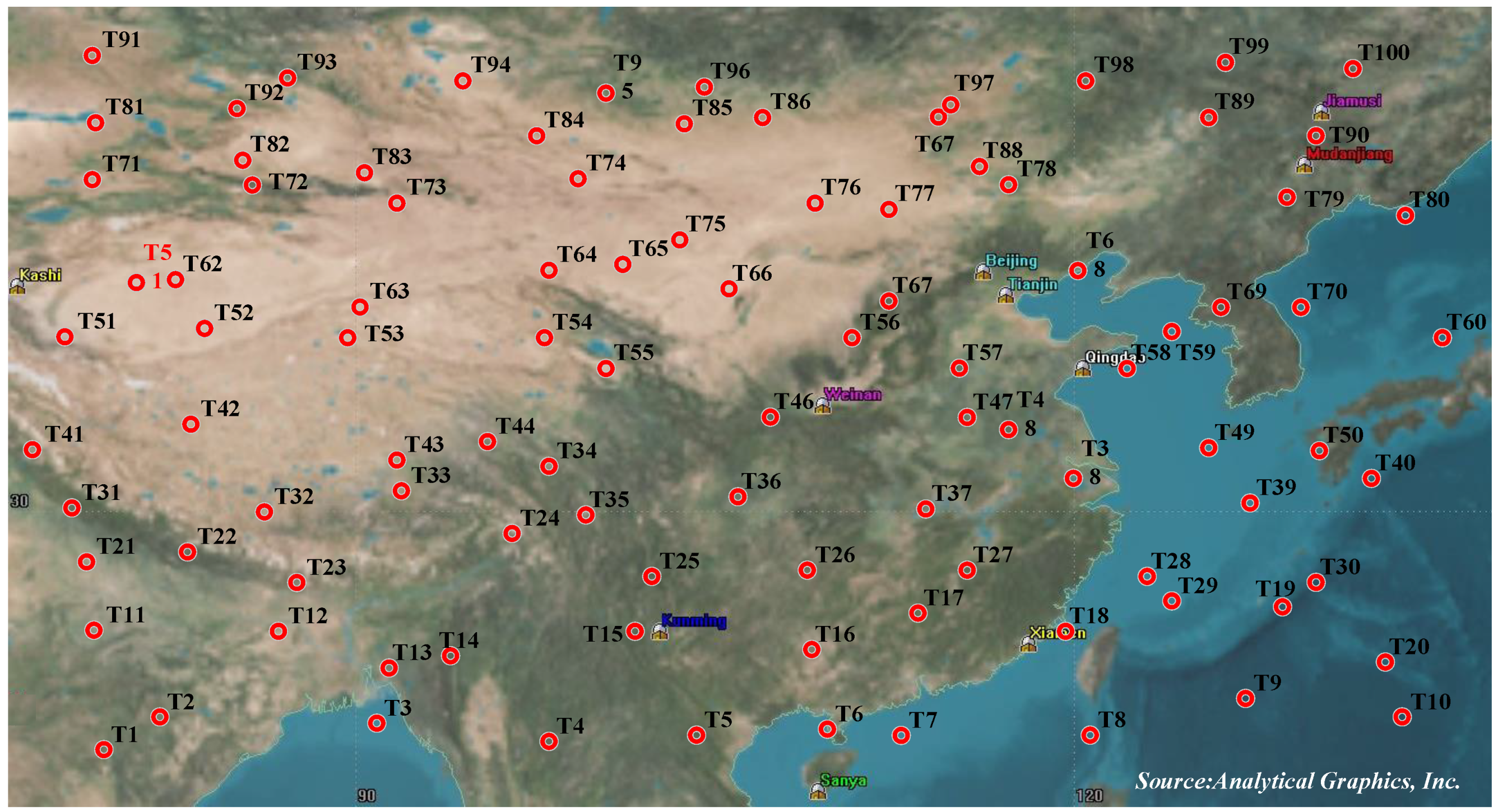
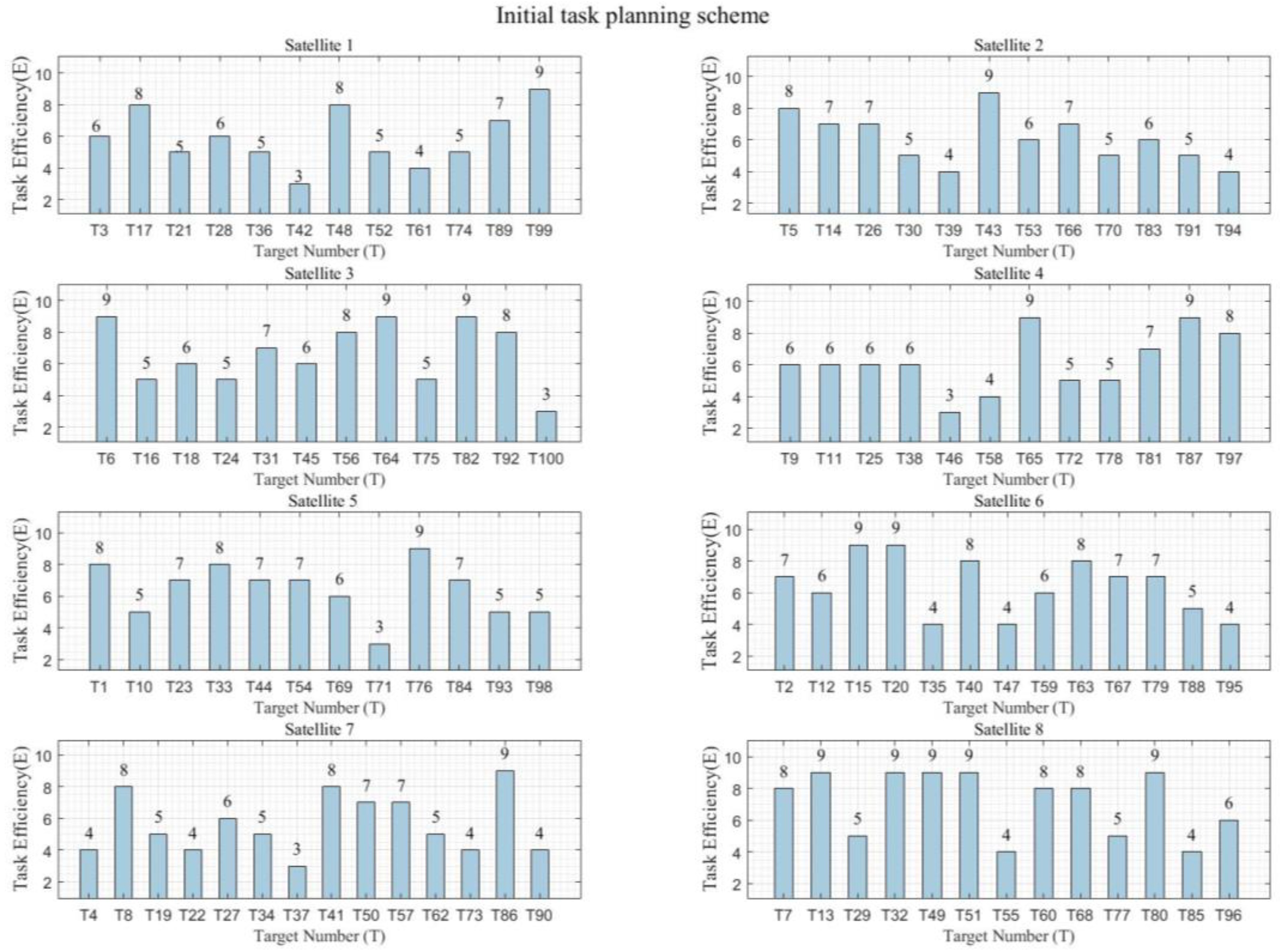
| T | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Sat | 5 | 6 | 1 | 7 | 2 | 3 | 8 | 7 | 4 | 5 | 4 | 6 | 8 | 2 | 6 | 3 | 1 | 3 | 7 | 6 |
| E | 8 | 7 | 6 | 4 | 8 | 9 | 8 | 8 | 6 | 5 | 6 | 6 | 9 | 7 | 9 | 5 | 8 | 6 | 5 | 9 |
| T | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Sat | 1 | 7 | 5 | 3 | 4 | 2 | 7 | 1 | 8 | 2 | 3 | 8 | 5 | 7 | 6 | 1 | 7 | 4 | 2 | 6 |
| E | 5 | 4 | 7 | 5 | 6 | 7 | 6 | 6 | 5 | 5 | 7 | 9 | 8 | 5 | 4 | 5 | 3 | 6 | 4 | 8 |
| T | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| Sat | 7 | 1 | 2 | 5 | 3 | 4 | 6 | 1 | 8 | 7 | 8 | 1 | 2 | 5 | 8 | 3 | 7 | 4 | 6 | 8 |
| E | 8 | 3 | 9 | 7 | 6 | 3 | 4 | 8 | 9 | 7 | 9 | 5 | 6 | 7 | 4 | 8 | 7 | 4 | 6 | 8 |
| T | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| Sat | 1 | 7 | 6 | 3 | 4 | 2 | 6 | 8 | 5 | 2 | 5 | 4 | 7 | 1 | 3 | 5 | 8 | 4 | 6 | 8 |
| E | 4 | 5 | 8 | 9 | 9 | 7 | 7 | 8 | 6 | 5 | 3 | 5 | 4 | 5 | 5 | 9 | 5 | 5 | 7 | 9 |
| Target | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| Sat | 4 | 3 | 2 | 5 | 8 | 7 | 4 | 6 | 1 | 7 | 2 | 3 | 5 | 2 | 6 | 8 | 4 | 5 | 1 | 3 |
| E | 7 | 9 | 6 | 7 | 4 | 9 | 9 | 5 | 7 | 4 | 5 | 8 | 5 | 4 | 4 | 6 | 8 | 5 | 9 | 3 |
| T | St | Et | T | St | Et | T | St | Et | T | St | Et |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | 16:35:34 | 16:38:54 | T26 | 19:41:38 | 19:43:50 | T51 | 00:22:34 | 00:27:07 | T76 | 12:12:20 | 12:14:12 |
| T2 | 22:15:26 | 22:17:47 | T27 | 19:41:38 | 19:43:50 | T52 | 17:23:38 | 17:24:36 | T77 | 23:43:21 | 23:47:16 |
| T3 | 20:26:49 | 20:27:17 | T28 | 04:00:00 | 04:03:23 | T53 | 05:05:38 | 05:08:36 | T78 | 07:42:53 | 07:45:03 |
| T4 | 19:22:14 | 19:25:34 | T29 | 16:36:26 | 16:38:40 | T54 | 14:10:47 | 14:13:11 | T79 | 04:38:34 | 04:40:52 |
| T5 | 11:04:41 | 11:06:16 | T30 | 12:57:50 | 13:01:00 | T55 | 18:33:15 | 18:40:27 | T80 | 12:29:36 | 12:31:55 |
| T6 | 06:20:24 | 06:22:00 | T31 | 16:28:02 | 16:32:15 | T56 | 01:10:03 | 01:16:53 | T81 | 03:08:00 | 03:12:01 |
| T7 | 18:34:31 | 18:41:45 | T32 | 21:39:51 | 21:43:06 | T57 | 01:51:31 | 01:58:47 | T82 | 12:43:23 | 12:45:48 |
| T8 | 08:06:47 | 08:08:56 | T33 | 19:19:48 | 19:23:09 | T58 | 13:34:30 | 13:37:36 | T83 | 03:02:25 | 03:04:22 |
| T9 | 02:47:24 | 02:49:43 | T34 | 03:48:16 | 03:55:19 | T59 | 20:10:24 | 20:16:55 | T84 | 10:56:14 | 11:00:01 |
| T10 | 11:30:27 | 11:32:19 | T35 | 06:17:34 | 06:19:54 | T60 | 06:28:54 | 06:31:13 | T85 | 11:06:20 | 11:12:44 |
| T11 | 14:17:07 | 14:18:59 | T36 | 04:00:00 | 04:04:19 | T61 | 17:32:30 | 17:35:41 | T86 | 14:20:49 | 14:23:14 |
| T12 | 02:22:44 | 02:25:37 | T37 | 00:10:40 | 00:16:36 | T62 | 20:36:05 | 20:38:03 | T87 | 06:53:16 | 06:56:07 |
| T13 | 12:55:33 | 12:57:45 | T38 | 12:39:35 | 12:41:50 | T63 | 16:04:37 | 16:06:46 | T88 | 15:14:17 | 15:16:34 |
| T14 | 10:59:22 | 11:01:13 | T39 | 03:29:17 | 03:34:52 | T64 | 01:26:30 | 01:29:21 | T89 | 01:53:20 | 02:00:40 |
| T15 | 00:53:08 | 00:56:29 | T40 | 11:10:18 | 11:12:39 | T65 | 06:26:29 | 06:28:34 | T90 | 01:56:14 | 01:58:18 |
| T16 | 15:14:48 | 15:20:08 | T41 | 16:17:02 | 16:21:31 | T66 | 15:54:28 | 15:56:04 | T91 | 09:33:09 | 09:35:00 |
| T17 | 14:16:45 | 14:24:00 | T42 | 09:25:40 | 09:27:32 | T67 | 20:02:46 | 20:05:30 | T92 | 15:30:03 | 15:32:28 |
| T18 | 07:02:35 | 07:05:37 | T43 | 17:06:50 | 17:12:23 | T68 | 07:27:19 | 07:34:22 | T93 | 17:26:06 | 17:28:06 |
| T19 | 12:39:44 | 12:47:04 | T44 | 07:58:05 | 08:04:57 | T69 | 03:03:12 | 03:05:35 | T94 | 07:39:16 | 07:46:39 |
| T20 | 01:26:19 | 01:33:35 | T45 | 20:31:33 | 20:33:42 | T70 | 05:56:33 | 05:58:39 | T95 | 23:17:12 | 23:19:51 |
| T21 | 05:47:29 | 05:53:38 | T46 | 12:18:17 | 12:20:35 | T71 | 14:46:43 | 14:50:11 | T96 | 03:08:56 | 03:11:21 |
| T22 | 13:34:05 | 13:36:33 | T47 | 22:22:59 | 22:23:26 | T72 | 10:12:24 | 10:15:40 | T97 | 01:38:46 | 01:40:19 |
| T23 | 06:00:56 | 06:07:44 | T48 | 14:54:37 | 15:01:20 | T73 | 04:11:12 | 04:13:29 | T98 | 21:52:57 | 21:57:37 |
| T24 | 11:36:34 | 11:39:09 | T49 | 10:31:17 | 10:33:26 | T74 | 23:46:30 | 23:48:07 | T99 | 16:38:35 | 16:41:21 |
| T25 | 17:52:10 | 17:53:19 | T50 | 23:35:08 | 23:37:21 | T75 | 21:33:47 | 21:40:44 | T100 | 14:09:03 | 14:12:14 |
| Instance | S | T | ||||
|---|---|---|---|---|---|---|
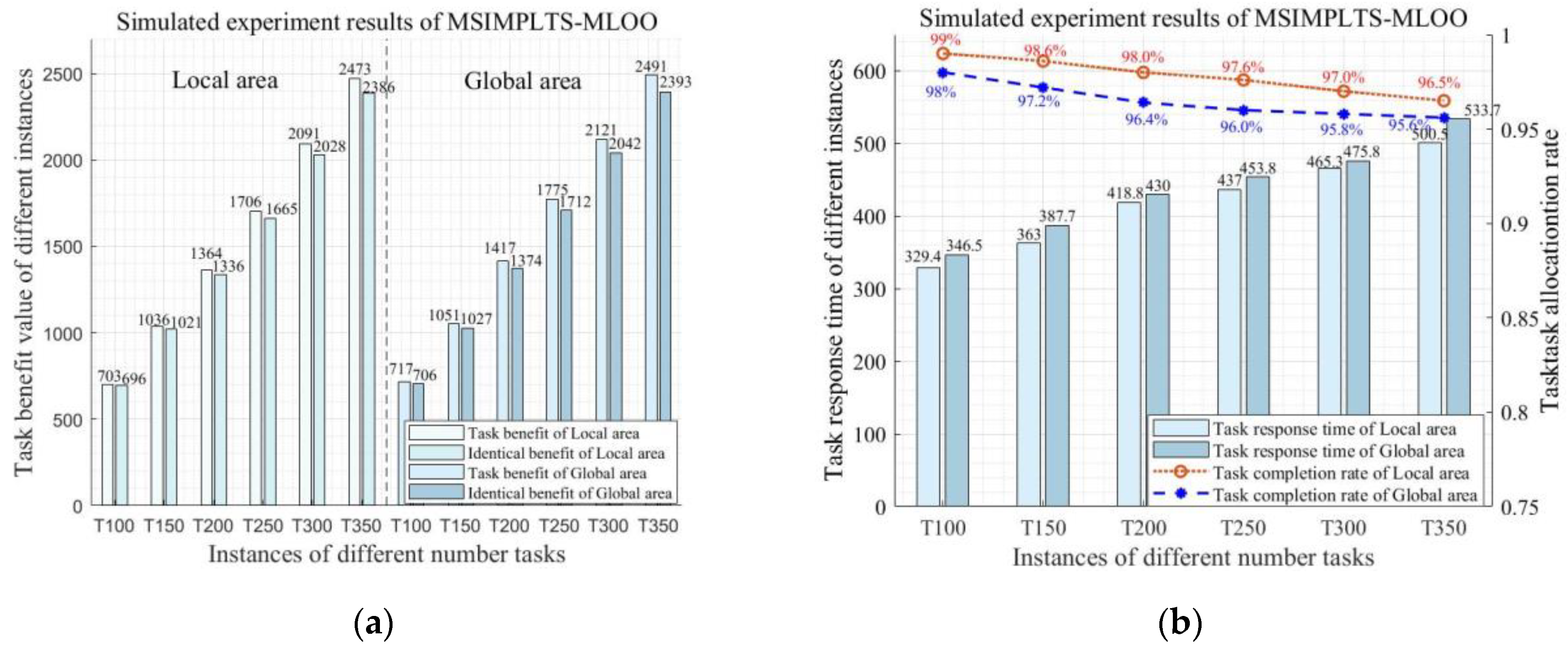
| LA_100 | 8 | 100 | 703 | 696 | 99.0% | 329.4 |
| GA_100 | 8 | 100 | 717 | 706 | 98.6% | 346.5 |
| LA_150 | 8 | 150 | 1036 | 1021 | 98.6% | 363.0 |
| GA_150 | 8 | 150 | 1051 | 1027 | 97.8% | 387.7 |
| LA_200 | 8 | 200 | 1364 | 1336 | 98.0% | 418.8 |
| GA_200 | 8 | 200 | 1417 | 1374 | 97.0% | 430.0 |
| LA_250 | 8 | 250 | 1706 | 1665 | 97.6% | 437.0 |
| GA_250 | 8 | 250 | 1775 | 1712 | 96.5% | 453.8 |
| LA_300 | 8 | 300 | 2091 | 2028 | 97.0% | 465.3 |
| GA_300 | 8 | 300 | 2121 | 2042 | 96.3% | 475.8 |
| LA_350 | 8 | 350 | 2473 | 2386 | 96.5% | 500.5 |
| GA_350 | 8 | 350 | 2491 | 2393 | 96.1% | 533.7 |
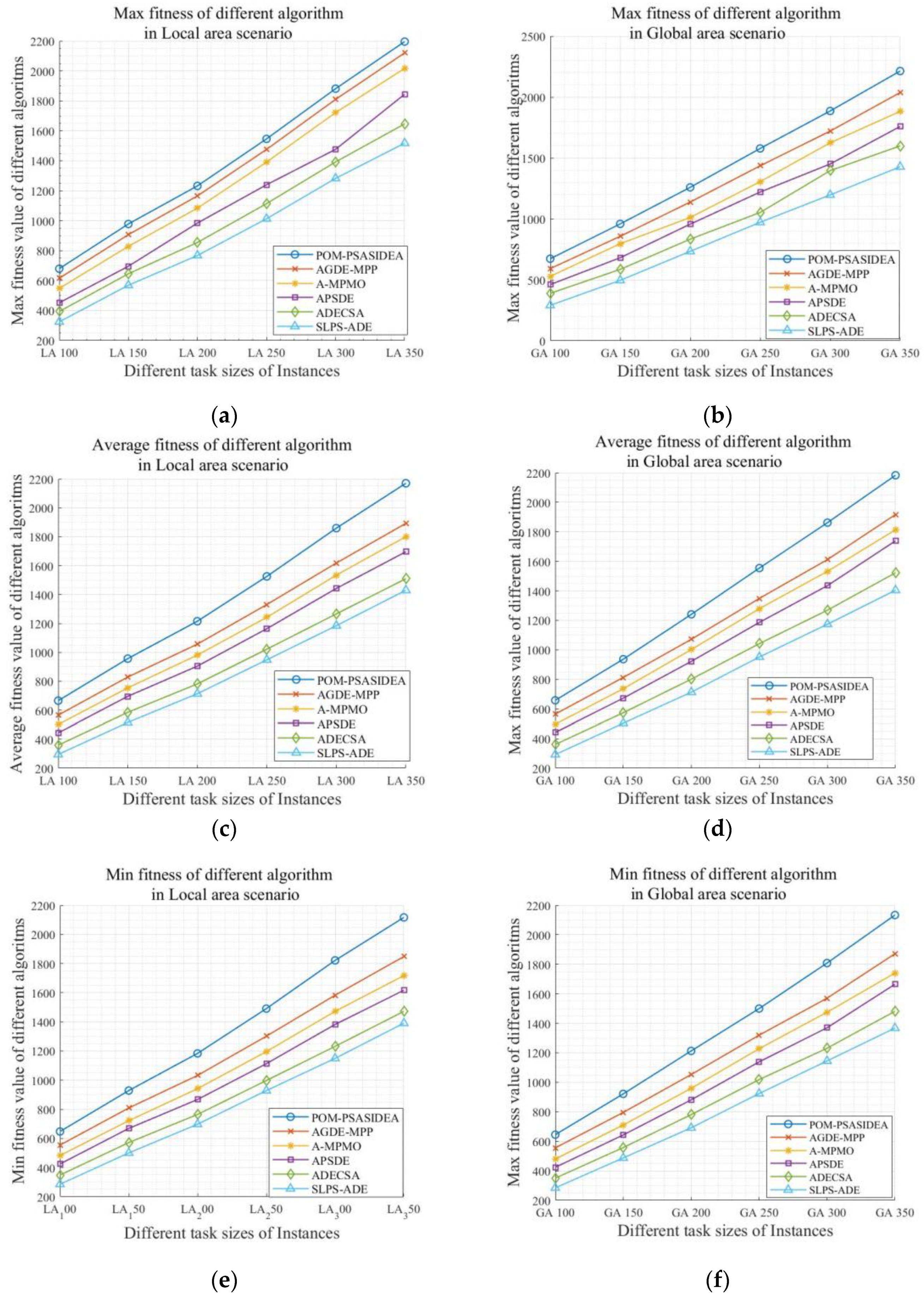
| Instances | POM-PSASIDEA | AGDE-MPP | A-MPMO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| LA_100 | 479.6 | 465.6 | 447.8 | 446 | 415.7 | 404.5 | 417.6 | 401.5 | 382.8 |
| LA_150 | 778.1 | 756.6 | 728.7 | 728.1 | 678.9 | 659.2 | 667.1 | 654 | 621.9 |
| LA_200 | 1032.2 | 1015.2 | 983.7 | 967.6 | 906.5 | 882.5 | 924.9 | 880.9 | 841.6 |
| LA_250 | 1346.0 | 1325.6 | 1290.9 | 1264.3 | 1180.9 | 1151.6 | 1222.5 | 1142.5 | 1095.8 |
| LA_300 | 1681.2 | 1659.7 | 1621.7 | 1571.6 | 1468.3 | 1432.9 | 1578.2 | 1434.7 | 1372.3 |
| LA_350 | 1995.6 | 1970.3 | 1916.7 | 1865.9 | 1742.8 | 1698.2 | 1734.7 | 1700.7 | 1617.7 |
| Avg | 1218.7 | 1198.8 | 1164.9 | 1140.5 | 1065.5 | 1038.2 | 1090.8 | 1035.7 | 988.7 |
| GA_100 | 473.2 | 458.1 | 445.2 | 442.2 | 414.8 | 405.8 | 428.8 | 397 | 380.3 |
| GA_150 | 759.1 | 737.1 | 721.6 | 707.2 | 663.2 | 646 | 696.7 | 636.7 | 610.7 |
| GA_200 | 1059.0 | 1041.0 | 1012.7 | 988 | 921.8 | 902.9 | 911.3 | 902.3 | 859 |
| GA_250 | 1378.0 | 1354.7 | 1299.9 | 1285.7 | 1199.1 | 1169.5 | 1205.9 | 1179.5 | 1127.8 |
| GA_300 | 1685.3 | 1662.5 | 1608.4 | 1570.3 | 1462.3 | 1420.1 | 1524.4 | 1432.4 | 1375.1 |
| GA_350 | 2013.2 | 1983.6 | 1934.0 | 1886.4 | 1767.4 | 1721.7 | 1782.3 | 1713.9 | 1640.7 |
| Avg | 1227.9 | 1206.1 | 1170.3 | 1146.6 | 1071.4 | 1044.3 | 1091.6 | 1043.6 | 998.9 |
| Instances | APSDE | ADECSA | SLPS-ADE | ||||||
| LA_100 | 401.8 | 393.9 | 374.8 | 370.2 | 359.4 | 348.9 | 350.4 | 345.2 | 335.8 |
| LA_150 | 697.2 | 645.6 | 618.8 | 614.1 | 584.9 | 571.7 | 573.1 | 565.6 | 550.8 |
| LA_200 | 931.3 | 854.4 | 817.5 | 851.7 | 781.4 | 764.8 | 771.4 | 763.6 | 747.7 |
| LA_250 | 1189.7 | 1113.7 | 1062.8 | 1093.3 | 1021.8 | 997.5 | 992.6 | 998.2 | 978.2 |
| LA_300 | 1476.2 | 1392.6 | 1332.3 | 1342.5 | 1266.5 | 1232 | 1234.1 | 1234.7 | 1199.6 |
| LA_350 | 1794.4 | 1646.3 | 1567 | 1540 | 1509.6 | 1472.3 | 1492 | 1480 | 1441 |
| Avg | 1081.8 | 1007.8 | 962.2 | 968.6 | 920.6 | 897.9 | 902.3 | 897.9 | 875.5 |
| GA_100 | 411.3 | 391.7 | 374.1 | 389.4 | 360.6 | 350.6 | 341 | 342.3 | 334.7 |
| GA_150 | 631.4 | 623.2 | 593.3 | 586 | 574.4 | 557.8 | 546.1 | 554 | 537.4 |
| GA_200 | 907.1 | 872.2 | 831.2 | 833.8 | 801.7 | 780.8 | 783.8 | 763.5 | 741.6 |
| GA_250 | 1170.5 | 1136.4 | 1088.6 | 1053 | 1042.6 | 1018.4 | 1022.3 | 1001.9 | 973.8 |
| GA_300 | 1400.5 | 1385.7 | 1319.8 | 1396.1 | 1269.2 | 1231.1 | 1246.9 | 1224.2 | 1194.9 |
| GA_350 | 1858.2 | 1689.3 | 1614.8 | 1599 | 1522.8 | 1481.7 | 1477.8 | 1454.5 | 1417.8 |
| Avg | 1063.2 | 1016.4 | 970.3 | 976.2 | 928.6 | 903.4 | 903.0 | 890.1 | 866.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Hu, M.; Huang, G.; Huang, F. Multi-Layer Objective Model and Progressive Optimization Mechanism for Multi-Satellite Imaging Mission Planning in Large-Scale Target Scenarios. Appl. Sci. 2024, 14, 8597. https://doi.org/10.3390/app14198597
Yang X, Hu M, Huang G, Huang F. Multi-Layer Objective Model and Progressive Optimization Mechanism for Multi-Satellite Imaging Mission Planning in Large-Scale Target Scenarios. Applied Sciences. 2024; 14(19):8597. https://doi.org/10.3390/app14198597
Chicago/Turabian StyleYang, Xueying, Min Hu, Gang Huang, and Feiyao Huang. 2024. "Multi-Layer Objective Model and Progressive Optimization Mechanism for Multi-Satellite Imaging Mission Planning in Large-Scale Target Scenarios" Applied Sciences 14, no. 19: 8597. https://doi.org/10.3390/app14198597
APA StyleYang, X., Hu, M., Huang, G., & Huang, F. (2024). Multi-Layer Objective Model and Progressive Optimization Mechanism for Multi-Satellite Imaging Mission Planning in Large-Scale Target Scenarios. Applied Sciences, 14(19), 8597. https://doi.org/10.3390/app14198597











