Comparison of the Wind Speed Estimation Algorithms of Wind Turbines Using a Drive Train Model and Extended Kalman Filter
Abstract
:1. Introduction
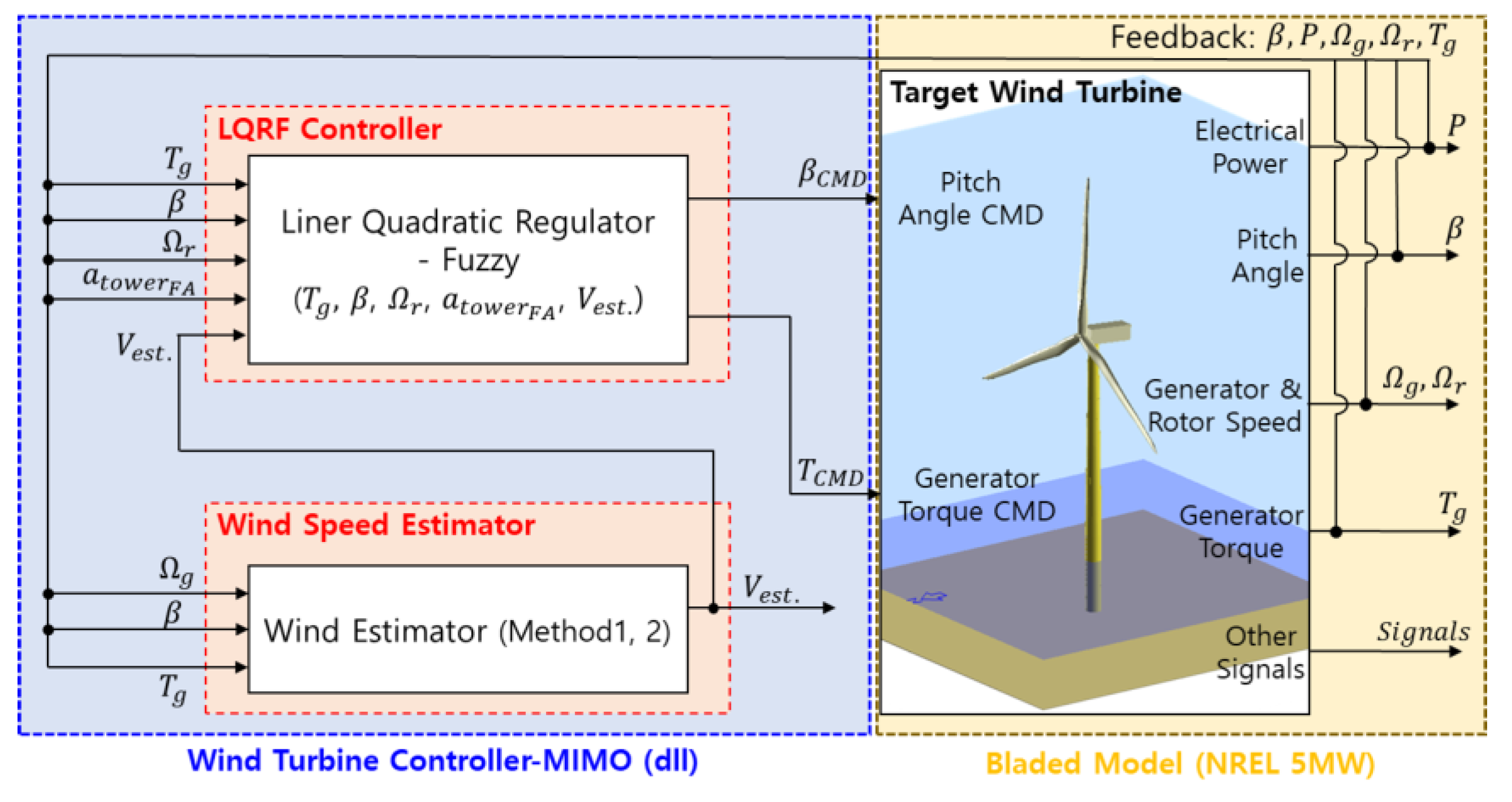
2. Wind Turbine and Control Algorithm
2.1. Target Wind Turbine
2.2. Control Algorithm
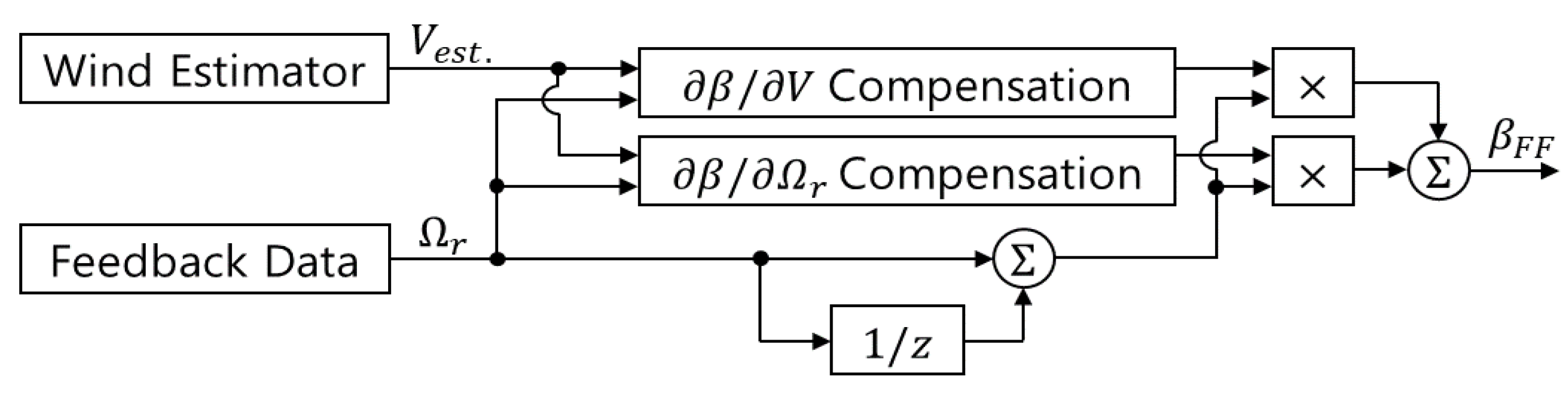
2.2.1. Feed-forward Control Algorithm
2.2.2. Available Power Estimator
2.2.3. Linear Quadratic Regulator Based on Fuzzy Control Algorithm
3. Wind Estimation Algorithms
3.1. Method Based on Drive Train Model for Wind Estimation
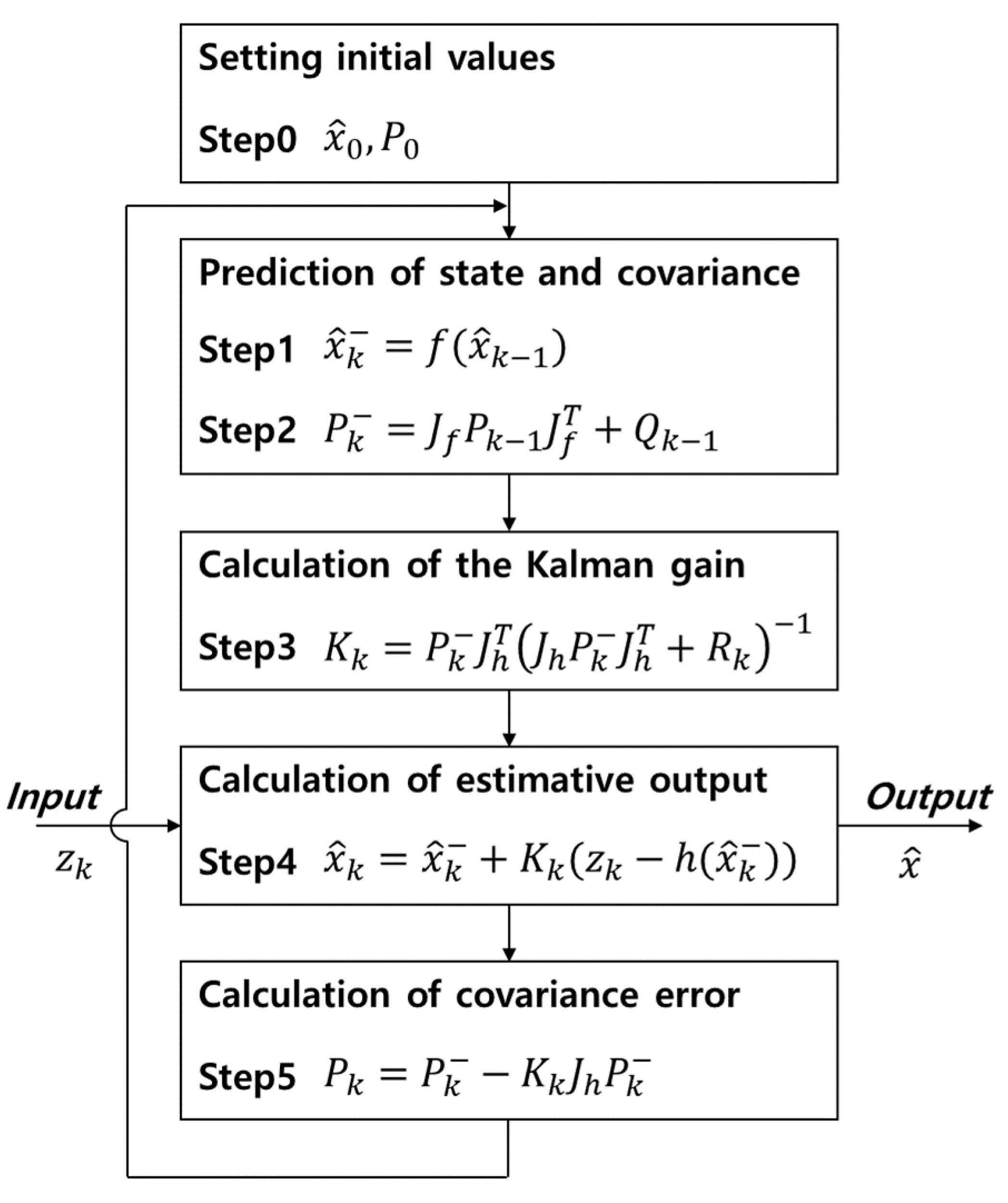
3.2. Method Based on Extended Kalman Filter for Wind Estimation
4. Simulation Validation
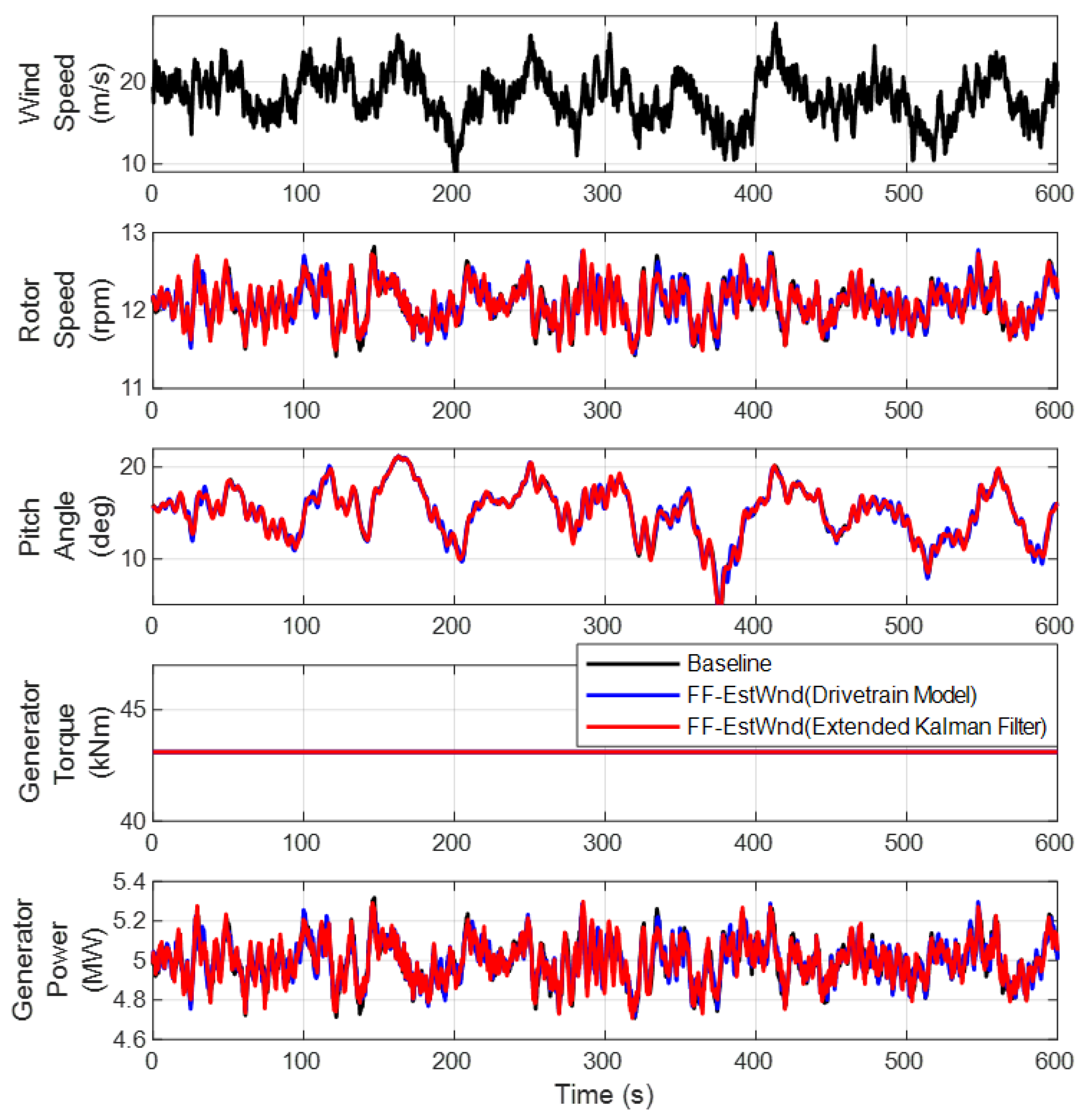
4.1. Validation 1: Feed-forward Control Algorithm
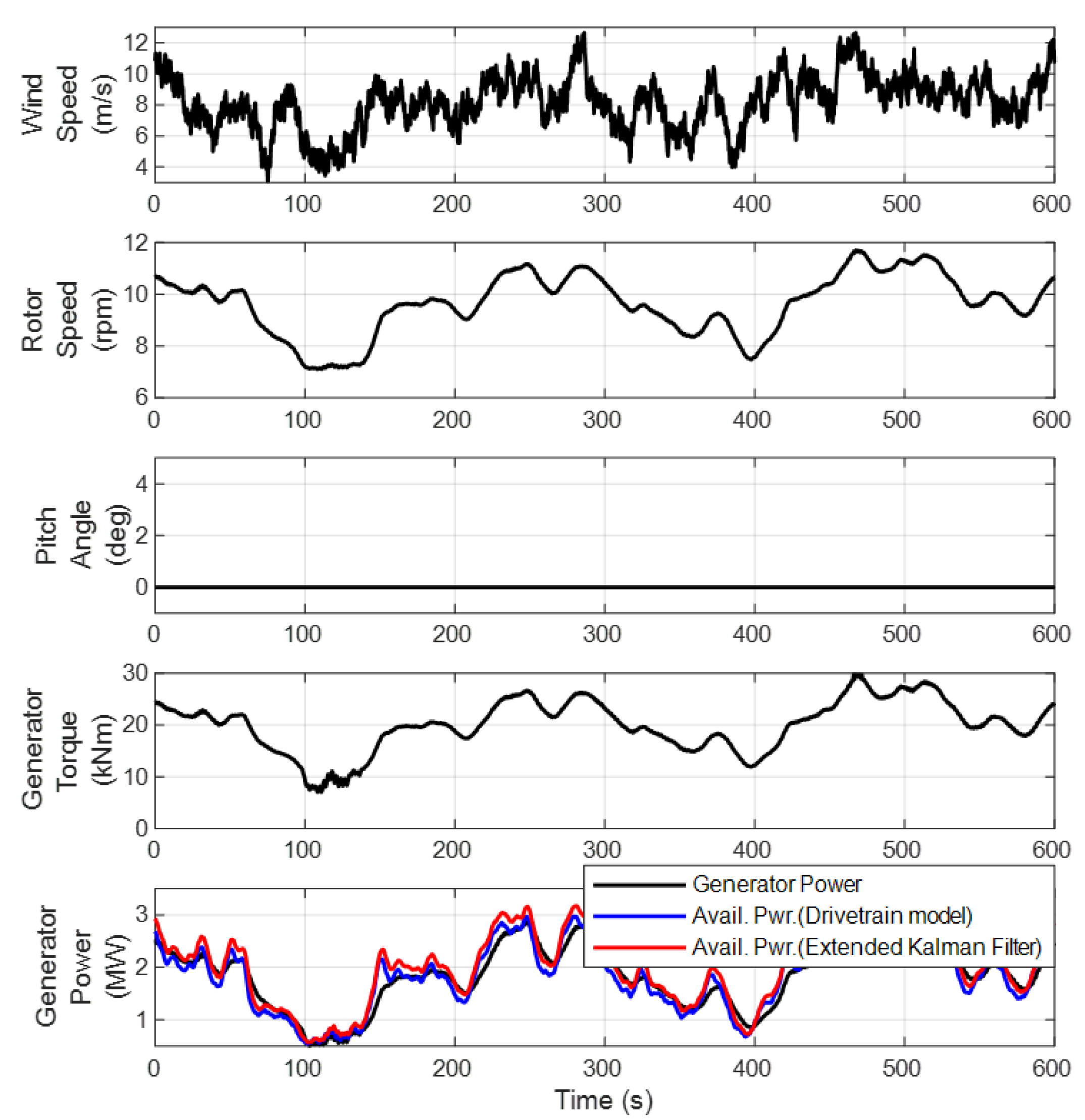
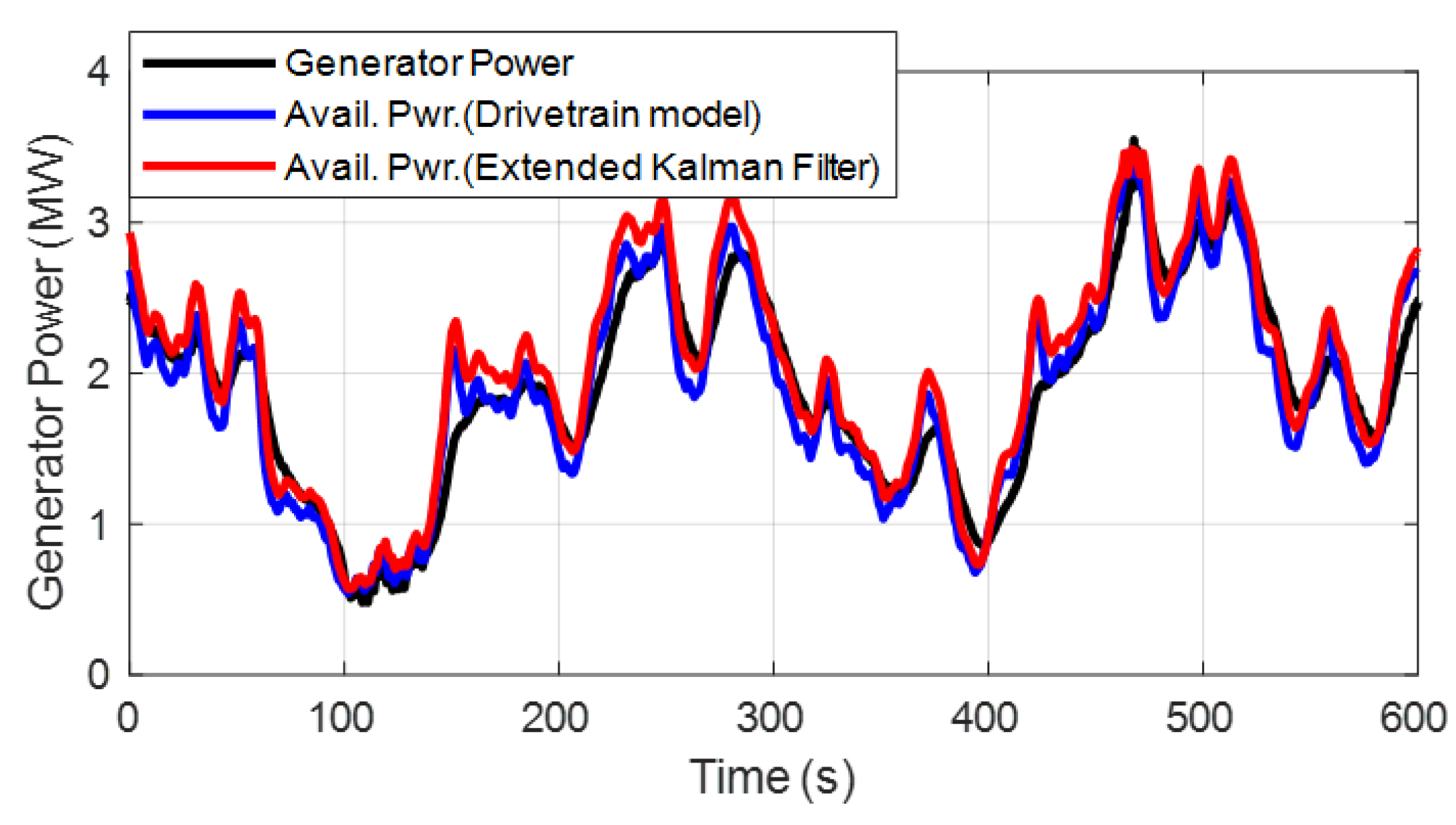
4.2. Validation 2: Available Power Estimator
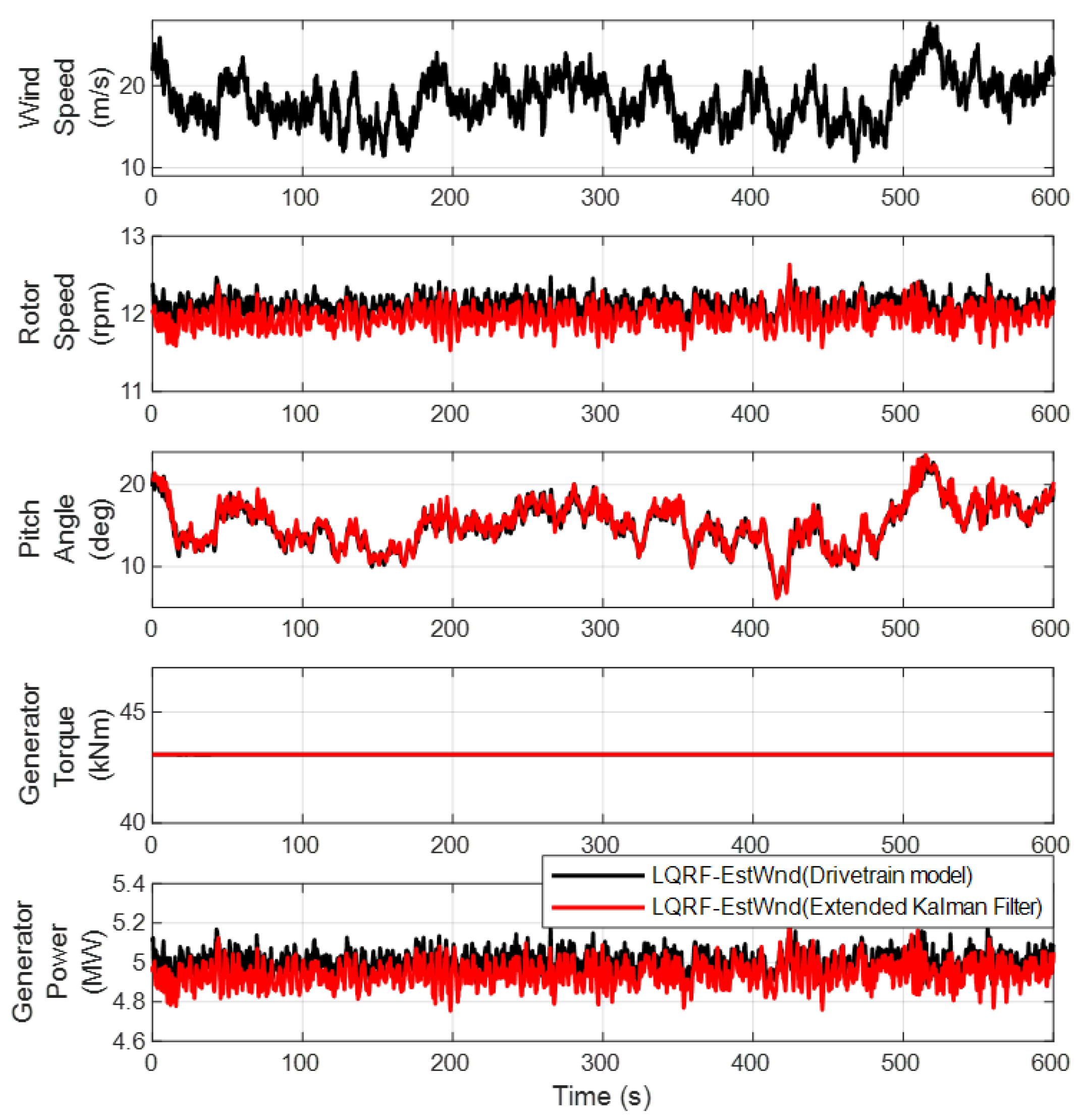
4.3. Validation 3: Linear Quadratic Regulator Based on Fuzzy Control Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| D | Dimensional |
| Diff | Difference |
| DLL | Dynamic link library |
| DPPT | Demanded power point tracking |
| DTM | Drive train model |
| EKF | Extended Kalman filter |
| HAWT | Horizontal axis wind turbine |
| LQR | Linear quadratic regulator |
| LQRF | Linear quadratic regulator based on fuzzy logic |
| MAE | Mean absolute error |
| MIMO | Multi-input–multi-output |
| MPPT | Maximum power point tracking |
| MSE | Mean square error |
| NREL | National Renewable Energy Laboratory |
| NTM | Normal turbulence model |
| P | Proportional |
| PI | Proportional integral |
| PID | Proportional integral derivative |
| RMSE | Root mean square error |
| ROSCO | Reference open-source controller |
| SISO | Single-input–single-output |
| TSR | Tip speed ratio |
| VSVP | Variable speed–variable pitch |
| Symbols | |
| Rotor swept area | |
| System matrix | |
| Generator damping coefficient | |
| Input matrix | |
| Rotor damping coefficient | |
| Output matrix | |
| Power coefficient | |
| Jacobian vector | |
| Generator moment of inertia | |
| Rotor moment of inertia | |
| Kalman gain | |
| Gear ratio | |
| Available power | |
| Predicted value of error covariance | |
| Noise covariance | |
| Torque command | |
| Aerodynamic torque | |
| Generator torque | |
| Estimated wind speed | |
| Measurement value | |
| Nacelle fore–aft displacement | |
| Nacelle fore–aft velocity | |
| u | Input vector |
| x | State vector |
| Time derivative of state vector | |
| y | Output vector |
| Estimated result | |
| Predicted value of system | |
| Change in wind speed | |
| Additional pitch command by feed-forward control | |
| Change in rotor speed | |
| Pitch angle | |
| Pitch rate | |
| Pitch command | |
| Rotor speed | |
| Electrical loss | |
| Mechanical loss | |
| Measurement noise | |
| System noise | |
| Applied air density | |
| Partial derivative of pitch angle | |
| Partial derivative of wind speed | |
| Partial derivative of rotor speed | |
References
- Nouriani, A.; Moradi, H. Variable speed wind turbine power control: A comparison between multiple MPPT based methods. Int. J. Dyn. Control 2021, 10, 654–667. [Google Scholar] [CrossRef]
- Navarrete, E.C.; Trejo Perea, M.; Jáuregui Correa, J.C.; Carrillo Serrano, R.V.; Moreno, G.J.R. Expert Control Systems Implemented in a Pitch Control of Wind Turbine: A Review. IEEE Access 2019, 7, 13241–13259. [Google Scholar] [CrossRef]
- Nam, Y. Wind Turbine System Control, 1st ed.; GS Intervision: Seoul, Republic of Korea, 2013. [Google Scholar]
- Njiri, J.G.; Beganovic, N.; Do, M.H.; Söffker, D. Consideration of lifetime and fatigue load in wind turbine control. Renew. Energy 2019, 131, 818–828. [Google Scholar] [CrossRef]
- Wang, S.S.; Moan, T.; Nejad, A.R. A comparative study of fully coupled and de-coupled methods on dynamic behaviour of floating wind turbine drivetrains. Renew. Energy 2021, 179, 1618–1635. [Google Scholar] [CrossRef]
- Bao, J.; Yue, H.; Leithead, W.E.; Wang, J.-Q. Feedforward control for wind turbine load reduction with pseudo-LIDAR measurement. Int. J. Autom. Comput. 2018, 15, 142–155. [Google Scholar] [CrossRef]
- Schlipf, D.; Cheng, P.W. Flatness-based feedforward control of wind turbines using lidar. In Proceedings of the 19th World Congress of the International Federation of Automatic Control, Cape Town, South Africa, 25–29 August 2014. [Google Scholar]
- Nam, Y.; Kim, J.; Paek, I.; Moon, Y.; Kim, S.; Kim, D. Feedforward Pitch Control Using Wind Speed Estimation. J. Power Electron. 2011, 11, 211–217. [Google Scholar] [CrossRef]
- Bossanyi, E. Individual blade pitch control for load reduction. Wind Energy 2003, 6, 119–128. [Google Scholar] [CrossRef]
- Ossmann, D.; Seiler, P. Field testing of multi-variable individual pitch control on a utility-scale wind turbine. Renew. Energy 2021, 170, 1245–1256. [Google Scholar] [CrossRef]
- Tian, D.; Tang, S.; Tao, L.; Li, B.; Wu, X. Peak shaving strategy for load reduction of wind turbines based on model predictive control. Energy Rep. 2023, 9, 338–349. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Wind turbine control for load reduction. Wind Energy 2003, 6, 229–244. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Siguerdidjane, H. Nonlinear control with wind estimation of a DFIG variable speed wind turbine for power capture optimization. Energy Convers. Manag. 2009, 50, 885–892. [Google Scholar] [CrossRef]
- Jeon, T.; Paek, I. Design and Verification of the LQR Controller Based on Fuzzy Logic for Large Wind Turbine. Energies 2021, 14, 230. [Google Scholar] [CrossRef]
- Sudarsana Reddy, K.; Mahalakshmi, R. A MIMO-Based Compatible Fuzzy Logic Controller for DFIG-Based Wind Turbine Generator. In Artificial Intelligence and Technologies; Raje, R.R., Hussain, F., Kannan, R.J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2022; Volume 806. [Google Scholar]
- Nayeh, R.F.; Moradi, H.; Vossoughi, G.J. Multivariable robust control of a horizontal wind turbine under various operating modes and uncertainties: A comparison on sliding mode and H∞ control. Int. J. Electr. Power Energy Syst. 2020, 115, 105474. [Google Scholar] [CrossRef]
- Stockhouse, D.; Pusch, M.; Damiani, R.; Sirnivas, S.; Pao, L. Robust Multi-Loop Control of a Floating Offshore Wind Turbine. Wind Energy 2023, 1–24. Available online: https://onlinelibrary.wiley.com/doi/10.1002/we.2864 (accessed on 26 September 2024).
- Kim, D.; Jeon, T.; Paek, I.; Kim, D. A Study on Available Power Estimation Algorithm and Its Validation. Energies 2022, 15, 2648. [Google Scholar] [CrossRef]
- Chen, P.; Han, D. Effective wind speed estimation study of the wind turbine based on deep learning. Energy 2022, 247, 123491. [Google Scholar] [CrossRef]
- Hur, S. Short-term wind speed prediction using Extended Kalman filter and machine learning. Energy Rep. 2021, 7, 1046–1054. [Google Scholar] [CrossRef]
- Hur, S. Estimation of Useful Variables in Wind Turbines and Farms Using Neural Networks and Extended Kalman Filter. IEEE Access 2019, 7, 24017–24028. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Dong, M.; Joo, Y.H. Kalman filter-based wind speed estimation for wind turbine control. Int. J. Control Autom. Syst. 2017, 15, 1089–1096. [Google Scholar] [CrossRef]
- Abbas, N.; Zalkind, D.; Pao, L.; Wright, A. A Reference Open-Source Controller for Fixed and Floating Offshore Wind Turbines. Wind Energ. Sci. 2022, 7, 53–73. Available online: https://wes.copernicus.org/articles/7/53/2022/ (accessed on 13 September 2024). [CrossRef]
- Song, D.; Yang, J.; Cai, Z.; Dong, M.; Su, M.; Wang, Y. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines. Appl. Energy 2017, 190, 670–685. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Kim, H.; Kim, K.; Paek, I. Model Based Open-loop wind farm control using active power for power increase and load reduction. Appl. Sci. 2017, 7, 1068. [Google Scholar] [CrossRef]
- Kim, H.; Kim, K.; Paek, I.; Bottasso, C.L.; Campagnolo, F. A Study on the Active Induction Control of Upstream Wind Turbines for total power increases. J. Phys. Conf. Ser. 2016, 753, 32016. [Google Scholar] [CrossRef]
- Grewal, M.S. Kalman Filtering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Knudsen, T.; Bak, T.; Soltani, M. Prediction models for wind speed at turbine locations in a wind farm. Wind Energy 2011, 14, 877–894. [Google Scholar] [CrossRef]



| Specification | Unit | Value |
|---|---|---|
| Wind Turbine Type | - | HAWT, VSVP, Upwind |
| Rated Power | MW | 5 |
| Rotor Diameter | m | 162 |
| Hub Height | m | 90 |
| Rated Wind Speed | m/s | 11.4 |
| Rated Rotor Speed | rpm | 12.1 |
| Fine Pitch Angle | deg | 0 |
| Optimal Tip Speed Ratio | - | 7.8 |
| Max-Cp | - | 0.48 |
| Gear Ratio | - | 1:97 |
| Condition | Wind Speed [m/s, %] | |||
|---|---|---|---|---|
| Mean | Error | Std. | Error | |
| Rotor Averaged | 17.80 | - | 1.94 | - |
| DTM | 18.26 | 2.58 | 2.05 | 5.67 |
| EKF | 18.29 | 2.75 | 2.01 | 3.61 |
| Condition | Rotor Speed [rpm, %] | Electrical Power [MW, %] | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Diff. | Std. | Diff. | Mean | Diff. | Std. | Diff. | |
| Baseline | 12.10 | - | 0.2482 | - | 5.00 | - | 0.1035 | - |
| DTM | 12.10 | 0 | 0.2332 | −6.04 | 5.00 | 0 | 0.0945 | −8.70 |
| EKF | 12.09 | −0.08 | 0.2431 | −2.05 | 5.00 | 0 | 0.1015 | −1.93 |
Method | Electrical Power (MW, %) | |||
|---|---|---|---|---|
| Mean | Error | Std. | Error | |
| Generator Power | 1.9041 | - | 0.6533 | - |
| Available Power-DTM | 1.8930 | −0.58 | 0.6799 | 4.07 |
| Available Power-EKF | 2.0429 | 7.29 | 0.7080 | 8.37 |
Method | Electrical Power (MW) | ||
|---|---|---|---|
| RMSE | MSE | MAE | |
| Available Power-DTM | 0.2061 | 0.0425 | 0.1672 |
| Available Power-EKF | 0.2332 | 0.0544 | 0.1818 |
| Condition | Rotor Speed [rpm, %] | Electrical Power [MW, %] | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Diff. | Std. | Diff. | Mean | Diff. | Std. | Diff. | |
| DTM | 12.11 | - | 0.1104 | - | 5.00 | - | 0.0482 | - |
| EKF | 11.96 | −1.24 | 0.1356 | 22.83 | 4.94 | −1.20 | 0.0582 | 20.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Jeon, T.; Paek, I.; Roynarin, W. Comparison of the Wind Speed Estimation Algorithms of Wind Turbines Using a Drive Train Model and Extended Kalman Filter. Appl. Sci. 2024, 14, 8764. https://doi.org/10.3390/app14198764
Kim D, Jeon T, Paek I, Roynarin W. Comparison of the Wind Speed Estimation Algorithms of Wind Turbines Using a Drive Train Model and Extended Kalman Filter. Applied Sciences. 2024; 14(19):8764. https://doi.org/10.3390/app14198764
Chicago/Turabian StyleKim, Dongmyoung, Taesu Jeon, Insu Paek, and Wirachai Roynarin. 2024. "Comparison of the Wind Speed Estimation Algorithms of Wind Turbines Using a Drive Train Model and Extended Kalman Filter" Applied Sciences 14, no. 19: 8764. https://doi.org/10.3390/app14198764
APA StyleKim, D., Jeon, T., Paek, I., & Roynarin, W. (2024). Comparison of the Wind Speed Estimation Algorithms of Wind Turbines Using a Drive Train Model and Extended Kalman Filter. Applied Sciences, 14(19), 8764. https://doi.org/10.3390/app14198764







