Multi-Layer QCA Reversible Full Adder-Subtractor Using Reversible Gates for Reliable Information Transfer and Minimal Power Dissipation on Universal Quantum Computer
Abstract
:1. Introduction
- Review of the structure, operation, and characteristics of existing excellent QCA-based RFAS circuits
- Design of a reversible quantum gate (RQG)-based RFAS after presenting the problems of implementing the existing QCA circuits
- Best performance in all aspects compared with the existing circuits and significant improvements of at least 67% and 54% in delay and energy dissipation, respectively.
- Remarkable improvements of 180% and 562% in two representative design costs, CostAD and CostED, respectively, compared to the best existing circuit
- Noise-free and high and stable output polarization, especially a significant improvement of 3.8% in the average output polarization
- Proposal of an efficient QCA-based RFAS that minimizes information loss and provides reliable information transmission through the best performance of the proposed reversible circuit
2. Related Works
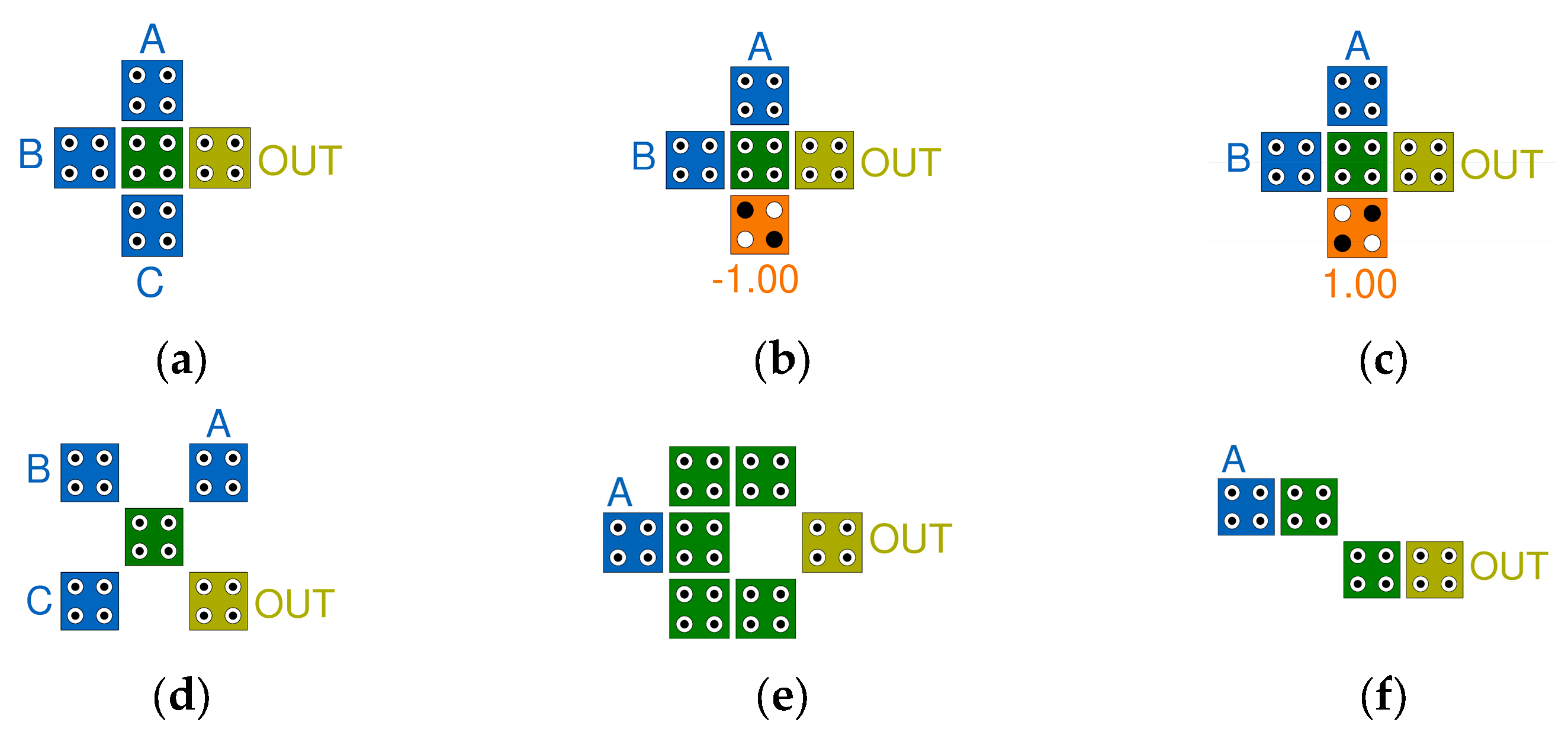
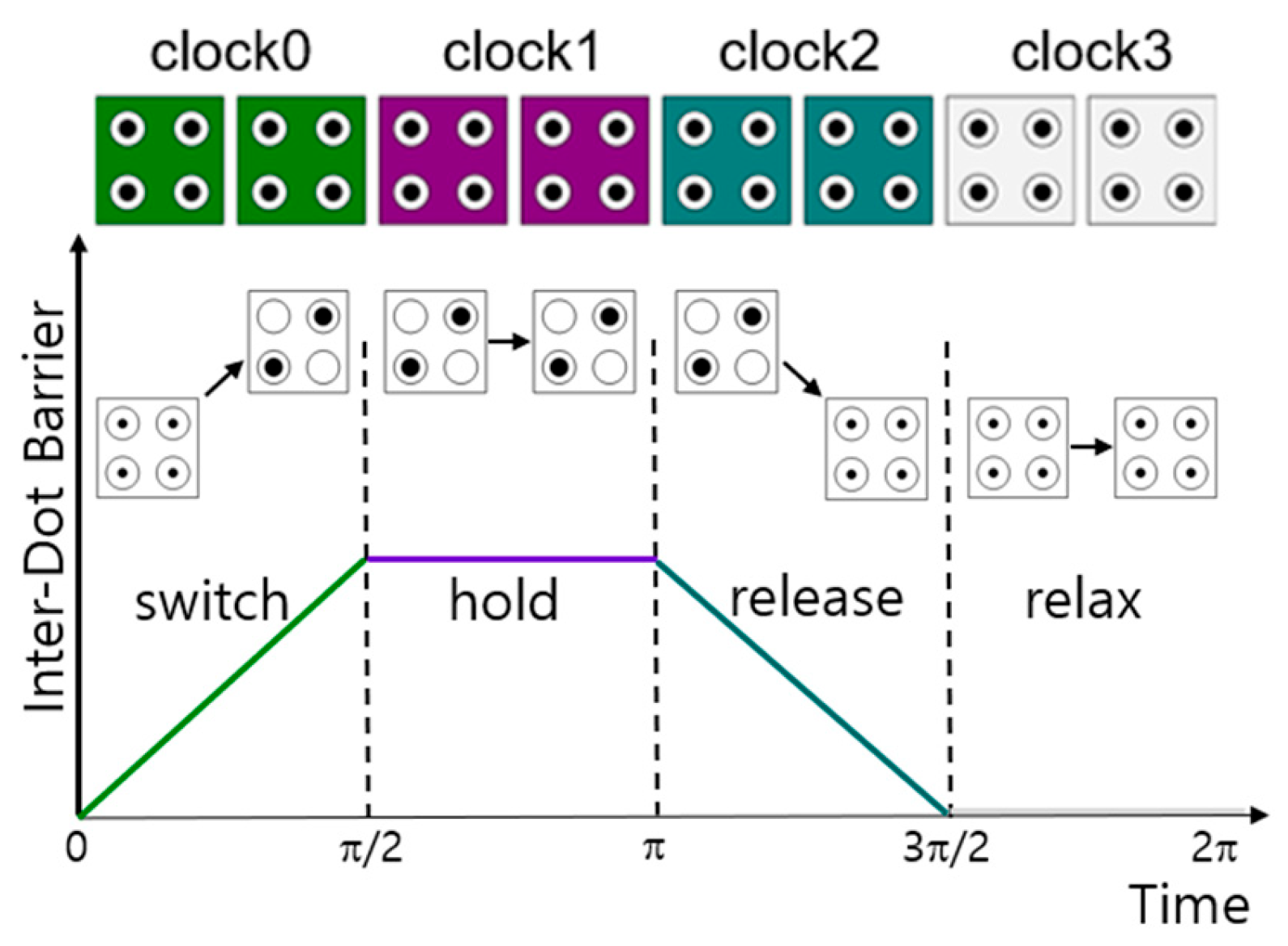
2.1. QCA Gates and Clock Sates
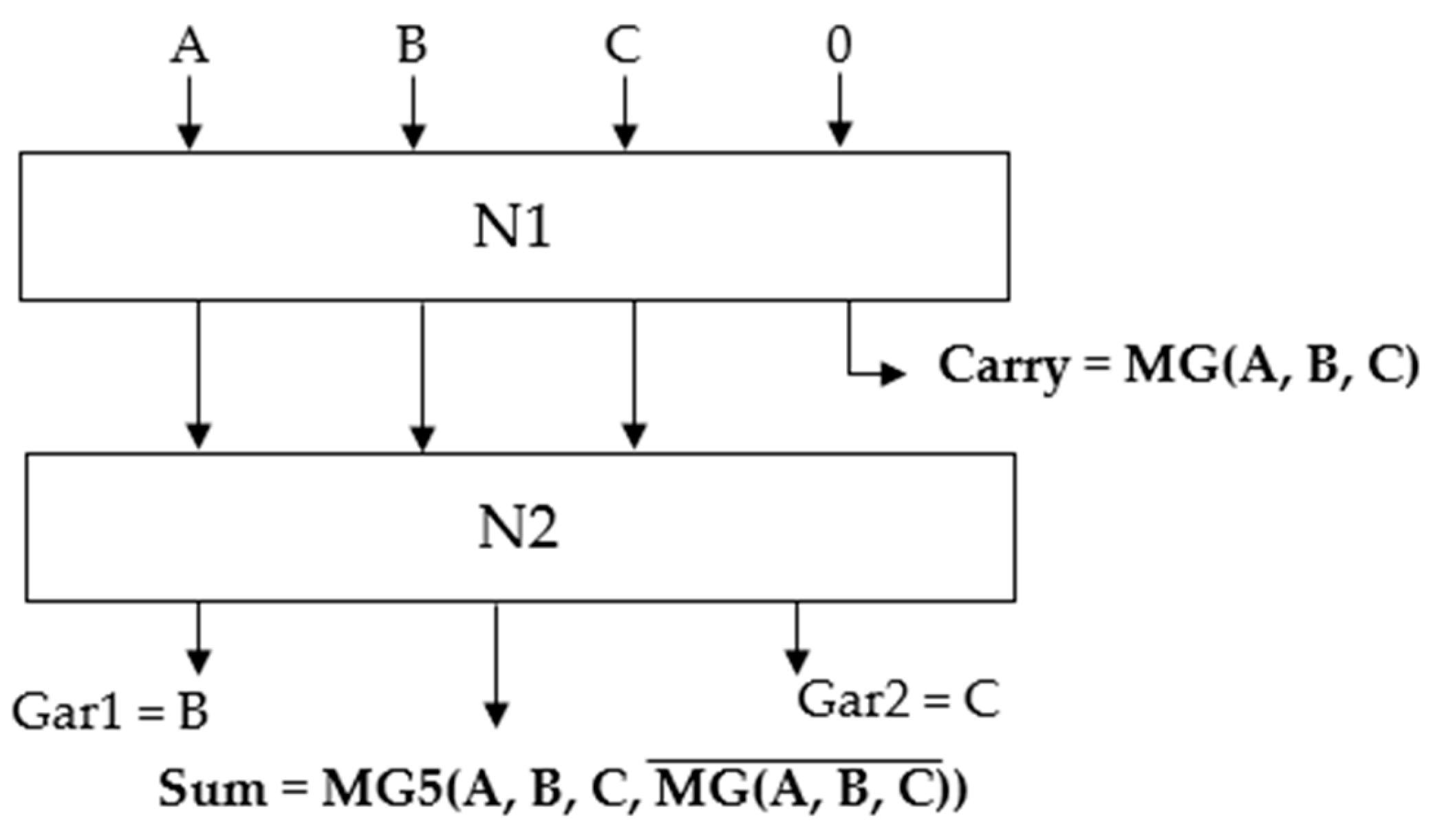
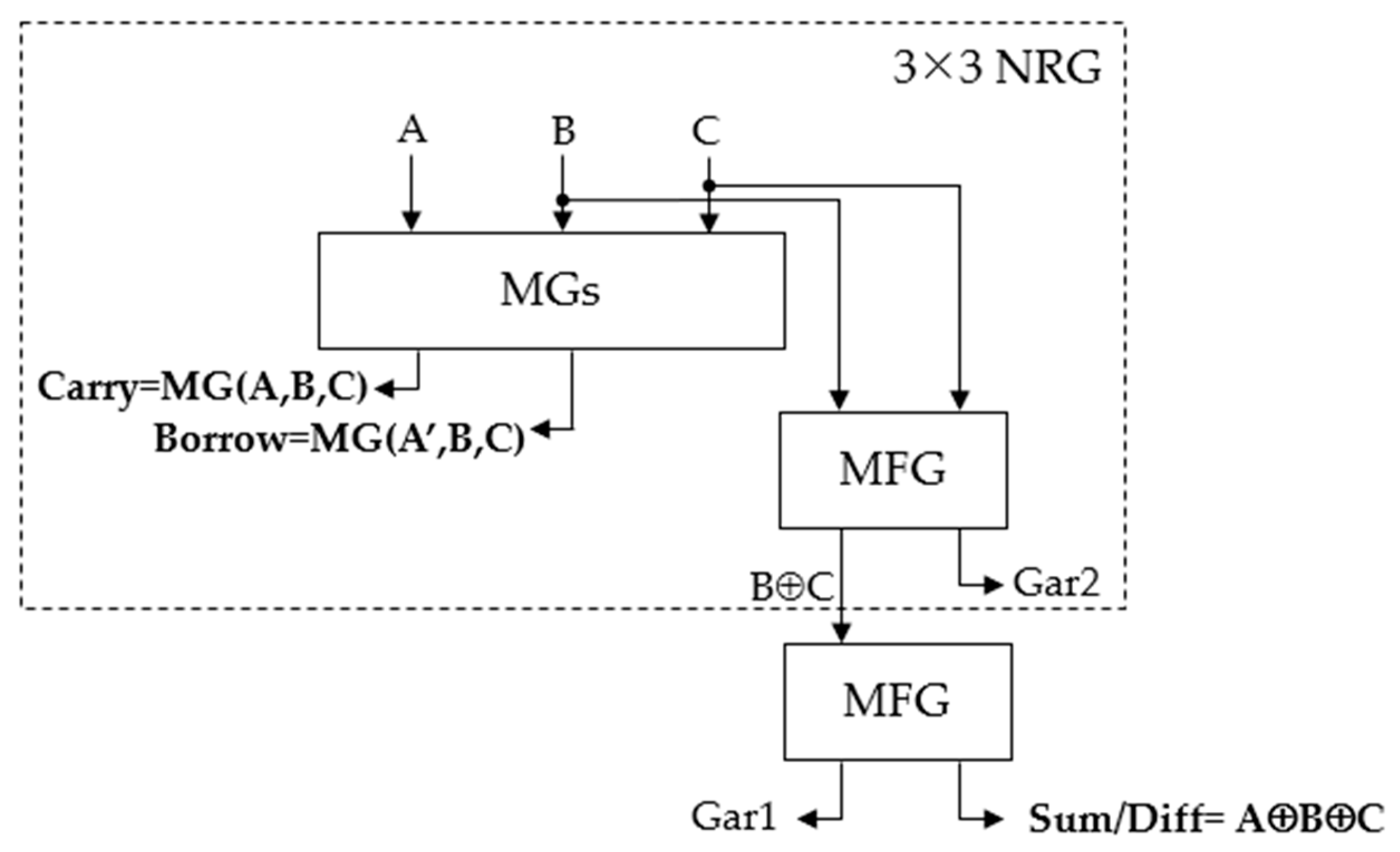
2.2. Conventional QCA Reversible Full Adder-Subtractors
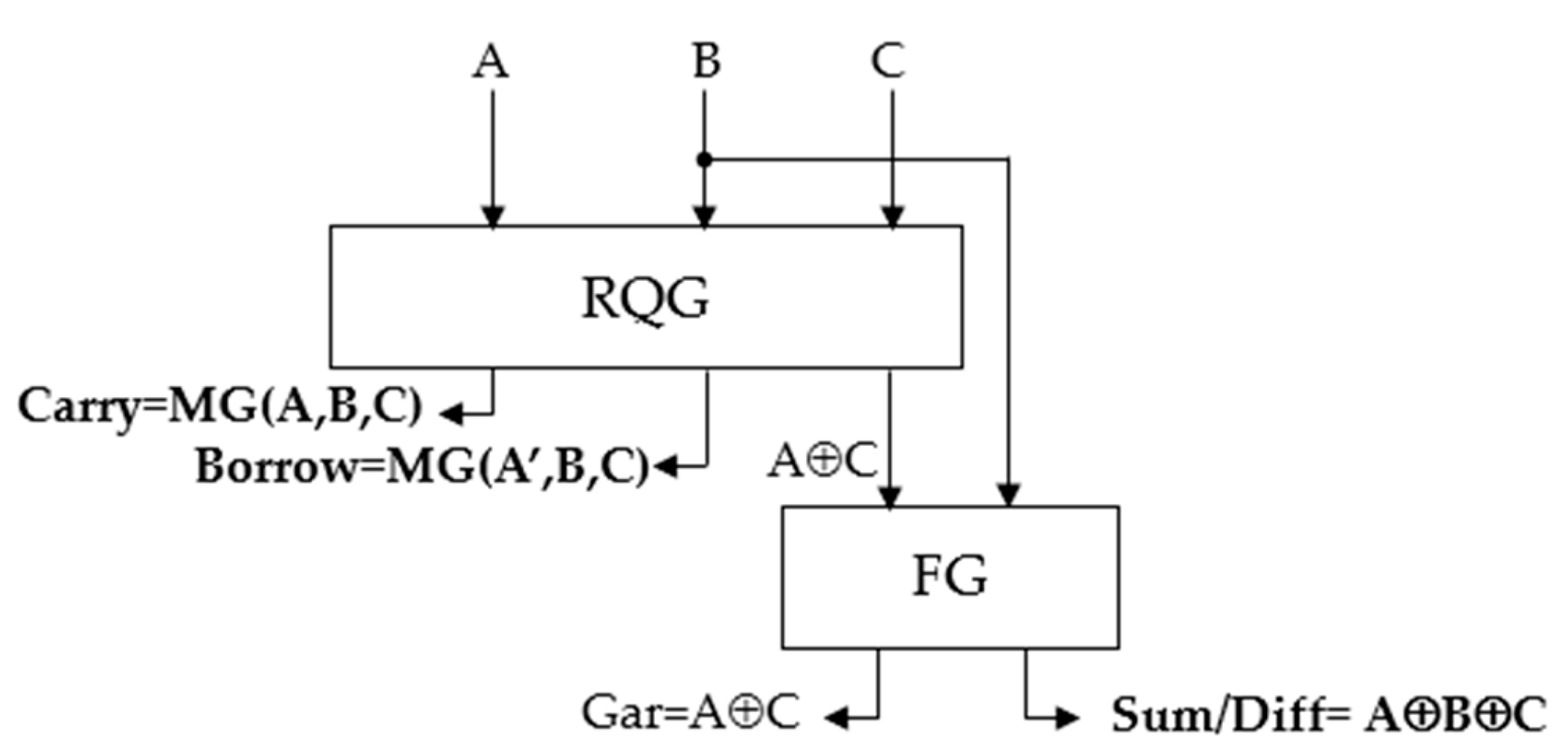
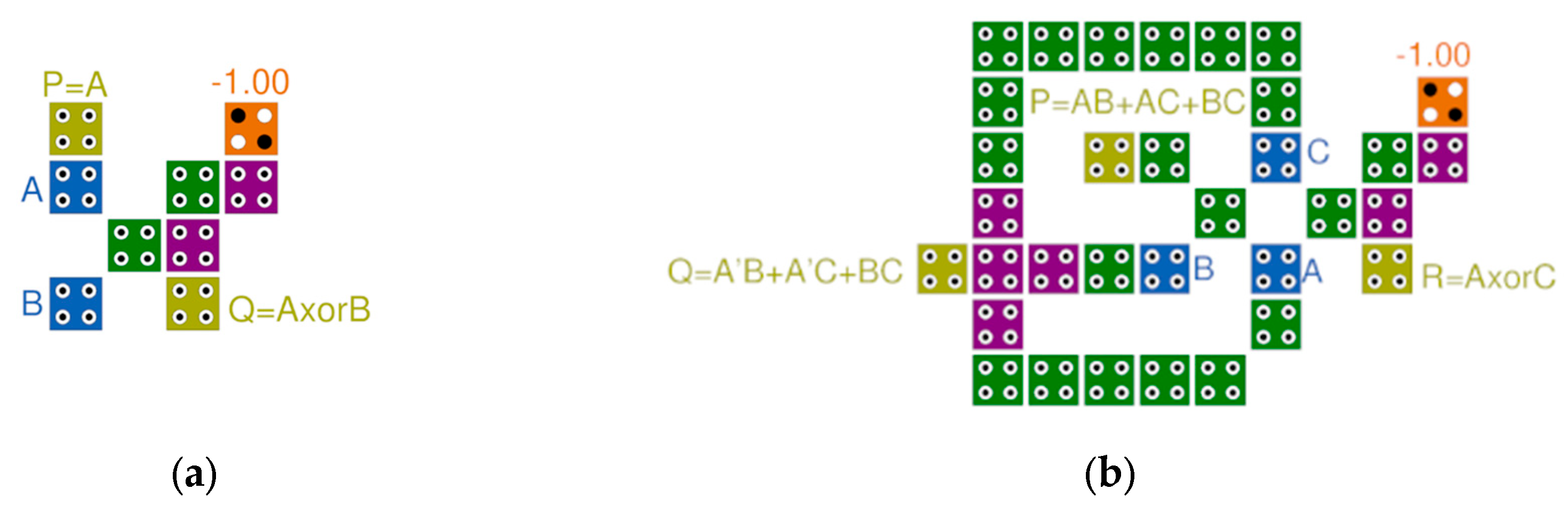
3. Proposed Reversible Full Adder-Subtractor
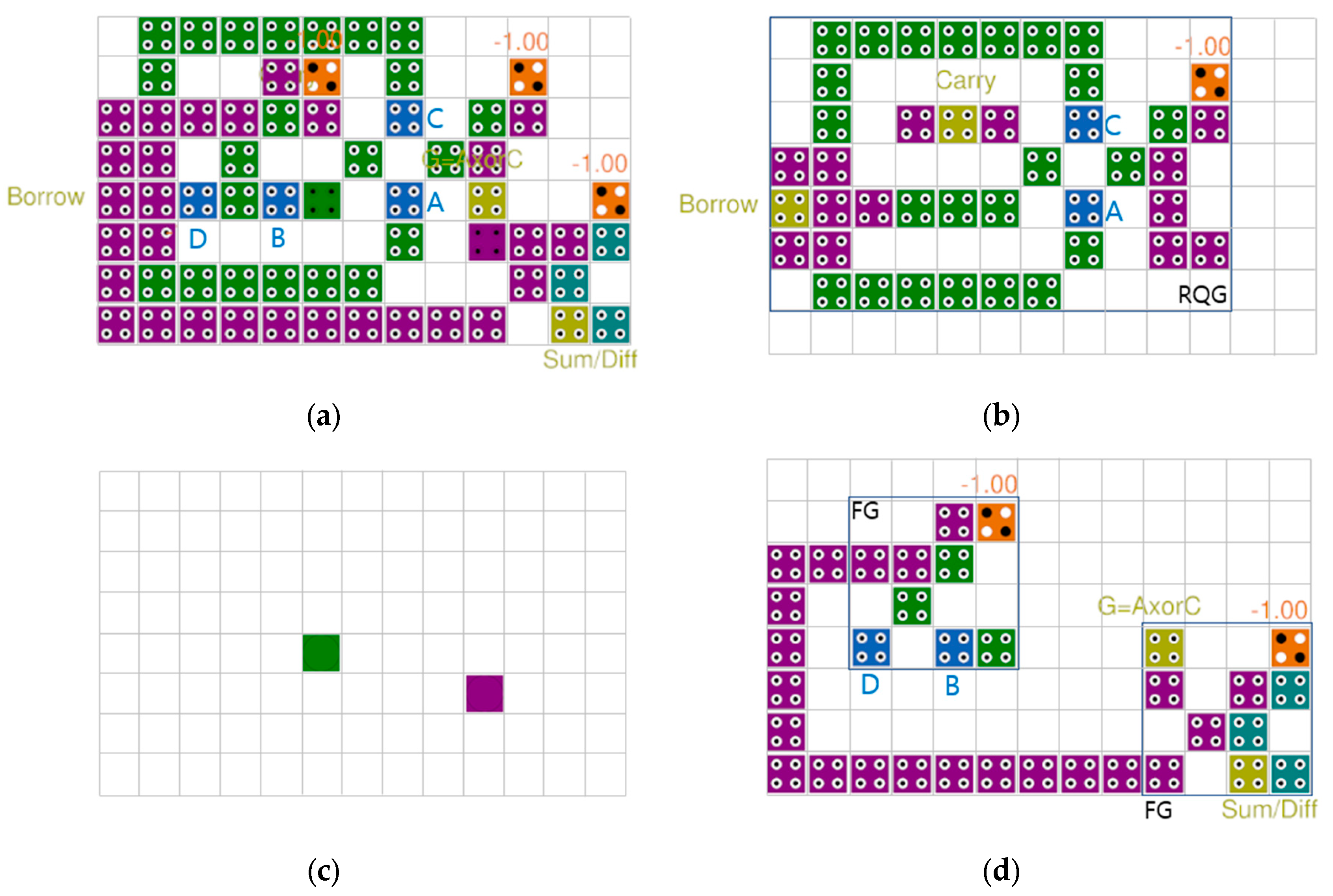
4. Simulation and Performance Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bilal, B.; Ahmed, S.; Kakkar, V. An insight into beyond CMOS Next generation computing using quantum-dot cellular automata nanotechnology. Int. J. Eng. Manuf. 2018, 8, 25–37. [Google Scholar] [CrossRef]
- Moore, G.E. No exponential is forever: But “Forever” can be delayed! [semiconductor industry]. In Proceedings of the 2003 IEEE International Solid-State Circuits Conference, 2003. Digest of Technical Papers, ISSCC, San Francisco, CA, USA, 13–13 February 2003; pp. 20–23. [Google Scholar]
- Dennard, R.H.; Gaensslen, F.H.; Kuhn, L.; Yu, H.N. Design of micron MOS switching devices. In Proceedings of the International Electron Devices Meeting, Washington, DC, USA, 4–6 January 1972; pp. 168–170. [Google Scholar]
- Iwai, H. Roadmap for 22 nm and beyond. Microelectron. Eng. 2009, 86, 1520–1528. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Song, Y.; Wu, Y.; Wu, S.; Li, D.; Wen, Q.; Qin, S.; Gao, F. A quantum federated learning framework for classical clients. Sci. China Phys. Mech. Astron. 2024, 67, 250311. [Google Scholar] [CrossRef]
- Toffoli, T. Reversible computing. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 1980; pp. 632–644. [Google Scholar]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [PubMed]
- Fredkin, E.; Toffoli, T. Conservative Logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Feynman, R. Quantum Mechanical Computers. Opt. News 1985, 11, 11–20. [Google Scholar] [CrossRef]
- Peres, A. Reversible logic and quantum computers. Phys. Rev. A 1985, 32, 3266–3276. [Google Scholar] [CrossRef]
- Sen, B.; Adak, T.; Anand, A.S.; Sikdar, B.K. Synthesis of reversible universal QCA gate structure for energy efficient digital design. In Proceedings of the IEEE Region 10 Conference TENCON, Bali, Indonesia, 21–24 November 2011; pp. 806–810. [Google Scholar]
- Sen, B.; Dutta, M.; Some, S.; Sikdar, B.K. Realizing Reversible Computing in QCA Framework Resulting in Efficient Design of Testable ALU. ACM J. Emerg. Technol. Comput. Syst. 2014, 11, 1–22. [Google Scholar] [CrossRef]
- Islam, M.S.; Abdullah-Al-Shafi, M.; Bahar, A.N. A new approach of presenting universal reversible gate in nanoscale. Int. J. Comput. Appl. 2016, 134, 1–4. [Google Scholar]
- Saravanan, S.; Vennila, I.; Mohanram, S. Design and Implementation of an Efficient Reversible Comparator Using TR Gate. Circuits Syst. 2016, 7, 2578–2592. [Google Scholar] [CrossRef]
- Chabi, A.M.; Roohi, A.; Khademolhosseini, H.; Sheikhfaal, S.; Angizi, S.; Navi, K.; De-Mara, R.F. Towards ultra-efficient QCA reversible circuits. Microprocess. Microsyst. 2017, 49, 127–138. [Google Scholar] [CrossRef]
- Moustafa, A.; Younes, A. Efficient Synthesis of Reversible Circuits Using Quantum Dot Cellular Automata. IEEE Access 2021, 9, 76662–76673. [Google Scholar] [CrossRef]
- Lent, C.; Tougaw, P. A device architecture for computing with quantum dots. Proc. IEEE 1997, 85, 541–557. [Google Scholar] [CrossRef]
- Srivastava, S.; Sarkar, S.; Bhanja, S. Power dissipation bounds and models for quantum-dot cellular automata circuits. In Proceedings of the 2006 Sixth IEEE Conference on Nanotechnology, Cincinnati, OH, US, 17–20 July 2006; Volume 1, pp. 375–378. [Google Scholar]
- Srivastava, S.; Sarkar, S.; Bhanja, S. Estimation of upper bound of power dissipation in QCA circuits. IEEE Trans. Nanotechnol. 2009, 8, 116–127. [Google Scholar] [CrossRef]
- Song, Z.; Xie, G.; Cheng, X.; Wang, L.; Zhang, Y. An Ultra-Low Cost Multilayer RAM in Quantum-Dot Cellular Automata. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3397–3401. [Google Scholar] [CrossRef]
- Heikalabad, S.R.; Salimzadeh, F.; Barughi, Y.Z. A unique three-layer full adder in quantum-dot cellular automata. Comput. Electr. Eng. 2020, 86, 106735. [Google Scholar] [CrossRef]
- Chu, Z.; Li, Z.; Xia, Y.; Wang, L.; Liu, W. BCD Adder Designs Based on Three-Input XOR and Majority Gates. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1942–1946. [Google Scholar] [CrossRef]
- Perri, S.; Spagnolo, F.; Frustaci, F.; Corsonello, P. Multibit Full Comparator Logic in Quantum-Dot Cellular Automata. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4508–4512. [Google Scholar] [CrossRef]
- Das, R.; Alam, M.S.; Ahmmed, K.T. An energy efficient design of a multi-layered crossover based 3:8 decoder using quantum-dot cellular automata. Heliyon 2022, 8, e11643. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Parameshwara, M.C.; Arya, R. Defects of quantum dot cellular automata computing devices: An extensive review, evaluation, and future directions. Microprocess. Microsyst. 2023, 101, 104912. [Google Scholar] [CrossRef]
- Khan, A.; Bahar, A.N.; Arya, R. Quad-functioning Parity Layout for Nanocomputing: A QCA Design. Nano Commun. Netw. 2024, 41, 100525. [Google Scholar] [CrossRef]
- Safoev, N.; Jeon, J.C. A novel controllable inverter and adder/subtractor in quantum-dot cellular automata using cell interaction based XOR gate. Microelectron. Eng. 2020, 222, 111197. [Google Scholar] [CrossRef]
- Safoev, N.; Jeon, J.C. Design of high-performance QCA incrementer/decrementer circuit based on adder/subtractor methodology. Microprocess. Microsyst. 2020, 72, 102927. [Google Scholar] [CrossRef]
- Erniyazov, S.; Jeon, J.C. Carry save adder and carry look ahead adder using inverter chain based coplanar QCA full adder for low energy dissipation. Microelectron. Eng. 2019, 211, 37–43. [Google Scholar] [CrossRef]
- Kianpour, M.; Sabbaghi-Nadooshan, R. Novel 8-bit reversible full adder/subtractor using a QCA reversible gate. J. Comput. Electron. 2017, 16, 459–472. [Google Scholar] [CrossRef]
- Hashemi, S.; Azghadi, M.R.; Navi, K. Design and analysis of efficient QCA reversible adders. J. Supercomput. 2018, 75, 2106–2125. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, S. Optimization of the area efficiency and robustness of a QCA-based reversible full adder. J. Comput. Electron. 2019, 18, 1478–1489. [Google Scholar] [CrossRef]
- Taherkhani, E.; Moaiyeri, M.H.; Angizi, S. Design of an ultra-efficient reversible full adder-subtractor in quantum-dot cellular automata. Optik 2017, 142, 557–563. [Google Scholar] [CrossRef]
- Ahmad, F.; Ahmed, S.; Kakkar, V.; Bhat, G.M.; Bahar, A.N.; Wani, S. Modular Design of Ultra-Efficient Reversible Full Adder-Subtractor in QCA with Power Dissipation Analysis. Int. J. Theor. Phys. 2018, 57, 2863–2880. [Google Scholar] [CrossRef]
- Vahabi, M.; Rahimi, E.; Lyakhov, P.; Bahar, A.N.; Wahid, K.A.; Otsuki, A. Novel Quan-tum-Dot Cellular Automata-Based Gate Designs for Efficient Reversible Computing. Sustainability 2023, 15, 2265. [Google Scholar] [CrossRef]
- Lent, C.S.; Tougaw, P.D.; Porod, W. Quantum cellular automata: The physics of computing with arrays of quantum dot molecules. In Proceedings of the Workshop on Physics and Computation, PhysComp ‘94, Dallas, TX, USA, 17–20 November 1994; pp. 5–13. [Google Scholar]
- Lent, C.S.; Tougaw, P.D. Logical devices implemented using quantum cellular automata. J. Appl. Phys. 1993, 75, 1818–1825. [Google Scholar]
- Jeon, J.C. “Multi-Layer QCA Shift Registers and Wiring Structure for LFSR in Stream Cipher with Low Energy Dissipation in Quantum Nanotechnology. Electronics 2023, 12, 4093. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Hussain, D.; Azimi, N.; Alenizi, F.A.; Safaiezadeh, B.; Ahmed, O.H.; Lee, S.-W.; Rahmani, A.M. Design and simulation of Full-Subtractor based on Quantum-Dot cellular automata technology. AEU—Int. J. Electron. Commun. 2023, 171, 154927. [Google Scholar] [CrossRef]
- Abutaleb, M.M. Utilizing charge reconfigurations of quantum-dot cells in building blocks to design nanoelectronic adder circuits. Comput. Electr. Eng. 2020, 86, 106712. [Google Scholar] [CrossRef]
- Walus, K.; Dysart, T.J.; Jullien, G.A.; Budiman, R.A. QCADesigner: A rapid design and simulation tool for quantum-dot cellular automata. IEEE Trans. Nanotechnol. 2004, 3, 26–31. [Google Scholar] [CrossRef]
- QCADesigner-E. Available online: https://github.com/FSillT/QCADesigner-E (accessed on 18 August 2024).
- Liu, W.; Lu, L.; O’Neill, M.; Swartzlander, E.E. A First Step toward Cost Functions for Quantum-Dot Cellular Automata Designs. IEEE Trans. Nanotechnol. 2014, 12, 476–487. [Google Scholar]
- Seo, D.K.; Jeon, J.C. QCA-Based Secure RAM Cell Structure Using Logic Transformation and Cell Interaction with Signal Reliability and Energy Dissipation in Quantum Computing. Appl. Sci. 2023, 13, 9998. [Google Scholar] [CrossRef]
- Jeon, J.C. Quantum-Dot CA-Based Fredkin Gate and Conservative D-latch for Reliability-Based Information Transmission on Reversible Computing. Electronics 2024, 13, 2872. [Google Scholar] [CrossRef]
- Timler, J.; Lent, C.S. Power gain and dissipation in quantum-dot cellular automata. J. Appl. Phys. 2002, 91, 823–831. [Google Scholar] [CrossRef]
- Torres, F.S.; Wille, R.; Niemann, P.; Drechsler, R. An Energy-Aware Model for the Logic Synthesis of Quantum-Dot Cellular Automata. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 3031–3041. [Google Scholar] [CrossRef]
- Jeon, J.C. Low-complexity QCA universal shift register design using multiplexer and D flip-flop based on electronic correlations. J. Supercomput. 2020, 76, 6438–6452. [Google Scholar] [CrossRef]
- Jeon, J.C. Designing nanotechnology QCA–multiplexer using majority function-based NAND for quantum computing. J. Supercomput. 2021, 77, 1562–1578. [Google Scholar] [CrossRef]
- Abdullah-Al-Shafi, M.; Bahar, A.N.; Bhuiyan, M.M.R.; Shamim, S.M.; Ahmed, K. Average out-put polarization dataset for signifying the temperature influence for QCA designed reversible logic circuits. Data Brief 2018, 19, 42–48. [Google Scholar] [CrossRef]


| Reference | Year | Structure | Major Contributions |
|---|---|---|---|
| [32] | 2017 | RFAS | 3 × 3 QCA Reversible (QR) gate using Toffoli and Fredkin gates |
| [33] | 2018 | RFA | 4 × 4 N1 and 3 × 3 N2 gates based on a 5-input majority gate |
| [34] | 2019 | RFA | Area optimization using a 5-input majority gate |
| [35] | 2017 | RFAS | 3 × 3 Reversible Quantum Gate (RQG) |
| [36] | 2018 | RFAS | 3 × 3-New Reversible Gate (NRG) and Modified Feynman Gate (MFG) |
| [37] | 2023 | RFAS | Optimization of RQG |
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| A | B | C | Carry | Borrow | Sum/Diff |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| QCADesigner 2.0.3 | QCADesigner-E 2.2 | |
|---|---|---|
| Parameters | Bistable Approximation | Coherence Vector with Energy |
| Cell size (nm) | 18 | 18 |
| Dot diameter (nm) | 5 | 5 |
| Cell separation (nm) | 2 | 2 |
| Layer separation (nm) | 11.5 | 11.5 |
| Clock high (J) | 9.8 × 10−22 | 9.8 × 10−22 |
| Clock low (J) | 3.8 × 10−23 | 3.8 × 10−23 |
| Clock shift | 0 | 0 |
| Clock amplitude factor | 2.0 | 2.0 |
| Relative permittivity | 12.9 | 12.9 |
| Radius of effect (nm) | 65 | 80 |
| Number of samples | 12,800 | - |
| Convergence tolerance | 1.0 × 10−3 | - |
| Maximum iterations per sample | 100 | - |
| Temperature (K) | - | 1 |
| Relaxation time (s) | - | 1.0 × 10−15 |
| Clock slope (s) | - | 1.0 × 10−12 |
| Time step (s) | - | 1.0 × 10−16 |
| Clock/input period (s) | - | 4.0 × 10−12 |
| Circuit | Cell Count | Area | Delay | CostAD | Operation | ||||
|---|---|---|---|---|---|---|---|---|---|
| no. | Ratio | µm2 | Ratio | Clock | Ratio | AD2 | Ratio | ||
| [32] | 399 | 5.18 | 0.50 | 4.2 | 2 | 2.67 | 2.00 | 29.6 | RFAS |
| [33] | 236 | 3.06 | 0.32 | 2.7 | 3.25 | 4.33 | 3.38 | 50.1 | RFA |
| [34] | 178 | 2.31 | 0.23 | 1.9 | 3.25 | 4.33 | 2.43 | 36.0 | RFA |
| [35] | 228 | 2.96 | 0.28 | 2.3 | 1.75 | 2.33 | 0.86 | 12.7 | RFAS |
| [36] | 121 | 1.57 | 0.14 | 1.2 | 1.25 | 1.67 | 0.22 | 3.2 | RFAS |
| [37] | 123 | 1.60 | 0.12 | 1.0 | 1.25 | 1.67 | 0.19 | 2.8 | RFAS |
| Ours | 77 | 1.00 | 0.12 | 1.0 | 0.75 | 1.00 | 0.07 | 1.0 | RFAS |
| Circuit | Avg_Ebath | Error_Avg | Sum_Ebath | Error_Sum | CostED | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10−3 eV | Ratio | −10−4 eV | Ratio | 10−2 eV | Ratio | −10−3 eV | Ratio | E2D2 | Ratio | |
| [33] | 5.39 | 2.74 | 4.21 | 2.52 | 5.93 | 2.73 | 4.63 | 2.52 | 371.43 | 140.23 |
| [34] | 4.90 | 2.49 | 3.95 | 2.37 | 5.38 | 2.48 | 4.35 | 2.36 | 305.73 | 115.42 |
| [35] | 4.66 | 2.37 | 3.45 | 2.07 | 5.13 | 2.36 | 3.79 | 2.06 | 80.60 | 30.43 |
| [36] | 3.52 | 1.79 | 3.01 | 1.80 | 3.87 | 1.78 | 3.31 | 1.80 | 23.40 | 8.83 |
| [37] | 3.04 | 1.54 | 2.49 | 1.49 | 3.35 | 1.54 | 2.74 | 1.49 | 17.54 | 6.62 |
| Ours | 1.97 | 1.00 | 1.67 | 1.00 | 2.17 | 1.00 | 1.84 | 1.00 | 2.65 | 1.00 |
| Circuit | Carry | Borrow | Sum/Diff | Total | ||||
|---|---|---|---|---|---|---|---|---|
| AOP | Ratio | AOP | Ratio | AOP | Ratio | AOP | Ratio | |
| [33] | 9.540 | 0.967 | - | - | 9.550 | 0.969 | 9.545 | 0.966 |
| [34] | 9.540 | 0.967 | - | - | 9.550 | 0.969 | 9.545 | 0.966 |
| [35] | 9.540 | 0.967 | 9.550 | 0.963 | 9.540 | 0.968 | 9.543 | 0.966 |
| [36] | 9.540 | 0.967 | 9.530 | 0.961 | 9.530 | 0.967 | 9.533 | 0.965 |
| [37] | 9.540 | 0.967 | 9.530 | 0.961 | 9.475 | 0.961 | 9.515 | 0.963 |
| Ours | 9.870 | 1.000 | 9.920 | 1.000 | 9.860 | 1.000 | 9.883 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, J.-C. Multi-Layer QCA Reversible Full Adder-Subtractor Using Reversible Gates for Reliable Information Transfer and Minimal Power Dissipation on Universal Quantum Computer. Appl. Sci. 2024, 14, 8886. https://doi.org/10.3390/app14198886
Jeon J-C. Multi-Layer QCA Reversible Full Adder-Subtractor Using Reversible Gates for Reliable Information Transfer and Minimal Power Dissipation on Universal Quantum Computer. Applied Sciences. 2024; 14(19):8886. https://doi.org/10.3390/app14198886
Chicago/Turabian StyleJeon, Jun-Cheol. 2024. "Multi-Layer QCA Reversible Full Adder-Subtractor Using Reversible Gates for Reliable Information Transfer and Minimal Power Dissipation on Universal Quantum Computer" Applied Sciences 14, no. 19: 8886. https://doi.org/10.3390/app14198886
APA StyleJeon, J.-C. (2024). Multi-Layer QCA Reversible Full Adder-Subtractor Using Reversible Gates for Reliable Information Transfer and Minimal Power Dissipation on Universal Quantum Computer. Applied Sciences, 14(19), 8886. https://doi.org/10.3390/app14198886






