Consensus Control of Leader–Follower Multi-Agent Systems with Unknown Parameters and Its Circuit Implementation
Abstract
:1. Introduction
- (1)
- The dynamic characteristics of the financial system are analyzed, and the results show that the system behavior can be effectively controlled through the parameters of the financial system.
- (2)
- According to Lyapunov stability theorem, linear state feedback controllers are designed to synchronize financial systems. Meanwhile, adaptive control laws are derived for synchronization of master–slave systems with unknown parameters, and numerical simulations are given to verify the theoretical results.
- (3)
- The consensus theorem of leader–follower multi-agent systems is proved based on complex financial systems. The circuit implementation of master–slave systems consensus is provided through variable synchronization and parameter identification.
2. Dynamic Analysis of the Financial System
2.1. Equilibrium Point of Financial System (1)
2.2. Bifurcation Analysis of Financial System (1)
| Algorithm 1: Algorithm of Bifurcation with Respect to Parameter c |
|
3. Consensus Control of Master–Slave Systems
3.1. Consensus Control of Master–Slave Financial Systems
3.2. Consensus of Master–Slave Systems with Unknown Parameters
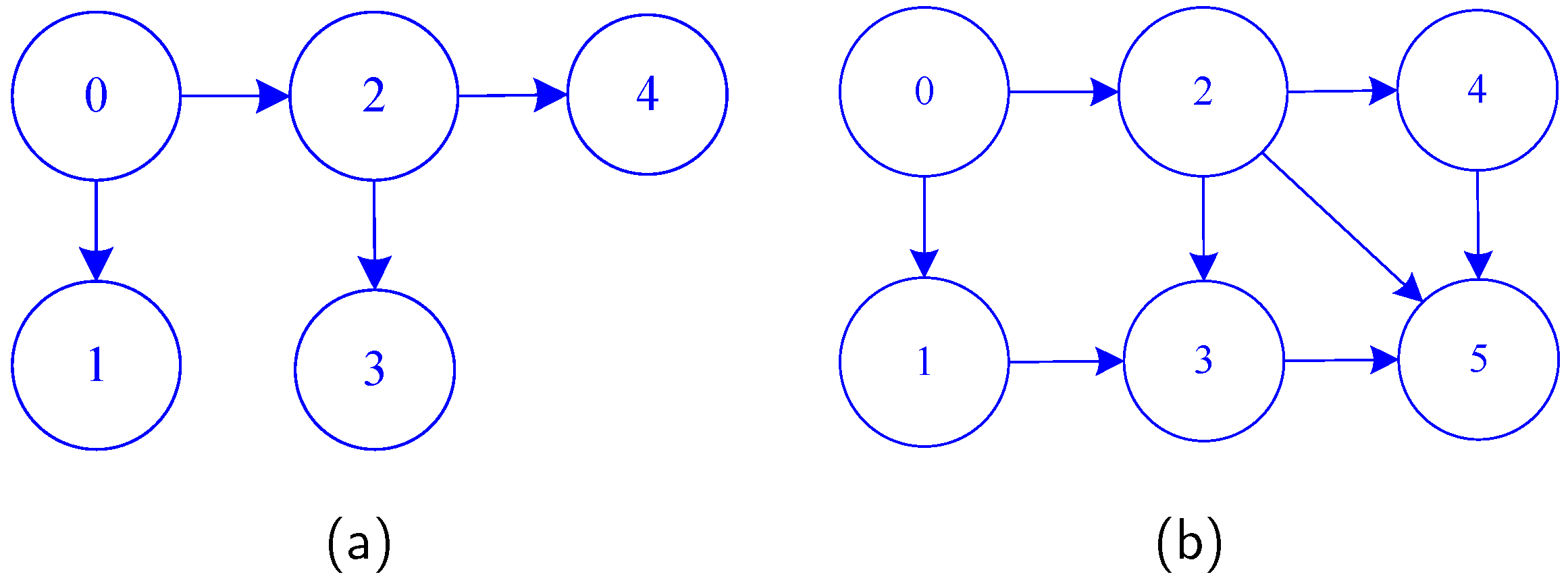
4. Consensus of Leader–Follower Multi-Agent Systems with Unknown Parameters
4.1. Consensus of Leader–Follower Multi-Agent Systems
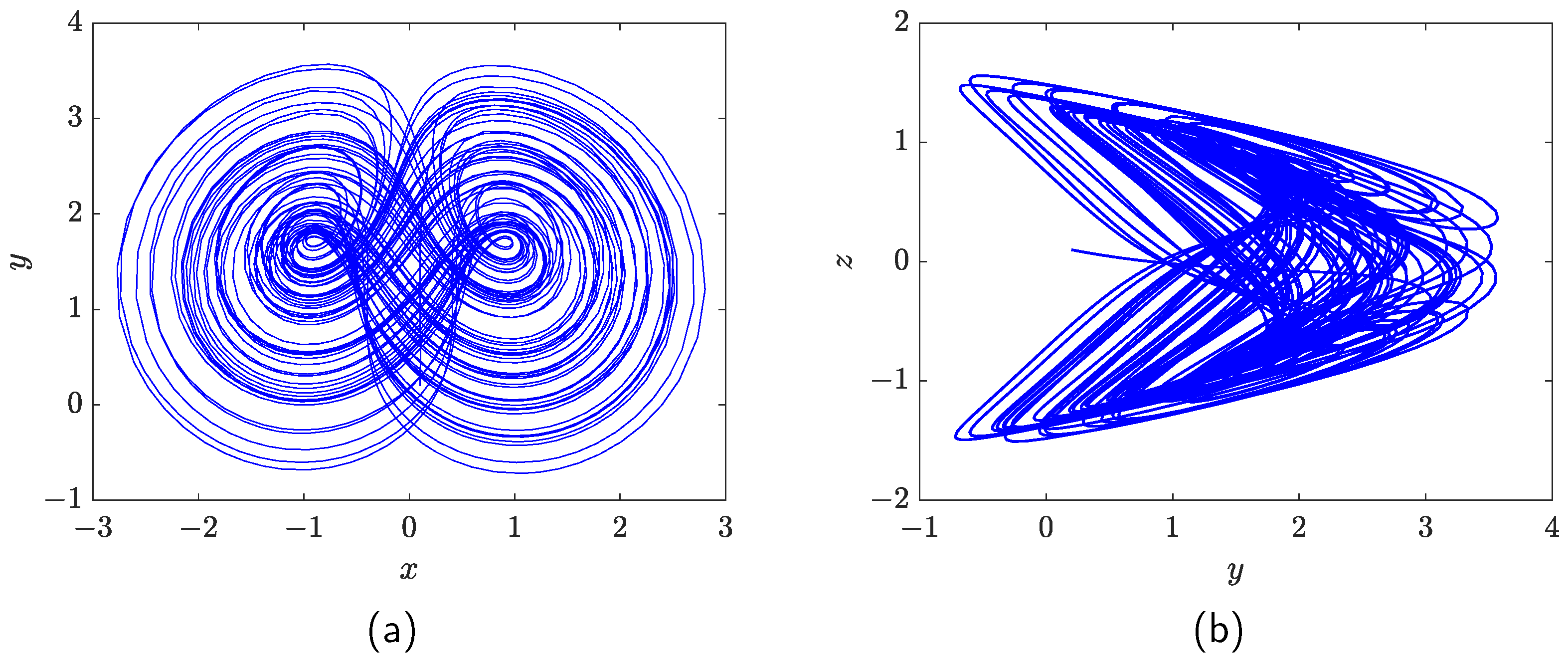
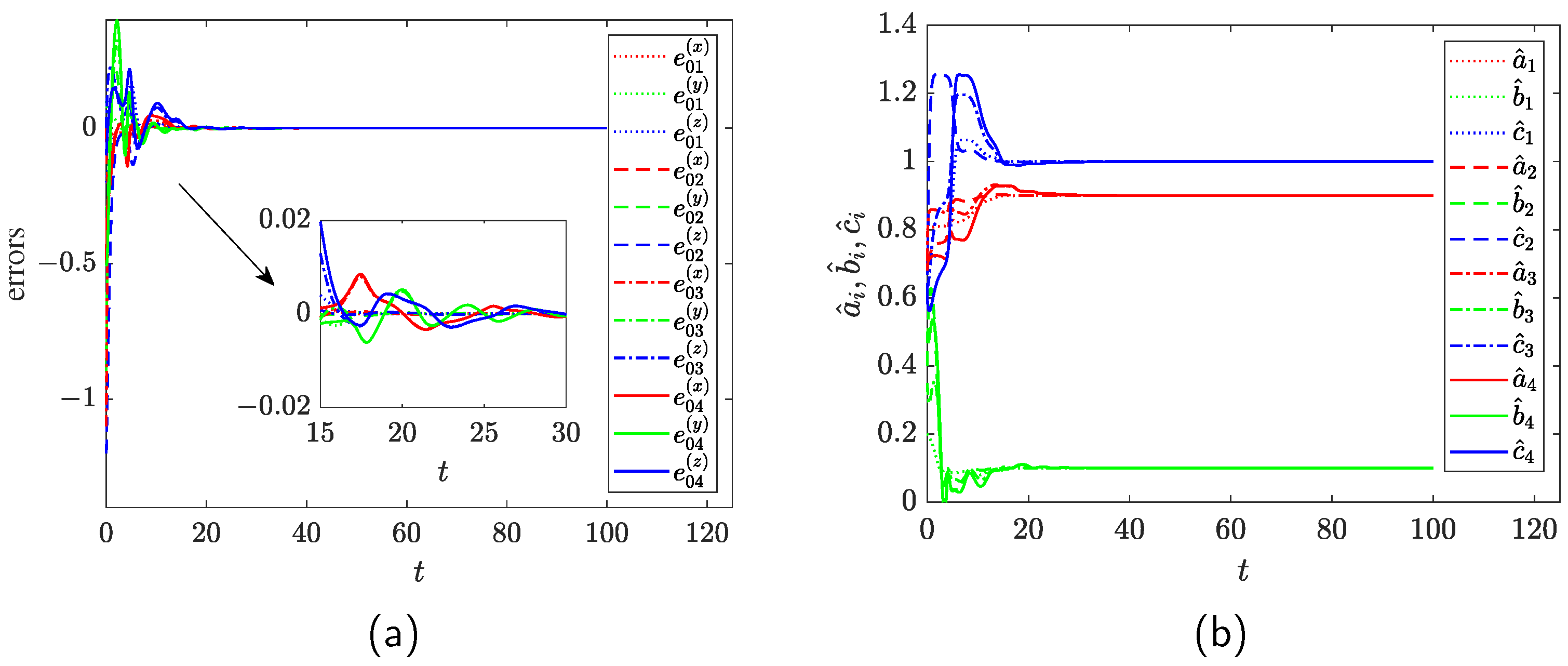
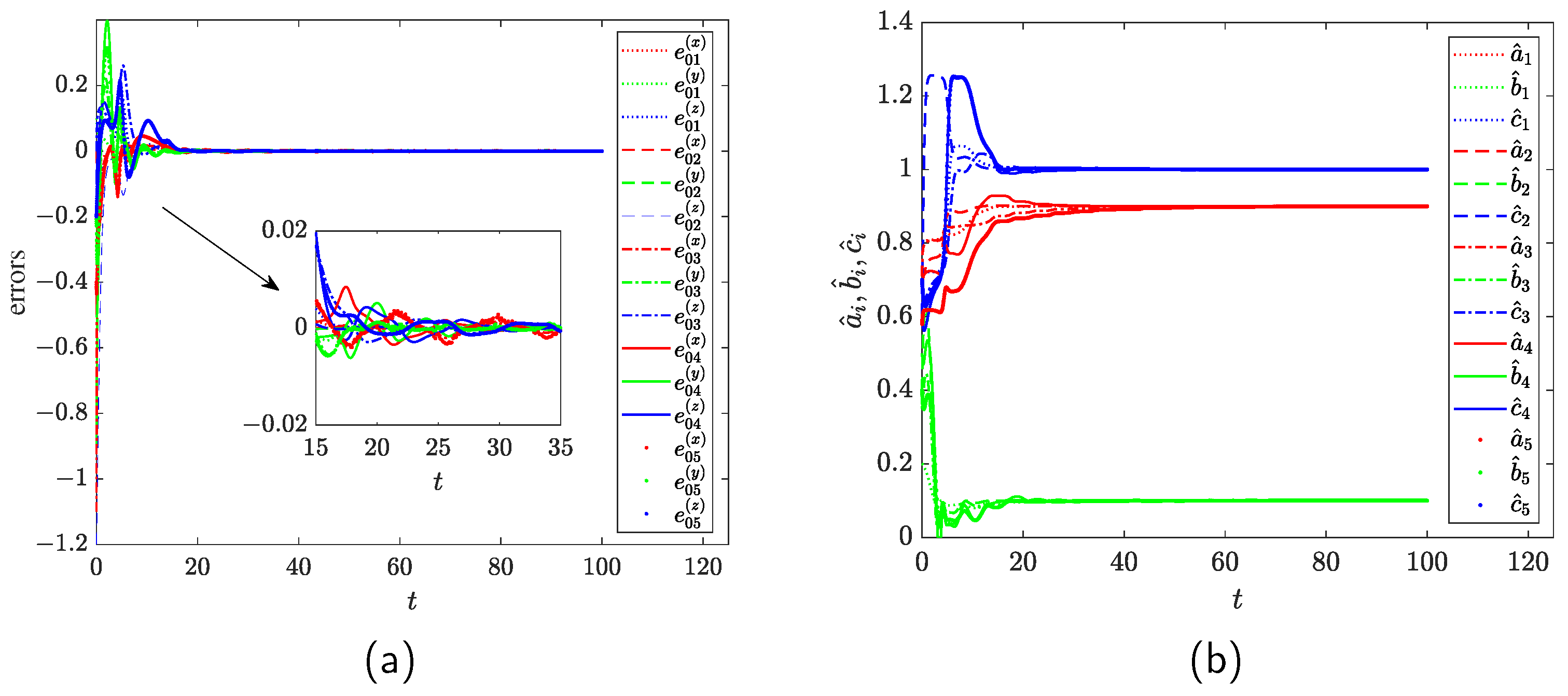
4.2. Numerical Simulations
4.3. Discussions of the Consensus for Multi-Agent Systems
- (1)
- The controller with only a linear term and a gain coefficient is simple and easy to implement;
- (2)
- The number of controllers is fewer, and only the first and second equations of slave financial system are added controllers;
- (3)
- The control cost is relatively low, and the linear feedback controller is easy to implement in hardware, such as the circuit implementation of master–slave synchronization.
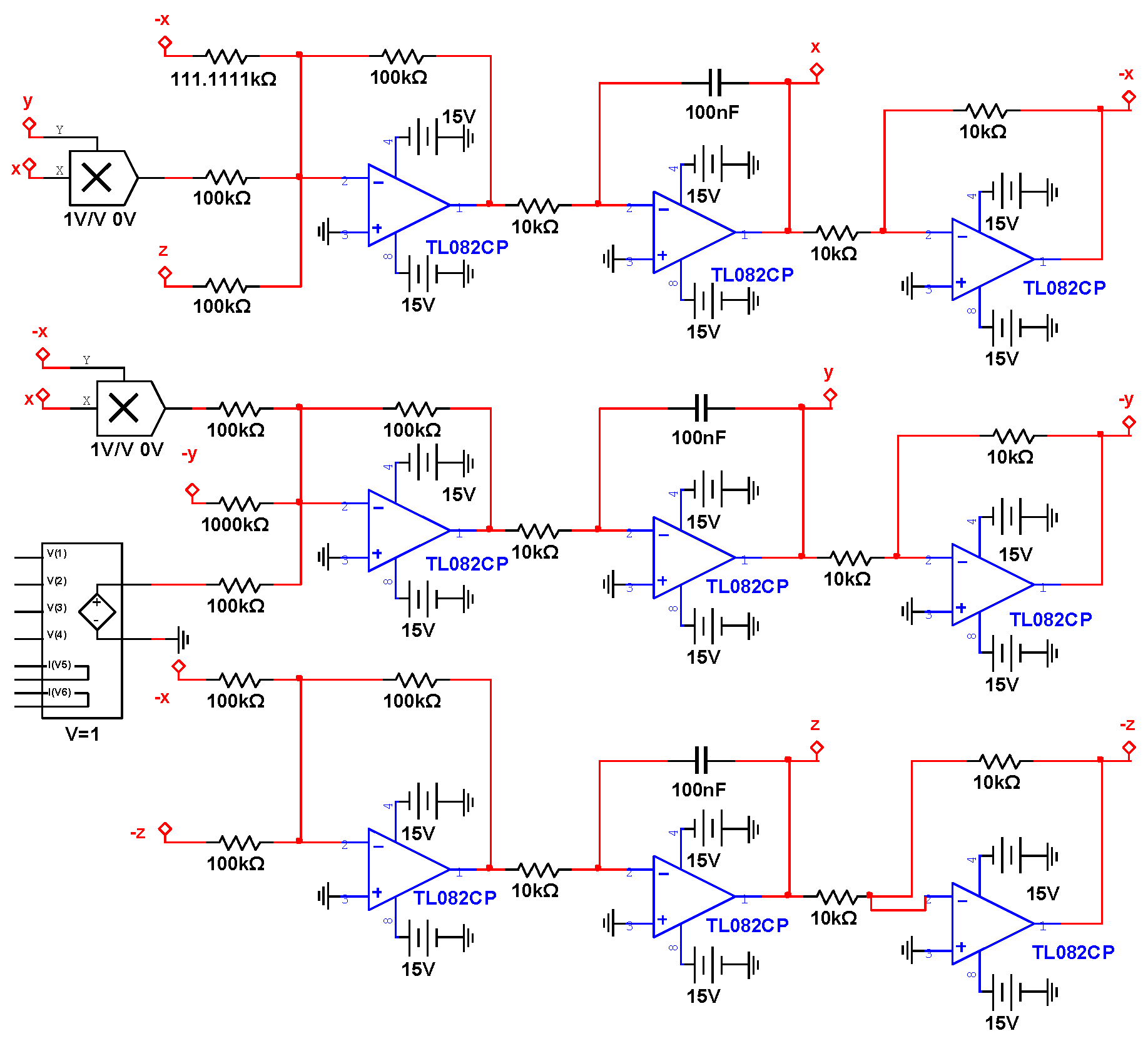
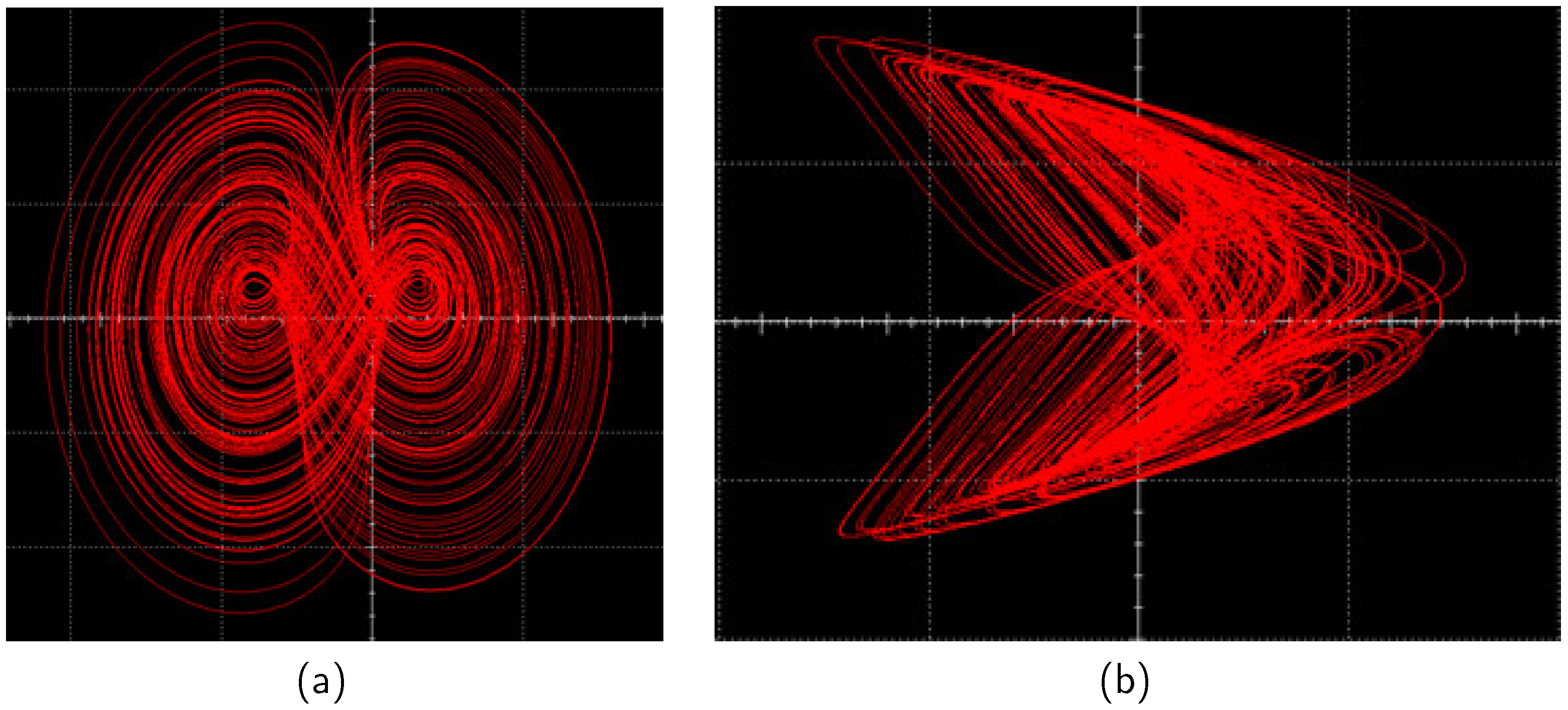
5. Circuit Implementation
5.1. Circuit Implementation of the Financial System
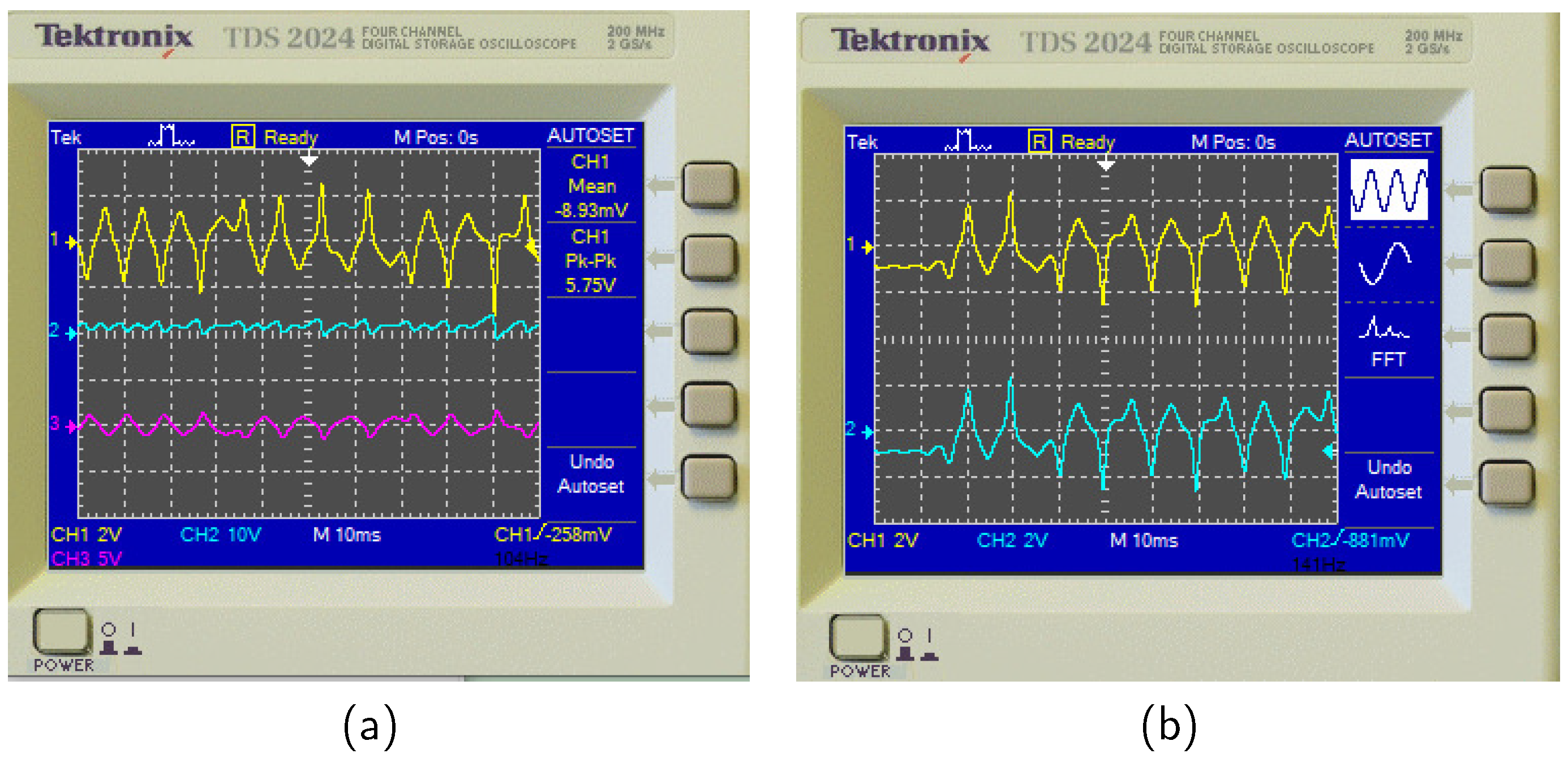
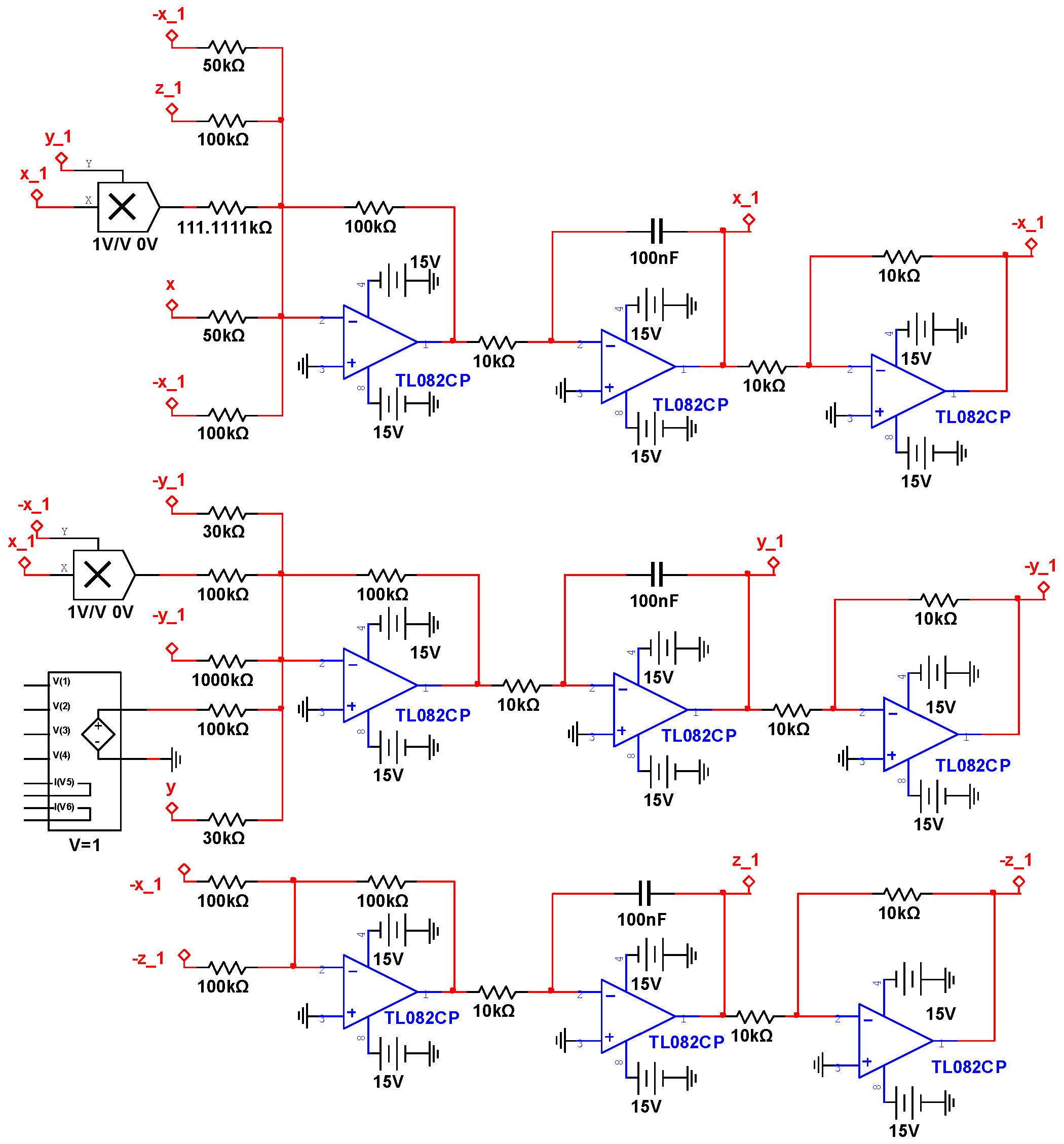
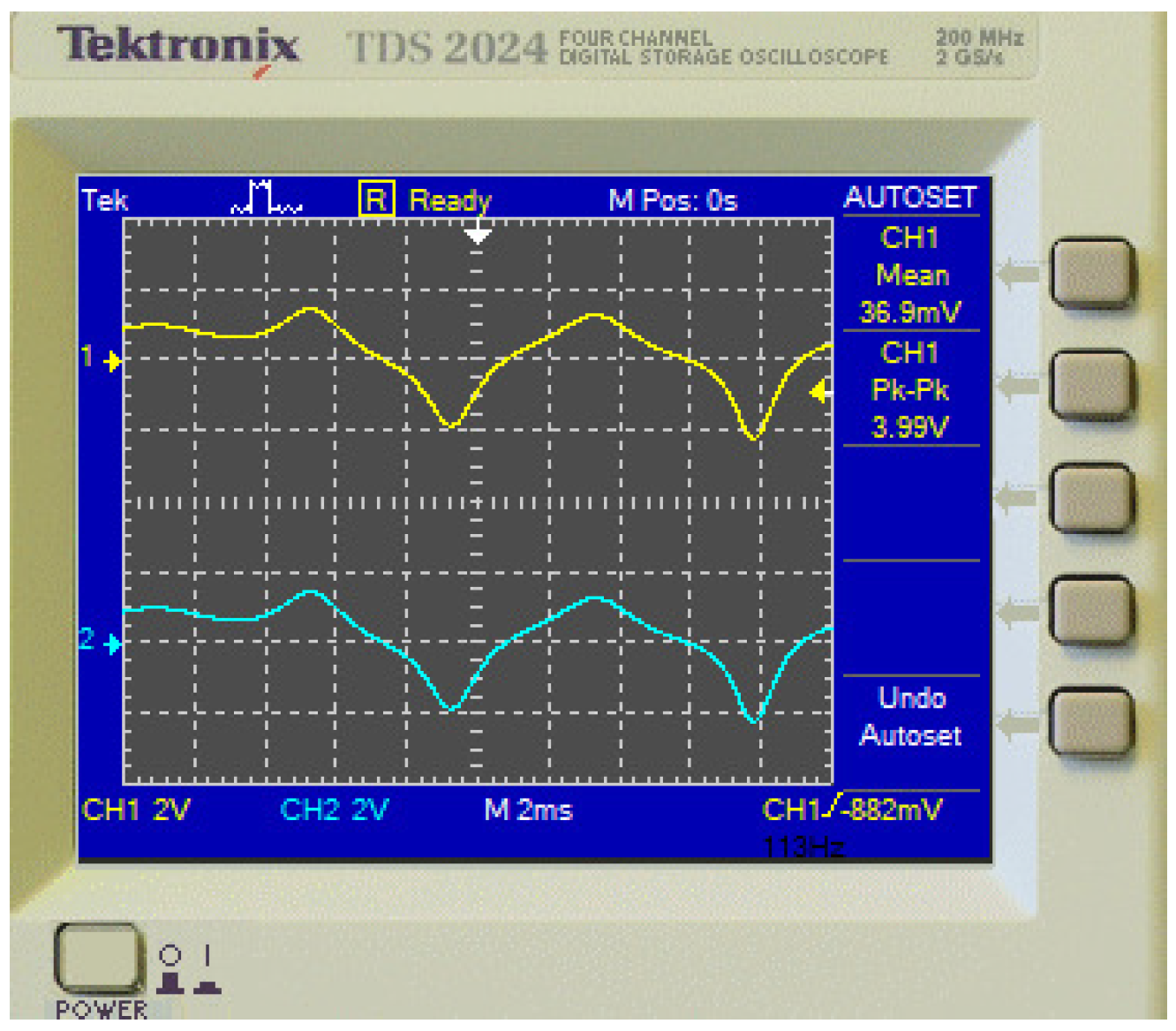
5.2. Circuit Implementation of Master–Slave Systems
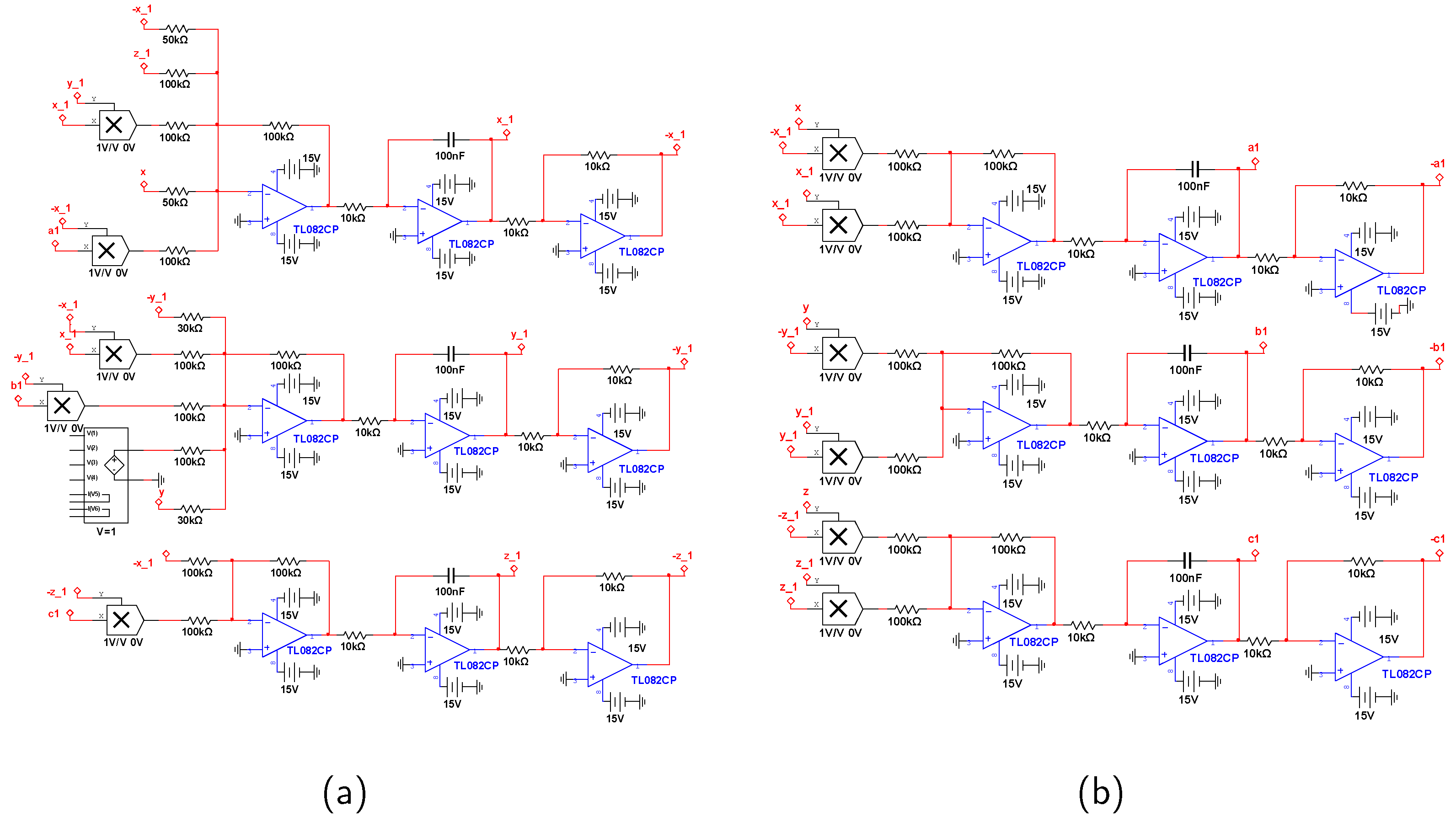
5.3. Circuit Implementation of Master–Slave Systems with Unknown Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matsumoto, T.; Chua, L.; Komuro, M. The double scroll. IEEE Trans. Circuits Syst. 1985, 32, 797–818. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Ben Slimane, N.; Bouallegue, K.; Machhout, M. Designing a multi-scroll chaotic system by operating Logistic map with fractal process. Nonlinear Dyn. 2017, 88, 1655–1675. [Google Scholar] [CrossRef]
- He, J.; Yu, S. Construction of higher-dimensional hyperchaotic systems with a maximum number of positive Lyapunov exponents under average eigenvalue criteria. J. Circuits Syst. Comput. 2019, 28, 1950151. [Google Scholar] [CrossRef]
- Kuate, P.D.K.; Tchendjeu, A.E.T.; Fotsin, H. A modified rössler prototype-4 system based on Chua’s diode nonlinearity: Dynamics, multistability, multiscroll generation and FPGA implementation. Chaos Solitons Fractals 2020, 140, 110213. [Google Scholar] [CrossRef]
- Sugandha, K.; Singh, P. Generation of a multi-scroll chaotic system via smooth state transformation. J. Comput. Electron. 2022, 21, 781–791. [Google Scholar] [CrossRef]
- Huang, D.; Li, H. Theory and Method of the Nonlinear Economics; Sichuan University Press: Chengdu, China, 1993. [Google Scholar]
- Xin, B.; Zhang, J. Finite-time stabilizing a fractional-order chaotic financial system with market confidence. Nonlinear Dyn. 2015, 79, 1399–1409. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.; Pano-Azucena, A.D.; Obeso-Rodelo, P.; Nuñez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Yildirim, M. Optical color image encryption scheme with a novel DNA encoding algorithm based on a chaotic circuit. Chaos Solitons Fractals 2022, 155, 111631. [Google Scholar] [CrossRef]
- Kaur, G.; Agarwal, R.; Patidar, V. Color image encryption scheme based on fractional Hartley transform and chaotic substitution–permutation. Vis. Comput. 2022, 38, 1027–1050. [Google Scholar] [CrossRef]
- Zhao, K.; He, J. Design of higher-dimensional hyperchaotic system based on combined control and its encryption application. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 869–879. [Google Scholar] [CrossRef]
- Gámez-Guzmán, L.; Cruz-Hernández, C.; López-Gutiérrez, R.; García-Guerrero, E. Synchronization of Chua’s circuits with multi-scroll attractors: Application to communication. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2765–2775. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, L.; Chen, Q.; Chen, G. Design and performance analysis of generalised carrier index M-ary differential chaos shift keying modulation. IET Commun. 2018, 12, 1324–1331. [Google Scholar] [CrossRef]
- Jiang, G.P.; Tang, W.K.S.; Chen, G. A simple global synchronization criterion for coupled chaotic systems. Chaos Solitons Fractals 2003, 15, 925–935. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J. Active control strategy for synchronization and anti-synchronization of a fractional chaotic financial system. Phys. A: Stat. Mech. Its Appl. 2017, 473, 262–275. [Google Scholar] [CrossRef]
- Aydogmus, F.; Tosyali, E. Master-slave synchronization in a 4D dissipative nonlinear fermionic system. Int. J. Control 2022, 95, 620–625. [Google Scholar] [CrossRef]
- Kuntanapreeda, S. Adaptive control of fractional-order unified chaotic systems using a passivity-based control approach. Nonlinear Dyn. 2016, 84, 2505–2515. [Google Scholar] [CrossRef]
- Mohadeszadeh, M.; Pariz, N. An application of adaptive synchronization of uncertain chaotic system in secure communication systems. Int. J. Model. Simul. 2022, 42, 143–152. [Google Scholar] [CrossRef]
- Zhou, J.; Tong, D.; Chen, Q.; Zhou, W. Master-slave synchronization of neural networks with time-varying delays via the event-triggered control. Math. Comput. Model. Dyn. Syst. 2020, 26, 357–373. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, J.; Liang, J.; Cao, J.; Perc, M. Pinning synchronization of nonlinear coupled Lur’e networks under hybrid impulses. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 432–436. [Google Scholar] [CrossRef]
- Tang, Z.; Park, J.H.; Zheng, W.X. Distributed impulsive synchronization of Lur’e dynamical networks via parameter variation methods. Int. J. Robust Nonlinear Control 2018, 28, 1001–1015. [Google Scholar] [CrossRef]
- Nowzari, C.; Garcia, E.; Cortés, J. Event-triggered communication and control of networked systems for multi-agent consensus. Automatica 2019, 105, 1–27. [Google Scholar] [CrossRef]
- Huang, Y.; Bao, H. Master-slave synchronization of complex-valued delayed chaotic Lur’e systems with sampled-data control. Appl. Math. Comput. 2020, 379, 125261. [Google Scholar] [CrossRef]
- Arena, P.; Buscarino, A.; Fortuna, L.; Patanè, L. Lyapunov approach to synchronization of chaotic systems with vanishing nonlinear perturbations: From static to dynamic couplings. Phys. Rev. E 2020, 102, 012211. [Google Scholar] [CrossRef] [PubMed]
- Yalçin, M.E.; Suykens, J.A.; Vandewalle, J. Master-slave synchronization of Lur’e systems with time-delay. Int. J. Bifurc. Chaos 2001, 11, 1707–1722. [Google Scholar] [CrossRef]
- Htun, Y.H.T.; Hlaing, M.S.; Hla, T.T. Master-slave synchronization of robotic arm using PID controller. Indones. J. Electr. Eng. Informatics 2023, 11, 77–87. [Google Scholar] [CrossRef]
- Gu, Z.; Peng, S.; Huang, Y. Quasi-consensus of disturbed nonlinear multiagent systems with event-triggered impulsive control. Appl. Sci. 2022, 12, 7580. [Google Scholar] [CrossRef]
- Trakas, P.S.; Tantoulas, A.; Bechlioulis, C.P. Formation control of nonlinear multi-agent systems with nested input saturation. Appl. Sci. 2024, 14, 213. [Google Scholar] [CrossRef]
- Yang, J.; Lee, B.G. Distributed adaptive tracking control of hidden leader-follower multi-agent systems with unknown parameters. Mathematics 2024, 12, 1013. [Google Scholar] [CrossRef]
- Gu, R.; Sun, X. Fault-tolerant cooperative control of multiple uncertain Euler-Lagrange systems with an uncertain leader. Electronics 2024, 13, 2068. [Google Scholar] [CrossRef]
- Ding, K.; Han, Q.L. Master-slave synchronization criteria for horizontal platform systems using time delay feedback control. J. Sound Vib. 2011, 330, 2419–2436. [Google Scholar] [CrossRef]
- Wen, G.; Wan, Y.; Cao, J.; Huang, T.; Yu, W. Master-slave synchronization of heterogeneous systems under scheduling communication. IEEE Trans. Syst. Man Cybern. Syst. 2016, 48, 473–484. [Google Scholar] [CrossRef]
- Ramirez, J.P.; Garcia, E.; Alvarez, J. Master-slave synchronization via dynamic control. Commun. Nonlinear Sci. Numer. Simul. 2020, 80, 104977. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R. Control of a fractional-order economical system via sliding mode. Phys. A Stat. Mech. Its Appl. 2010, 389, 2434–2442. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Baleanu, D. New aspects of the adaptive synchronization and hyperchaos suppression of a financial model. Chaos Solitons Fractals 2017, 99, 285–296. [Google Scholar] [CrossRef]
- Jäntschi, L. Eigenproblem basics and algorithms. Symmetry 2023, 15, 2046. [Google Scholar] [CrossRef]
- Parks, P.C. AM Lyapunov’s stability theory–100 years on. IMA J. Math. Control Inf. 1992, 9, 275–303. [Google Scholar] [CrossRef]
- Sastry, S.; Sastry, S. Lyapunov stability theory. In Nonlinear Systems: Analysis, Stability, and Control; Springer: Berlin/Heidelberg, Germany, 1999; pp. 182–234. [Google Scholar]



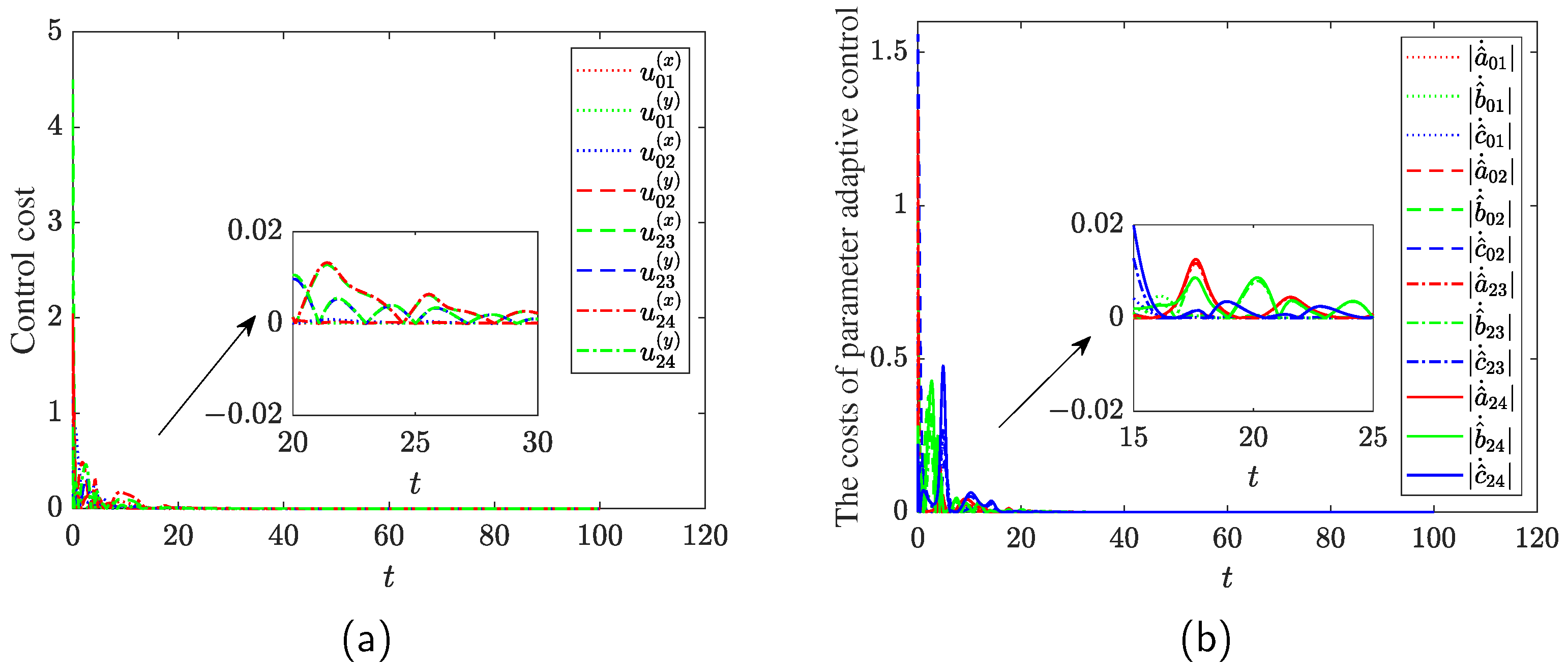
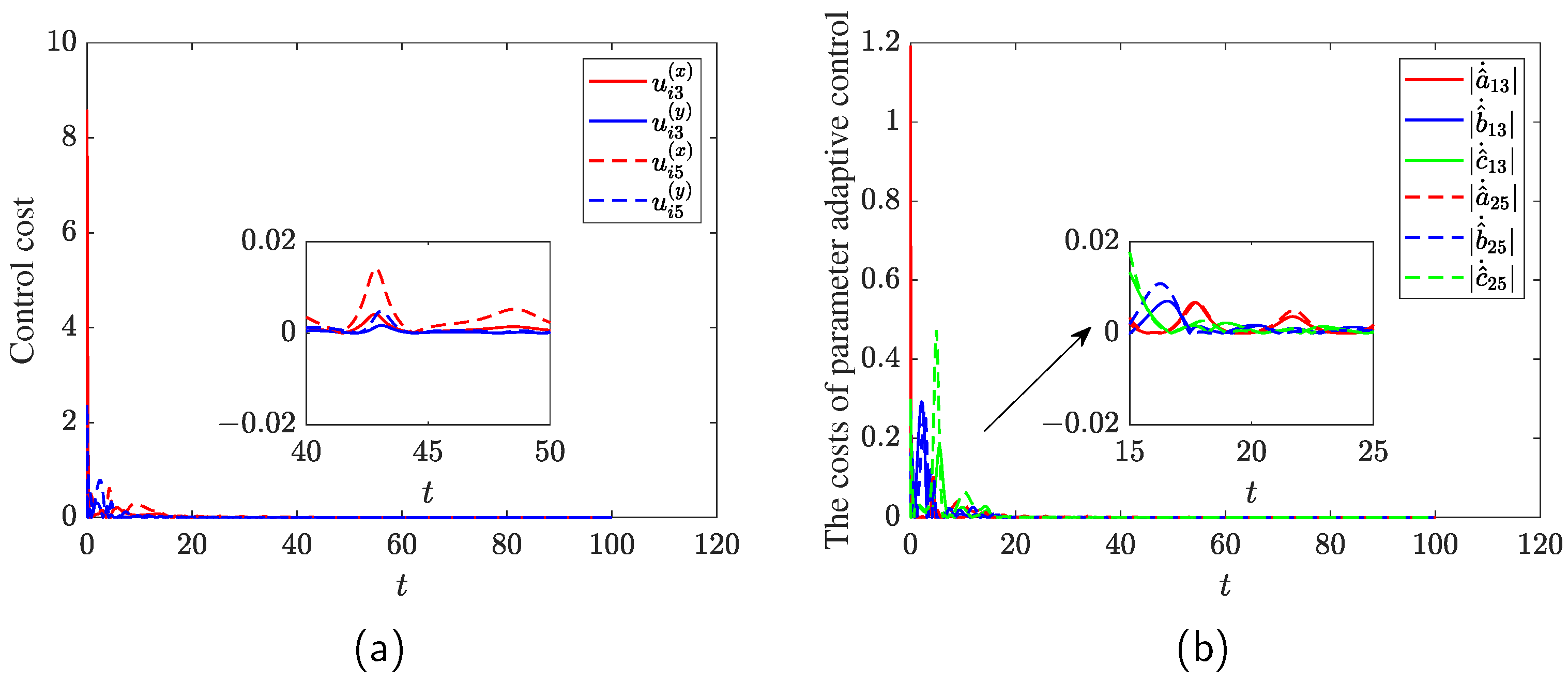

| Agent | Initial Errors ,, in Equation (20) | Control Time t When , | Control Costs of , and Total Cost |
|---|---|---|---|
| 1 | 0.1, 0.1, 0.2 | 14.19, 12.00 | {812.92, 311.68}, 1124.60 |
| 2 | 0.0, 0.9, 1.2 | 12.29, 8.49 | {1640.54, 1600.14}, 3240.68 |
| 3 | 1.1, 0.6, 1.2 | 21.98, 18.21 | {1814.09, 1145.51}, 2959.60 |
| 4 | 0.5, 0.4, 1.1 | 22.01, 20.24 | {1806.64, 1418.36}, 3225.00 |
| Agent | Initial Errors , , in Equation (21) | Control Time t When , | The Costs of , and Total Cost |
|---|---|---|---|
| 1 | 0.1, 0.1, 0.3 | 10.79, 12.02, 11.57 | {116.36,173.33,429.40}, 719.09 |
| 2 | 0.2, 0.3, 0.4 | 5.55, 8.43, 10.94 | {215.86,990.61,922.13}, 2128.60 |
| 3 | 0.19, 0.25, 0.36 | 17.88, 12.72, 15.14 | {348.54,796.55,790.29}, 1935.38 |
| 4 | 0.22, 0.4, 0.4 | 17.90, 12.76, 15.40 | {348.38,1042.67,1013.86}, 2404.91 |
| Agent | Initial Errors in Equation (20) of , | Control Time t When , | Control Costs of , and Total Cost |
|---|---|---|---|
| 3 | 1.1, 0.6, 1.2 | 21.98, 17.00 | {2228.17, 848.90}, 3077.07 |
| 5 | 0.4, 0.2, 0.2 | 14.24, 7.74 | {4149.07, 2747.63}, 6896.70 |
| Agent | Initial Errors , , in Equation (21) | Control Time t When | The Costs of , and Total Cost |
|---|---|---|---|
| 3 | 0.19, 0.25, 0.36 | 14.15, 8.11, 15.29 | {198.92,704.98,466.67}, 1370.57 |
| 5 | 0.32, 0.3, 0.3 | 14.50, 16.54, 15.39 | {355.26,673.66,967.35}, 1996.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; He, J. Consensus Control of Leader–Follower Multi-Agent Systems with Unknown Parameters and Its Circuit Implementation. Appl. Sci. 2024, 14, 8894. https://doi.org/10.3390/app14198894
Ye Y, He J. Consensus Control of Leader–Follower Multi-Agent Systems with Unknown Parameters and Its Circuit Implementation. Applied Sciences. 2024; 14(19):8894. https://doi.org/10.3390/app14198894
Chicago/Turabian StyleYe, Yinfang, and Jianbin He. 2024. "Consensus Control of Leader–Follower Multi-Agent Systems with Unknown Parameters and Its Circuit Implementation" Applied Sciences 14, no. 19: 8894. https://doi.org/10.3390/app14198894






