A Novel Approach of the Viscoelasticity of Axially Functional Graded Bar and Application of Harmonic Vibration Analysis of an Isotropic Beam as Support
Abstract
:1. Introduction
- -
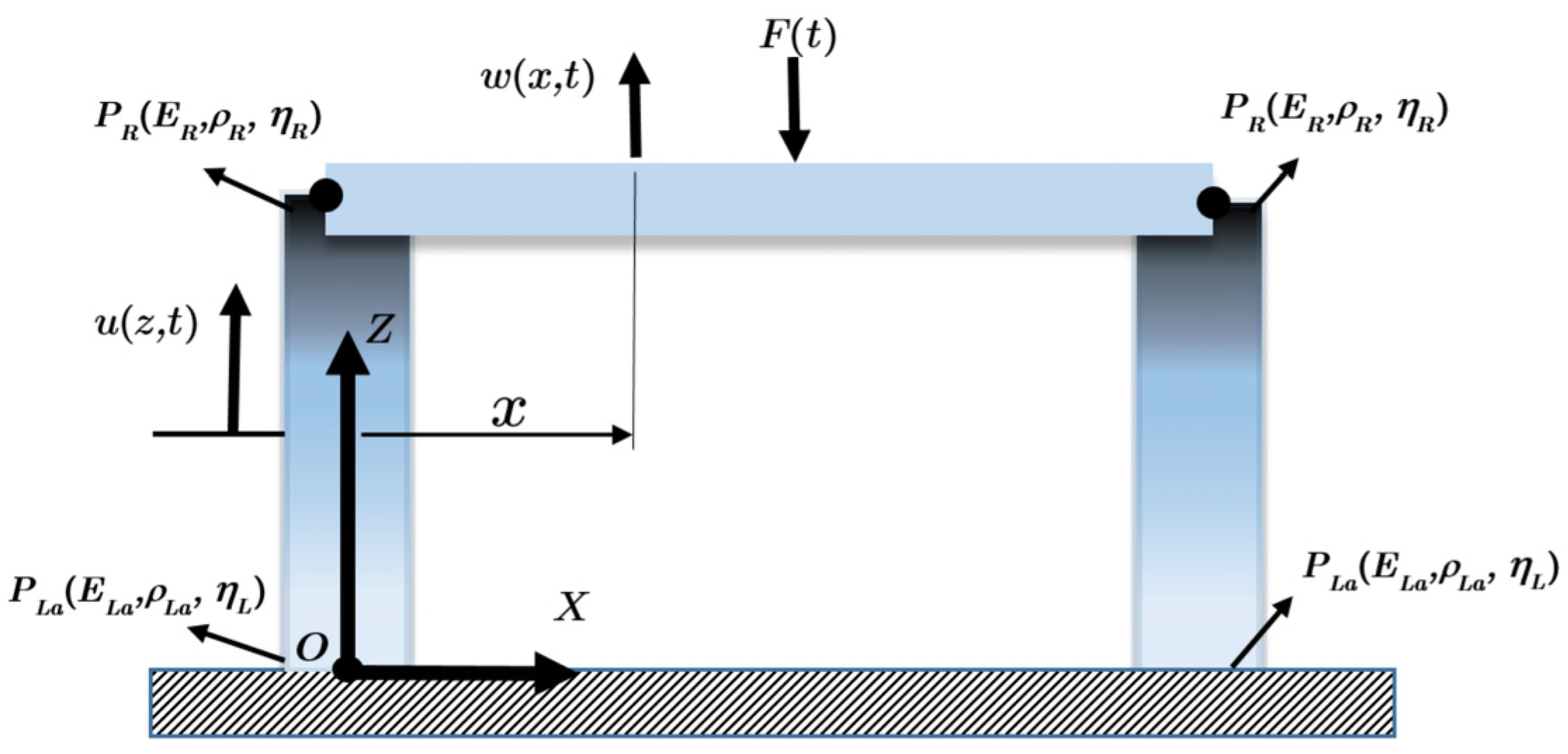
- The system consists of beam and AFG viscoelastic bars. The system or only AFG viscoelastic bars can be used as an alternative to the spring and damping system to minimise the force transmitted to the ground in the foundations of large mass machines and to minimise the vibration amplitudes of machines. Variable internal damping and stiffness values along the axis of the structure at the support provide advantages in terms of stress and amplitude compared to other structures;
- -
- Passive dampers are used in buildings against stimuli such as earthquakes, wind, etc. Such energy dissipation devices are called ADAS (Added Damping and Stiffness). The ADAS can dissipate a part of the seismic energy input to a structure by hysteretic contribution. The structure considered in the paper absorbs large displacements, especially between floors, by axially varying internal damping. It is also safe in terms of structural stress;
- -
- In anti-terrorist structures such as mushroom barriers, it will be possible to make more successful anti-terrorist equipment by using the advantage of the varying stiffness and material damping of the rods in the axial direction (collision direction) in the steel pipe.
2. Theory and Formulations
2.1. Finite Element Modelling of the Axial FG Element with Material Damping
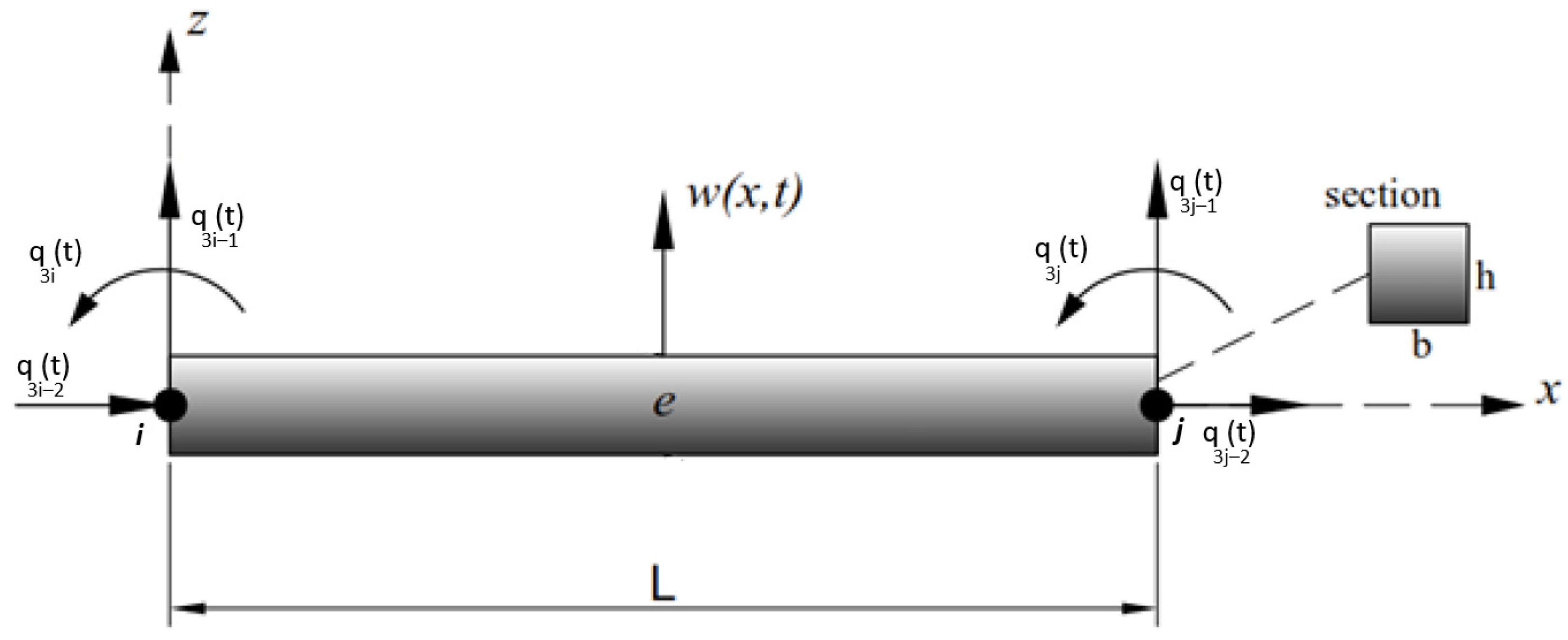
2.2. Modelling Beam Element
2.3. Assembling the Matrices of System
K(m + i, m + j) = KB(i, j), i = 1…pb, j = 1…pb
K(p + 1 − i, p + 1 − j) = KA(i, j), i = 1…m, j = 1…m
K(m + 2, m) = KA(m + 1, m);
K(m + 2, m + 2) = KA(m + 1, m + 1) + K(m + 2, m + 2);
K(4m + 2, 4m + 4) = KA(p, p−1);
K(4m + 4, 4m + 2) = KA(p−1, p);
K(4m + 2, 4m + 2) = KA(p, p) + K(4m + 2, 4m + 2);
3. Numerical Formulations
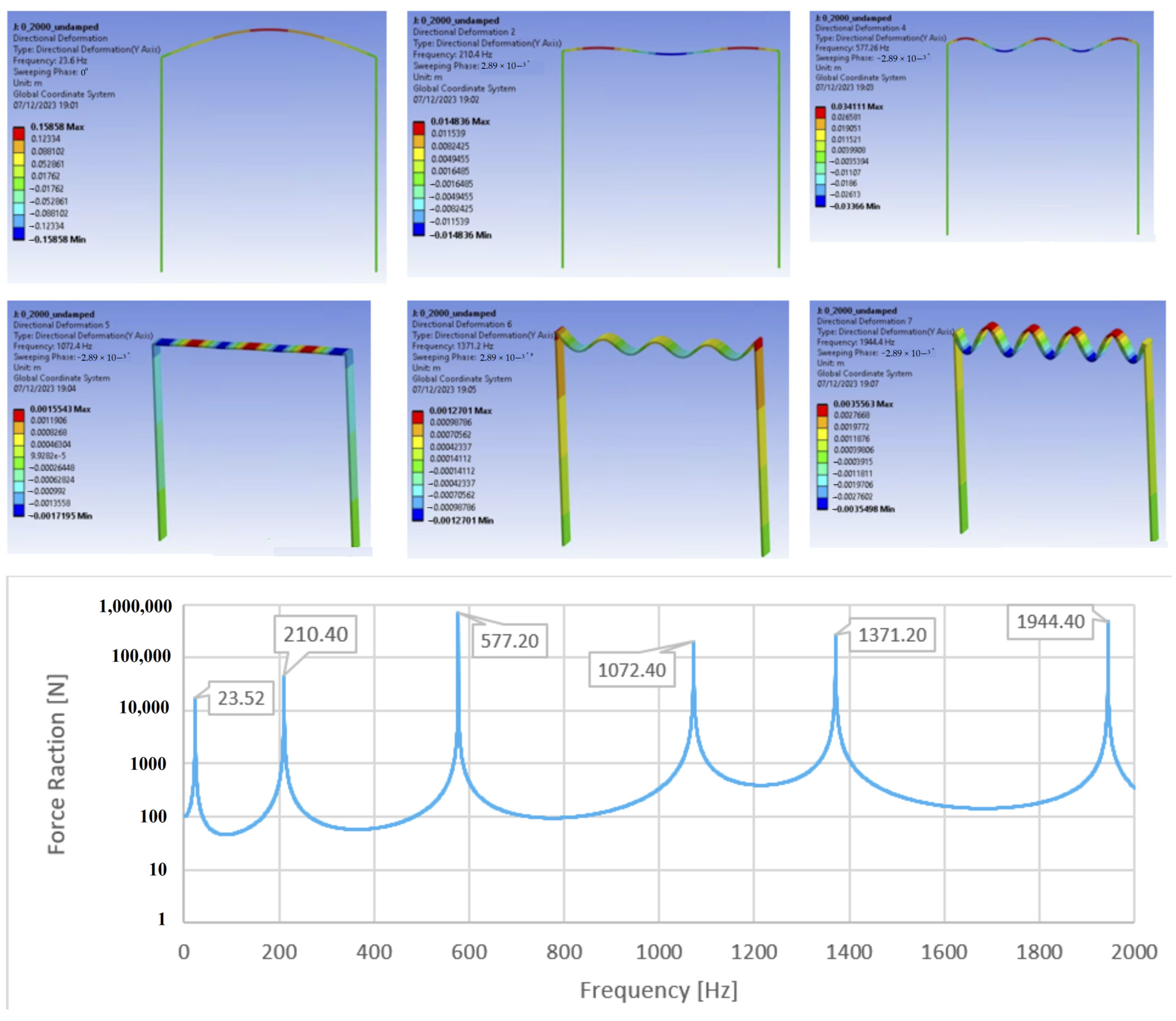
4. Verification Studies
5. Parameterisation Studies
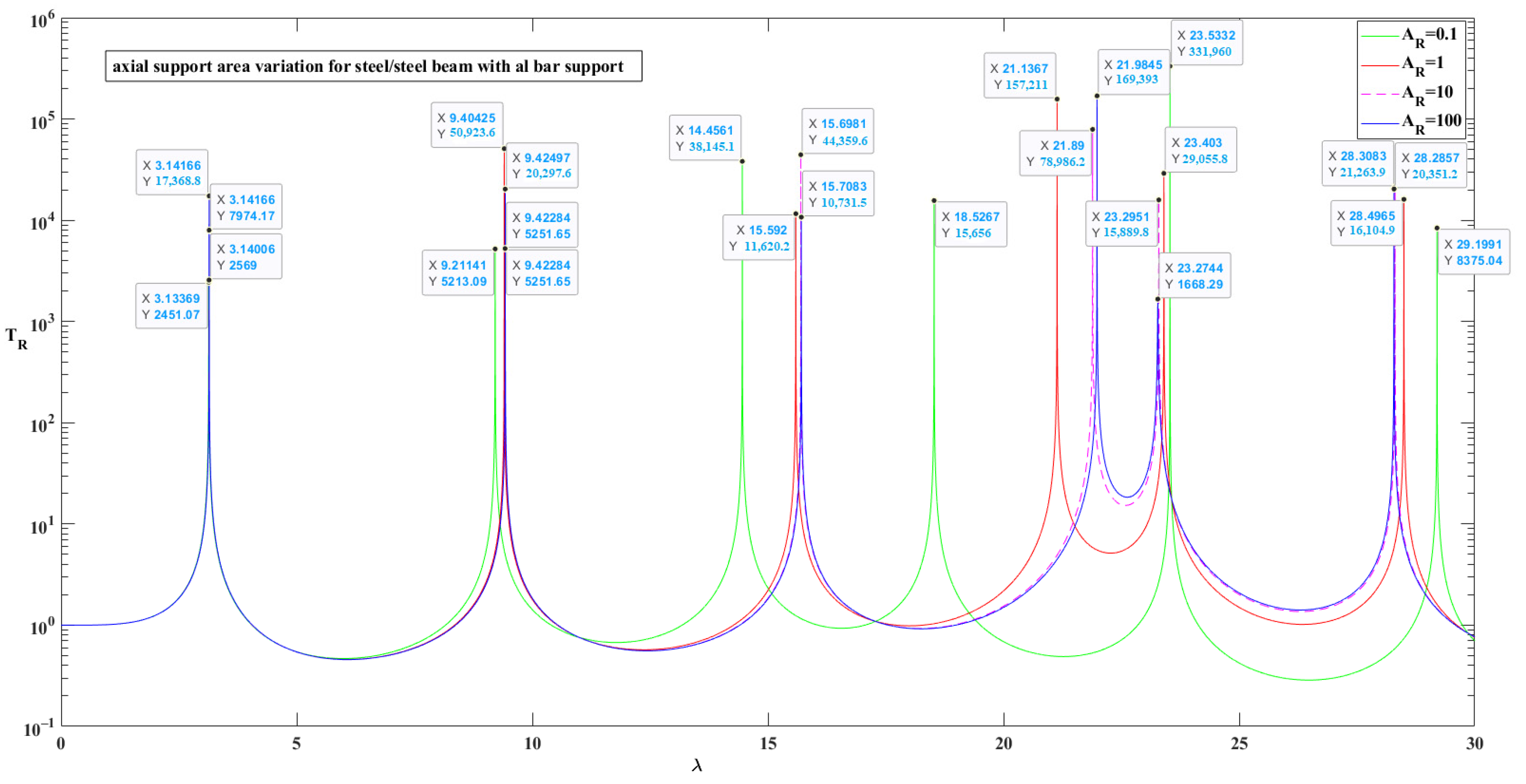
5.1. The Area of Support Bars
5.2. Material Damping Effect
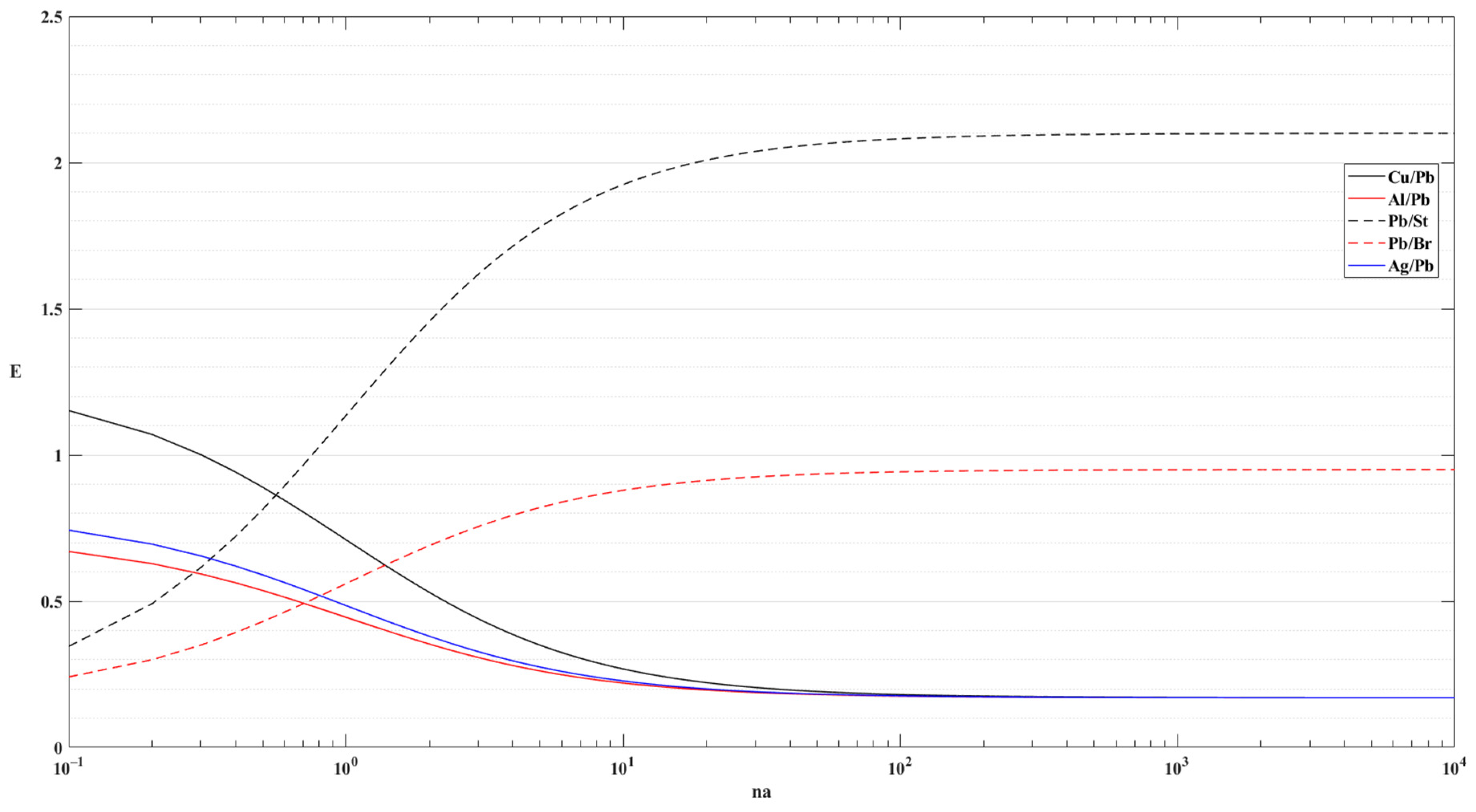
5.3. Material Pairs for Bar Support
5.4. The Limits of Material Distribution Coefficient “na”
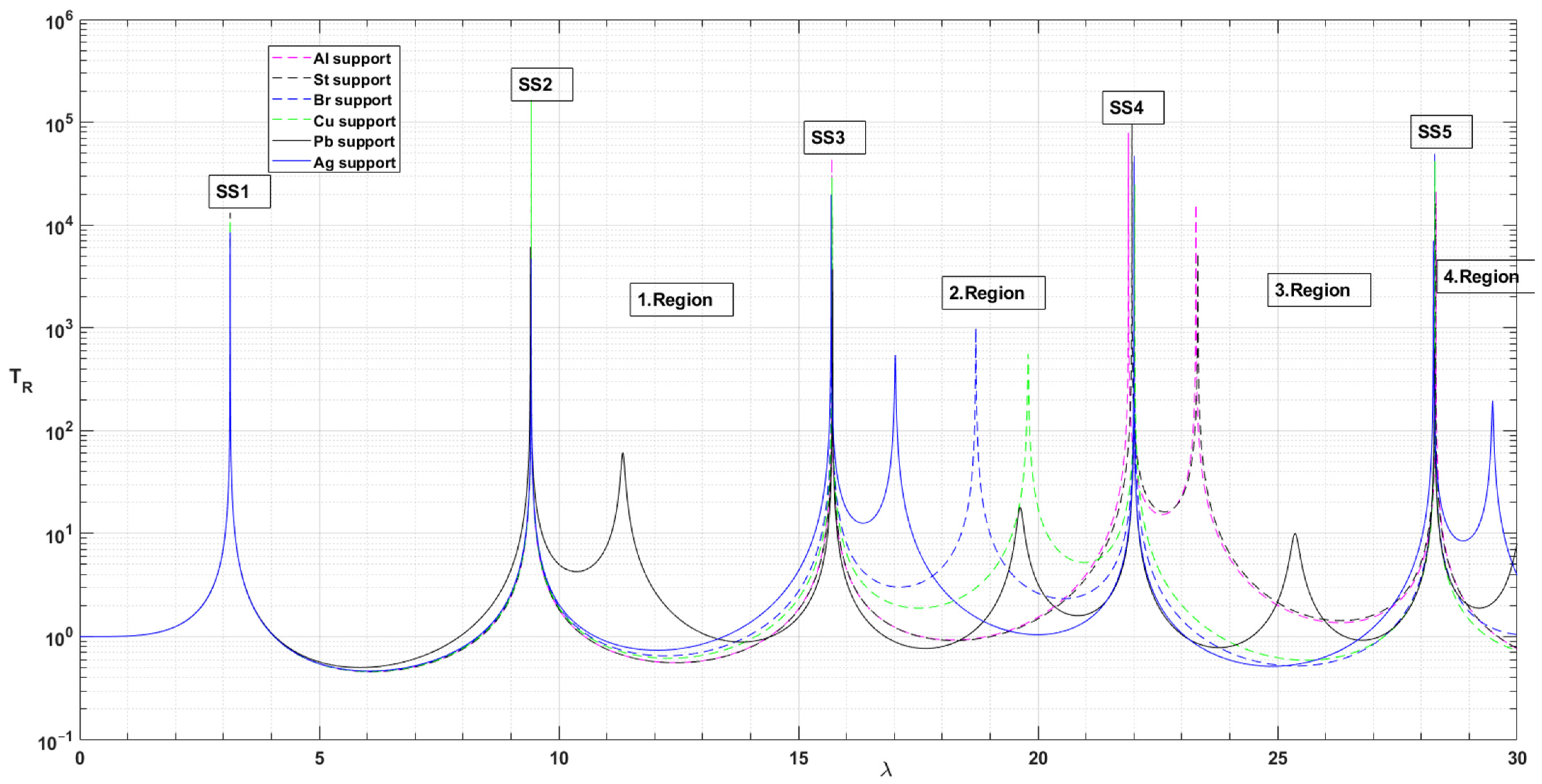
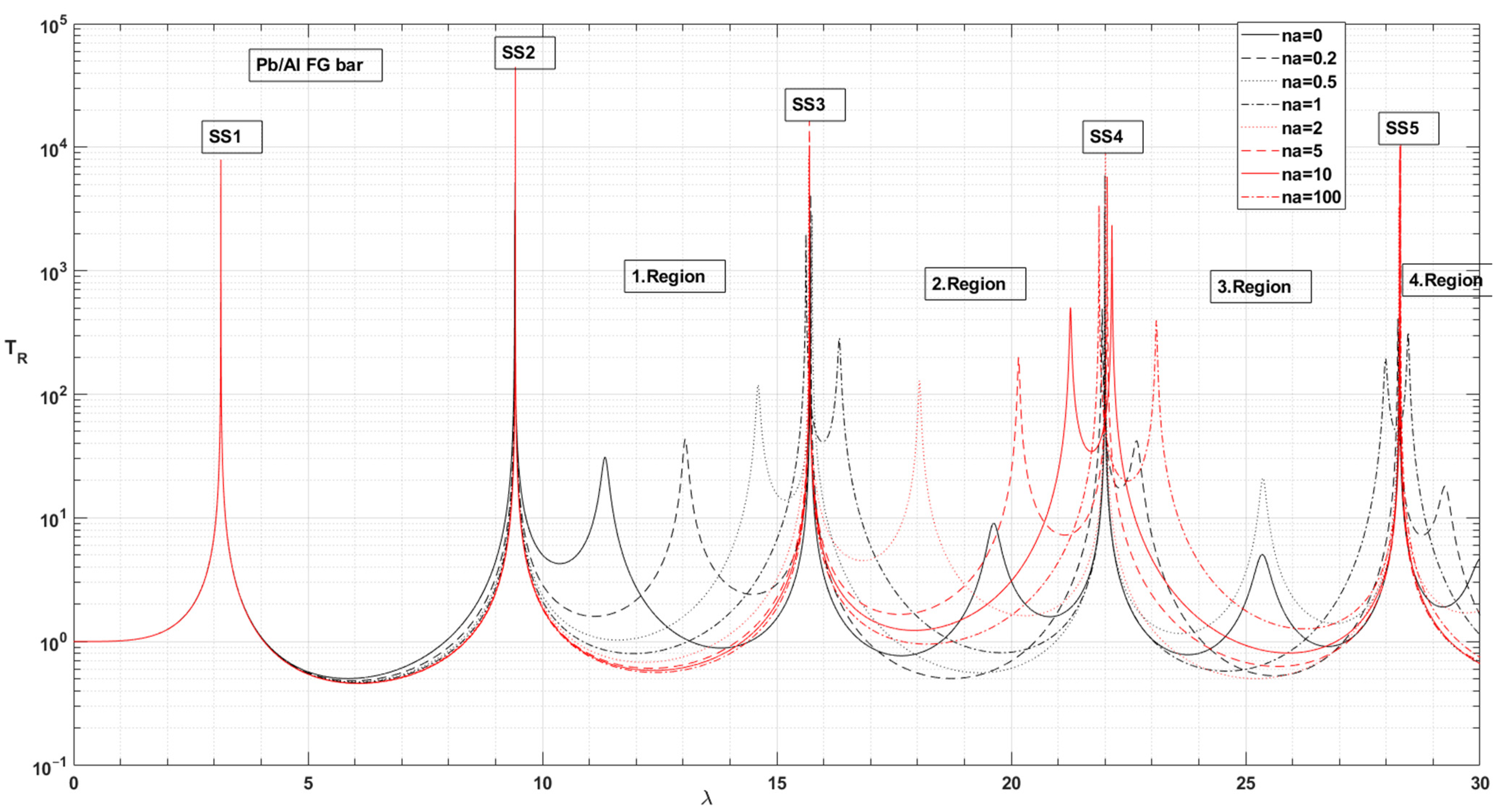
6. Investigation of Force Transmission of Axial FG Bar Supported Steel Beam According to Material Distribution Coefficient “na”
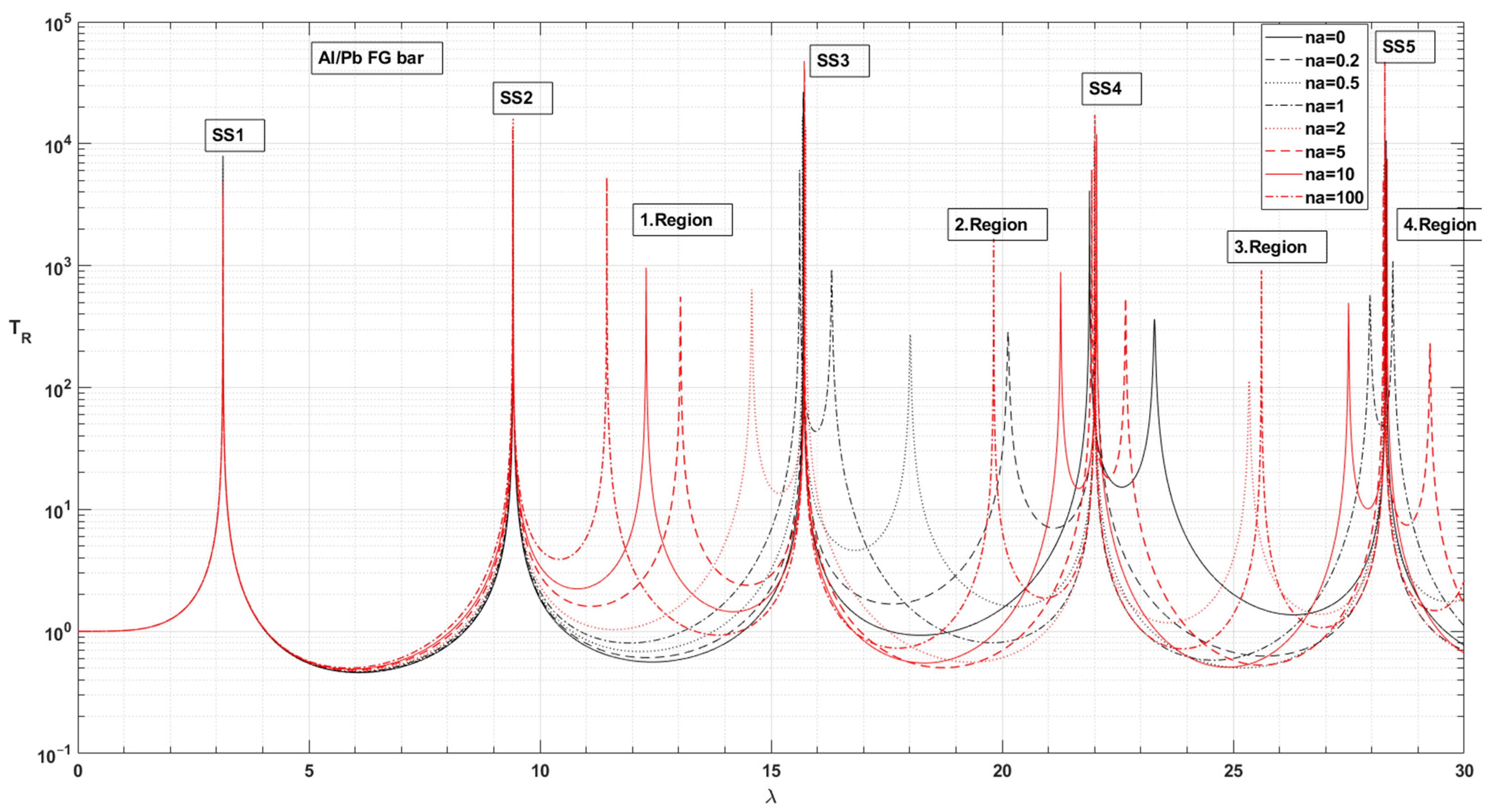
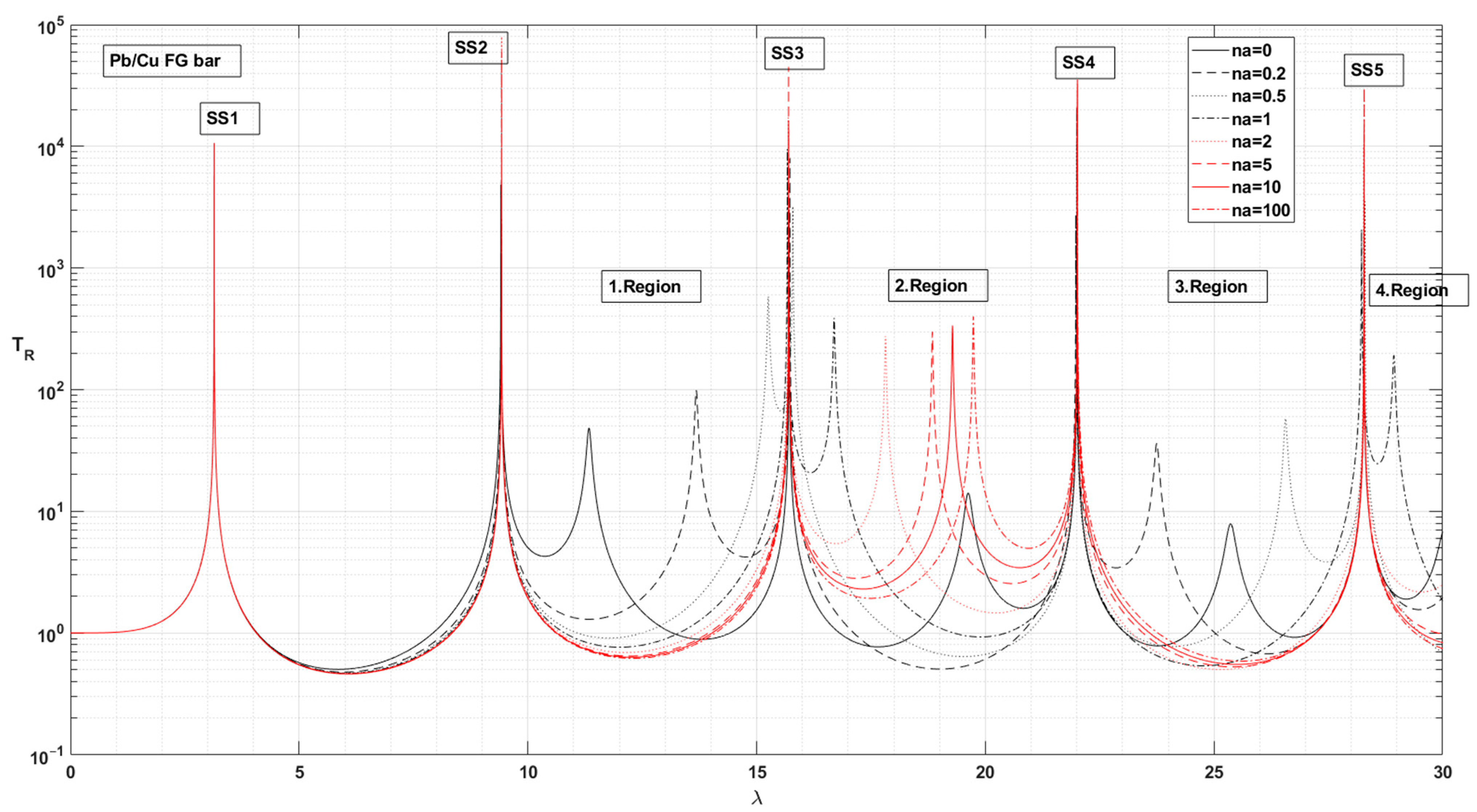
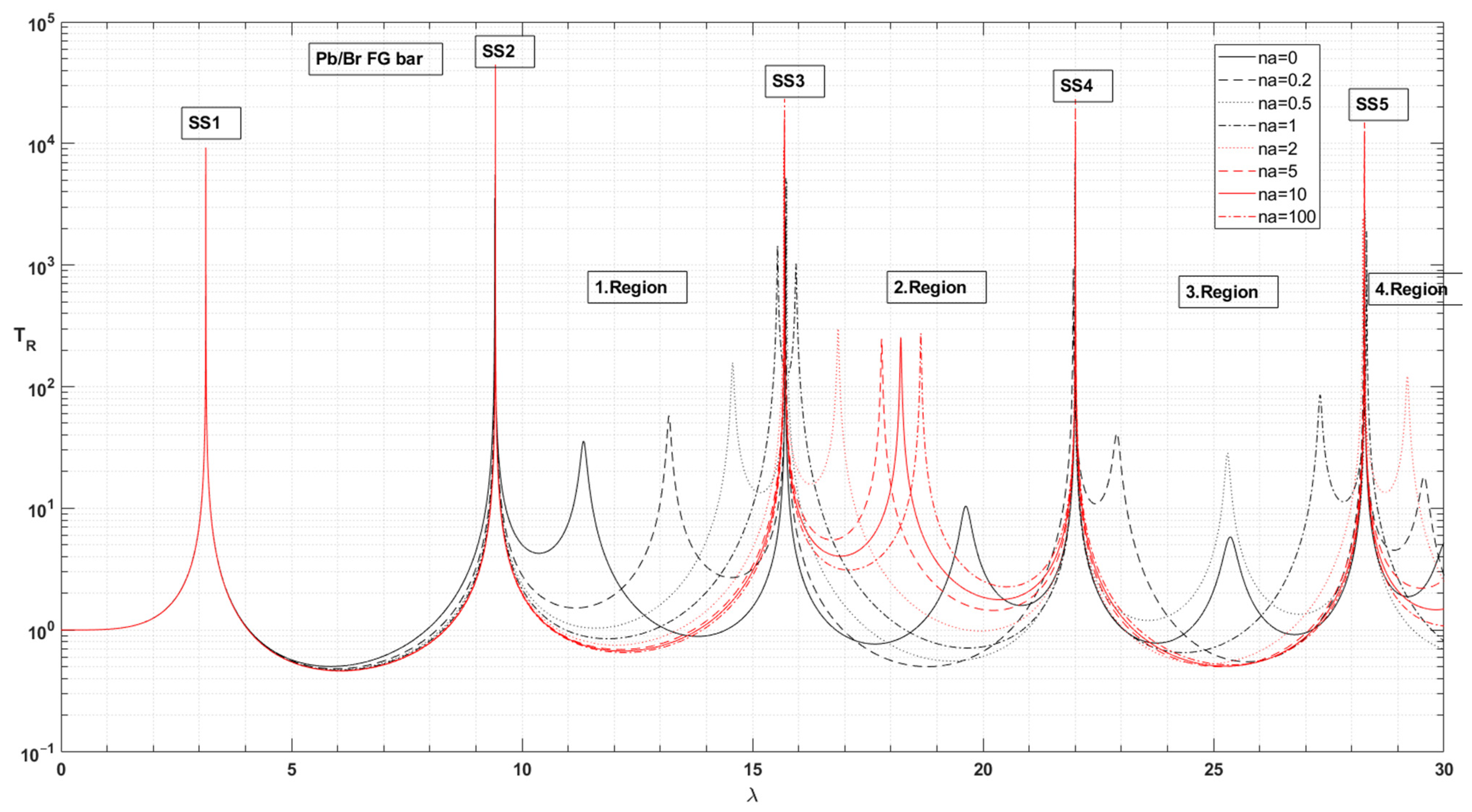
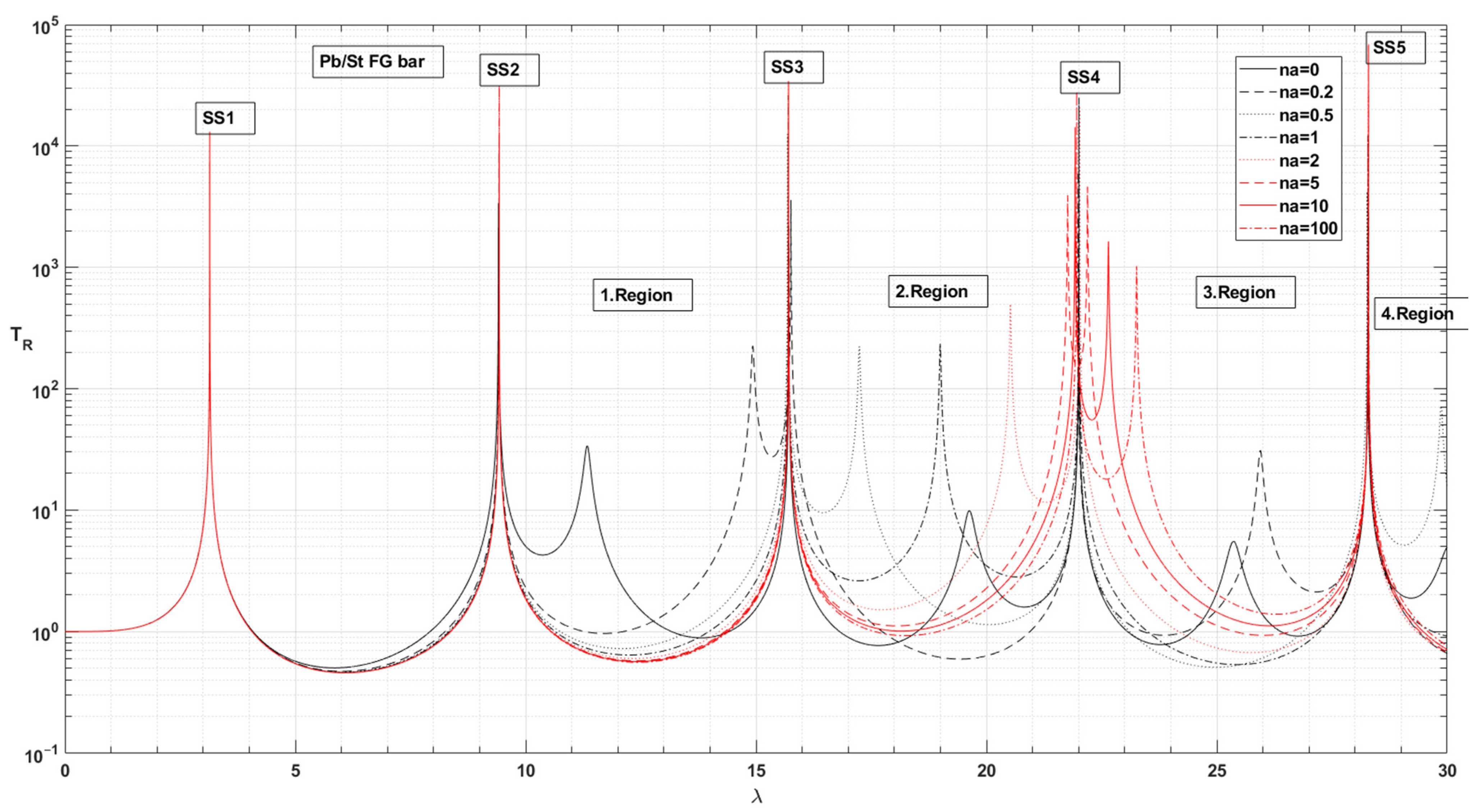
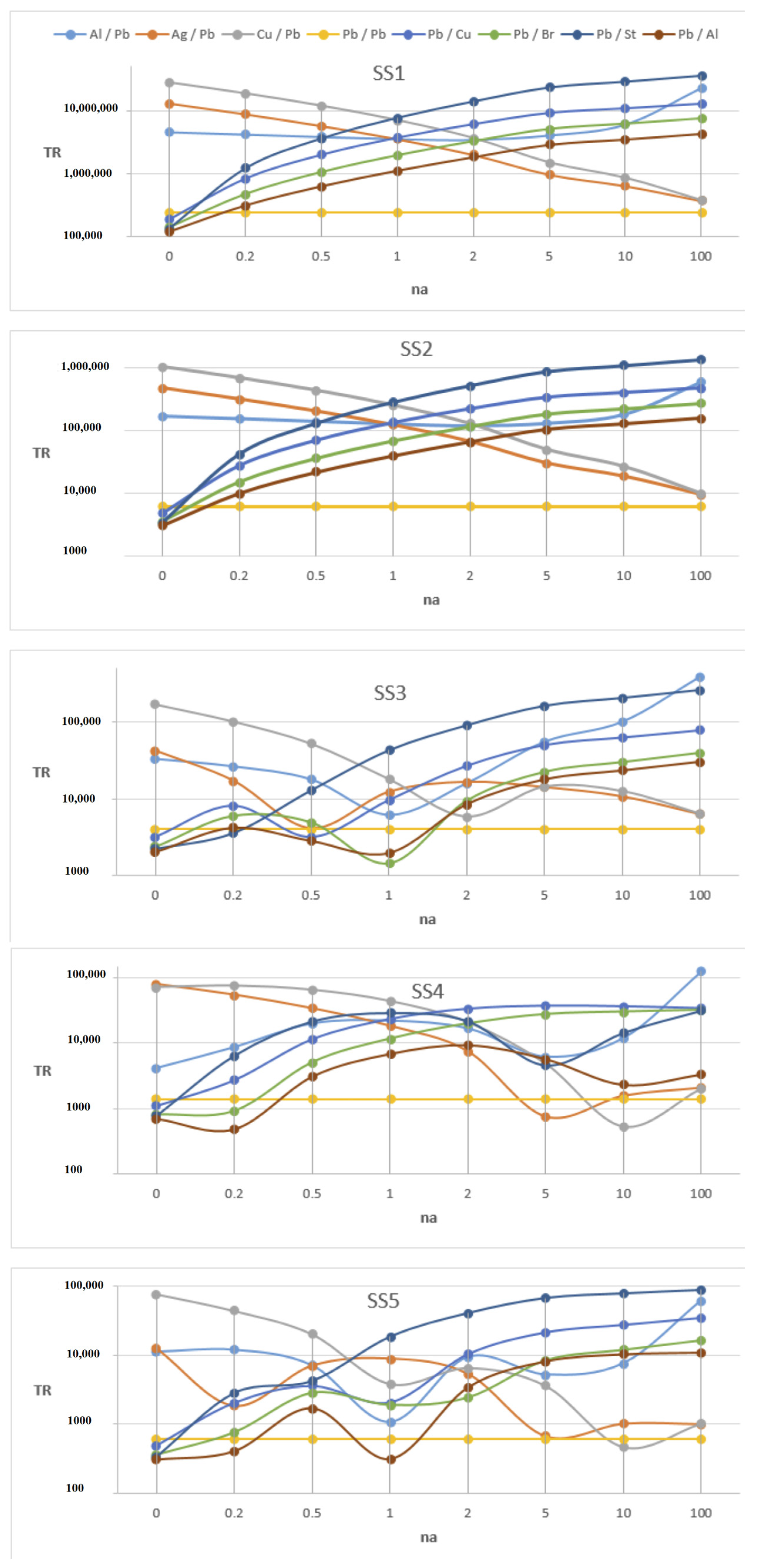
- For the system with the Pb/Cu, Pb/Br, Pb/St and Pb/Al support bars, cAratio > 1 and for the frequency parameters SS1 and SS2, the TR force transmission values increase with increasing na. The values of the TR force transmission decrease with increasing cAratio if cAratio > 1 (Figure 20 and Table 8).
- In the frequency parameters SS1 and SS2, the bar material pairs with cAratio > 1 Pb/Cu, Pb/Br, Pb/St and Pb/Al are ranked in insulation quality as the na value increased towards 100. Excluding Pb/St, TR is ranked according to the cAratio value (Table 5). It can be seen that the Eratio for the Pb/St pair is very low when other material pairs are considered (Table 5). The support bar made of the Pb/Al material pair with the highest cAratio value provides better insulation (Table 8, Figure 20).
- When cAratio > 1, the system with Pb/Al bars provides the best insulation for all values of na. On the other hand, when na = 0, although the bar material behaves like Pb, the insulation is better than the system supported by the pure Pb bar. The change in force transmissibility of the system using pure Pb bar supports is shown in Figure 3 and Table 3. Table 6 shows that for the frequency parameter SS1, the TR value decreases from 243,782 in the Pb bar-supported system to 123,496 in the Pb/Al bar-supported system; for the frequency parameter SS2, the TR value decreases from 6144 in the Pb supported system to 3108 in the Pb/Al supported system. The lowest TR value of the frequency parameter SS1, na = 0, is 4,584,299 for the Al/Pb material pair bar-supported system. Whether the Pb material is at the bottom or the top affects the transmissibility (Table 7 and Table 8, Figure 20).
- In the frequency parameters SS1 and SS2, the bar material pairs with cAratio < 1 Al/Pb, Ag/Pb and Cu/Pb are ranked in terms of insulation quality as the na value increased towards 100 until the na = 1 value. Excluding Al/Pb, the TR is ranked according to the cAratio value (Table 5). The TR of the system with the Al/Pb bar material pair has a turning point at na = 2 and then increases. The support bar made of the Al/Pb and Ag/Pb material pairs with the lowest cAratio value provides better insulation for the different na regions (Table 6, Figure 20). When other material pairs are considered, it is seen that the cAratio is very low in the Pb/Al pair (Table 6).
- For the SS frequency parameters of the system with the Ag/Pb and Cu/Pb material pairs under the condition of cAratio < 1, the TR values are maximum for na = 0, while the TR values are minimum for na = 100. Although there are exceptional cases, the general trend is in this direction. In contrast to the other material pairs with cAratio < 1, for the SS frequency parameters of the system with the Al/Pb material pair, the TR values are maximum for na = 100, while the TR values are minimum for na = 0 and the various na values (Table 6, Figure 20).
- In the frequency responses of SS3, SS4 and SS5, in the case of cAratio > 1, although the trend is for TR to increase with increasing na, the trend has minima at different na values. The minimum values of TR are lower than the value of pure Pb. In the case of cAratio < 1, except for the Al/Pb material pair, the decreasing TR trend continues after making minima at different na values. For SS4 and SS5 frequency responses, the minimum values of TR are lower than the values of pure Pb. For SS3, SS4 and SS5 frequency parameters, the best isolation of the force transmission is achieved at different na values. The material pairs and na values that provide better isolation than the pure Pb bar system are as follows:
- SS3 frequency response: for Pb/Al, Pb/Br material pairs at na = 1 and Pb/Cu at na = 0.5, the best isolation is achieved with Pb/Br material at na = 0.5;
- SS4 frequency response: for Pb/Al, Pb/Br material pairs at na = 0.2 and Ag/Pb material at na = 5 and for Cu/Pb material at na = 10 with minimum transmission, the best isolation is achieved with Pb/Al material pair at na = 0.2;
- In the regions where the bar motion is dominant, 1.region and others, there is a minimum force transmission for na = 0 for the materials with cAratio > 1, while maximum TR values occur for different values of na. For the materials with cAratio < 1, there is a minimum force transmission for na = 100 except for the Al/Pb material pair. There is a maximum force transmission for na = 100, while minimum TR values occur for different values of na for the Al/Pb material pair (Table 6 and Table 8).
- In 1. Region, there is a trend for the transmissibility of the side frequency parameters. This distribution shows a trend according to na less than and greater than 1 for the other regions. For the material pairs with cAratio > 1 and Al/Pb material (cAratio < 1), TR values increase with increasing na. For the material pairs with cAratio < 1, the TR values decrease with increasing na (Table 6 and Table 8 and Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19).
- The TR values decrease as the frequency parameters increase for 1. Region, 2. Region and 3. Region for na = 100 and cAratio < 1 (i.e., TR values, 1. Region: 5305, 2. Region: 1681, 3. Region: 919 for the Al/Pb material pair at na = 100 in Table 6). This trend occurs for maxima values for Al/Pb and the minima values for Ag/Pb and Cu/Pb material pairs (Table 6).
- The TR values decrease as the frequency parameters increase in 1. Region, 2. Region and 3. Region for na = 0 and cAratio >1 (i.e., TR values, 1. Region: 31, 2. Region: 9, 3. Region: 5 for the Pb/Al material pair at na = 0 in Table 8).
- The na values of material pairs that minimise force transmission in the side frequency regions can be written as follows:
- Bar with Al/Pb material: 1. Region and before at na = 0, 2. Region at na = 5, 3. Region at na = 0.5;
- Bar with Ag/Pb material: 1. Region and before na = 0, 2. Region na = 2, 3. Region na = 5;
- Bar with Cu/Pb material; 1. Region and before na = 0, 2. Region na = 5, 3. Region na = 10;
- Bar with Pb/Cu material: 1. Region and before na = 100, 2. Region na = 0.2, 3. Region na = 5;
- Bar with Pb/Br material: 1. Region and before na = 100, 2. Region na = 0.2, 3. Region na = 10;
- Bar with Pb/St material: 1. Region and before na = 100, 2. Region na = 0.2, 3. Region na = 0.5;
- 17.
- 18.
- For the system with the Al/Pb, Ag/Pb and Cu/Pb support bars, cAratio < 1, the frequency parameters decrease with increasing na in the 1. Region (Table 6). The contrast in TR force transmission (TR) between material pairs with cAratio < 1 is not seen here. This situation appears to be the effect of material damping and Young’s modulus.
- 19.
- 20.
- In 1. Region, for the system with bars of Pb/Cu, Pb/Br, Pb/St and Pb/Al material pairs, cAratio > 1, the frequency parameters increase with increasing na (Table 8).
- 21.
- 22.
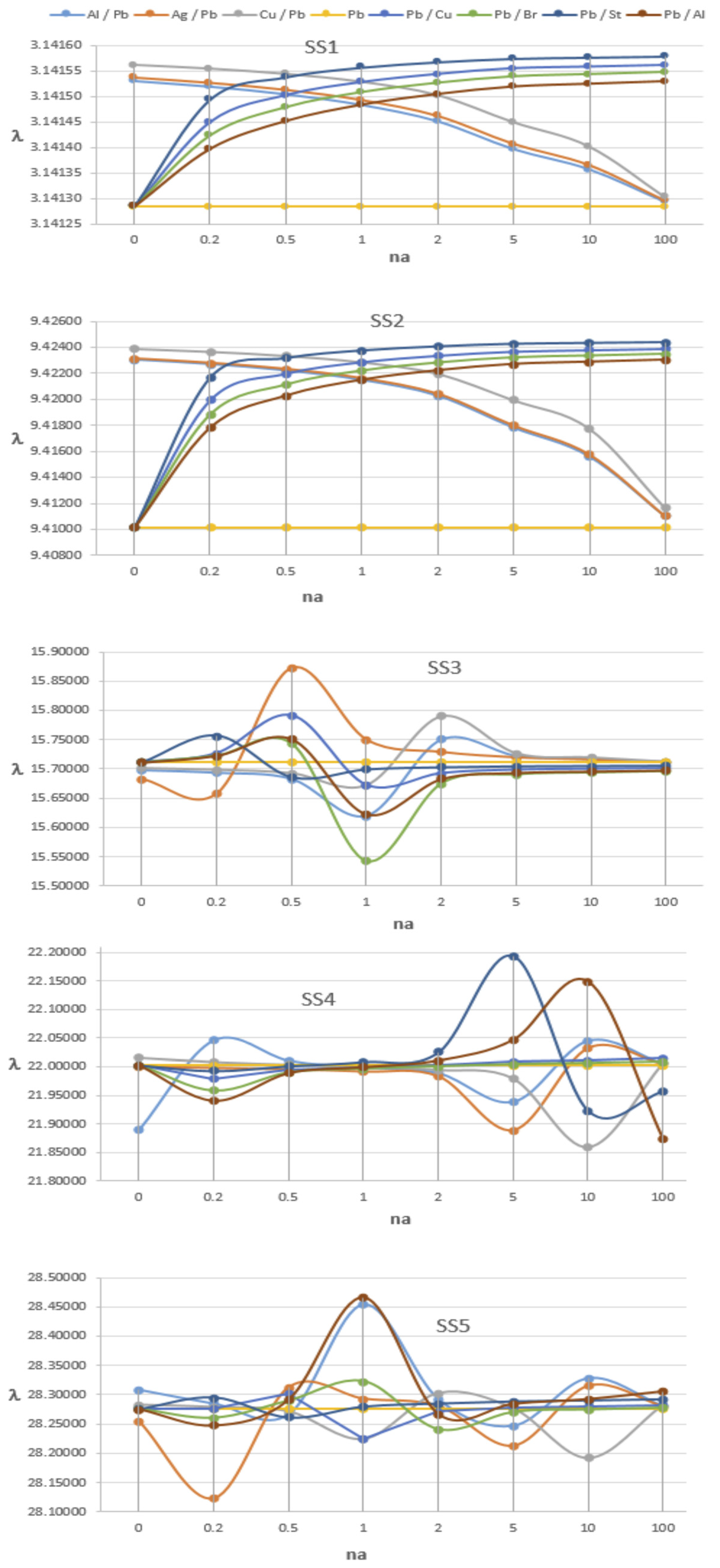
- The side frequencies show an ordered distribution as a function of na over 0–30 Hz. In other frequency ranges, as the bar begins to dominate the overall motion, it is difficult to see a trend due to the dependence of the frequency parameters on specific mass and Young’s modulus. Although there are approaches in the literature to overcome this situation by considering the specific mass ratio as 1, in this study, since beam isolation is the main concern, real material properties are used for the bar. However, the graph for SS3 in Figure 21 shows that the frequency parameters remain constant when na > 5, whereas the graph for SS4 shows that the frequency parameters remain constant in the range 0.5 < na < 2 (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 21 and Table 6, Table 7 and Table 8).
- 23.
- Since it is possible to influence the elasticity and mass distribution with na, isolation in the form of a dynamic absorber will be possible for the relevant frequency. While the peak value is minimised at a certain frequency, the frequency is decomposed as two different peak values. This may be a different approach to the study of minimising the vibration made by Mi and Song [28]. As an example of this situation, Figure 13, Figure 15, Figure 17 and Figure 18 show that for the material pair Al/Pb, SS3 and SS5 for na = 1; for the material pair Cu/Pb, SS5 for na = 10; for the material pair Pb/Br, SS3 for na = 1; and for the material pair Pb/St, SS4 frequency can be given as na = 5.
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, Z.-J.; Lee, J.-H.; Kang, K.-H.; Kim, K.-J. The Forced Vibration Of A Beam with Viscoelastic Boundary Supports. J. Sound Vib. 1998, 210, 673–682. [Google Scholar] [CrossRef]
- Jacquot, R.G. Optimal Damper Location for Randomly Forced Cantilever Beams. J. Sound Vib. 2004, 269, 623–632. [Google Scholar] [CrossRef]
- Abu-Hilal, M.; Mohsen, M. Vibration Of Beams with General Boundary Conditions Due To A Moving Harmonic Load. J. Sound Vib. 2000, 232, 703–717. [Google Scholar] [CrossRef]
- Wang, D.; Wen, M. Vibration Attenuation of Beam Structure with Intermediate Support under Harmonic Excitation. J. Sound Vib. 2022, 532, 117008. [Google Scholar] [CrossRef]
- Jacquot, R.G. Random Vıbratıon of Damped Modıfıed Beam Systems. J. Sound Vib. 2000, 234, 441–454. [Google Scholar] [CrossRef]
- Jacquot, R.G. The Spatial Average Mean Square Motion as an Objective Function for Optimizing Damping in Damped Modified Systems. J. Sound Vib. 2003, 259, 955–965. [Google Scholar] [CrossRef]
- Baz, A.M. Active and Passive Vibration Damping; John Wiley & Sons Ltd: Oxford, UK, 2018; pp. 1–55. [Google Scholar]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure-Borne Sound, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 149–232. [Google Scholar]
- He, J.; Fu, Z.F. Modal Analysis; Butterworth-Heinemann: Oxford, UK, 2001; pp. 123–139. [Google Scholar]
- Petyt, M. Introduction to Finite Element Vibration Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 352–355. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson: London, UK, 2004; pp. 192–197. [Google Scholar]
- Maia, N. Reflections on the Hysteretic Damping Model. Shock. Vib. 2009, 16, 529–542. [Google Scholar] [CrossRef]
- Lisitano, D.; Slavič, J.; Bonisoli, E.; Boltežar, M. Strain Proportional Damping in Bernoulli-Euler Beam Theory. Mech. Syst. Signal Process 2020, 145, 106907. [Google Scholar] [CrossRef]
- Pan, D.; Fu, X.; Qi, W. The Direct Integration Method with Virtual Initial Conditions on the Free and Forced Vibration of a System with Hysteretic Damping. Appl. Sci. 2019, 9, 3707. [Google Scholar] [CrossRef]
- Tsai, T.-C.; Tsau, J.-H.; Chen, C.-S. Vibration Analysis of a Beam with Partially Distributed Internal Viscous Damping. Int. J. Mech. Sci. 2009, 51, 907–914. [Google Scholar] [CrossRef]
- Chen, W.-R. Bending Vibration of Axially Loaded Timoshenko Beams with Locally Distributed Kelvin–Voigt Damping. J. Sound Vib. 2011, 330, 3040–3056. [Google Scholar] [CrossRef]
- Kocatürk, T.; Şimşek, M. Vibration of Viscoelastic Beams Subjected to an Eccentric Compressive Force and a Concentrated Moving Harmonic Force. J. Sound Vib. 2006, 291, 302–322. [Google Scholar] [CrossRef]
- Freundlich, J. Transient Vibrations of a Fractional Kelvin-Voigt Viscoelastic Cantilever Beam with a Tip Mass and Subjected to a Base Excitation. J. Sound Vib. 2019, 438, 99–115. [Google Scholar] [CrossRef]
- Chen, W.-R. Parametric studies on bending vibration of axially-loaded twisted Timoshenko beams with locally distributed Kelvin–Voigt damping. Int. J. Mech. Sci. 2014, 88, 61–70. [Google Scholar] [CrossRef]
- Sepehri-Amin, S.; Faal, R.T.; Das, R. Analytical and Numerical Solutions for Vibration of a Functionally Graded Beam with Multiple Fractionally Damped Absorbers. Thin-Walled Struct. 2020, 157, 106711. [Google Scholar] [CrossRef]
- Demir, C.; Oz, F.E. Free Vibration Analysis of a Functionally Graded Viscoelastic Supported Beam. J. Vib. Control 2013, 20, 2464–2486. [Google Scholar] [CrossRef]
- Deng, H.; Chen, K.; Cheng, W.; Zhao, S. Vibration and Buckling Analysis of Double-Functionally Graded Timoshenko Beam System on Winkler-Pasternak Elastic Foundation. Comp. Struct. 2017, 160, 152–168. [Google Scholar] [CrossRef]
- Duy, H.T.; Van, T.N.; Noh, H.C. Eigen Analysis of Functionally Graded Beams with Variable Cross-Section Resting on Elastic Supports and Elastic Foundation. Struct. Eng. Mech. 2014, 52, 1033–1049. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Fageehi, Y.A.; Assie, A.E.; Eltaher, M.A. Dynamic Analysis of Viscoelastic Functionally Graded Porous Thick Beams under Pulse Load. Eng. Comput. 2020, 38, 365–377. [Google Scholar] [CrossRef]
- Nikolić, A. Free Vibration Analysis of a Non-Uniform Axially Functionally Graded Cantilever Beam with a Tip Body. Arch. Appl. Mech. 2017, 87, 1227–1241. [Google Scholar] [CrossRef]
- Huang, Y.; Rong, H.-W. Free Vibration of Axially Inhomogeneous Beams That Are Made of Functionally Graded Materials. Int. J. Acoust. Vib. 2017, 22, 68–73. [Google Scholar] [CrossRef]
- Demir, E.; Sayer, M.; Callioglu, H. An Approach for Predicting Longitudinal Free Vibration of Axially Functionally Graded Bar by Artificial Neural Network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 237, 2245–2255. [Google Scholar] [CrossRef]
- Mi, X.; Song, Z. A Mode Localization Inspired Vibration Control Method Based on the Axially Functionally Graded Design for Beam Structures. Comp. Struct. 2024, 343, 118300. [Google Scholar] [CrossRef]
- Demir, C. Natural Frequencies of a Viscoelastic Supported Axially Functionally Graded Bar with Tip Masses. Int. J. Acoust. Vib. 2023, 28, 50–64. [Google Scholar] [CrossRef]






| E (GPa) | ρ (kg/m3) | Flexural Loss Factor | Longitudinal Loss Factor * | (GPa) | |
|---|---|---|---|---|---|
| Al/Aluminium | 72 | 2700 | (0.3–10) × 10−5 | 1 × 10−4 | 72 × 105 |
| St/Steel | 210 | 7800 | (0.2–3) × 10−4 | 3 × 10−4 | 630 × 105 |
| Br/Brass | 95 | 8500 | (0.2–1) × 10−3 | 1 × 10−3 | 950 × 105 |
| Ag/Silver | 80 | 10,500 | 4 × 10−4 | 3 × 10−3 | 2400 × 105 |
| Cu/Copper (polycrystalline) | 125 | 8900 | 2 × 10−3 | 2 × 10−3 | 2500 × 105 |
| Pb/Lead(pure) | 17 | 11,300 | (5–30) × 10−2 | 2 × 10−2 | 3400 × 105 |
| Matlab Calculated Results | Rao’s Analytical Solution [11] | Ansys Workbench Modal Analysis | Ansys Workbench Harmonic Analysis | ||||
|---|---|---|---|---|---|---|---|
| Non-Dimensional | Hz. | Non-Dimensional | Hz. | Non-Dimensional | Hz. | Non-Dimensional | |
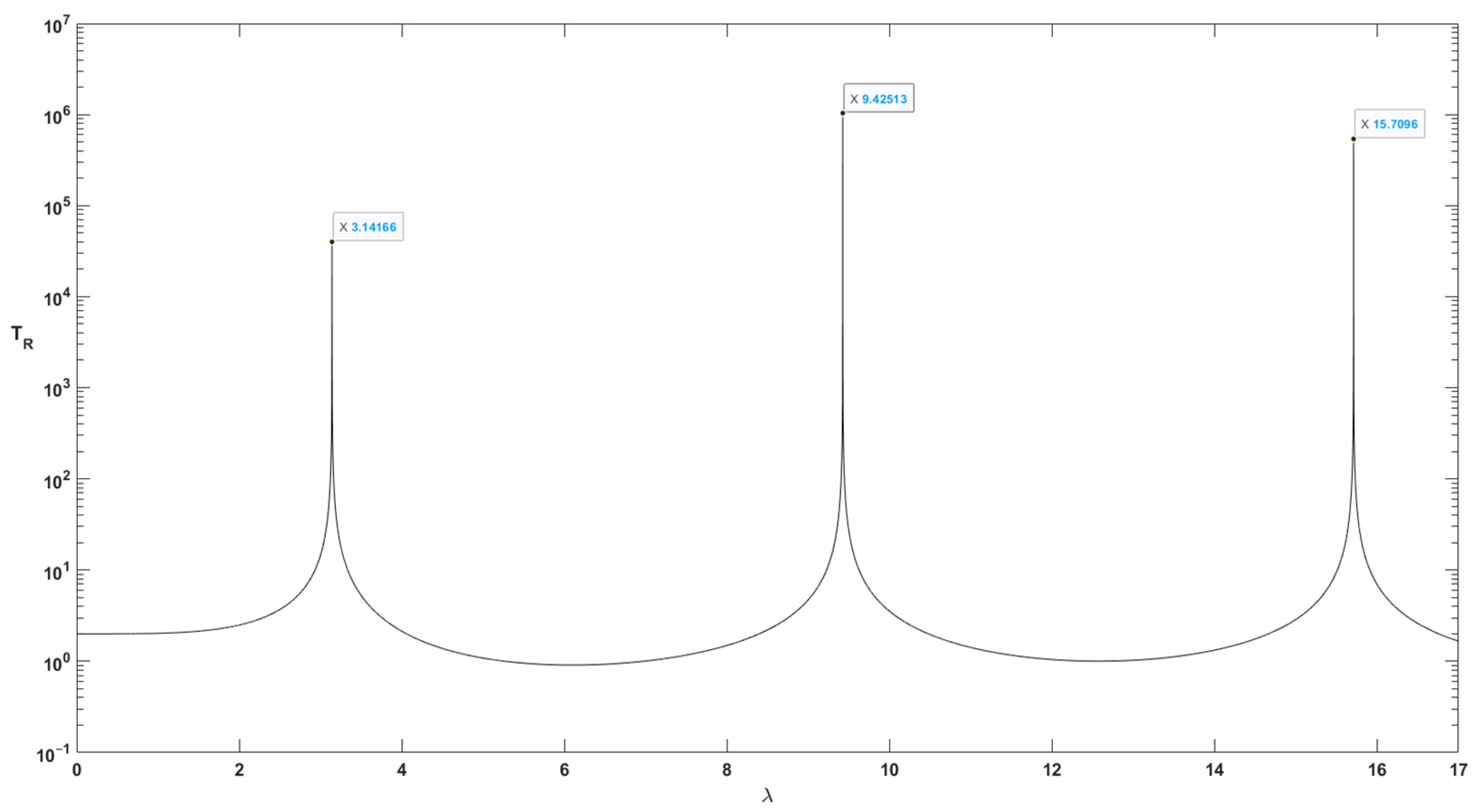
| SS1 | 3.14166 | 23.5293 | 3.1416 | 23.524 | 3.1413 | 23.52 | 3.14166 |
| - | - | - | 94.05 | 6.2798 | - | - | |
| SS2 | 9.42497 | 211.764 | 9.4248 | 211.44 | 9.4177 | 210.48 | 9.40425 |
| - | - | - | 375.45 | 12.5389 | - | - | |
| SS3 | 15.7096 | 588.3315 | 15.708 | 585.76 | 15.6752 | 577.2 | 15.592 |
| Pb Bar | SS1.Mod | SS2.Mod | 1.Region | SS3.Mod | 2.Region | |||||
| λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | |
| η = 0 | 3.141285 | 4,906,936 | 9.410127 | 11,465,955 | 11.33643 | 16,651,019 | 15.71125 | 62,202,302 | 19.62624 | 19,008,059 |
| η = 0.2 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 |
| SS4.Mod | 3.Region | SS5.Mod | ||||||||
| λ | TR | λ | TR | λ | TR | |||||
| η = 0 | 22.00275 | 44,959,291 | 25.3654 | 101,320,433 | 28.27558 | 11,728,774 | ||||
| η = 0.2 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 |
| (a) | ||||||||||||
| Bar Material | Pb | Cu | Ag | Br | St | Al | ||||||
| Mode Number | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| SS1 | 3.14128 | 243,782 | 3.14156 | 14,412,284 | 3.14154 | 1,789,396 | 3.14155 | 2,004,509 | 3.14158 | 8,340,324 | 3.14153 | 8,287,499 |
| SS2 | 9.41013 | 6144 | 9.42390 | 651,465 | 9.42313 | 271,842 | 9.42349 | 983,524 | 9.42441 | 3,849,090 | 9.42304 | 6,501,443 |
| 1.Region | 11.33643 | 61 | ||||||||||
| SS3 | 15.71125 | 4056 | 15.70121 | 108,121 | 15.68292 | 24,358 | 15.69666 | 143,805 | 15.70562 | 1,432,198 | 15.69806 | 1,460,498 |
| 2.Region | 19.62722 | 18 | 19.79233 | 558 | 17.01995 | 544 | 18.70356 | 998 | ||||
| SS4 | 22.00275 | 1412 | 22.01536 | 45,711 | 22.00044 | 46,618 | 22.00860 | 115,014 | 21.95969 | 183,227 | 21.88989 | 186,157 |
| 3.Region | 25.36540 | 10 | 23.33434 | 5348 | 23.29497 | 16,457 | ||||||
| SS5 | 28.27558 | 619 | 28.28267 | 48,419 | 28.25448 | 7200 | 28.27770 | 61,126 | 28.29214 | 476,127 | 28.30824 | 499,885 |
| 4.Region | 29.48704 | 195 | ||||||||||
| (b) | ||||||||||||
| Bar Material | St | Cu | Br | Ag | Al | Pb | ||||||
| Mode Number | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| SS1 | 3.14158 | 8,340,324 | 3.14156 | 14,412,284 | 3.14155 | 2,004,509 | 3.14154 | 178,9396 | 3.14153 | 8,287,499 | 3.14128 | 243,782 |
| SS2 | 9.42441 | 3,849,090 | 9.42390 | 651,465 | 9.42349 | 983,524 | 9.42313 | 271,842 | 9.42304 | 6,501,443 | 9.41013 | 6144 |
| 1.Region | 11.33643 | 61 | ||||||||||
| SS3 | 15.70562 | 1,432,198 | 15.70121 | 108,121 | 15.69666 | 143,805 | 15.68292 | 24,358 | 15.69806 | 1,460,498 | 15.71125 | 4056 |
| 2.Region | 19.79233 | 558 | 18.70356 | 998 | 17.01995 | 544 | 19.62722 | 18 | ||||
| SS4 | 21.95969 | 183,227 | 22.01536 | 45,711 | 22.00860 | 115,014 | 22.00044 | 46,618 | 21.88989 | 186,157 | 22.00275 | 1412 |
| 3.Region | 23.33434 | 5348 | 23.29497 | 16,457 | 25.36540 | 10 | ||||||
| SS5 | 28.29214 | 476,127 | 28.28267 | 48,419 | 28.27770 | 61126 | 28.25448 | 7200 | 28.30824 | 499,885 | 28.27558 | 619 |
| 4.Region | 29.48704 | 195 | ||||||||||
| E Ratio | ρRatio | ηRatio | CA (Eη) Ratio | |
|---|---|---|---|---|
| Al/Pb | 4.235294118 | 0.238938053 | 0.005 | 0.021176 |
| Ag/Pb | 4.705882 | 0.929204 | 0.15 | 0.705882 |
| Cu/Pb | 7.352941176 | 0.787610619 | 0.1 | 0.735294 |
| Pb/Pb | 1 | 1 | 1 | 1 |
| Pb/Cu | 0.136 | 1.269662921 | 10 | 1.36 |
| Pb/Br | 0.178947368 | 1.329411765 | 20 | 3.578947 |
| Pb/St | 0.080952381 | 1.448717949 | 66.66667 | 5.396825 |
| Pb/Al | 0.236111111 | 4.185185185 | 200 | 47.22222 |
| Al/Pb | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.14153 | 4,584,299 | 9.42304 | 167,778 | 15.69806 | 32,607 | 21.89002 | 4121 | 23.29653 | 364 | 28.30827 | 11,053 | ||||||
| 0.2 | 3.14152 | 4,207,768 | 9.42270 | 152,565 | 15.69360 | 26,052 | 20.12809 | 288 | 22.04616 | 8639 | 28.28465 | 11,791 | ||||||
| 0.5 | 3.14150 | 3,862,223 | 9.42221 | 138,182 | 15.68285 | 17,694 | 18.01204 | 272 | 22.01073 | 20,042 | 28.26654 | 7038 | ||||||
| 1 | 3.14148 | 3,580,055 | 9.42148 | 125,492 | 15.61944 | 6135 | 16.3106 | 939 | 21.99940 | 22,155 | 27.95853 | 572 | 28.45400 | 1083 | ||||
| 2 | 3.14145 | 3,462,921 | 9.42027 | 117,195 | 14.58257 | 635 | 15.75101 | 15,768 | 21.98918 | 16,872 | 25.34486 | 114 | 28.29201 | 9297 | ||||
| 5 | 3.14140 | 4,079,769 | 9.41782 | 128,369 | 13.03908 | 556 | 15.72294 | 54,267 | 21.93939 | 6176 | 22.67103 | 543 | 28.24702 | 5210 | 29.25848 | 230 | ||
| 10 | 3.14136 | 6,035,680 | 9.41561 | 177,822 | 12.29681 | 962 | 15.71748 | 98,712 | 21.26622 | 887 | 22.04542 | 11,981 | 27.49573 | 495 | 28.32821 | 7589 | ||
| 100 | 3.14129 | 22,650,047 | 9.41101 | 584,055 | 11.44642 | 5305 | 15.71201 | 380,530 | 19.81652 | 1681 | 22.00516 | 126,262 | 25.61121 | 919 | 28.28022 | 60,951 | ||
| Ag/Pb | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.14154 | 13,158,012 | 9.42314 | 466,260 | 15.68292 | 41,757 | 17.0200 | 933 | 22.00044 | 79,919 | 28.25449 | 12,346 | 29.48763 | 335 | ||||
| 0.2 | 3.14153 | 8,873,608 | 9.42280 | 311,797 | 15.65846 | 17,146 | 16.40639 | 1293 | 21.99842 | 54,963 | 28.12347 | 1839 | 28.51182 | 1289 | ||||
| 0.5 | 3.14151 | 5,779,456 | 9.42233 | 200,653 | 15.48819 | 3065 | 15.87273 | 4152 | 21.99590 | 34,187 | 27.1014 | 203 | 28.31277 | 6937 | ||||
| 1 | 3.14149 | 3,562,337 | 9.42162 | 121,426 | 14.8179 | 589 | 15.75018 | 12,243 | 21.99206 | 18,399 | 25.7453 | 89 | 28.29311 | 8803 | ||||
| 2 | 3.14146 | 2,010,061 | 9.42043 | 66,390 | 13.9188 | 235 | 15.72914 | 16,487 | 21.98348 | 7521 | 24.1620 | 69 | 28.28054 | 5306 | ||||
| 5 | 3.14141 | 973,785 | 9.41800 | 30,124 | 12.8090 | 124 | 15.71993 | 14,074 | 21.88856 | 756 | 22.31571 | 255 | 28.21306 | 673 | 28.76369 | 103 | ||
| 10 | 3.14137 | 643,107 | 9.41578 | 18,741 | 12.2010 | 100 | 15.71644 | 10,660 | 21.11088 | 76 | 22.03336 | 1575 | 27.291 | 41 | 28.31509 | 1020 | ||
| 100 | 3.14130 | 373,432 | 9.41106 | 9617 | 11.4399 | 87 | 15.71195 | 6270 | 19.80615 | 28 | 22.00495 | 2087 | 25.59731 | 15 | 28.27998 | 1002 | ||
| Cu/Pb | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.141562 | 28,114,214 | 9.42390 | 1,017,914 | 15.70121 | 168,945 | 19.79246 | 872 | 22.01536 | 81,417 | 28.28267 | 75,668 | ||||||
| 0.2 | 3.141555 | 18,833,545 | 9.42368 | 678,206 | 15.69838 | 101,115 | 18.83889 | 608 | 22.00813 | 75,307 | 28.27891 | 43,397 | ||||||
| 0.5 | 3.141545 | 12,000,457 | 9.42336 | 428,744 | 15.69245 | 52,117 | 17.81276 | 537 | 22.00351 | 65,012 | 28.27133 | 20,057 | ||||||
| 1 | 3.141529 | 7,077,611 | 9.42287 | 249,716 | 15.67188 | 18,040 | 16.68968 | 732 | 21.99957 | 43,784 | 28.22471 | 3846 | 28.92619 | 364 | ||||
| 2 | 3.141503 | 3,674,291 | 9.42198 | 126,709 | 15.25034 | 1053 | 15.79087 | 5870 | 21.99452 | 20,816 | 26.55739 | 105 | 28.30251 | 6522 | ||||
| 5 | 3.141450 | 1,499,524 | 9.41995 | 48,985 | 13.67858 | 175 | 15.72676 | 14,428 | 21.97888 | 4853 | 23.74623 | 64 | 28.27621 | 3604 | ||||
| 10 | 3.141403 | 855,290 | 9.41777 | 26,337 | 12.75307 | 111 | 15.71968 | 12,581 | 21.85889 | 534 | 22.24804 | 291 | 28.19220 | 472 | 28.65825 | 118 | ||
| 100 | 3.141304 | 376,660 | 9.41166 | 9854 | 11.51472 | 84 | 15.71244 | 6362 | 19.93583 | 28 | 22.00662 | 2034 | 25.76523 | 15 | 28.28288 | 1034 |
| Pb/Pb | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 0.2 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 0.5 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 1 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 2 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 5 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 10 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 | ||
| 100 | 3.141285 | 243,782 | 9.410127 | 6144 | 11.33643 | 61 | 15.71125 | 4056 | 19.627 | 18 | 22.00275 | 1412 | 25.3654 | 10 | 28.27558 | 619 |
| Pb/Cu | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.14128 | 193,155 | 9.41013 | 4859 | 11.33616 | 48 | 15.71126 | 3207 | 19.62689 | 14 | 22.00274 | 1116 | 25.36241 | 8 | 28.27551 | 489 | ||
| 0.2 | 3.14145 | 849,163 | 9.41995 | 27,746 | 13.68093 | 99 | 15.72678 | 8160 | 21.97891 | 2752 | 23.74845 | 36 | 28.27619 | 2041 | ||||
| 0.5 | 3.14150 | 2,020,898 | 9.42198 | 69,706 | 15.25409 | 584 | 15.79143 | 3205 | 21.99452 | 11,449 | 26.56335 | 58 | 28.30255 | 3576 | ||||
| 1 | 3.14153 | 3,768,639 | 9.42287 | 132,984 | 15.67205 | 9650 | 16.69442 | 388 | 21.99957 | 23,295 | 28.22535 | 2069 | 28.93241 | 192 | ||||
| 2 | 3.14154 | 6,162,435 | 9.42336 | 220,193 | 15.69248 | 26,814 | 17.81772 | 275 | 22.00352 | 33,341 | 28.27135 | 10,319 | ||||||
| 5 | 3.14156 | 9,284,181 | 9.42368 | 334,349 | 15.69839 | 49,885 | 18.84243 | 300 | 22.00814 | 37,076 | 28.27891 | 21,399 | ||||||
| 10 | 3.14156 | 10,969,268 | 9.42379 | 396,089 | 15.69988 | 62,487 | 19.28222 | 337 | 22.01092 | 36,341 | 28.28084 | 27,475 | ||||||
| 100 | 3.14156 | 12,970,765 | 9.42389 | 469,499 | 15.70109 | 77,545 | 19.73765 | 400 | 22.01479 | 33,999 | 28.28249 | 34,676 | ||||||
| Pb/Br | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.141285 | 134,651 | 9.41014 | 3573 | 11.33569 | 36 | 15.71126 | 2358 | 19.62808 | 10 | 22.00273 | 820 | 25.36269 | 6 | 28.27557 | 359 | ||
| 0.2 | 3.141495 | 1,218,623 | 9.41884 | 15,124 | 13.18836 | 58 | 15.72276 | 5941 | 21.95877 | 933 | 22.9042 | 42 | 28.26020 | 760 | 29.56703 | 18 | ||
| 0.5 | 3.141539 | 3,629,187 | 9.42113 | 35,766 | 14.56947 | 158 | 15.74291 | 4901 | 21.99007 | 5108 | 25.30386 | 28 | 28.28987 | 2848 | ||||
| 1 | 3.141558 | 7,750,313 | 9.42219 | 67,918 | 15.54333 | 1448 | 15.94383 | 1029 | 21.99647 | 11,693 | 27.3117 | 86 | 28.32286 | 1903 | ||||
| 2 | 3.141568 | 14,129,968 | 9.42281 | 114,927 | 15.67537 | 9356 | 16.85613 | 300 | 22.00043 | 19,956 | 28.24040 | 2434 | 29.20481 | 122 | ||||
| 5 | 3.141575 | 23,578,274 | 9.42321 | 181,572 | 15.69094 | 22,021 | 17.80223 | 247 | 22.00412 | 27,593 | 28.27019 | 8453 | ||||||
| 10 | 3.141577 | 29,201,923 | 9.42335 | 220,150 | 15.69408 | 29,492 | 18.21691 | 254 | 22.00599 | 30,154 | 28.27438 | 11,992 | ||||||
| 100 | 3.141579 | 36,374,675 | 9.42348 | 268,457 | 15.69642 | 38,917 | 18.65109 | 275 | 22.00829 | 31,984 | 28.27741 | 16,476 | ||||||
| Pb/St | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.14128 | 134,640 | 9.41015 | 3388 | 11.33556 | 34 | 15.71126 | 2236 | 19.62814 | 10 | 22.00273 | 778 | 25.36191 | 6 | 28.27556 | 340 | ||
| 0.2 | 3.14150 | 1,218,530 | 9.42169 | 41,670 | 14.92799 | 225 | 15.75657 | 3587 | 21.99268 | 6457 | 25.94335 | 31 | 28.29503 | 2839 | ||||
| 0.5 | 3.14154 | 1,221,260 | 9.42318 | 128,935 | 15.68624 | 12,862 | 17.24097 | 223 | 22.00132 | 21,564 | 28.26153 | 4252 | 29.86814 | 72 | ||||
| 1 | 3.14156 | 1,604,090 | 9.42376 | 279,392 | 15.69930 | 42,581 | 18.99723 | 237 | 22.00860 | 29,102 | 28.27974 | 18,434 | ||||||
| 2 | 3.14157 | 2,233,350 | 9.42408 | 513,287 | 15.70291 | 89,978 | 20.51953 | 498 | 22.02528 | 21,758 | 28.28477 | 40,453 | ||||||
| 5 | 3.14157 | 2,390,880 | 9.42428 | 860,539 | 15.70462 | 16,1363 | 21.76179 | 3931 | 22.19388 | 4625 | 28.28834 | 66,851 | ||||||
| 10 | 3.14158 | 11,638,600 | 9.42434 | 1,067,479 | 15.70513 | 20,4208 | 21.92315 | 14,467 | 22.64737 | 1638 | 28.28996 | 77,837 | ||||||
| 100 | 3.14158 | 12,410,100 | 9.42440 | 1,331,584 | 15.70558 | 259,091 | 21.95759 | 31,565 | 23.25824 | 1024 | 28.29188 | 87,303 | ||||||
| Pb/Al | ||||||||||||||||||
| SS1 | SS2 | 1.Region | SS3 | 2.Region | SS4 | 3.Region | SS5 | 4.Region | ||||||||||
| na | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR | λ | TR |
| 0 | 3.141286 | 123,496 | 9.41015 | 3108 | 11.33522 | 31 | 15.71126 | 2050 | 19.62677 | 9 | 22.00269 | 713 | 25.35513 | 5 | 28.27538 | 310 | ||
| 0.2 | 3.141398 | 319,056 | 9.41782 | 10,051 | 13.0478 | 44 | 15.72298 | 4229 | 21.94089 | 493 | 22.67207 | 42 | 28.24748 | 411 | 29.25086 | 18 | ||
| 0.5 | 3.141452 | 639,406 | 9.42027 | 21,664 | 14.59998 | 119 | 15.75164 | 2866 | 21.98919 | 3123 | 25.36936 | 21 | 28.29198 | 1705 | ||||
| 1 | 3.141484 | 1,125,549 | 9.42149 | 39,492 | 15.62259 | 1997 | 16.33198 | 285 | 21.99941 | 6945 | 27.98499 | 195 | 28.46568 | 317 | ||||
| 2 | 3.141505 | 1,838,666 | 9.42221 | 65,829 | 15.68313 | 8512 | 18.04323 | 129 | 22.01086 | 9458 | 28.26668 | 3383 | ||||||
| 5 | 3.141519 | 2,874,258 | 9.42270 | 104,253 | 15.69367 | 17,868 | 20.15779 | 199 | 22.04706 | 5797 | 28.28462 | 8040 | ||||||
| 10 | 3.141525 | 3,490,783 | 9.42287 | 127,182 | 15.69604 | 23,334 | 21.26336 | 503 | 22.14850 | 2342 | 28.29257 | 10,151 | ||||||
| 100 | 3.141530 | 4,282,465 | 9.42302 | 156,660 | 15.69787 | 30,284 | 21.87354 | 3366 | 23.09514 | 397 | 28.30585 | 10,744 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demir, C. A Novel Approach of the Viscoelasticity of Axially Functional Graded Bar and Application of Harmonic Vibration Analysis of an Isotropic Beam as Support. Appl. Sci. 2024, 14, 8974. https://doi.org/10.3390/app14198974
Demir C. A Novel Approach of the Viscoelasticity of Axially Functional Graded Bar and Application of Harmonic Vibration Analysis of an Isotropic Beam as Support. Applied Sciences. 2024; 14(19):8974. https://doi.org/10.3390/app14198974
Chicago/Turabian StyleDemir, Cihan. 2024. "A Novel Approach of the Viscoelasticity of Axially Functional Graded Bar and Application of Harmonic Vibration Analysis of an Isotropic Beam as Support" Applied Sciences 14, no. 19: 8974. https://doi.org/10.3390/app14198974






