Abstract
To improve acquisition efficiency and achieve super high-resolution reconstruction, a computational integral imaging reconstruction (CIIR) method based on the generative adversarial network (GAN) network is proposed. Firstly, a sparse camera array is used to generate an elemental image array of the 3D object. Then, the elemental image array is mapped to a low-resolution sparse view image. Finally, a lite GAN super-resolution network is presented to up-sample the low-resolution 3D images to high-resolution 3D images with realistic image quality. By removing batch normalization (BN) layers, reducing basic blocks, and adding intra-block operations, better image details and faster generation of super high-resolution images can be achieved. Experimental results demonstrate that the proposed method can effectively enhance the image quality, with the structural similarity (SSIM) reaching over 0.90, and can also reduce the training time by about 20%.
1. Introduction
Integral imaging is a popular method to achieve a 3D display without the need to wear glasses. This approach provides full parallax and all-depth cues, enabling a more immersive experience [1,2,3,4]. Previously, the pickup and display all relied on a lenslet array [5]. With the advancement of computers, computer-generated and computational reconstruction have experienced rapid progress, and many efforts have been devoted to realistic high-quality 3D images, including increasing the sampling rate to improve the resolution of each view [6], changing rendering algorithms to accelerate and generate high-quality 3D images [7,8], as well as the use of convolutional neural networks (CNNs) to eliminate the noise of 3D images [9].
Computational integral imaging reconstruction (CIIR) is based on the technique of optical mapping [10,11,12], which involves mapping elemental images to a 3D space and combining them at a certain depth plane to generate a 3D scene. Optical mapping-based CIIR methods have been extensively studied for improving 3D imagery due to their straightforward ray optics model [13,14]. These methods consist of mapping the pixels in elemental images to the 3D space, either directly or after applying windowing or convolution. Pixel mapping methods, in which each pixel is individually mapped using a lens array, effectively reduce computational costs and improve the visual quality of reconstructed images [15,16,17,18,19]. Windowing methods involve weighting the elemental images with a window function before mapping [20], which helps eliminate blurring and lens array artifacts, thereby improving the quality of the reconstructed image [21,22]. Convolutional methods have been recently introduced to extract depth information through the use of convolutions and delta functions. This approach has resulted in improved image quality and greater control over depth resolution [23,24,25,26,27,28,29,30].
The reconstruction of super high-resolution 3D images with lower optical sampling presents a substantial challenge, notwithstanding the valuable insights offered by the aforementioned research in the field of 3D image generation and reconstruction.
In recent years, deep learning has become a popular technique in computer vision and has made significant progress in various areas such as speech and image recognition and classification [31], novel view synthesis [32], and image super-resolution (SR) [33]. Image SR is a technique used to restore high-resolution images with more details from low-resolution images. It aims to restore lost details, improve image clarity, and enhance visual quality, making the images more informative and realistic. In surveillance systems, it can be used to improve video quality and aid in target recognition and tracking. In medical imaging, it can assist doctors in more accurate diagnosis of patients [34,35]. In satellite imaging and other related fields, it can enhance image clarity and analytical capabilities, helping scientists gain a better understanding of earth, weather, and astronomical phenomena. Single image super-resolution (SISR) has been the subject of extensive research over the past few decades and serves as the foundation for multiple image super-resolution [36]. Super-resolution convolutional neural networks (SRCNNs) utilize an end-to-end learning approach to directly generate high-resolution images from low-resolution ones, eliminating the need for multiple stages in traditional methods [37]. Very deep super-resolution (VDSR) [38] and residual dense networks (RDNs) [39] further explore the mechanisms and effectiveness of deep convolutional neural networks. VDSR, consisting of 20 convolutional layers, can better capture the minute details in images. On the other hand, RDNs utilize the structure of residual skip connections and dense connections to effectively handle complex textures and structures, resulting in the generation of realistic images. The super-resolution generative adversarial network (SRGAN) applies the concept of generative adversarial networks (GANs) to the field of image generation for producing high-resolution photo-realistic images [40]. Compared to traditional methods, they are better at capturing complex patterns and creating intricate textures. Similarly, an enhanced super-resolution generative adversarial network (ESRGAN) was proposed, which utilizes GANs to generate realistic high-resolution images with improved detail and sharpness [41].
Computational efficiency is also a concern in image SR, and the fast super-resolution convolutional neural network (FSRCNN) simplifies the network structure [42], achieving faster speeds compared to each camera viewpoint independent rendering (ECVIR) [43]. Another approach [44] simplifies the generation network to only consist of two convolutions, an activation function, and a deconvolution. While this accelerates computation, designing the generation network too simply can limit its ability to capture texture details.
The traditional SRGAN network utilizes convolutional layers with batch normalization (BN) to extract feature maps during training. BN normalizes the data along the channel dimension for each batch, ensuring that the values of each layer are within a specific range. This helps alleviate the problem of vanishing gradients during the training process. However, BN also introduces additional computational complexity and memory usage. Furthermore, BN only considers the statistical characteristics of the internal batch data during normalization and ignores the inter-batch correlations, which can lead to artifacts and impact the generalization ability of the network [45]. Therefore, in this study, we chose to remove the BN layers to reduce computational complexity and improve the network’s generalization ability. Additionally, addition and subtraction operations are added between the basic blocks to increase the inter-block correlation and enhance the reconstruction effect.
This paper proposes a method for CIIR based on GAN super-resolution. First, a low-resolution reconstructed 3D image based on pixel mapping is generated, which allows for obtaining a view image in less time, and then a lite GAN is employed to super-resolve the low-resolution 3D image. Eliminating the BN layer from SRGAN leads to improvements in generalization and increased high-frequency texture details while reducing computational complexity and memory usage. The residual network layers are then added together to form a dense residual network, which allows for greater connectivity between each residual block. This approach ensures that there is more communication between each residual block and improves the overall performance of the network. After the process of the lite GAN network, super-high resolution reconstructed 3D images are obtained. The experimental results show that the proposed method achieves SSIM above 0.95 in different 3D models and reduces network training time by about 20%.
This article is structured as follows: Section 2 introduces the fundamental principles of the algorithm. Section 2.1 provides an overview of ray tracing and pixel mapping, explaining how to generate low-resolution images from elemental image arrays. Section 2.2 focuses on high-resolution 3D image generation based on GAN, explaining how to enhance the effect of the reconstructed image. Section 3 presents the experimental results and engages in comprehensive discussions. Finally, Section 4 draws conclusions based on the research conducted.
2. Principle
The proposed method is shown in Figure 1. Firstly, a sparse camera array is established to quickly obtain the elemental image array of the 3D model. Then, view images are generated by pixel mapping. Due to the limited number of cameras, only low-resolution view images can be reconstructed. Therefore, a lite GAN network is utilized for super-resolution of the view images. This enables high-resolution integral imaging reconstruction to be achieved with fewer cameras.
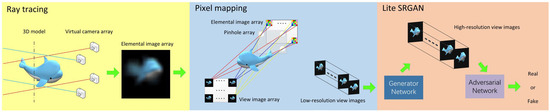
Figure 1.
The overall approach of our proposed method.
2.1. Ray Tracing and Pixel Mapping
The difference between the computational integral imaging and the all-optical integral imaging is that the reconstructed 3D image is synthesized in the computer by using a simulated lens array (or pinhole array, camera array), rather than using a combination of a display device and a lens array. At present, there are two kinds of methods to reconstruct the 3D image in integral imaging [13]. One is to synthesize the pinhole array model by computer and reconstruct the 3D image by ray tracing. The other is to extract and model the depth of the collected 3D information.
Ray tracing is a fundamental process to generate an elemental image array, as shown in Figure 2a. Any point on the surface of a 3D object is imaged through the lenslet array. Each elemental image represents the imaging mapping of the 3D object through the corresponding optical center. The elemental images record the information of the rays emitted from every point on the surface of a 3D object. Therefore, a ray can be determined by selecting any point in the elemental image array. We can use ray tracing to analyze the recording process of integral imaging.
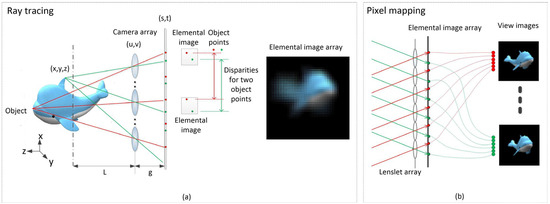
Figure 2.
The process of (a) ray tracing and (b) pixel mapping.
According to the dual-plane light field parameterization method [46], the imaging range of the lenslet is located behind it, and all of the optical axes of the lenslet are perpendicular to the elemental image array. The optical center of the lenslet corresponds to the elemental image array. Based on geometric optics, from Figure 2a we can derive that
where are the coordinates of the ray, it passes through the lenslet array plane , and imaging on the elemental image arrays is . Then the light field distribution of the elemental image array can be written as:
The light field information recorded by integral imaging is:
Therefore, the recorded is equivalent to , and can be reconstructed from .
To reconstruct view images, pixel mapping is used to generate images from different perspectives, as shown in Figure 2b. According to the optical mapping between elemental images and view images [47], parallel rays with the same incident angle (e.g., red or green in Figure 2b) refracted by the lens array will produce corresponding view images at the imaging plane under the corresponding angle. Different angles of light will generate different view images. By using pixel mapping, the pixels with the same viewpoint can be extracted from the elemental image array to reconstruct the view image.
Parallel light rays with the same incident angle are refracted by the lenslet array and generate view images at corresponding angles on the imaging plane. Different angles of light rays will generate view images from different perspectives. The pixel mapping between elemental image and view image can be expressed as:
where subscript represent the coordinates of the elemental image, and are the pixels in each elemental image. Equation (4) shows that the resolution of the reconstructed view image is equal to the number of elemental images, which means increasing the resolution of view images requires an increase in the number of cameras. For example, a 50 × 50 camera array can only reconstruct a 3D image with a resolution of 50 × 50. To improve the rendering efficiency, it is necessary to avoid increasing the number of cameras. Therefore, a lite GAN is used to convert the low-resolution 3D image to super-resolution.
2.2. High-Resolution 3D View Image Generation Based on GAN
Based on the method described in Section 2.1, it is possible to generate a low-resolution view image. In order to achieve efficient generation of super high-resolution 3D images, a refined SRGAN network is proposed.
Traditional CNN-based super-resolution reconstruction algorithms usually use mean squared error (MSE) as the loss function, which cannot guarantee the perceptual consistency between the generated images and the real images. SRGAN introduces perceptual loss, which calculates the feature differences between the generated images and the real images using a pre-trained feature extraction network, thereby better preserving the perceptual details of the images. In addition, the discriminator of the SRGAN network adopts a deep convolutional neural network, which can effectively learn the differences between the generated images and the real images. This enables SRGAN to generate more realistic and natural high-resolution images, avoiding the issues of excessive smoothness or over-sharpening.
To prevent the issues of gradient diffusion and degradation caused by an increasing number of network layers, the generator network has incorporated a skip-connection residual network structure. Each residual block includes two convolutional layers, followed by batch normalization and leaky rectified linear unit (LReLU) activation function. Furthermore, the visual geometry group (VGG) network is employed to compute the content loss instead of the traditional MSE. All convolutional kernels have a 3 × 3 structure with 64 feature maps, aiding in the extraction of richer feature information.
We can input a low-resolution image and perform convolution on the convolutional layer with parameters set to 3 × 3 × 64, meaning there are 64 convolution kernels with a 3 × 3 structure and step size of 1. LReLU is used as the activation function, followed by training in 6 residual block networks before entering the convolutional layer. Finally, the image is upscaled by a factor of 2 using the scaling convolution method. The nearest-neighbor interpolation is employed to upscale the image by 2 times, and then it is passed through the convolutional layer. After that, a convolution operation is performed, and a high-resolution image is outputted.
This article is based on an improved SRGAN network that removes the BN layer from the previous SRGAN. The BN layer is implemented by normalizing each batch of data in the channel dimension by subtracting the mean of the batch and dividing it by the standard deviation of the feature values of each sample. In this way, the feature values of each layer are in a specific range, which reduces the problem of gradient disappearance during training. However, since the BN layer only considers the statistical properties of the current batch data, the correlation between different batches is ignored. This means that if there are differences in the data distribution between batches, the BN layer may not be able to completely eliminate these differences, introducing an artifact problem. Such artifacts can manifest themselves as unnatural textures or color deviations in the generated images, among others. Moreover, since the BN layer only exploits the statistical properties of the local batch data, it may affect the generalization ability of the network. Because the generalization ability requires the network to be able to adapt to different distributions of data, the normalization process of the BN layer is only carried out on the local batch data, which cannot fully consider the global characteristics of the entire data set. Therefore, removing BN layers can reduce this artifact problem and improve the generalization ability of the network by increasing the correlation between the basic blocks. Such improvement measures help to improve the accuracy of the reconstruction task and the quality of the generated images.
The residual network layers are added together to form a dense residual network, allowing for more connections between each residual block, as shown in Figure 3.
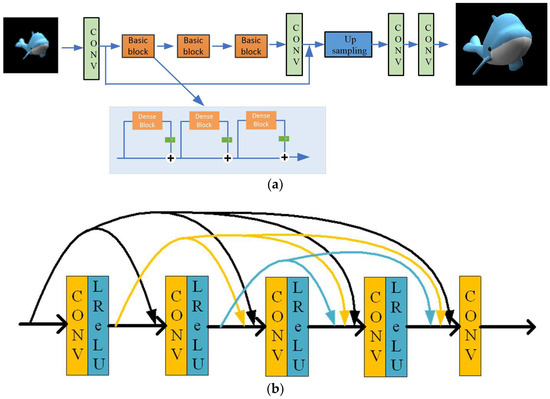
Figure 3.
The architecture of the proposed networks: (a) generative network and (b) dense block.
We use relatively few basic blocks to compose the generative network, which can reduce the training time and the time required to generate high-resolution images. The GAN uses content loss and adversarial loss to improve the realism of the output image and generate high-frequency information. The loss function is expressed as follows:
where is the adversarial loss, which is the loss incurred when the discriminator identifies the generated images from the generator as natural images. The content loss is divided into two parts: , which is the MSE loss of the generator network, and , which is the feature loss obtained by inputting the generated images into the VGG network. The weight of the adversarial loss is l = 10–3.
The MSE loss is a commonly used loss function to measure the difference between the high-resolution images generated by the generative network and the real images. If the loss function only consists of the MSE loss, it can be represented as:
where and represent the width and height of the image, is the magnification factor for super-resolution, is the pixel value of the original image , and represents the reconstructed image output by the generative network. The VGG loss function utilizes the feature vectors from a pre-trained VGG-19 network to measure the perceptual similarity between the generated image and the original image. This loss is calculated by comparing the feature values produced by the VGG network for both images. The VGG loss can be expressed as:
where represent the feature maps output after the convolutional layer and before the max pooling layer. It is the feature value obtained through the VGG network.
The purpose of the generative network is to generate realistic images to deceive the discriminative network and produce high-quality images. Therefore, the adversarial loss is used to measure the similarity between the generated image and the real image. The adversarial loss is:
where is the probability that the discriminator classifies the generated image by the generator as a real image.
The VOC2012 dataset was used to train the network, which contains a large number of high-quality images and has wide applicability, making it suitable for SR training [48]. The training dataset consists of images with varying complexity captured using different sets of lenses, enabling the network to have better generalization ability. To expand the dataset, the images in the dataset can be cropped, rotated, mirrored, etc., to increase the number of samples. During training, the high-resolution images were first down-sampled using bicubic interpolation to obtain low-resolution images which were then upscaled and compared with the original images to train the network parameters. To generate low-resolution and high-resolution image pairs for training, we first cropped all images in the dataset to 88 × 88 images, then downsampled to the corresponding low-resolution image. The adaptive moment estimation (Adam) was used with a learning rate of 10–4 for gradient descent during training. The network was trained for 100 epochs with a batch size of 16.
3. Experimental Results
In the experiments, the PC hardware configuration consists of Intel(R) Core(TM) i7-11,800H CPU @ 2.30GHz with 16GB RAM and NVIDIA GeForce RTX 3060 laptop GPU. The parameters of the ray tracing are shown in Table 1.

Table 1.
Parameters of the ray tracing.
The test objects encompass a simple textured dolphin, a complex textured warcraft, and a hamburger. Figure 4 shows the elemental image array generated by ray tracing, as well as upper, lower, left, and right view images resulting from pixel mapping.
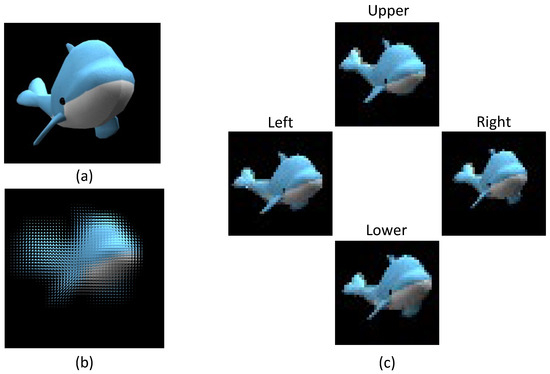
Figure 4.
(a) 3D model dolphin (b) elemental image array (c) view images.
In order to quickly obtain high-resolution 3D images, light generative networks and deep discriminative networks can be used to achieve better results in image super-resolution, while reducing the time required for the generation network to produce high-resolution images. While SRGAN uses 16 basic blocks to increase the complexity of the network, this paper uses fewer basic blocks to improve training speed while reducing complexity, as shown in Table 2.

Table 2.
Number of basic blocks and training time.
Table 2 shows that the structural similarity index measure (SSIM) and peak signal to noise ratio (PSNR) obtained using 16 basic blocks in SRGAN are not significantly different from those obtained using 6 basic blocks, but the training time is greatly reduced by about 20%. On the other hand, the training time difference between 6 basic blocks and 3 basic blocks is not significant, yet the SSIM and PSNR values are much lower than those obtained using 16 basic blocks. This indicates that while maintaining the same image output quality, appropriately reducing the number of basic blocks can lead to faster training of network parameters. To enhance the training speed while ensuring that the image reconstruction quality remains unaffected, a comparison was also made between the traditional SRGAN and the proposed method. The training results of traditional SRGAN showed a PSNR of 23.9041 dB and an SSIM of 0.7091, while the training results of the proposed method showed a PSNR of 23.8863 dB and an SSIM of 0.7102. It can be observed that there is not a significant difference in the training results between the two methods. This indicates that the proposed method can train the network quickly without compromising on the image reconstruction quality. In summary, the proposed method in this paper offers both time efficiency and quality preservation.
Due to the limited number of cameras, through pixel mapping, we can only reconstruct the view images with lower resolution. Therefore, super-resolution is used to improve these reconstructed images; the results are shown in Figure 5.

Figure 5.
Reconstructed images using (a) proposed method, (b) SRCNN, (c) bicubic interpolation, and (d) pixel mapping.
To verify the feasibility of the proposed method, a comparison of reconstructed 3D images is made between our method, SRCNN [37], bicubic interpolation [37], and pixel mapping [13]. For simplicity, we select a specific viewpoint for super-resolution reconstruction. From the local zoom-in effect, it can be observed that the proposed method provides reconstructed images with sharper texture details and better subjective image quality than others.
In addition, SSIM is used as an objective quantitative metric for the reconstructed image quality evaluation, as shown in Table 2.
From Figure 5 and Table 2 and Table 3, it can be observed that the proposed method has better view effects for the three different complexity 3D models. It also exhibits better generalization ability, displays more high-frequency information, and ensures a better 3D imaging effect as perceived by the human eye. The proposed method not only achieves improvements in SSIM but also reduces the training time by about 20%.

Table 3.
SSIM of super-resolution reconstructed images for different models.
In summary, using the improved light GAN network can quickly reconstruct the low-resolution view images at high resolution and improve the 3D image display quality, so as to better represent the details and texture information. By removing the BN layer, better extraction of high-frequency information from images can be achieved, as the BN layer may introduce unnecessary smoothing to high-frequency details in the images. Removing the BN layer allows the network to preserve image details and texture features more effectively. Furthermore, reducing the number of basic blocks brings two benefits. Firstly, it reduces the number of parameters and computational load, thereby accelerating network training and high-resolution image generation. Secondly, reducing the number of basic blocks prevents the network from becoming overly complex and helps avoid overfitting issues, resulting in generated images with better generalization ability. Increasing intra-block operations enhances connectivity between layers, allowing the network to better propagate and utilize information. This improves the network’s ability to capture image details, leading to the generation of more realistic and clear high-resolution images.
The VOC2012 dataset was used for training, which includes a large number of scene images covering various types of images such as people, landscapes, etc. The dataset was augmented using techniques such as rotation and scaling to increase its diversity, which improves the model’s ability to generalize to different scenes and enhances its performance. Although the training time is long, once the model is trained, the subsequent super-resolution can be applied directly without the need for further training. It only takes about 1 s to super-resolve a new input image using the trained model, as shown in Table 2. Therefore, it is feasible to use super-resolution for computational integral imaging reconstruction. Reference [44] also indicates that using super-resolution methods can improve the reconstruction speed of integral imaging. To verify the feasibility of the proposed method, three models with different complexities were evaluated, and image quality evaluation metrics such as PSNR and SSIM were used for comparison. The results showed that the proposed method exhibited higher PSNR and SSIM values while reducing training time. This means that the proposed method can better preserve image details, improve image fidelity, and significantly enhance image reconstruction quality. Through extensive testing on a large amount of data, we confirmed that the performance difference of the proposed method is significant and not just due to random errors. Therefore, we can conclude that the proposed improvement method has statistical significance and is effectively reflected in the image quality evaluation metrics.
It should be noted that the proposed method performs well in SR for images with relatively high resolutions. However, if the resolution of the view images is too small, the method may suffer from distortion issues. In particular, when dealing with images of size 25 × 25 pixels, the performance is not ideal. While the current performance may not be ideal for such low-resolution images, ongoing research and advancements in SR algorithms hold promise for further enhancing the method’s effectiveness in handling smaller image sizes. Thus, future work could focus on refining the proposed method to improve its performance even for images with extremely low resolutions.
4. Conclusions
A light SRGAN is used to generate super high-resolution 3D images from low-resolution 3D images. This method eliminates the BN layer from SRGAN, reduces basic blocks, and adds intra-block operations, which helps to improve generalization, increase high-frequency texture details, and enhance the reconstruction effect and speed. The experimental results show that the proposed method can synthesize better 3D images with lower training time than the existing reconstruction method, and the value of SSIM is over 0.95, which demonstrates that the image quality can be acceptable. This method enables observers to see the details and structures in 3D images more clearly. This is of great significance in fields such as medical imaging, geological exploration, and industrial inspection, as it can enhance the analysis and diagnostic capabilities of images.
Author Contributions
Conceptualization, W.W. and Z.Q.; methodology, W.C. and S.W.; software, W.W. and Z.Q.; validation, W.W, S.W. and Z.Q.; formal analysis, W.C.; investigation, Y.Z.; resources, C.Z.; data curation, Y.C.; writing—original draft preparation, W.W.; writing—review and editing, W.W.; visualization, C.Z.; supervision, W.C.; project administration, S.W. and W.C.; funding acquisition, W.W. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (NSFC) (61631009 and 61901187) and Science and Technology Development Plan of Jilin Province (20220101127JC and 20210201027GX).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to acknowledge support from the State Key Laboratory of New Communications Technologies at Jilin University.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, W.; Wang, S.G. Integral Imaging with Full Parallax Based on Mini LED Display Unit. IEEE Access 2019, 7, 32030–32036. [Google Scholar] [CrossRef]
- Balram, N.; Tošić, I. Light-field imaging and display systems. Inf. Disp. 2016, 32, 6–13. [Google Scholar] [CrossRef]
- Sang, X.Z.; Gao, X. Interactive floating full-parallax digital three-dimensional light-field display based on wavefront recomposing. Opt. Express 2018, 26, 8883–8889. [Google Scholar] [CrossRef] [PubMed]
- Li, H.N.; Wang, S.G. Large-scale elemental image array generation in integral imaging based on scale invariant feature transform and discrete viewpoint acquisition. Displays 2021, 69, 102025. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.G. Performance metric and objective evaluation for displayed 3D images generated by different lenslet arrays. Opt. Commun. 2018, 426, 635–641. [Google Scholar] [CrossRef]
- Yanaka, K. Integral photography using hexagonal fly’s eye lens and fractional view. Proc. SPIE 2008, 6803, 68031K. [Google Scholar]
- Halle, M. Multiple viewpoint rendering. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; pp. 243–254. [Google Scholar]
- Xing, S.; Sang, X.Z. High-efficient computer-generated integral imaging based on the backward ray-tracing technique and optical reconstruction. Opt. Express 2017, 25, 330–338. [Google Scholar] [CrossRef]
- Li, Y.; Sang, X.Z. Real-time optical 3D reconstruction based on Monte Carlo integration and recurrent CNNs denoising with the 3D light field display. Opt. Express 2019, 27, 22198–22208. [Google Scholar] [CrossRef]
- Hong, S.H.; Jang, J.S. Three-dimensional volumetric object reconstruction using computational integral imaging. Opt. Express 2004, 12, 483–491. [Google Scholar] [CrossRef]
- Shin, D.H.; Yoo, H. Image quality enhancement in 3D computational integral imaging by use of interpolation methods. Opt. Express 2007, 15, 12039–12049. [Google Scholar] [CrossRef]
- Arimoto, H.; Javidi, B. Integral three-dimensional imaging with digital reconstruction. Opt. Lett. 2001, 26, 157–159. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Cho, H. Computational Integral Imaging Reconstruction via Elemental Image Blending without Normalization. Sensors 2023, 23, 5468. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Ren, Z. Analysis of the noise in back projection light field acquisition and its optimization. Appl. Opt. 2017, 56, F20–F26. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.H.; Yoo, H. Computational integral imaging reconstruction method of 3D images using pixel-to-pixel mapping and image interpolation. Opt. Commun. 2009, 282, 2760–2767. [Google Scholar] [CrossRef]
- Inoue, K.; Lee, M.C. Improved 3D integral imaging reconstruction with elemental image pixel rearrangement. J. Opt. 2018, 20, 025703. [Google Scholar] [CrossRef]
- Cho, M.; Javidi, B. Computational reconstruction of three-dimensional integral imaging by rearrangement of elemental image pixels. J. Disp. Technol. 2009, 5, 61–65. [Google Scholar] [CrossRef]
- Inoue, K.; Cho, M. Visual quality enhancement of integral imaging by using pixel rearrangement technique with convolution operator (CPERTS). Opt. Lasers Eng. 2018, 111, 206–210. [Google Scholar] [CrossRef]
- Qin, Z.; Chou, P.Y. Resolution-enhanced light field displays by recombining subpixels across elemental images. Opt. Lett. 2019, 44, 2438–2441. [Google Scholar] [CrossRef]
- Shin, D.H.; Yoo, H. Scale-variant magnification for computational integral imaging and its application to 3D object correlator. Opt. Express 2008, 16, 8855–8867. [Google Scholar] [CrossRef]
- Yoo, H. Artifact analysis and image enhancement in three-dimensional computational integral imaging using smooth windowing technique. Opt. Lett. 2011, 36, 2107–2109. [Google Scholar] [CrossRef]
- Yoo, H.; Shin, D.H. Improved analysis on the signal property of computational integral imaging system. Opt. Express 2007, 15, 14107–14114. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.Y.; Shin, D.H. Improved 3-D image reconstruction using the convolution property of periodic functions in curved integral-imaging. Opt. Lasers Eng. 2014, 54, 14–20. [Google Scholar] [CrossRef]
- Llavador, A.; Sánchez-Ortiga, E. Free-depths reconstruction with synthetic impulse response in integral imaging. Opt. Express 2015, 23, 30127–30135. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.Y.; Shin, D.H. Optical three-dimensional refocusing from elemental images based on a sifting property of the periodic δ-function array in integral imaging. Opt. Express 2014, 22, 1533–1550. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Wang, Q.H. Optical arbitrary-depth refocusing for large-depth scene in integral imaging display based on reprojected parallax image. Opt. Commun. 2019, 433, 209–214. [Google Scholar] [CrossRef]
- Ai, L.Y.; Dong, X.B. Optical full-depth refocusing of 3-D objects based on subdivided-elemental images and local periodic δ-functions in integral imaging. Opt. Express 2016, 24, 10359–10375. [Google Scholar] [CrossRef]
- Jang, J.Y.; Ser, J.I. Depth extraction by using the correlation of the periodic function with an elemental image in integral imaging. Appl. Opt. 2012, 51, 3279–3286. [Google Scholar] [CrossRef]
- Yoo, H.; Jang, J.-Y. Intermediate elemental image reconstruction for refocused three-dimensional images in integral imaging by convolution with -function sequences. Opt. Lasers Eng. 2017, 97, 93–99. [Google Scholar] [CrossRef]
- Ai, L.Y.; Kim, E.S. Refocusing-range and image-quality enhanced optical reconstruction of 3-D objects from integral images using a principal periodic δ-function array. Opt. Commun. 2018, 410, 871–883. [Google Scholar] [CrossRef]
- Nadeem, M.I.; Ahmed, K. SHO-CNN: A Metaheuristic Optimization of a Convolutional Neural Network for Multi-Label News Classification. Electronics 2023, 12, 113. [Google Scholar] [CrossRef]
- Liu, C.L.; Shih, K.T. Light Field Synthesis by Training Deep Network in the Refocused Image Domain. IEEE Trans. Image Proc. 2020, 29, 6630–6640. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ying, X. Symmetric parallax attention for stereo image super resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 766–775. [Google Scholar]
- Oyelade, O.N.; Ezugwu, A.E. Characterization of abnormalities in breast cancer images using nature-inspired metaheuristic optimized convolutional neural networks model. Concurr. Comput. Pract. Exper. 2022, 34, e6629. [Google Scholar] [CrossRef]
- Zivkovic, M.; Bacanin, N. Hybrid CNN and XGBoost Model Tuned by Modified Arithmetic Optimization Algorithm for COVID-19 Early Diagnostics from X-ray Images. Electronics 2022, 11, 3798. [Google Scholar] [CrossRef]
- Anwar, S.; Khan, S. A deep journey into super-resolution: A survey. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Zhang, Y.; Tian, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Ledig, C.; Theis, L. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Rakotonirina, N.C.; Rasoanaivo, A. ESRGAN+: Further improving enhanced super-resolution generative adversarial network. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3637–3641. [Google Scholar]
- Dong, C.; Loy, C.C. Accelerating the super-resolution convolutional neural network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar]
- Ren, H.; Wang, Q.H. Super-multiview integral imaging scheme based on sparse camera array and CNN super-resolution. Appl. Opt. 2019, 58, A190–A196. [Google Scholar] [CrossRef]
- Guo, X.; Sang, X.Z. Real-time optical reconstruction for a three-dimensional light-field display based on path-tracing and CNN super-resolution. Opt. Express 2021, 29, 37862–37876. [Google Scholar] [CrossRef]
- Wang, X.T.; Yu, K. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Volume 11133, pp. 63–79. [Google Scholar]
- Levoy, M.; Hanrahan, P. Light field rendering. In Seminal Graphics Papers: Pushing the Boundaries; ACM: New York, NY, USA, 1996; pp. 31–42. [Google Scholar]
- Park, J.H.; Lee, B. Recent progress in three-dimensional information processing based on integral imaging. Appl. Opt. 2009, 48, H77–H94. [Google Scholar] [CrossRef]
- Everingham, M.; Eslami, S.M.A. The PASCAL visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).