Evolution Mechanism of Interlayer Properties of CRTS III Slab Track during Construction
Abstract
:1. Introduction
2. Methods
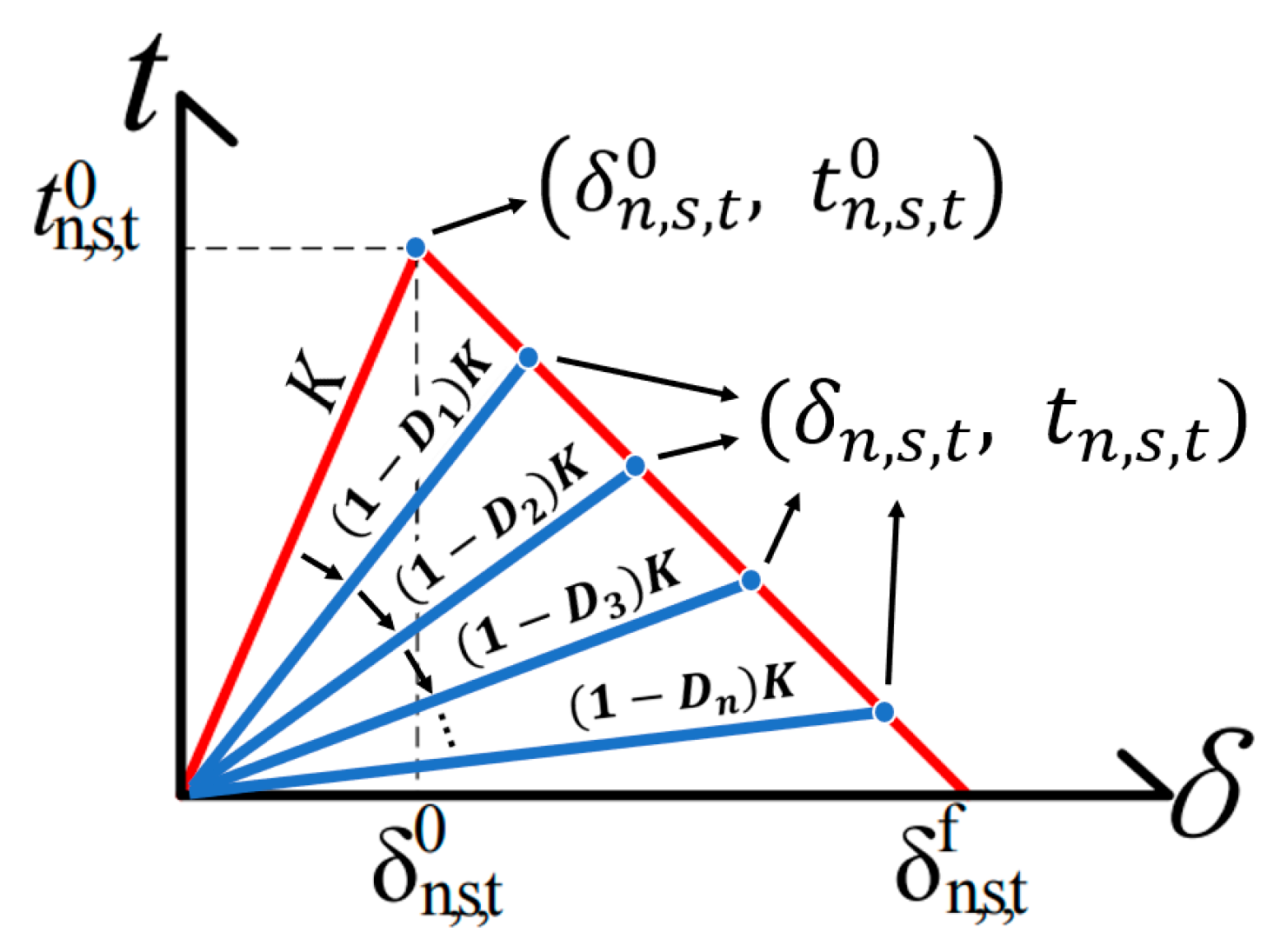
2.1. Interface Constitutive
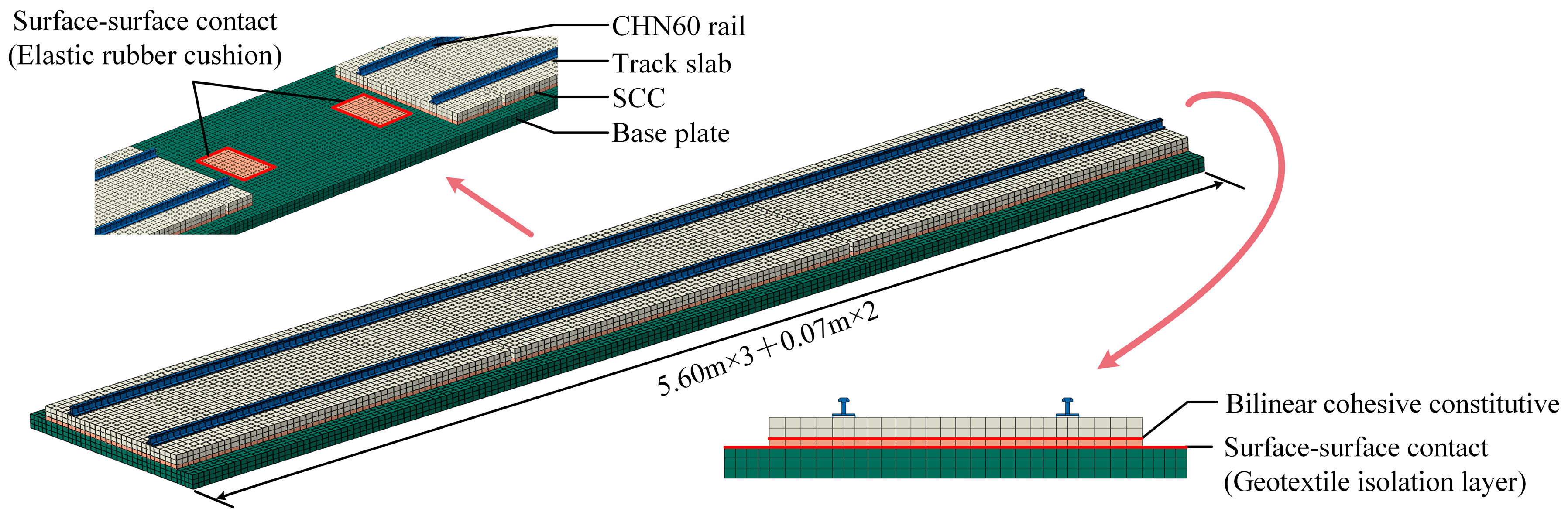
2.2. FEM of CRTS III Slab Track
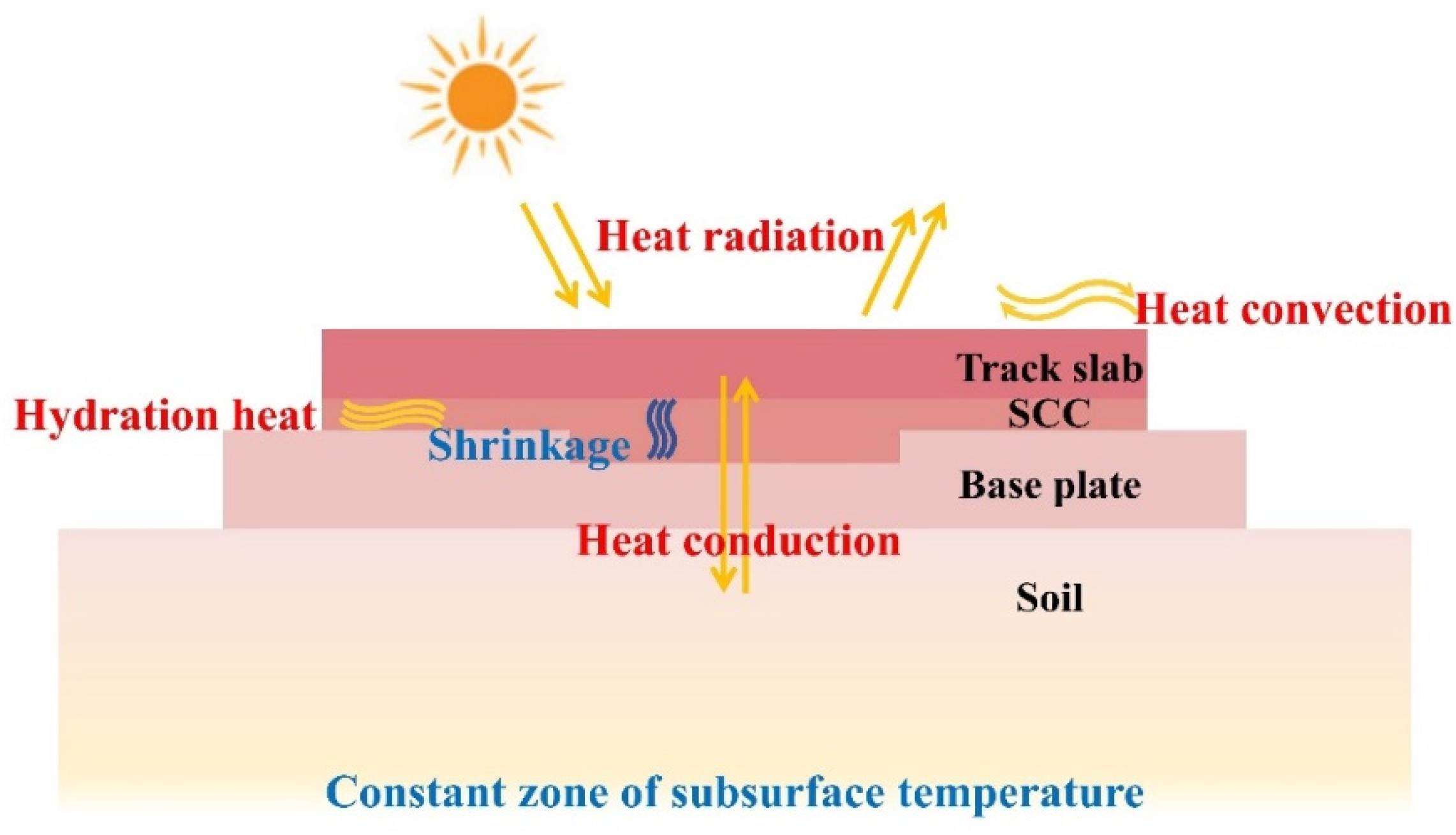
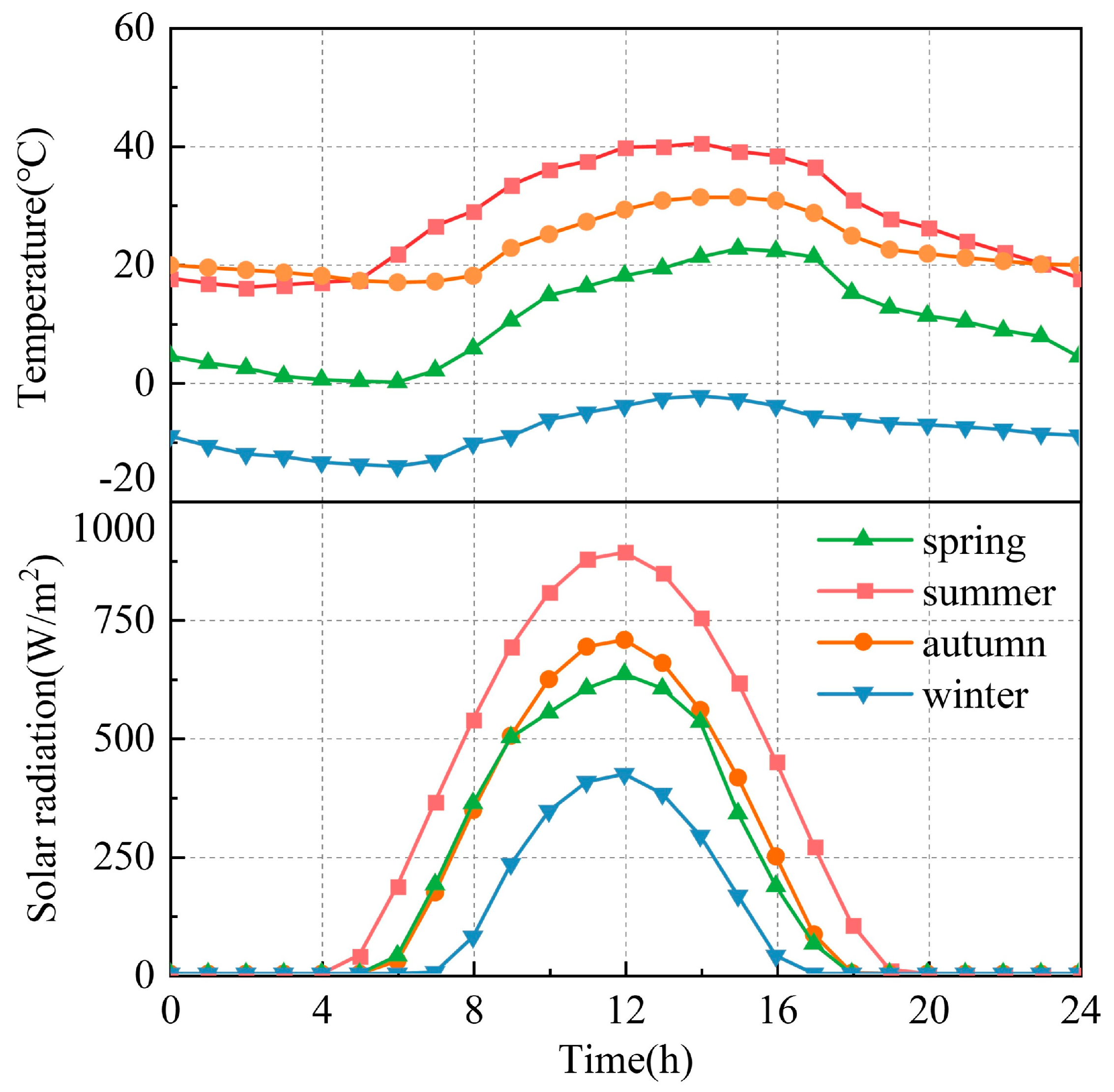
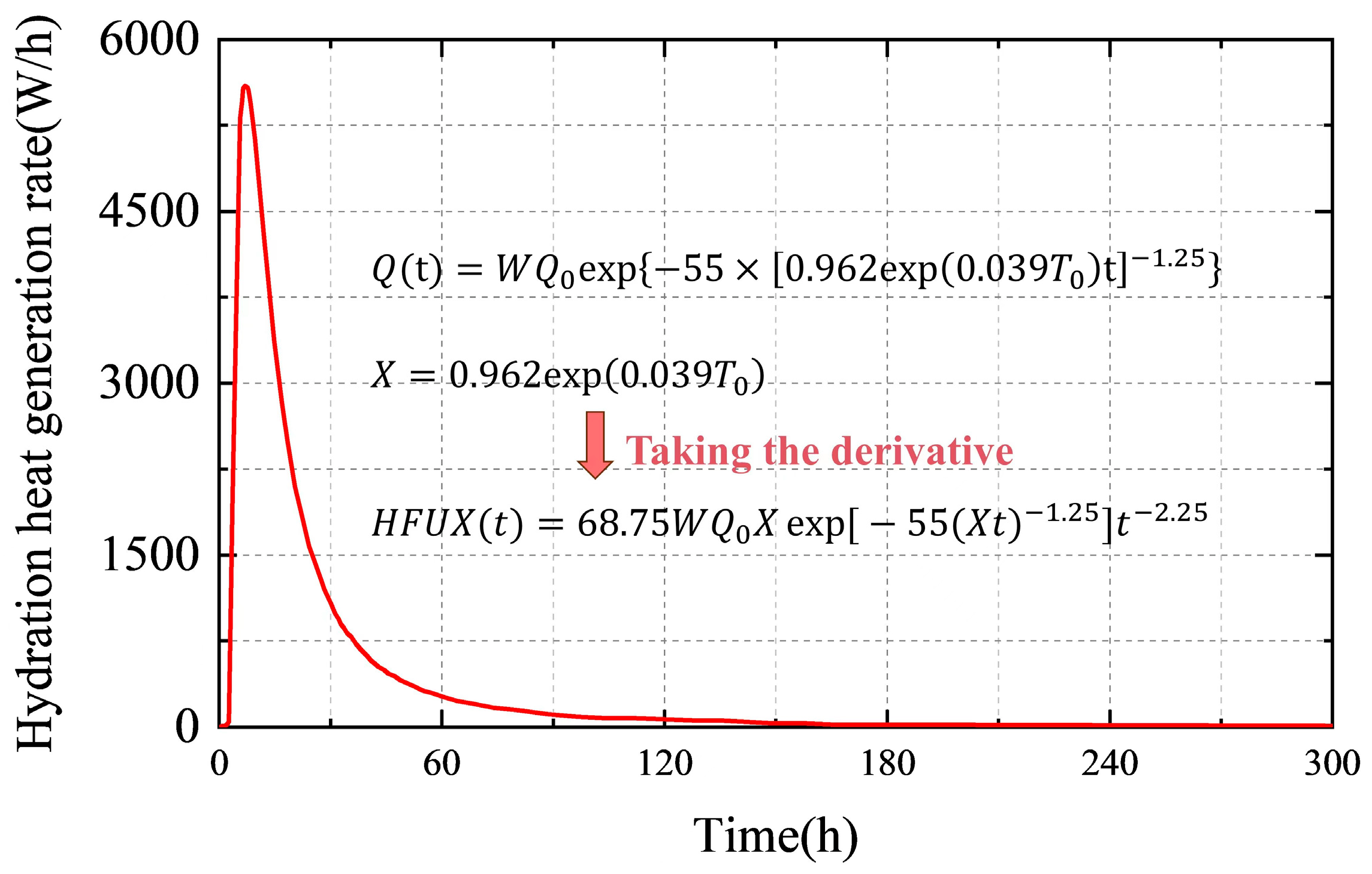
2.3. Coupling of Multiple Loads
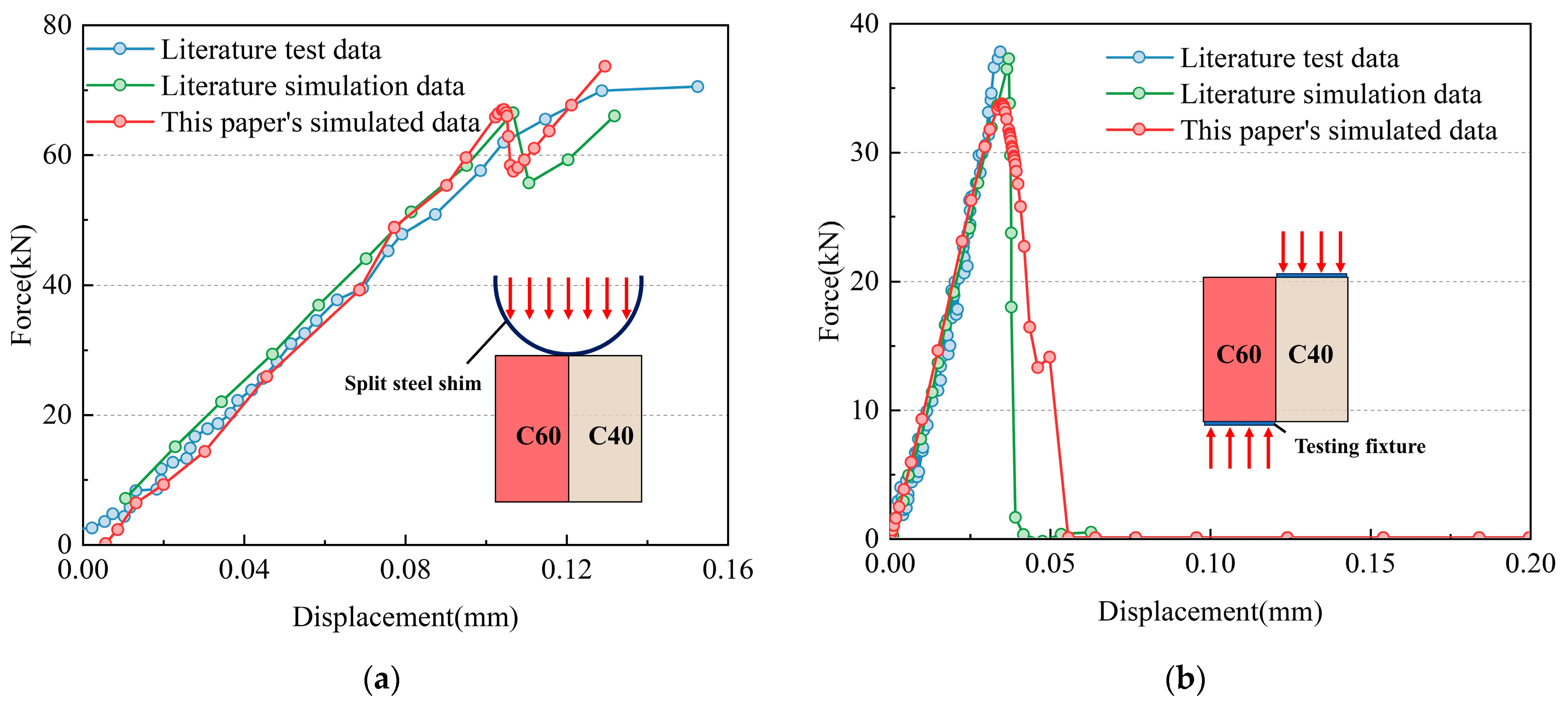
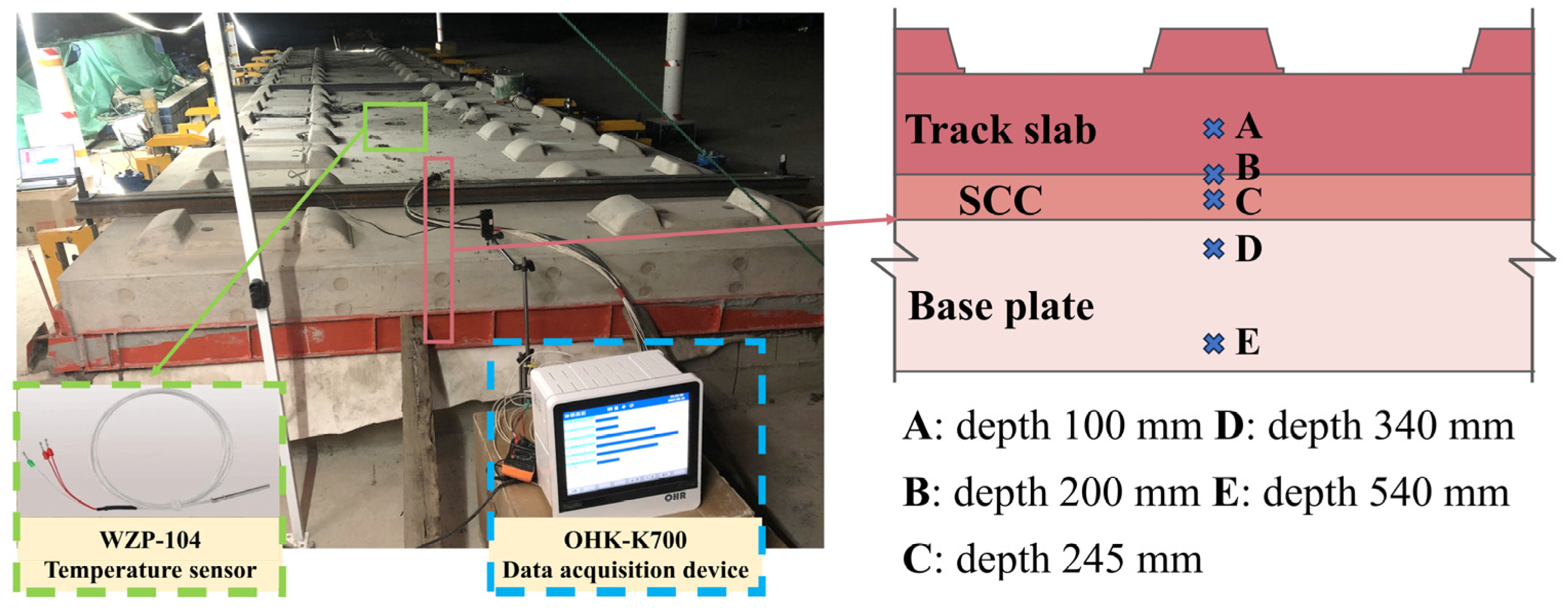
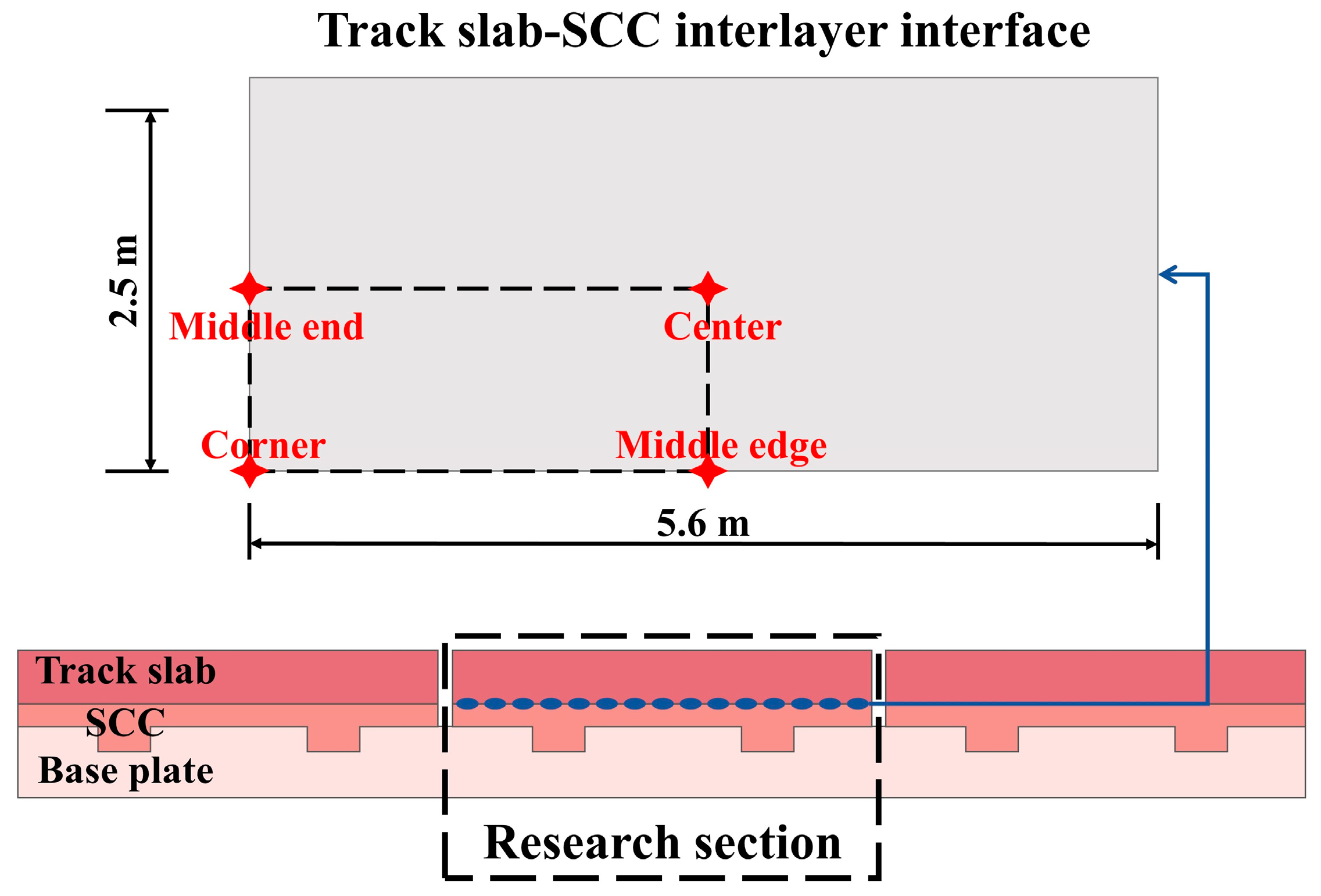
2.4. Model Verification
3. Results and Discussion
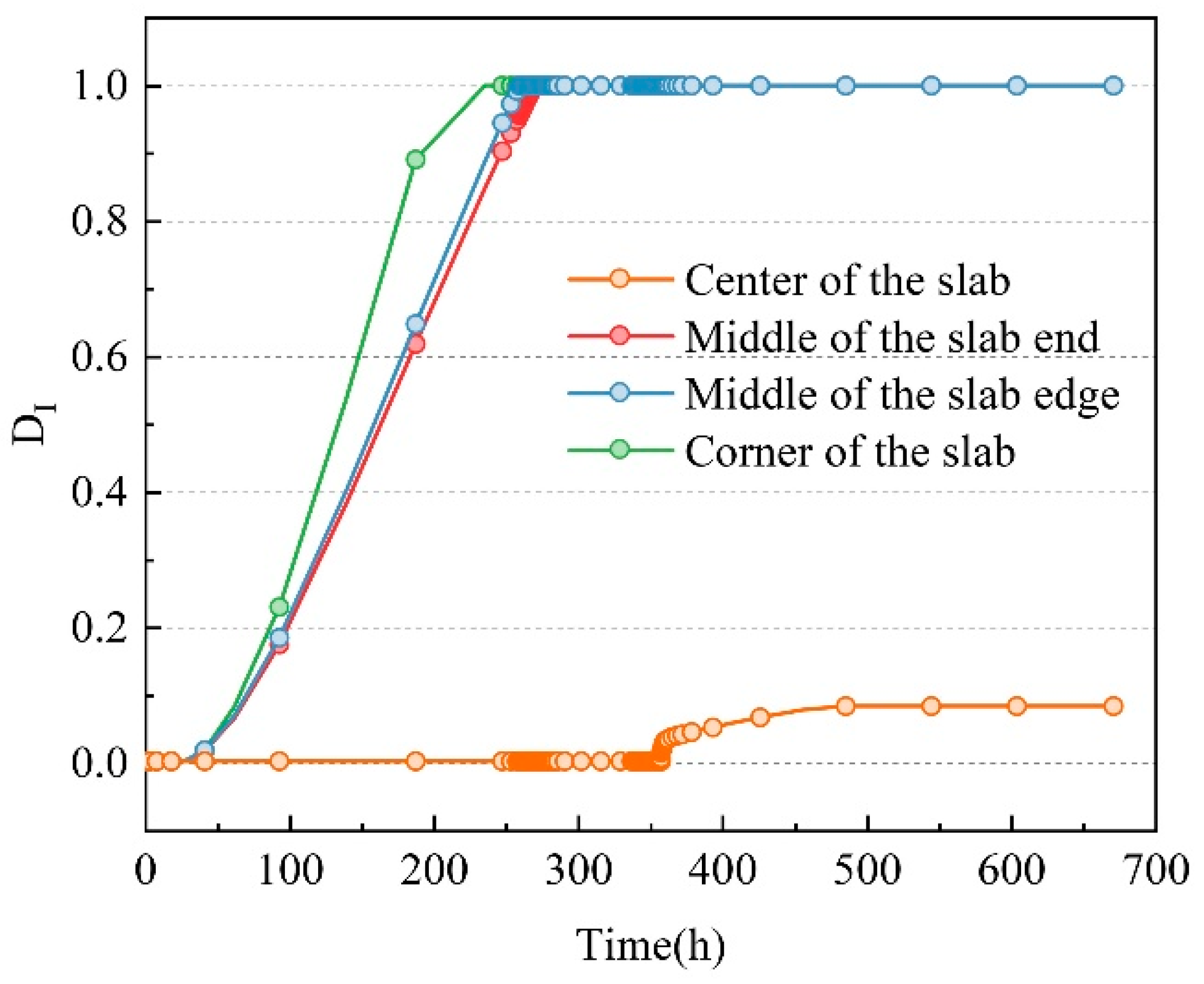
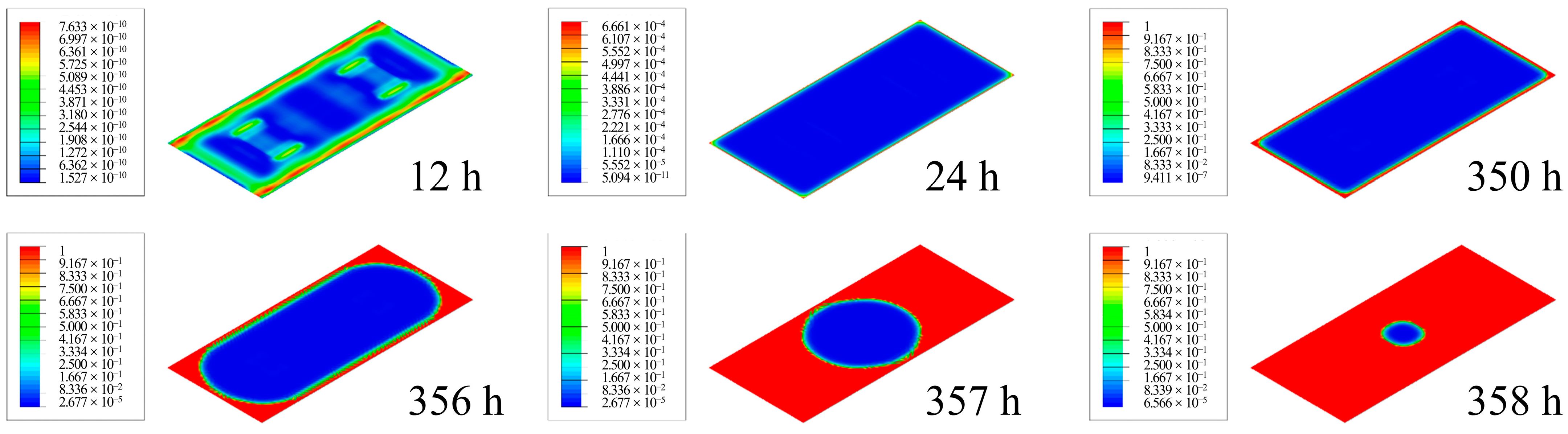
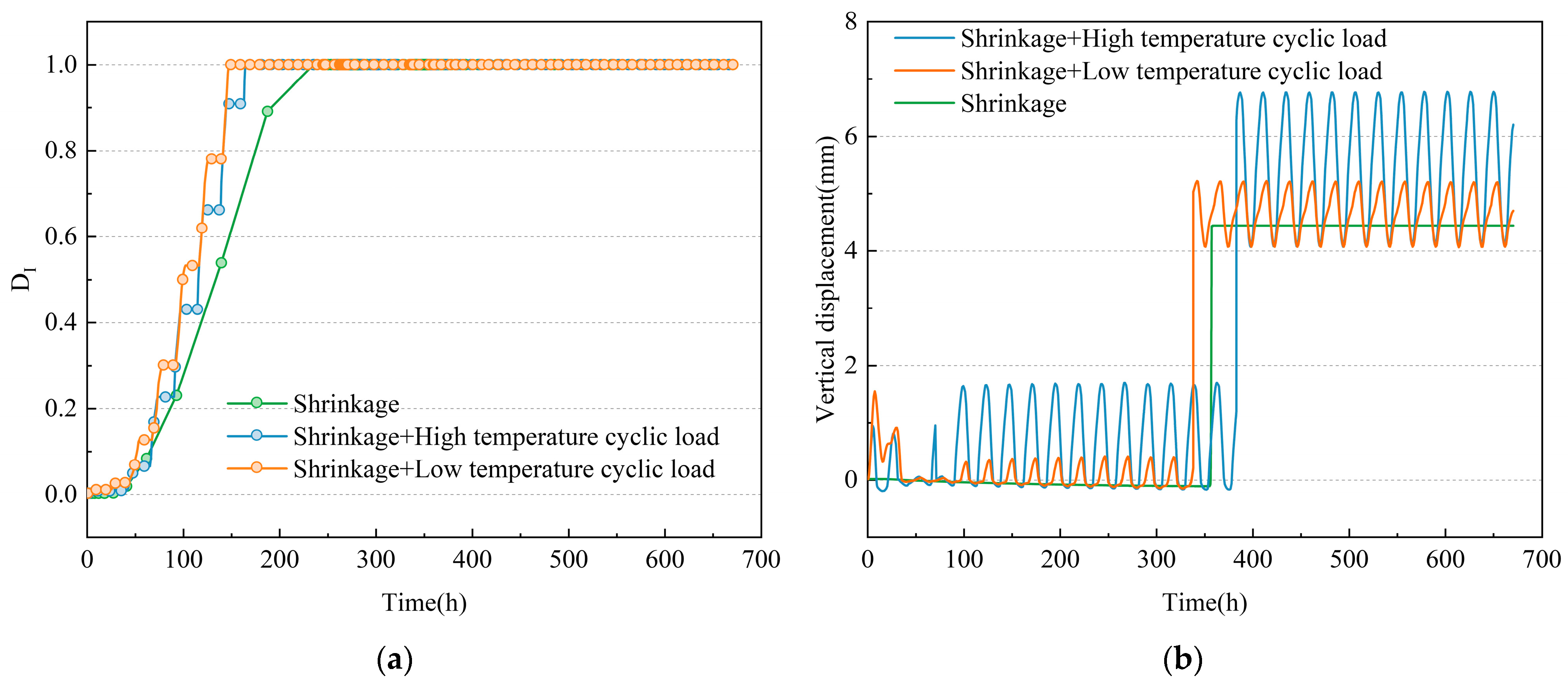
3.1. Evolution Process of Interlayer Damage
3.2. Mechanical Characteristics of Slab Track after Interlayer Damage
3.3. Influence of Key Factors on the Evolution of Interlayer Damage
3.3.1. Interlayer Bonding Property
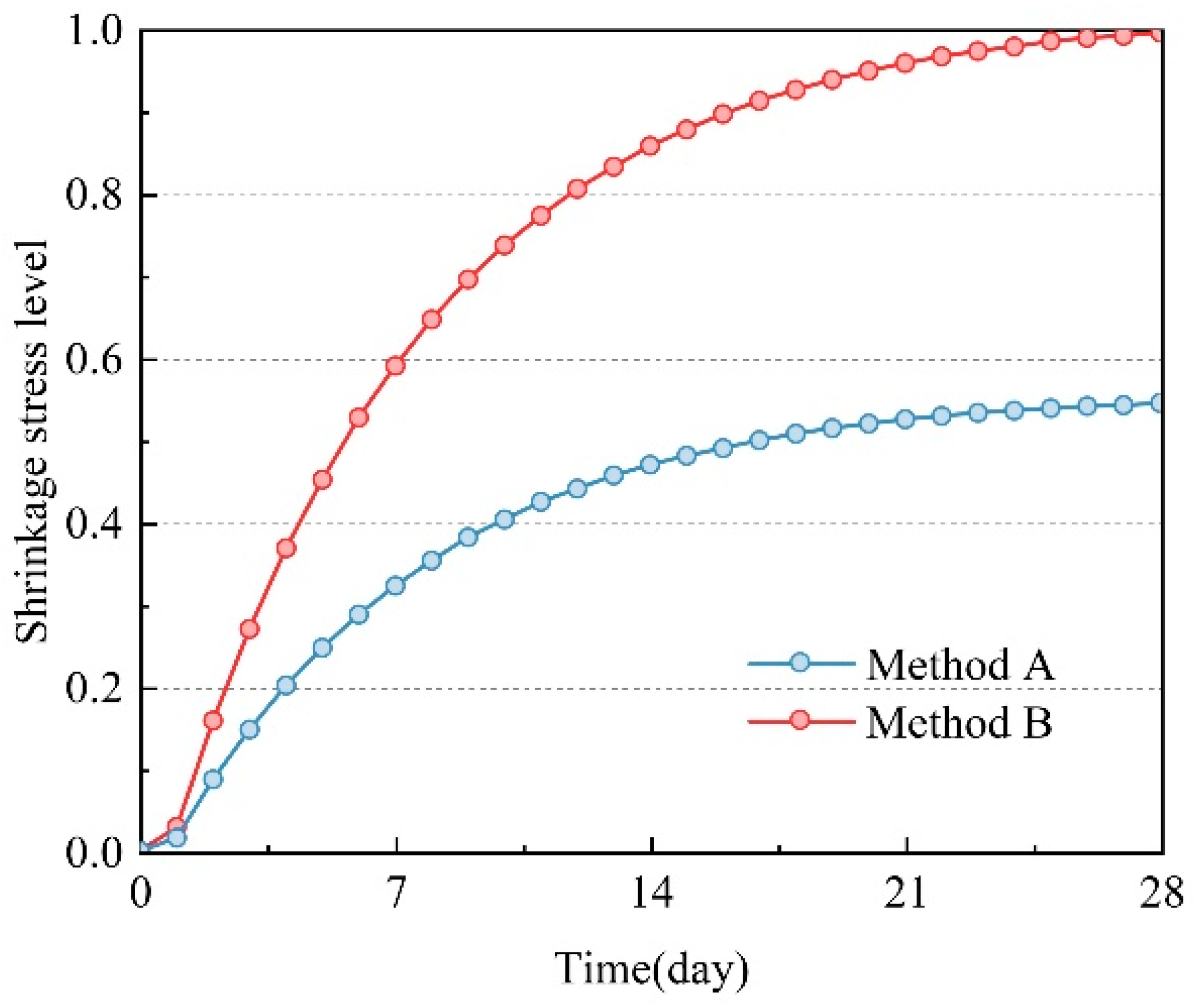
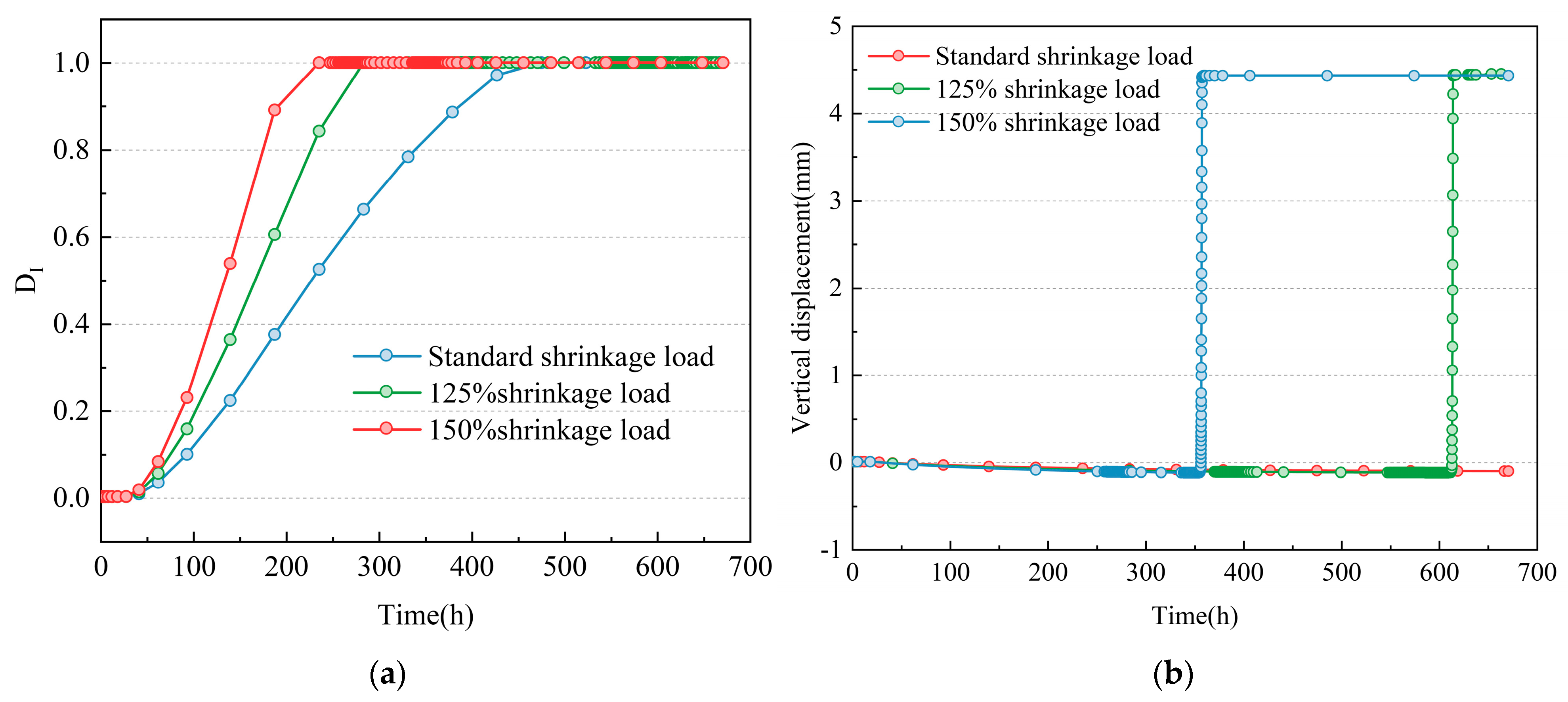
3.3.2. Shrinkage Performance of SCC
3.3.3. Construction Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, S.; Zhang, Y.; Ren, J.; Yang, K.; Liu, K.; Liu, M. Evaluation index of CRTS III prefabricated slab track cracking condition based on interval AHP. Int. J. Struct. Stab. Dyn. 2021, 21, 2140013. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Q.; Wang, Q.; Cui, X.; Dong, B. Effects of the subgrade differential arch on damage characteristics of CRTS III slab track and vehicle dynamic response. Constr. Build. Mater. 2022, 327, 126982. [Google Scholar] [CrossRef]
- Zeng, R.; Zhang, J.; Hu, W.; Jin, C. Study on the Evolution Characteristics of Temperature Field in CRTS III Ballastless Track Slab. Railw. Stand. Des. 2022, 66, 35. [Google Scholar]
- Jiang, W.; Xie, Y.; Li, W.; Long, G. Influence of bubble defects on the bonding performance of the interlayer interface of the CRTS III slab ballastless track structure. Constr. Build. Mater. 2021, 307, 125003. [Google Scholar] [CrossRef]
- Liu, R.; Song, L.; Cao, J.; Xia, Z.; Yu, Z. Early warping deformation of high-speed railway CRTS III track slabs. Eng. Struct. 2023, 294, 116651. [Google Scholar] [CrossRef]
- Bhogone, M.; Subramaniam, K.V. Improvement in early-age cracking performance of concrete with hybrid steel-macropolypropylene fiber blends. Mater. Today Proc. 2022, 65, 1589–1593. [Google Scholar] [CrossRef]
- Li, L.; Dao, V.; Lura, P. Autogenous deformation and coefficient of thermal expansion of early-age concrete: Initial outcomes of a study using a newly-developed Temperature Stress Testing Machine. Cem. Concr. Compos. 2021, 119, 103997. [Google Scholar] [CrossRef]
- Shaofei, L. Cause Analysis of Interlayer Seams of CRTS III Slab Ballastless Track. Railw. Eng. 2017, 4, 106–109. [Google Scholar]
- Wei, C.; Yang, R.; Zhang, G.; Chang, F.; Sun, Z. Research on the Early Temperature Field of Self-compacting Concrete of Ballastless Track and its lnfluence. Railw. Stand. Des. 2021, 65, 22–27. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Q.; Zhang, Y.; Wang, Q.; Luo, B.; Yang, G.; Lau, A. Deformation law and control limit of CRTSIII slab track under subgrade frost heave. Appl. Sci. 2021, 11, 3520. [Google Scholar] [CrossRef]
- Du, W.; Ren, J.; Zhang, K.; Deng, S.; Zhang, S. Two-stage identification of interlayer contact loss for CRTS III prefabricated slab track based on multi-index fusion. J. Zhejiang Univ. Sci. A 2023, 24, 497–515. [Google Scholar] [CrossRef]
- Zhu, K.; Wu, B.; Zeng, Z.; Liu, B. Reason Analysis of the Gap between CRTS Slab and Self Compacting Concrete. In Proceedings of the International Conference on Education, Management, Computer and Society, Shenyang, China, 1–3 January 2016; pp. 626–629. [Google Scholar]
- Sun, S.; Xu, Q. Experimental study on the interface fatigue between track slab and self-compacting concrete for CRTS III slab track. Eng. Fail. Anal. 2023, 150, 107302. [Google Scholar] [CrossRef]
- Sheng, X.-W.; Zheng, W.-Q.; Zhu, Z.-H.; Qin, Y.-P.; Guo, J.-G. Full-scale fatigue test of unit-plate ballastless track laid on long-span cable-stayed bridge. Constr. Build. Mater. 2020, 247, 118601. [Google Scholar] [CrossRef]
- Wang, J.; Gao, L.; Zhao, W.; Zhong, Y.; Tong, F.; Wang, Q. Evolution mechanism of interlayer fatigue properties of CRTS III slab track. Constr. Build. Mater. 2022, 360, 129459. [Google Scholar] [CrossRef]
- Zhong, Y.; Gao, L.; Zhang, Y. Effect of daily changing temperature on the curling behavior and interface stress of slab track in construction stage. Constr. Build. Mater. 2018, 185, 638–647. [Google Scholar] [CrossRef]
- Cai, X.-P.; Luo, B.-C.; Zhong, Y.-L.; Zhang, Y.-R.; Hou, B.-W. Arching mechanism of the slab joints in CRTSII slab track under high temperature conditions. Eng. Fail. Anal. 2019, 98, 95–108. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, K.; Gao, L.; Yan, S.; Cai, X. Study on the interlayer debonding and its effects on the mechanical properties of CRTS II slab track based on viscoelastic theory. Constr. Build. Mater. 2019, 224, 387–407. [Google Scholar] [CrossRef]
- Cui, X.; Du, B.; Xiao, H.; Zhou, R.; Guo, G.; Liu, H. Interface damage and arching mechanism of CRTS II slab track under temperature load. Constr. Build. Mater. 2021, 291, 123258. [Google Scholar] [CrossRef]
- Su, M.; Xie, H.; Kang, C.; Li, S. Determination of the interfacial properties of longitudinal continuous slab track via a field test and ANN-based approaches. Eng. Struct. 2021, 246, 113039. [Google Scholar] [CrossRef]
- Zhou, R.; Zhu, X.; Ren, W.-X.; Zhou, Z.; Yao, G.; Ma, C.; Du, Y. Thermal evolution of CRTS II slab track under various environmental temperatures: Experimental study. Constr. Build. Mater. 2022, 325, 126699. [Google Scholar] [CrossRef]
- Shi, T.; Lou, P. Time-variant reliability of interlayer damage of CRTS-II slab track by combining the second-order fourth-moment and outcrossing method. Constr. Build. Mater. 2023, 400, 132790. [Google Scholar] [CrossRef]
- Rosso, M.M.; Asso, R.; Aloisio, A.; Di Benedetto, M.; Cucuzza, R.; Greco, R. Corrosion effects on the capacity and ductility of concrete half-joint bridges. Constr. Build. Mater. 2022, 360, 129555. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Guan, J.; Xie, C.; Khan, M. Normal statistical fracture analysis of Roller-compacted concrete on the basis of non-linear elastic fracture mechanics. Compos. Struct. 2023, 324, 117543. [Google Scholar] [CrossRef]
- Liu, H.; Song, L.; Liu, R.; Yu, Z. Temperature field and thermal effect analysis of CRTS III ballastless track structure under the outdoor natural environment. Constr. Build. Mater. 2022, 358, 129383. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, X.; Zhong, Y.; Chen, Z.; Wang, C. Temperature field and thermal effects of the longitudinal connected slab track based on the measurement data and thermal-fluid-structure coupling analysis. Constr. Build. Mater. 2022, 343, 128121. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, X.; Zhang, Y.; Wang, T.; Zhong, Y. Real-time temperature field and thermal deformation of slab track on cable-stayed bridge. Case Stud. Therm. Eng. 2023, 51, 103582. [Google Scholar] [CrossRef]
- Topkaya, C.; Yura, J.A.; Williamson, E.B. Composite shear stud strength at early concrete ages. J. Struct. Eng. 2004, 130, 952–960. [Google Scholar] [CrossRef]
- Han, J.; Zhao, G.; Zhang, L. Experimental research on fracture properties of adjerence for new to old concrete. China Civ. Eng. J. 2003, 36, 31–35. [Google Scholar]
- Li, X.; Ren, J.; Wang, J.; Yang, R.; Shi, L.; Liu, X. Drying shrinkage of early-age concrete for twin-block slab track. Constr. Build. Mater. 2020, 243, 118237. [Google Scholar] [CrossRef]
- Du, W.; Deng, S.-J.; Ren, J.-J.; Zhao, Z.-M.; Wei, Z.; Zhang, K.-Y.; Ye, W.-L. Debonding analysis and identification of the interface between sleeper and track slab for twin-block slab tracks. Int. J. Struct. Stab. Dyn. 2021, 21, 2140011. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Papaelias, M.; Roberts, C. Wet/dry influence on behaviors of closed-cell polymeric cross-linked foams under static, dynamic and impact loads. Constr. Build. Mater. 2018, 187, 1092–1102. [Google Scholar] [CrossRef]
- Xin, T.; Ding, Y.; Wang, P.; Gao, L. Application of rubber mats in transition zone between two different slab tracks in high-speed railway. Constr. Build. Mater. 2020, 243, 118219. [Google Scholar] [CrossRef]
- Zbiciak, A.; Kraśkiewicz, C.; Dudziak, S.; Al-Sabouni-Zawadzka, A.; Pełczyński, J. An accurate method for fast assessment of under slab mats (USM) performance in ballastless track structures. Constr. Build. Mater. 2021, 300, 123953. [Google Scholar] [CrossRef]
- GB 50176-2016; Code for Thermal Design of Civil Building. Ministry of Housing and Urban-Rural Development: Beijing, China, 2017.
- Cristofari, C.; Notton, G.; Louche, A. Study of the thermal behaviour of a production unit of concrete structural components. Appl. Therm. Eng. 2004, 24, 1087–1101. [Google Scholar] [CrossRef]
- Tan, Y.; Li, H.; Xie, Y.; Yi, Z. Research on Deformation Properties of Scc Used In High Speed Railway Slab Ballastless Track of CRTSb. In Proceedings of the 3rd International Symposium on Design, Performance and Use of Self-Consolidating Concrete, Xiamen, China, 5–8 June 2014; p. 286. [Google Scholar]
- Niknezhad, D.; Kamali-Bernard, S.; Mesbah, H.-A. Self-compacting concretes with supplementary cementitious materials: Shrinkage and cracking tendency. J. Mater. Civ. Eng. 2017, 29, 04017033. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, M.; Zhai, W.; Cai, C.; Zhao, C.; Zeng, D.; Zhang, J. Mechanical property and damage evolution of concrete interface of ballastless track in high-speed railway: Experiment and simulation. Constr. Build. Mater. 2018, 187, 460–473. [Google Scholar] [CrossRef]
- Oliveira, M.J.; Ribeiro, A.n.B.; Branco, F.G. Shrinkage of self-compacting concrete. A comparative analysis. J. Build. Eng. 2017, 9, 117–124. [Google Scholar] [CrossRef]
- Aslani, F.; Nejadi, S. Shrinkage behavior of self-compacting concrete. J. Zhejiang Univ. Sci. A 2012, 13, 407–419. [Google Scholar] [CrossRef]






| Parameter Name | Unit | Value |
|---|---|---|
| Normal interfacial stiffness | Pa/m | 5 × 1011 |
| Tangential interfacial stiffness | Pa/m | 1.5 × 1011 |
| Normal interfacial strength | MPa | 1.4 |
| Tangential interfacial strength | MPa | 1.8 |
| Normal interfacial fracture energy | J/m2 | 14 |
| Tangential interfacial fracture energy | J/m2 | 40 |
| Main Structures | Size (m) | Elastic Modulus (Pa) | Poisson’s Ratio | Density (kg/m3) | Specific Heat Capacity J/(kg·°C) | Coefficient of Heat Conduction W/(m·°C) |
|---|---|---|---|---|---|---|
| Rail | 16.94 | 3.65 × 1010 | 0.3 | 7830 | ||
| Track slab | 5.6 × 2.5 × 0.2 | 2.05 × 1011 | 0.2 | 2500 | 900 | 1.75 |
| SCC | 5.6 × 2.5 × 0.09 | Time-varying | 0.2 | 2500 | 1000 | 3.1 |
| Convex platform | 0.7 × 1.0 × 0.1 | - | - | - | - | - |
| Base plate | 16.94 × 3.1 × 0.3 | 2.8 × 1010 | 0.2 | 2500 | 920 | 1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gao, L.; Wang, L.; Zhao, W.; Qin, Y.; Hua, C.; Li, Y. Evolution Mechanism of Interlayer Properties of CRTS III Slab Track during Construction. Appl. Sci. 2024, 14, 704. https://doi.org/10.3390/app14020704
Wang J, Gao L, Wang L, Zhao W, Qin Y, Hua C, Li Y. Evolution Mechanism of Interlayer Properties of CRTS III Slab Track during Construction. Applied Sciences. 2024; 14(2):704. https://doi.org/10.3390/app14020704
Chicago/Turabian StyleWang, Ji, Liang Gao, Ludong Wang, Wenqiang Zhao, Ying Qin, Chen Hua, and Yuanwei Li. 2024. "Evolution Mechanism of Interlayer Properties of CRTS III Slab Track during Construction" Applied Sciences 14, no. 2: 704. https://doi.org/10.3390/app14020704
APA StyleWang, J., Gao, L., Wang, L., Zhao, W., Qin, Y., Hua, C., & Li, Y. (2024). Evolution Mechanism of Interlayer Properties of CRTS III Slab Track during Construction. Applied Sciences, 14(2), 704. https://doi.org/10.3390/app14020704






