Study on the Residual Strength of Nonlinear Fatigue-Damaged Pipeline Structures
Abstract
:1. Introduction
2. Residual Strength Model of Materials with Fatigue Damage Accumulation
2.1. Fatigue Life Prediction
2.2. Peak Stress Response
2.3. Residual Strength Model
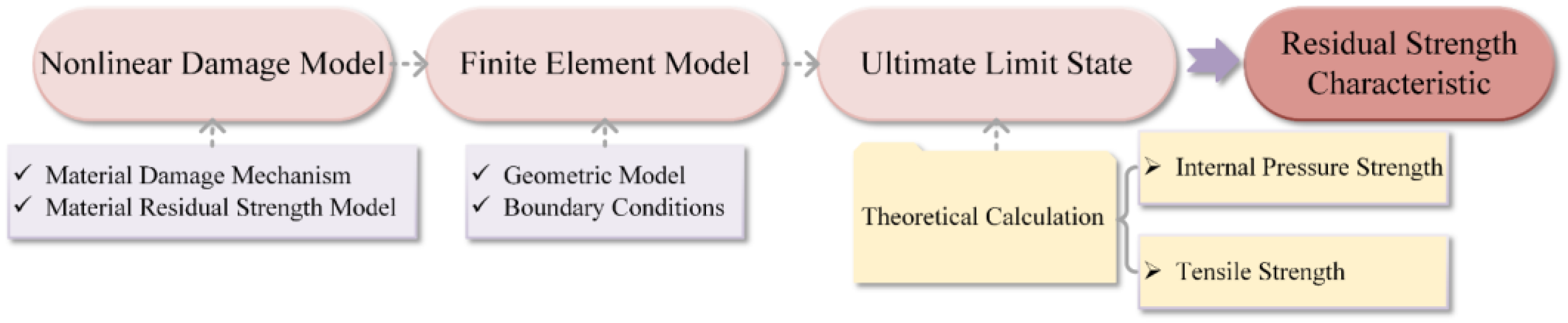
3. Stress–Strain Analysis of Nonlinear Damaged Pipeline Structure
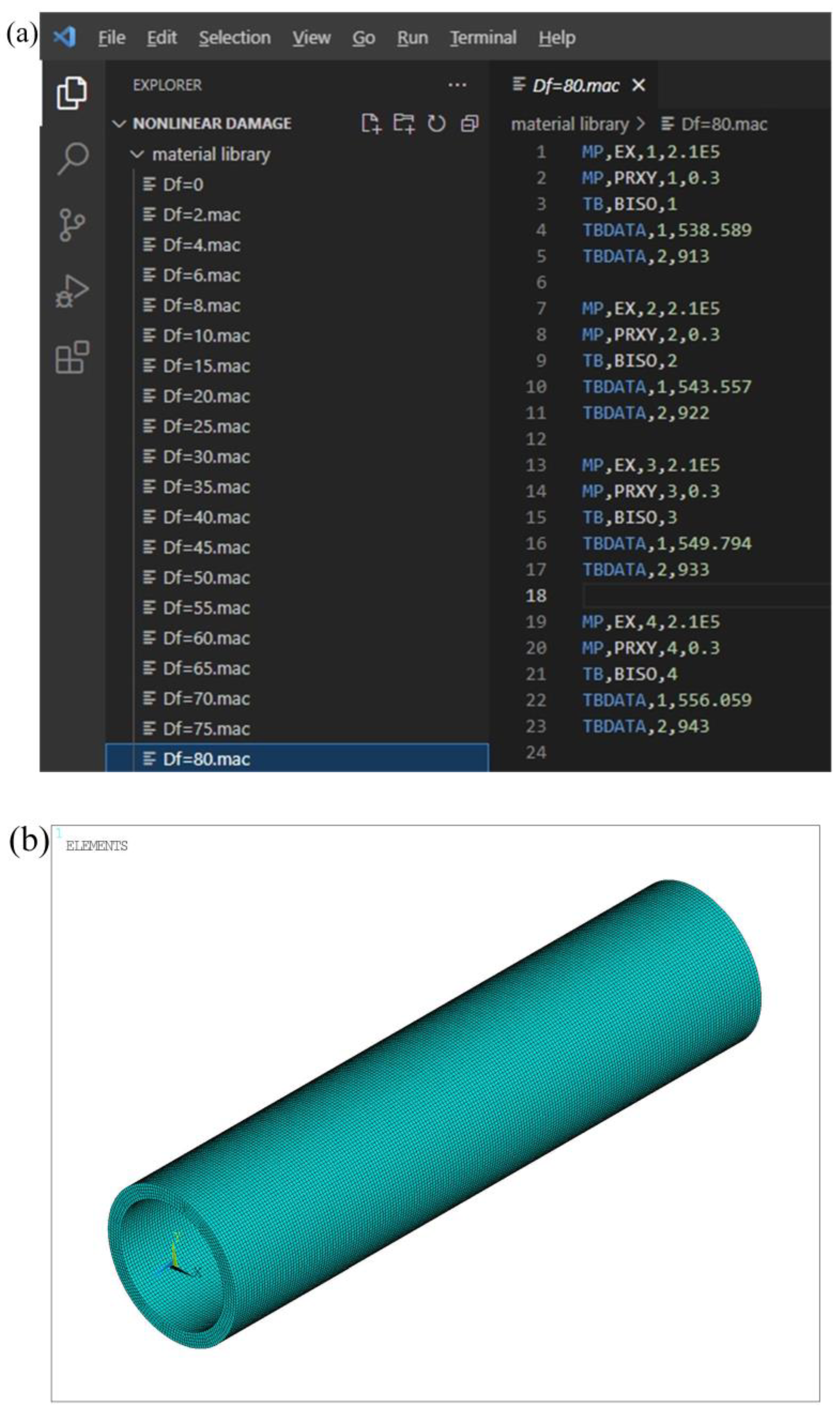
3.1. Research Methods and Content
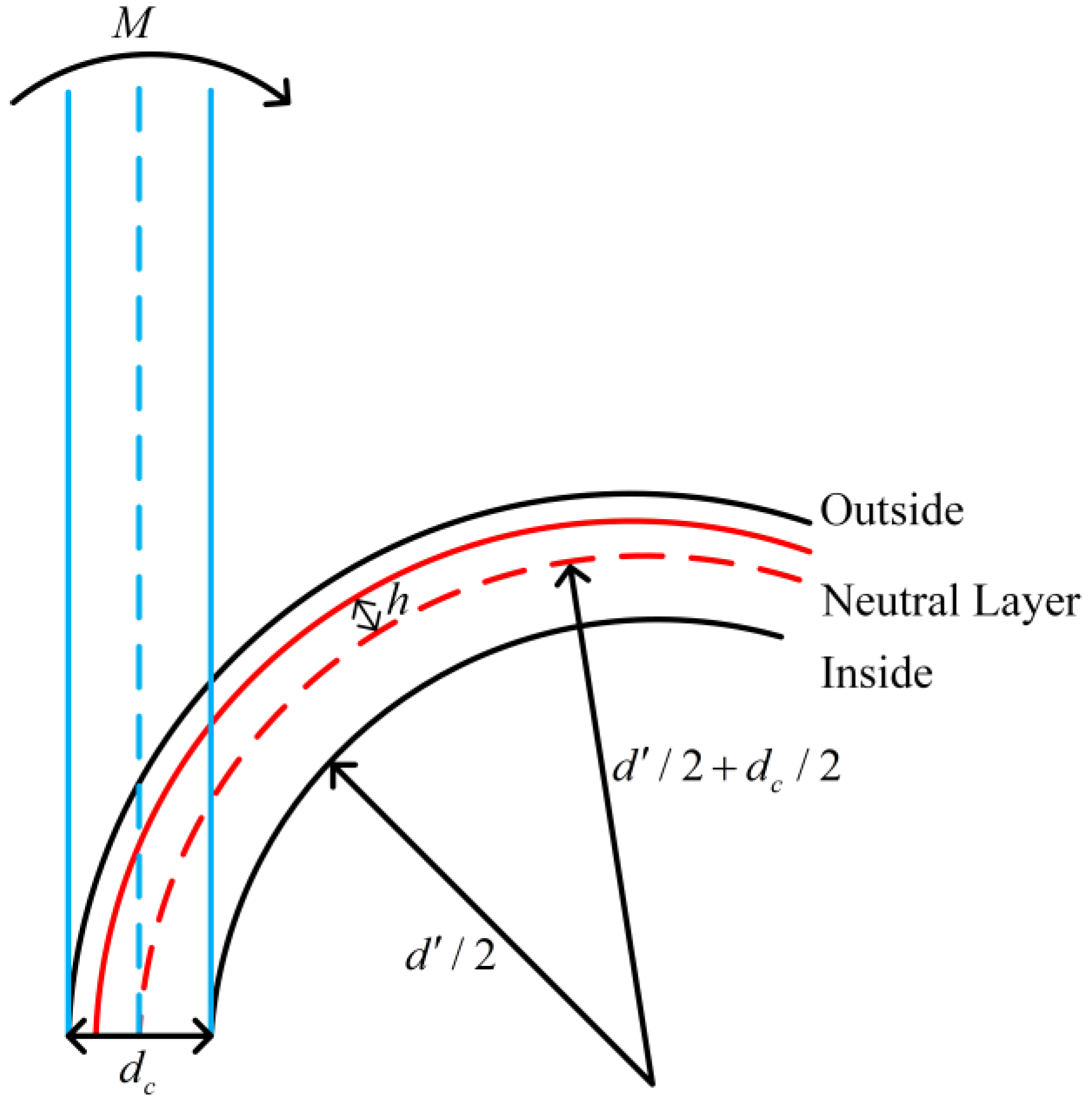
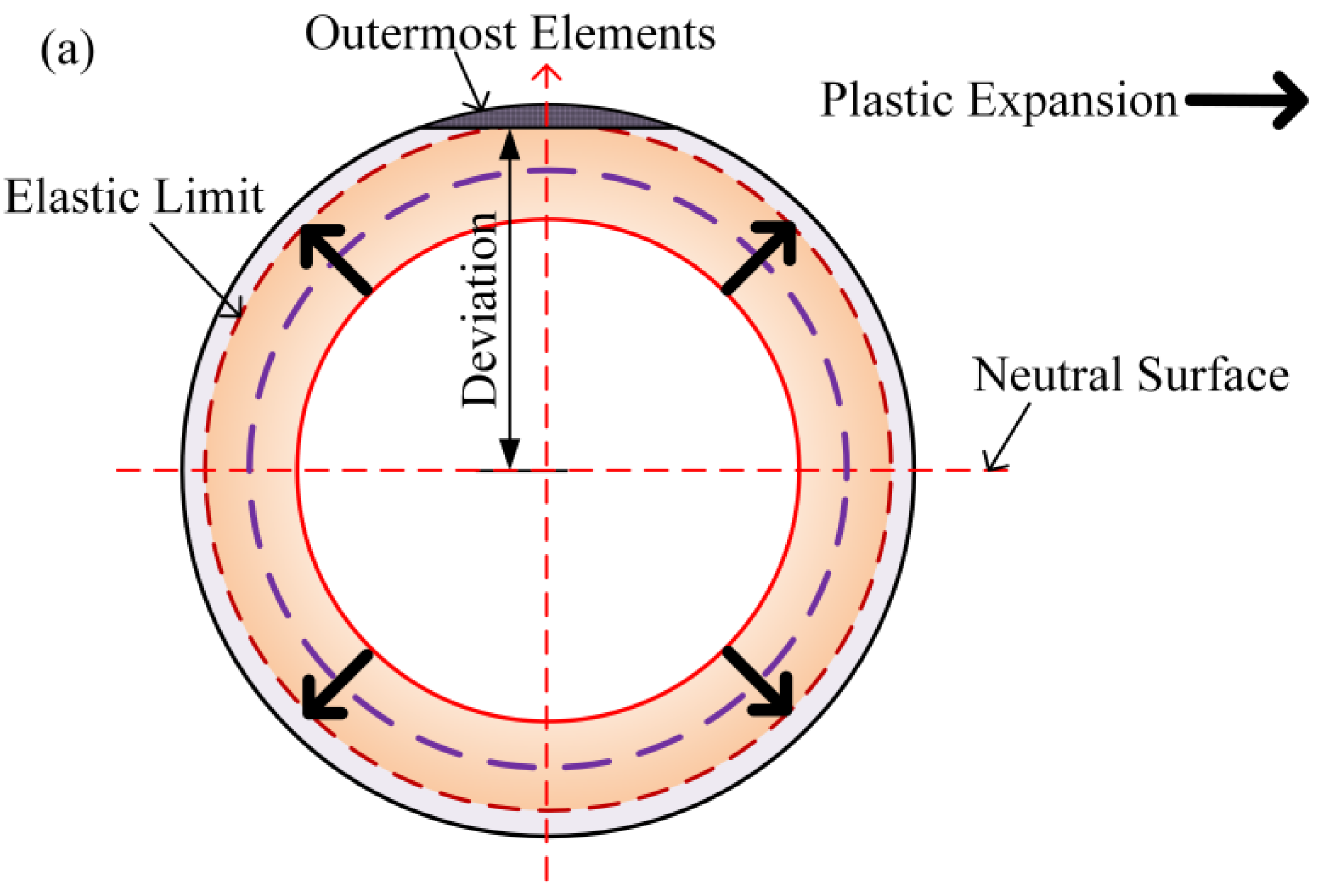
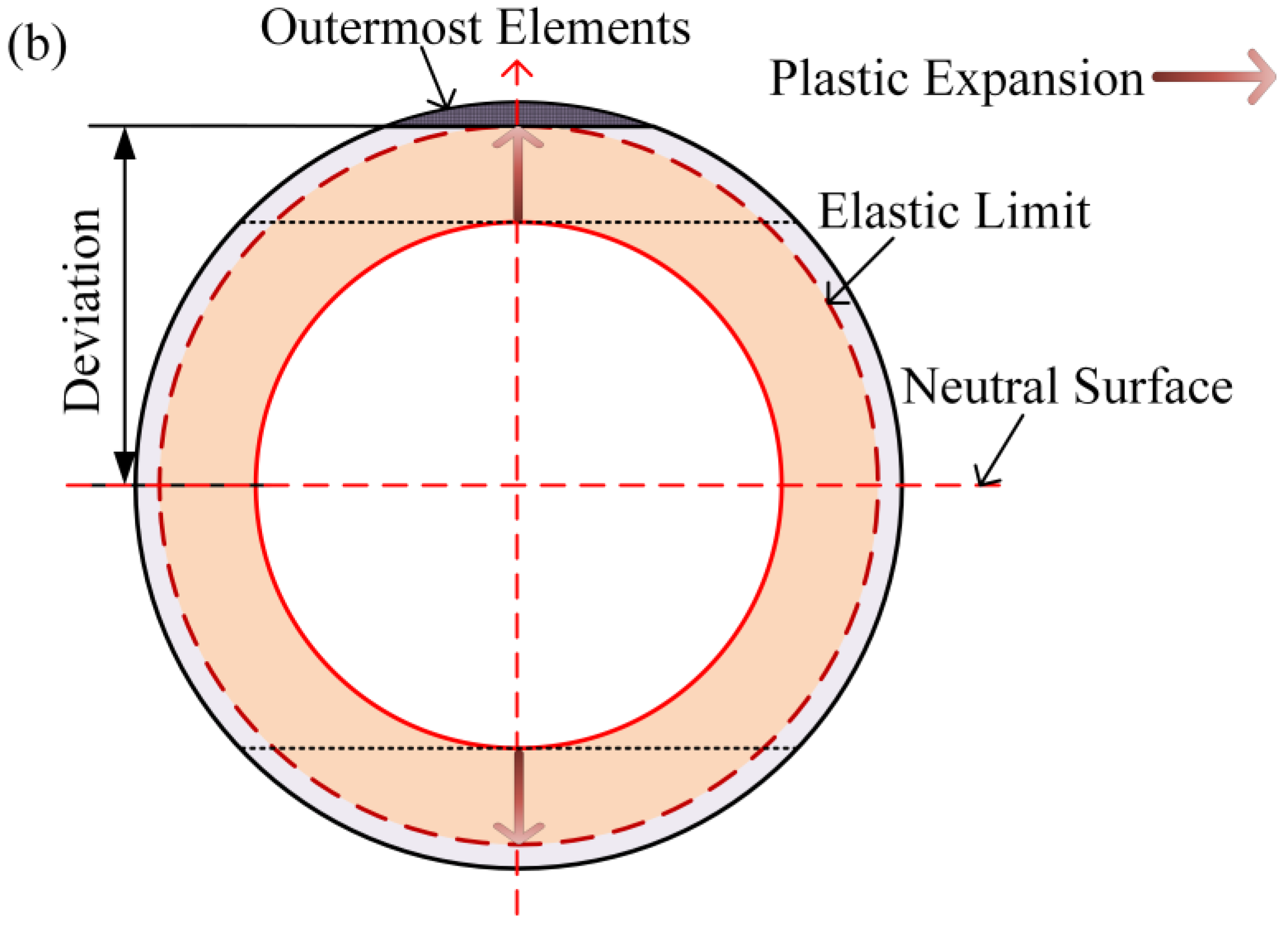
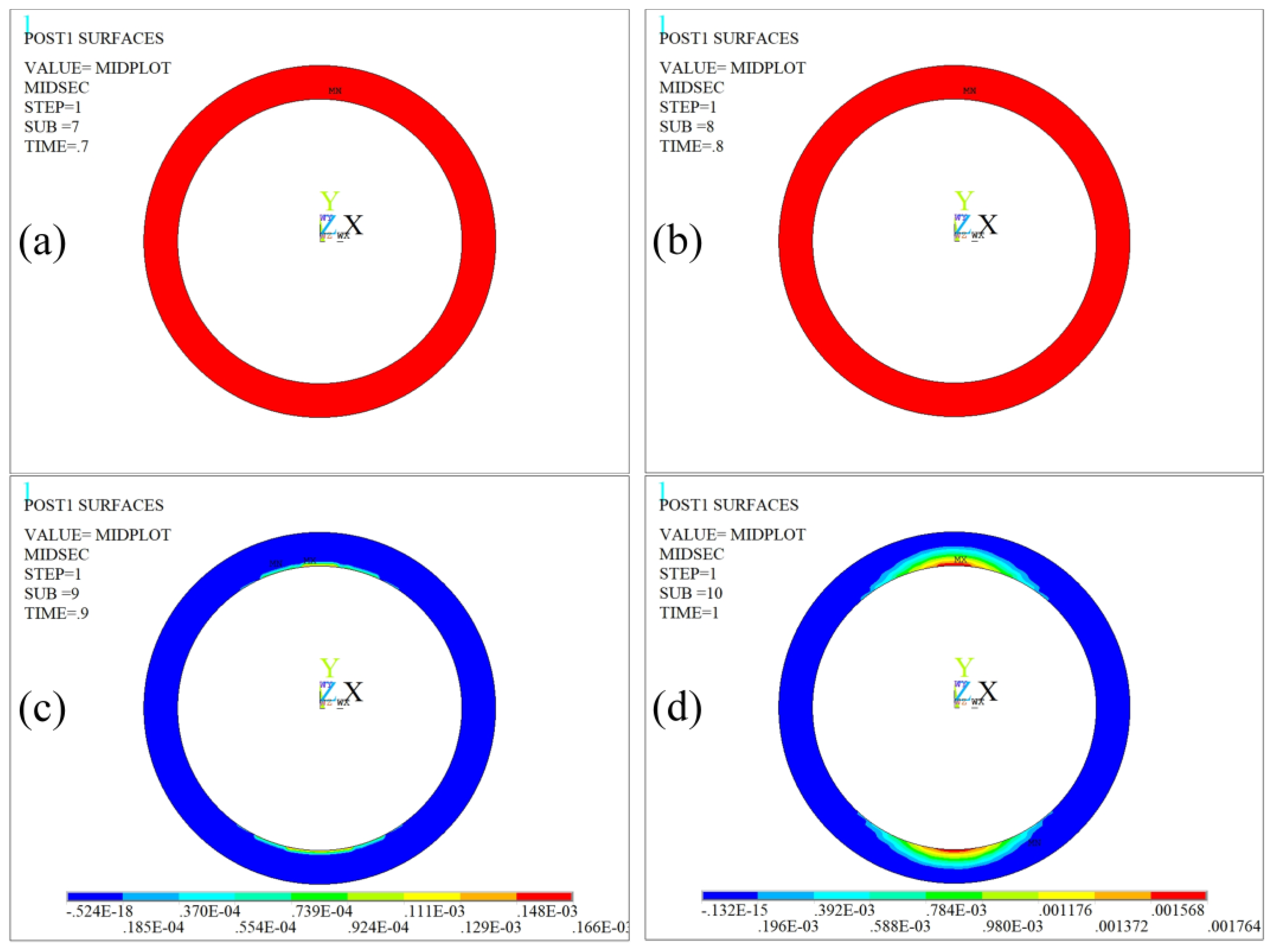
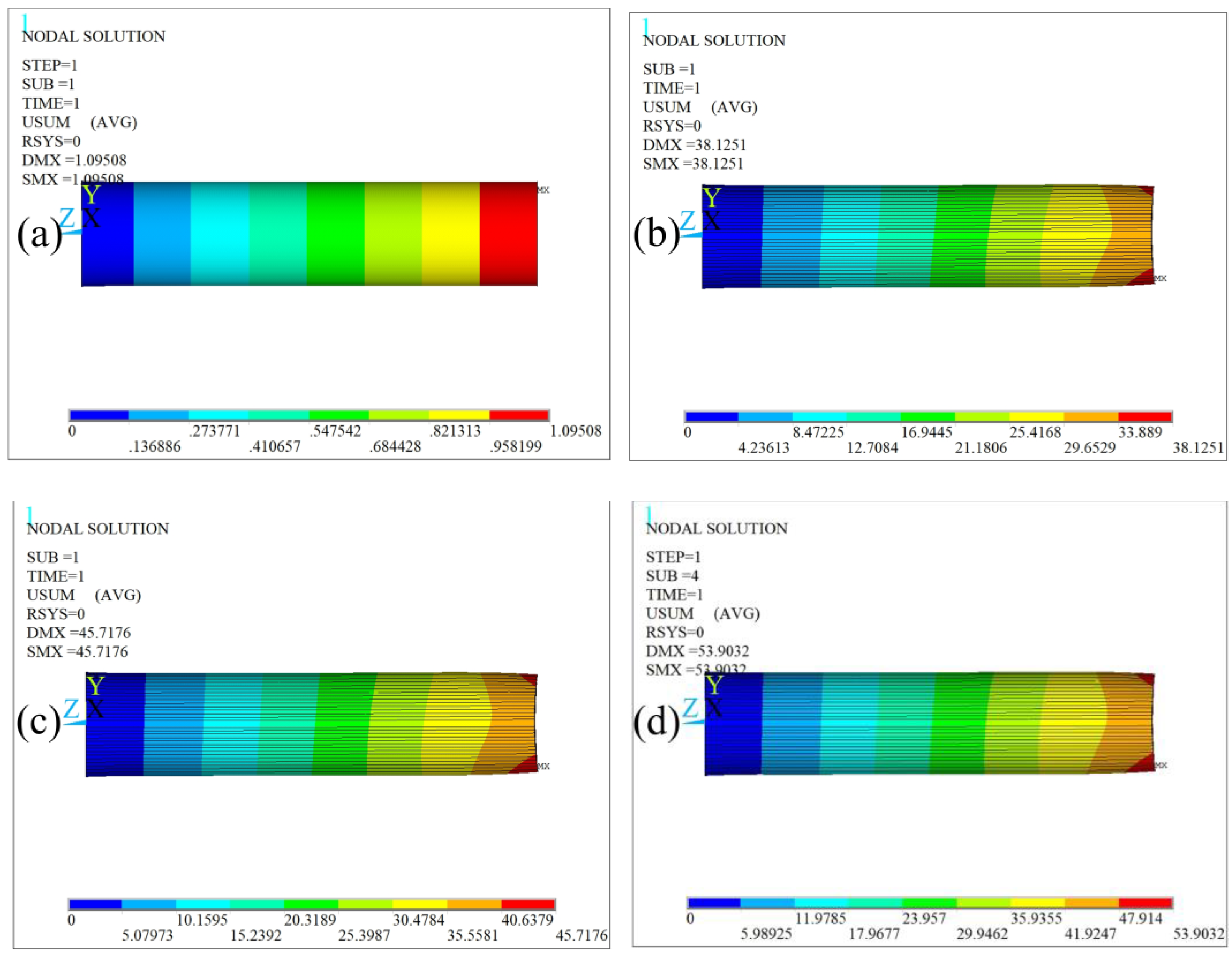
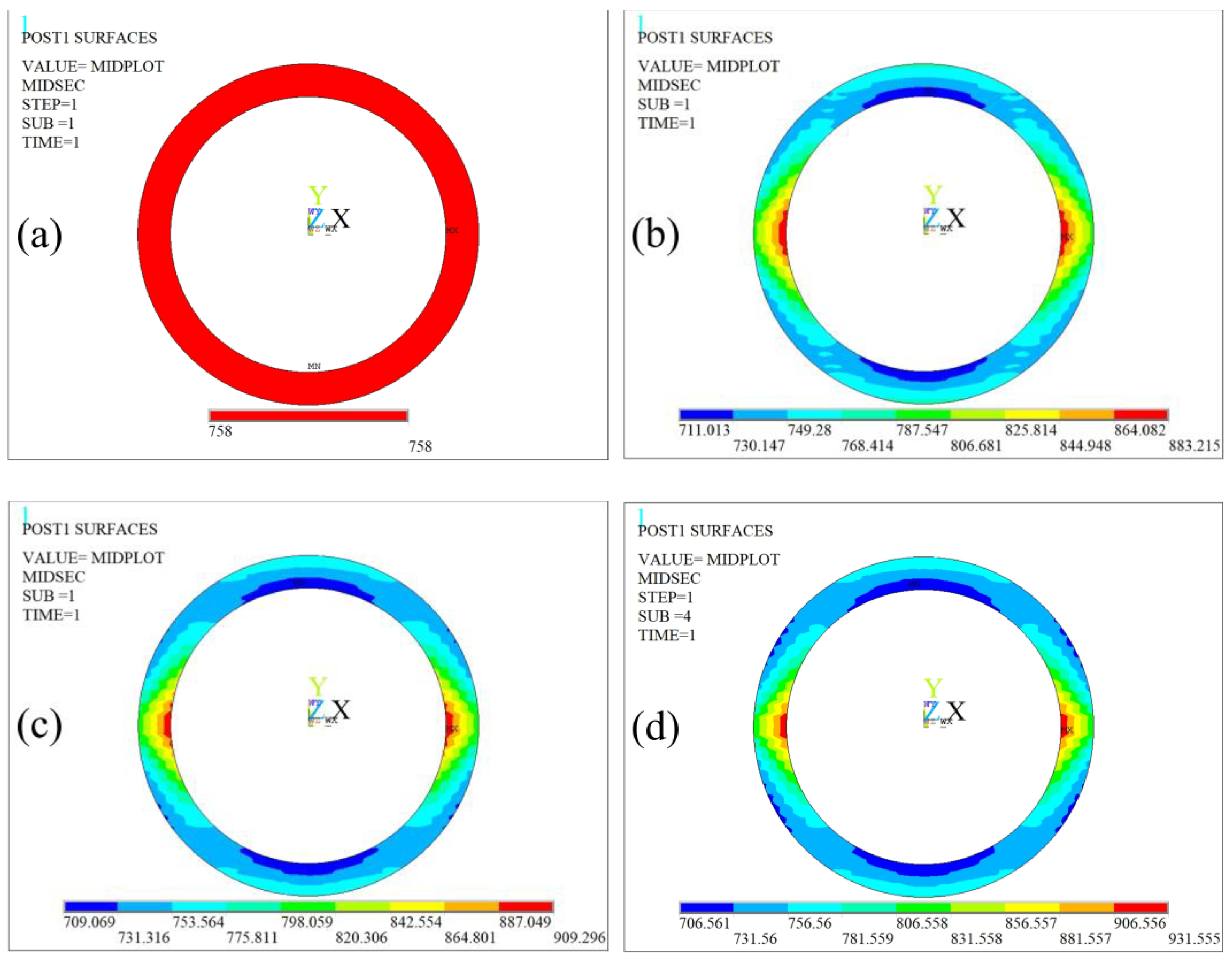
3.2. Stress–Strain Analysis
4. Results and Discussion
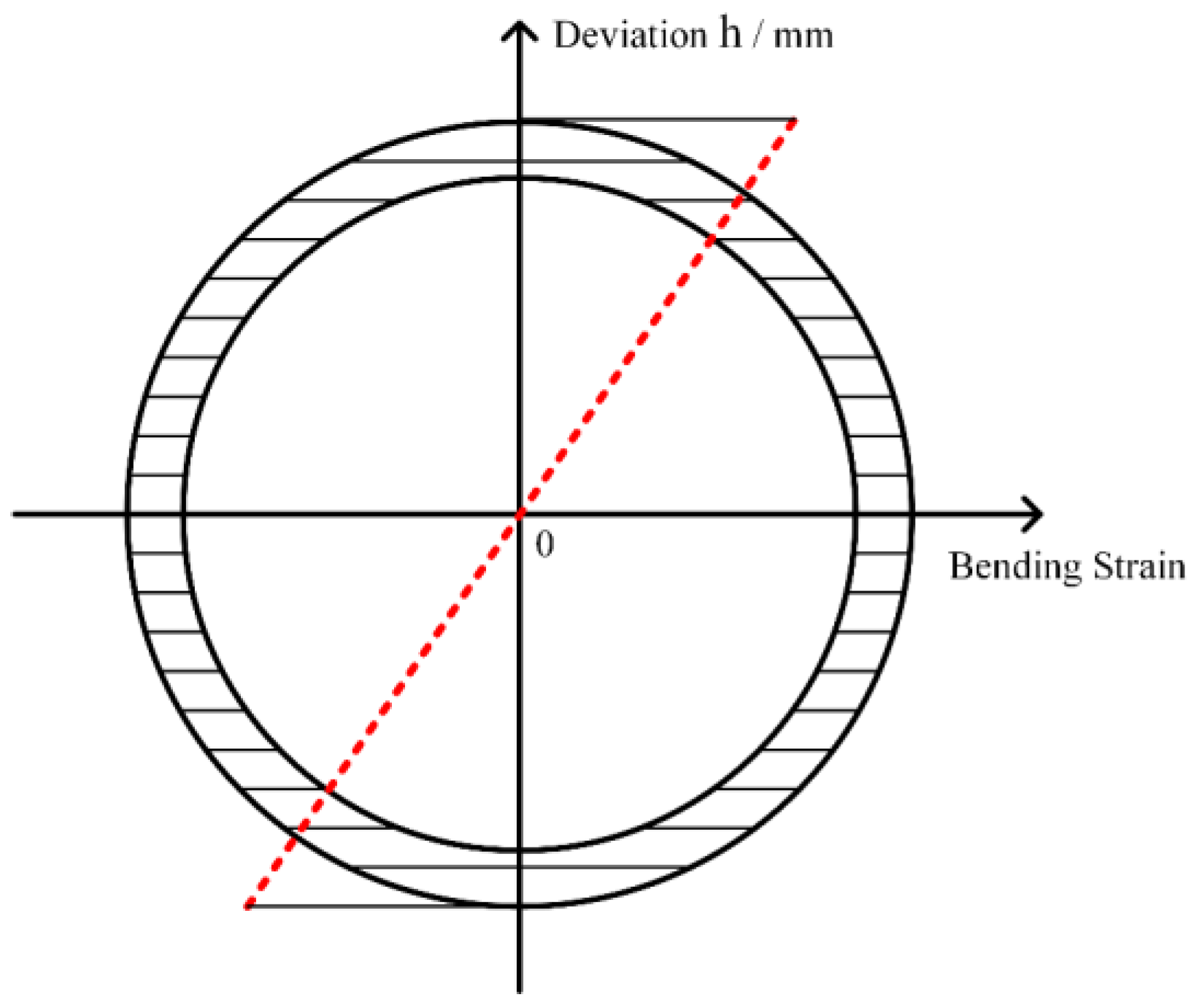
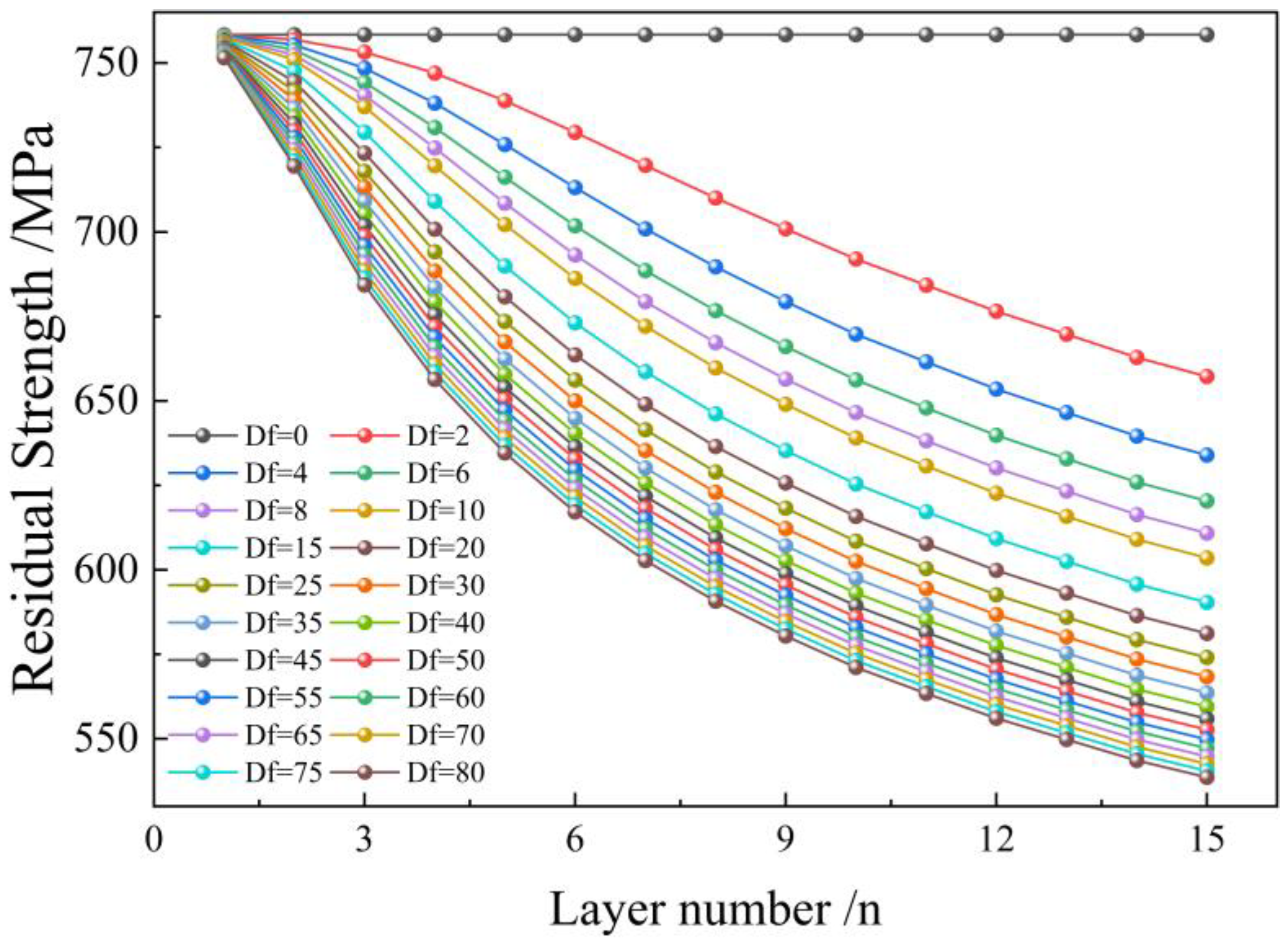
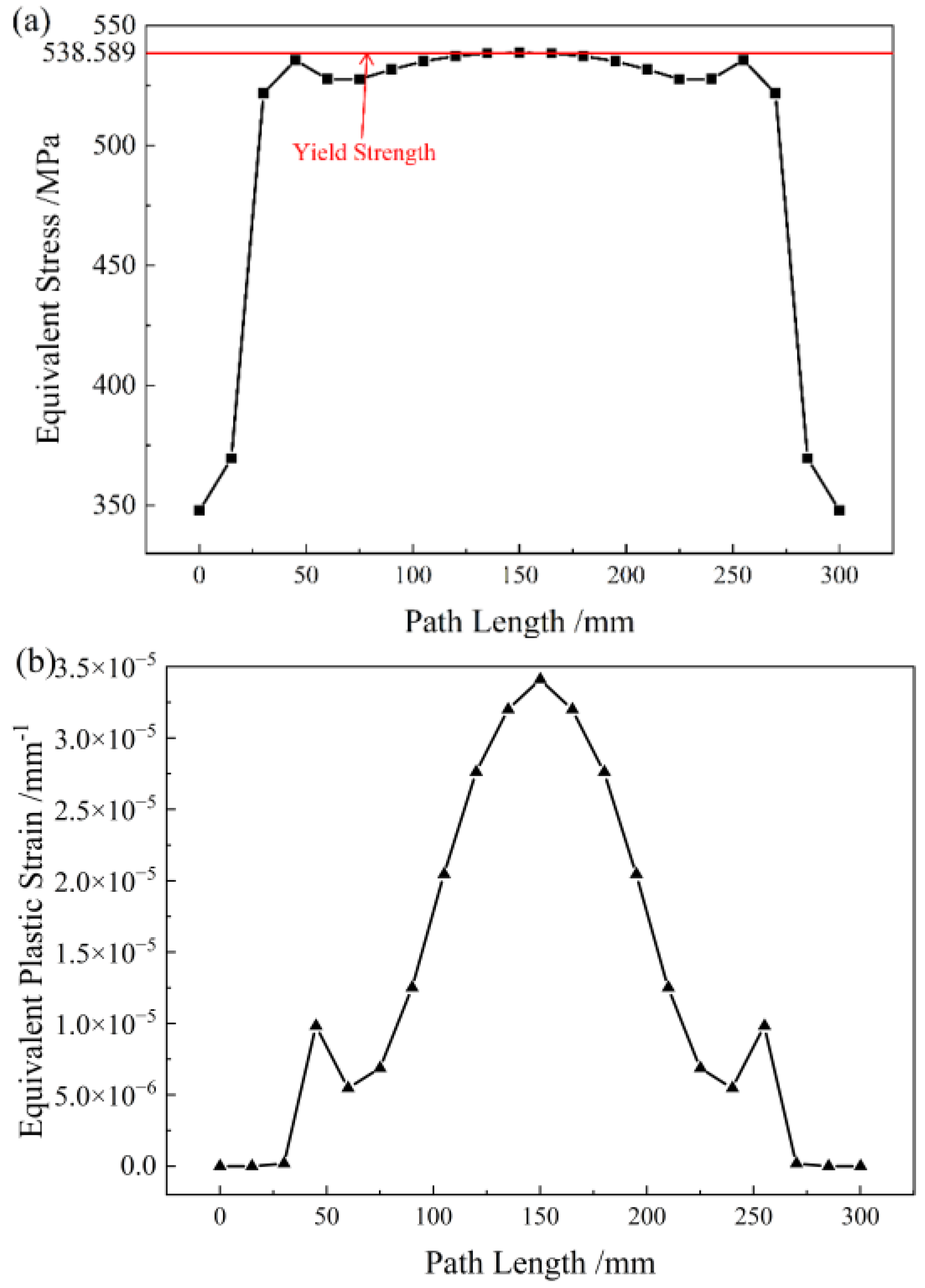
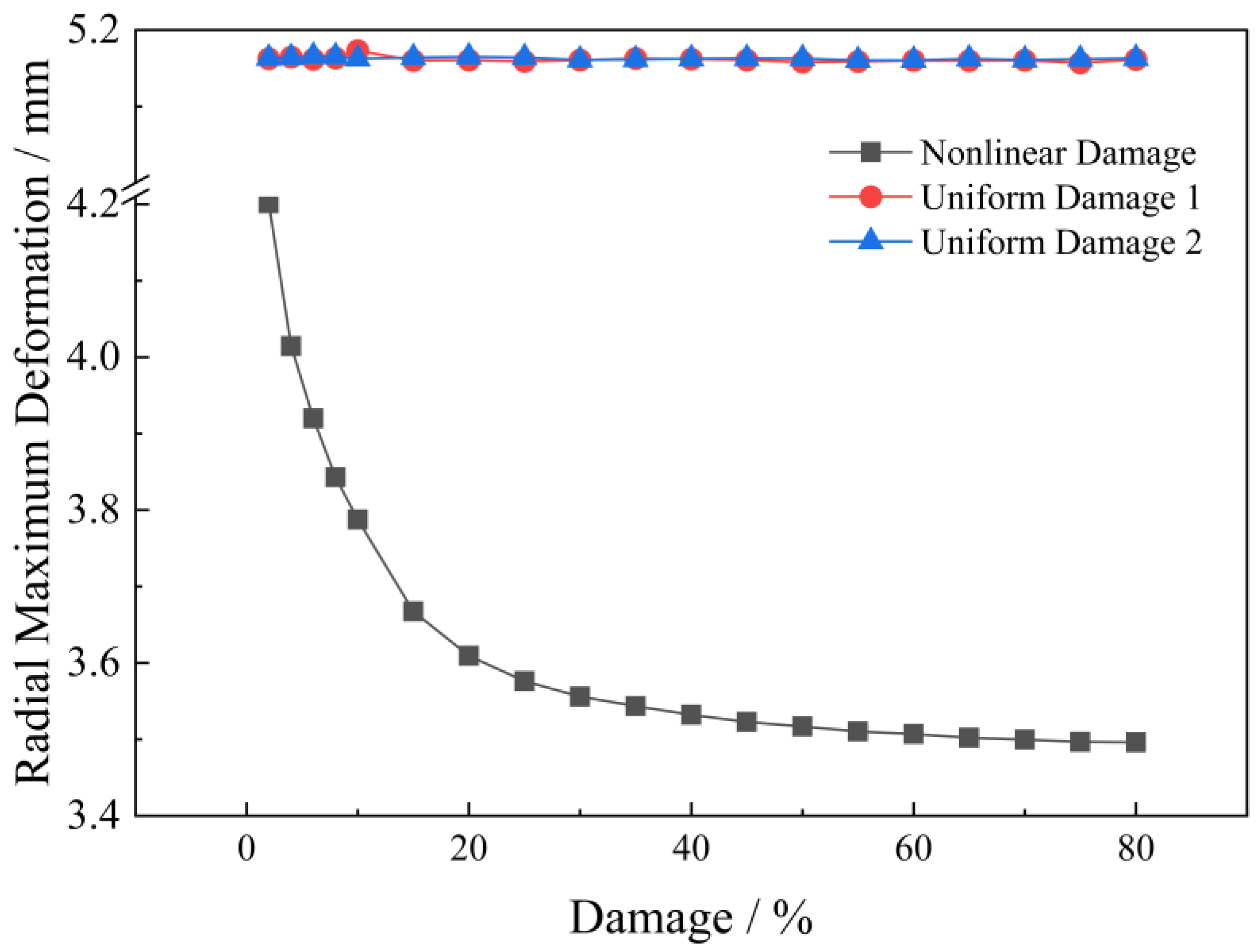
4.1. Residual Strength Characteristics of the Pipe Body under the Influence of Low-Cycle Fatigue
4.2. Tensile Strength Characteristics of Nonlinear Damaged Pipe Body
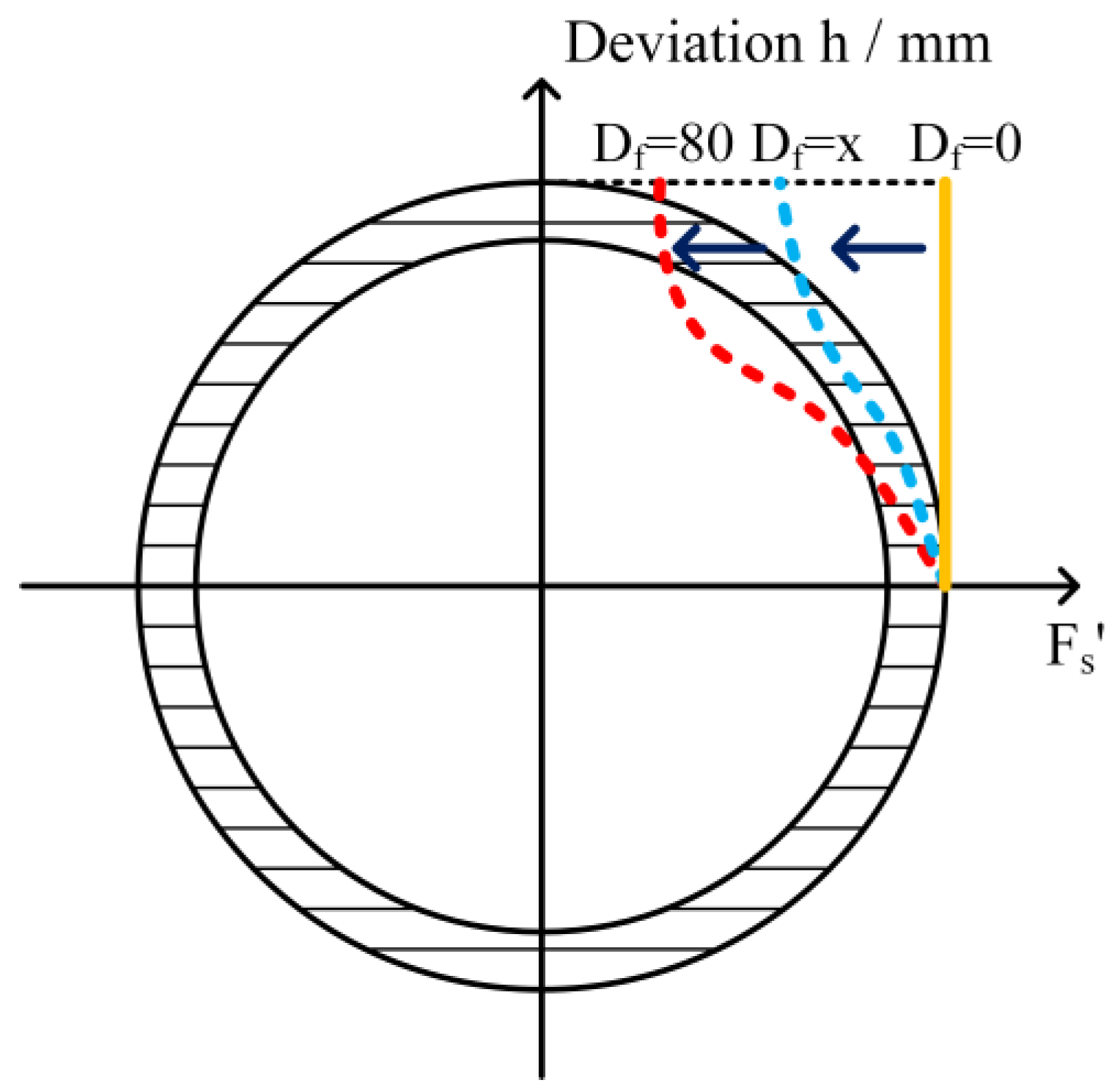
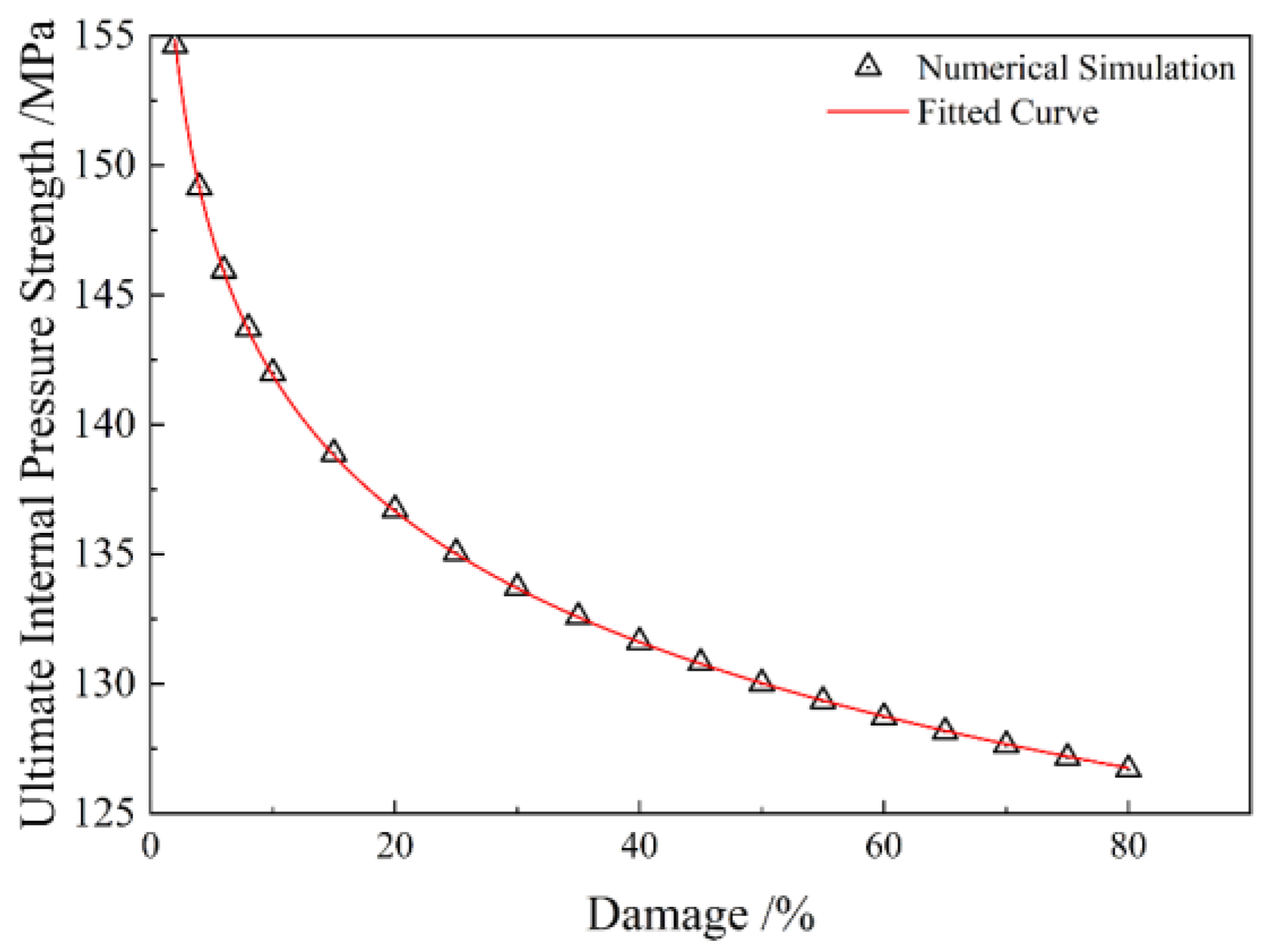
4.3. Ultimate Internal Pressure Strength Characteristics of Nonlinear Damaged Pipe Body
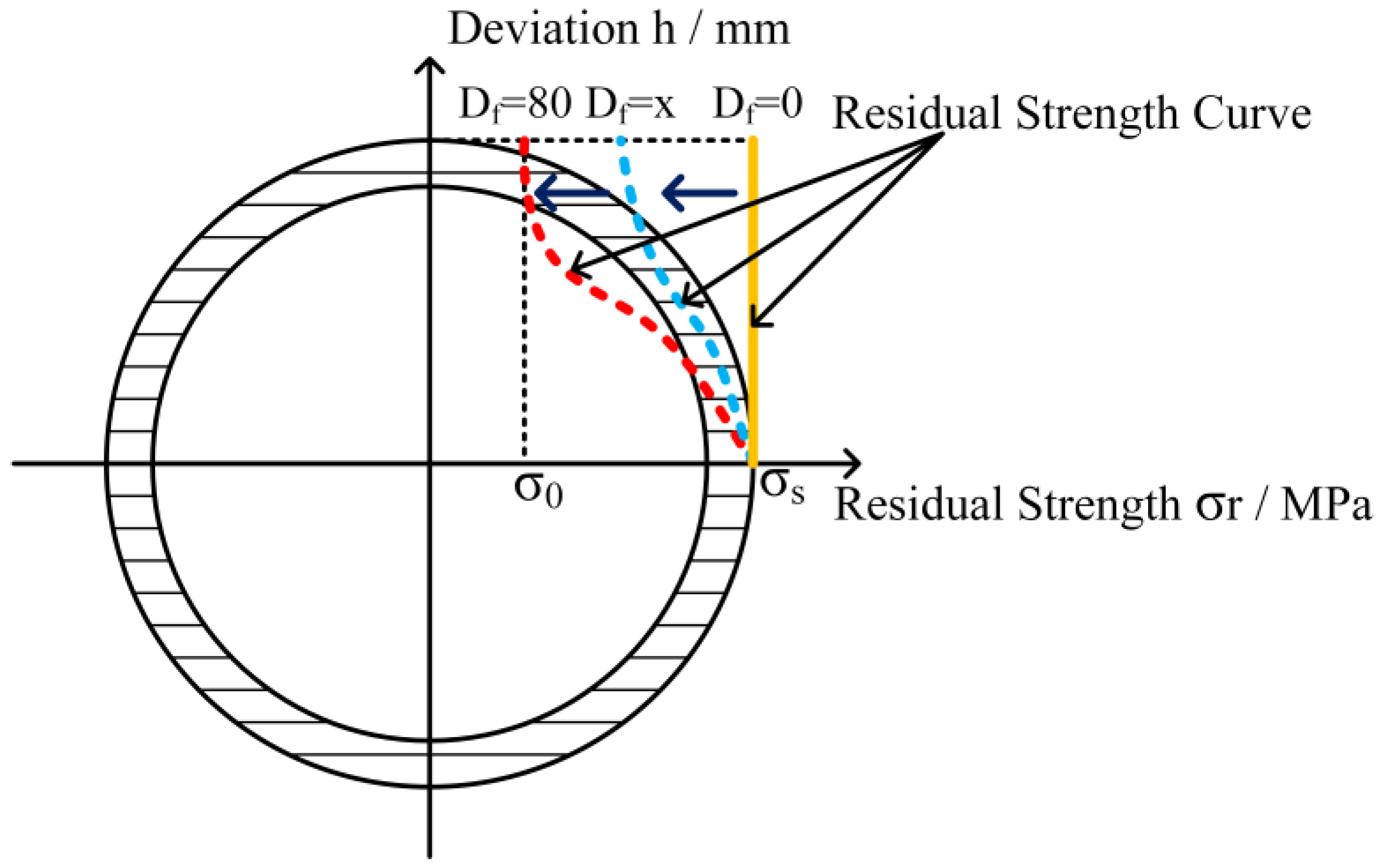
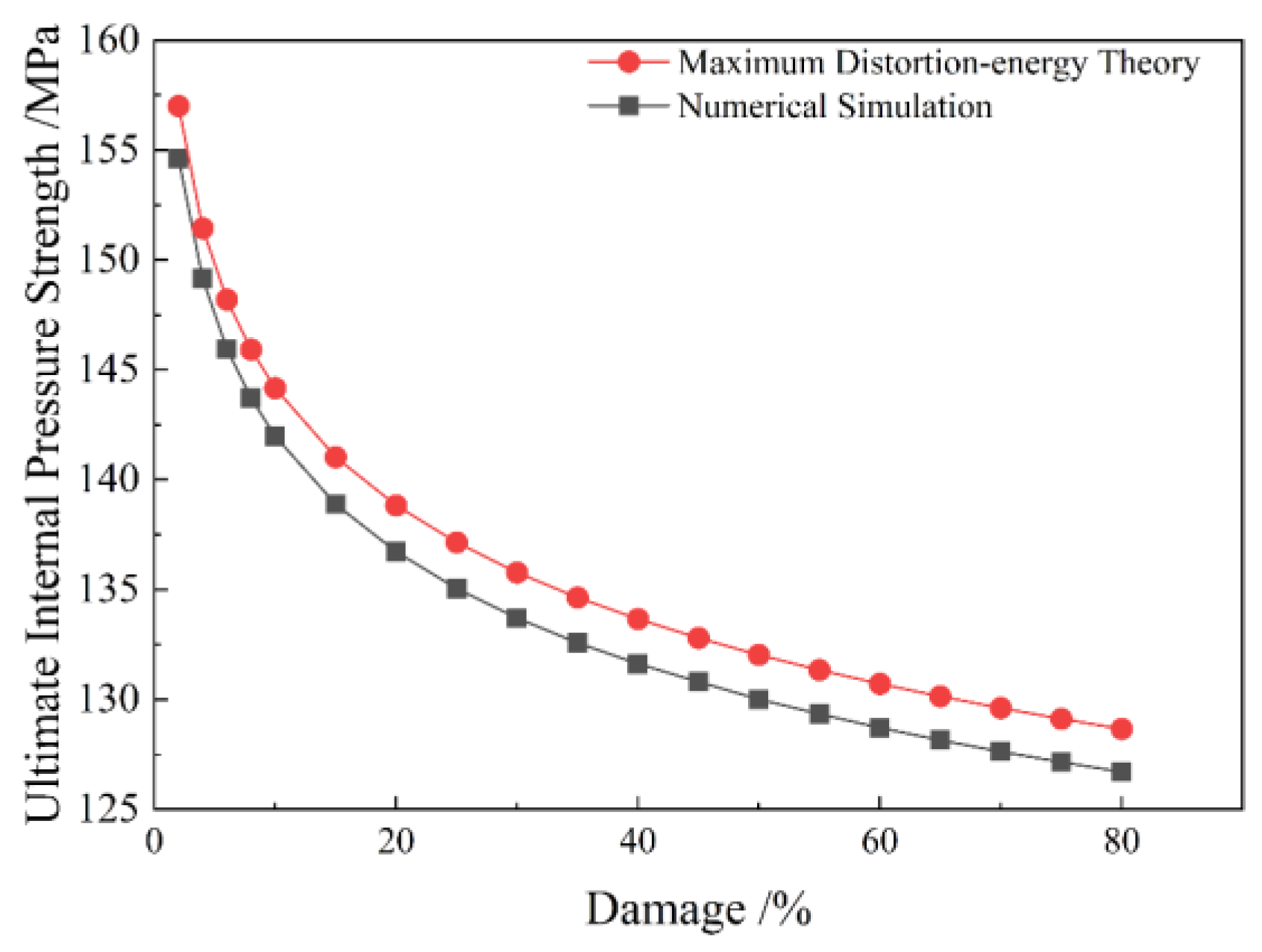
4.4. Theoretical Verification of Ultimate Internal Pressure Strength
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, W.; Feng, Y.; Han, L.; Zhang, Q.; Zhang, J. Cyclic Hardening and Dynamic Strain Aging during Low-Cycle Fatigue of Cr-Mo Tempered Martensitic Steel at Elevated Temperatures. Mater. Sci. Eng. A 2018, 734, 20–26. [Google Scholar] [CrossRef]
- Wei, W.L.; Guo, L.L.; Ju, L.Y.; Han, L.H.; Feng, Y.R.; Zhang, J.B.; Zhang, Q.B. Failure Analysis and Service Life Prediction of 80SH Casing Steel under Thermal Cycle Service Environment. Mater. Sci. Forum 2020, 993, 1293–1300. [Google Scholar] [CrossRef]
- Dou, Y.; Wei, W.; Cao, Y.; Cui, L. Strengthening Mechanism of Low Cycle Fatigue Resistance for Cr-Mo Tempered Martensite Steel at 350 °C. J. Mater. Eng. Perform. 2021, 30, 2083–2090. [Google Scholar] [CrossRef]
- Shao, B.; Wang, X.; Yan, Y.; Yan, X. A Study on the Mechanical Stability of Strings of Thermal Production Wells in Steam Injection. J. Phys. Conf. Ser. 2020, 1635, 012106. [Google Scholar] [CrossRef]
- Wei, W.; Feng, Y.; Han, L.; Zhang, J.; Wang, H. High-Temperature Low-Cycle Fatigue Behavior of HS80H Ferritic–Martensitic Steel Under Dynamic Strain Aging. J. Mater. Eng. Perform. 2018, 27, 6629–6635. [Google Scholar] [CrossRef]
- Han, L.; Wang, H.; Wang, J.; Xie, B.; Tian, Z.; Wu, X. Strain-Based Casing Design for Cyclic-Steam-Stimulation Wells. SPE Prod. Oper. 2017, 33, 409–418. [Google Scholar] [CrossRef]
- Han, L.; Wang, H.; Wang, J.; Zhu, L.; Xie, B.; Tian, Z. Strain Based Design and Field Application of Thermal Well Casing String for Cyclic Steam Stimulation Production. In Proceedings of the SPE Canada Heavy Oil Technical Conference, Calgary, AB, Canada, 7 June 2016. [Google Scholar]
- Wang, J.; Yang, S.; Xue, C.; Han, L.; Wang, H. Strain Design Method for Casing Strings in Heavy Oil Thermal Recovery Well. Zhongguo Shiyou Daxue Xuebao Ziran Kexue Ban J. China Univ. Pet. Ed. Nat. Sci. 2017, 41, 150–155. [Google Scholar] [CrossRef]
- Gou, Y.; Shuang, Y.; Zhou, Y.; Cai, W.; Dai, J.; Mao, F.; Ding, X.; Zhao, C. Damage and Wall Thickness Variation of Magnesium Alloy Tube in Large Curvature and No-Mandrel Bending Process. Xiyou Jinshu Cailiao Yu Gongcheng Rare Met. Mater. Eng. 2018, 47, 2422–2428. [Google Scholar]
- Baldwin, A.J.; Hess, K.M. Mechanics of Materials. In A Programmed Review Of Engineering Fundamentals; Baldwin, A.J., Hess, K.M., Eds.; Springer: Boston, MA, USA, 1978; pp. 204–226. ISBN 978-1-4757-1223-0. [Google Scholar]
- Cheng, G.; Plumtree, A. A Fatigue Damage Accumulation Model Based on Continuum Damage Mechanics and Ductility Exhaustion. Int. J. Fatigue 1998, 20, 495–501. [Google Scholar] [CrossRef]
- Correia, J.A.F.O.; Raposo, P.; Muniz-Calvente, M.; Blasón, S.; Lesiuk, G.; De Jesus, A.M.P.; Moreira, P.M.G.P.; Calçada, R.A.B.; Canteli, A.F. A Generalization of the Fatigue Kohout-Věchet Model for Several Fatigue Damage Parameters. Eng. Fract. Mech. 2017, 185, 284–300. [Google Scholar] [CrossRef]
- Djebli, A.; Aid, A.; Bendouba, M.; Amrouche, A.; Benguediab, M.; Benseddiq, N. A Non-Linear Energy Model of Fatigue Damage Accumulation and Its Verification for Al-2024 Aluminum Alloy. Int. J. Non-Linear Mech. 2013, 51, 145–151. [Google Scholar] [CrossRef]
- Bai, S.; Li, Y.-F.; Huang, H.-Z.; Ma, Q.; Lu, N. A Probabilistic Combined High and Low Cycle Fatigue Life Prediction Framework for the Turbine Shaft with Random Geometric Parameters. Int. J. Fatigue 2022, 165, 107218. [Google Scholar] [CrossRef]
- Aid, A.; Amrouche, A.; Bouiadjra, B.B.; Benguediab, M.; Mesmacque, G. Fatigue Life Prediction under Variable Loading Based on a New Damage Model. Mater. Des. 2011, 32, 183–191. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Gao, J.-W.; Correia, J.; Calçada, R.; Lesiuk, G. Generalized Strain Energy Density-Based Fatigue Indicator Parameter. Int. J. Mech. Sci. 2023, 254, 108427. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Liao, D.; Liu, Q.; Correia, J.A.F.O.; De Jesus, A.M.P. Nonlinear Fatigue Damage Accumulation: Isodamage Curve-Based Model and Life Prediction Aspects. Int. J. Fatigue 2019, 128, 105185. [Google Scholar] [CrossRef]
- Chin, C.H.; Abdullah, S.; Singh, S.S.K.; Schramm, D.; Ariffin, A.K. Strain Generation for Fatigue-Durability Predictions Considering Load Sequence Effect of Random Vibration Loading. Int. J. Fatigue 2023, 166, 107242. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, G.; Liu, X.; Yang, X. An Improved Strength Degradation Model for Fatigue Life Prediction Considering Material Characteristics. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 275. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. Cumulative Damage and Life Prediction Models for High-Cycle Fatigue of Metals: A Review. Metals 2021, 11, 204. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Jiang, C.; Wang, X.; Wang, X. Prediction and Evaluation of Fatigue Life for Mechanical Components Considering Anelasticity-Based Load Spectrum. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 129–140. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, Y.; Li, Y.; Xue, Q. Fatigue Life Prediction Based on a Novel Improved Version of the Corten-Dolan Model Considering Load Interaction Effect. Eng. Struct. 2020, 221, 111036. [Google Scholar] [CrossRef]
- Huang, B.; Wang, S.; Geng, S.; Liu, X. Improved Numerical Model for Fatigue Cumulative Damage of Mechanical Structure Considering Load Sequence and Interaction. Adv. Mech. Eng. 2021, 13, 1687814021995309. [Google Scholar] [CrossRef]
- Abbasali Ayubali, A.; Prabu Shanmugavel, B.; Padmanabhan, K.A. On Material-Agnostic Fatigue Life Prediction Using Buckingham Pi Theorem. Eng. Fract. Mech. 2023, 280, 109021. [Google Scholar] [CrossRef]
- Huffman, P.J.; Beckman, S.P. A Non-Linear Damage Accumulation Fatigue Model for Predicting Strain Life at Variable Amplitude Loadings Based on Constant Amplitude Fatigue Data. Int. J. Fatigue 2013, 48, 165–169. [Google Scholar] [CrossRef]
- Subramanyan, S. A Cumulative Damage Rule Based on the Knee Point of the S-N Curve. J. Eng. Mater. Technol. 1976, 98, 316–321. [Google Scholar] [CrossRef]
- Rege, K.; Pavlou, D.G. A One-Parameter Nonlinear Fatigue Damage Accumulation Model. Int. J. Fatigue 2017, 98, 234–246. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, Y.; Ye, N. An Improved Fatigue Accumulation Damage Model Based on Load Interaction and Strength Degradation. Int. J. Fatigue 2022, 156, 106636. [Google Scholar] [CrossRef]
- Araújo, L.M.; Ferreira, G.V.; Neves, R.S.; Malcher, L. Fatigue Analysis for the Aluminum Alloy 7050-T7451 Performed by a Two Scale Continuum Damage Mechanics Model. Theor. Appl. Fract. Mech. 2020, 105, 102439. [Google Scholar] [CrossRef]
- Tumanov, A.; Shlyannikov, V.N.; Zakharov, A.P. Crack Growth Rate Prediction Based on Damage Accumulation Functions for Creep-Fatigue Interaction. Frat. Ed Integrità Strutt. 2020, 14, 299–309. [Google Scholar] [CrossRef]
- Manson, S.S.; Halford, G.R. Practical Implementation of the Double Linear Damage Rule and Damage Curve Approach for Treating Cumulative Fatigue Damage. Int. J. Fract. 1981, 17, 169–192. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A Cumulative Damage Theory of Fatigue Failure. Mater. Sci. Eng. 1978, 34, 147–160. [Google Scholar] [CrossRef]
- Aeran, A.; Siriwardane, S.C.; Mikkelsen, O.; Langen, I. A New Nonlinear Fatigue Damage Model Based Only on S-N Curve Parameters. Int. J. Fatigue 2017, 103, 327–341. [Google Scholar] [CrossRef]
- Liu, Z.; Tipton, S.; Sukumar, D. Latest Development in Physics-Based Modeling of Coiled Tubing Plasticity and Fatigue. SPE J. 2022, 27, 1275–1286. [Google Scholar] [CrossRef]
- Tipton, S.M. Multiaxial Plasticity and Fatigue Life Prediction in Coiled Tubing. In Proceedings of the Advances in Fatigue Lifetime Predictive Techniques; ASTM International: West Conshohocken, PA, USA, 1993; Volume 3, pp. 283–304. [Google Scholar]
- Behenna, F.; Myrick, D.; Stanley, R.; Tipton, S.; Hammond, W. Field Validation of a Coiled Tubing Fatigue Model. In Proceedings of the SPE/ICoTA Coiled Tubing Conference and Exhibition, Houston, TX, USA, 8–9 April 2003. [Google Scholar] [CrossRef]
- Wei, W.; Han, L.; Wang, H.; Wang, J.; Zhang, J.; Feng, Y.; Tian, T. Low-Cycle Fatigue Behavior and Fracture Mechanism of HS80H Steel at Different Strain Amplitudes and Mean Strains. J. Mater. Eng. Perform. 2017, 26, 1717–1725. [Google Scholar] [CrossRef]
- Ellyin, F. Cyclic Stress-Strain Response. In Fatigue Damage, Crack Growth and Life Prediction; Ellyin, F., Ed.; Springer: Dordrecht, The Netherlands, 1997; pp. 33–76. ISBN 978-94-009-1509-1. [Google Scholar]







| Parameter | Symbol | Value |
|---|---|---|
| Fatigue strength coefficient | σf′ | 17,407 |
| Fatigue strength exponent | b | −0.51453 |
| Fatigue ductility coefficient | εf′ | 0.04965 |
| Fatigue ductility exponent | c | −0.029159 |
| Function fitting coefficient | k | 685.719 |
| Function fitting exponent | d | −0.055 |
| Corrected value | ΔC | 0.16 |
| Parameter | Symbol | Value |
|---|---|---|
| Outside diameter | Φ | 73.02 mm |
| Wall thickness | t | 7.01 mm |
| Poisson’s ratio | ν | 0.3 |
| Elastic modulus | E | 210 GPa |
| Yield strength | σs | 758 MPa |
| Tensile strength | σb | 947.5 MPa |
| Parameter | Value |
|---|---|
| a1 | 160.774 |
| b1 | −0.0543 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, W.; Zhang, R.; Zhang, Y.; Cheng, J.; Cao, Y.; Fang, F. Study on the Residual Strength of Nonlinear Fatigue-Damaged Pipeline Structures. Appl. Sci. 2024, 14, 754. https://doi.org/10.3390/app14020754
Wei W, Zhang R, Zhang Y, Cheng J, Cao Y, Fang F. Study on the Residual Strength of Nonlinear Fatigue-Damaged Pipeline Structures. Applied Sciences. 2024; 14(2):754. https://doi.org/10.3390/app14020754
Chicago/Turabian StyleWei, Wenlan, Rui Zhang, Yuwen Zhang, Jiarui Cheng, Yinping Cao, and Fengying Fang. 2024. "Study on the Residual Strength of Nonlinear Fatigue-Damaged Pipeline Structures" Applied Sciences 14, no. 2: 754. https://doi.org/10.3390/app14020754






