Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks
Abstract
:1. Introduction
2. Test Design Scheme
2.1. Preparing the Specimen
2.2. Loading Scheme and Test Equipment
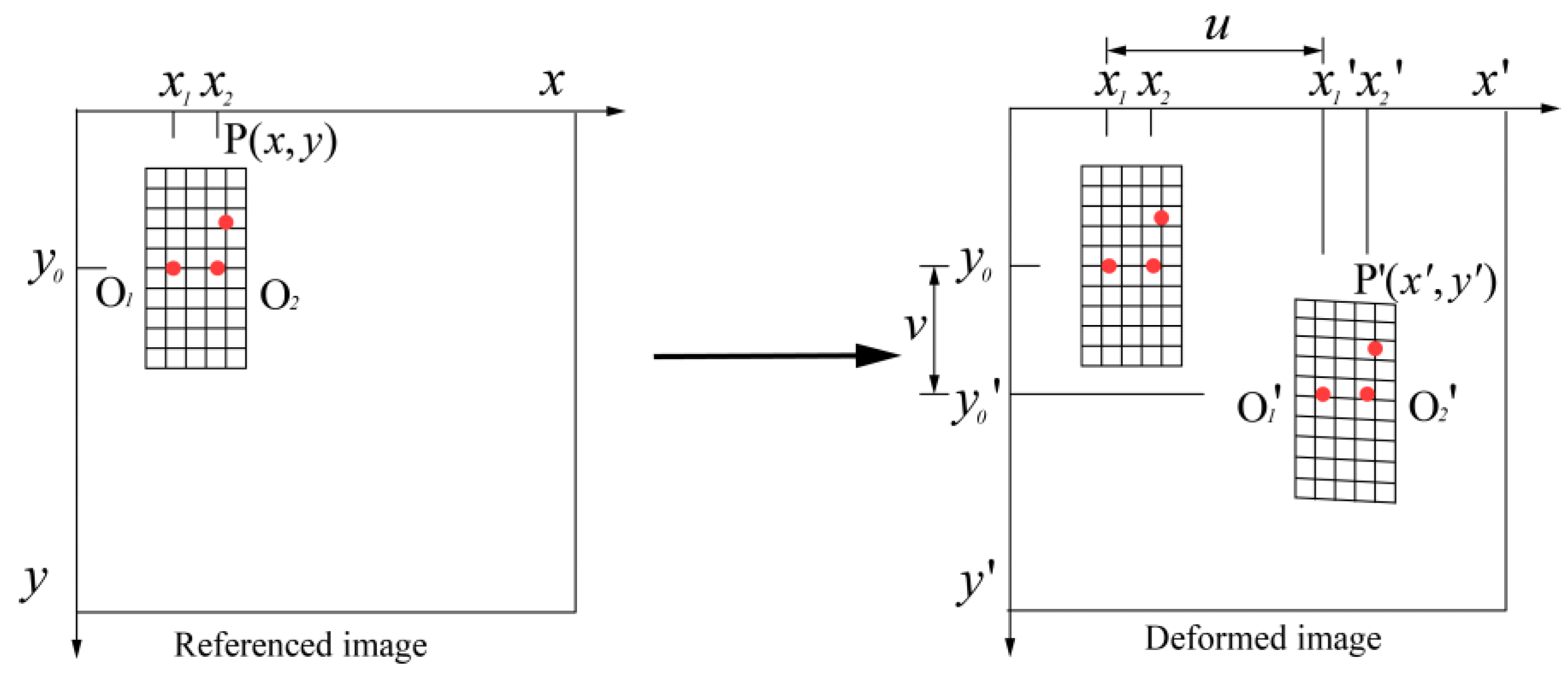
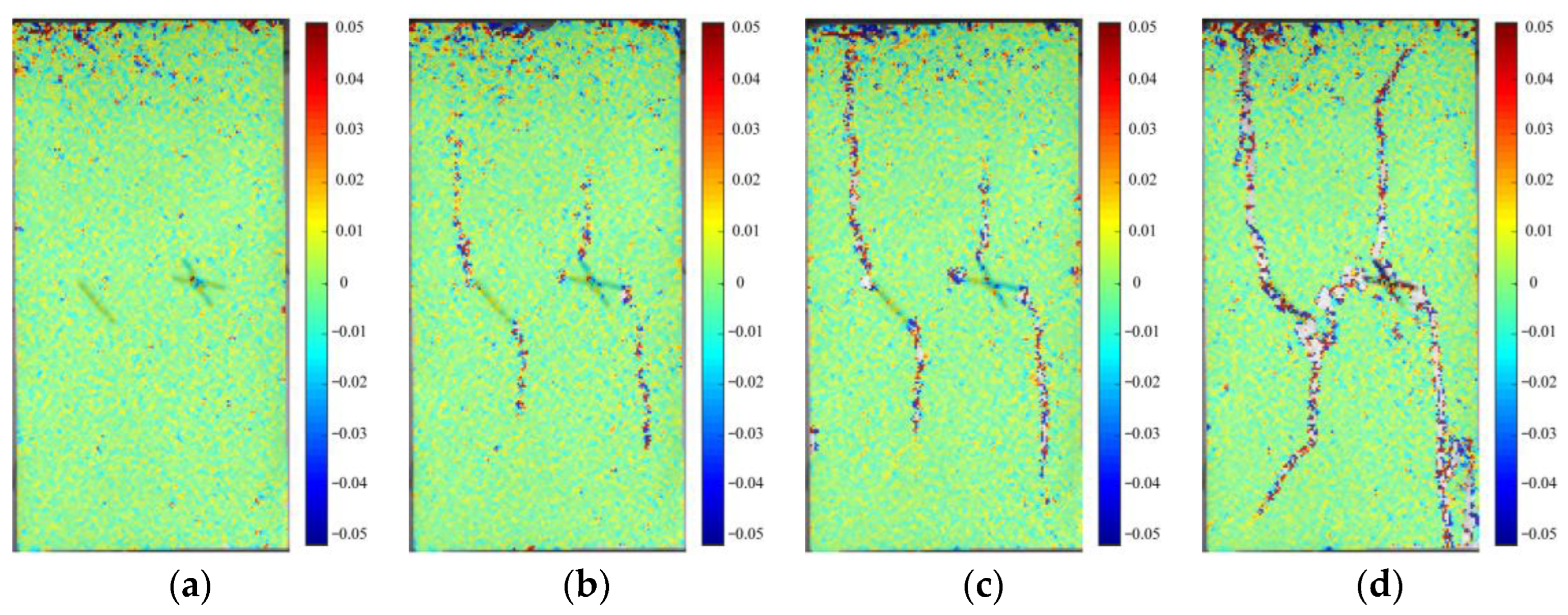
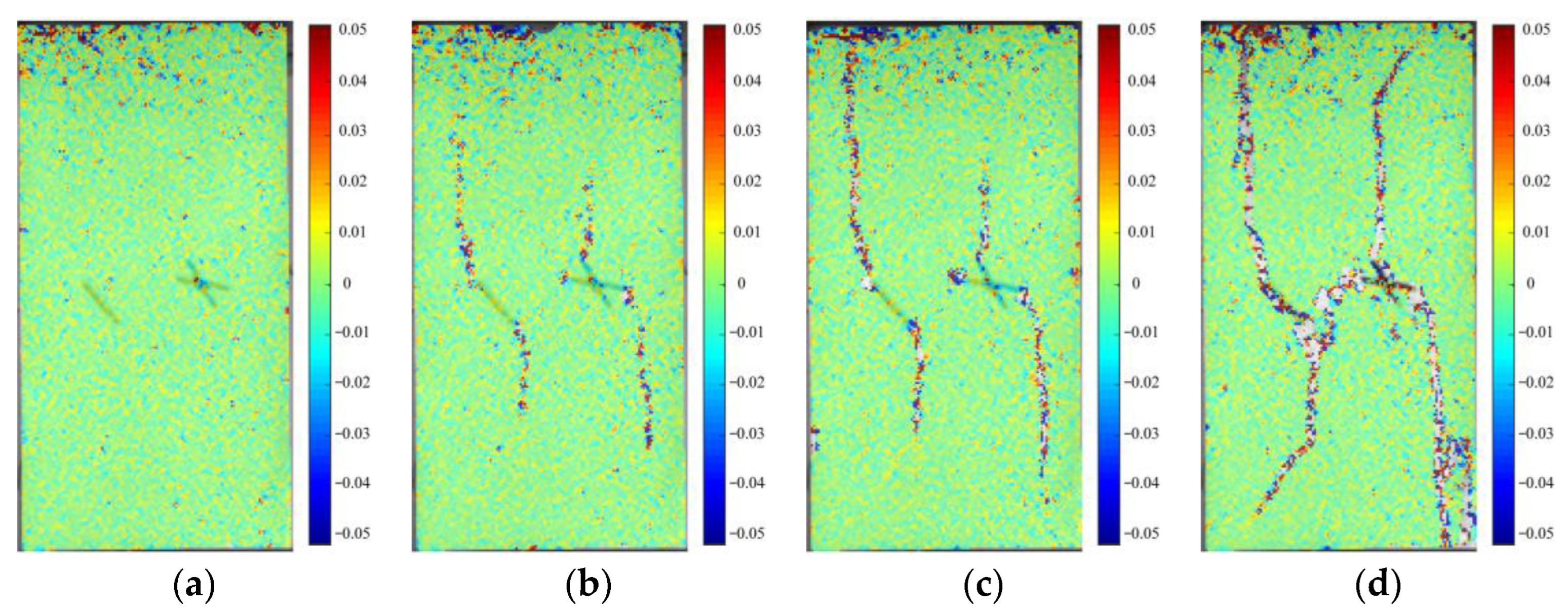
2.3. Digital Image Correlation Technique
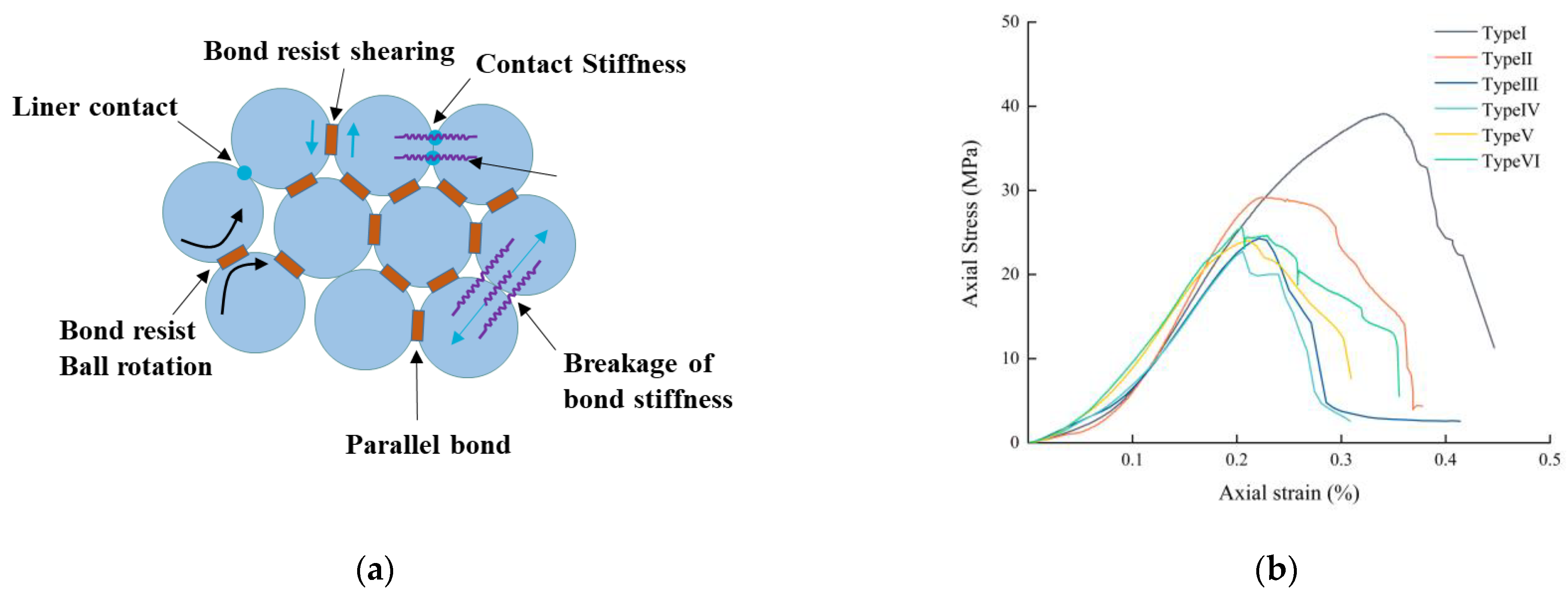
3. Model Establishment and Parameter Selection
4. Test Result Analysis
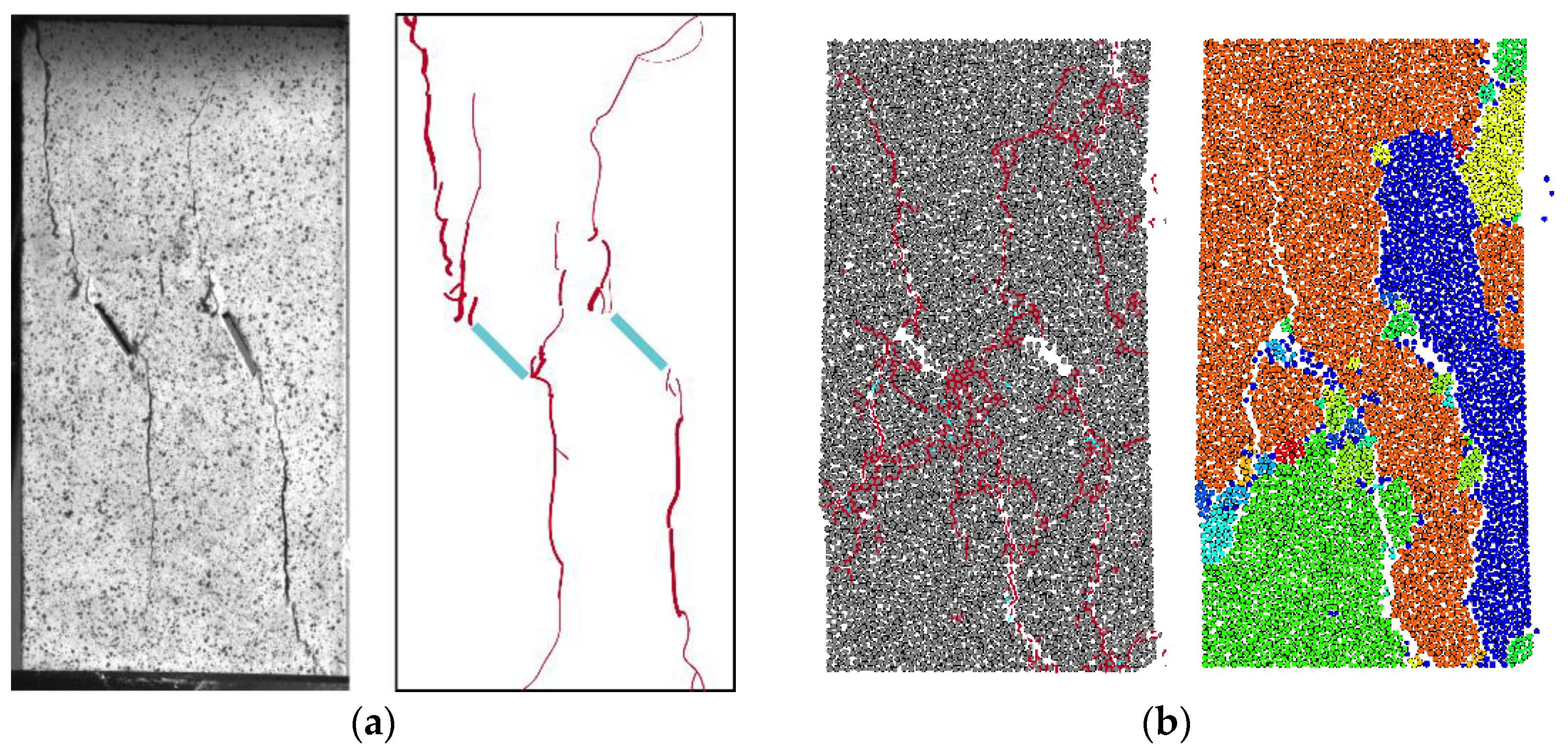
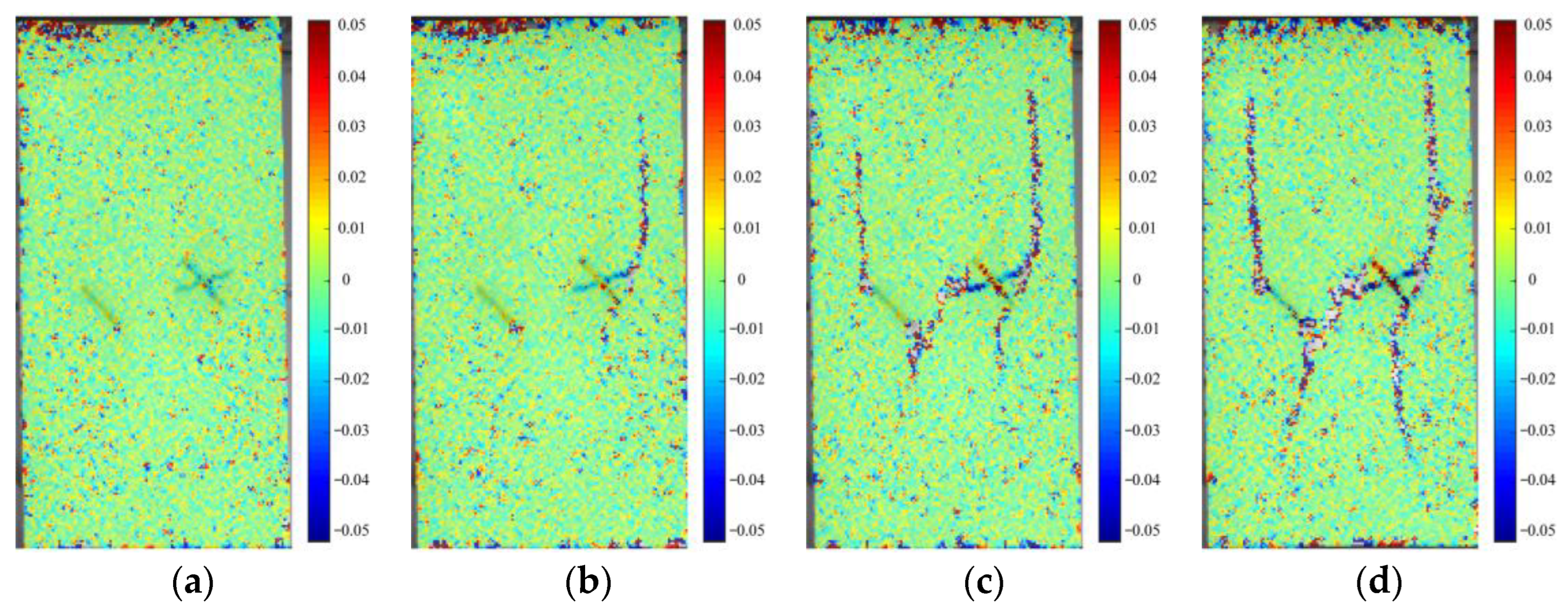
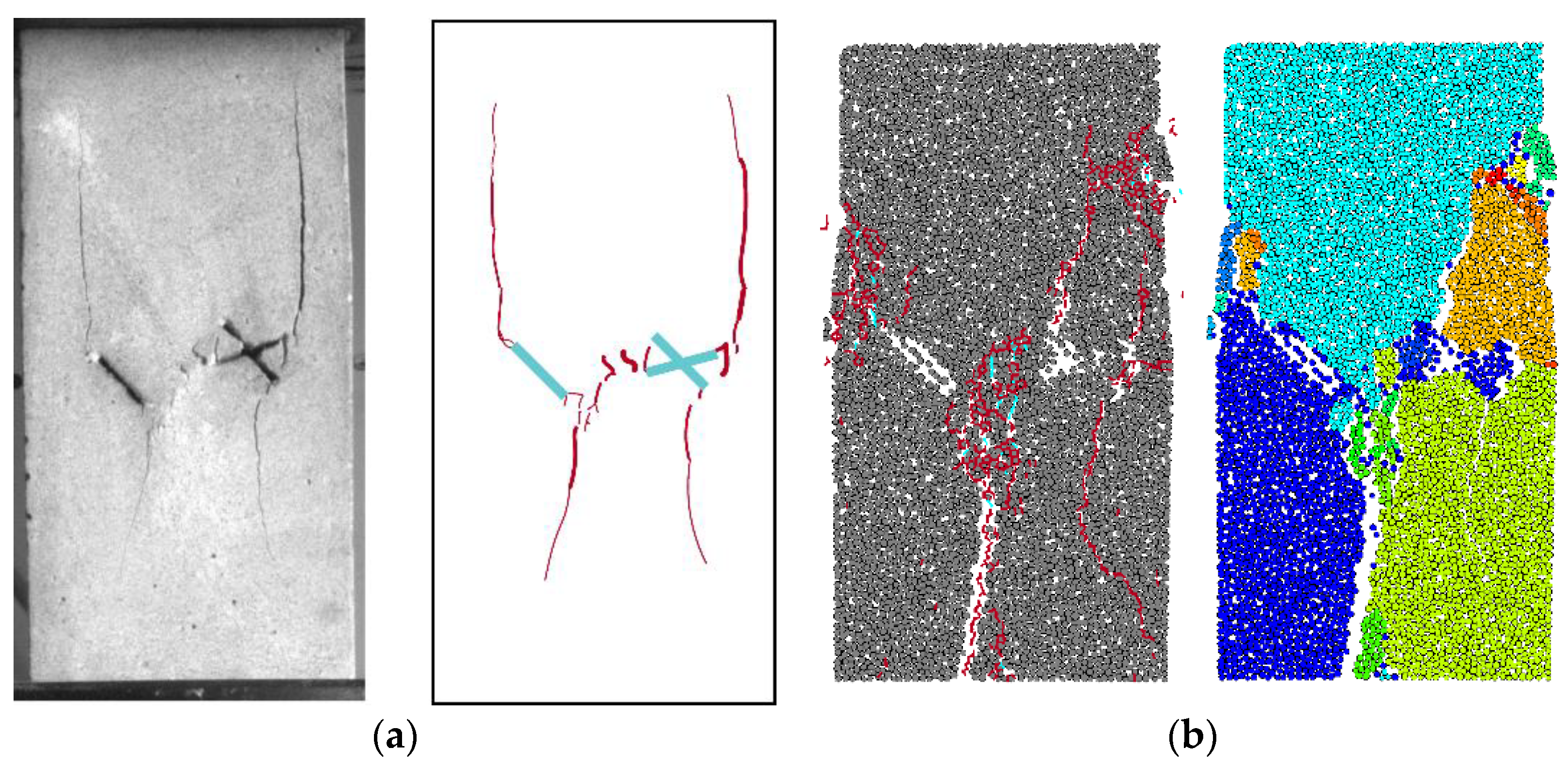
4.1. Type I and Type II Failure Modes
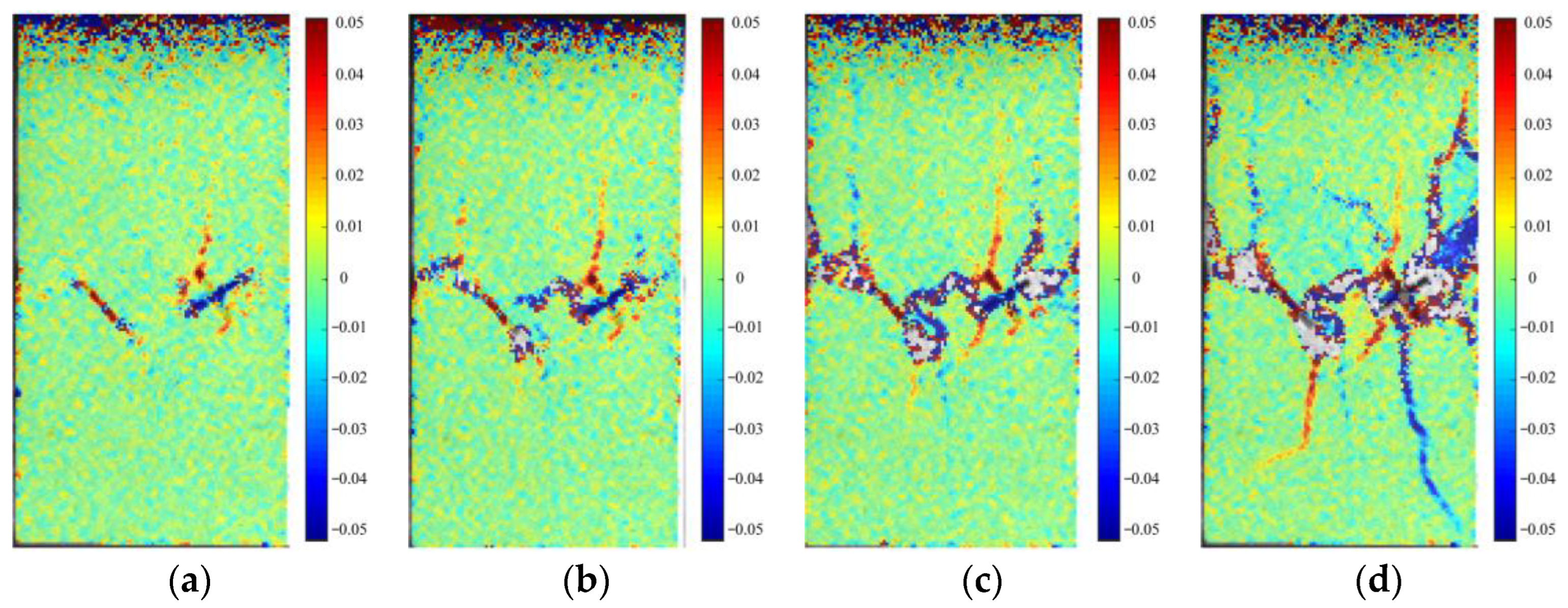
4.2. Failure Effect of Crossed Fractures
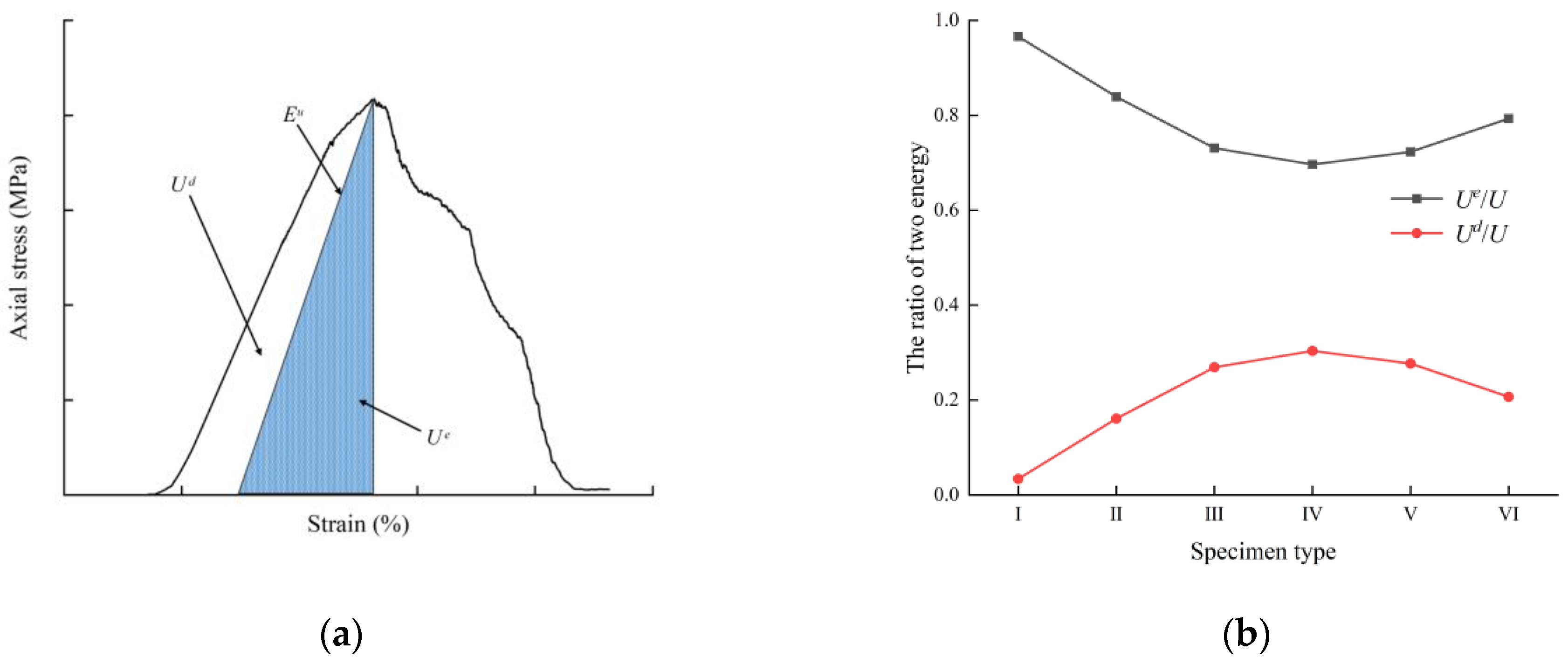
5. Energy Characteristics and Damage Mechanism
6. Discussion
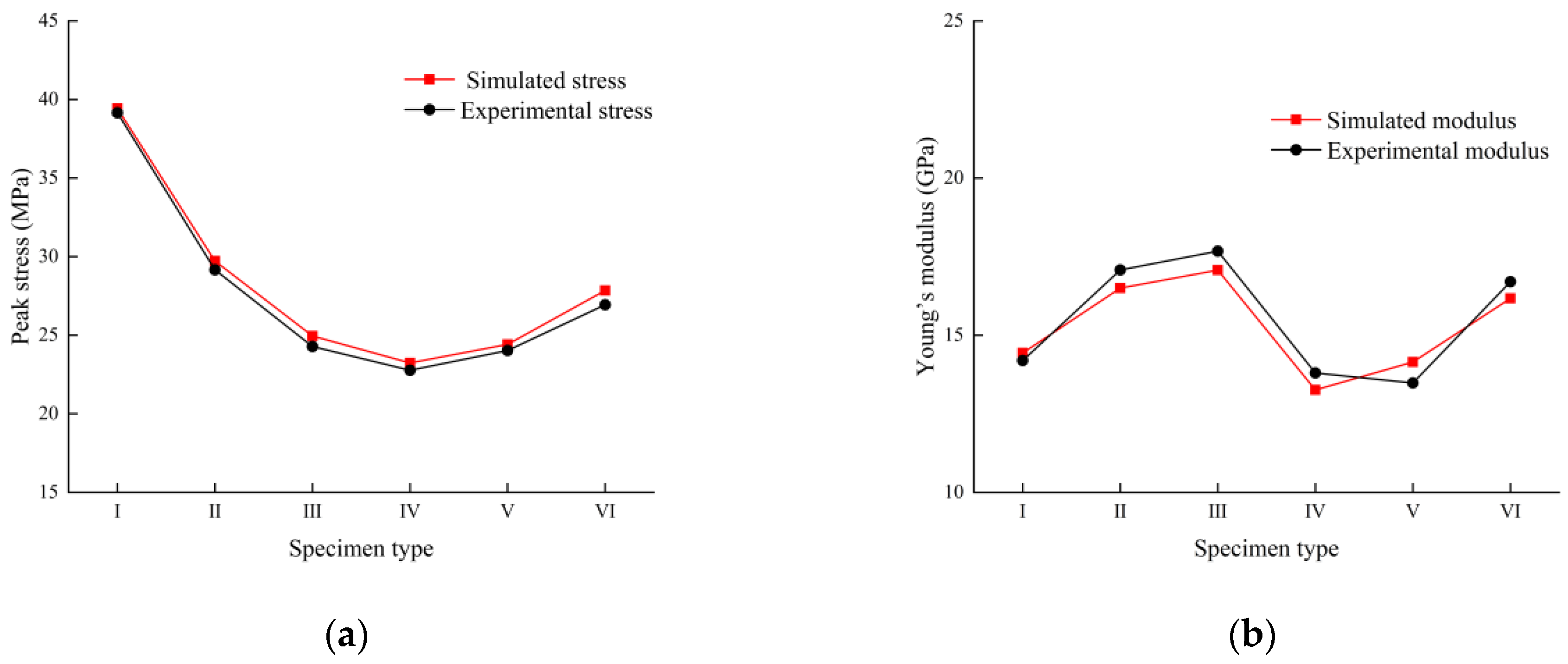
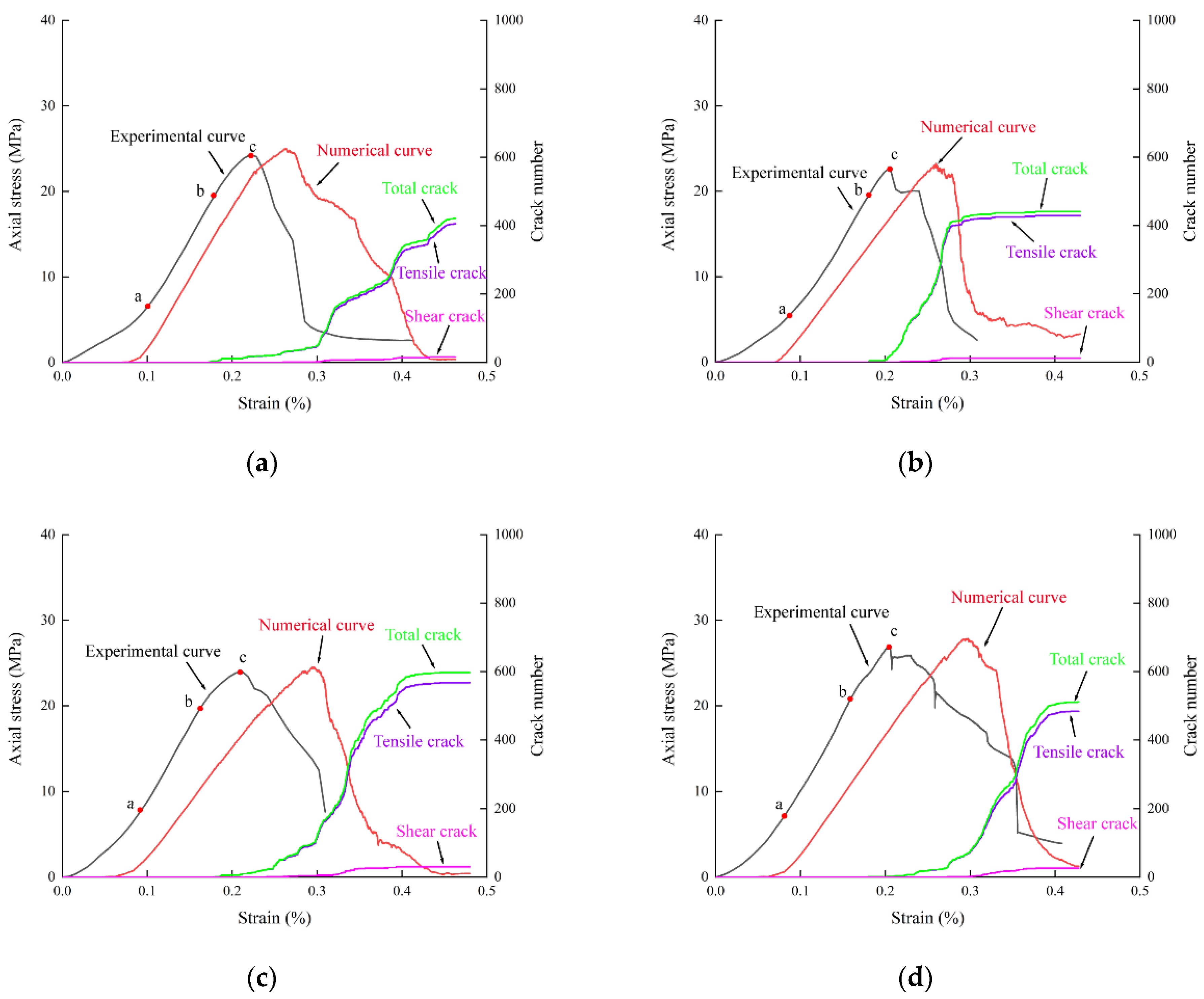
6.1. Mechanical Properties
6.2. Aggregation Patterns of Cleavage
7. Conclusions
- The peak strength of specimens containing a combination of both single and conjugate cracks is related to the β-angle within the prefabricated conjugate cracks. Under the same conditions, as the β angle increases from 30° to 90°, the peak strength decreases and then increases, reaching a minimum at β = 45° (Type IV).
- The geometry of the conjugate crack affects the location of the crack clusters in the rock specimens. Except for the conjugate cracks with β = 45°, the positions of crack clusters in specimens with conjugate crack clusters are biased towards the lower part of the specimen. The numerical simulation results show that the damage caused by secondary cracks generated by tensile cracks dominates the crack extension process and is the main controlling crack leading to the decrease in rock-bearing capacity;
- The positive correlation between specimen integrity and energy dissipation rate was verified using the energy dissipation rate method. The crack development law of multiple conjugate crack combination specimens under uniaxial compression conditions was obtained, which helps to infer the process of crack initiation, expansion, and merging in fractured pressure-bearing rock bodies in actual engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.Q.; Yang, D.S.; Jing, H.W.; Li, Y.H.; Wang, S.Y. An experimental study of the fracture coalescence behaviour of brittle sandstone specimens containing three fissures. Rock Mech. Rock Eng. 2011, 45, 563–582. [Google Scholar] [CrossRef]
- Shi, G.H.; Goodman, R.E. Generalization of two-dimensional discontinuous deformation analysis for forward modelling. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 359–380. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Dong, P.; Wu, B.; Xia, K.; Wang, Q. Fracture modes of single-flawed rock-like material plates subjected to dynamic compression. Int. J. Geomech. 2020, 20, 04020145. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Discontinuity spacings in rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 135–148. [Google Scholar] [CrossRef]
- Bobet, A.; Einstein, H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Afolagboye, L.O.; He, J.; Wang, S. Experimental study on cracking behaviour of moulded gypsum containing two non-parallel overlapping flaws under uniaxial compression. Acta Mech. Sin. 2017, 33, 394–405. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Heuze, F.E. Finite element models for rock fracture mechanics. Int. J. Numer. 1980, 4, 25–43. [Google Scholar] [CrossRef]
- Yang, S.Q.; Huang, Y.H.; Jing, H.W.; Liu, X.R. Discrete element modeling on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression. Eng. Geol. 2014, 178, 28–48. [Google Scholar] [CrossRef]
- Hoek, E.; Bieniawski, Z.T. Brittle fracture propagation in rock under compression. Int. J. Fract. 1973, 1, 137–155. [Google Scholar] [CrossRef]
- Bahat, D.; Frid, V.; Rabinovitch, A.; Palchik, V. Exploration via electromagnetic radiation and fractographic methods of fracture properties induced by compression in glass-ceramic. Int. J. Fract. 2002, 116, 179–194. [Google Scholar] [CrossRef]
- Bombolakis, E.G. Study of the brittle fracture process under uniaxial compression in crystalline rock. Tectonophysics 1973, 18, 231–248. [Google Scholar] [CrossRef]
- Vallejo, L.E. The influence of fissures in a stiff clay subjected to direct shear. Géotechnique 1987, 37, 69–82. [Google Scholar] [CrossRef]
- Cao, R.H.; Cao, P.; Lin, H.; Pu, C.Z.; Ou, K. Mechanical behavior of brittle rock-like specimens with pre-existing fissures under uniaxial loading: Experimental studies and particle mechanics approach. Rock Mech. Rock Eng. 2016, 49, 763–783. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Sahouryeh, E.; Jewell, R.J.; Joer, H.; Ustinov, K.B. Influence of shape and locations of initial 3-D cracks on their growth in uniaxial compression. Eng. Fract. Mech. 2003, 70, 2115–2136. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F.; Fan, P.; Xu, N.; Dong, L. Experimental investigation of the influence of joint geometric configurations on the mechanical properties of intermittent jointed rock models under cyclic uniaxial compression. Rock Mech. Rock Eng. 2017, 50, 1453–1471. [Google Scholar] [CrossRef]
- Rabinovitch, A.; Zlotnikov, R.; Bahat, D. Flaw length distribution measurement in brittle materials. J. Appl. Phys. 2000, 87, 7720–7725. [Google Scholar] [CrossRef]
- Rabinovitch, A.; Bahat, D. Differentiation of crack branching types in fractured glass. Europhys. Lett. 2011, 95, 16003. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T.; Tang, C.A.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flawsFPart I: Experimental approach. Int. J. Rock Mech. Min. Sci. 2001, 38, 909–924. [Google Scholar] [CrossRef]
- Le, H.; Sun, S.; Kulatilake, P.H.S.W.; Wei, J. Effect of Grout on Mechanical Properties and Cracking Behavior of Rock-Like Specimens Containing a Single Flaw under Uniaxial Compression. Int. J. Geomech. 2018, 18, 04018129. [Google Scholar] [CrossRef]
- Sivakumar, G.; Maji, V.B. Crack growth in rocks with preexisting narrow flaws under uniaxial compression. Int. J. Geomech. 2021, 21, 04021032. [Google Scholar] [CrossRef]
- Hosseini-Tehrani, P.; Hosseini-Godarzi, A.R.; Tavangar, M. Boundary element analysis of stress intensity factor KI in some two-dimensional dynamic thermoelastic problems. Eng. Anal. Bound. Elem. 2005, 29, 232–240. [Google Scholar] [CrossRef]
- Lu, X.; Wu, W.-l. A subregion DRBEM formulation for the dynamic analysis of two-dimensional cracks. Math. Comput. Model. 2006, 43, 76–88. [Google Scholar] [CrossRef]
- Damjanac, B.; Board, M.; Lin, M.; Kicker, D.; Leem, J. Mechanical degradation of emplacement drifts at Yucca Mountain—A modeling case study. Int. J. Rock Mech. Min. Sci. 2007, 44, 368–399. [Google Scholar] [CrossRef]
- Xu, H.; Qin, Y.; Wang, G.; Fan, C.; Wu, M.; Wang, R. Discrete element study on mesomechanical behavior of crack propagation in coal samples with two prefabricated fissures under biaxial compression. Powder Technol. 2020, 375, 42–59. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Bai, J.; Dou, L.; Li, X.; Ma, X.; Lu, F.; Han, Z. Evolution Laws of Stress–Energy and Progressive Damage Mechanisms of Surrounding Rock Induced by Mining Disturbance. Appl. Sci. 2023, 13, 7759. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y.; Yang, T.; Bai, W.; Gao, S.; Yan, Y. Study on the Co-Evolution Mechanism of Key Strata and Mining Fissure in Shallow Coal Seam Mining. Appl. Sci. 2023, 13, 8036. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wong, L.N.Y. Crack initiation, propagation and coalescence in rock-like material containing two flaws: A numerical study based on bonded-particle model approach. Rock Mech. Rock Eng. 2013, 46, 1001–1021. [Google Scholar] [CrossRef]
- Fan, P.; Liu, J.; Zuo, W.; Wang, M.; Zhang, D. Experimental Study of Rock-like Materials with Two Unequal Parallel Preexisting Fissures under Uniaxial Compression. Appl. Sci. 2022, 12, 10404. [Google Scholar] [CrossRef]
- Wu, B.; Liu, Q.; Fu, Q.; Yang, Q.; Chen, Q. Damage Mechanism of Prefabricated Fracture-Grouted Rock Specimens under the Action of Dry and Wet Cycles. Appl. Sci. 2023, 13, 3631. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Cao, R.; Dai, H.; Yao, R.; Lin, H.; Li, K. Failure Behaviour of Jointed Rock Masses with 3D Nonpenetrating Joints under Uniaxial Compression: Insights from Discrete Element Method Modelling. Appl. Sci. 2022, 12, 11027. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation, propagation and coalescence from frictional flaws in uniaxial compression. Eng. Fract. Mech. 2010, 77, 2727–2748. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.; Yang, X.Y.; Li, S.C.; Liu, B.; Xu, Z.H.; Pei, Y. Influence of two cross-flaws geometry on the strength and crack coalescence of eock-like material specimens under uniaxial compression. Int. J. Geomech. 2020, 20, 04020134. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, N.; Liu, H.; Fukuda, D.; Rong, H. Hybrid finite-discrete element simulator based on GPGPU-parallelized computation for modelling crack initiation and coalescence in sandy mudstone with prefabricated cross-flaws under uniaxial compression. Eng. Fract. Mech. 2021, 247, 107658. [Google Scholar] [CrossRef]
- Li, K.S.; Zhao, Z.; Ma, D.P.; Liu, C.X.; Zhang, J.P. Acoustic emission and mechanical characteristics of rock-like material containing single crack under uniaxial compression. Arab. J. Sci. Eng. 2022, 47, 4749–4761. [Google Scholar] [CrossRef]
- GB/T 2015-2017; White Portland Cement. Standards Press of China: Beijing, China, 2017.
- GB/T 14684-2022; Sand for Construction. Standards Press of China: Beijing, China, 2022.
- Zhou, X.-P.; Zhang, J.-Z.; Wong, L.N.Y. Experimental study on the growth, coalescence and wrapping behaviors of 3D cross-embedded flaws under uniaxial compression. Rock Mech. Rock Eng. 2018, 51, 1379–1400. [Google Scholar] [CrossRef]
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Feng, P.; Xu, Y.; Dai, F. Effects of dynamic strain rate on the energy dissipation and fragment characteristics of cross-fissured rocks. Int. J. Rock Mech. Min. Sci. 2021, 138, 104600. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of Digital.Image-CorrelationTechniques to Experimental Mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Potyondy, D.O. Simulating stress corrosion with a bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 677–691. [Google Scholar] [CrossRef]
- Yao, D.; Jiang, N.; Wang, X.; Jia, X.; Lv, K. Mechanical behaviour and failure characteristics of rocks with composite defects of different angle fissures around hole. Bull. Eng. Geol. Environ. 2022, 81, 290. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Gao, Y.; Chen, H.; Xie, T. Influence of prefabricated fissure combinations on strength and failure characteristics of rock-like specimens under uniaxial compression. Int. J. Geomech. 2023, 23, 04022279. [Google Scholar] [CrossRef]
- Guo, W.Y.; Zhang, D.X.; Zhao, T.B.; Li, Y.R.; Zhao, Y.Q.; Wang, C.W.; Wu, W.B. Influence of rock strength on the mechanical characteristics and energy evolution law of gypsum-rock combination specimen under cyclic loading-unloading condition. Int. J. Geomech. 2022, 22, 16. [Google Scholar] [CrossRef]
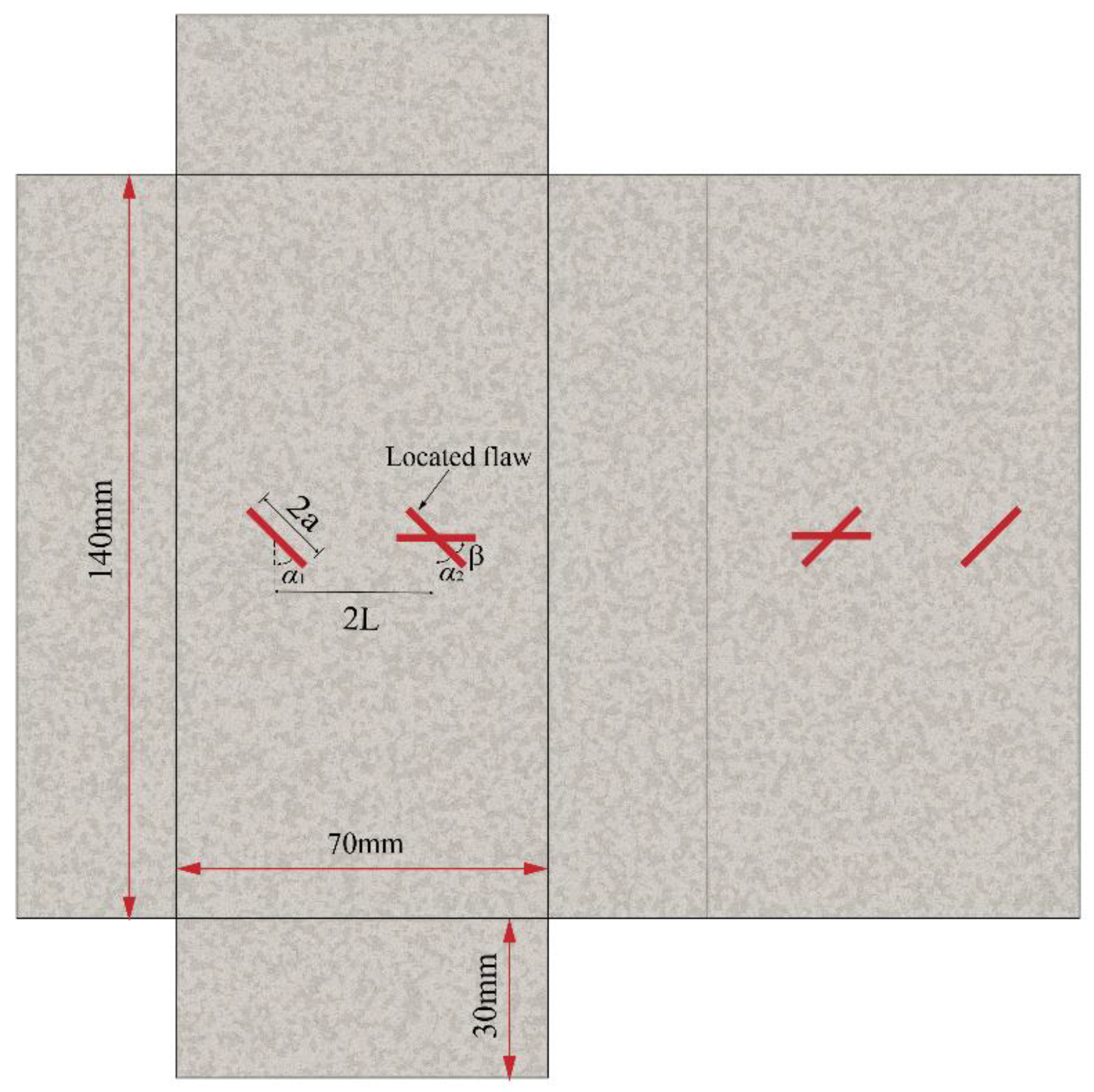




| Specimen | Geometric Angle | Geometrical Length |
|---|---|---|
| Type I: intact sample | / | / |
| Type II | 45°, 0° | 2 = 20 mm, 2 = 30 mm |
| Type III | 45°, 30° | |
| Type IV | 45°, 45° | |
| Type V | 45°, 60° | |
| Type VI | 45°, 90° |
| Materials | Rock-like Materials | Value |
|---|---|---|
| Rock-like materials | Poisson ratio | 0.238 |
| Young’s modulus (GPa) | 14.435 | |
| Uniaxial compressive strength, UCS (MPa) | 39.419 | |
| Particle parameters | R (mm) | 0.6–0.9 |
| Particle stiffness ratio () | 1.15 | |
| Particle friction | 1.6 | |
| Parameters of simulated specimen | Tensile strength (MPa) | 39.6 |
| Cohesion (MPa) | 39.6 | |
| Elastic modulus (MPa) | 18.7 | |
| Particle porosity | 0.04 | |
| Density | 2387 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Wang, K.; Zhou, W.; Yao, Y.; Xie, T. Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks. Appl. Sci. 2024, 14, 823. https://doi.org/10.3390/app14020823
Zhou J, Wang K, Zhou W, Yao Y, Xie T. Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks. Applied Sciences. 2024; 14(2):823. https://doi.org/10.3390/app14020823
Chicago/Turabian StyleZhou, Jie, Kezhong Wang, Weidi Zhou, Yilin Yao, and Tian Xie. 2024. "Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks" Applied Sciences 14, no. 2: 823. https://doi.org/10.3390/app14020823
APA StyleZhou, J., Wang, K., Zhou, W., Yao, Y., & Xie, T. (2024). Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks. Applied Sciences, 14(2), 823. https://doi.org/10.3390/app14020823





