Are There Seven Symbols for the Nucleotide-Based Genetic Code?
Abstract
:1. Introduction
1.1. The Power-Law Phenomena
1.2. The Linguistic Approach in Genome Studies
1.3. The Hypothesis Statements
2. Materials and Methods
2.1. Data
2.2. The Experiment Design
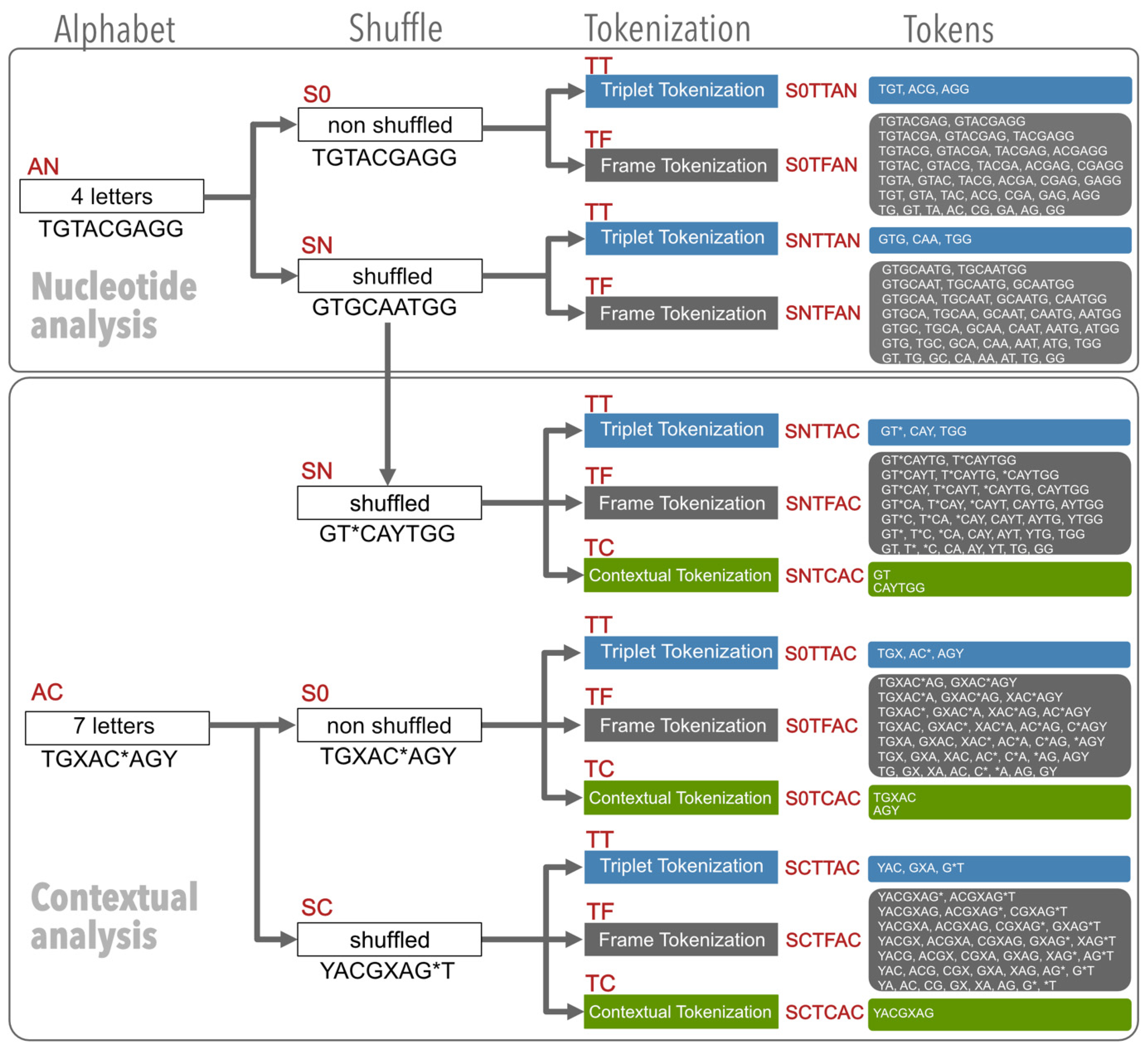
2.2.1. The Nucleotide Analysis
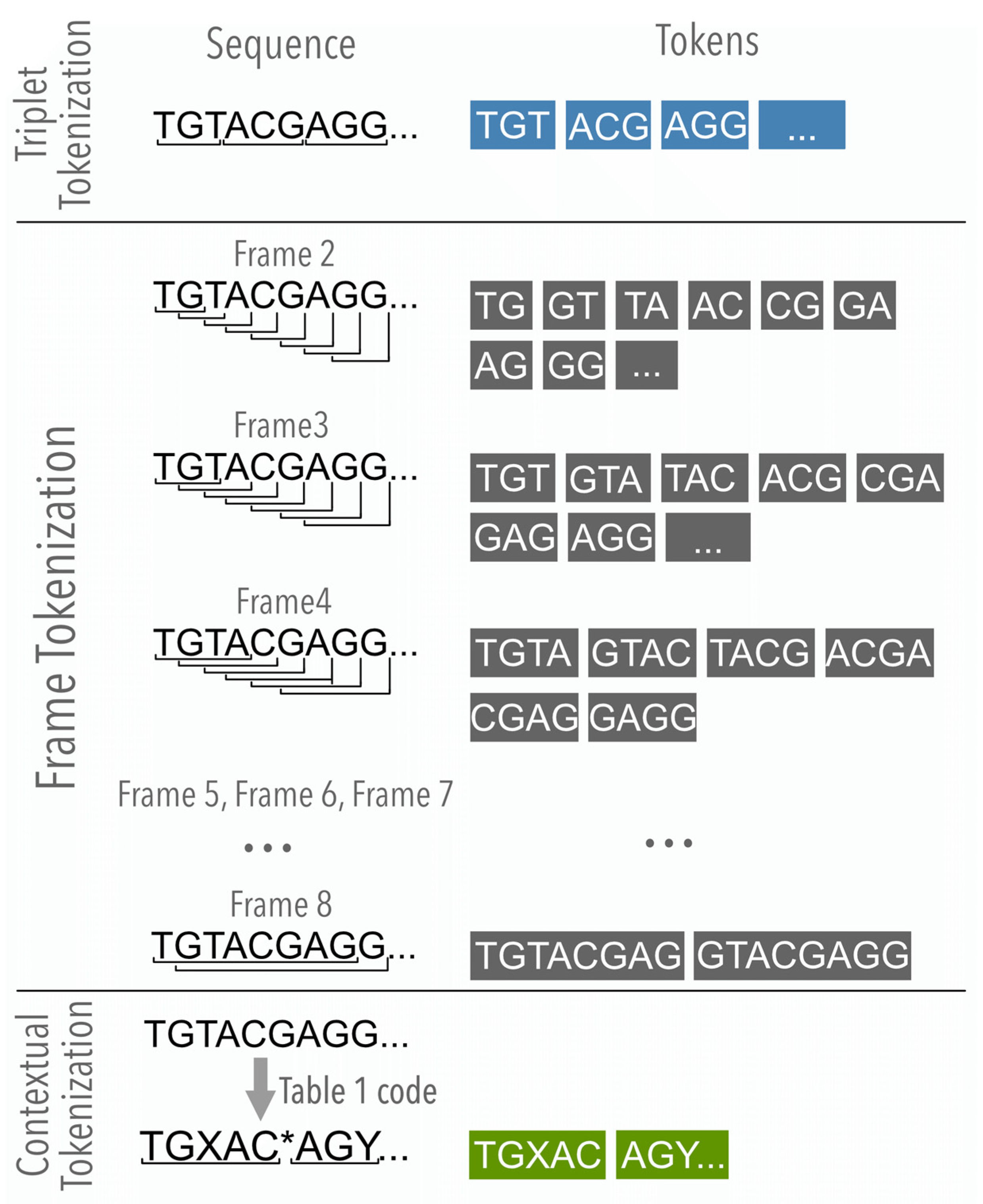
2.2.2. The Contextual Analysis
2.3. Computational Programs and Statistical Tools Applied
3. Results
3.1. The Genomic Texts Analysis
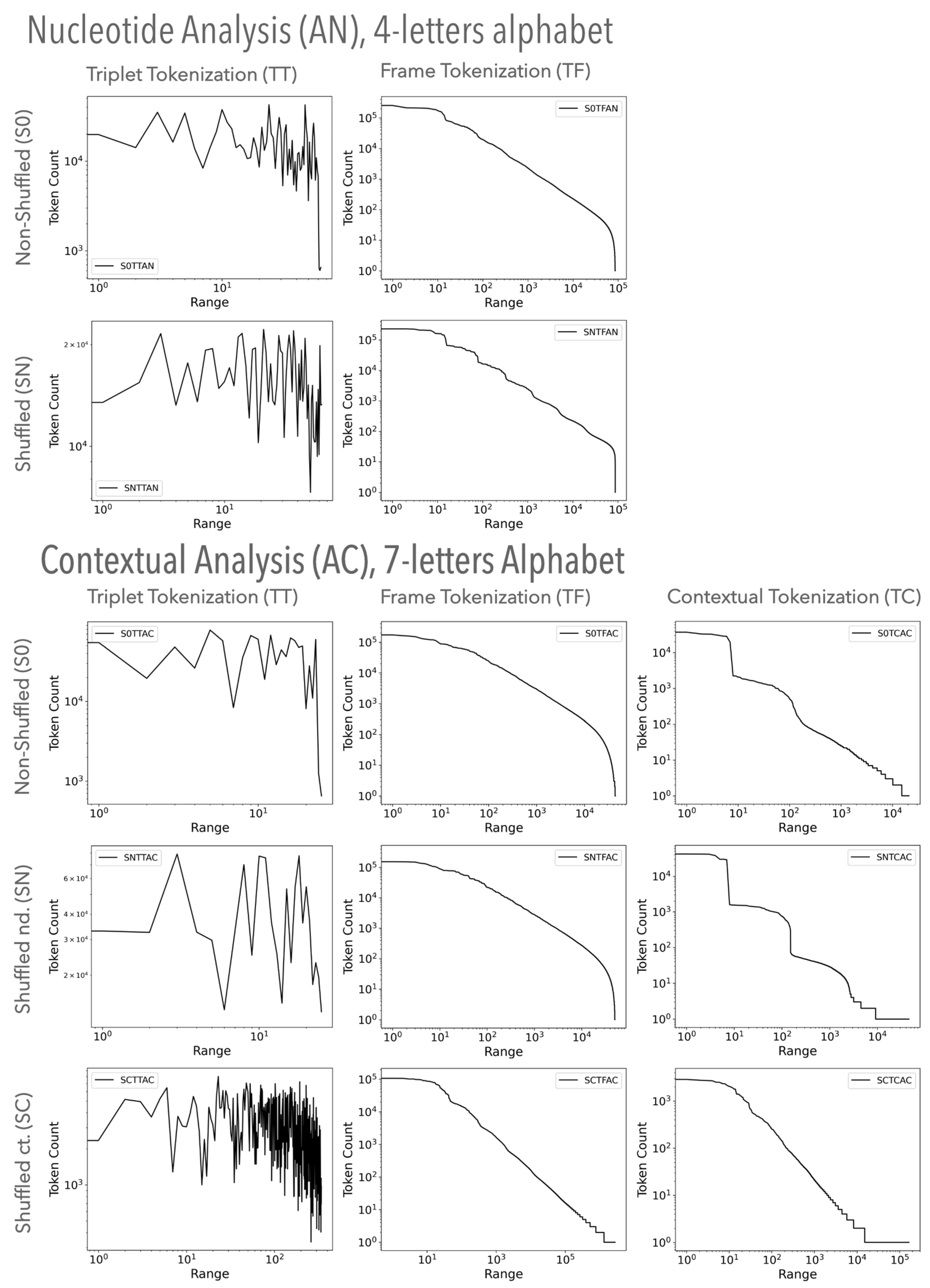
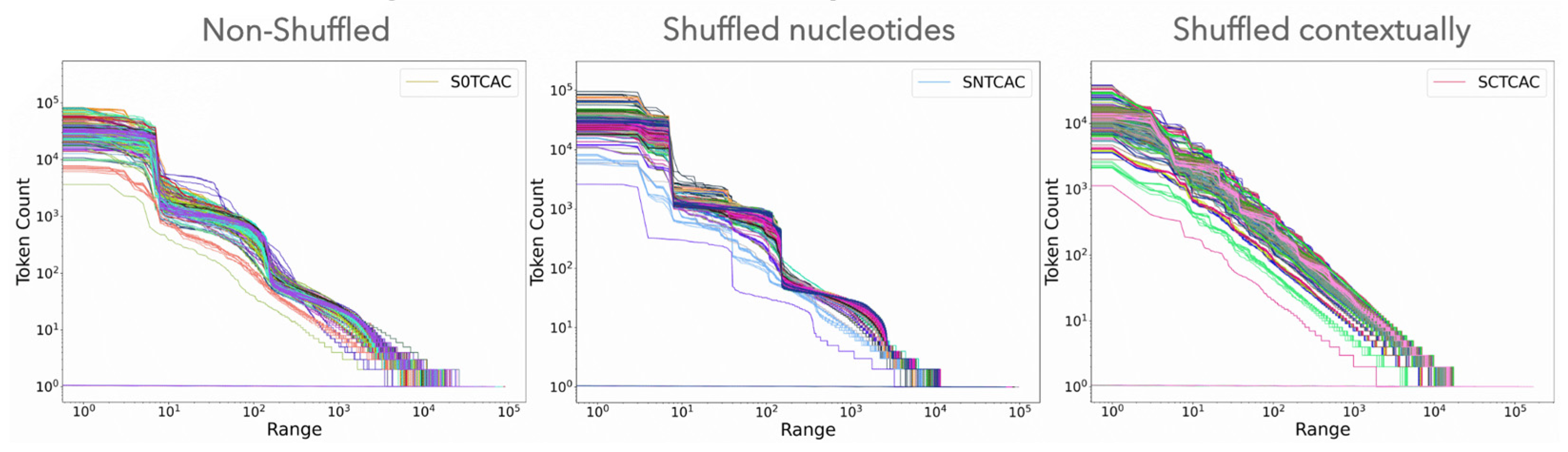
3.1.1. Visual Examination of Genomic Texts
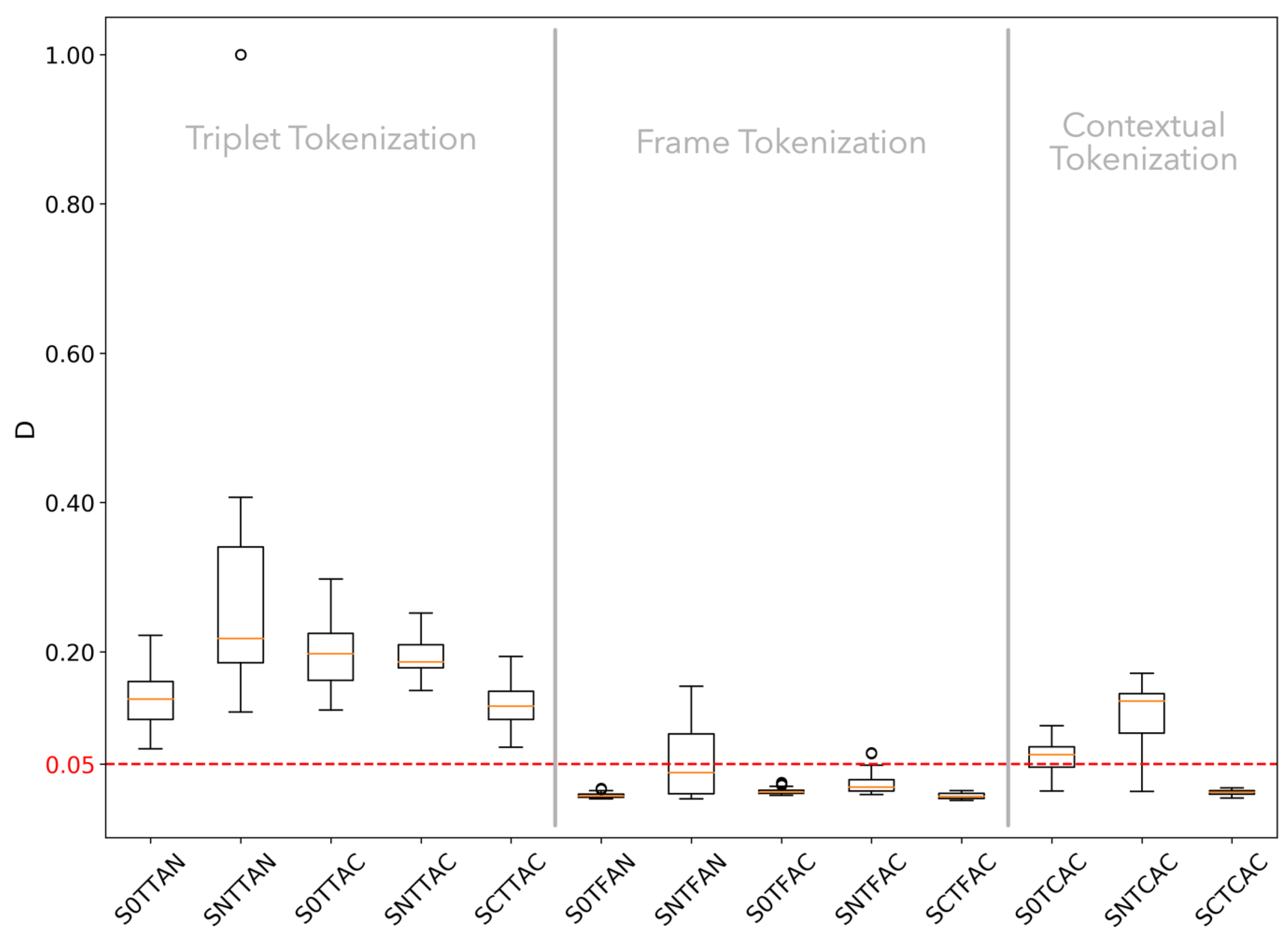
3.1.2. K-S Statistic Test of Genomic Texts
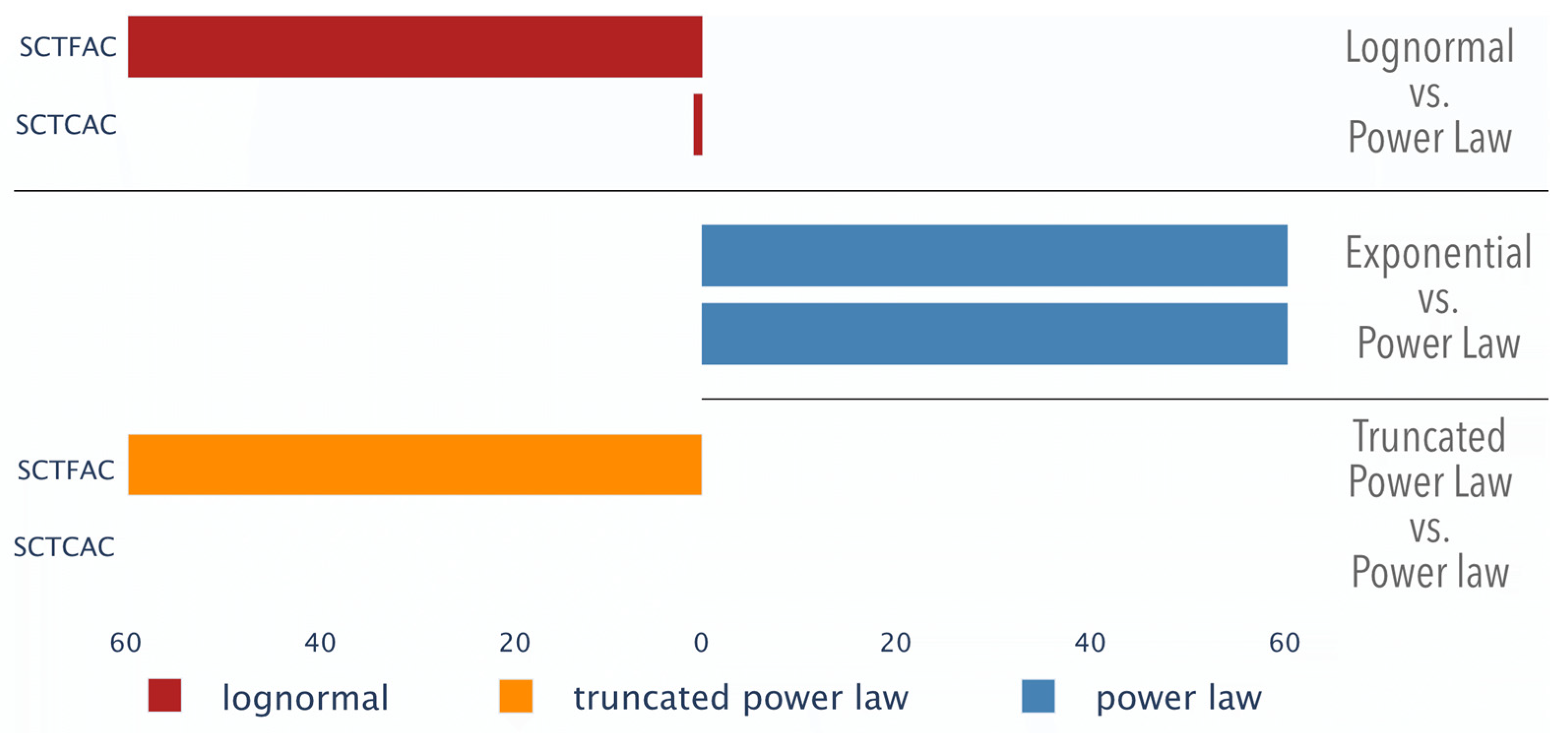
3.1.3. Distribution Comparison of Genomic Texts
3.1.4. Hypothesis Testing
3.2. Random Texts Analysis
3.2.1. Visual Examination of Random Texts
3.2.2. K-S Statistic of Random Texts
3.2.3. Distribution Comparison of Random Texts
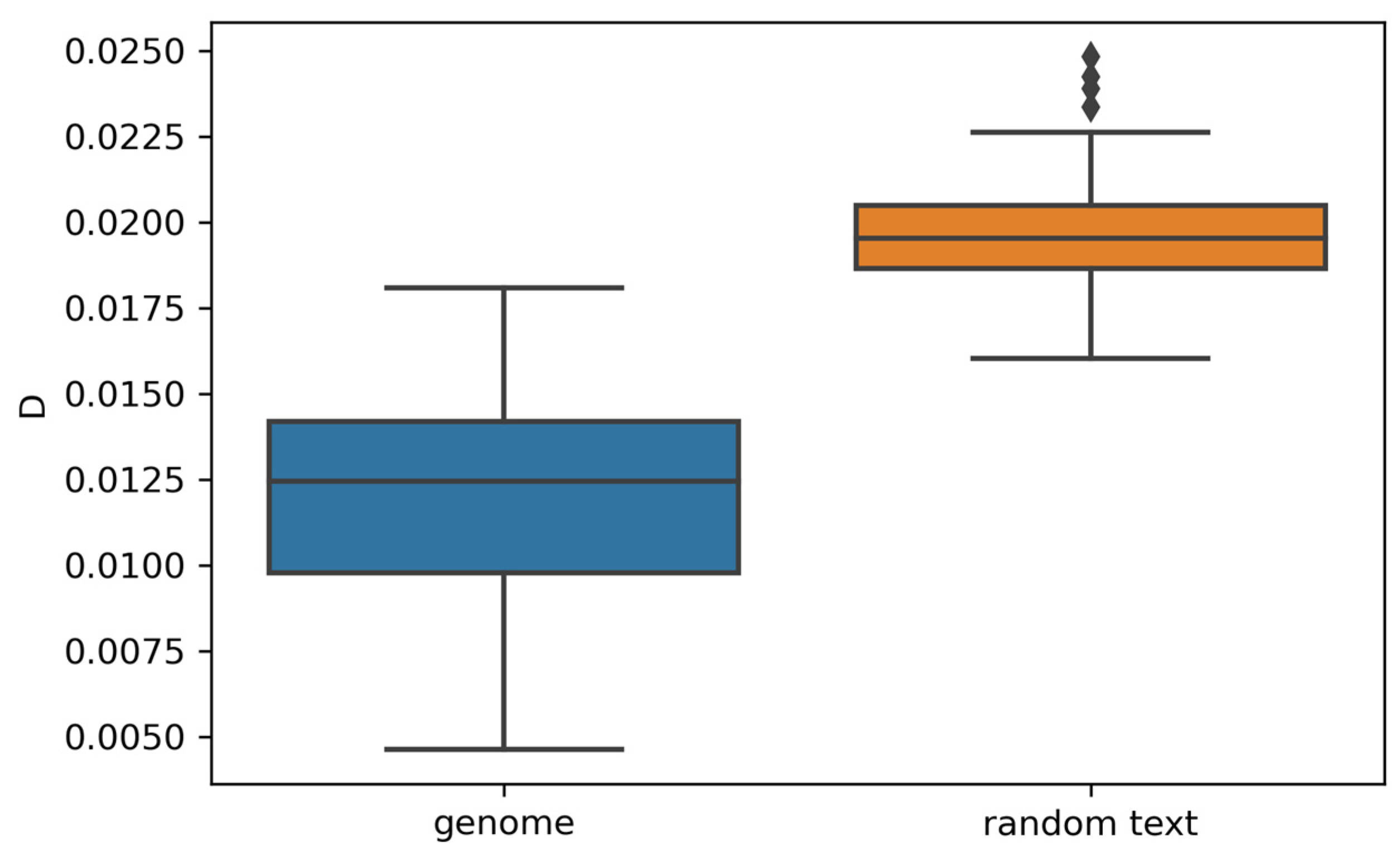
3.3. Random vs. Genomic Texts
3.4. Summary of Results
4. Discussion
- The frequency-range dependency of tokens generated via triplet tokenization consistently fails to follow a power-law distribution, suggesting that the conventional nucleotide sequence tokenization method is inadequate for representing semiotic information in genomic sequences.
- The genomic corpora generated by frame tokenization in most cases followed the Zipf distribution, supporting the claim of hidden informational structures within genomic sequences.
- The excellent power-law performance of shuffled contextual genomic texts (SCTCAC) corroborates our hypothesis that genomic sequences should be analyzed using a seven-character alphabet system.
- The moderate performance of original contextual tokenization genomic corpora (S0TCAC) indicates notable differences between genomic texts and natural language structures.
- Observed differences in word frequency distributions between random texts and genomes provide evidence that our findings regarding genomic sequences are not attributable to random chance.
- These results collectively suggest that novel tokenization methods, particularly those employing a seven-character alphabet, may offer insightful approaches to analyzing the informational content of genomic sequences.
4.1. Triplet Tokenization Does Not Represent Semiotic Information
4.2. Frame Tokenization Detects Semiotic Information
4.3. Contextual Tokenization Represents Semiotic Information
4.4. Differences between Genomic and Natural Languages Texts
4.5. Comparative Analysis of Random Texts and Genomes
4.6. Possible Practical Applications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chapman, S.; Watkins, N. Avalanching and Self Organised Criticality, a paradigm for geomagnetic activity? Space Sci. Rev. 2001, 95, 293–307. [Google Scholar] [CrossRef]
- Manor, A.; Shnerb, N.M. Multiplicative noise and second order phase transitions. Phys. Rev. Lett. 2009, 103, 030601. [Google Scholar] [CrossRef] [PubMed]
- Landini, G. Evidence of linguistic structure in the Voynich manuscript using spectral analysis. Cryptologia 2001, 25, 275–295. [Google Scholar] [CrossRef]
- Smith, R. Investigation of the Zipf-plot of the extinct Meroitic language. arXiv 2008, arXiv:0808.2904. [Google Scholar]
- Ferrer-I-Cancho, R.; Elvevåg, B. Random texts do not exhibit the real ZIPF’s Law-Like rank distribution. PLoS ONE 2010, 5, e9411. [Google Scholar] [CrossRef]
- Gustafson, K.B.; Proctor, J.L. Identifying spatio-temporal dynamics of Ebola in Sierra Leone using virus genomes. J. R. Soc. Interface 2017, 14, 20170583. [Google Scholar] [CrossRef]
- Klaus, A.; Yu, S.; Plenz, D. Statistical analyses support power law distributions found in neuronal avalanches. PLoS ONE 2011, 6, e19779. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.M.; Machado, J.A.T. Power law behaviour in complex systems. Entropy 2018, 20, 671. [Google Scholar] [CrossRef]
- Huynen, M.A.; van Nimwegen, E. The frequency distribution of gene family sizes in complete genomes. Mol. Biol. Evol. 1998, 15, 583–589. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, W.; Lages, N.; Borcherds, W.; Wang, D. Relationship between gene duplicability and diversifiability in the topology of biochemical networks. BMC Genom. 2014, 15, 577. [Google Scholar] [CrossRef]
- Baek, S.K.; Bernhardsson, S.; Minnhagen, P. Zipf’s law unzipped. New J. Phys. 2011, 13, 043004. [Google Scholar] [CrossRef]
- Jung, H.C.; Kim, S.H.; Lee, J.H.; Kim, J.H.; Han, S.W. Gene Regulatory Network Analysis for Triple-Negative Breast neoplasms by using gene expression data. J. Breast Cancer 2017, 20, 240. [Google Scholar] [CrossRef]
- Hansen, M.E.B.; Kulathinal, R.J. Sex-Biased networks and nodes of sexually antagonistic conflict in Drosophila. Int. J. Evol. Biol. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Bornholdt, S.; Kauffman, S. Ensembles, dynamics, and cell types: Revisiting the statistical mechanics perspective on cellular regulation. J. Theor. Biol. 2019, 467, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Kalankesh, L.R.; Stevens, R.; Brass, A. The language of gene ontology: A Zipf’s law analysis. BMC Bioinform. 2012, 13, 127. [Google Scholar] [CrossRef]
- Monod, J. Chance and Necessity; Vintage Books: New York, NY, USA, 1971. [Google Scholar]
- Pollack, R. Signs of Life: The Language and Meanings of DNA; Penguin: Harmondsworth, UK, 1995. [Google Scholar]
- Ratner, V.A. The genetic language: Grammar, semantics, evolution. Genetika 1993, 29, 709–719. [Google Scholar]
- Yandell, M.D.; Majoros, W.H. Genomics and natural language processing. Nat. Rev. Genet. 2002, 3, 601–610. [Google Scholar] [CrossRef]
- Zipf, K.G. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology; Addison-Wesley Press: New York, NY, USA, 1949. [Google Scholar]
- Cancho, R.F.I.; Solé, R.V. Least effort and the origins of scaling in human language. Proc. Natl. Acad. Sci. USA 2003, 100, 788–791. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.K.; Simons, M.; Stanley, H.E. Linguistic features of noncoding DNA sequences. Phys. Rev. Lett. 1994, 73, 3169–3172. [Google Scholar] [CrossRef]
- Czirók, A.; Stanley, H.E.; Vicsek, T. Possible origin of power-law behavior inn-tuple Zipf analysis. Phys. Rev. E 1996, 53, 6371–6375. [Google Scholar] [CrossRef]
- Gan, X.; Wang, D.; Han, Z. N-Tuple ZIPF analysis and modeling for language, computer program and DNA. arXiv 2009. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Elsner, J.B.; Tsonis, P.A. Is DNA a language? J. Theor. Biol. 1997, 184, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Naranan, S.; Balasubrahmanyan, V.K. Information Theory and Algorithmic Complexity: Applications to linguistic discourses and DNA sequences as complex systems Part I: Efficiency of the genetic code of DNA. J. Quant. Linguist. 2000, 7, 129–151. [Google Scholar] [CrossRef]
- Malevergne, Y.; Pisarenko, V.; Sornette, D. Gibrat’s Law for Cities: Uniformly most powerful unbiased test of the pareto against the lognormal. SSRN Electron. J. 2009, 09-40. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. powerlaw: A Python Package for Analysis of Heavy-Tailed Distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef]
- De Boer, B. Self-organization in vowel systems. J. Phon. 2000, 28, 441–465. [Google Scholar] [CrossRef]
- DeGiuli, E. Random Language Model. Phys. Rev. Lett. 2019, 122, 128301. [Google Scholar] [CrossRef]
- Ke, J.; Holland, J.H. Language Origin from an Emergentist Perspective. Appl. Linguist. 2006, 27, 691–716. [Google Scholar] [CrossRef]
- Grzybek, P.; Köhler, R. Exact Methods in the Study of Language and Text; De Gruyter Mouton: Berlin, Germany, 2007. [Google Scholar] [CrossRef]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Sci. Nat. 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle: A Principle of Natural Self-Organization; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Joyce, G.F. RNA evolution and the origins of life. Nature 1989, 338, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Hockett, C. The problem of universals in language. In Universals of Language; Greenberg, J.H., Ed.; MIT Press: Cambridge, MA, USA, 1963; pp. 1–29. [Google Scholar]
- Milewski, T. Jezykoznawstwo; Panstwowe Wydawnictwo Naukowe: Warsaw, Poland, 1967. [Google Scholar]
- Martinet, A. Double articulation as a criterion of linguisticity. Lang. Sci. 1984, 6, 31–38. [Google Scholar] [CrossRef]
- Barbieri, M. The Organic Codes: An Introduction to Semantic Biology; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Barbieri, M. Code Biology: A New Science of Life; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Miller, G.A.; Newman, E.; Friedman, E. Some effects of intermittent silence. Am. J. Psychol. 1957, 70, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B. Information Theory and Psycholinguistics; Oldfield, R.C., Marchall, J.C., Eds.; Penguin Books: Harmondsworth, UK, 1968. [Google Scholar]
- Li, W. Random texts exhibit Zipf’s-law-like word frequency distribution. IEEE Trans. Inf. Theory 1992, 38, 1842–1845. Available online: http://sfi-edu.s3.amazonaws.com/sfi-edu/production/uploads/sfi-com/dev/uploads/filer/a5/07/a507be1c-7232-422b-8657-d24dcf24a35d/91-03-016.pdf (accessed on 1 August 2024). [CrossRef]
- Rapoport, A. Zipf’s law re-visited. Quant. Linguist. 1982, 16, 1–28. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Ferrer-I-Cancho, R.; Forns, N.; Hernández-Fernández, A.; Bel-Enguix, G.; Baixeries, J. The challenges of statistical patterns of language: The case of Menzerath’s law in genomes. Complexity 2012, 18, 11–17. [Google Scholar] [CrossRef]
- Piantadosi, S.T. Zipf’s word frequency law in natural language: A critical review and future directions. Psychon. Bull. Rev. 2014, 21, 1112–1130. [Google Scholar] [CrossRef]


| Codon Set | Amino Acid | Codon Set | Amino Acid |
|---|---|---|---|
| AC * | Threonine | AAX | Asparagine |
| CC * | Proline | CAX | Histidine |
| GC * | Alanine | GAX | Aspartic acid |
| GG * | Glycine | TGX | Cysteine |
| GT * | Valine | TTX | Phenylalanine |
| CG * | Arginine | AGX | Serine |
| CT * | Leucine | ATX | Isoleucine |
| UC * | Serine | TAX | Tyrosine |
| AAY | Lysine | ATG | Methionine |
| CAY | Glutamine | TGG | Tryptophan |
| GAY | Glutamic acid | ATA | Isoleucine |
| AGY | Arginine | TGA | Stop |
| TTY | Leucine | ||
| TAY | Stop |
| Shuffle | Tokenization | Alphabet | |||
|---|---|---|---|---|---|
| S | T | A | |||
| 0 | non-shuffled | T | triplet | N | nucleotide |
| N | shuffled nucleotides | F | frame | C | contextual |
| C | shuffled contextually | C | contextual | ||
| Nucleotide analysis: | |||||
| (A) triplet tokenization | |||||
| S0TTAN—the original (non-shuffled) text tokenized by triplet tokenization and analyzed at the nucleotide level | |||||
| SNTTAN—the shuffled text tokenized by triplet tokenization and analyzed at the nucleotide level | |||||
| (B) frame tokenization | |||||
| S0TFAN—the original text tokenized via frame tokenization and analyzed at the nucleotide level | |||||
| SNTFAN—the text shuffled on the nucleotide level, then tokenized with the frame method and analyzed at the nucleotide level | |||||
| Contextual analysis: | |||||
| (A) triplet tokenization | |||||
| S0TTAC—the original text tokenized according to triplet tokenization and contextually analyzed | |||||
| SNTTAC—the text shuffled at the nucleotide level, then translated into the 7-letter alphabet and tokenized by triplet tokenization | |||||
| SCTTAC—the text contextually analyzed (using the 7-letter alphabet), then shuffled and subjected to triplet tokenization | |||||
| (B) frame tokenization | |||||
| S0TFAC—the non-shuffled text translated into the 7-letter alphabet and then tokenized by the frame method | |||||
| SNTFAC—the original (using the 4-letter alphabet) text shuffled at the nucleotide level; next contextually analyzed (using the 7-letter alphabet) and then tokenized by the frame method | |||||
| SCTFAC—the text contextually analyzed (the 7-letter alphabet) and then shuffled, tokenized by the frame method | |||||
| (C) contextual tokenization | |||||
| S0TCAC—the original text contextually analyzed (using the 7-letter alphabet) and tokenized (by the “any nucleotide” character) | |||||
| SNTCAC—the original text shuffled at the nucleotide level, then contextually analyzed (using the 7-letter alphabet) and contextually tokenized | |||||
| SCTCAC—the text contextually analyzed (using the 7-letter alphabet), then shuffled and contextually tokenized | |||||
| Random Texts | Genomes | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PL Fit | % PT | % EXP | % LN | Visual | No | Analysis | No | Visual | % LN | % EXP | % PT | PL Fit | ||
| - | --- | --- | --- | - | --- | 0/60 | S0TTAN | 0/60 | --- | - | --- | --- | --- | - |
| - | --- | --- | --- | - | --- | 0/60 | SNTTAN | 0/60 | --- | - | --- | --- | --- | - |
| - | --- | --- | --- | - | --- | 0/60 | S0TTAC | 0/60 | --- | - | --- | --- | --- | - |
| - | --- | --- | --- | - | --- | 0/60 | SNTTAC | 0/60 | --- | - | --- | --- | --- | - |
| - | --- | --- | --- | - | --- | 0/60 | SCTTAC | 0/60 | --- | - | --- | --- | --- | - |
| - | --- | --- | --- | + | --- | 0/60 | S0TFAN | 60/60 | 0.008 ± 0.003 | +++ | 10% | 0% | 100% | +++ |
| - | --- | --- | --- | + | --- | 0/60 | SNTFAN | 33/60 | 0.019 ± 0.014 | ++ | 3% | 0% | 94% | + |
| - | --- | --- | --- | ++ | --- | 0/60 | S0TFAC | 60/60 | 0.013 ± 0.004 | +++ | 32% | 0% | 100% | ++ |
| - | --- | --- | --- | ++ | --- | 0/60 | SNTFAC | 58/60 | 0.022 ± 0.010 | ++ | 12% | 0% | 100% | + |
| - | 100% | 0% | 100% | +++ | 0.017 ± 0.000 | 60/60 | SCTFAC | 60/60 | 0.008 ± 0.004 | +++ | 28% | 0% | 100% | +++ |
| - | --- | --- | --- | + | --- | 0/60 | S0TCAC | 19/60 | 0.038 ± 0.010 | + | 26% | 0% | 5% | + |
| - | --- | --- | --- | +/− | --- | 0/60 | SNTCAC | 4/60 | 0.029 ± 0.011 | +/- | 0% | 0% | 0% | - |
| ++ | 0% | 0% | 2% | +++ | 0.020 ± 0.002 | 60/60 | SCTCAC | 60/60 | 0.012 ± 0.003 | +++ | 0% | 0% | 88% | +++ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kłóś, A.; Płonka, P.M.; Baczyński, K. Are There Seven Symbols for the Nucleotide-Based Genetic Code? Appl. Sci. 2024, 14, 9176. https://doi.org/10.3390/app14209176
Kłóś A, Płonka PM, Baczyński K. Are There Seven Symbols for the Nucleotide-Based Genetic Code? Applied Sciences. 2024; 14(20):9176. https://doi.org/10.3390/app14209176
Chicago/Turabian StyleKłóś, Adam, Przemysław M. Płonka, and Krzysztof Baczyński. 2024. "Are There Seven Symbols for the Nucleotide-Based Genetic Code?" Applied Sciences 14, no. 20: 9176. https://doi.org/10.3390/app14209176
APA StyleKłóś, A., Płonka, P. M., & Baczyński, K. (2024). Are There Seven Symbols for the Nucleotide-Based Genetic Code? Applied Sciences, 14(20), 9176. https://doi.org/10.3390/app14209176






