High-Precision Elastoplastic Four-Node Quadrilateral Shell Element
Abstract
:1. Introduction
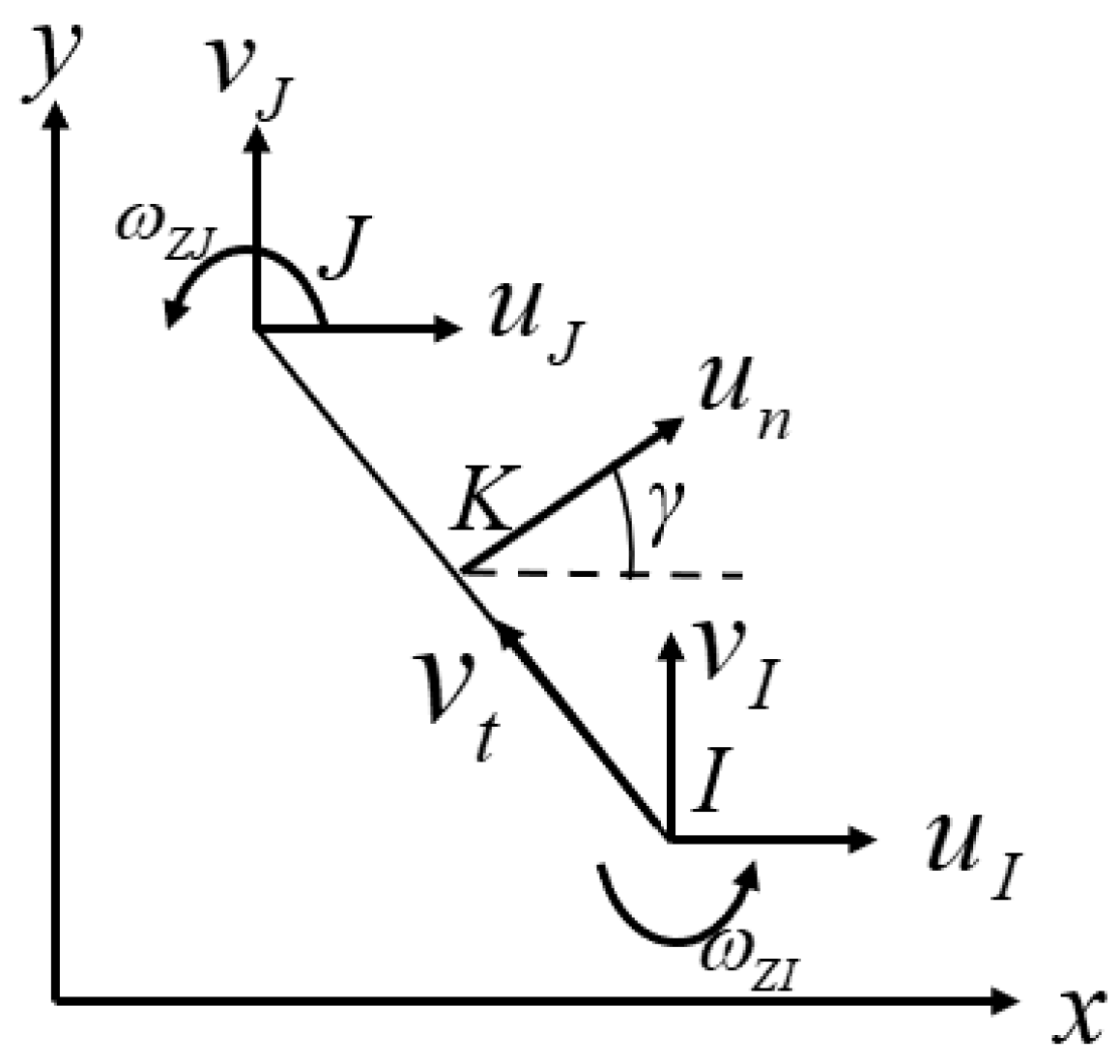
2. Introduction to DOF of Rotation around Element Normal
3. Assumed Strain Rate Interpolation
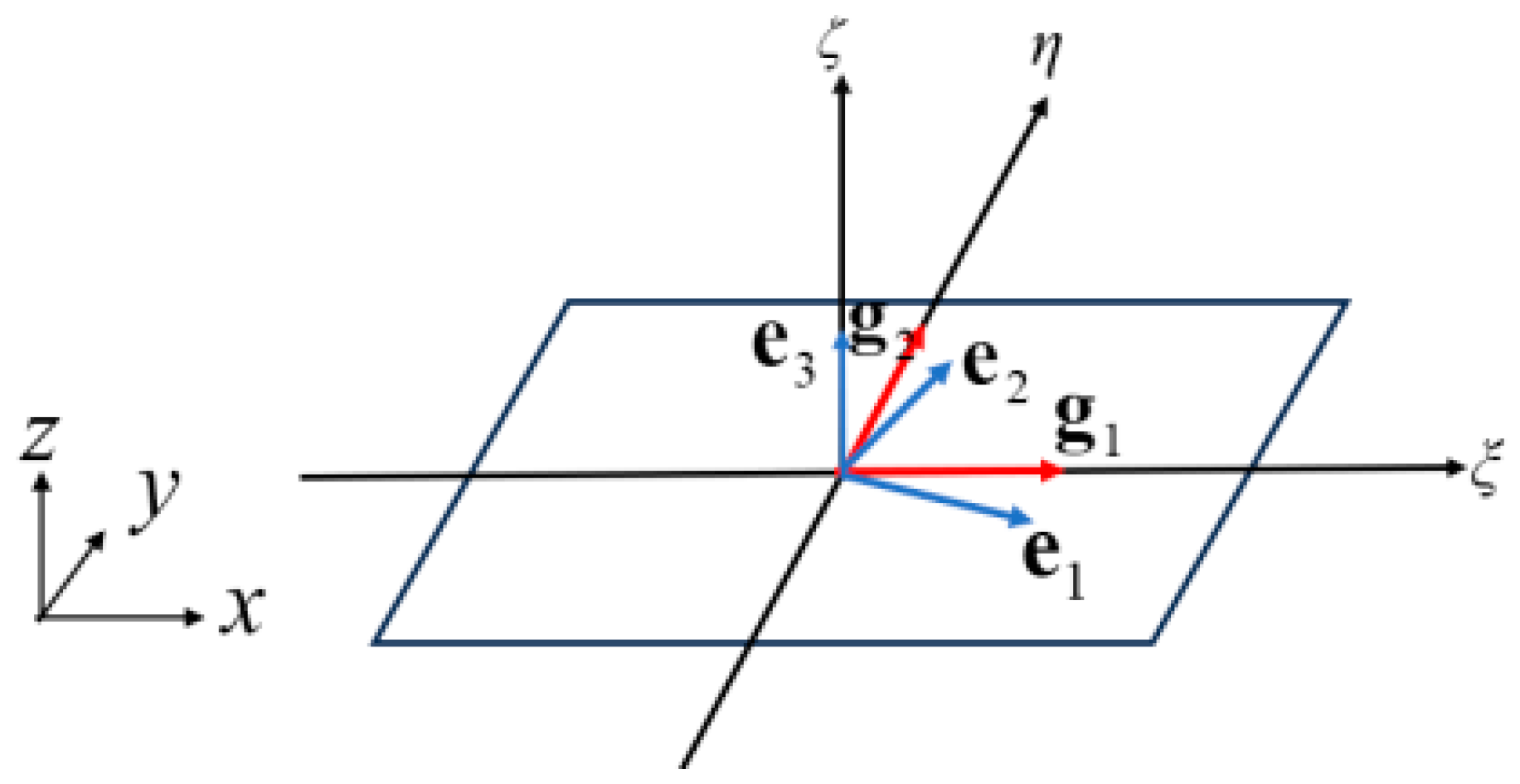
3.1. In-Plane Strainrate Interpolation
3.2. Transverse Shear–Velocity–Strain Interpolation
3.3. Elimination of Corotational Zero-Energy Mode
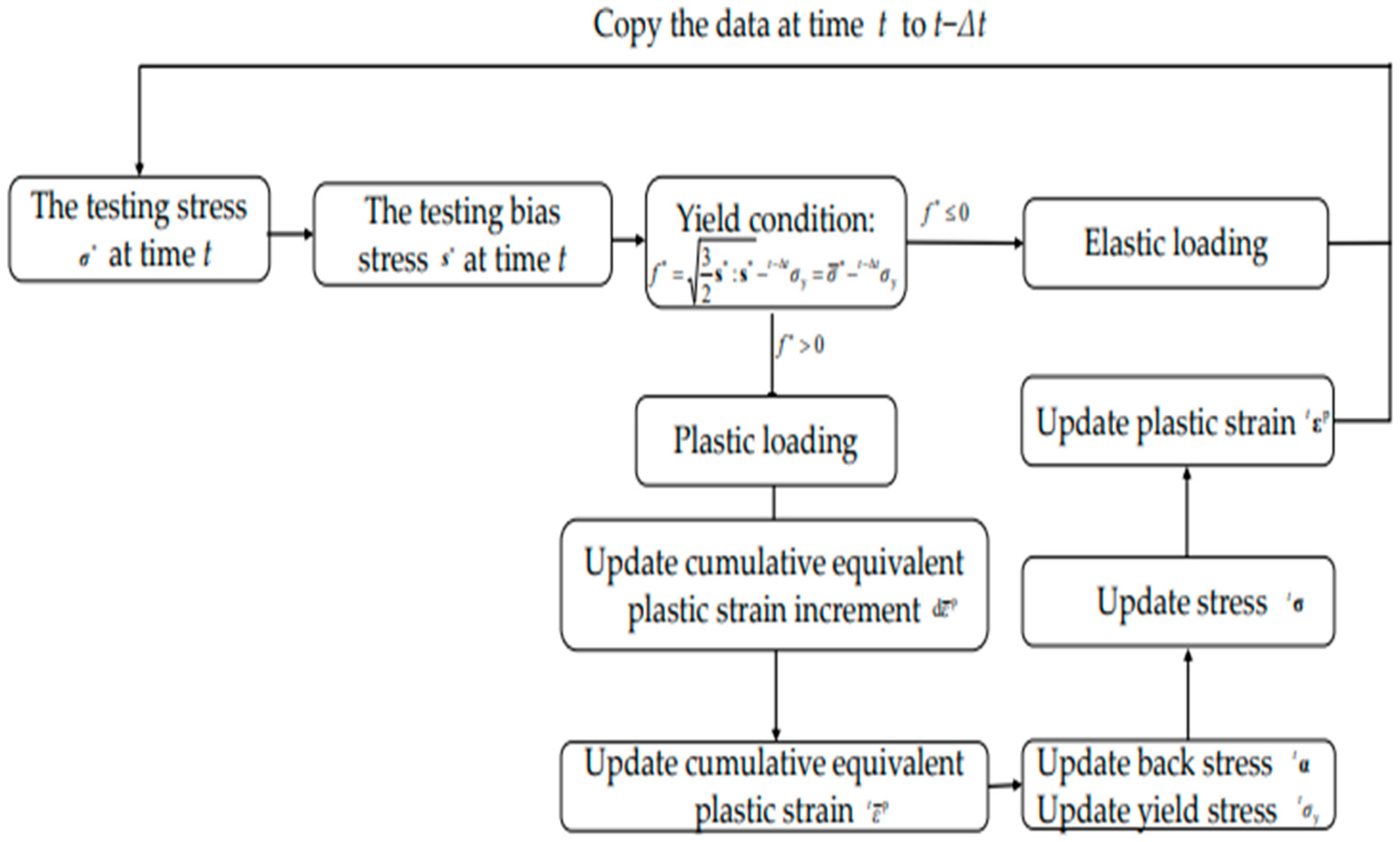
4. Plastic Analysis
5. Numerical Results
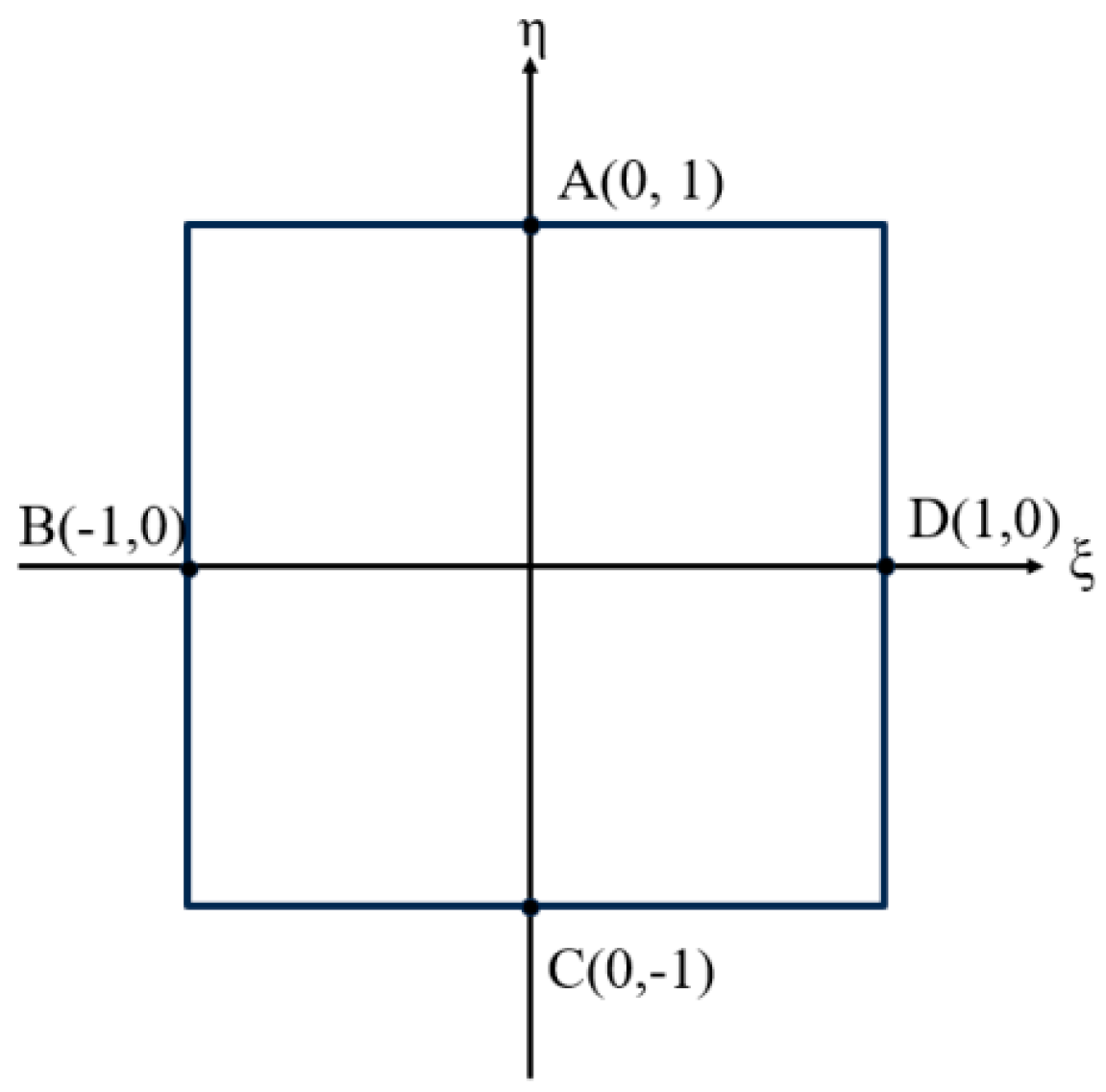
5.1. In-Plane Patch Test
5.2. Bending Patch Test
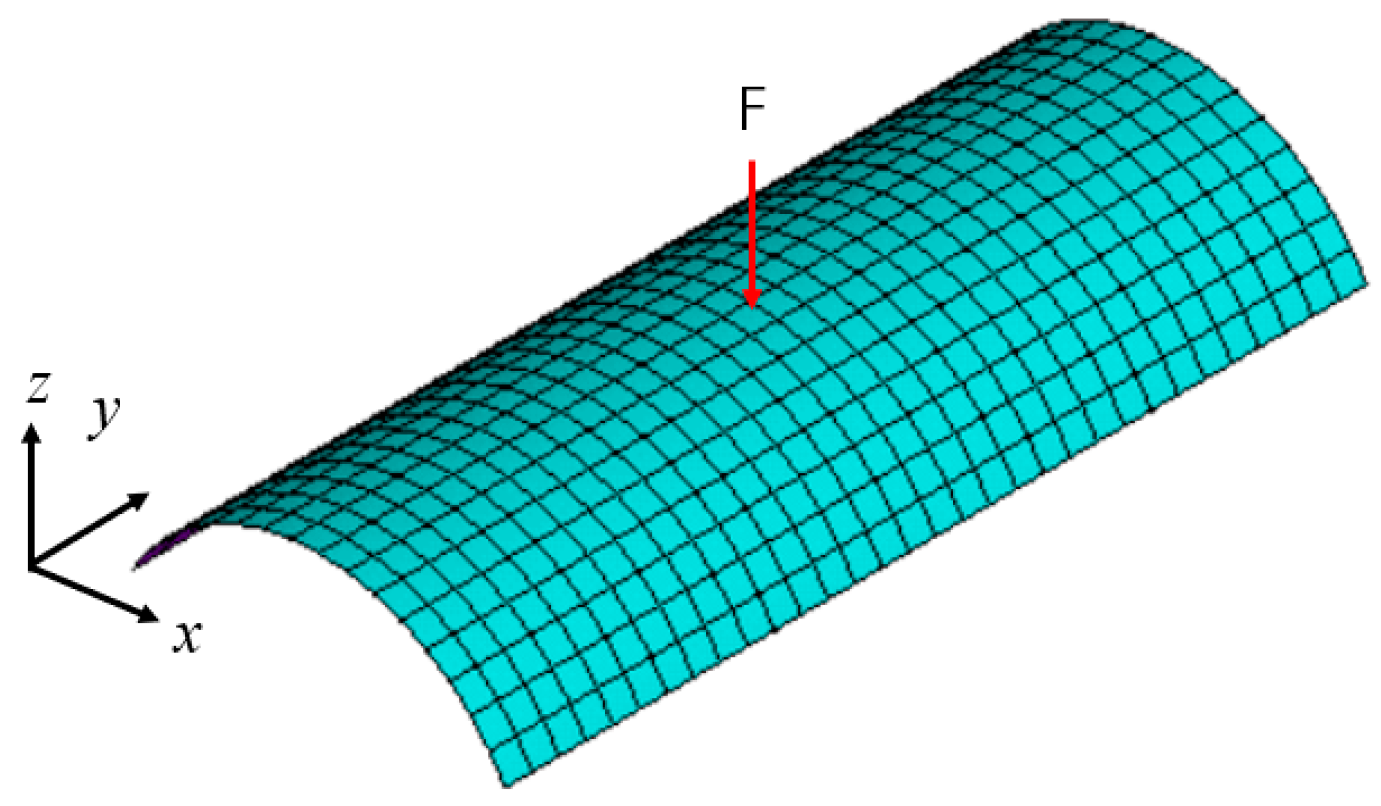
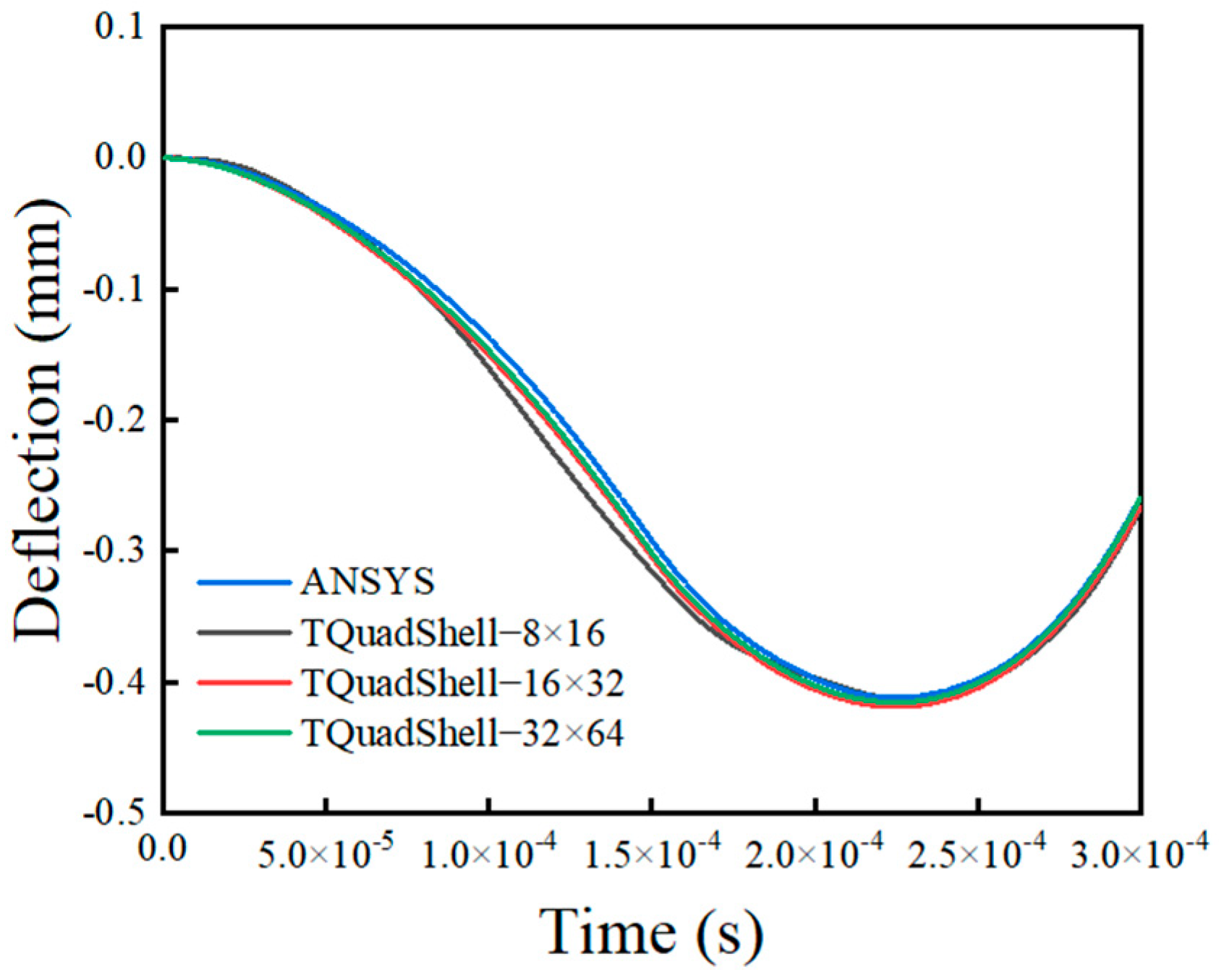
5.3. Cylindrical Shells Subjected to Impact Loads
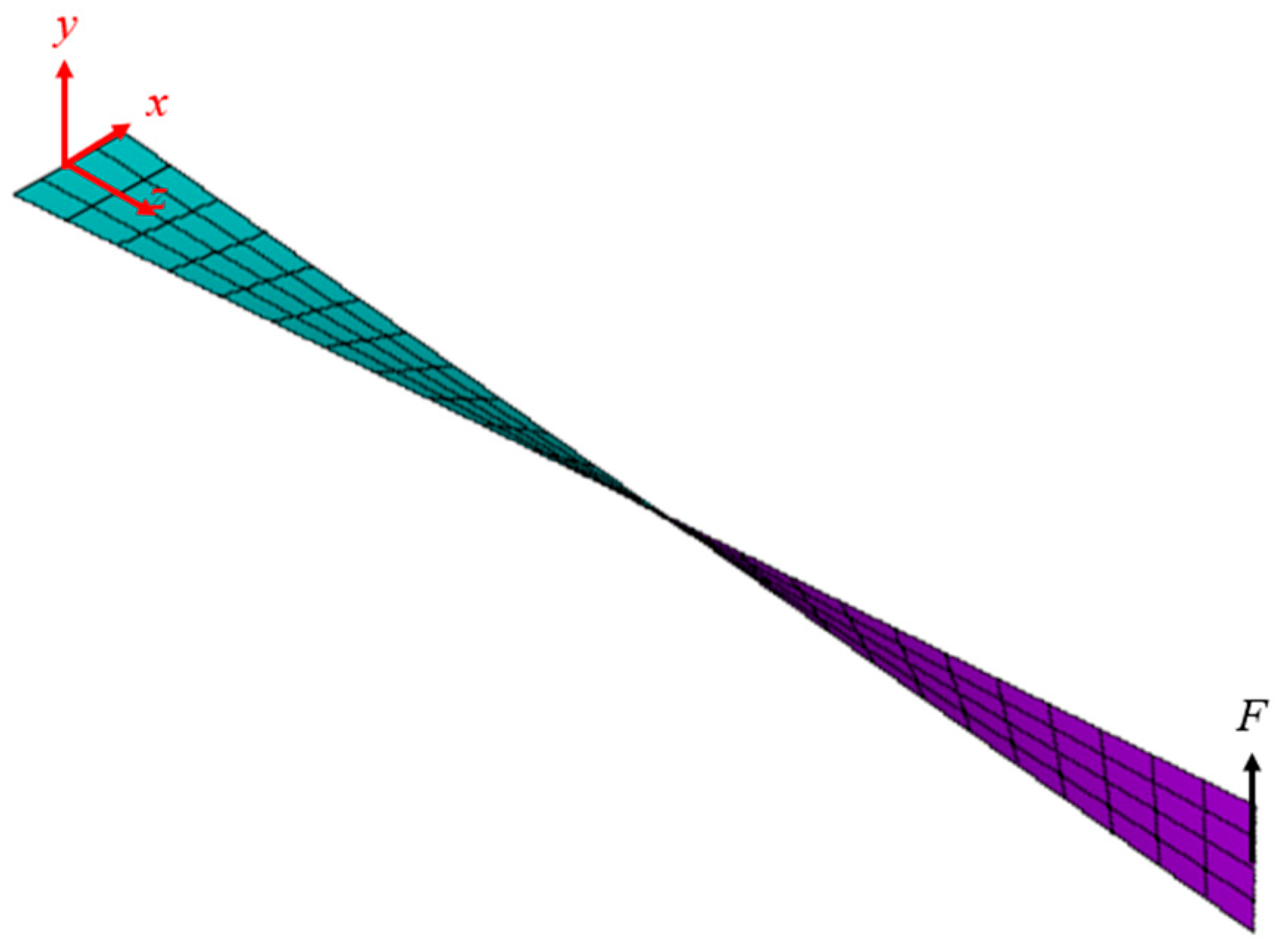
5.4. Twisted Cantilever Beam Subjected to Step Load
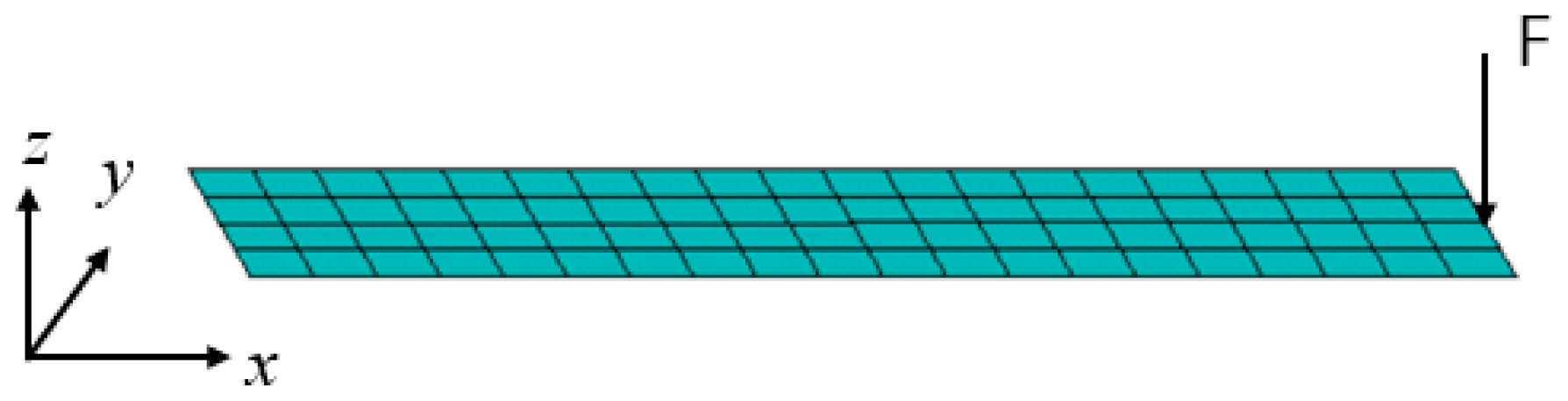
5.5. Rectangular Sheet Subjected to Impact Loads
5.6. Ideal Elastic–Plastic Rectangular Sheet Subjected to Impact Loads
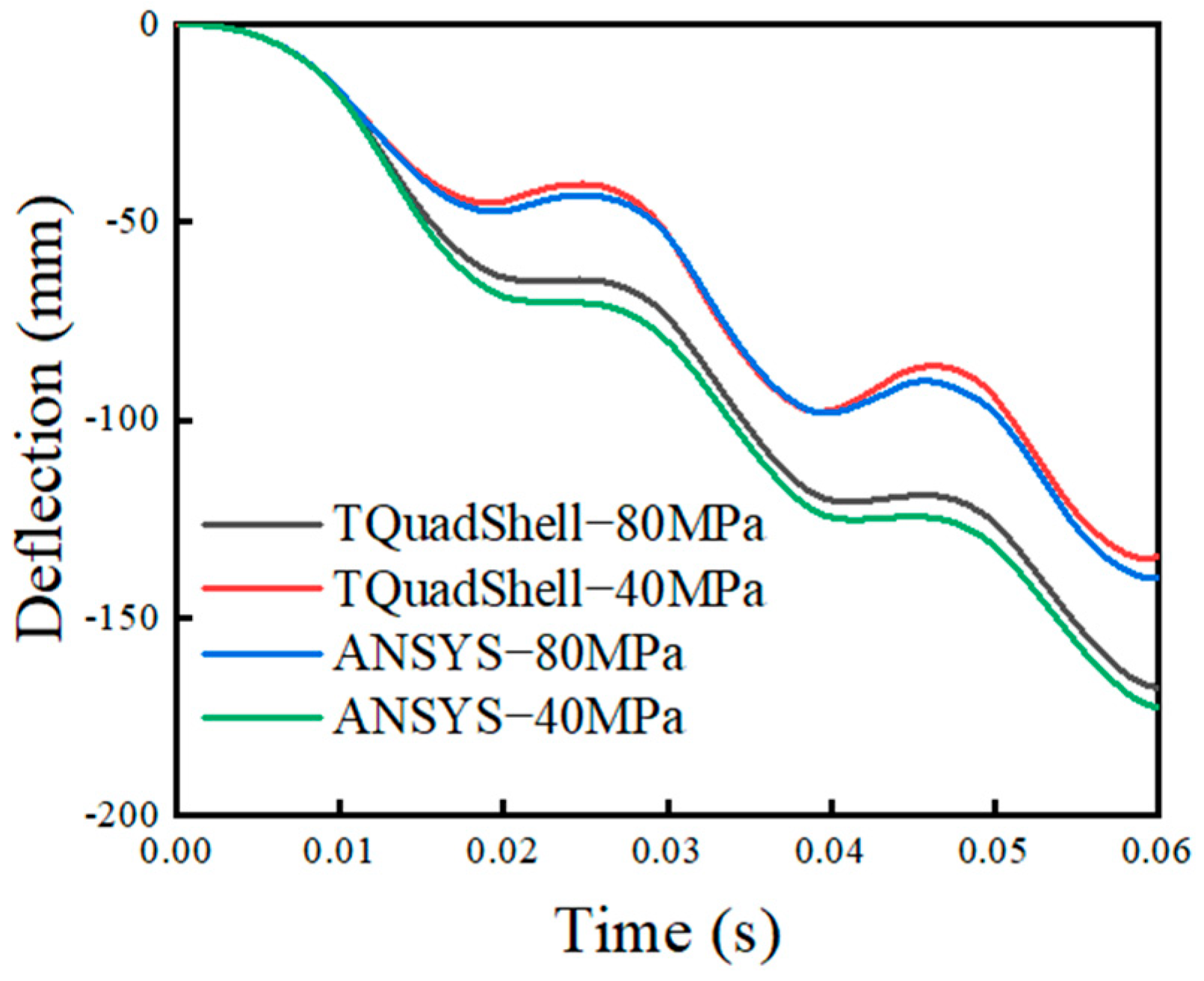
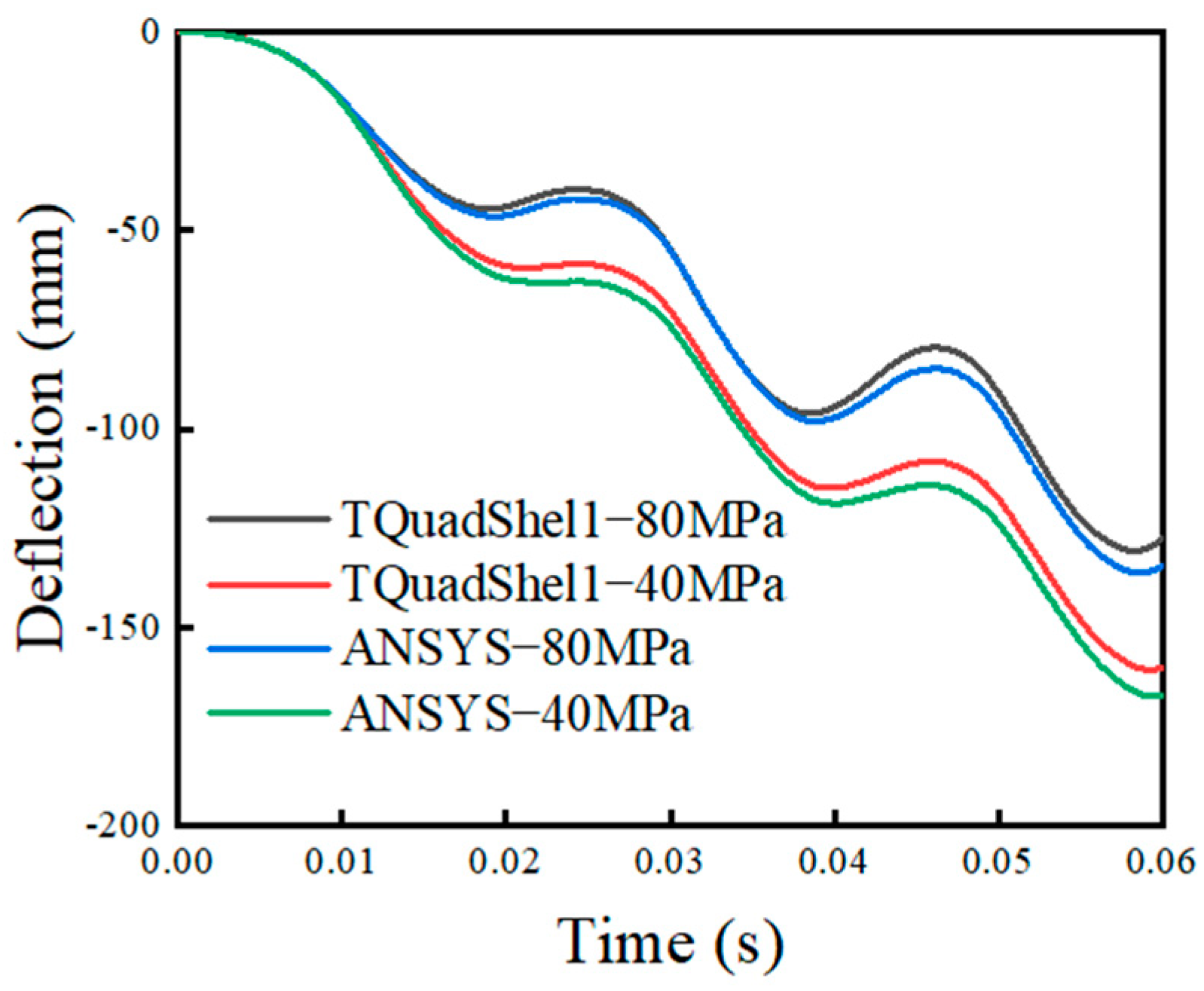
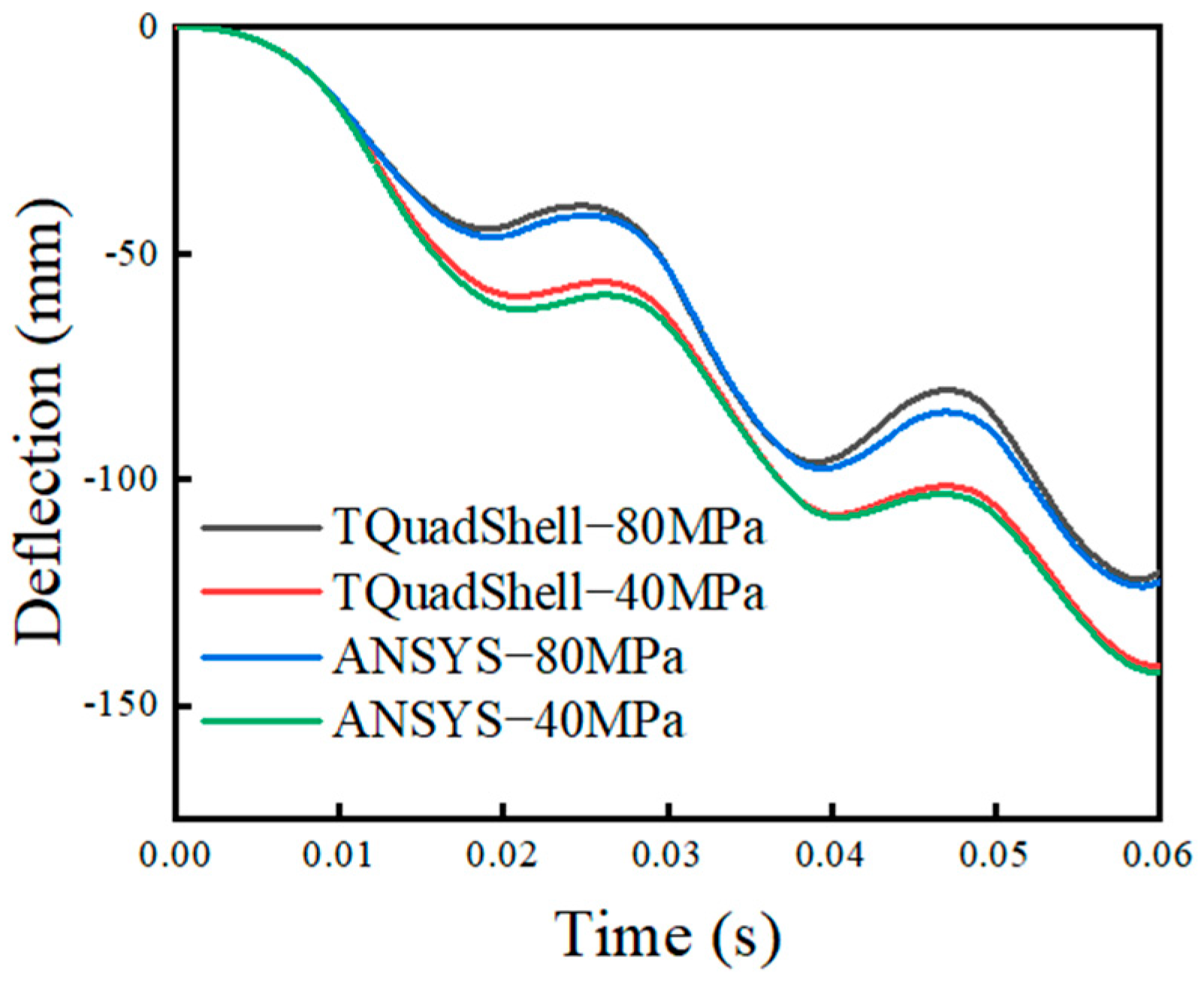
5.7. Isotropically Strengthened and Motion-Strengthened Elastoplastic Rectangular Thin Plates Subjected to Impact Loads
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dvorkin, E.N.; Bathe, K.J. A continuum mechanics based four-node shell element for general non-linear analysis. Eng. Comput. 1984, 1, 77–88. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Q. Corotational nonlinear analyses of laminated shell structures using a 4-node quadrilateral flat shell element with drilling stiffness. Acta Mech. 2014, 30, 418–429. [Google Scholar] [CrossRef]
- Ahmed, A.; Kapuria, S. A four-node facet shell element for laminated shells based on the third order zigzag theory. Compos. Struct. 2016, 158, 112–127. [Google Scholar] [CrossRef]
- Versino, D.; Gherlone, M.; Di Sciuva, M. Four-node shell element for doubly curved multilayered composites based on the refined zigzag theory. Compos. Struct. 2014, 118, 392–402. [Google Scholar] [CrossRef]
- Sussman, T.; Bathe, K.J. 3D-shell elements for structures in large strains. Comput. Struct. 2013, 122, 2–12. [Google Scholar] [CrossRef]
- Kim, D.N.; Bathe, K.J. A triangular six-node shell element. Comput. Struct. 2009, 87, 1451–1460. [Google Scholar] [CrossRef]
- Videla, J.; Natarajan, S.; Bordas, S.P.A. A new locking-free polygonal plate element for thin and thick plates based on Reissner-Mindlin plate theory and assumed shear strain fields. Comput. Struct. 2019, 220, 32–42. [Google Scholar] [CrossRef]
- Bathe, K.J.; Lee, P.S.; Hiller, J.F. Towards improving the MITC9 shell element. Comput. Struct. 2003, 81, 477–489. [Google Scholar] [CrossRef]
- Chapelle, D.; Bathe, K.J. Fundamental considerations for the finite element analysis of shell structures. Comput. Struct. 1998, 66, 19–36. [Google Scholar] [CrossRef]
- Lee, P.S.; Bathe, K.J. On the asymptotic behavior of shell structures and the evaluation in finite element solutions. Comput. Struct. 2002, 80, 235–255. [Google Scholar] [CrossRef]
- Bucalem, M.L.; Bathe, K.J. Higher-order MITC general shell elements. Int. J. Numer. Meth Eng. 1993, 36, 3729–3754. [Google Scholar] [CrossRef]
- Bucalem, M.L.; Bathe, K.J. Finite element analysis of shell structures. Arch. Comput. Meth Eng. 1997, 4, 3–61. [Google Scholar] [CrossRef]
- Belytschko, T.; Tsay, C.S. A stabilization procedure for the quadrilateral plate element with one-point quadrature. Int. J. Numer. Methods Eng. 1983, 19, 405–419. [Google Scholar] [CrossRef]
- Koschnick, F.; Bischoff, M.; Camprubí, N.; Bletzinger, K.U. The discrete strain gap method and membrane locking. Comp. Meth Appl. Mech. Eng. 2005, 194, 2444–2463. [Google Scholar] [CrossRef]
- Choi, C.K.; Paik, J.G. An efficient four node degenerated shell element based on the assumed covariant strain. Struct. Eng. Mech. 1994, 2, 17–34. [Google Scholar] [CrossRef]
- Belytschko, T.; Leviathan, I. Projection schemes for one-point quadrature shell elements. Comput. Methods Appl. Mech. Eng. 1994, 115, 277–286. [Google Scholar] [CrossRef]
- Allman, D.J. A Compatible Triangular Element Including Vertex Rotations For Plane Elasticity Analysis. Comput. Struct. 1984, 19, 1–4. [Google Scholar] [CrossRef]
- Cook, R.D. On The Allman Triangle and a Related Quadilateral Element. Comput. Struct. 1986, 22, 1065–1067. [Google Scholar] [CrossRef]
- Yunus, S.M. A Study of Different Hybrid Elements with and without Rotational DOF for Plane Stress/Plane Strain Problems. Comput. Struct. 1988, 30, 1127–1133. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, Z.; Shen, C. An effective planar triangular element with drilling rotation. Finite Elem. Anal. Des. 2010, 46, 1031–1036. [Google Scholar] [CrossRef]
- MacNeal, R.H.; Harder, R.L. A refined four-noded membrane element with rotational degrees of freedom. Comput. Struct. 1988, 28, 75–84. [Google Scholar] [CrossRef]
- Bathe, K.J.; Dvorkin, E.N. A formulation of general shell elements—The use of mixed interpolation of tensorial components. Int. J. Numer. Methods Eng. 1986, 22, 697–722. [Google Scholar] [CrossRef]
- Bucalem, M.L.; Bathe, K.J. Locking behavior of isoparametric curved beam finite elements. Appl. Mech. Rev. 1995, 48, S25–S29. [Google Scholar] [CrossRef]
- Ko, Y.; Lee, P.S.; Bathe, K.J. The MITC4+ shell element and its performance. Comput. Struct. 2016, 169, 57–68. [Google Scholar] [CrossRef]
- Lee, P.S.; Bathe, K.J. The quadratic MITC plate and MITC shell elements in plate bending. Adv. Eng. Softw. 2010, 41, 712–728. [Google Scholar] [CrossRef]
- Abedian, A.; Parvizian, J.; Düster, A.; Rank, E. The finite cell method for the J2 flow theory of plasticity. Finite Elem. Anal. Des. 2013, 69, 37–47. [Google Scholar] [CrossRef]
- Szabó, L. A semi-analytical integration method for J2 flow theory of plasticity with linear isotropic hardening. Comput. Methods Appl. Mech. Eng. 2009, 198, 2151–2166. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Fleck, N.A. Mode I crack tip fields: Strain gradient plasticity theory versus J2 flow theory. Eur. J. Mech.-A/Solids 2019, 75, 381–388. [Google Scholar] [CrossRef]
- de Borst, R. A generalisation of J2-flow theory for polar continua. Comput. Methods Appl. Mech. Eng. 1993, 103, 347–362. [Google Scholar] [CrossRef]
- Mousavi, F.; Jafarzadeh, S.; Bobaru, F. An ordinary state-based peridynamic elastoplastic 2D model consistent with J2 plasticity. Int. J. Solids Struct. 2021, 229, 111146. [Google Scholar] [CrossRef]
- Yu, B.; Yin, X.; Jiang, L.; Xiao, X.; Wang, C.; Yuan, H.; Chen, X.; Xie, W.; Wang, H.; Ding, H. Analysis of plastic yield behavior during impact of a rigid sphere on an elastic-perfectly plastic half-space. Int. J. Mech. Sci. 2023, 237, 107774. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Elastic-plastic analysis with pre-integrated beam finite element based on state diagrams: Elastic-perfectly plastic flow. Eur. J. Mech.-A/Solids 2023, 97, 104837. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, C.; Wu, P.; Yoon, J.W. New geometry-inspired numerical convex analysis method for yield functions under isotropic and anisotropic hardenings. Int. J. Solids Struct. 2024, 286, 112582. [Google Scholar] [CrossRef]
- Roubaud, F.; Morin, L.; Remmal, A.; Marie, S.; Leblond, J.B. A Gurson-type layer model for ductile porous solids containing ellipsoidal voids with isotropic and kinematic hardening. Eur. J. Mech. -A/Solids 2024, 104, 105114. [Google Scholar] [CrossRef]
- Mehani, N.; Roy, S.C. Modified isotropic and kinematic hardening equations for 304L SS under low cycle fatigue. Comput. Mater. Sci. 2024, 240, 112999. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Krabbenhøft, J. Simplified kinematic hardening plasticity framework for constitutive modelling of soils. Comput. Geotech. 2021, 138, 104146. [Google Scholar] [CrossRef]
- Yu, H.Y.; Chen, S.J. A mixed hardening model combined with the transformation-induced plasticity effect. J. Manuf. Process. 2017, 28, 390–398. [Google Scholar] [CrossRef]
- Lei, P.; Meng, S.; Wu, J.; Liu, Z.; Imtiaz, H.; Feng, H.; Zhou, J.; Liu, B. Is the Jaumann Stress Rate Applicable?—Discussions on Choosing Proper Rate Expressions of a Finite Deformation Constitutive Model. Int. J. Appl. Mech. 2023, 15, 2350097. [Google Scholar] [CrossRef]
- Belytschko, T.; Lin, J.I.; Chen-Shyh, T. Explicit algorithms for the nonlinear dynamics of shells. Comput. Methods Appl. Mech. Eng. 1984, 42, 225–251. [Google Scholar] [CrossRef]
- Belytschko, T.; Leviathan, I. Physical stabilization of the 4-node shell element with one point quadrature. Comp. Meth App Mech. Eng. 1994, 113, 321–350. [Google Scholar] [CrossRef]



| Node No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| x | 0 | 0 | 10 | 10 | 2 | 8 | 8 | 4 |
| y | 10 | 0 | 0 | 10 | 2 | 3 | 7 | 7 |
| Node No. | u | v | |
|---|---|---|---|
| 5 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 |
| Node No. | x | y | u | v | |
|---|---|---|---|---|---|
| 1 | 0 | 10 | 0.013 | 0.019 | 0.001 |
| 2 | 0 | 0 | 0.003 | 0.004 | 0.001 |
| 3 | 10 | 0 | 0.023 | 0.034 | 0.001 |
| 4 | 10 | 10 | 0.033 | 0.049 | 0.001 |
| 5 | 2 | 2 | 0.009 | 0.013 | 0.001 |
| 6 | 8 | 3 | 0.022 | 0.0325 | 0.001 |
| 7 | 8 | 7 | 0.026 | 0.0385 | 0.001 |
| 8 | 4 | 7 | 0.018 | 0.0265 | 0.001 |
| Node No. | u | v | |
|---|---|---|---|
| 5 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, M.; Wei, Y. High-Precision Elastoplastic Four-Node Quadrilateral Shell Element. Appl. Sci. 2024, 14, 9186. https://doi.org/10.3390/app14209186
Tian M, Wei Y. High-Precision Elastoplastic Four-Node Quadrilateral Shell Element. Applied Sciences. 2024; 14(20):9186. https://doi.org/10.3390/app14209186
Chicago/Turabian StyleTian, Mingjiang, and Yongtao Wei. 2024. "High-Precision Elastoplastic Four-Node Quadrilateral Shell Element" Applied Sciences 14, no. 20: 9186. https://doi.org/10.3390/app14209186





