Changing the Position of the Vehicle’s Center of Gravity as a Result of Different Load Distribution
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Proposal of Measurement Methodology
- Ensuring that vehicle tanks—fuel tank, washer fluid tank, etc.—are either full or empty. Ensuring that any cargo in the vehicle cannot move freely.
- Ensuring correct tire pressure. The correct tire pressure is prescribed by the manufacturer.
- Determination of the wheelbase value from the vehicle’s technical documentation or by measuring the distance between the wheel centers of adjacent axles.
- Selection of suitable pallets, prisms, beams, grates, or thick boards strong enough to support the weight of the vehicle.
- Check the weighing accuracy of the pallet truck with a scale. Verification of the calibration sheet of the pallet truck with a scale and other technical documentation. Checking the accuracy of weighing using weights with a known weight. Instead of a pallet truck with a scale, pallet scales can also be used if they have a weighing division of 0.5 kg or less.
- Determination of the weight of pallets, prisms, beams, grates, or thick boards to be stored under individual vehicle axles.
- Positioning the vehicle on pallets, prisms, grates, beams, or thick boards. Let there be a pallet truck with a scale or pallet scales under one of the axles. In that case, there are pallets, prisms, grates, beams, or thick boards between the pallet truck or pallet scale and the wheels of the vehicle. If there are two pallet trucks with scales or pallet scales available, let them be stored under both axles.
- For the most accurate measurement, it is necessary that the wheels of the front and rear axles are in a horizontal position. Horizontality is also required between the right and left sides of the vehicle. It is advisable to check the horizontality only after the vehicle has been positioned, as deformations of the base may occur. The level can be checked using a spirit level. With a flat surface, horizontality can also be measured as the distance between the lower part of the wheel and the surface, i.e., the floor.
- Measurement of the weight falling on one of the axles and subsequently on the other axle. If two pallet trucks are available, the weights are determined faster.
- Measurements of axle weights must be repeated and deviations between individual measurements must be evaluated. To determine the accuracy of the measurements, it is necessary to use the available known statistical methods. Deviations between measurements arise mainly due to failure to maintain the horizontality of the axles during measurements. The levelness must be checked before each weight measurement. If the weighing is carried out with a person or persons in the vehicle, it is necessary that the persons are in the same position and body position every time. The accuracy of the measurement can also be verified by adding a known weight to the vehicle and assessing the difference in the weights of an empty vehicle and a vehicle with a known weight.
- After determining the weight falling on the axles and the axle wheelbase, the distance of the center of gravity from the front axle is calculated:
- 12.
- After determining the position of the center of gravity in the horizontal direction, it is also possible to calculate the height of the center of gravity. To calculate the height of the center of gravity, it is necessary to know the difference between the weight of the axles in the plane and the weight of the axles when one of the axles is lifted.
- 13.
- The lifting of one of the axles can be ensured by gradually supporting it by other pallets, prisms, grates or thick boards, according to availability. The weight of the underlying material must be subtracted from the weight of the axle. The lifting angle is as large as possible, but one that does not yet cause visible deformation of the suspension, damping, and tires. After noticing the deformation of suspension, damping or tires, it is necessary to slightly reduce the angle of lift of the axle. The second option is to ensure suspension and damping with stops so that it does not deform. The third option is to record the amount of suspension deformation and then take it into account when calculating the height of the center of gravity.
- 14.
- After lifting one of the axles, it is necessary to determine the weight of one of the axles. Depending on the circumstances, the weight of the axle is determined for which it is easier. If possible, it is advisable to find out the weight of both axles for the sake of greater accuracy, but it is not necessary.
- 15.
- While determining the weight of an axle or both axles, the vehicle must not be braked. There must be a plane under all wheels to prevent the vehicle from moving when the vehicle brakes are released. Measurements cannot be performed on an inclined plane, as it would be necessary to derive braking forces or the need to otherwise secure the vehicle against movement—for example, with wedges.
- 16.
- Determination of the axle’s lift height. A length gauge is needed to determine the lift height of one of the axles. The lifting height of one of the axles needs to be determined as precisely as possible. It is recommended to take measurements on both sides of the vehicle.
- 17.
- In the same way as during measurements in the plane, to verify the accuracy of the measurement, it is necessary to repeat the measurements with the axle raised in order to verify the measurement results. To determine the accuracy of the repeated measurement, it is advisable to use known statistical methods.
- 18.
- After determining the angle of lift of the vehicle and differences in weight on any axle, the height of the center of gravity is calculated as follows:
3.2. Practical Verification of Measurement Methodology
3.3. Measurements with Hatchback
- -
- Empty vehicle, with a driver only, weighing 50.5 kg;
- -
- Load in the luggage compartment;
- -
- Load on the rear seats;
- -
- Load on the rear seats and in the roof box;
- -
- Load in the luggage compartment and the empty roof box;
- -
- Load on the rear seats and the empty roof box.
3.4. Measurements with SUV
- -
- The empty vehicle with the driver only weighing 50.5 kg;
- -
- Load in the roof box weighing 72.5 kg;
- -
- Load in the load compartment, on the lowered rear seats and on the floor in front of the lowered rear seats, and on the floor in front of the front seats weighing 472.5 kg;
- -
- Load in the load compartment, on the lowered rear seats weighing 400 kg, and in the roof box weighing 72.5 kg;
- -
- Load on the floor in front of the rear seats and on the floor in front of the front seat weighing 72.5 kg.
3.5. Measurements with Electric, Hybrid, and VAN
4. Results and Discussion
4.1. Measurement Results with Hatchback
4.2. Measurement Results with SUV
4.3. Measurement Results with Electric, Hybrid, and VAN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Yang, X.; Liu, Y.; Wang, L.; Li, P.; Li, H.; Luo, Y.; Li, Y.; Liu, Q. TruckSim-based study of the rollover accident mechanisms of container semitrailers on freeway interchange loop ramps. PLoS ONE 2024, 19, e0309139. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Yoo, H.; Shin, M.; Oh, J.; Shim, S.-B. Analysis of Overturning Stability of Small off-Road Vehicle. J. Biosyst. Eng. 2024, 48, 309–318. [Google Scholar] [CrossRef]
- Peng, C.; Wei, C.; Solernou, A.; Hagenzieker, M.; Merat, N. User comfort and naturalness of automated driving: The effect of vehicle kinematic and proxemic factors on subjective response. Appl. Ergon. 2025, 122, 104397. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, B. Mass properties and automotive directional stability. In Proceedings of the 80th SAWE International Conference on Mass Properties Engineering, Cocoa Beach, FL, USA, 2–6 October 2021. [Google Scholar]
- Figueira, M.; Guo, Z. The Influence of Weight Distribution on the Handling Characteristics of Intercity Bus under Steady State Vehicle Cornering Condition. In Proceedings of the 5th International Conference on Transportation and Traffic Engineering (ICTTE), Lucerne, Switzerland, 6–10 July 2016. [Google Scholar]
- Wang, X.; Gan, Y.; Lian, M.; Bi, B.; Tang, Y. Identification of Risk Sources of Abnormal Driving Vehicles of Expressway in Port City. J. Coast. Res. 2020, 104, 317–321. [Google Scholar] [CrossRef]
- Solmaz, S.; Akar, M.; Shorten, R.; Kalkkuhl, J. Real-time multiple-model estimation of centre of gravity position in automotive vehicles. Veh. Syst. Dyn. 2008, 46, 763–788. [Google Scholar] [CrossRef]
- Dontu, A.; Gaiginschi, L.; Barsanescu, P. Reducing the urban pollution by integrating weigh-in-motion sensors into intelligent transportation systems. In Proceedings of the State of the art and future trends, IOP Conference Series: Materials Science and Engineering, Modern Technologies in Industrial Engineering VII (ModTech2019), Iasi, Romania, 19–22 June 2019; Volume 591. [Google Scholar] [CrossRef]
- Jablonicky, J.; Tulik, J.; Bártová, S.; Tkáč, Z.; Kosiba, J.; Kuchar, P.; Čorňák, Š.; Kollárová, K.; Kaszkowiak, J.; Tomić, M.; et al. Influence of Decarbonization on Selected Parameters of ICE. Atmosphere 2023, 14, 1271. [Google Scholar] [CrossRef]
- Tautkus, A.; Miceviciene, D.; Vaitiekunas, T. Investigation of the load of three axled semi-trailer. In Proceedings of the 11th International Conference on Intelligent Technologies in Logistics and Mechatronics Systems (ITELMS), Panevezys, Lithuania, 28–29 April 2016. [Google Scholar]
- Vida, G.; Torok, A. Expected effects of accident data recording technology evolution on the identification of accident causes and liability. Eur. Transp. Res. Rev. 2023, 15, 17. [Google Scholar] [CrossRef]
- Gao, X.; Tang, Y.; Xu, H.; Xu, X.; Xu, L.; Yan, L. Vertical load distribution strategy of amphibious wheel-track vehicle using neural network and particle swarm optimization. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 563–587. [Google Scholar] [CrossRef]
- Imani, M.; Nasyis, T.; Pramujati, B.; Nurahmi, L.; Maulana, H.S.; Faranka, M.A.; Azzuri, M.S.; Wijaya, C.H. Dynamic Analysis of Forklift AGV based on Center of Gravity. In Proceedings of the International Electronics Symposium: Shaping the Future: Society 5.0 and Beyond, IES 2024, Denpasar, Indonesia, 6–8 August 2024. [Google Scholar] [CrossRef]
- Khandekar, P.; Badiger, K.; Gautam, A.; Soni, L. A Novel Approach for Combi Braking System Design Considering Tire’s Nonlinear Behavior. In Proceedings of the 18th Symposium on International Automotive Technology, SIAT, SAE Technical Paper, Warsaw, Poland, 23–24 January 2024. [Google Scholar] [CrossRef]
- Fan, Y.; Du, C.; Wang, Q. Study on the Influence of the Center of Gravity of Fuel Cell City Bus on its Handling Characteristics. Mechanika 2020, 26, 416–425. [Google Scholar] [CrossRef]
- Transport and Environment. Cars Are Getting 1 cm Wider Every Two Years—Research. Available online: https://www.transportenvironment.org/articles/cars-are-getting-1-cm-wider-every-two-years-research (accessed on 7 October 2024).
- IEA. Trends in Electric Vehicle Charging, Global EV Outlook 2024. Available online: https://www.iea.org/reports/global-ev-outlook-2024/trends-in-electric-vehicle-charging (accessed on 7 October 2024).
- Navarro, H.; Canale, A. Influences of the load center of gravity on heavy vehicle acceleration. Int. J. Heavy Veh. Syst. 2001, 8, 17–47. [Google Scholar] [CrossRef]
- Skrucany, T.; Vrabel, J.; Kazimir, P. The influence of the cargo weight and its position on the braking characteristics of light commercial vehicles. Open Eng. 2020, 10, 154–165. [Google Scholar] [CrossRef]
- Skrucany, T.; Vrabel, J.; Kendra, M.; Kazimir, P. Impact of Cargo Distribution on the Vehicle Flatback on Braking Distance in Road Freight Transport. In Proceedings of the 18th International Scientific Conference on LOGI, Ceske Budejovice, Czech Republic, 19 October 2017; Volume 134. [Google Scholar] [CrossRef]
- Radzajewski, P.; Guzek, M. Assessment of the Impact of Selected Parameters of Tractor-Semitrailer Set on the Braking Safety Indicators. Appl. Sci. 2023, 13, 5336. [Google Scholar] [CrossRef]
- Nicolescu, B.; Macarie, T.; Petrescu, T. On the vehicle planar motion. Acta Tech. Napoc. Ser.-Appl. Math. Mech. Eng. 2015, 58, 349–360. [Google Scholar]
- Majdan, R.; Abraham, R.; Kollárová, K.; Tkáč, Z.; Matejková, E.; Kubík, Ľ. Alternative Models for Calculation of Static Overturning Angle and Lateral Stability Analysis of Subcompact and Universal Tractors. Agriculture 2021, 11, 861. [Google Scholar] [CrossRef]
- TRID. Traffic Safety Facts 2018: A Compilation of Motor Vehicle Crash Data; DOT HS 812 981; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2020. [Google Scholar]
- Tengler, S.; Harlecki, A. Dynamics of vehicles with high gravity center. Theor. Appl. Mech. Lett. 2012, 2, 043014. [Google Scholar] [CrossRef]
- Brandt, A.; Jacobson, B.; Sebben, S. High speed driving stability of road vehicles under crosswinds: An aerodynamic and vehicle dynamic parametric sensitivity analysis. Veh. Syst. Dyn. 2021, 60, 2334–2357. [Google Scholar] [CrossRef]
- Raessa, M.; Fanni, M.; Mohamed, A. Dynamics Analysis and Control of All-Terrains Wearable Vehicle. In Proceedings of the IEEE International Conference on Industrial Technology (ICET), Taipei, Taiwan, 14–17 March 2016. [Google Scholar] [CrossRef]
- Lugner, P.; Edelmann, J. Basics of Vehicle Dynamics, Vehicle Models. Veh. Dyn. Mod. Passeng. Cars 2019, 582, 1–45. [Google Scholar] [CrossRef]
- Kutluay, E.; Winner, H. Validation of vehicle Dynamics simulation models—A review. Veh. Syst. Dyn. 2014, 52, 186–200. [Google Scholar] [CrossRef]
- Ersal, T.; Kittirungsi, B.; Fathy, H.; Stein, J.L. Model reduction in vehicle Dynamics using importance analysis. Veh. Syst. Dyn. 2009, 47, 851–865. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, L.; Shan, H.; Liu, H.; Liu, Y. Estimation of the vehicle’s center of gravity based on a braking model. Veh. Syst. Dyn. 2015, 53, 1520–1533. [Google Scholar] [CrossRef]
- Sar, H.; Fundowics, P. Empirical equations for determining the height of the center of mass of a passenger car. In Proceedings of the 11th International Scientific and Technical Conference on Automotive Safety, Casta Papiernicka, Slovakia, 18–20 April 2018. [Google Scholar] [CrossRef]
- Krauze, P. Modelling and Identification of Magneto theological Vehicle Suspension. In Proceedings of the 17th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2012. [Google Scholar] [CrossRef]
- Xu, Q.; Fu, R.; Wu, F.; Wang, B. Road side estimation of a vehicle’s center of gravity height based on an improved single-stage detection algorithm and regression prediction technology. IEEE Sens. J. 2021, 21, 24520–24530. [Google Scholar] [CrossRef]
- Lin, C.; Gong, X.; Xiong, R.; Cheng, X. A novel H-infinity and EKF joint estimation method for determining the center of gravity position of electric vehicles. Appl. Energy 2017, 194, 609–616. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Real-time estimation of center of gravity position for light weight vehicles using combined AKF-EKF method. IEEE Trans. Veh. Technol. 2014, 63, 4221–4231. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. Center of gravity height real-time estimation for lightweight vehicles using tire instant effective radius. Control. Eng. Pract. 2013, 21, 370–380. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, S.; Lee, J.; Choi, S.B.; Kim, M.; Lee, H. Estimation of TireLoad and Vehicle Parameters Using Intelligent Tires Combined with Vehicle Dynamics. IEEE Trans. Instrum. Meas. 2020, 70, 9502712. [Google Scholar] [CrossRef]
- Braghin, H.; Brusarosco, M.; Cheli, F.; Cigada, A.; Manzoni, S.; Mancosu, F. Measurement of contact forces and patch features by means of accelerometers fixed inside the tire to improve future caractive control. Veh. Syst. Dyn. 2006, 44, 3–13. [Google Scholar] [CrossRef]
- Jeong, D.; Lee, J.; Choi, S.; Kim, M. Load Estimation of Intelligent Tires Equipped with Acceleration Sensors. In Proceedings of the 2019 IEEE Sensors Applications Symposium (SAS), Conference Proceedings, Sophia Antipolis, France, 11–13 March 2019. [Google Scholar] [CrossRef]
- Lee, H.; Tahery, S. Intelligent tires—A review of tire characterization literature. EEE Intell. Transp. Syst. Mag. 2017, 9, 114–135. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y. Vehicle Rollover Propensity Detection Based on a Mass-Center-Position Metric: A Continuous and Completed Method. IEEE Trans. Veh. Technol. 2019, 68, 1. [Google Scholar] [CrossRef]
- Doumiati, M.; Victorino, A.; Charara, A.; Lechner, D. Lateral load transfer and normal forces estimation for vehicle safety: Experimental test. Veh. Syst. Dyn. 2009, 47, 1511–1533. [Google Scholar] [CrossRef]
- Markovsky, I.; Huffel, V. Overview of total least-squares methods. Signal Procesing 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Hylier, T.; Bevly, D. Vehicle Load Estimation Using Recursive Total Least Squares for Rollover Detection; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, H.; Zong, C.; Chen, Y. Vehicle Mass Estimation for Heavy Duty Vehicle; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Kubica, P. Device for Measuring the Height Position of the Center of Gravity of the Vehicle. Available online: http://hdl.handle.net/11012/39436 (accessed on 17 November 2023).
- Schiller GmbH: Vehicle Inertia Measuring Machine. Available online: http://cfm-schiller.de/pdf/CFM%20Schiller%20VIMM%20%20Vehicle%20Inertia%20Measuring%20Machine%20en.pdf (accessed on 17 November 2023).
- Center of Gravity and Inertia Testing. Available online: https://sealimited.com/capability/center-of-gravity-and-inertia/ (accessed on 17 November 2023).
- Win, T.; Alakin, V.; Plakhov, S. Development of a Methodology and Study of the Center of Gravity of a Vehicle. In Lecture Notes in Mechanical Engineering, Proceedings of the 8th International Conference on Industrial Engineering; Springer: Berlin/Heidelberg, Germany, 2023; pp. 411–420. [Google Scholar] [CrossRef]
- Khorosandi, F.; Ayers, P.; Freeland, R.; Wang, X. Modeling the effect of liquid movement on the center of gravity calculation of agricultural vehicles. J. Terramechanics 2018, 75, 37–48. [Google Scholar] [CrossRef]
- Axle Weighers, Axle Scale by Weigh Capacities. Available online: https://www.cublift.com/axle-scales/ (accessed on 4 May 2023).
- Widner, A.; Bári, G. Comparison of Center of Gravity Height Estimation Methods. Lect. Notes Mech. Eng. 2021, 22, 293–301. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Ayers, P.D.; Su, S.; Yuan, C. The influence of the lift angle on the center of gravity: Measurements for zero turning radius mowers. Appl. Eng. Agric. 2016, 32, 189–199. [Google Scholar] [CrossRef]
- Fuerbeth, U. Centre of gravity of motor vehicles. Forensic Sci. Int. 2024, 31, 112073. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Wang, Z.; Yang, J.; Ikiela, N.V.O.; Yin, G. A Novel Methodology for Inertial Parameter Identification of Lightweight Electric Vehicle via Adaptive Dual Unscented Kalman Filter. Int. J. Automot. Technol. 2024, 25, 1113–1125. [Google Scholar] [CrossRef]
- Wu, F.; Sun, C.; Li, H.; Zheng, S. Real-Time Center of Gravity Estimation for Intelligent Connected Vehicle Based on HEKF-EKF. Electronics 2023, 12, 386. [Google Scholar] [CrossRef]
- Lin, C.; Cheng, X.; Zhang, H.; Gong, X. Estimation of Center of Gravity Position for Distributed Driving Electric Vehicles Based on Combined H-infinity-EKF Method. Energy Proc. 2016, 88, 970–977. [Google Scholar] [CrossRef]
- Jin, X.; Yang, J.; Xu, L.; Wei, C.; Wang, Z.; Yin, G. Combined Estimation of Vehicle Dynamic State and Inertial Parameter for Electric Vehicles Based on Dual Central Difference Kalman Filter Method. Chin. J. Mech. Eng. 2023, 36, 91. [Google Scholar] [CrossRef]
- Reyneh, M.; Enqvist, M.; Gustafsson, F. IMU-based vehicle load estimation under normal driving conditions. In Proceedings of the IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; Volume 2015, pp. 3376–3381. [Google Scholar] [CrossRef]
- Redl, J.; Boyko, G.; Kalantari, D. Prediction of Machine’s Centre of Gravity Dislocation with Monte Carlo Simulation. Acta Technol. Agric. 2024, 27, 133–141. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Yan, X.; Liu, M.; Xu, L. Real-time estimation of barycenter position for fuel cell distributed drive electric tractor based on derived UKF. Veh. Syst. Dyn. 2024, 62, 2661–2685. [Google Scholar] [CrossRef]
- Skrúcaný, T.; Synák, F.; Semanová, Š.; Ondruš, J.; Rievaj, V. Detection of road vehicle gravity. In Proceedings of the 2018 11th International Science and Technical Conference Automotive Safety, Casta Papiernicka, Slovakia, 18–20 April 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Janosko, I.; Polonec, T.; Simor, R.; Blazek, J.; Brabec, P.; Vozenilek, R. Electronic encyclopaedia of construction engines and vehicles. In Proceedings of the 41st International Scientific Conference of Czech and Slovak University Departments and Institutions Dealing with the Research of Internal Combustion Engines, Liberec, Czech Republic, 6–7 September 2010; pp. 232–238, ISBN 978-80-7372-632-4. [Google Scholar]
- Technical Data Kia. Available online: https://www.cars-data.com/en/ (accessed on 6 September 2024).
- Technical Data VW. Available online: https://www.carfolio.com/search/results/?terms=volkswagen (accessed on 6 September 2024).
- User Manual for KPZ 52E-7/1. Available online: https://kpzwagi.pl/wagi-przemyslowe/panele-sterujace/panel-steruj-cy-kpz-52e-7-1/ (accessed on 4 May 2023).
- Frequently Asked Questions on Pallet Truck Scales. Available online: https://www.camaweigh.com/blog/post/faqs-on-pallet-truck-scales/, (accessed on 17 November 2023).
- Rievaj, V.; Vrábel, J.; Synák, F.; Bartuška, L. The effects of vehicle load on driving characteristics. Adv. Sci. Technol.-Res. J. 2018, 12, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Kim, Y.; Park, H.; Kim, Y.; Woo, S.; Uyeh, D.D.; Ha, Y. Rollover Safety and Workable Boundary Suggestion of an Agricultural Platform with Different Attachments. Agriculture 2022, 12, 1148. [Google Scholar] [CrossRef]
- Zhao, N.; Dong, Y.; Yan, D.; Feng, X.; Cui, L. Enhanced assessment framework of static stability of tracked vehicles in consideration of multi-directional loading. J. Terramechanics 2024, 115, 100984. [Google Scholar] [CrossRef]
- Filo, M.; Puskar, M.; Kelemenova, T.; Kelemen, M.; Kolarikova, I.; Kral, J. Calibration Tool for Tilt Sensors for Checking the Instability of Motor Vehicles. MM Sci. J. 2024, 7260–7264. [Google Scholar] [CrossRef]
- User Manual for LP7516. Available online: https://www.topmaq.co.nz/content/products/pallet-weigh-platform-with-digital-scales-2ton-mapa1900-mapa1900-man1.pdf?srsltid=AfmBOoqzr1TZLRe75V02O2HKzJKmtySLOMaOPKicvk5wKcWeuazu_3q2 (accessed on 6 September 2024).
- Kamain, Y.; Zhukov, M.; Panickhin, A.; Redelin, A. Modeling of load lifting process with unknown center of gravity position. IOP Conf. Ser.-Mater. Sci. Eng. 2018, 327, 022054. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, X.; Yang, C.; Mo, J. Dynamic distribution method of multi-axle vehicle’s driving axle load on test bench. Zhejiang DaxueXuebao/J. Zhejiang Univ. (Eng. Sci.) 2014, 48, 1080–1085. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Zhao, W.; Duan, T. Torque Distribution of Electric Vehicle with Four In-Wheel Motors Based on Road Adhesion Margin; Transactions of Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2019; Volume 36. [Google Scholar] [CrossRef]
- Hosseinian, A.; Melzi, S. Numerical analysis of the influence of an actively controlled spoiler on the handling of a sports car. J. Vib. Control. 2018, 24, 5437–5448. [Google Scholar] [CrossRef]
- Preda, I.; Ciolan, G.; Covaciu, D. Aspects Regarding the Stability Performances Calculation of the Wheeled Vehicles While Turning. In Proceedings of the 30th SIAR International Congress of Automotive and Transport Engineering, Craiova, Romania, 23 – 25 October 2020; pp. 614–623. [Google Scholar] [CrossRef]
- Arslan, T.A.; Çelik, I.; Aysal, F.E.; Bayrakçeken, H. Investigation of the Effects of Axle Load on Tire Behaviour in Vehicle. J. Polytech. 2024, 27, 603–614. [Google Scholar] [CrossRef]
- Jilek, P.; Nemec, J. System for changing the radial response on car wheels. Acta Univ. Agric. Silvic. 2020, 68, 39–47. [Google Scholar] [CrossRef]
- Sharaf, A.; Yacoub, M.; Elhefnawy, A. Improving the stability of a bullet proofed vehicle using modified suspension system. In Proceedings of the ASME International Design Engineering Technical Conferences/Computers and Information in Engineering Conference (IDETC-CIE), Anaheim, CA, USA, 17–19 August 2020. [Google Scholar] [CrossRef]
- Sabouri, M.; Hamidi, A. Introducing a revised model for determination of rollover threshold speed of buses. Int. J. Heavy Veh. Syst. 2020, 27, 723–742. [Google Scholar] [CrossRef]
- Bruni, S.; Meijaard, J.; Rill, G.; Schwab, A. State-of-the-art and challenges of railway and road vehicle dynamics with multi body dynamics approaches. Multi Body Syst. Dyn. 2020, 49, 1–32. [Google Scholar] [CrossRef]
- Skrucany, T.; Gnap, J. The Effect of the Crosswinds on the Stability of the Moving Vehicles. In Proceedings of the 6th International Scientific Conference on Dynamic of Civil Engineering and Transport Structures and Wind Engineering (DYN-WIND), Donovaly, Slovakia, 25–29 May 2014; Volume 617, pp. 296–301. [Google Scholar] [CrossRef]
- Jurco, A. Study of the influence of roof luggage box on a vehicle aerodynamics. Ingeniria Automob. 2021, 58, 15–18. [Google Scholar]
- LLatif, M.A.; Hashim, M.; Rashid, M.; Azhari, M.; Othman, M. Roof Box Shape Streamline Adaptation and the Impact towards Fuel Consumption. Eng. Technol. Int. Conf. (ETIC) 2017, 97, 6. [Google Scholar] [CrossRef]
- Makihara, T.; Kitamura, T.; Yamashita, T.; Maeda, K.; Kato, C.; Takayama, T.; Yamamoto, K.; Yamade, Y.; Suzuki, Y. Identification of Vortical Structure that Drastically Worsens Aerodynamic Drag on a 2-Box Vehicle using Large-scale Simulations. SAE Int. J. Passeng. Cars-Mech. Syst. 2016, 9, 592–602. [Google Scholar] [CrossRef]
- Mashadi, B.; Ebrahimi, N.; Marzbanrad, J. Effect of front-wheel drive or rear-wheel drive on the limit handling behaviour of passenger vehicles. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2007, 221, 393–403. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Shen, J.; Yan, J. Study on Improvement of Climbing Ability of Multi-Motor Driven Vehicle. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 032182. [Google Scholar] [CrossRef]
- Majdan, R.; Abraham, R.; Tkac, Z.; Tkáč, Z.; Drlička, R.; Matejková, E.; Kollárová, K.; Mareček, J. Static Lateral Stability of Tractor with Rear Wheel Ballast Weights: Comparison of ISO 16231-2 (2015) with Experimental Data Regarding Tire Deformation. Appl. Sci. 2021, 11, 381. [Google Scholar] [CrossRef]
- Wang, X.; Ayers, P.; Womac, A. Static Simulation and Analyses of Mower’s ROPS Behavior in a Finite Element Model. J. Agric. Saf. Health 2009, 15, 335–352. [Google Scholar] [CrossRef]
- Wiesalla, J.; Mao, Y.; Esser, F. Using Generic Tire Parameters for Low Friction Surfaces in Full Vehicle Simulations. SAE Int. J. Veh. Dyn. Stab. NVH 2017, 1, 190–197. [Google Scholar] [CrossRef]
- Beal, C.; Brennan, S. Modeling and friction estimation for automotive steering torque at very low speeds. Veh. Syst. Dyn. 2020, 59, 458–484. [Google Scholar] [CrossRef]
- Kondakov, S.; Pavlovskaya, O.; Aliukov, S.; Smirnov, V. Modeling of the Automatic Power Distribution System Among the Traction Motors of the Driving Wheels of a Multi-Axle Vehicle; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Dubrovskiy, A.; Aliukov, S.; Keller, A.; Dubrovskiy, S.; Alyukov, A. Adaptive Suspension of Vehicles with Wide Range of Control; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, N.; Du, H. Investigation into untripped rollover of light vehicles in the modified fishhook and the sine manoeuvres, part II: Effects of vehicle inertia property, suspension and tire characteristics. Veh. Syst. Dyn. 2011, 49, 949–968. [Google Scholar] [CrossRef]
- Hejtmanek, P.; Blatak, O.; Vancura, J. New Approach to measure the Vehicle Center of Gravity Height. Perner’s Contacts 2015, 10, 18–27. [Google Scholar]
- Kim, Y.Y.; Noh, J.S.; Shin, S.Y.; Byoungln, K.; Hong, S.J. Improved Method for Determining the Height of Center of Gravity of Agricultural Tractors. J. Biosyst. Eng. 2016, 41, 170–176. [Google Scholar] [CrossRef]
- Load Expert Software, Axle Load Calculation Software. Available online: https://www.loadxpert.com/axle-load-calculation-software/ (accessed on 7 October 2024).
- NTEA Vehicle Center of Gravity Axle Weight Calculator. Available online: https://www.ntea.com/weightcalculator (accessed on 7 October 2024).
- Corner Balance Calculator. Available online: https://robrobinette.com/corner_weight_calc.htm#google_vignette (accessed on 7 October 2024).
- NZ Transport Agency, Axle Weights Calculator. Available online: https://www.nzta.govt.nz/vehicles/choosing-the-right-vehicle/choosing-and-operating-a-heavy-vehicle/axle-weights-calculator/ (accessed on 7 October 2024).
- Axle Load Calculator. Available online: https://donbur.co.uk/gb-en/calculator/trailer-axle-load/index.php (accessed on 7 October 2024).
- Truck Stow. Available online: https://truck-stow-tudent.software.informer.com/ (accessed on 7 October 2024).
- Trends in Vehicle Centre of Gravity Height and Static Stability Factor from 1971 to 2020 using the NHTSA LVIPD and NCAP Rollover Stability Measurements. Available online: https://kktse.github.io/jekyll/update/2022/07/28/trends-in-vehicle-cg-height-and-ssf.html (accessed on 6 September 2024).









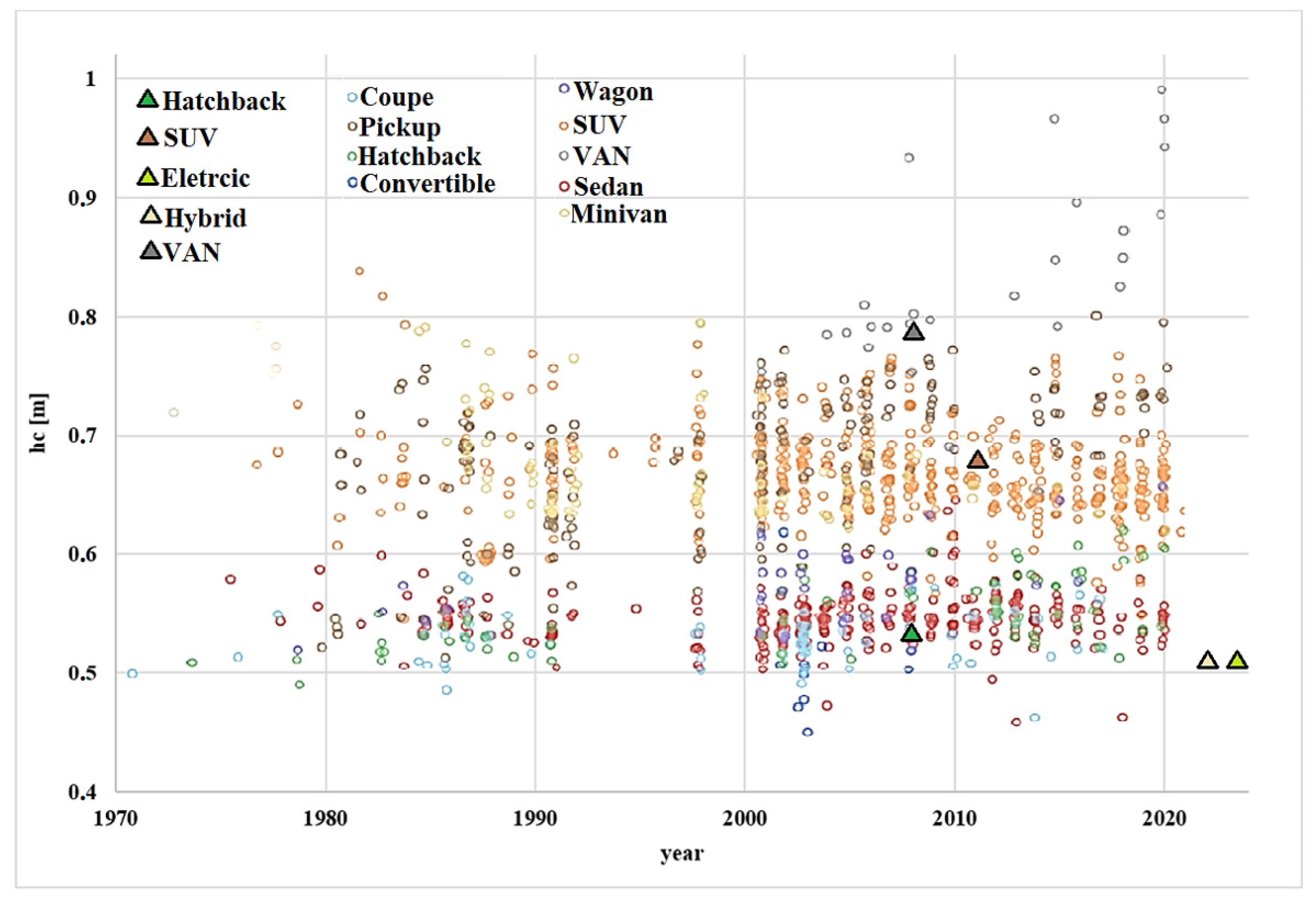

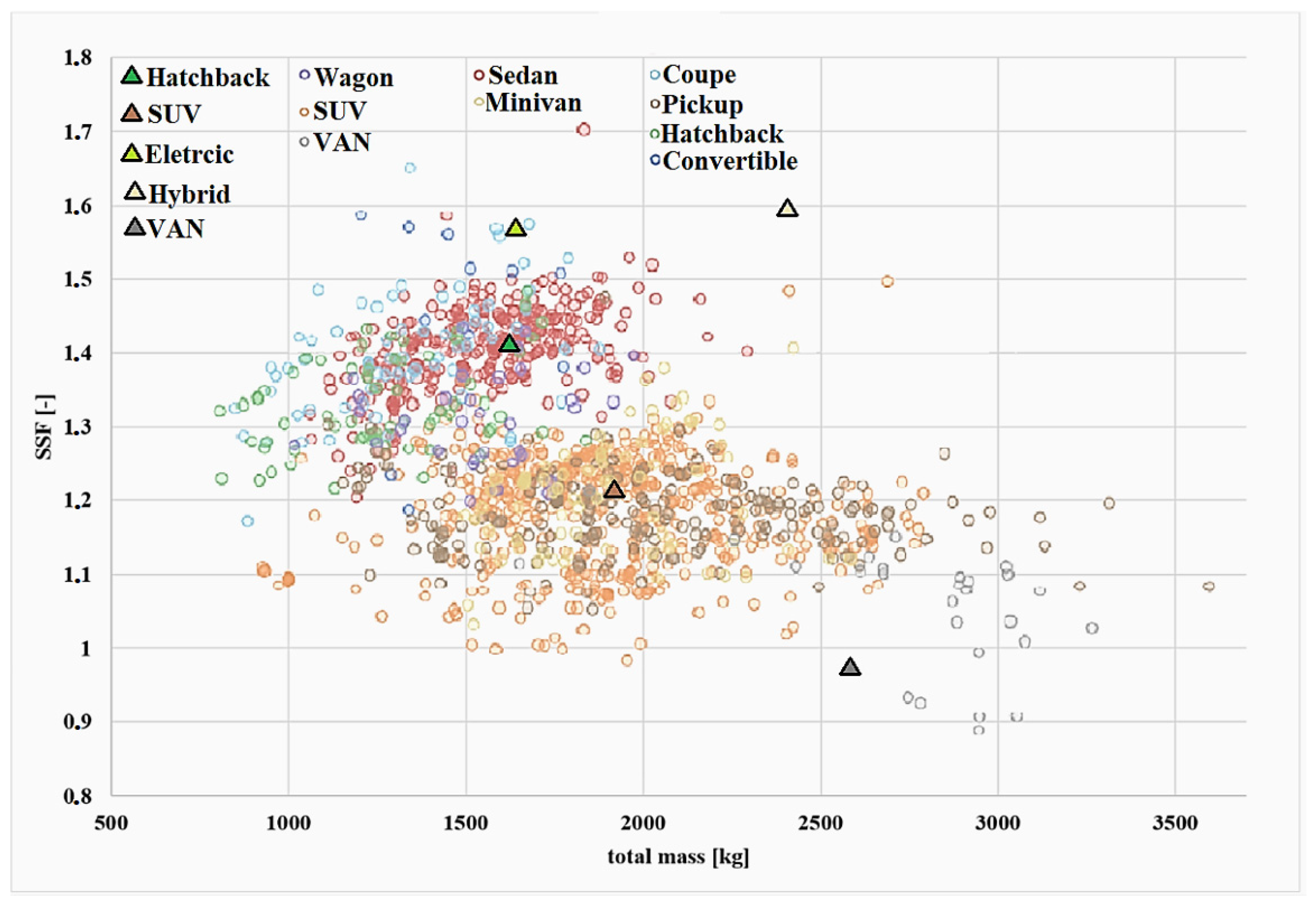
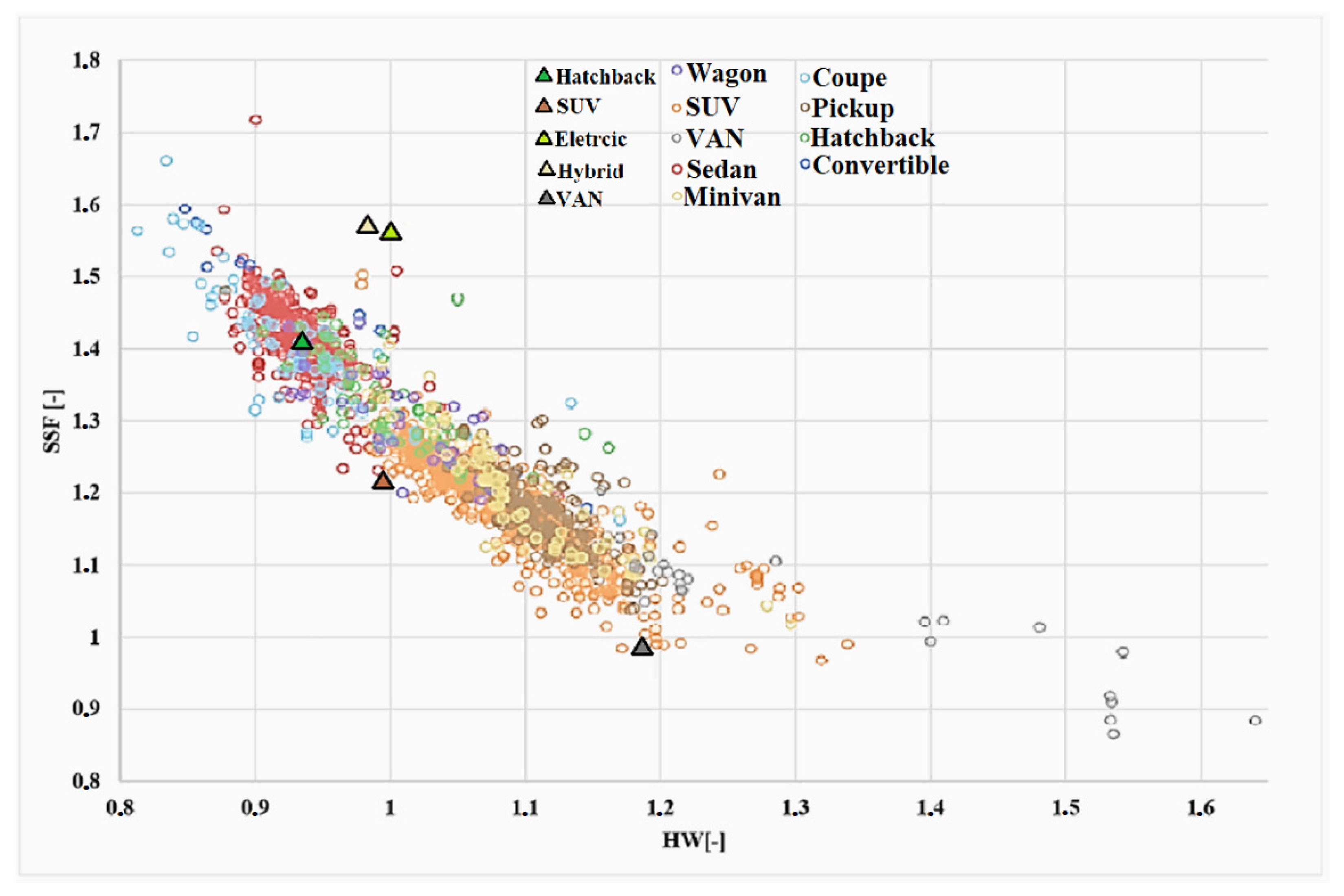
| Author and Year | Research Focus |
|---|---|
| Sar, H., Fundowics, P, 2018 [32], Redl, J., Boyko, G., Kalantari, D, 2024 [61] | Use of the Monte Carlo method and using known vehicle parameters. Neglecting the impact of suspension, damping, and tire characteristics on the change in the center of gravity’s height. |
| Yue, H, Zhang, L., Shan, S., et al., 2015 [31] Li, X., Zhang, M., Yan, X., et al., 2024 [62] | Estimation of the center of gravity’s height based on data obtained from displacement and velocity sensors. Such estimations have mean absolute errors of 14.2% and 5.0% of the state amplitude, respectively. |
| Xu, Q., Fu, R., Wu, F., et al., 2021, [34] | Identification of a specific vehicle model by sensors and subsequent assignment of the center of gravity’s position from a database, regardless of the actual vehicle load. |
| Lee, H., Tahery, S. 2017, [41] Doumiati, M., Victorino, A., Charara, A., et al., 2009, [43] | Estimation of the center of gravity’s position based on data obtained from specialized sensors in the tires, with errors exceeding 30%. |
| Kubica, P., 2023, [47] | Experimental measurements based on the vehicle’s moments of inertia. The equipment is very money-demanding with deviations exceeding 20%. |
| Schiller, 2023 [48] | |
| This publication | Experimental measurements using readily available tools and aids. |
| Vehicle | Kia Ceed, 1.6 CVVT (Hatchback) | Kia Sportage (SUV) | BMW i3s (Electric) | Kia Sportage Plug-in (Hybrid) | Volkswagen Transporter (VAN) |
|---|---|---|---|---|---|
| Engine | 1.6 CVVT | 1.7 CRDI, | Electric motor | 1.6 GDi | 1.9TDI |
| Engine power, engine type | 93 kW, spark-ignition | 85 kW, compression ignition | 75 kW Synchronous | 44 kW, ignition + electric | 62 kW, compression ignition |
| Outside size, body size (l/w/h) (mm) | 4235/1790/ 1480 | 4440/1855/ 1635 | 4011/1775/ 1598 | 4515/1865/ 1650 | 4890/1904/ 1990 |
| Wheelbase (mm) | 2650 | 2640 | 2574 | 2685 | 3013 |
| Total mass | 1710 | 1940 | 1730 | 2415 | 2600 |
| Kerb mass (kg) | 1263 | 1390 | 1365 | 1922 | 1800 |
| Wheelbase (kg) | 447 | 550 | 365 | 493 | 800 |
| Roof load (kg) | 80 | 100 | 75 | 80 | 80 |
| Variant | Front Axle (kg) | Rear Axle (kg) | Lifted front Axle (kg) |
|---|---|---|---|
| Empty vehicle | 789.0 | 516.5 | 768.5 |
| Load in the luggage compartment | 776.5 | 734.5 | 745.5 |
| Load on the rear seats | 827.5 | 684.0 | 804.0 |
| Load in the luggage compartment and in the roof box | 806.0 | 716.0 | 773.5 |
| Load in the roof box only | 815.0 | 573.0 | 785.5 |
| Load on the rear seats and in the roof box | 841.0 | 681.5 | 807.0 |
| Load on the rear seats, empty roof box | 831 | 692 | 800.5 |
| Load in the luggage compartment, empty roof box | 778 | 745 | 748.5 |
| Empty vehicle, empty roof box | 792.5 | 524.5 | 771.5 |
| Variant | Measured Vehicle Mass (kg) | Theoretical Vehicle Mass (kg) | Deviation (%) |
|---|---|---|---|
| Load in the luggage compartment | 1511.0 | 1510.5 | +0.03 |
| Load on the rear seats | 1511.5 | 1510.5 | +0.06 |
| Load in the luggage compartment and in the roof box | 1522.0 | 1522.0 | 0.00 |
| Load in the roof box only | 1388.0 | 1381.0 | +0.50 |
| Load on the rear seats and in the roof box | 1522.5 | 1522.0 | +0.03 |
| Load on the rear seats, empty roof box | 1523.0 | 1522.0 | +0.06 |
| Load in the luggage compartment, empty roof box | 1523.0 | 1522.0 | +0.06 |
| Empty vehicle, empty roof box | 1317.0 | 1317.0 | 0.00 |
| Variant | Front Axle Load (%) | Rear Axle Load (%) | Change (%) | L1 (m) | L2 (m) | Change (m) |
|---|---|---|---|---|---|---|
| Empty vehicle | 60.44 | 39.56 | 0.00 | 1.05 | 1.60 | 0.00 |
| Load in the luggage compartment | 51.39 | 48.61 | 9.05 | 1.29 | 1.36 | 0.24 |
| Load on the rear seats | 54.75 | 45.25 | 5.69 | 1.20 | 1.45 | 0.15 |
| Load in the luggage compartment and in the roof box | 52.96 | 47.04 | 7.48 | 1.25 | 1.40 | 0.20 |
| Load in the roof box only | 58.72 | 41.28 | 1.72 | 1.09 | 1.56 | 0.04 |
| Load on the rear seats and in the roof box | 55.24 | 44.76 | 5.20 | 1.19 | 1.46 | 0.14 |
| Load on the rear seats, empty roof box | 54.56 | 45.44 | 5.88 | 1.20 | 1.45 | 0.15 |
| Load in the luggage compartment, empty roof box | 51.08 | 48.92 | 9.36 | 1.30 | 1.35 | 0.25 |
| Empty vehicle, empty roof box | 60.17 | 39.83 | 0.27 | 1.06 | 1.59 | 0.01 |
| Variant | hc (m) | Change (%)/ (m) | Theoretical Speed Limit (km·h−1) | Change (%)/ (km·h−1) | Theoretical Rollover Angle (°) |
|---|---|---|---|---|---|
| Empty vehicle | 0.56 | 0 /0 | 87.65 | 0/0 | 50.71 |
| Load in the luggage compartment | 0.62 | 10.71/0.06 | 83.20 | −5.07/−4.45 | 51.70 |
| Load on the rear seats | 0.63 | 12.5/0.07 | 82.53 | −5.84/−5.12 | 51.25 |
| Load in the luggage compartment and in the roof box | 0.65 | 16.07/0.09 | 81.23 | −7.33/−6.42 | 50.37 |
| Load in the roof box only | 0.66 | 17.86/0.10 | 80.60 | −8.04/−7.05 | 49.94 |
| Load on the rear seats and in the roof box | 0.67 | 19.64/0.11 | 79.99 | −8.74/−7.66 | 49.51 |
| Load on the rear seats, empty roof box | 0.63 | 12.5/0.07 | 82.53 | −5.84/−5.12 | 51.25 |
| Load in the luggage compartment, empty roof box | 0.62 | 10.71/0.06 | 83.20 | −5.08/−4.45 | 51.70 |
| Empty vehicle, empty roof box | 0.56 | 0/0 | 87.65 | 0.00/0.00 | 50.71 |
| Variant | Front Axle (kg) | Rear Axle (kg) | Lifted Front Axle (kg) |
|---|---|---|---|
| Empty vehicle | 911.0 | 582.0 | 873.5 |
| Load in the roof box only, 72 kg | 927.0 | 638.5 | 682.5 |
| Load in the luggage compartment, on the lowered rear seats, 400 kg, on the floor in front of the lowered rear seats, and on the floor in front of the front seat, 72.5 kg | 927.0 | 638.5 | 883.0 |
| Load in the load compartment, on the lowered rear seats, 400 kg, and in the roof box, 72.5 kg | 942.0 | 1029.5 | 882.0 |
| Load on the floor, 72.5 kg | 943.0 | 623.5 | 905.0 |
| Variant | Measured Vehicle Mass (kg) | Theoretical Vehicle Mass (kg) | Deviation (%) |
|---|---|---|---|
| Load in the roof box only, 72 kg | 1565.5 | 1565.5 | 0.00 |
| Load in the luggage compartment, on the lowered rear seats, 400 kg, on the floor in front of the lowered rear seats, and on the floor in front of the front seat, 72.5 kg | 1969.0 | 1965.5 | +0.18 |
| Load in the load compartment, on the lowered rear seats, 400 kg, and in the roof box, 72.5 kg | 1971.5 | 1965.5 | +0.31 |
| Load on the floor, 72.5 kg | 1165.5 | 1565.5 | 0.00 |
| Variant | Front Axle Load (%) | Rear Axle Load (%) | Change (%) | L1 (m) | L2 (m) | Change (m) |
|---|---|---|---|---|---|---|
| Empty vehicle | 61.02 | 38.98 | 0.00 | 1.03 | 1.61 | 0.00 |
| Load in the roof box only, 72 kg | 59.21 | 40.79 | 1.81 | 1.08 | 1.56 | 0.05 |
| Load in the luggage compartment, on the lowered rear seats, 400 kg, on the floor in front of the lowered rear seats, and on the floor in front of the front seat, 72.5 kg | 48.63 | 51.37 | 12.39 | 1.36 | 1.28 | 0.33 |
| Load in the load compartment, on the lowered rear seats, 400 kg, and in the roof box, 72.5 kg | 47.78 | 52.22 | 13.24 | 1.38 | 1.26 | 0.35 |
| Load on the floor, 72.5 kg | 60.20 | 39.80 | 0.82 | 1.05 | 1.59 | 0.02 |
| Variant | hc (m) | Change (%)/ (m) | Theoretical Speed Limit (km·h−1) | Change (%)/ (km·h−1) | Theoretical Rollover Angle (°) |
|---|---|---|---|---|---|
| Empty vehicle | 0.67 | 0.00/0.00 | 81.12 | 0.00/0.00 | 50.23 |
| Load in the roof box only, 72 kg | 0.71 | 5.97/0.04 | 78.77 | −2.90/−2.35 | 48.66 |
| Load in the luggage compartment, on the lowered rear seats, 400 kg, on the floor in front of the lowered rear seats, and on the floor in front of the front seat, 72.5 kg | 0.69 | 2.99/0.02 | 79.91 | −1.49/−1.21 | 49.47 |
| Load in the load compartment, on the lowered rear seats, 400 kg, and in the roof box, 72.5 kg | 0.74 | 10.45/0.07 | 77.14 | −4.91/−3.98 | 49.47 |
| Load on the floor, 72.5 kg | 0.66 | −1.49/−0.01 | 81.74 | +0.76/+0.62 | 50.73 |
| Vehicle | Front Axle (kg) | Rear Axle (kg) | Measured/Theoretical Vehicle Mass (kg) | Difference (kg)/(%) |
|---|---|---|---|---|
| Electric | 646.5/672.5 | 707.5/732 | 1404.5/1404.5 | 0/0 |
| Hybrid | 1106/1130 | 789/815.5 | 1945.5/1945.5 | 0/0 |
| VAN | 1101.5/1130 | 696.5/718.5 | 1848.5/1848.5 | 0/0 |
| Vehicle | Front Axle (%) | Rear Axle (%) | L1 (m) | L2 (m) |
|---|---|---|---|---|
| Electric | 47.74/47.88 | 52.26/52.12 | 1.34/1.34 | 1.23/1.23 |
| Hybrid | 58.36/58.08 | 41.64/41.92 | 1.12/1.12 | 1.56/1.56 |
| VAN | 61.26/61.13 | 38.74/38.87 | 1.17/1.17 | 1.84/1.84 |
| Vehicle | hc (m) | Theoretical Speed Limit (km·h−1) | Theoretical Rollover Angle (°) |
|---|---|---|---|
| Electric | 0.52/0.53 | 89.55/88.60 | 55.44/54.85 |
| Hybrid | 0.52/0.52 | 92.24/92.24 | 57.10/57.10 |
| VAN | 0.89/0.91 | 69.78/68.99 | 43.20/72.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Synák, F.; Nedeliaková, E. Changing the Position of the Vehicle’s Center of Gravity as a Result of Different Load Distribution. Appl. Sci. 2024, 14, 9328. https://doi.org/10.3390/app14209328
Synák F, Nedeliaková E. Changing the Position of the Vehicle’s Center of Gravity as a Result of Different Load Distribution. Applied Sciences. 2024; 14(20):9328. https://doi.org/10.3390/app14209328
Chicago/Turabian StyleSynák, František, and Eva Nedeliaková. 2024. "Changing the Position of the Vehicle’s Center of Gravity as a Result of Different Load Distribution" Applied Sciences 14, no. 20: 9328. https://doi.org/10.3390/app14209328
APA StyleSynák, F., & Nedeliaková, E. (2024). Changing the Position of the Vehicle’s Center of Gravity as a Result of Different Load Distribution. Applied Sciences, 14(20), 9328. https://doi.org/10.3390/app14209328






