Research on Optimal Control of Treadmill Shock Absorption Based on Ground Reaction Force Constraint
Abstract
:1. Introduction
2. Establishment of the Mathematical Model
2.1. Biomechanical Motion Model
2.2. Airbag Model
2.3. Foot Pressure Model
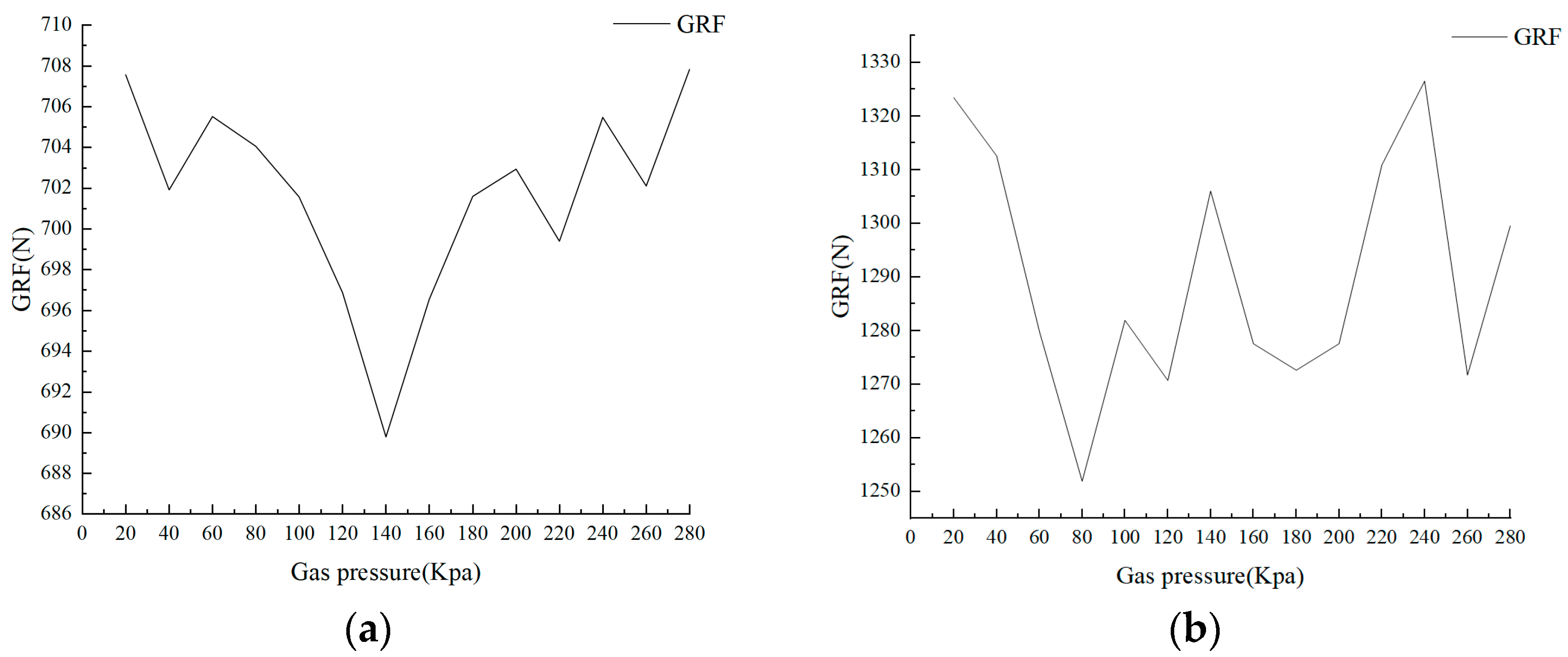
2.3.1. Air Pressure and Foot Pressure
2.3.2. Speed and Foot Pressure
2.3.3. Model of Air Pressure, Foot Pressure, and Speed
2.4. Establishing a System Stability Model
2.4.1. Establishing the System Dynamics Equation
2.4.2. Linearized System Dynamics Equations
2.4.3. Stability Analysis
2.4.4. Stability Control Strategy
3. Overall Design of Active Control System for Treadmill Shock Absorption
4. Experimental Data Collection
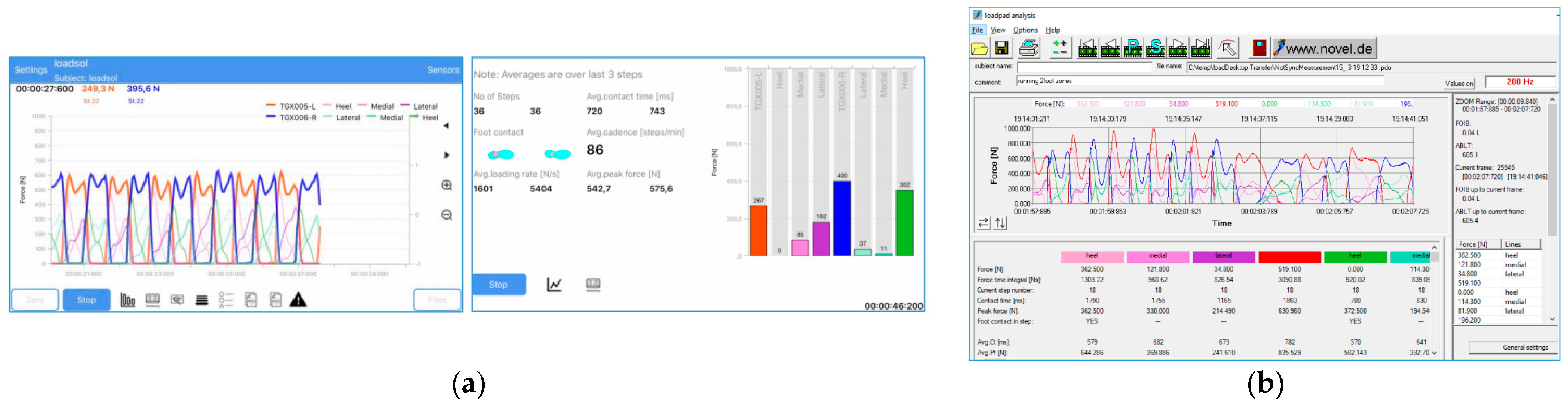
4.1. Foot Pressure Testing System
4.1.1. Dataset Creation
4.1.2. Data Processing
5. Experimental Data
5.1. Establishment of the Dataset
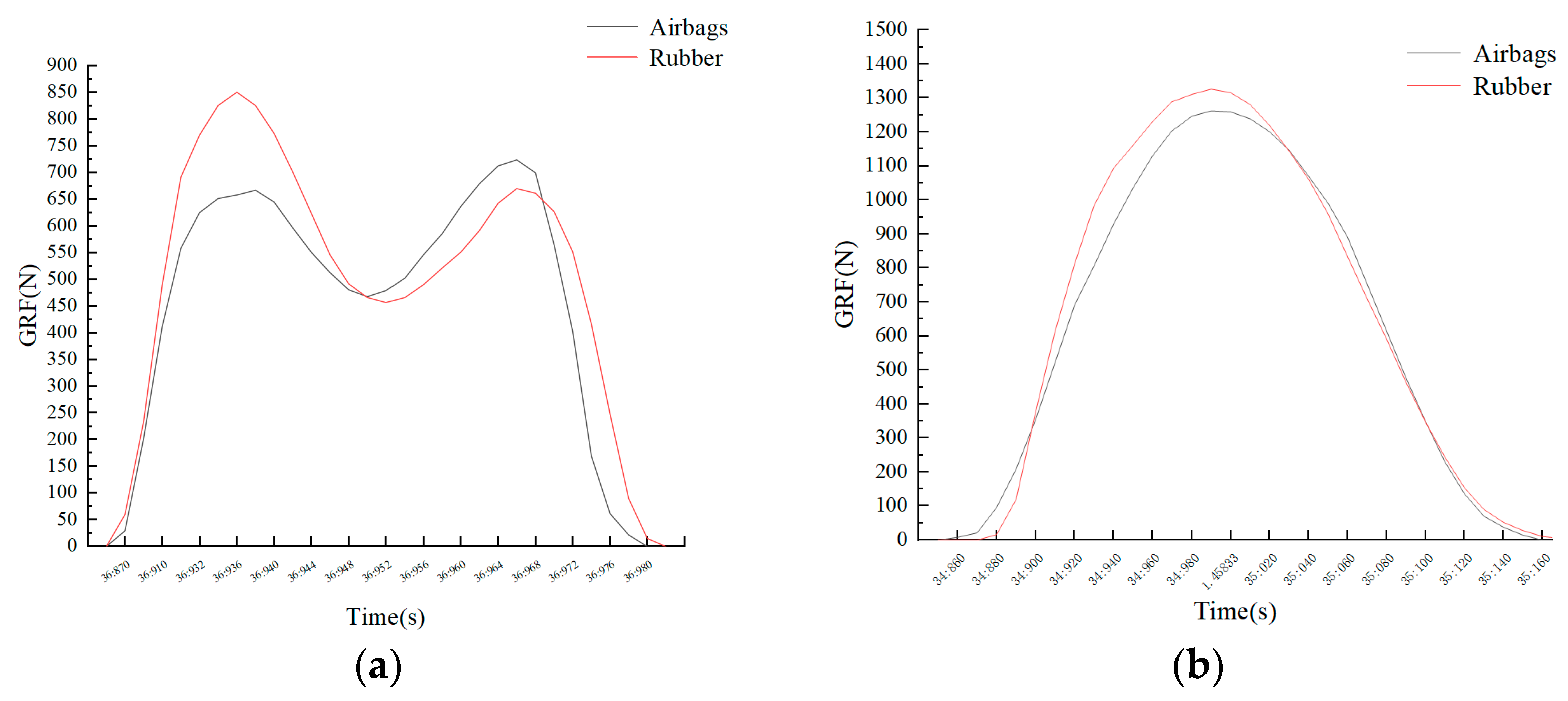
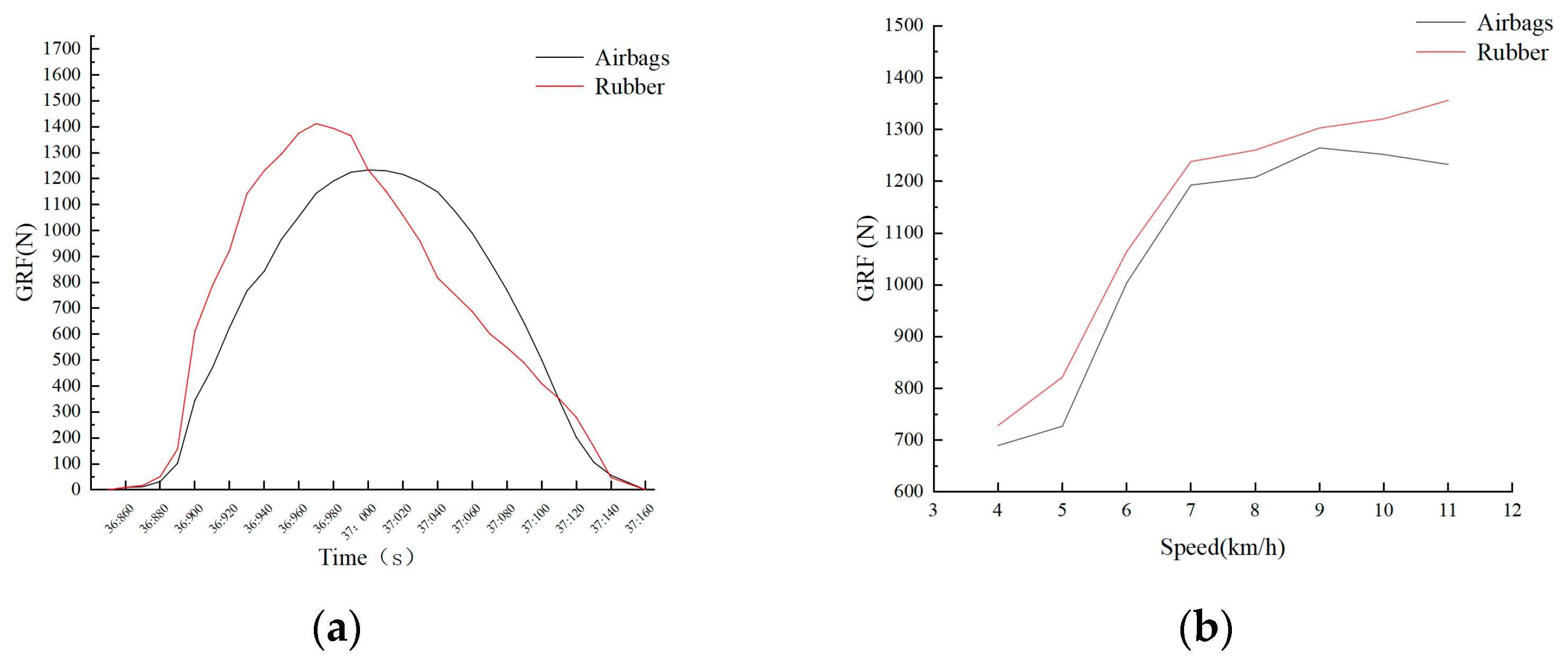
5.2. Comparison of GRF
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munro, C.F.; Miller, D.I.; Fuglevand, A.J. Ground reaction forces in running: A reexamination. J. Biomech. 1987, 20, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Besier, T.; Lloyd, D.G.; Wilkie, J.C.; Ackland, T. External loading of the knee joint during running and cutting maneuvers. Med. Sci. Sports Exerc. 2001, 33, 1168–1175. [Google Scholar] [CrossRef] [PubMed]
- Fields, K.B.; Sykes, J.C.; Walker, K.M.; Jackson, J.C. Prevention of running injuries. Curr. Sports Med. Rep. 2010, 9, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Hreljac, A. Impact and overuse injuries in runners. Med. Sci. Sports Exerc. 2004, 36, 845–849. [Google Scholar] [CrossRef] [PubMed]
- Winter, D. Moments of force and mechanical power in jogging. In Proceedings of the 1999 ICRA, Detroit, MI, USA, 10–15 May 1999; pp. 368–374. [Google Scholar]
- Colino, E.; Felipe, J.L.; Van Hooren, B.; Gallardo, L.; Meijer, K.; Lucia, A.; Lopez-Fernandez, J.; Garcia-Unanue, J. Mechanical properties of treadmill surfaces compared to other overground sport surfaces. Sensors 2020, 20, 3822. [Google Scholar] [CrossRef] [PubMed]
- Ricard, M.D.; Veatch, S. Effect of running speed and aerobic dance jump height on vertical ground reaction forces. J. Appl. Biomech. 1994, 10, 14–27. [Google Scholar] [CrossRef]
- Wank, V.; Frick, U.; Schmidtbleicher, D. Kinematics and electromyography of lower limb muscles in overground and treadmill running. Int. J. Sports Med. 1998, 19, 455–461. [Google Scholar] [CrossRef]
- Rodden, P.T. Treadmill with Elastomeric-Spring Mounted Deck. U.S. Patent 5,336,144, 9 August 1994. [Google Scholar]
- Yuegang, M.A. Shock Absorption Mechanism for Treadmill. U.S. Patent 16/360,998, 18 June 2020. [Google Scholar]
- Moser, G. Treadmill. U.S. Patent 15/798,373, 15 February 2018. [Google Scholar]
- Nigg, B.M.; Wakeling, J.M. Impact forces and muscle tuning: A new paradigm. Exerc. Sport Sci. Rev. 2001, 29, 37–41. [Google Scholar] [CrossRef]
- Nikooyan, A.A.; Zadpoor, A.A. An improved cost function for modeling of muscle activity during running. J. Biomech. 2011, 44, 984–987. [Google Scholar] [CrossRef]
- Putti, A.B.; Arnold, G.P.; Cochrane, L.; Abboud, R.J. The Pedar® in-shoe system: Repeatability and normal pressure values. Gait Posture 2007, 25, 401–405. [Google Scholar] [CrossRef]
- Boyd, L.; Bontrager, E.; Mulroy, S.; Perry, J. The reliability and validity of the novel Pedar system of in-shoe pressure measurement during free ambulation. Gait Posture 1997, 5, 165. [Google Scholar] [CrossRef]
- Bus, S.A.; Ulbrecht, J.S.; Cavanagh, P.R. Pressure relief and load redistribution by custom-made insoles in diabetic patients with neuropathy and foot deformity. Clin. Biomech. 2004, 19, 629–638. [Google Scholar] [CrossRef] [PubMed]
- Owings, T.M.; Apelqvist, J.; Stenström, A.; Becker, M.; Bus, S.A.; Kalpen, A.; Ulbrecht, J.S.; Cavanagh, P.R. Plantar pressures in diabetic patients with foot ulcers which have remained healed. Diabet. Med. 2009, 26, 1141–1146. [Google Scholar] [CrossRef] [PubMed]



| Ac | a | b | c | d | e | |
|---|---|---|---|---|---|---|
| Hard footwear | 2.0 | 1.38 | 0.75 | 1 | ||
| Soft footwear | 2.0 | 1.38 | 0.75 | 1 |
| Speed (km/h) | 4 km/h | 5 km/h | 6 km/h | 7 km/h | 8 km/h | 9 km/h | 10 km/h | 11 km/h |
|---|---|---|---|---|---|---|---|---|
| Airbag (N) | 689.7 | 726.9 | 1003.7 | 1192.7 | 1207.9 | 1264.7 | 1251.9 | 1232.5 |
| Rubber (N) | 728.4 | 821.9 | 1064.1 | 1238.2 | 1260.2 | 1303.0 | 1320.5 | 1356.4 |
| Difference (N) | 38.6 | 95.0 | 60.3 | 45.4 | 52.3 | 38.2 | 68.6 | 123.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Wang, X.; Wang, Z.; Wu, X. Research on Optimal Control of Treadmill Shock Absorption Based on Ground Reaction Force Constraint. Appl. Sci. 2024, 14, 9509. https://doi.org/10.3390/app14209509
Huang L, Wang X, Wang Z, Wu X. Research on Optimal Control of Treadmill Shock Absorption Based on Ground Reaction Force Constraint. Applied Sciences. 2024; 14(20):9509. https://doi.org/10.3390/app14209509
Chicago/Turabian StyleHuang, Lang, Xiancheng Wang, Zeng Wang, and Xueguang Wu. 2024. "Research on Optimal Control of Treadmill Shock Absorption Based on Ground Reaction Force Constraint" Applied Sciences 14, no. 20: 9509. https://doi.org/10.3390/app14209509
APA StyleHuang, L., Wang, X., Wang, Z., & Wu, X. (2024). Research on Optimal Control of Treadmill Shock Absorption Based on Ground Reaction Force Constraint. Applied Sciences, 14(20), 9509. https://doi.org/10.3390/app14209509





