Optimization of Rotary Drilling Rig Mast Structure Based on Multi-Dimensional Improved Salp Swarm Algorithm
Abstract
1. Introduction
2. Working Conditions and Mathematical Modelling of Masts
2.1. Introduction to Rotary Drilling Rig
2.2. Classification of Working Conditions
2.3. Optimization Models
2.4. Limitations
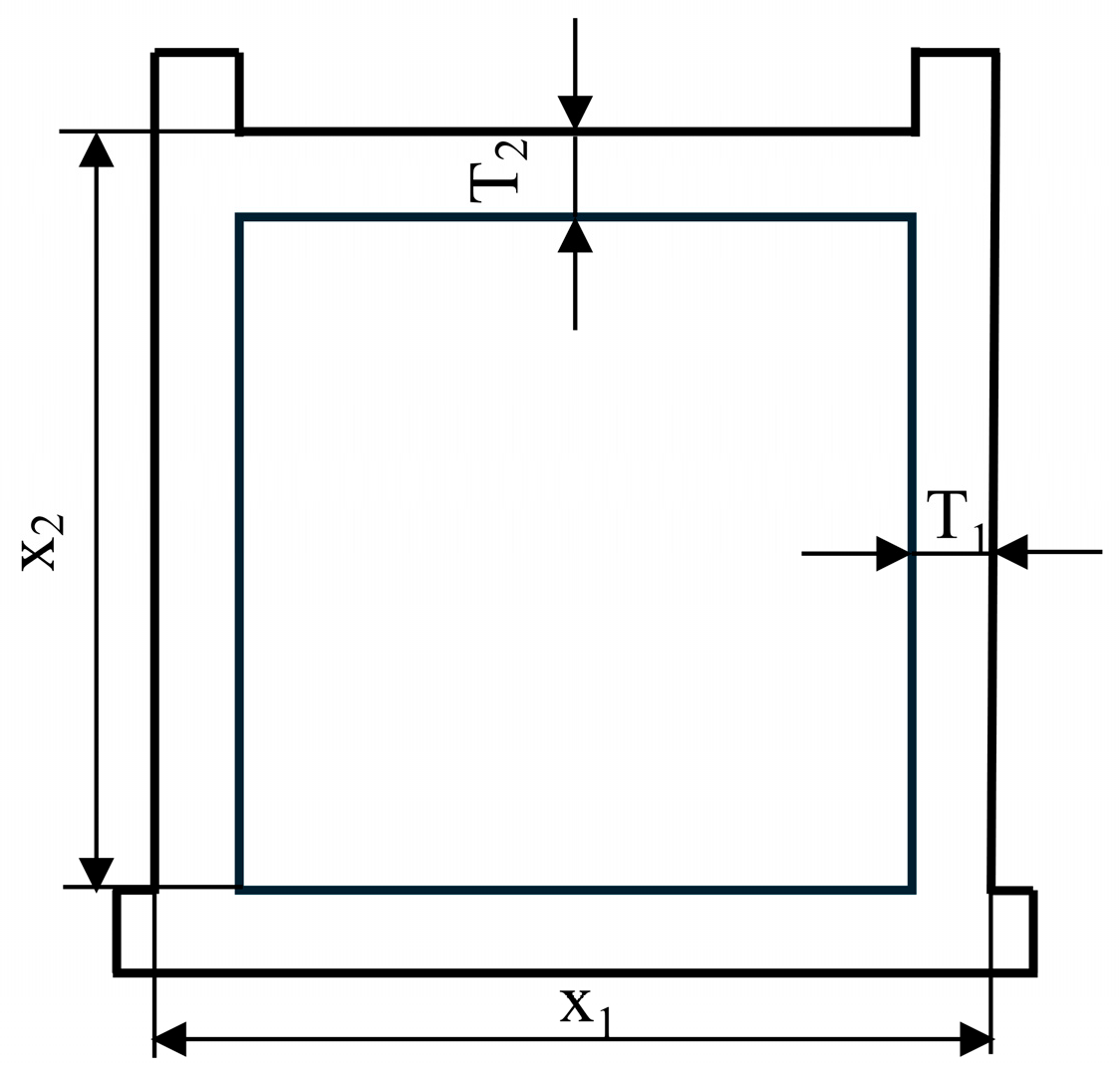
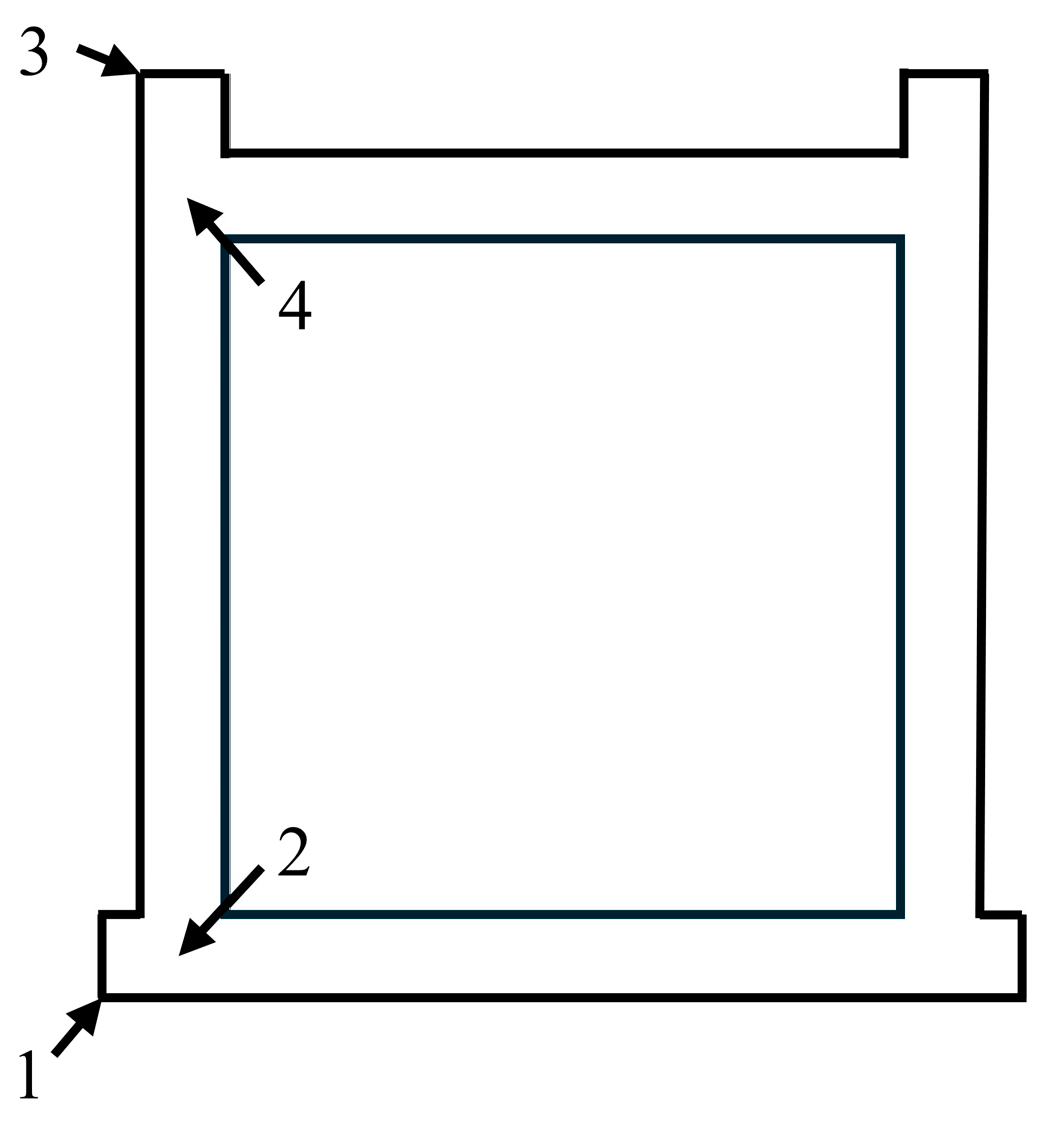
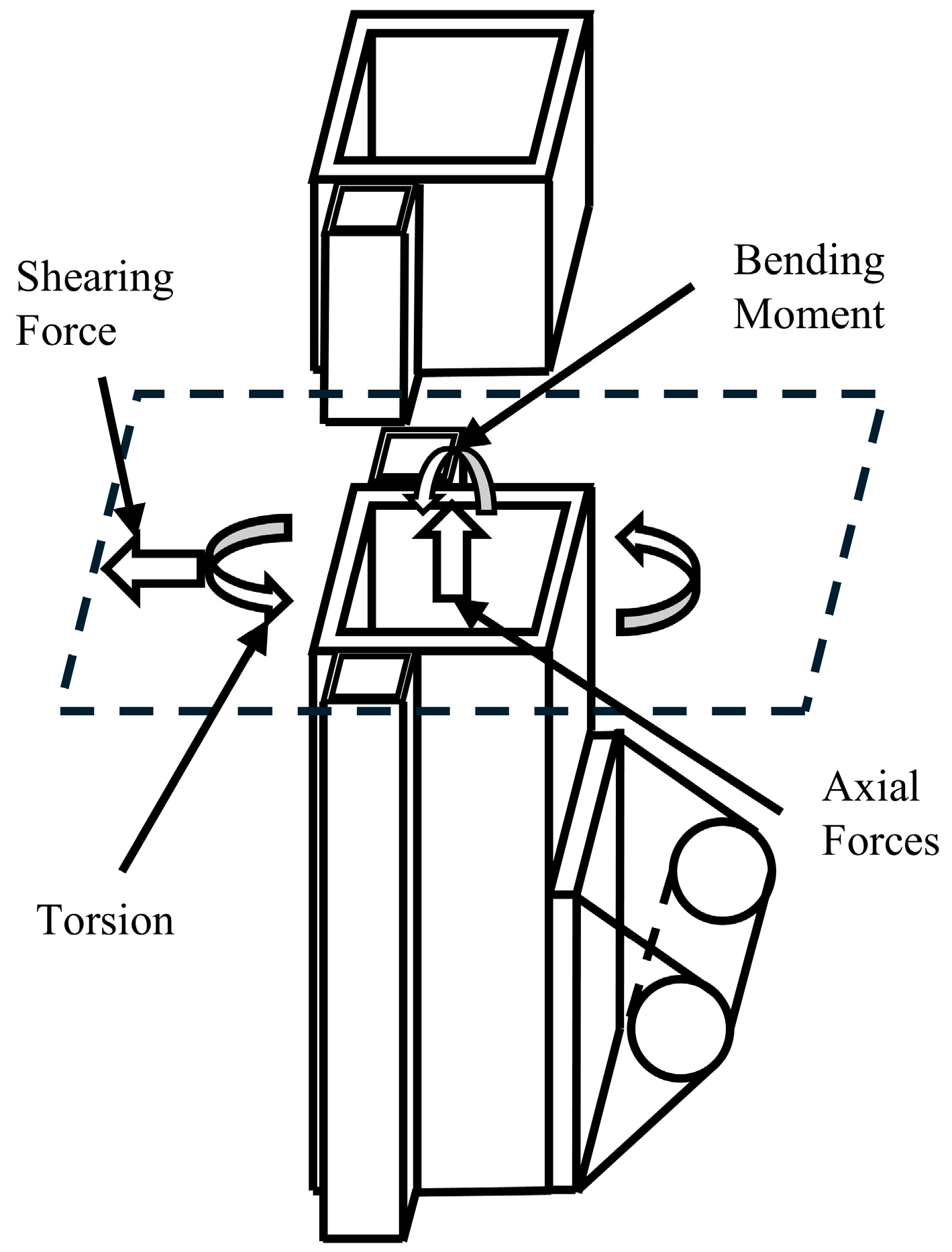
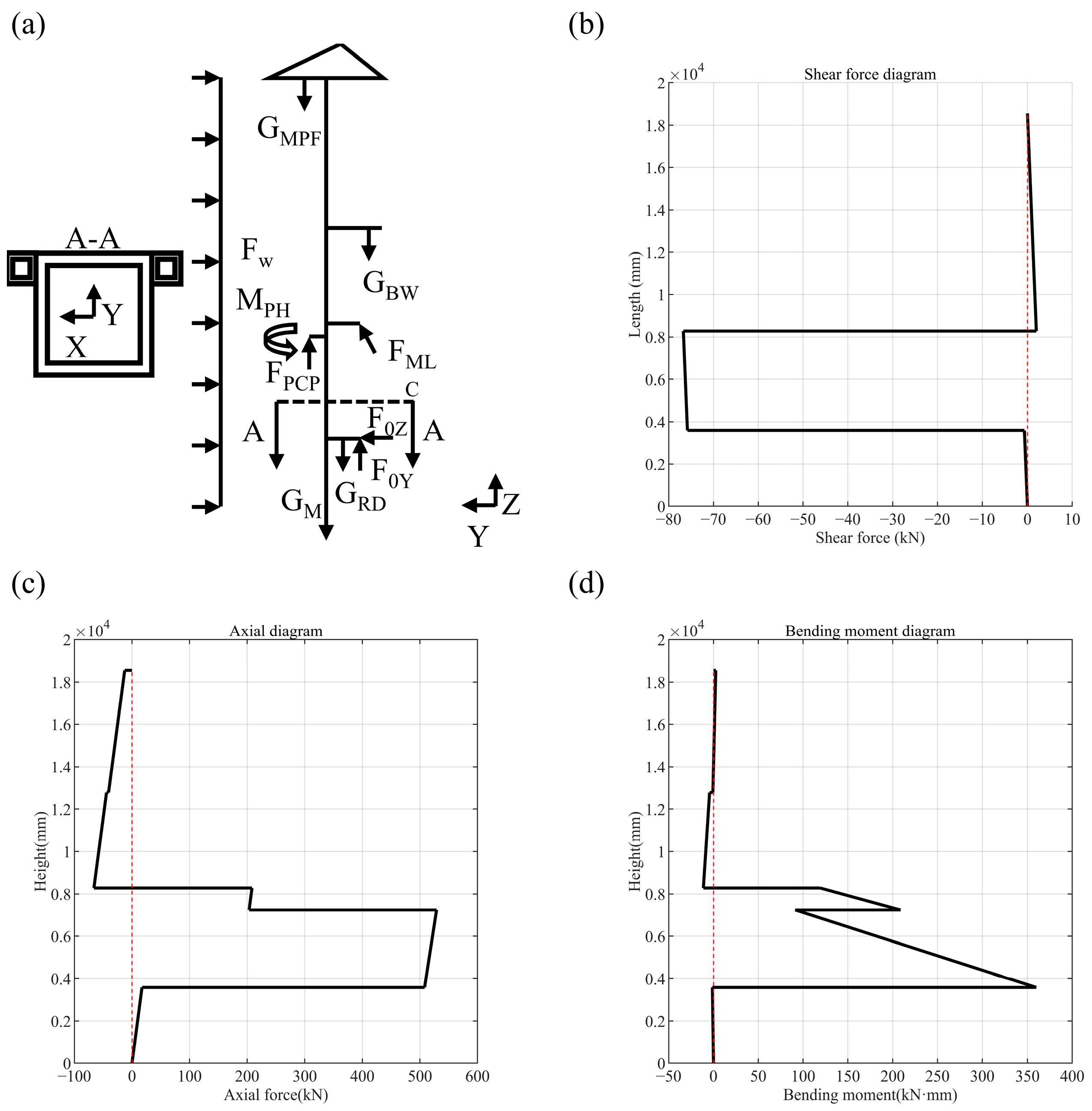
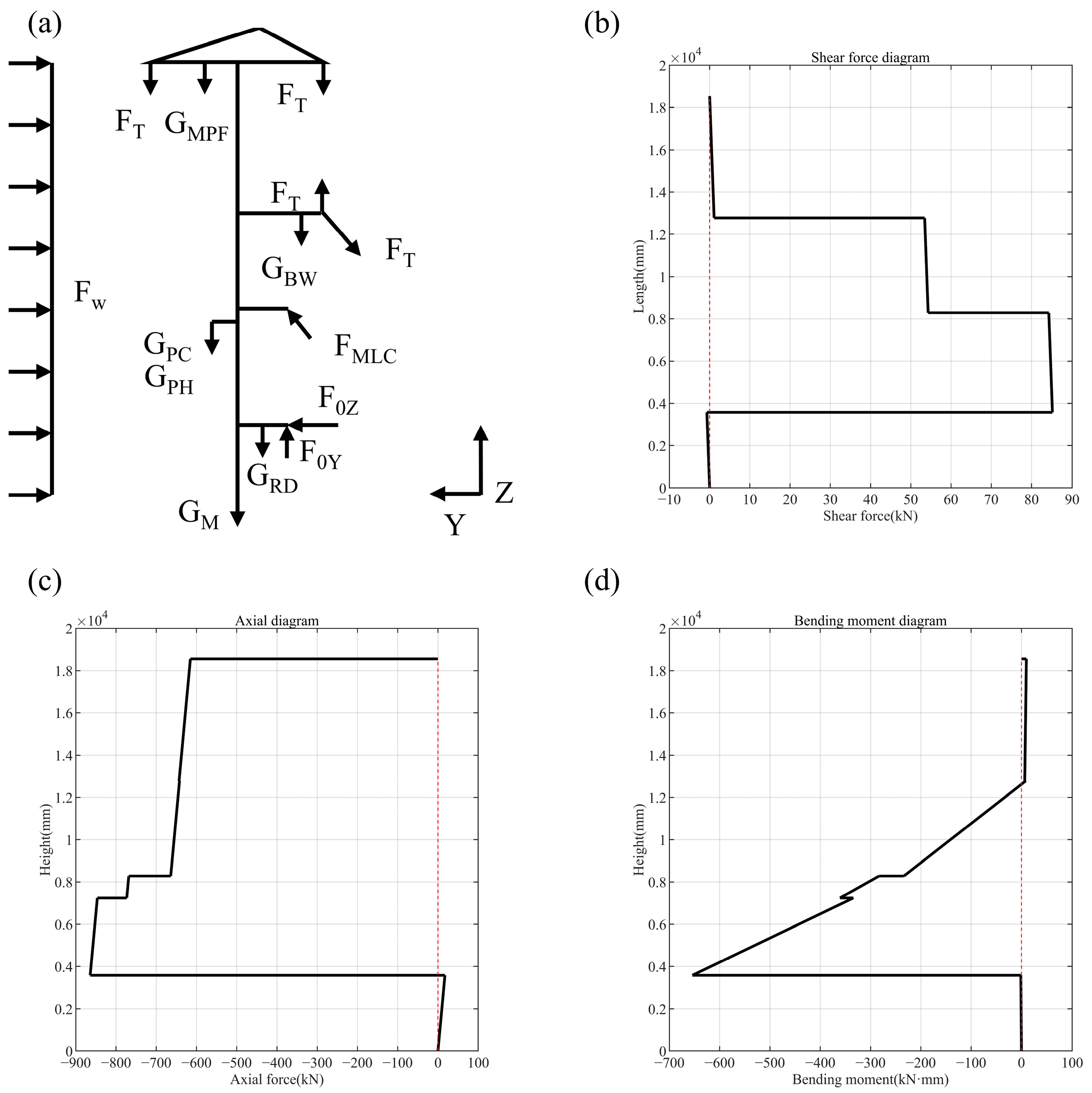
2.4.1. Selection of Hazardous Points for Mast Calibration Section
2.4.2. Static Strength Checks and Constraints
2.4.3. Fatigue Calculations and Constraints
2.4.4. Stiffness Calculations and Constraints
2.4.5. Stability Calculations and Constraints
2.4.6. Process Constraints
3. Improvement of Salp Swarm Algorithm
3.1. Principles of the Salp Swarm Algorithm
| Algorithm 1 SSA Flow | |
| 1: | Initialization parameters: Population size N and maximum number of iterations L |
| 2: | |
| 3: | Selection of food sources F. |
| 4: | for l = 1:L |
| 5: | for i = 1:N |
| 6: | if (i < N/2) |
| 7: | Updating the leader |
| 8: | |
| 9: | else |
| 10: | Update followers |
| 11: | |
| 12: | end if |
| 13: | end for |
| 14: | Updating of food source F |
| 15: | end while |
| 16: | Output optimal solution |
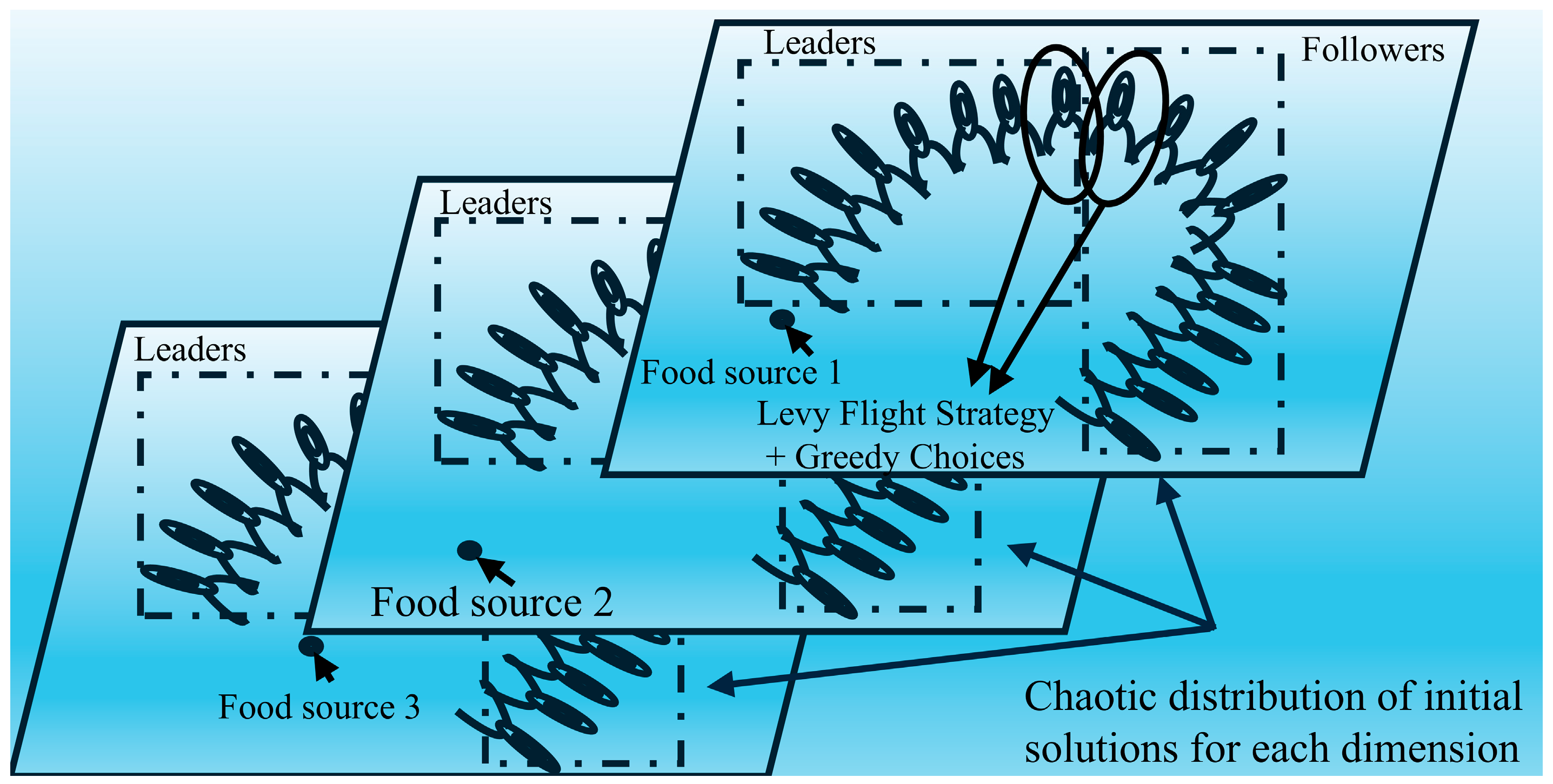
3.2. Improved Salp Swarm Algorithm
3.2.1. Algorithmic Multidimensional Settings
3.2.2. Population Initialization
3.2.3. Leader Renewal
3.2.4. Follower Updates
| Algorithm 2 Pseudo-Code of Proposed ISSA | |
| 1: | Initialization |
| 2: | Define the population size M, algorithm dimension N, maximum iteration times L. |
| 3: | The variables for the initial population in each dimension were chaotically distributed and rounded (The following variables are the variables x1 and x2, unless otherwise specified). |
| 4: | Find the optimal initial values for each dimension and select for each dimension food source. |
| 5: | for l = 1:L |
| 6: | for n = 1:N |
| 7: | for m = 1:M |
| 8: | if i ≤ M/2 update leader position |
| 9: | Leaders in each dimension move toward the food source in each dimension |
| 10: | else |
| 11: | Updating individual variables of followers in each dimension using Levy flight perturbation and greedy selection strategy |
| 12: | end if |
| 13: | end for |
| 14: | Calculating adaptation, updating the food source for each dimension and recording the global optimal food source |
| 15: | end for |
| 16: | end for |
| 17: | Update the optimal solution in all dimensions |
| 18: | Finish |
4. Experiments
4.1. Parameterization
4.2. Constraints
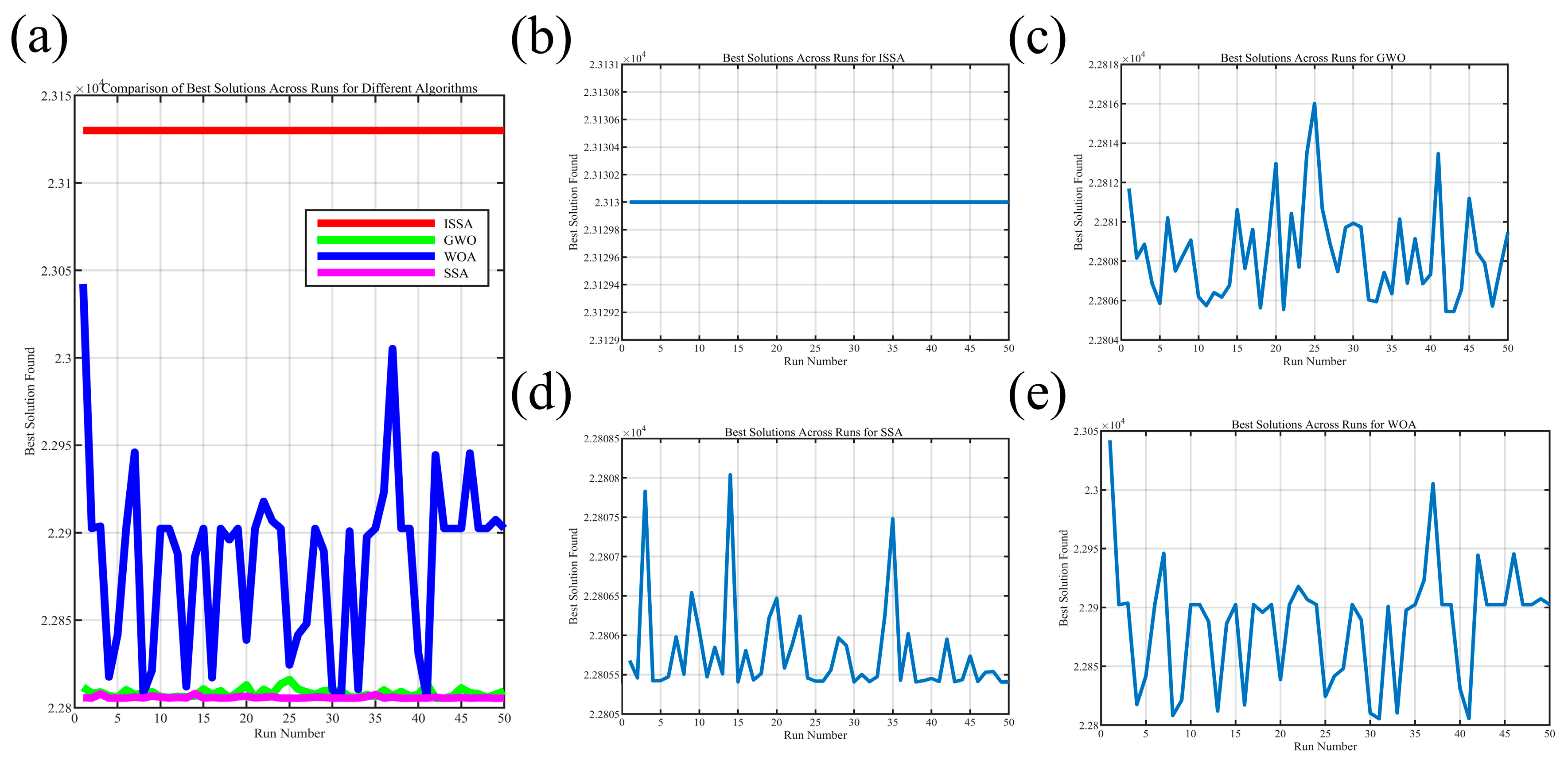
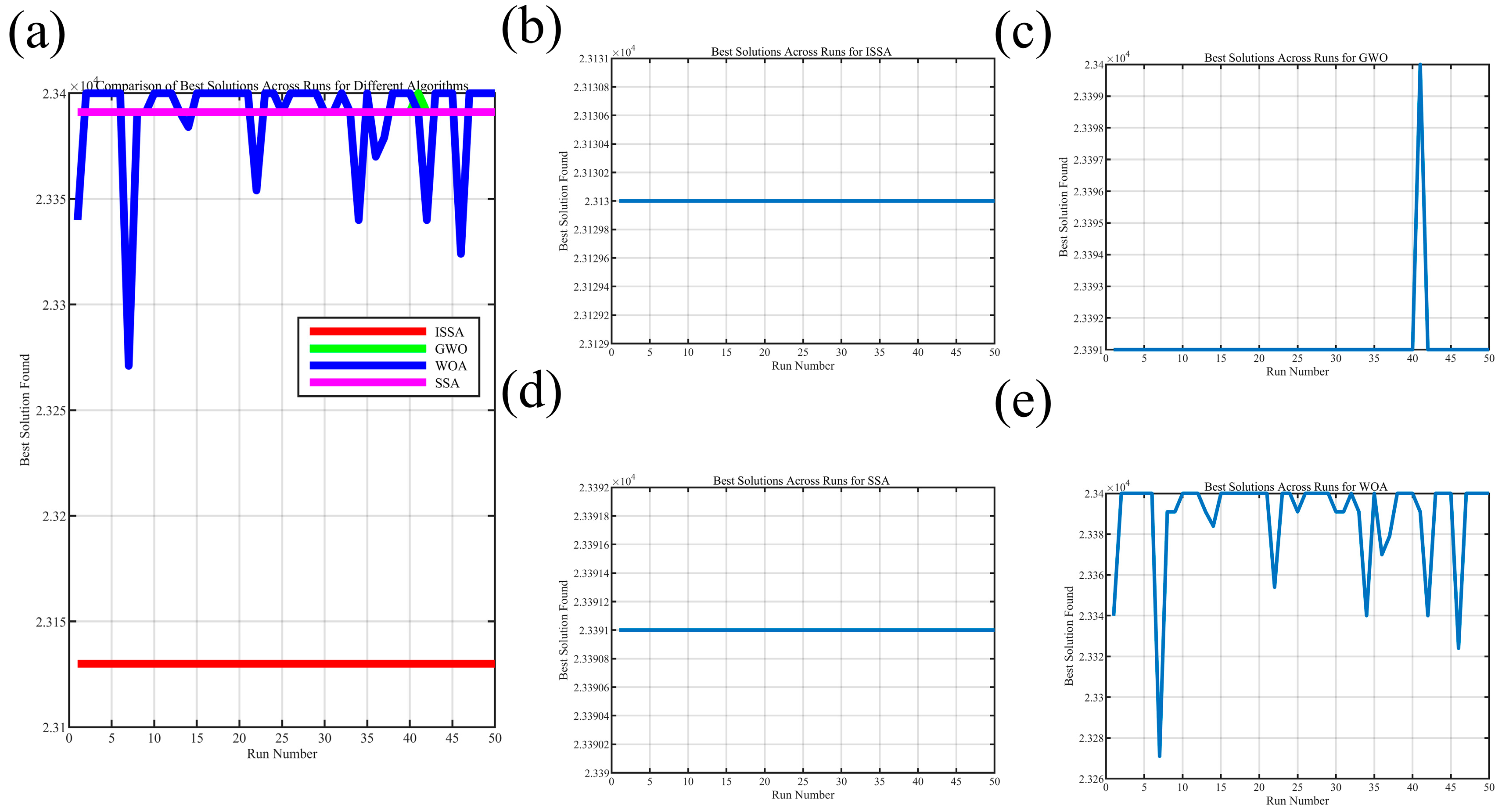
4.3. Comparison and Analysis of Optimization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Savković, M.M.; Bulatović, R.R.; Gašić, M.M.; Pavlović, G.V.; Stepanović, A.Z. Optimization of the box section of the main girder of the single-girder bridge crane by applying biologically inspired algorithms. Eng. Struct. 2017, 148, 452–465. [Google Scholar] [CrossRef]
- Cheng, B.; Qian, Q.; Sun, H. Steel truss bridges with welded box-section members and bowknot integral joints, Part II: Minimum weight optimization. J. Constr. Steel Res. 2013, 80, 475–482. [Google Scholar] [CrossRef]
- Qi, Q.; Yu, Y.; Dong, Q.; Xu, G.; Xin, Y. Lightweight and green design of general bridge crane structure based on multi-specular reflection algorithm. Adv. Mech. Eng. 2021, 13, 16878140211051220. [Google Scholar] [CrossRef]
- Pavlović, G.V.; Zdravković, N.B.; Savković, M.M.; Bulatović, R.R.; Marković, G.Đ. Light-weight design of an overhead crane’s girder with a non-symmetric box cross-section. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 666–676. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Minh, H.-L.; Khatir, S.; Wahab, M.A.; Tran, M.T.; Mirjalili, S. A novel version of Cuckoo search algorithm for solving optimization problems. Expert Syst. Appl. 2021, 186, 115669. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. An improved ant colony optimization for constrained engineering design problems. Eng. Comput. 2010, 27, 155–182. [Google Scholar] [CrossRef]
- Pavlović, G.; Savković, M. Analysis and optimization of the main girder of the bridge crane with an asymmetric box cross-section. Sci. Tech. Rev. 2022, 72, 3–11. [Google Scholar] [CrossRef]
- Hijjawi, M.; Alshinwan, M.; Khashan, O.A.; Alshdaifat, M.; Almanaseer, W.; Alomoush, W.; Garg, H.; Abualigah, L. Accelerated arithmetic optimization algorithm by cuckoo search for solving engineering design problems. Processes 2023, 11, 1380. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Wang, G.-G.; Sangaiah, A.K.; Rushdy, E. Krill herd algorithm based on cuckoo search for solving engineering optimization problems. Multimed. Tools Appl. 2019, 78, 3861–3884. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Singh, S.; Singh, G.; Mittal, N. Self-adaptive salp swarm algorithm for engineering optimization problems. Appl. Math. Model. 2021, 89, 188–207. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018, 48, 3462–3481. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Kassaymeh, S.; Makhadmeh, S.N.; Fraihat, S.; Abdullah, S. Feedforward neural network-based augmented salp swarm optimizer for accurate software development cost forecasting. Appl. Soft Comput. 2023, 149, 111008. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, D.; Zhang, L. DV-Hop localization algorithm based on simulated annealing and optimization of salp swarm. Transducer Microsyst. Technol. 2024, 43, 125–129. [Google Scholar]
- Tang, X.; Cheng, Y.; Pan, S. Look-ahead distance optimization method for pure pursuit control based on time delay compensation. J. Chin. Inert. Technol. 2023, 31, 876–882. [Google Scholar]
- Altay, O.; Cetindemir, O.; Aydogdu, I. Size optimization of planar truss systems using the modified salp swarm algorithm. Eng. Optim. 2024, 56, 469–485. [Google Scholar] [CrossRef]
- Hichri, A.; Hajji, M.; Mansouri, M.; Nounou, H.; Bouzrara, K. Supervised machine learning-based salp swarm algorithm for fault diagnosis of photovoltaic systems. J. Eng. Appl. Sci. 2024, 71, 12. [Google Scholar] [CrossRef]
- Barhoush, M.; Abed-alguni, B.H.; Al-qudah, N.E.A. Improved discrete salp swarm algorithm using exploration and exploitation techniques for feature selection in intrusion detection systems. J. Supercomput. 2023, 79, 21265–21309. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Kang, H.; He, Q.; Xie, Y. Mechanics analysis of rotary drilling rig under drilling-bucket-lifting conditions. Eng. Mech. 2010, 27, 214–218. [Google Scholar]
- Kang, H. Study on Mechanical Properties and Optimization of Working Device of Rotary Drilling Rig; Central South University: Changsha, China, 2013. [Google Scholar]
- Mohamed, A.W. A novel differential evolution algorithm for solving constrained engineering optimization problems. J. Intell. Manuf. 2017, 29, 659–692. [Google Scholar] [CrossRef]
- Dan, L.; Qiang, H.; Li, J. Chaotic optimization algorithm based on Tent map. Control. Decis. 2005, 20, 179–182. [Google Scholar]
- Lu, X.-L.; He, G. QPSO algorithm based on Lévy flight and its application in fuzzy portfolio. Appl. Soft Comput. 2021, 99, 106894. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
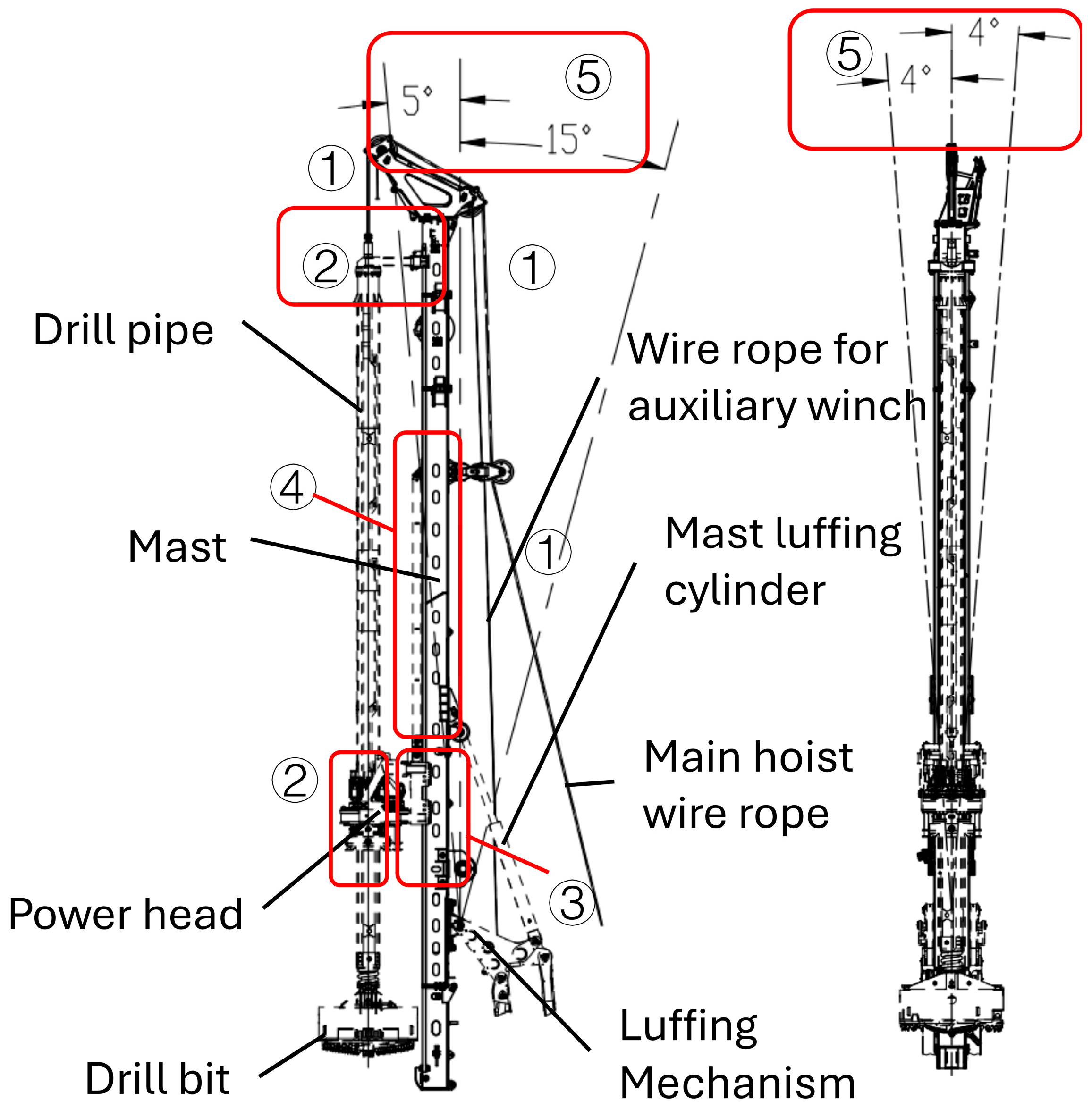


| Working Condition | Description |
|---|---|
| Drilling condition B1 | The mast is perpendicular to the ground, the drill bit is in contact with the ground, the pressure cylinder applies maximum pressure downward, and the power head drives the drill rod bit to dig downward. |
| Out-of-hole lifting condition B2 | The mast of the rotary drilling rig is perpendicular to the ground, the winch lifts outside the hole, and the self-weight of the power head is borne by the pressure cylinder [20], which does not provide lifting force. |
| In-hole lifting condition B3 | The mast is perpendicular to the ground and the main winch lifts the drill pipe and bit in the hole. |
| Dumping condition B4 | The power head can unload the soil in the drill bit by turning it forward and backward. |
| Shaking soil condition B5 | The rotary drilling rig starts and stops continuously through the winch mechanism, rises and lowers the drill pipe to unload the soil using inertia. |
| Walking condition B6 | With the drill pipe fully retracted and the mast perpendicular to the ground, the rotary drilling rig moves to advance to the next construction position. |
| Rotating condition B7 | The drill pipe is fully recovered, the mast is perpendicular to the ground, and the body is rotated for dumping, shaking, and changing bits. |
| B1 | B3 | |
|---|---|---|
| Point 1 Point 3 | Maximum positive free bending stress | |
| Unidirectional state of stress at points 1 and 3 | ||
| Point 2 Point 4 | 1. Positive free bending stress 2. Maximum positive stress in constrained bending 3. Constrained torsional stress 4. Bending shear stress 5. Torsional shear stress | 1. Positive free bending stress 2. Maximum positive bending stress 3. Bending shear stress |
| Points 2 and 4 are three-way stress states | ||
| Parameters | Numerical Value |
|---|---|
| Mast deadweight | GM = 70.71 kN |
| Self-weight of rotary disk | GRD = 5.13 kN |
| Back wheel deadweight | GBK = 2.76 kN |
| Main pulley frame deadweight | GMPF = 9.89 kN |
| Pressure cylinder deadweight | GPC = 6.79 kN |
| Pressure cylinder pressurization | FPCP = 210 kN |
| Pressure cylinder lifting force | FT1 = 210 kN |
| The main hoist lifting force | FT = 190 kN |
| Power head torque | MPH = 210 kN·m |
| Self-weight of power head | GPH = 50.51 kN |
| ISSA | GWO | SSA | WOA | |
|---|---|---|---|---|
| x1 | 591 | 600 | 600 | 600 |
| x2 | 591 | 600 | 600 | 600 |
| x3 | 10 | 10.34 | 10.42 | 11.20 |
| x4 | 20 | 18.66 | 18.58 | 17.87 |
| g1 | −89.33 | −85.50 | −85.06 | −81.35 |
| g2 | −123.10 | −121.20 | −121.06 | −119.88 |
| g3 | −60.77 | −57.36 | −56.87 | −51.95 |
| g4 | −83.82 | −84.55 | −84.46 | −83.63 |
| g5 | 0 | 0 | 0 | 0 |
| g6 | −0.33 | 0 | 0 | 0 |
| Degree of adaptation | 23,130 | 22,808.40 | 22,805.90 | 22,842.80 |
| ISSA | GWO | SSA | WOA | |
|---|---|---|---|---|
| x1 | 591 | 600 | 600 | 600 |
| x2 | 591 | 600 | 600 | 600 |
| x3 | 10 | 11 | 11 | 12 |
| x4 | 20 | 19 | 19 | 18 |
| Degree of adaptation | 23,130 | 23,391 | 23,391 | 23,384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Ren, Y.; Xu, G. Optimization of Rotary Drilling Rig Mast Structure Based on Multi-Dimensional Improved Salp Swarm Algorithm. Appl. Sci. 2024, 14, 10040. https://doi.org/10.3390/app142110040
Yang H, Ren Y, Xu G. Optimization of Rotary Drilling Rig Mast Structure Based on Multi-Dimensional Improved Salp Swarm Algorithm. Applied Sciences. 2024; 14(21):10040. https://doi.org/10.3390/app142110040
Chicago/Turabian StyleYang, Heng, Yuhang Ren, and Gening Xu. 2024. "Optimization of Rotary Drilling Rig Mast Structure Based on Multi-Dimensional Improved Salp Swarm Algorithm" Applied Sciences 14, no. 21: 10040. https://doi.org/10.3390/app142110040
APA StyleYang, H., Ren, Y., & Xu, G. (2024). Optimization of Rotary Drilling Rig Mast Structure Based on Multi-Dimensional Improved Salp Swarm Algorithm. Applied Sciences, 14(21), 10040. https://doi.org/10.3390/app142110040





