Optimization and Experimental Verification of Lower Articulation for Low-Floor Tram Using Meta-Model
Abstract
:1. Introduction
2. Optimization Model for Lower Articulation
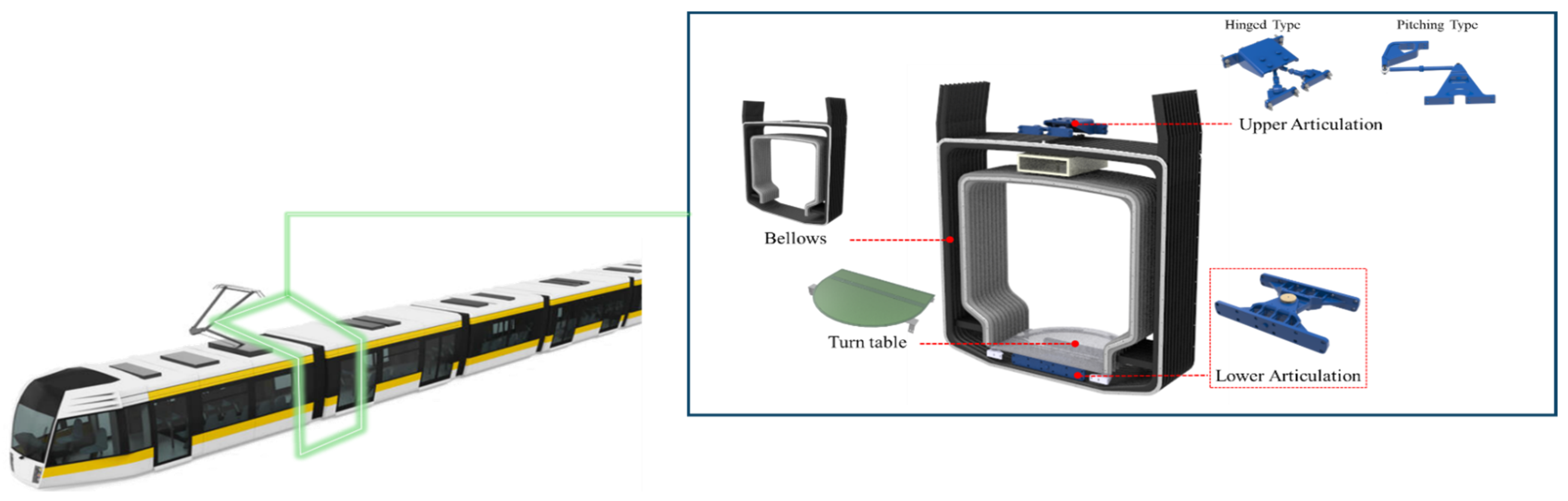
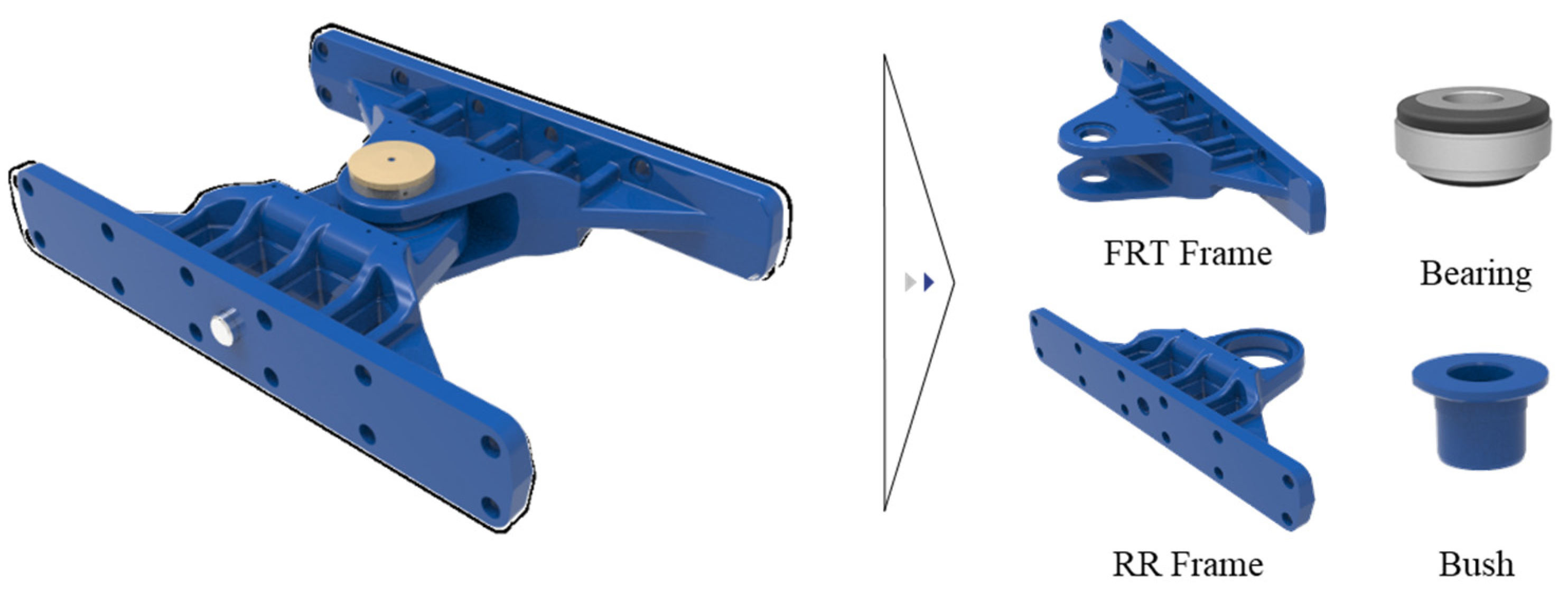
2.1. Lower Articulation
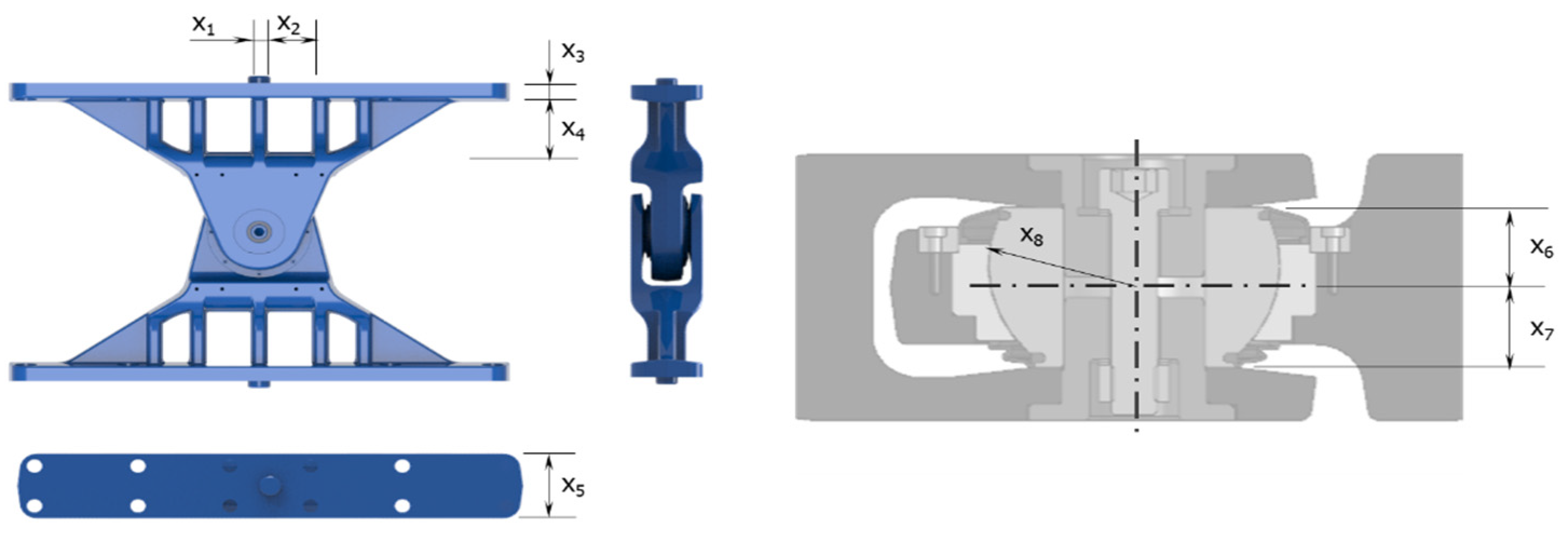
2.2. Design Variable of Lower Articulation
2.2.1. Structural Analysis
2.2.2. Design Variable
2.3. Structure and Fatigue Life Evaluation of Optimized Lower Articulation
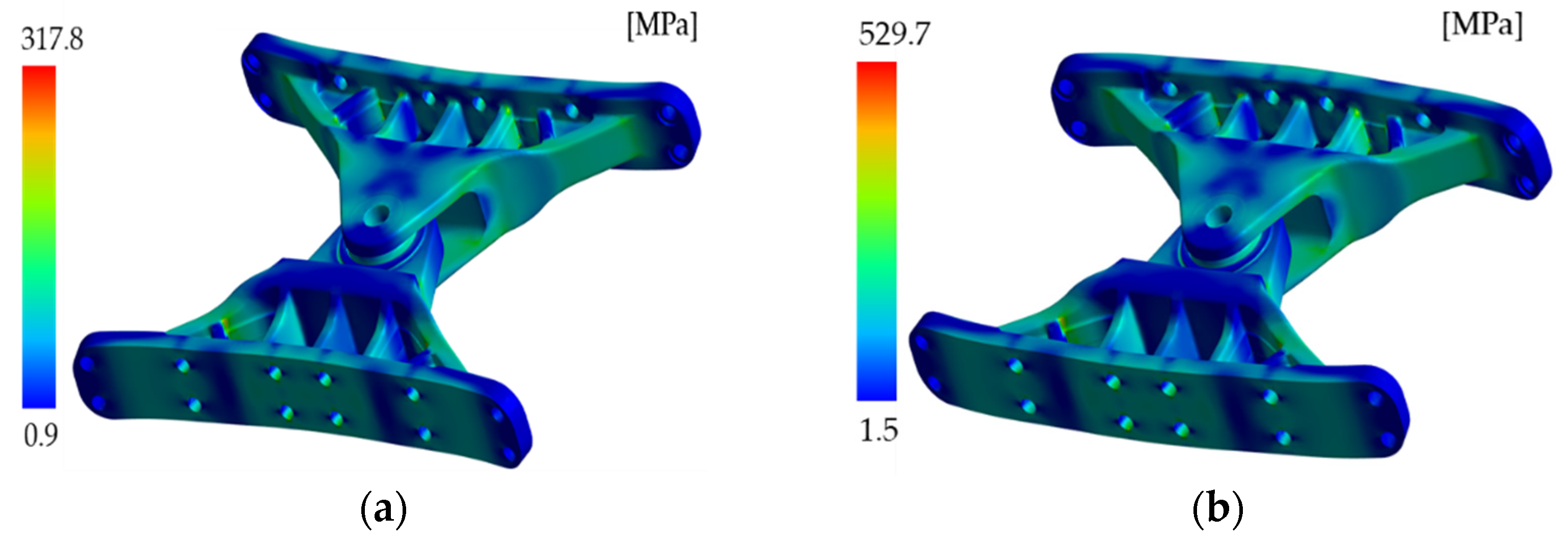
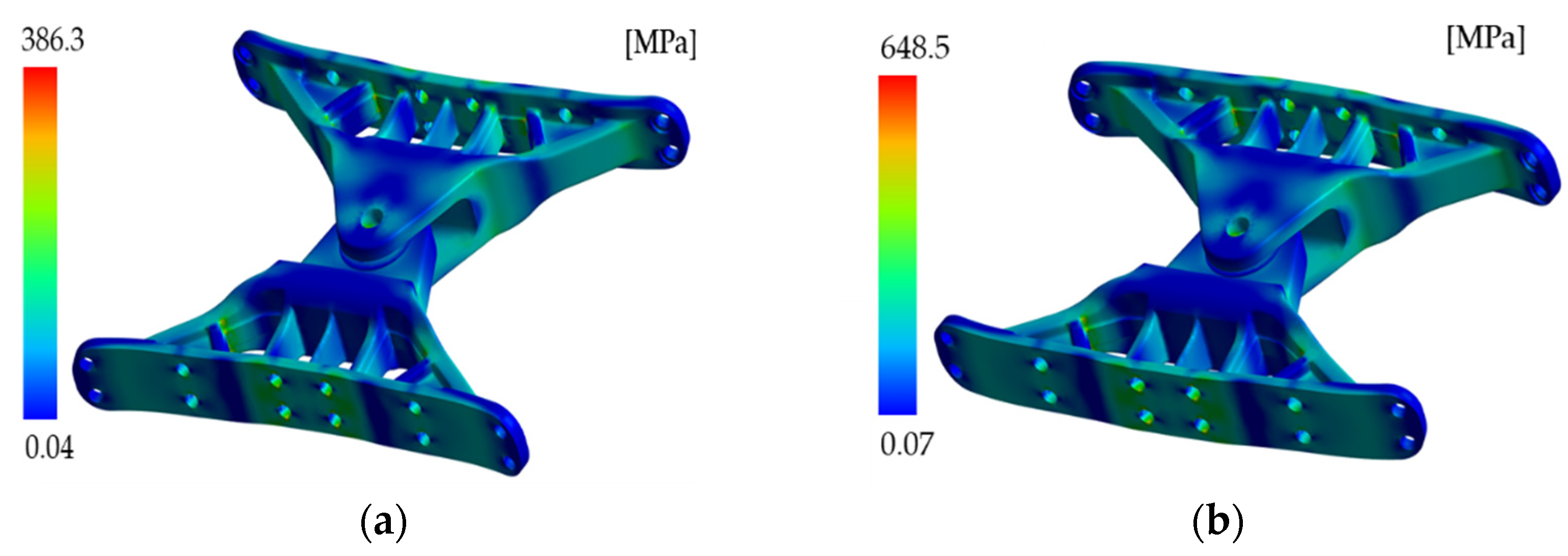
2.3.1. Structural Design Using Meta-Model
2.3.2. Sensitivity Analysis
3. Experimental Verification of Lower Articulation
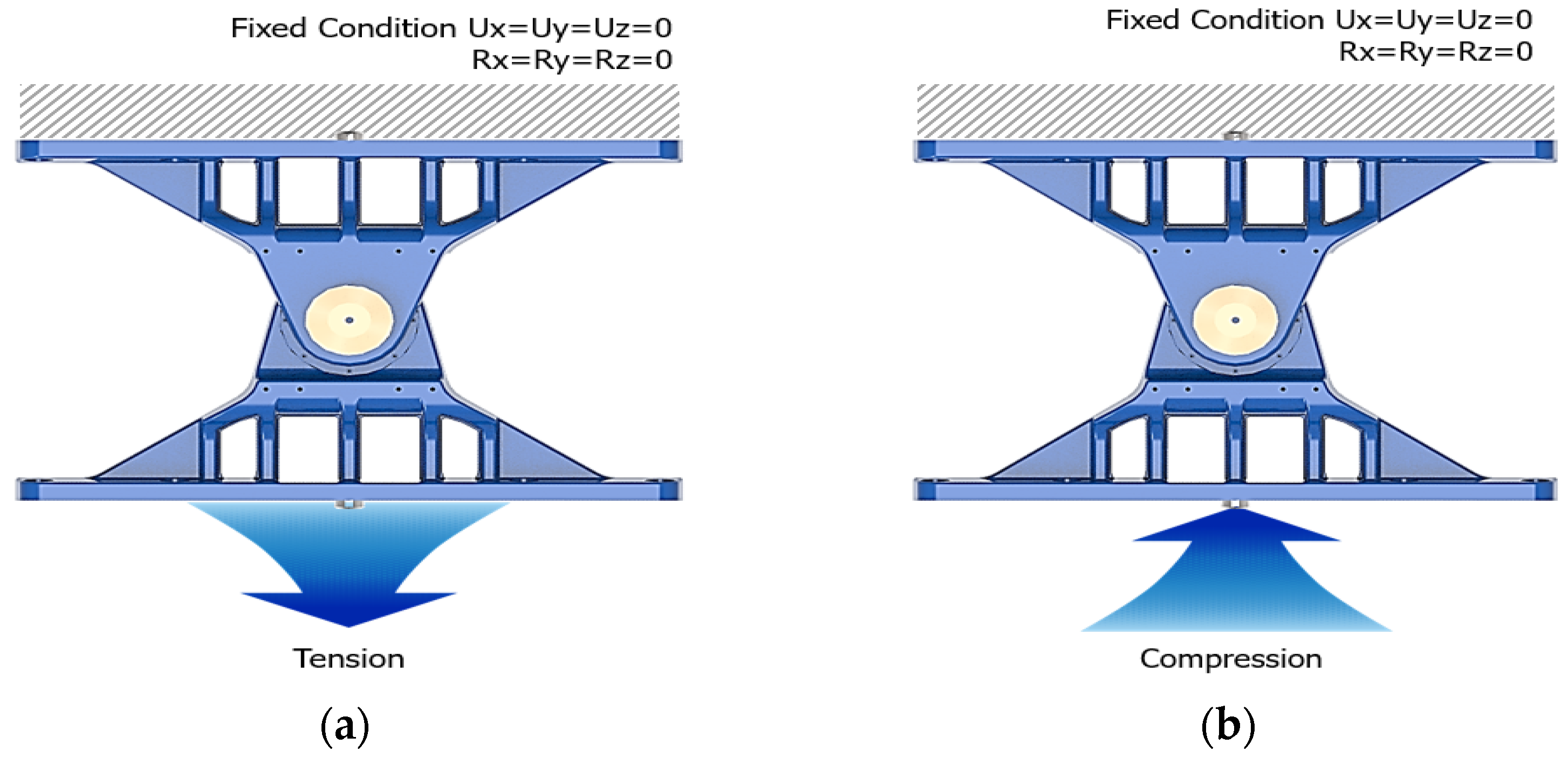
3.1. Structural Test
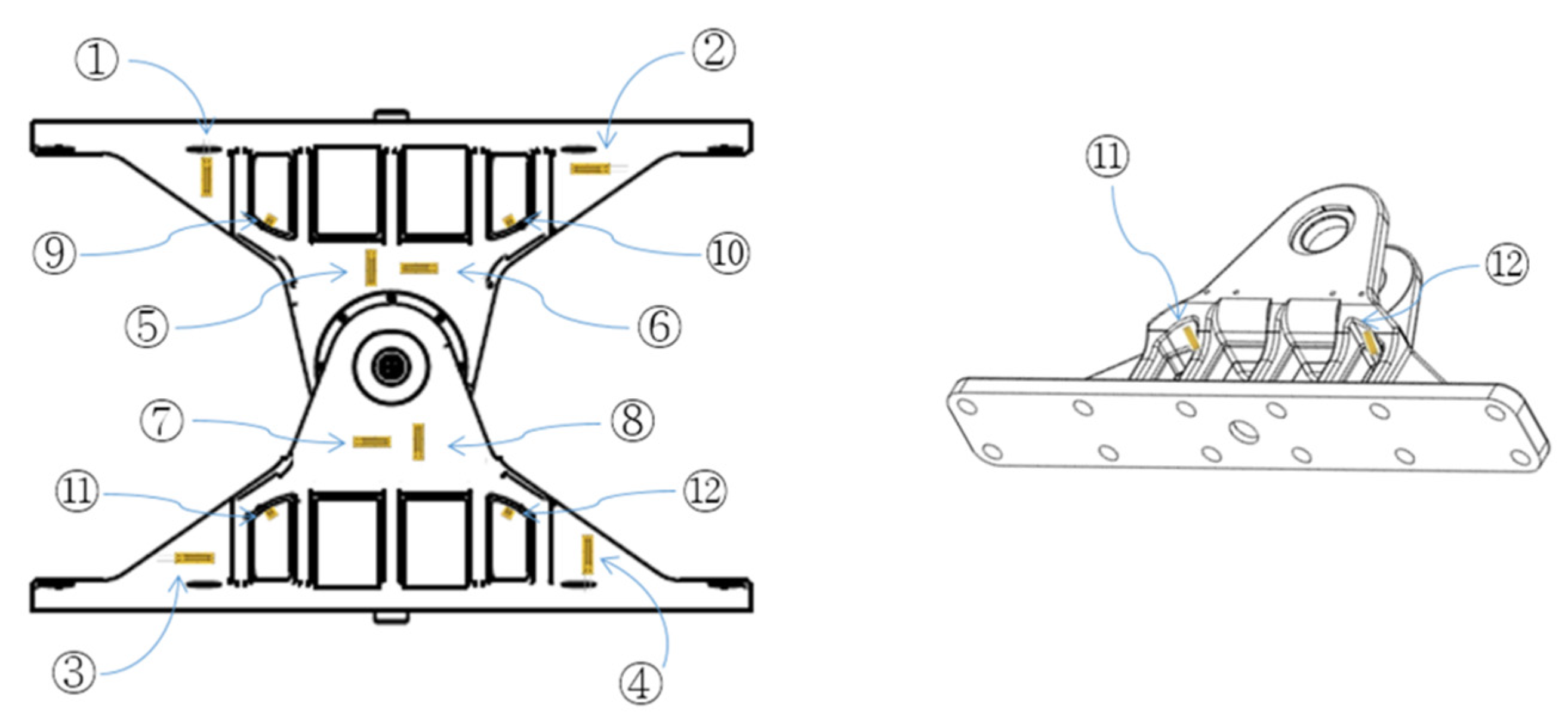
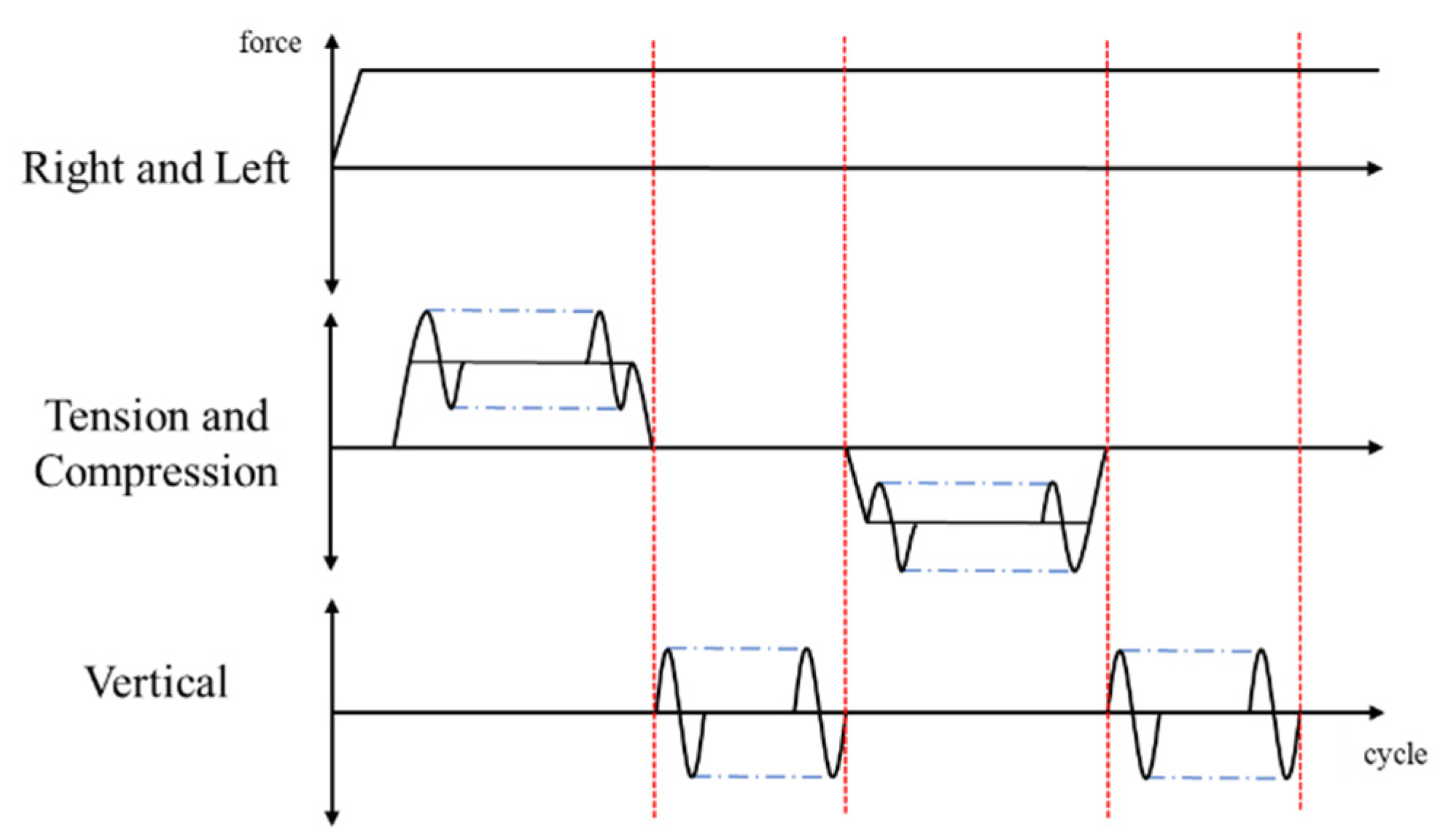
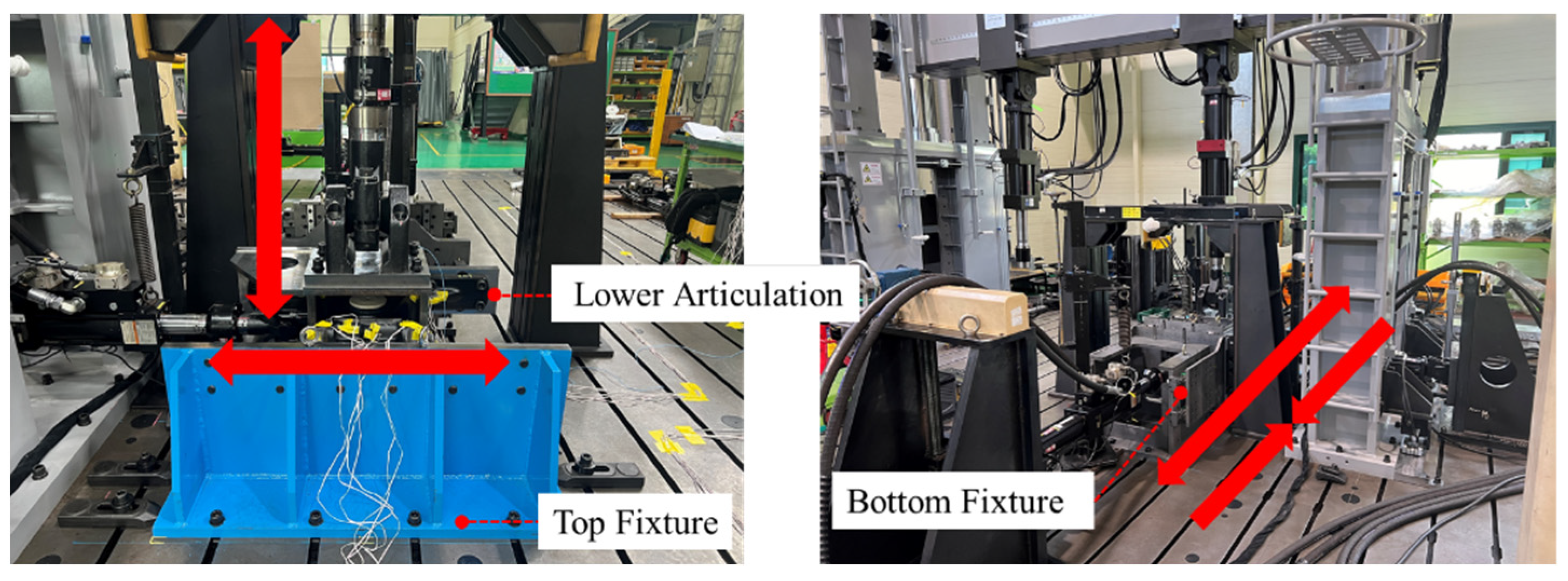
3.1.1. Structural Test Method
3.1.2. Structural Test Results
3.2. Fatigue Test
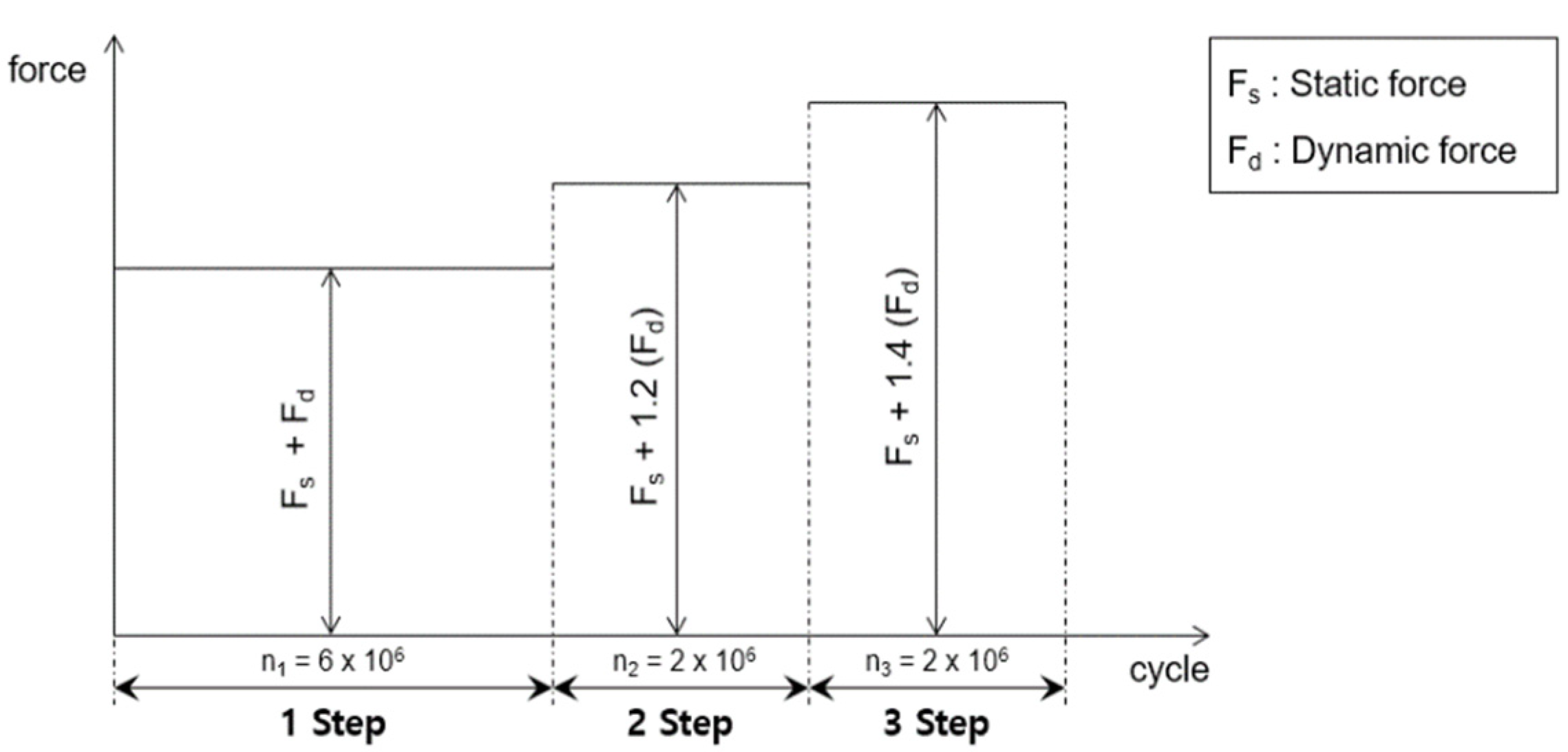
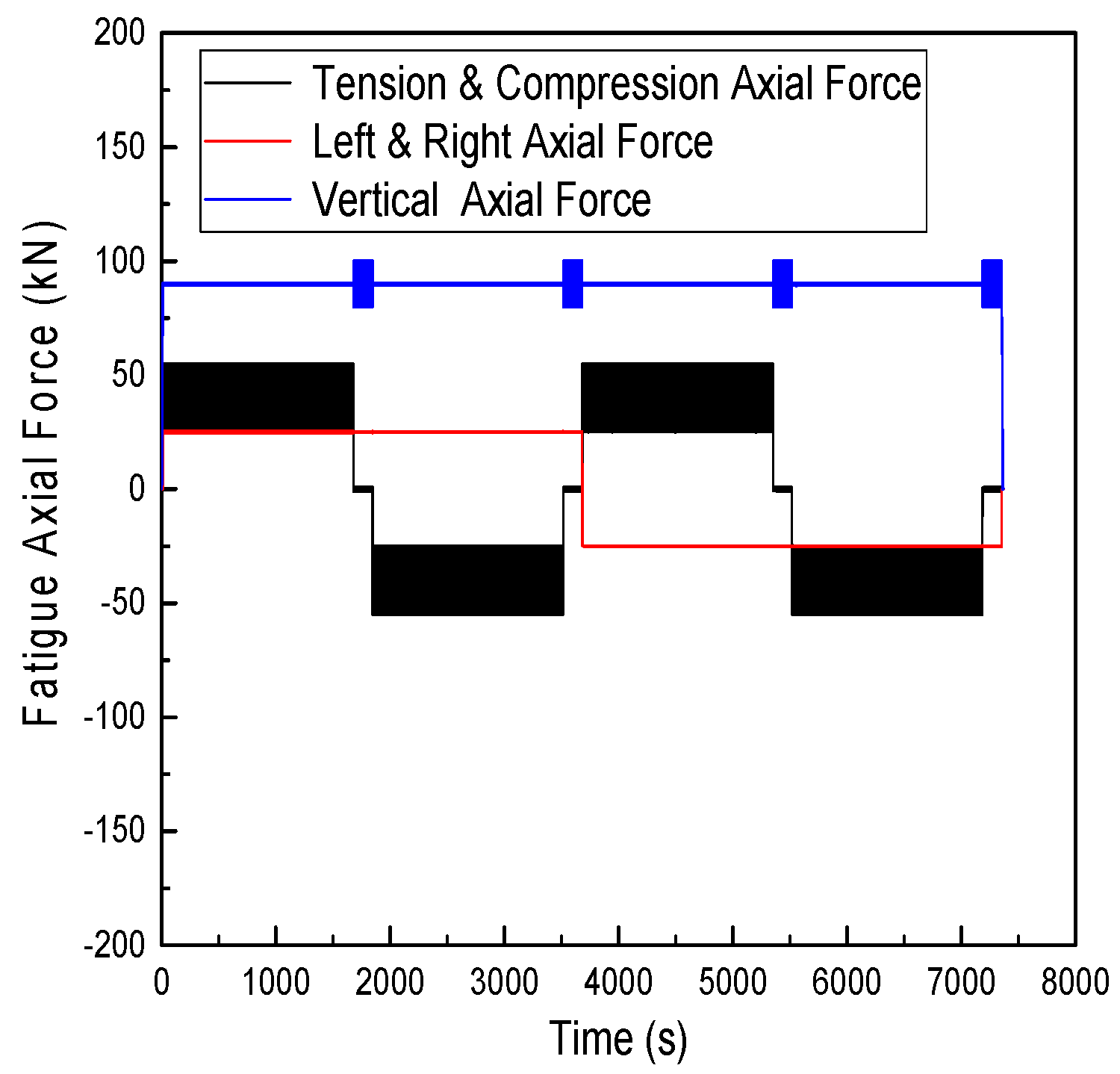
3.2.1. Fatigue Test Method
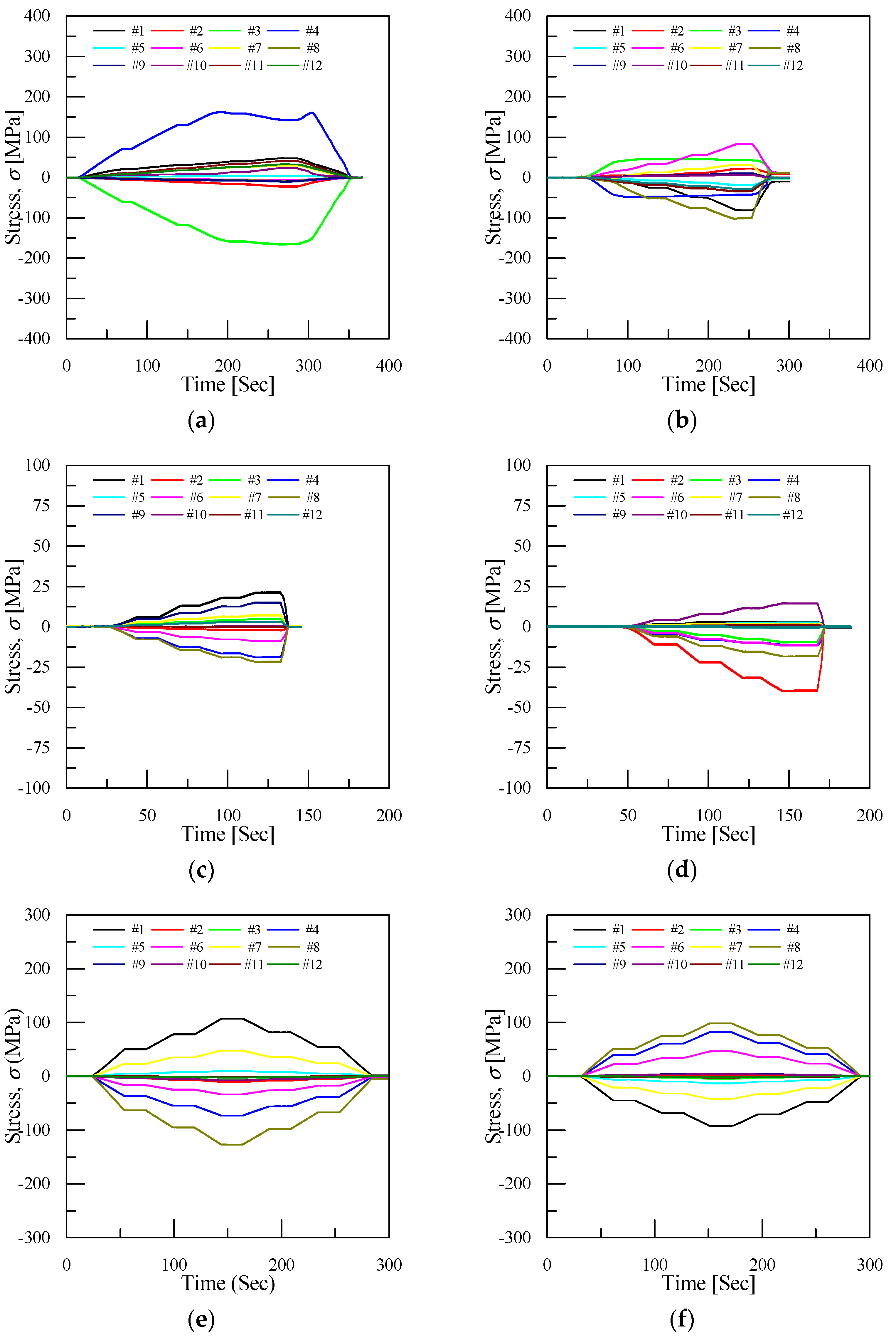
3.2.2. Fatigue Test Results
4. Conclusions
- Eight factors affecting the structural safety of the lower articulation were identified, and their correlations with stress and weight were established.
- The ISCD-II technique was employed to minimize the number of analyses to 16. Sensitivity analyses were used to identify the primary design factors significantly influencing stress and weight.
- The structural safety of the optimized lower articulation was evaluated through both a structural analysis and experimental validation.
- A comparison between the structural analysis and test results revealed an average error within 10% for each load direction, thereby validating the accuracy of the analysis.
- Non-destructive testing conducted after completing the fatigue tests confirmed the absence of fatigue cracks, indicating that adequate durability was achieved.
- The performance and durability of the lower articulation can be tested and verified through real vehicle tests by installing it on a low-floor tram.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uhl, T.; Chudzikiewicz, A. Analytical and experimental investigation of low floor tram dynamics. Veh. Syst. Dyn. 2002, 37, 702–713. [Google Scholar] [CrossRef]
- Lee, S.B.; Ahn, S.; Lee, J.H.; Jang, I.G. Optimization of the wireless power transfer system in an electric railway. In Proceedings of the 2014 IEEE Wireless Power Transfer Conference, Jeju Island, Republic of Korea, 8–9 May 2014; pp. 158–161. [Google Scholar]
- Shimauchi, T. Luxembourg tram system Catenary-free hybrid technology to reduce visual damage to the historical cityscape. Stud. Sci. Technol. 2020, 9, 141–148. [Google Scholar]
- Chudzikiewicz, A.; Korzeb, J. Simulation study of wheels wear in low-floor tram with independently rotating wheels. Arch. Appl. Mech. 2018, 88, 175–192. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Q.; Duan, H.; Liu, C. Energy Storage System Design for Catenary Free Modern Trams. In Proceedings of the 4th International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2019: Novel Traction Drive Technologies of Rail Transportation, Qingdao, China, 25–27 October 2019; Springer: Singapore, 2020; pp. 613–621. [Google Scholar]
- Li, J.; Zhu, X.; Robineau, C. Non-linear stiffness analyzing of a hydraulic assisted turning system in low-floor trams. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics (FPM), Harbin, China, 5–7 August 2015; IEEE: New York, NY, USA, 2015; pp. 529–535. [Google Scholar]
- Jeong, N.T.; Choi, S.U.; Lee, H.Y.; Baek, K.H.; Han, S.Y.; Kim, W.K.; Suh, M.W. A study on the optimum design of high-speed low-floor bogie with independently rotating wheels. J. Mech. Sci. Technol. 2017, 31, 2105–2115. [Google Scholar] [CrossRef]
- Chudzikiewicz, A.; Maciejewski, I.; Krzyżyński, T.; Krzyszkowski, A.; Stelmach, A. Electric Drive Solution for Low-Floor City Transport Trams. Energies 2022, 15, 4640. [Google Scholar] [CrossRef]
- Kalina, T.; Heller, P.; Chval, Z.; Sedláček, F.; Křížek, M.; Bartoň, L. Numerical simulation and experimental testing of two-axle chassis of low-floor trams. Manuf. Technol. 2018, 18, 248–254. [Google Scholar] [CrossRef]
- Lee, J.I.; Jang, S.C.; Eom, K.; Lee, J.Y.; Kim, K.J. The Application of Articulation Systems based on the Number of Carbody Modules of the Low-Floor Tram. In Proceedings of the KSR Conference; The Korean Society for Railway: Busan, Republic of Korea, 2011; pp. 842–848. [Google Scholar]
- Megna, G.; Bracciali, A. Technical comparison of commercially available trams and review of standardization frame and design principles. Urban Rail Transit 2022, 8, 16–31. [Google Scholar] [CrossRef]
- Ding, W.S.; Song, X.L. Analysis of the anti-kink hydraulic system and running mode of low-floor trams. J. Eng. 2020, 14, 966–969. [Google Scholar] [CrossRef]
- Konowrocki, R.; Kalinowski, D.; Szolc, T.; Marczewski, A. Identification of safety hazards and operating conditions of the low-floor tram with independently rotating wheels with various drive control algorithms. Eksploat. Niezawodn. 2021, 23, 21–33. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Xiang, K.; Zuo, A. Mechanism and performance of a passive auxiliary steering device for low-floor light rail vehicle. Veh. Syst. Dyn. 2024, 1–26. [Google Scholar] [CrossRef]
- Viqaruddin, M.; Reddy, D.R. Structural optimization of control arm for weight reduction and improved performance. Mater. Today Proc. 2017, 4, 9230–9236. [Google Scholar] [CrossRef]
- Li, J.; Tan, J.; Dong, J. Lightweight Design of front suspension upright of electric formula car based on topology optimization method. World Electr. Veh. J. 2020, 11, 15. [Google Scholar] [CrossRef]
- Song, X.G.; Jung, J.H.; Son, H.J.; Park, J.H.; Lee, K.H.; Park, Y.C. Metamodel-based optimization of a control arm considering strength and durability performance. Comput. Math. Appl. 2010, 60, 976–980. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar]
- Ansys®. Ansys Workbench, Release 18.1; ANSYS Inc.: Canonsburg, PA, USA, 2017.
- EasyDesign, Design Optimization Inc.: Seoul, Republic of Korea, 2022.
- EN 12663-1:2010+A1:2014; Railway Applications–Structural Requirements of Railway Vehicle Bodies–Part 1: Locomotives and Passenger Rolling Stock (and Alternative Method for Freight Wagons). European Committee for Standardization: Brussels, Belgium, 2014.
- EN 13749:2011; Railway Applications-Wheelsets and Bogies-Method of Specifying the Structural Requirements of Bogie Frames. European Committee for Standardization: Brussels, Belgium, 2011.





| Young’s Modulus [GPa] | Poisson’s Ratio | Density [kg/m3] | |
|---|---|---|---|
| SCM440 | 205 | 0.29 | 7850 |
| STB2 | 210 | 0.30 | 7850 |
| SM45C | 205 | 0.29 | 7850 |
| Design Variable | Min | Max |
|---|---|---|
| x1 (Middle Frame) | 5 | 15 |
| x2 (Frame Hold Width) | 70 | 90 |
| x3 (Frame Edge Width) | 25 | 45 |
| x4 (Frame Neck Length) | 54 | 64 |
| x5 (Frame Width) | 120 | 140 |
| x6 (Core Upper Length) | 25.5 | 31.5 |
| x7 (Core Lower Length) | 33.5 | 39.5 |
| x8 (Core Radius) | 58 | 66 |
| Case | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | Stress [MPa] | Mass [kg] |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.0 | 70.0 | 45.0 | 54.0 | 140 | 25.5 | 39.5 | 58.0 | 1046.6 | 162.5 |
| 2 | 5.0 | 90.0 | 45.0 | 64.0 | 120 | 25.5 | 39.5 | 58.0 | 886.1 | 144.4 |
| 3 | 15.0 | 90.0 | 25.0 | 64.0 | 140 | 31.5 | 33.5 | 58.0 | 1300.0 | 136.2 |
| 4 | 5.0 | 70.0 | 45.0 | 64.0 | 140 | 31.5 | 39.5 | 66.0 | 1321.7 | 156.2 |
| 5 | 5.0 | 90.0 | 25.0 | 54.0 | 120 | 31.5 | 39.5 | 66.0 | 1393.4 | 129.2 |
| 6 | 5.0 | 70.0 | 25.0 | 64.0 | 140 | 25.5 | 33.5 | 66.0 | 702.7 | 134.2 |
| 7 | 15.0 | 70.0 | 25.0 | 64.0 | 120 | 31.5 | 39.5 | 58.0 | 1302.1 | 128.9 |
| 8 | 15.0 | 70.0 | 45.0 | 54.0 | 120 | 31.5 | 33.5 | 66.0 | 904.9 | 151.0 |
| 9 | 15.0 | 90.0 | 45.0 | 64.0 | 120 | 25.5 | 33.5 | 58.0 | 795.0 | 147.8 |
| 10 | 5.0 | 90.0 | 45.0 | 54.0 | 140 | 31.5 | 33.5 | 58.0 | 673.5 | 159.8 |
| 11 | 15.0 | 90.0 | 25.0 | 54.0 | 140 | 25.5 | 39.5 | 66.0 | 533.2 | 139.6 |
| 12 | 5.0 | 70.0 | 25.0 | 54.0 | 120 | 25.5 | 33.5 | 58.0 | 666.1 | 130.5 |
| 13 | 10.0 | 80.0 | 35.0 | 59.0 | 130 | 28.5 | 36.5 | 62.0 | 529.7 | 143.7 |
| SAO #1 | 13.9 | 89.6 | 25 | 108.7 | 134.5 | 26.3 | 51.5 | 66 | 649.5 | 134.4 |
| SAO #2 | 5.1 | 70.4 | 25.3 | 107.3 | 120 | 25.5 | 46.5 | 59.5 | 650.1 | 128.7 |
| SAO #3 | 5.1 | 70.4 | 25.4 | 107.2 | 120 | 25.5 | 46.5 | 59.5 | 648.5 | 128.7 |
| Direction of Structural Testing | Test Equipment | Load Conditions | Testing Speed |
|---|---|---|---|
| Tension and Compression | MTS Tension and Compression Tester | 1000 kN | 2 mm/min |
| Right and Left | MTS Hydraulic Actuator | 100 kN | 2 mm/min |
| Vertical | MTS Hydraulic Actuator | 100 kN | 5 mm/min |
| Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tension | Analysis (MPa) | −59.50 | 15.29 | 39.94 | −52.12 | −15.54 | 69.56 | 38.02 | −124.78 | 8.84 | 4.44 | −32.57 | −24.42 |
| Experimental (MPa) | −66.74 | 15.65 | 45.74 | −59.89 | −16.52 | 71.10 | 38.83 | −127.71 | 9.94 | 5.72 | −34.74 | −27.85 | |
| Error (%) | 10.9 | 2.3 | 12.7 | 13.0 | 6.0 | 2.2 | 2.1 | 2.3 | 11.1 | 22.4 | 6.3 | 12.3 | |
| Compression | Analysis (MPa) | 47.22 | −21.61 | −160.24 | 153.32 | 3.76 | −6.01 | 28.39 | 21.79 | −7.88 | −10.11 | 38.70 | 28.64 |
| Experimental (MPa) | 48.21 | −22.91 | −164.18 | 159.65 | 4.37 | −7.18 | 29.11 | 23.84 | −8.10 | −10.59 | 40.37 | 32.69 | |
| Error (%) | 2.1 | 5.7 | 2.4 | 4.0 | 13.9 | 16.4 | 2.5 | 8.6 | 2.7 | 4.5 | 4.1 | 12.4 | |
| Right | Analysis (MPa) | 19.55 | −2.12 | 4.89 | −17.35 | 3.19 | −8.88 | 7.25 | −20.86 | 14.11 | 0.59 | −0.38 | 3.01 |
| Experimental (MPa) | 21.42 | −2.43 | 5.01 | −19.00 | 3.35 | −9.01 | 7.33 | −21.93 | 15.15 | 0.62 | −0.43 | 3.40 | |
| Error (%) | 6.8 | 6.6 | 6.9 | 3.3 | 4.7 | 15.2 | 6.7 | 11.1 | 7.0 | 8.9 | 11.7 | 9.4 | |
| Left | Analysis (MPa) | 3.04 | −37.49 | −9.22 | −11.36 | 2.65 | −9.97 | 1.97 | −16.52 | −0.60 | 13.41 | 1.25 | 0.36 |
| Experimental (MPa) | 3.26 | −40.15 | −9.90 | −11.75 | 2.78 | −11.76 | 2.11 | −18.58 | −0.65 | 14.72 | 1.42 | 0.40 | |
| Error (%) | 8.7 | 12.7 | 2.5 | 8.7 | 4.9 | 1.4 | 1.1 | 4.9 | 6.9 | 5.3 | 10.4 | 11.7 | |
| Vertical Up | Analysis (MPa) | −91.13 | 0.91 | −4.45 | 81.26 | −12.51 | 32.50 | −41.98 | 96.08 | 4.36 | 4.36 | −2.11 | −1.38 |
| Experimental (MPa) | −92.68 | 1.10 | −4.80 | 82.67 | −13.23 | 46.60 | −42.27 | 98.83 | 4.65 | 4.41 | −2.94 | −1.65 | |
| Error (%) | 1.7 | 17.4 | 7.2 | 1.7 | 5.5 | 30.3 | 0.7 | 2.8 | 6.1 | 1.2 | 28.3 | 16.1 | |
| Vertical Down | Analysis (MPa) | 102.96 | −10.22 | −6.95 | −70.43 | 9.34 | −32.50 | 46.31 | −123.16 | −7.41 | −7.72 | −1.13 | −2.25 |
| Experimental (MPa) | 107.47 | −11.06 | −7.10 | −73.31 | 10.21 | −33.59 | 48.09 | −127.02 | −7.73 | −7.82 | −1.47 | −2.79 | |
| Error (%) | 4.2 | 7.5 | 2.1 | 3.9 | 8.5 | 3.3 | 3.7 | 3.0 | 4.2 | 1.3 | 23.1 | 19.5 | |
| Direction of Fatigue Testing | Test Equipment | Fatigue Load Conditions | Testing Speed |
|---|---|---|---|
| Tension and Compression | MTS Hydraulic Actuator | ±40 ± 15 kN | 3 mm/min |
| Right and Left | MTS Hydraulic Actuator | ±25 kN | 3 mm/min |
| Vertical | MTS Hydraulic Actuator | −90 ± 10 kN | 3 mm/min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, J.-W.; Lee, J.; Choi, J.; Ji, H.; Hwang, W.-J. Optimization and Experimental Verification of Lower Articulation for Low-Floor Tram Using Meta-Model. Appl. Sci. 2024, 14, 9618. https://doi.org/10.3390/app14219618
Jin J-W, Lee J, Choi J, Ji H, Hwang W-J. Optimization and Experimental Verification of Lower Articulation for Low-Floor Tram Using Meta-Model. Applied Sciences. 2024; 14(21):9618. https://doi.org/10.3390/app14219618
Chicago/Turabian StyleJin, Ji-Won, Jaewon Lee, Jeonghwan Choi, Haeyoung Ji, and Won-Ju Hwang. 2024. "Optimization and Experimental Verification of Lower Articulation for Low-Floor Tram Using Meta-Model" Applied Sciences 14, no. 21: 9618. https://doi.org/10.3390/app14219618
APA StyleJin, J.-W., Lee, J., Choi, J., Ji, H., & Hwang, W.-J. (2024). Optimization and Experimental Verification of Lower Articulation for Low-Floor Tram Using Meta-Model. Applied Sciences, 14(21), 9618. https://doi.org/10.3390/app14219618







