Dynamic Optimization of Exclusive Bus Lane Location Considering Reliability: A Case Study of Beijing
Abstract
:1. Introduction
2. Literature Review
- (1)
- Travel time is concentrated more in EBL location research. However, in the real-world case, traffic congestions and crowded waiting environments may cause transit systems to become more and more unreliable, which could be the most important factor to dynamic demand.
- (2)
- With different EBL location plans, travel time and reliability of different bus lines can be changed when part of the trip operates on an EBL. The number of passengers taking related bus lines will be changed correspondingly. This dynamic demand should be analyzed in detail.
- (3)
- Previous studies were always conducted under numerical grid networks, and different EBL locations and key parameters were tested. However, in big cities, the traffic conditions are complex, and traffic is heavily congested during peak hours. It is indicated that most quantitative analyses resulting from the numerical studies have a larger gap with the actual ones. Therefore, with more detailed travel data from advanced IC card systems and on-vehicle GPS equipment, case studies should be conducted to examine the effect of the EBL location optimization model.
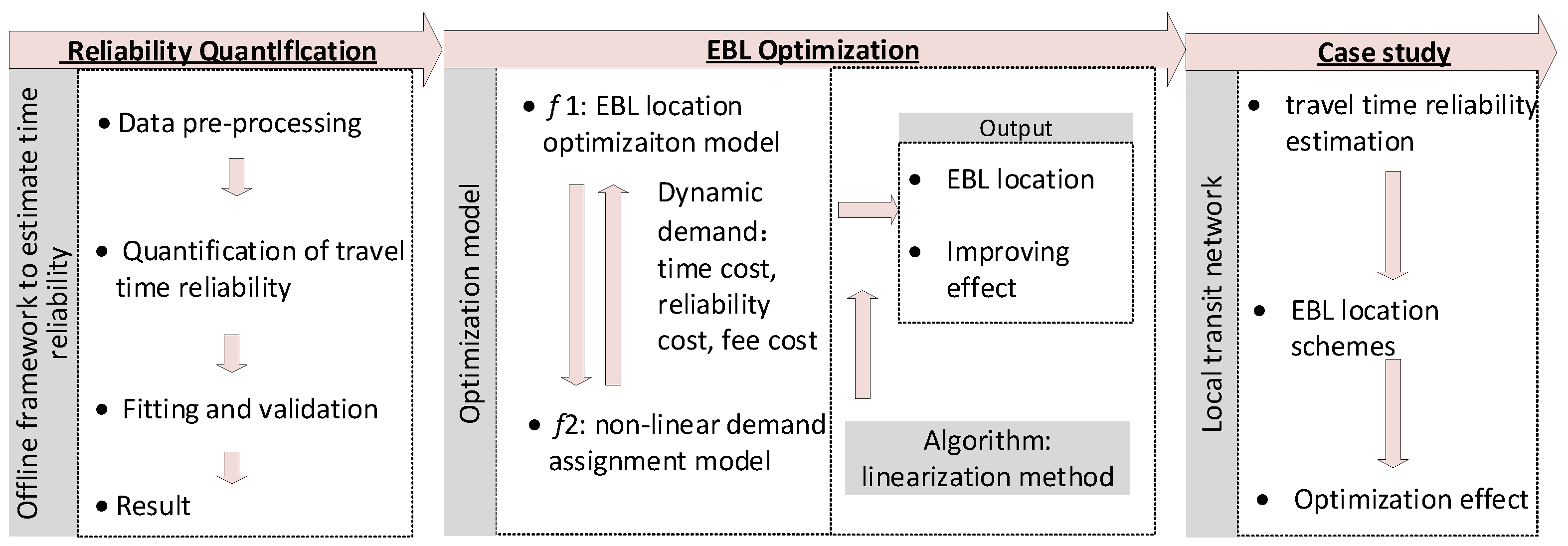
3. Materials and Methods
3.1. Descriptions
3.2. Estimation of Travel Time Reliability
3.3. Model Formulation and Analysis
3.3.1. General Cost
- (1)
- Formulation cost of a transit passenger
- (2)
- Formulation of the private car passenger cost
- (3)
- Formulation of EBL construction cost
3.3.2. Model Formulation
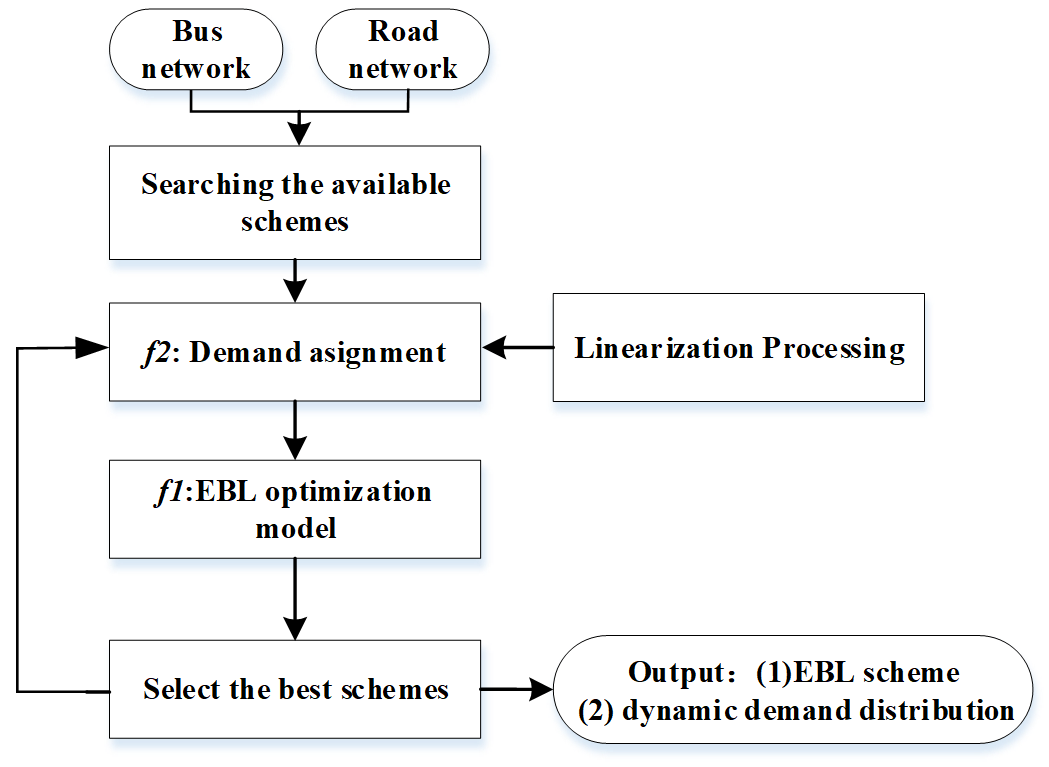
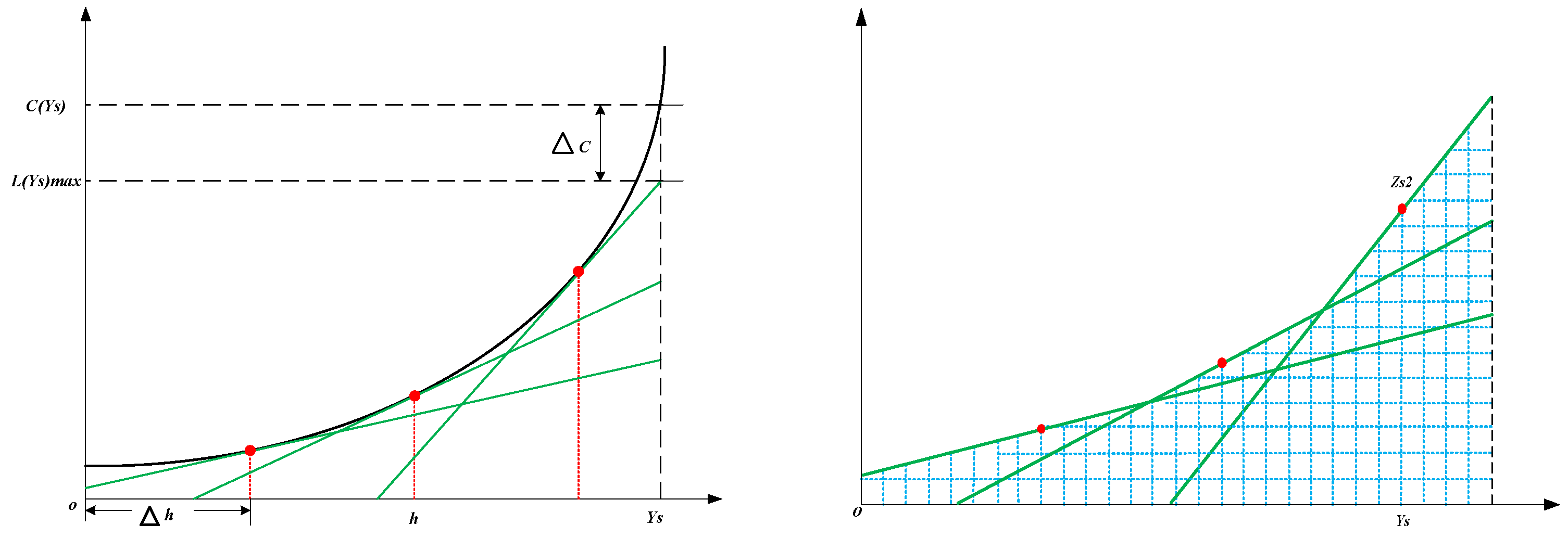
3.3.3. Solution Algorithm
4. Case Study
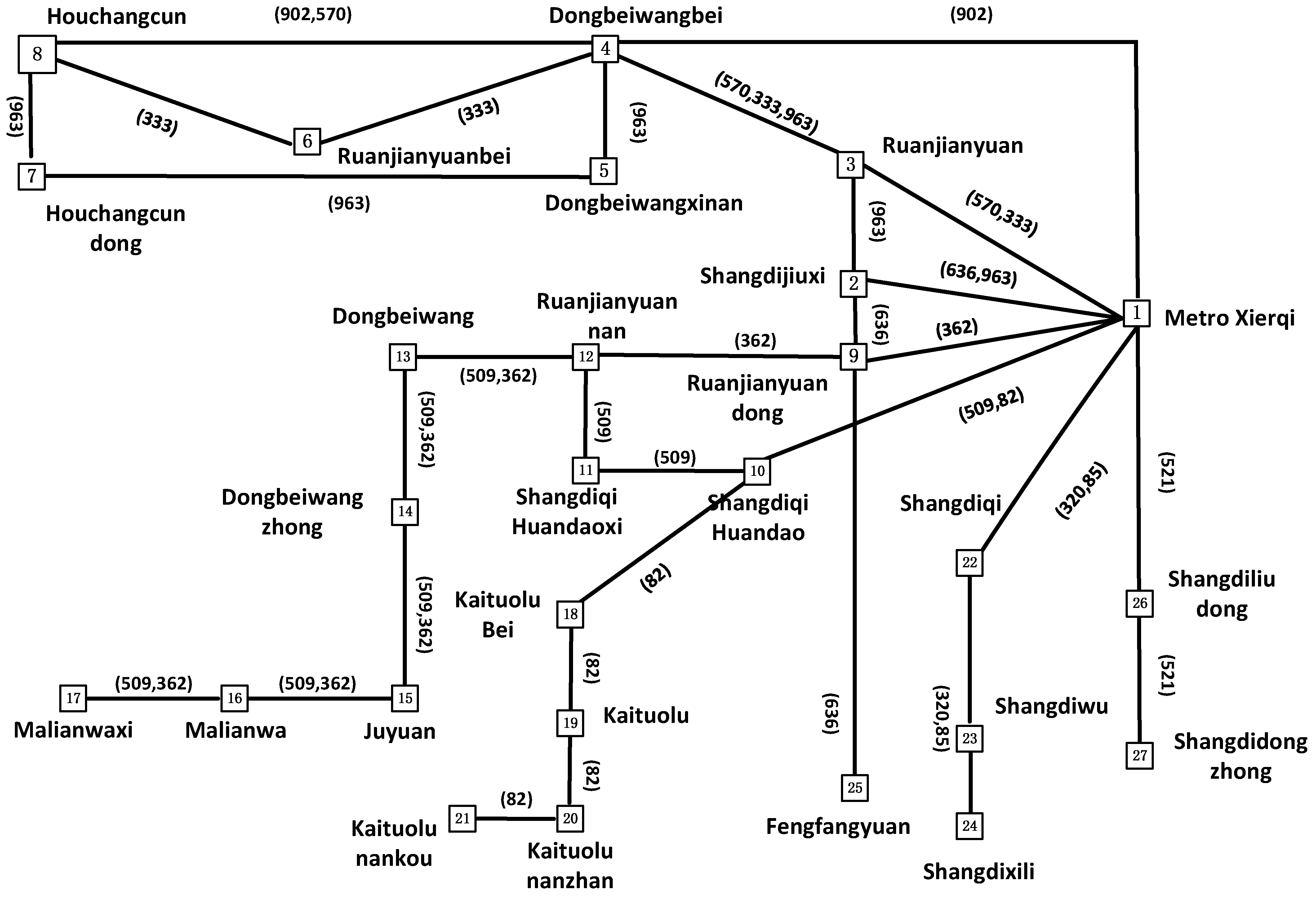
4.1. Local Bus Network
4.2. Travel Time Reliability Estimation
5. Result and Discussions
6. Conclusions
- (1)
- The indicator based on buffer time is defined to quantify the transit passenger travel time reliability, which is composed by passenger reliability preference and time volatility. Comparing the traditional methods of traffic models, the methodology proposed in this paper uses statistical modeling and fitting analysis to evaluate travel time and reliability, based on actual AVL data. Data are collected from bus lines that are operating on the EBL of the Third Ring Road in Beijing during peak hours. Calculation results show that unit expectation and standard deviations of travel time are 1.59 min/km and 1.15 min/km, respectively, which can be important parameters to reflect the fluctuation of passenger travel time reliability in the optimization model.
- (2)
- A relatively complete framework of a reliability-based EBL location optimization model is established, and is composed of the EBL location and demand assignment optimization. The transit passengers’ dynamic choices are considered under different EBL location schemes. A two-stage solution algorithm on the basis of iteration is designed to solve the nonlinear programming model. To solve the complex nonlinear problem, a linearization method is proposed by cutting tangent lines on the concave curves.
- (3)
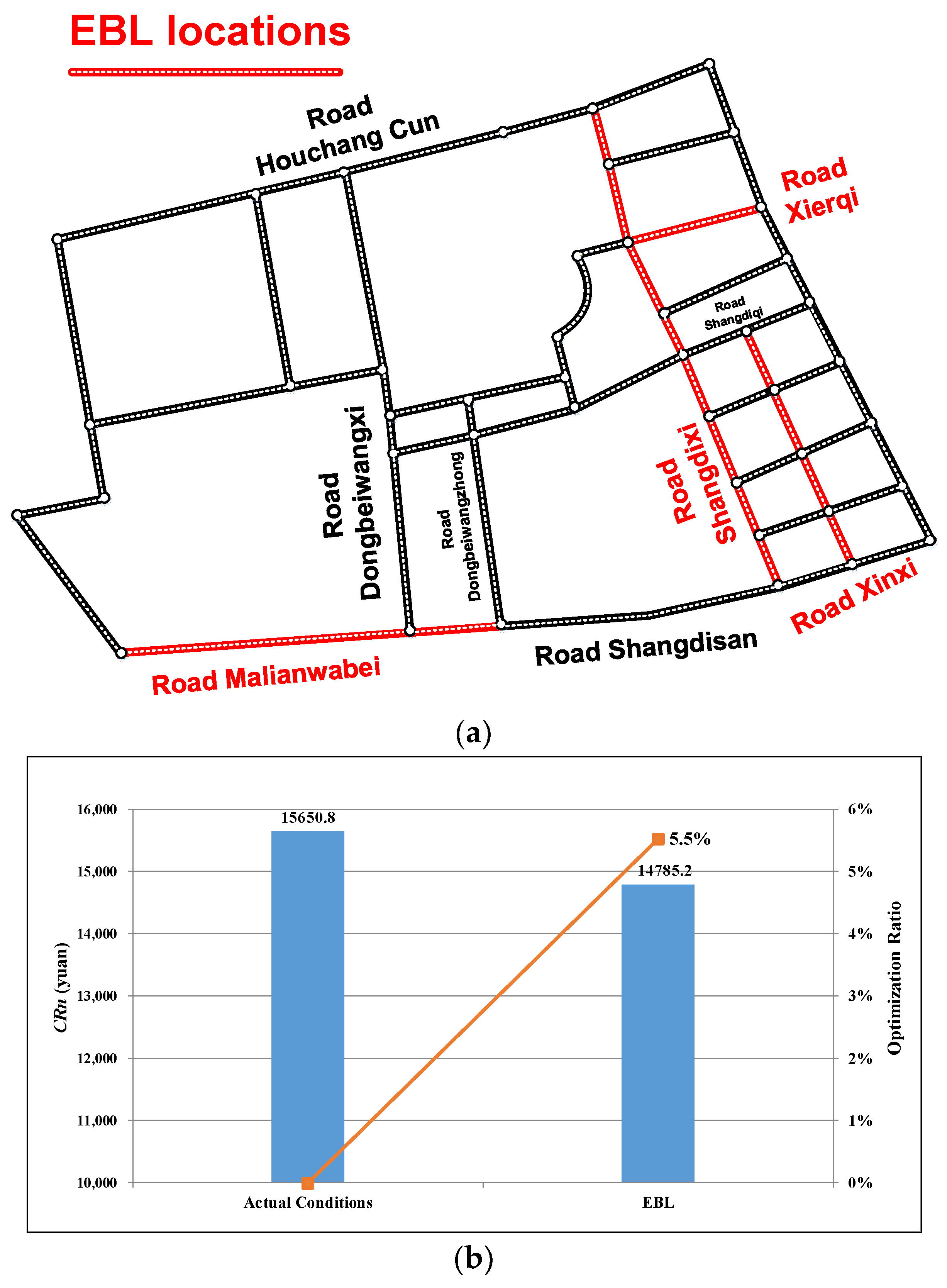
- To validate the model’s quality and robustness, the case study is analyzed in Beijing. Results show that the best-performing bus lane locations mainly depend on travel demand, road structure, and traffic conditions. For the network of bus passengers and private car passengers, the best EBL location scheme resulting from the proposed model can evidently improve the travel time reliability by 5.5% in the case study. In addition, comparing with other cities that have applied the EBL like Los Angeles, Beijing has more business districts and office areas, and commuters have higher requirements for the reliability of bus systems. Therefore, the implementation of an EBL can better improve the service level of the public transportation system within the area of highly concentrated demand. It will attract more passengers to choose the bus for commuting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guler, S.I.; Kan, W. Optimizing transit signal priority implementation along an arterial. Transp. Res. Record. 2018, 2672, 215–227. [Google Scholar]
- Christofa, E.; Papamichail, I.; Skabardonis, A. Person-Based Traffic Responsive Signal Control Optimization. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1278–1289. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Maitra, B.; Boltze, M. Implementation of bus priority with queue jump lane and pre-signal at urban intersections with mixed traffic operations: Lessons learned? Transp. Res. Record. 2019, 2673, 646–657. [Google Scholar] [CrossRef]
- Truong, L.T.; Sarvi, M.; Currie, G. An investigation of multiplier effects generated by implementing queue jump lanes at multiple intersections. J. Adv. Transp. 2016, 50, 1699–1715. [Google Scholar] [CrossRef]
- Chiabaut, N.; Barcet, A. Demonstration and evaluation of an intermittent bus lane strategy. Public Transp. 2019, 11, 443–456. [Google Scholar] [CrossRef]
- Bayrak, M.; Guler, S.I. Optimization of dedicated bus lane location on a transportation network while accounting for traffic dynamics. Public Transp. 2021, 13, 325–347. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, X. Improving the Operational Efficiency of Buses with Dynamic Use of Exclusive Bus Lane at Isolated Intersections. IEEE Trans. Intell. Transp. Syst. 2018, 20, 642–653. [Google Scholar] [CrossRef]
- Tang, Q.; Hu, X.; Lu, J.; Zhou, X. Analytical characterization of multi-state effective discharge rates for bus-only lane conversion scheduling problem. Transp. Res. Part B Methodol. 2021, 148, 106–131. [Google Scholar] [CrossRef]
- Wu, P.; Chu, F.; Che, A. Mixed-integer programming for a new bus-lane reservation problem. In Proceedings of the 18th International Conference on Intelligent Transportation Systems (ITSC), Gran Canaria, Spain, 2 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2782–2787. [Google Scholar]
- Gao, K.; Sun, L.; Tu, H.; Li, H. Heterogeneity in Valuation of Travel Time Reliability and In-Vehicle Crowding for Mode Choices in Multimodal Networks. J. Transp. Eng. Part A Syst. 2018, 144, 04018061. [Google Scholar] [CrossRef]
- Jeason, D.; Ferreira, L. Assessing travel time impacts of measure to enhance bus operation. Part II: Assessment criteria and main findings. Road Transp. Res. J. 2000, 9, 3–18. [Google Scholar]
- Chen, Q. An optimization model for the selection of bus-only lanes in a city. PLoS ONE 2015, 10, e0133951. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Kong, L.; Sun, Y.; Yao, B.; Gao, Z.Y. A bi-level programming for bus lane network design. Transp. Res. Part C Emerg. Technol. 2015, 55, 310–327. [Google Scholar] [CrossRef]
- Yao, J.; Shi, F.; An, S.; Wang, J. Evaluation of exclusive bus lanes in a bi-modal degradable road network. Transp. Res. Part C Emerg. Technol. 2015, 60, 36–51. [Google Scholar] [CrossRef]
- Khoo, H.L.; Teoh, L.E.; Meng, Q. A bi-objective optimization approach for exclusive bus lane selection and scheduling design. Eng. Optim. 2013, 46, 987–1007. [Google Scholar] [CrossRef]
- Truong, L.T.; Sarvi, M.; Currie, G. Exploring Multiplier Effects Generated by Bus Lane Combinations. Transp. Res. Rec. J. Transp. Res. Board 2015, 2533, 68–77. [Google Scholar] [CrossRef]
- Sun, X.; Lu, H.; Fan, Y. Optimal bus lane infrastructure design. Transp. Res. Rec. J. Transp. Res. Board 2014, 2467, 1–11. [Google Scholar] [CrossRef]
- Xu, H.; Zheng, M. Impact of Bus-Only Lane Location on the Development and Performance of the Logic Rule-Based Bus Rapid Transit Signal Priority. J. Transp. Eng. 2012, 138, 293–314. [Google Scholar] [CrossRef]
- Wu, J.; Hounsell, N. Bus priority using pre-signals. Transp. Res. Part A Policy Pract. 1998, 32, 563–583. [Google Scholar] [CrossRef]
- Chen, B.Y.; Lam, W.H.K.; Sumalee, A.; Shao, H. An efficient solution algorithm for solving multi-class reliability-based traffic assignment problem. Math. Comput. Model. 2011, 54, 1428–1439. [Google Scholar] [CrossRef]
- Sun, X.; Wu, J. Combinatorial optimization of bus lane infrastructure layout and bus operation management. Adv. Mech. Eng. 2017, 9, 1687814017703341. [Google Scholar] [CrossRef]
- Bingfeng, S.; Ming, Z.; Xiaobao, Y.; Ziyou, G. Bi-level Programming Model for Exclusive Bus Lanes Configuration in Multimodal Traffic Network. Transp. Res. Procedia 2017, 25, 652–663. [Google Scholar] [CrossRef]
- Mesbah, M.; Sarvi, M.; Ouveysi, I.; Currie, G. Optimization of transit priority in the transportation network using a decomposition methodology. Transp. Res. Part C Emerg. Technol. 2011, 19, 363–373. [Google Scholar] [CrossRef]
- Vedagiri, P.; Arasan, V. Estimating Modal Shift of Car Travelers to Bus on Introduction of Bus Priority System. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 120–129. [Google Scholar] [CrossRef]
- McLeod, D.S.; Morgan, G. Florida’s Mobility Performance Measures and Experience; Florida Department of Transportation: Tallahassee, FL, USA, 2011. Available online: https://www.fdot.gov/docs/default-source/planning/FTO/mobility/trbmpmpaper16.pdf (accessed on 20 October 2024).
- Kou, W.; Chen, X.; Yu, L.; Qi, Y.; Wang, Y. Urban commuters’ valuation of travel time reliability based on stated preference survey: A case study of Beijing. Transp. Res. Part A Policy Pr. 2017, 95, 372–380. [Google Scholar] [CrossRef]
- Wahba, M.; Shalaby, A. Large-scale application of MILATRAS: Case study of the Toronto transit network. Transportation 2011, 38, 889–908. [Google Scholar] [CrossRef]
- Yao, B.; Hu, P.; Lu, X.; Gao, J.; Zhang, M. Transit network design based on travel time reliability. Transp. Res. Part C Emerg. Technol. 2014, 43, 233–248. [Google Scholar] [CrossRef]
- McLeod, F. Estimating bus passenger waiting times from incomplete bus arrivals data. J. Oper. Res. Soc. 2007, 58, 1518–1525. [Google Scholar] [CrossRef]
- Chen, X.; Yu, L.; Zhang, Y.; Guo, J.F. Analyzing urban bus service reliability at the stop, route, and network levels. Transp. Res. Part A Policy Pract. 2009, 43, 722–734. [Google Scholar] [CrossRef]
- Barabino, B.; Francesco, M.D. Diagnosis of irregularity sources by automatic vehicle location data. IEEE Intell. Transp. Syst. Mag. 2021, 13, 152–165. [Google Scholar] [CrossRef]
- Barabino, B.; Di Francesco, M.; Mozzoni, S. An Offline Framework for the Diagnosis of Time Reliability by Automatic Vehicle Location Data. IEEE Trans. Intell. Transp. Syst. 2016, 18, 583–594. [Google Scholar] [CrossRef]
- Berbeglia, G.; Cordeau, J.F.; Laporte, G. Dynamic Pickup and Delivery Problems. Eur. J. Oper. Res. 2010, 202, 8–15. [Google Scholar] [CrossRef]
- Li, Y.; Soleimani, H.; Zohal, M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives. J. Clean. Prod. 2019, 227, 1161–1172. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Braekers, K.; Masmoudi, M.; Dammak, A. A Hybrid Genetic Algorithm for the Heterogeneous Dial-A-Ride Problem. Comput. Oper. Res. 2017, 81, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Hu, S.; Fan, W.; Deng, K. Modeling an enhanced ridesharing system with meet points and time windows. PLoS ONE 2018, 13, e0195927. [Google Scholar] [CrossRef]
- Jiang, Y.; Szeto, W. Reliability-based stochastic transit assignment: Formulations and capacity paradox. Transp. Res. Part B: Methodol. 2016, 93, 181–206. [Google Scholar] [CrossRef]
- Kou, W. Improvement Strategy Modeling for Transit Passengers’ Travel Time Reliability. Ph.D. Dissertation, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Szeto, W.Y.; Jiang, Y.; Wong, K.I.; Solayappan, M. Reliability-based stochastic transit assignment with capacity constraints: For-mulation and solution method. Transp. Res. Part C Emerg. Technol. 2013, 35, 286–304. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Solayappan, M.; Jiang, Y. Reliability-Based Transit Assignment for Congested Stochastic Transit Networks. Comput. Civ. Infrastruct. Eng. 2011, 26, 311–326. [Google Scholar] [CrossRef]
- Liu, C.; Lin, B.; Wang, J.; Xiao, J.; Liu, S.; Wu, J.; Li, J. Flow assignment model for quantitative analysis of diverting bulk freight from road to railway. PLoS ONE 2017, 12, e0182179. [Google Scholar] [CrossRef]
- Wu, J.; Lin, B.; Wang, J.; Liu, S. A Network-Based Method for the EMU Train High-Level Maintenance Planning Problem. Appl. Sci. 2017, 8, 2. [Google Scholar] [CrossRef]
- Kou, W.; Wang, J.; Liu, Y.; Li, C. Last-Mile Shuttle Planning for Improving Bus Commuters’ Travel Time Reliability: A Case Study of Beijing. J. Adv. Transp. 2022, 2022, 1–15. [Google Scholar] [CrossRef]




| Parameters | Descriptions |
|---|---|
| Bus arrival time samples of stop i and j. | |
| Sample time from i to j. | |
| Reliability-based in-vehicle time. | |
| E() | Expectation of IVT. |
| Standard deviation (SD) of ij. | |
| Reliability preference parameter. | |
| N | Number of samples. |
| w | Sample waiting time. |
| Reliability-based waiting time. | |
| E() | Expectation of WT for all the samples. |
| D(w) | Deviation of sample waiting time |
| Standard deviation of w. | |
| zw | Expectation of passenger arrival time/bus arrival interval. |
| s | Travel arc. |
| Cs | General cost of Travel arc s. |
| u | Unit travel time cost (yuan/h). |
| Set of in-vehicle travel arc. | |
| Set of waiting arc. | |
| Extra delay time. | |
| Number of waiting passengers. | |
| Parameter that determines whether travel arc s passes on path p from node o to node d | |
| Number of passengers on available path p from nodes ij | |
| K | Vehicle capacity. |
| , n | Parameters to be estimated. |
| Set of transfer arc. | |
| Unit construction cost. | |
| the length of EBL. | |
| Unit travel time of car under free flow velocity | |
| Volume of car. | |
| H | Passenger arrival headway |
| whether the EBL is set on the arc s. |
| Bus Stop | Bus Stop | Distance (km) | Bus Stop | Bus Stop | Distance (km) | Bus Stop | Bus Stop | Distance (km) |
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 1.5 | 2 | 3 | 0.5 | 10 | 11 | 0.3 |
| 4 | 8 | 1.9 | 1 | 9 | 1 | 11 | 12 | 0.4 |
| 1 | 3 | 1 | 9 | 12 | 0.5 | 2 | 9 | 0.6 |
| 3 | 4 | 0.5 | 12 | 13 | 0.3 | 9 | 25 | 1.5 |
| 4 | 6 | 1 | 13 | 14 | 1.8 | 1 | 26 | 1.3 |
| 6 | 8 | 0.9 | 14 | 15 | 0.7 | 26 | 27 | 0.7 |
| 4 | 5 | 0.7 | 15 | 16 | 0.6 | 1 | 22 | 1.3 |
| 5 | 7 | 0.8 | 16 | 17 | 0.7 | 22 | 23 | 0.6 |
| 1 | 2 | 0.3 | 1 | 10 | 1.1 | 23 | 24 | 0.8 |
| OD (Person) | S2 | S3 | S5 | S8 | S9 | S10 | S12 | S13 | S14 | S15 | S16 | S17 | S18 | S22 | S23 | S24 | S26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 2 | 6 | 96 | 209 | 371 | 2 | 270 | 2 | 29 | 149 | 2 | 327 | 139 | 91 | 3 | ||
| S3 | 3 | 10 | |||||||||||||||
| S9 | 59 | 23 | 46 | ||||||||||||||
| S11 | 19 | 4 | |||||||||||||||
| S13 | 13 | 23 | |||||||||||||||
| S15 | 6 | 6 | |||||||||||||||
| S22 | 15 | 23 | |||||||||||||||
| S23 | 14 |
| Parameter | IVT | WT | K | n | |||
|---|---|---|---|---|---|---|---|
| E | SD | E | SD | ||||
| Value | 3.38 min/km | 2.35 min/km | 4.18 min | 6.18 min | 80 person | 3 | 0.5 |
| Parameter | u | C | |||||
| Value | Travel time yuan/h | Travel time reliability yuan/h | 14.7 yuan/km | 600 pcu/lane | |||
| 11.34 | 19.27 | ||||||
| Road Name | Xierqi | Houchang Cun | Malianwa N | Xinxi | Dongbeiwang M | Shangdiqi | Shangdisan |
| Traffic Volume (pcu/h/lane) | 549 | 1116 | 692 | 160 | 130 | 634 | 420 |
| Road Name | Shangdixi | Dongbeiwang W | |||||
| Traffic Volume (pcu/h/lane) | 880 | 201 | |||||
| Line | Gaussian | Weibull | Laplace | Lognormal | Parameters of Best Fit | |
|---|---|---|---|---|---|---|
| 300 N | R-square | 0.900 | 0.882 | 0.909 | 0.973 | a = 0.799 b = 0.356 |
| RMSE | 0.055 | 0.060 | 0.052 | 0.028 | ||
| 300 W | R-square | 0.898 | 0.873 | 0.903 | 0.967 | a = 0.728 b = 0.385 |
| RMSE | 0.053 | 0.059 | 0.051 | 0.030 | ||
| 300 KN | R-square | 0.958 | 0.897 | 0.936 | 0.953 | a = 0.915 b = 1.877 c = 0.506 |
| RMSE | 0.050 | 0.078 | 0.061 | 0.052 | ||
| Line | IVT (min/km) | |
|---|---|---|
| E | SD | |
| 330 N | 1.96 | 1.27 |
| 300 W | 1.92 | 1.25 |
| 300 KN | 0.88 | 0.92 |
| Average | 1.59 | 1.15 |
| Line | IVT (min/km) | WT (min) | ||
|---|---|---|---|---|
| E | SD | E | SD | |
| 902 | 3.7 | 3.3 | 2.4 | 5.7 |
| 320 | 3.7 | 2.4 | 5.1 | 5.6 |
| 333 | 3.7 | 2.4 | 3.6 | 5.6 |
| 362 | 2.9 | 2 | 3.6 | 5.6 |
| 509 | 3.3 | 2.2 | 5.1 | 6.8 |
| 521 | 3.7 | 2.7 | 4.1 | 6.4 |
| 570 | 3 | 1.9 | 5.1 | 6.8 |
| 963 | 3.8 | 2.6 | 2.4 | 5.7 |
| 636 | 3.2 | 2.2 | 4.4 | 6.2 |
| 85 | 3 | 1.9 | 5.1 | 6.8 |
| 82 | 3.2 | 2.2 | 5.1 | 6.8 |
| Average | 3.38 | 2.35 | 4.18 | 6.18 |
| Road Name | Xierqi | Houchang Cun | Dongbeiwangzhong | Shangdiqi | Dongbeiwangxi |
|---|---|---|---|---|---|
| φ | 1 | 0 | 0 | 0 | 0 |
| Road name | Malianwabei | Xinxi | Shangdisan | Shangdixi | |
| φ | 1 | 1 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, W.; Zhang, S.; Liu, F.; Pang, L. Dynamic Optimization of Exclusive Bus Lane Location Considering Reliability: A Case Study of Beijing. Appl. Sci. 2024, 14, 9777. https://doi.org/10.3390/app14219777
Kou W, Zhang S, Liu F, Pang L. Dynamic Optimization of Exclusive Bus Lane Location Considering Reliability: A Case Study of Beijing. Applied Sciences. 2024; 14(21):9777. https://doi.org/10.3390/app14219777
Chicago/Turabian StyleKou, Weibin, Shijie Zhang, Fei Liu, and Lan Pang. 2024. "Dynamic Optimization of Exclusive Bus Lane Location Considering Reliability: A Case Study of Beijing" Applied Sciences 14, no. 21: 9777. https://doi.org/10.3390/app14219777
APA StyleKou, W., Zhang, S., Liu, F., & Pang, L. (2024). Dynamic Optimization of Exclusive Bus Lane Location Considering Reliability: A Case Study of Beijing. Applied Sciences, 14(21), 9777. https://doi.org/10.3390/app14219777





