A Novel Approach to Transient Fourier Analysis for Electrical Engineering Applications
Abstract
1. Introduction
- A method that employs the Laplace–Carson (L-C) transform in the complex domain, significantly simplifying the computation of the original function.
- The use of Fourier transform techniques to analyze transient states, particularly in electrical and electronic applications.
- Introduction.
- Fourier Analysis in Time and Complex Domains, including the method of complex conjugate amplitudes and transient analysis under non-harmonic excitation.
- Transient Analysis of Power Electronic Systems (PESs) using Fourier integral transforms, illustrated with two application examples from the EE field.
- Validation of System States using Matlab/Simulink.
- Discussion and Conclusion.
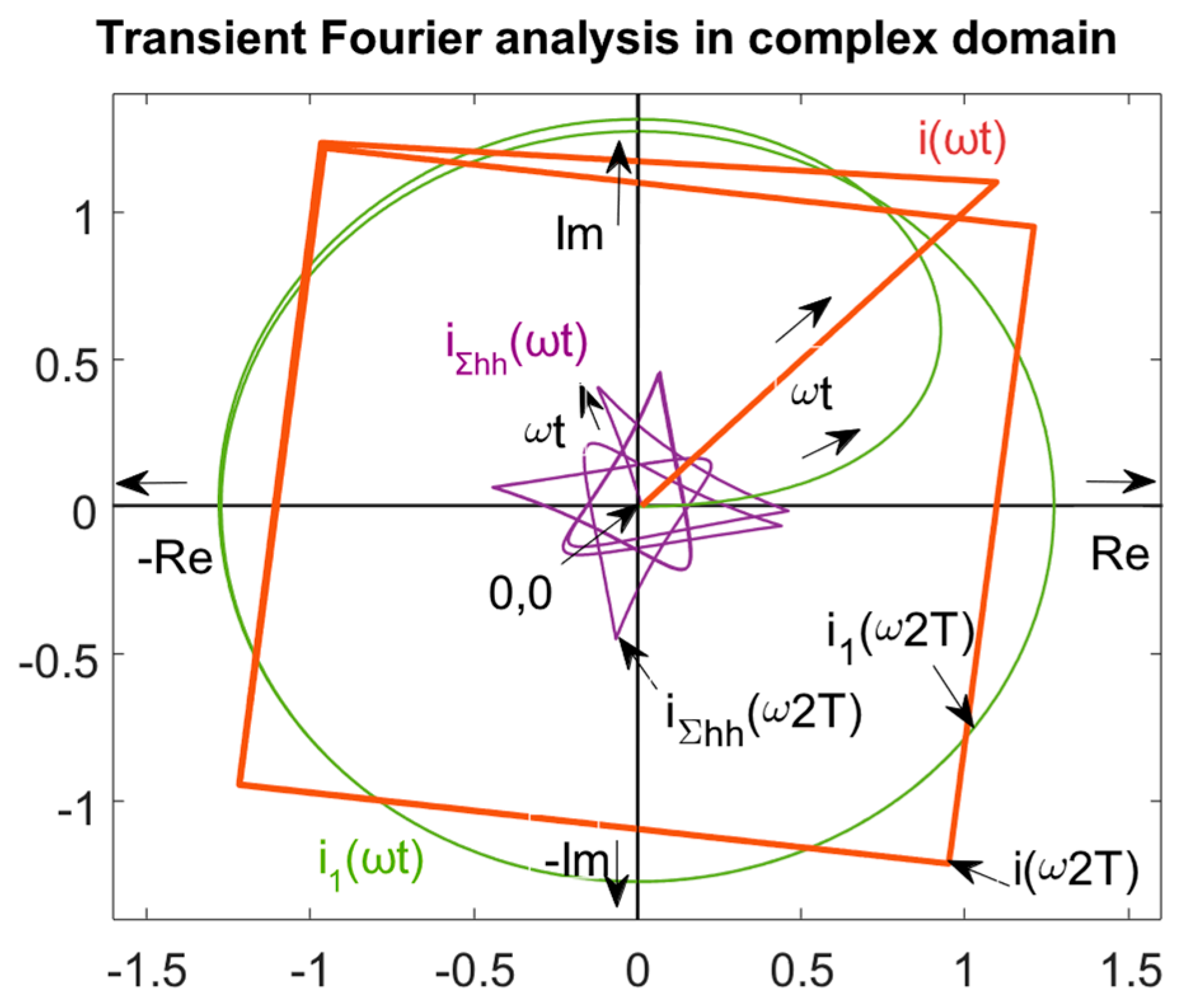
2. Fourier Analysis in the Time and Complex Domains
Analytical Solutions of Transient Values Using Fourier Series Using the Laplace–Carson Transform and Complex Time Vectors Inside One Period
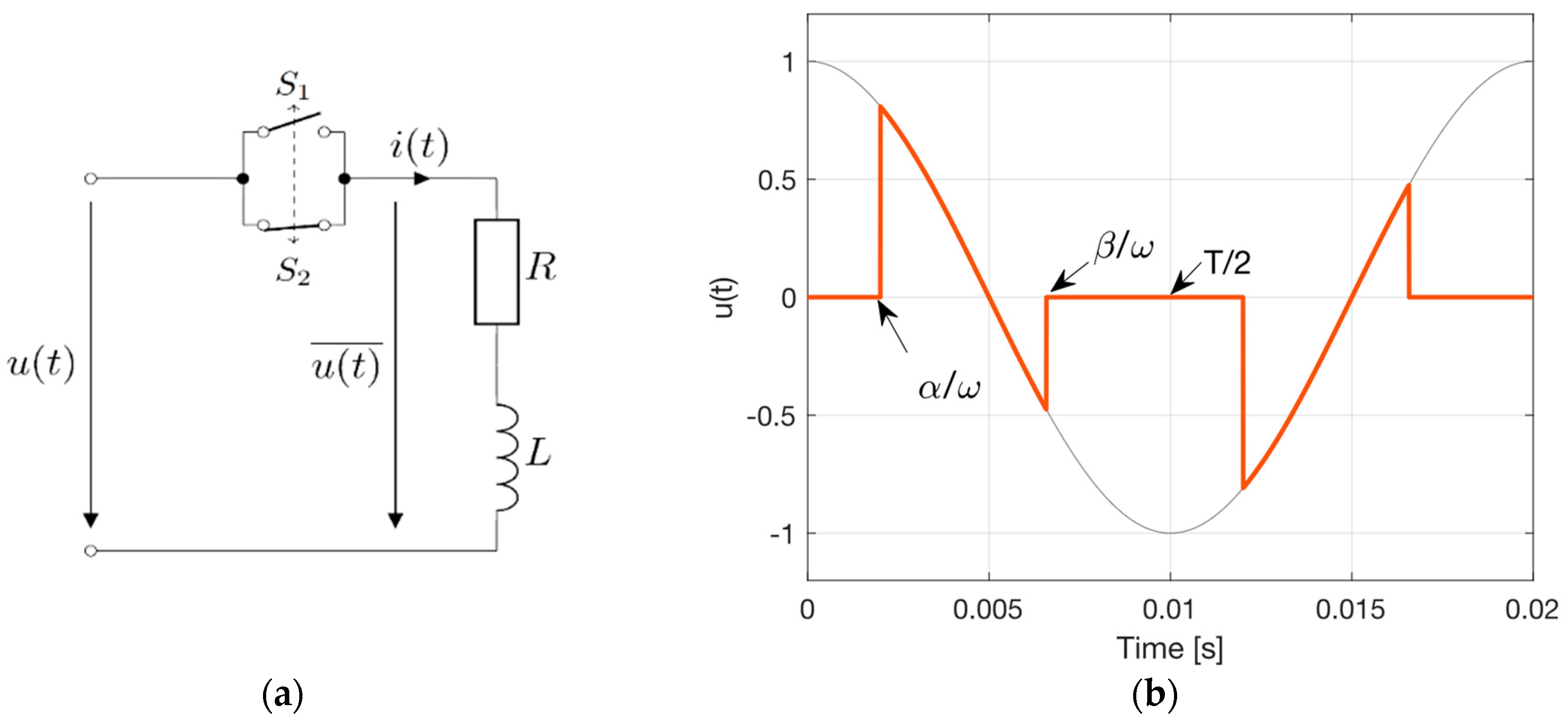
3. Transient Analysis of PES System Using Fourier Integral Transform
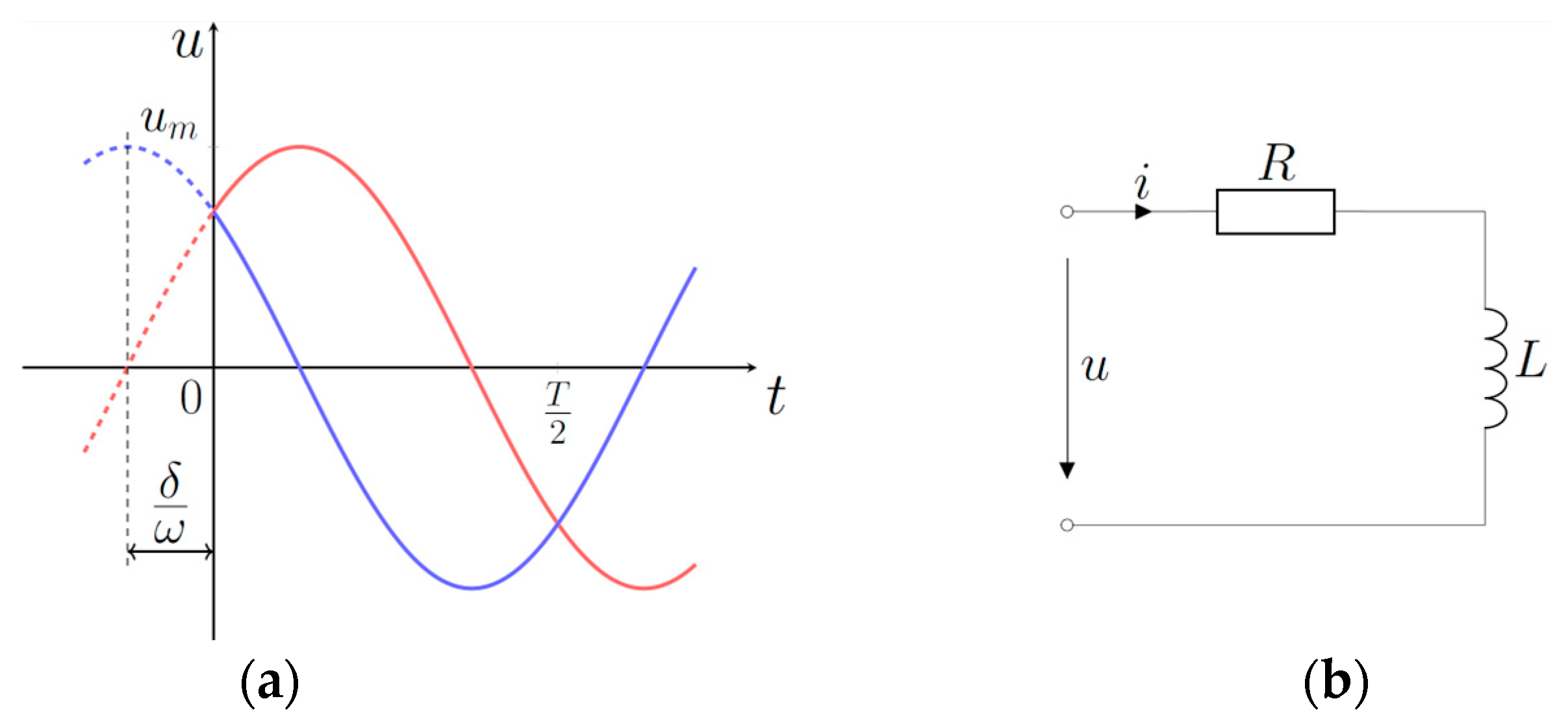
3.1. Case of Passive Resistive-Inductive Load Without Back-Electromotive Force (emf)
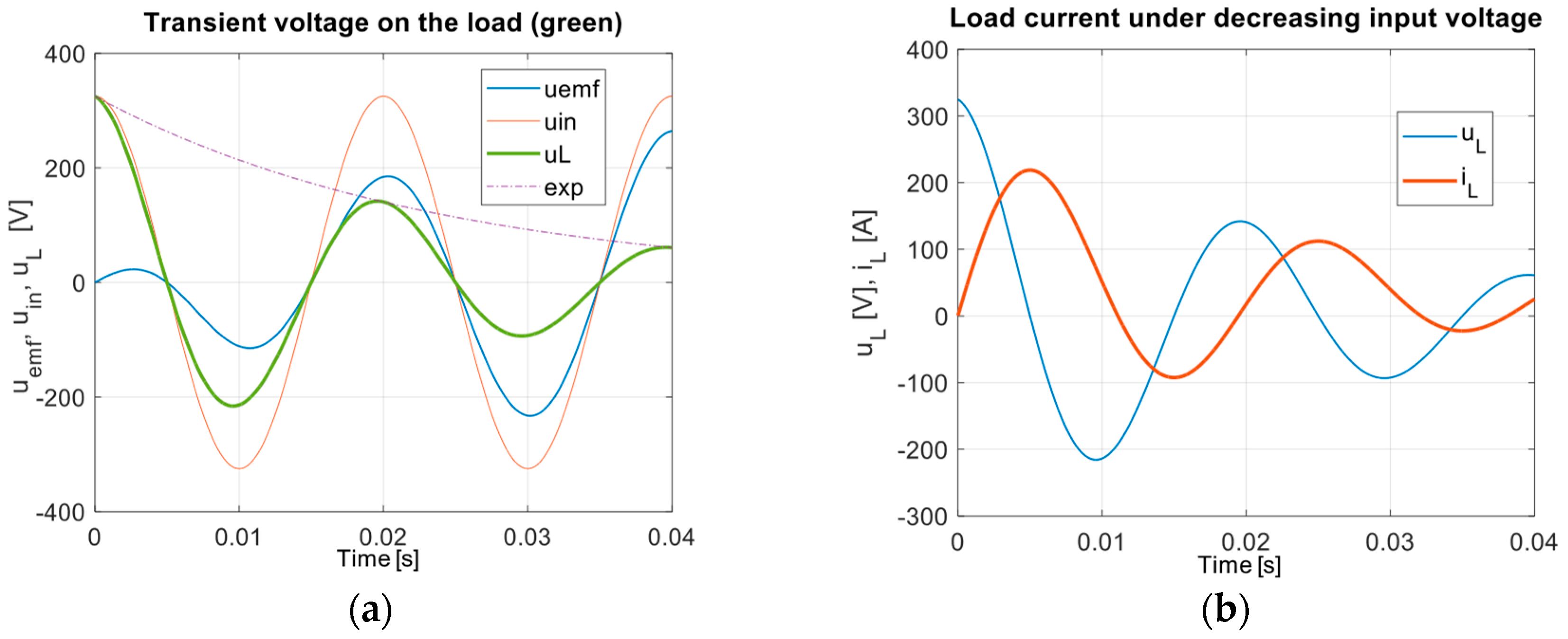
3.2. Case of Active-Inductive Load with Back-Emf
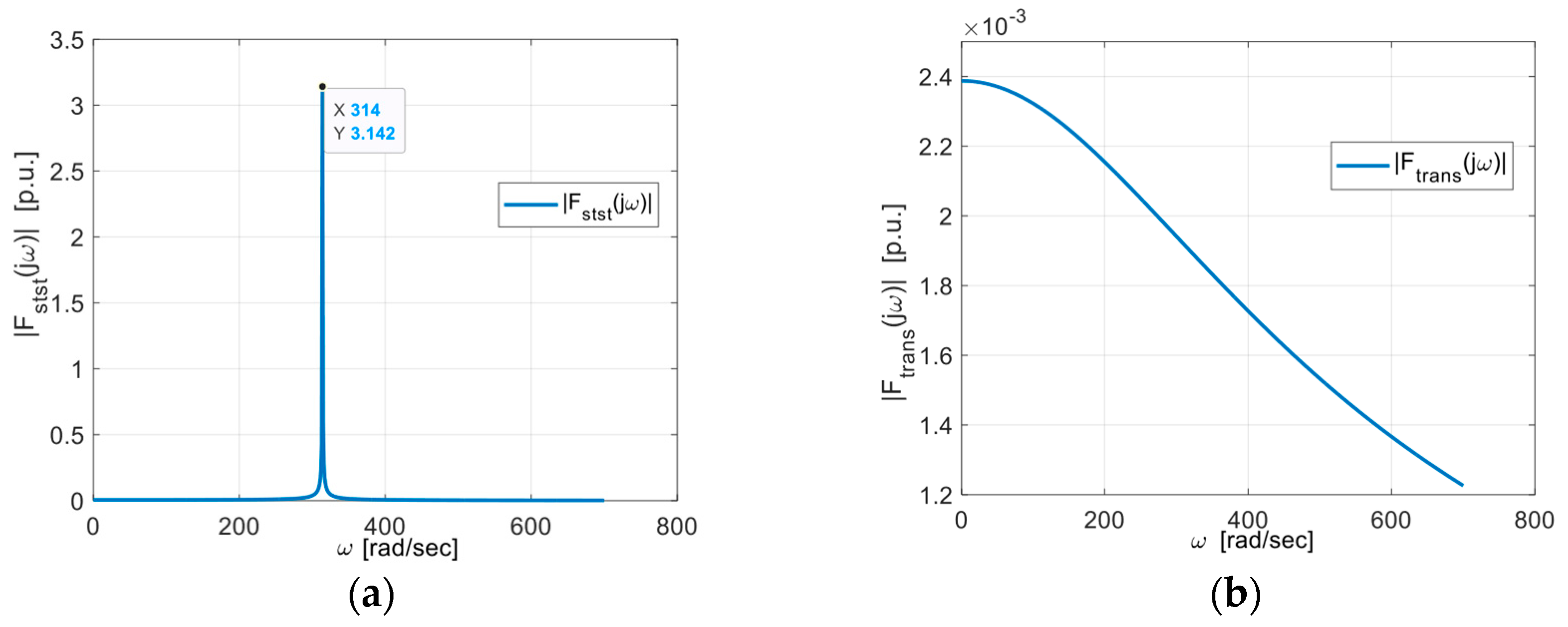
3.3. Transient Analysis Using Fourier Transform (and Under Decreasing Cosine Function)
4. Discussion and Conclusions
- It provides insight into the harmonic content of the signal;
- It allows for the straightforward calculation of harmonic distortion [12].
- The unique ability of this transformation to provide magnitude and phase frequency spectra, which are not easily obtained through other methods, demonstrates its utility [13].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Shenkman, A.L. Transient analysis using the Fourier transform. In Transient Analysis of Electric Power Circuits Handbook; Springer: Dordrecht, The Netherlands, 2005; Chapter 4; pp. 213–263. ISBN 10 0-387-28799-X. [Google Scholar]
- Bai, H.; Mi, C. Transients of Modern Power Electronics; John Wiley & Sons, Ltd.: Chichester, UK, 2011; ISBN 978-0-470-68664-5. [Google Scholar]
- Beerends, R.J.; Morsche, H.G.; Berg, J.C.; Vrie, E.M. Fourier and Laplace Transforms; Cambridge University Press: Cambridge, UK, 2003; Part 4; pp. 267–330. [Google Scholar]
- Kreyszig, E.; Kreyszig, H.; Norminton, E.J. Advanced Engineering Mathematics; John Wiley & Sons, Inc.: New York, NY, USA, 2011; Chapter 6; pp. 203–255. ISBN 978-0-470-45836-5. [Google Scholar]
- Simonová, A.; Hargaš, L.; Koniar, D.; Loncová, Z.; Hrianka, M. Mathematical analysis of complete operation cycle of a system with two-position controller. In Proceedings of the 2016 ELEKTRO, Strbske Pleso, Slovakia, 16–18 May 2016; pp. 213–215. [Google Scholar] [CrossRef]
- Takeuchi, T.J. Theory of SCR Circuit and Application to Motor Control; Electrical Engineering College Press: Tokyo, Japan, 1968; 284p, ASIN no. B000O026. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Aramovich, J.G.; Lunts, G.L.; Elsgolts, L.C. Complex Variable Functions, Operator Calculus, Theory of Stability; ALFA Publisher: Bratislava, Slovakia, 1973; Chapter 7; pp. 157–228. (In Slovak) [Google Scholar]
- Oršanský, P. Complex Variable Theory; Textbook UNIZA: Žilina, Slovakia, 2020; ISBN 978-80-554-1764-6. (In Slovak) [Google Scholar]
- Smith, S.W. The Complex Fourier Transform. In The Scientist and Engineer’s Guide to Digital Signal Processing; California Technical Publishing: San Diego, CA, USA, 1997–2007; Chapter 31; pp. 567–580. ISBN 0-9660176-3-3. [Google Scholar]
- Dobrucký, B.; Kaščák, S.; Šedo, J. Power Components Mean Values Determination Using New Ip-Iq Method for Transients. Energies 2024, 17, 2720. [Google Scholar] [CrossRef]
- Blagouchine, I.V.; Moreau, E. Analytic method for the computation of the total harmonic distortion by the Cauchy method of residues. IEEE Trans. Commun. 2011, 59, 2478–2491. [Google Scholar] [CrossRef]
- Choi, M.-J.; Park, I.-H. Transient analysis of magneto-dynamic systems using Fourier transform and frequency sensitivity. IEEE Trans. Magn. 1999, 35, 1155–1158. [Google Scholar] [CrossRef]





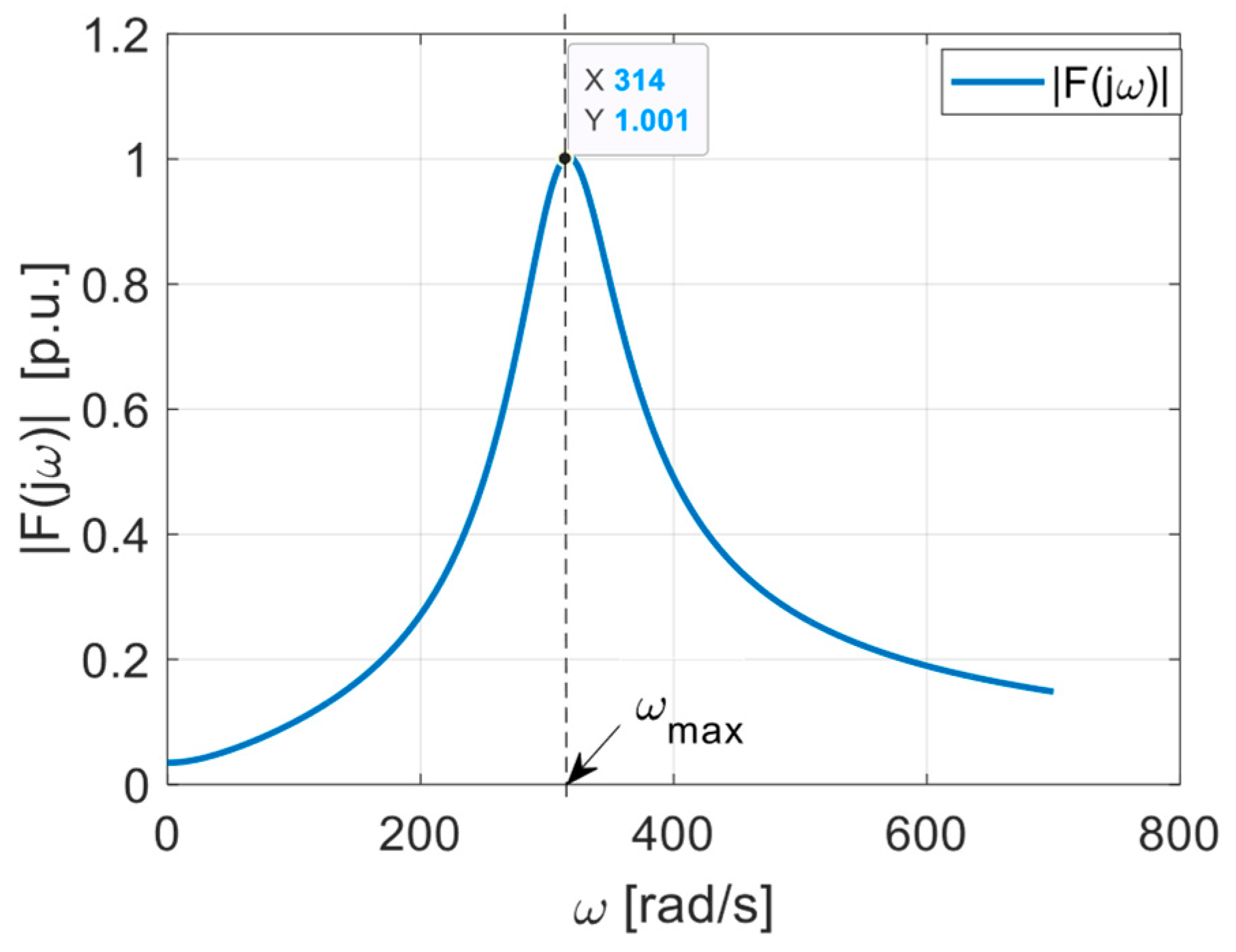
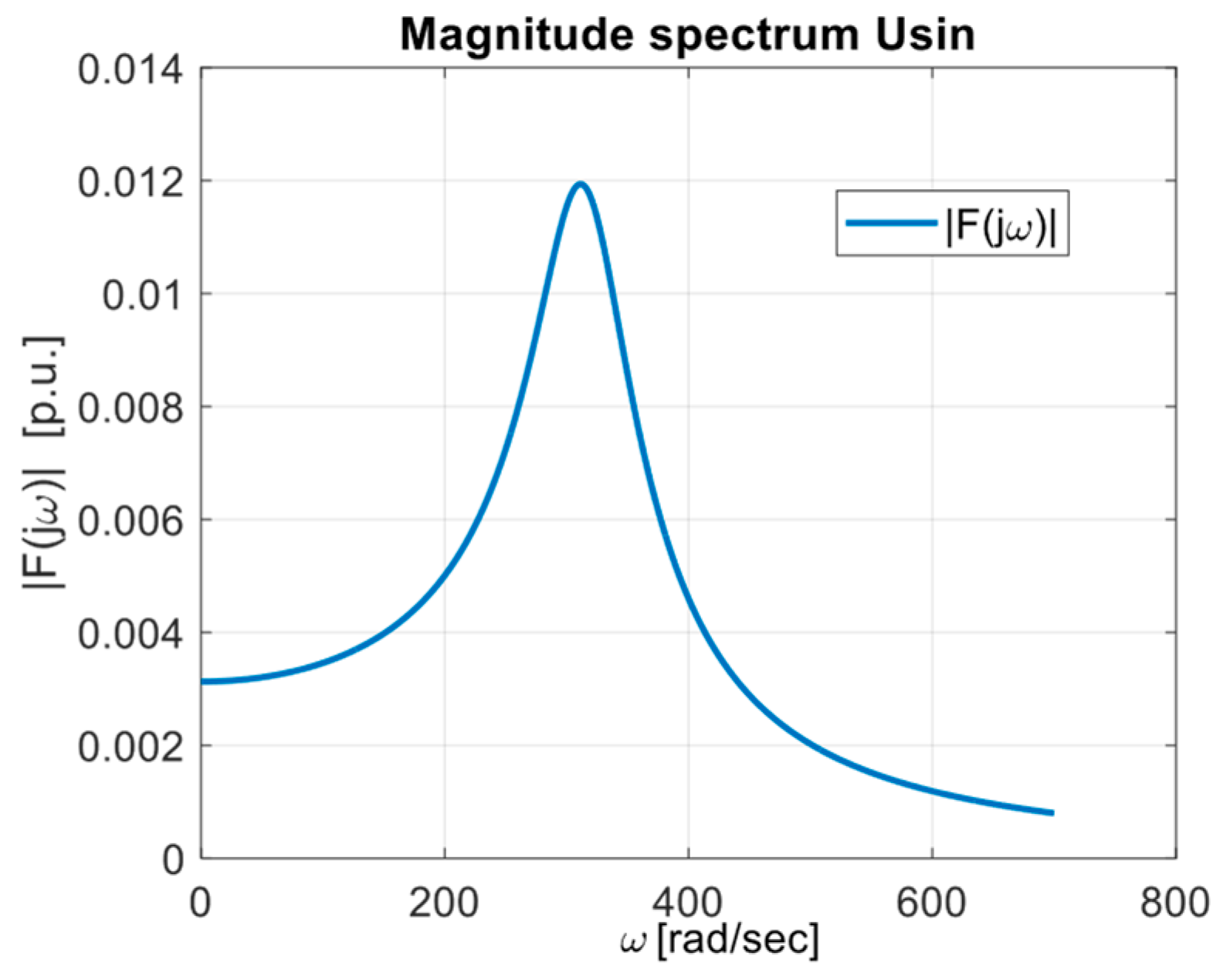
| Um [V] | [Hz] | R [W] | L [mH] | Z [W] | [ms] | [deg] |
|---|---|---|---|---|---|---|
| 325 | 50 | 18.4 | 43.93 | 23 | 2.3875 | 36.76 |
| Um [V] | [Hz] | R [W] | L [mH] | Z [W] | [ms] | [deg] |
|---|---|---|---|---|---|---|
| 325 | 50 | 18.4 | 43.93 | 23 | 10 τ1 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beňová, M.; Dobrucký, B.; Šedo, J.; Praženica, M.; Koňarik, R.; Šimko, J.; Kuchař, M. A Novel Approach to Transient Fourier Analysis for Electrical Engineering Applications. Appl. Sci. 2024, 14, 9888. https://doi.org/10.3390/app14219888
Beňová M, Dobrucký B, Šedo J, Praženica M, Koňarik R, Šimko J, Kuchař M. A Novel Approach to Transient Fourier Analysis for Electrical Engineering Applications. Applied Sciences. 2024; 14(21):9888. https://doi.org/10.3390/app14219888
Chicago/Turabian StyleBeňová, Mariana, Branislav Dobrucký, Jozef Šedo, Michal Praženica, Roman Koňarik, Juraj Šimko, and Martin Kuchař. 2024. "A Novel Approach to Transient Fourier Analysis for Electrical Engineering Applications" Applied Sciences 14, no. 21: 9888. https://doi.org/10.3390/app14219888
APA StyleBeňová, M., Dobrucký, B., Šedo, J., Praženica, M., Koňarik, R., Šimko, J., & Kuchař, M. (2024). A Novel Approach to Transient Fourier Analysis for Electrical Engineering Applications. Applied Sciences, 14(21), 9888. https://doi.org/10.3390/app14219888






