Reliability Analysis of Complex Structures Under Multi-Failure Mode Utilizing an Adaptive AdaBoost Algorithm

Abstract

A reliability analysis can become intricate when addressing issues related to nonlinear implicit models of complex structures. To improve the accuracy and efficiency of such reliability analyses, this paper presents a surrogate model based on an adaptive AdaBoost algorithm. This model employs an adaptive method to determine the optimal training sample set, ensuring it is as evenly distributed as possible on both sides of the failure curve and fully contains the information it represents. Subsequently, with the integration and iterative characteristics of the AdaBoost algorithm, a simple binary classifier is iteratively applied to build a high-precision alternative model for complex structural fault diagnosis to cope with multiple failure modes. Then, the Monte Carlo simulation technique is employed to meticulously assess the failure probability. The accuracy and stability of the proposed method’s iterative convergence process are validated through three numerical examples. The findings of the study illuminate that the proposed method is not only remarkably precise but also exceptionally efficient, capable of addressing the challenges related to the reliability evaluation of complex structures under multi-failure mode. The method proposed in this paper enhances the application of mechanical structures and facilitates the utilization of complex mechanical designs.

1. Introduction

The aim of the structural reliability analysis is to meticulously quantify the failure probability that arises from a multitude of uncertain factors, such as the geometric size error, variations in material properties, and external applied load [1,2]. To improve system reliability and simplify the reliability-based design problems widely applied in various engineering practices [3,4], many scholars have studied the reliability of multi-failure mode systems [5,6,7,8,9,10]. For example, Marozaua et al. [7] conducted a reliability assessment to solve specific safety assessment problems, analyzed the underlying causes of micro-electro-mechanical system device failure, and carried out a failure test using a typical micro-electro-mechanical system device package structure. Wang et al. [8] introduced a probabilistic analysis framework aimed at evaluating the reliability of turbine discs while accounting for the interdependencies among various failure modes. Meng et al. [9] proposed a hybrid reliability-based topology optimization method to deal with cognitive and cognitive uncertainty. Yang et al. [10] proposed an innovative reliability analysis method that integrates Markov chain Monte Carlo method with random forest algorithms. J. Guadalupe Monjardin-Quevedo, Alfredo Reyes-Salazar, et al. [11] explored the properties of steel by evaluating the seismic reliability of deep column smf. The first-order reliability method, response surface method, and an advanced probability scheme were adopted. The efficiency and accuracy of the proposed method were verified by the traditional Monte Carlo simulation method. German Michel Guzman-Acevedo, Juan A. Quintana-Rodriguez, Jose Ramon Gaxiola-Camacho, et al. [12] evaluated the Usumacinta Bridge in Mexico based on probabilistic methods, The Sentinel-1 image was used to define structural reliability. The case for selecting probabilistic methods integrates the reliability of the structure. Displacement theory and probability density function obtained by InSAR technique (pdf).

Common structural reliability analysis methods include the digital simulation method [13,14], approximate analytical method [15,16] and surrogate model methods. The Monte Carlo method [17] is a relatively straightforward digital simulation method. However, the large number of samples required for obtaining an accurate solution makes the method less efficient. Another digital simulation method known as importance sampling [18] utilizes the design point of the limit state equation as its sampling center, thereby enhancing sampling efficiency to a certain extent. However, this design point must be predetermined, which limits the applicability of this method to complex structures. Approximate analytic methods, such as the first-order second-moment method [19], necessitate minimal computational effort but yield large relative errors. Consequently, these methods are only suitable for solving the reliability problem associated with an explicit limit state equation. In view of the nonlinear implicit characteristics of complex mechanical structures, surrogate modeling methods such as the Kriging algorithm [20], neural network algorithm [21], and support vector machines algorithm [22] are frequently utilized to assess the reliability of these intricate mechanical structures. However, these algorithms are simple extensions of the single traditional classification algorithm for specific data, and they inevitably inherit the inherent shortcomings of the original algorithm [23]. Simultaneously, these algorithms rely on relatively idealized assumptions regarding probability distribution and data types when dealing with data uncertainty, which consequently hampers their widespread applicability in practical projects [24].

Traditional reliability analysis methods have accuracy problems, large errors, and low computational efficiency, making it difficult to effectively apply them in practical engineering. To address these challenges, this paper proposes a new reliability analysis method for complex structural systems with multiple failure modes, utilizing an adaptive AdaBoost model that enhances both accuracy and effectiveness in assessing the reliability of complex structures. Adaptive iteration continuously optimizes the sampling center through proactive sampling. During this process, the effectiveness of the sample is quantitatively evaluated by measuring the ratio of the number of samples falling into the ineffective region to the total number of samples. The AdaBoost algorithm is a strong integrated learning method for low-bias prediction tasks, which are not easy to overfit during training [25]. The method employs a training dataset with different weights to construct different weak basis classifiers. Each data sample is then assigned a weight that indicates its importance as a training sample, and all samples have the same weight in the first iteration. In the ensuing iterations, the weight assigned to misclassified samples is elevated (or alternatively, the weight attributed to correctly classified samples is proportionately diminished), causing the new classifier to pay increasing attention to misclassified samples that may gather near the classification edge, thereby ultimately reducing the error rate [26,27,28]. Many scholars around the world have actively engaged in in-depth research on the AdaBoost algorithm, evaluating its application effects and proposing practical and feasible improvements [29,30,31,32,33,34]. For example, Liu et al. [31] presented an innovative approach to the naval gun hydraulic system fault diagnosis based on the BP-AdaBoost model. Zhou et al. [32] proposed a new polynomial chaos expansion surrogate modeling method utilizing AdaBoost for uncertainty quantification. Lou [33] artfully integrated the enhanced AdaBoost algorithm with the backpropagation neural network model, employing an evolutionary optimization algorithm to refine the model and proposing a mechanical structure reliability calculation method grounded in this advanced framework. Du et al. [34] proposed a real BP AdaBoost algorithm based on weighted information entropy to solve the problems of low prediction accuracy and poor reliability of the software reliability model of the single neural network. Meng et al. [35,36,37] proposed a new hybrid adaptive Kriging model and a water-cycle algorithm based on reliability assessment learning and optimization strategies, subsequently applying it to offshore wind turbine monopole and offshore wind power towers. N. Asgarkhani, F. Kazemi, et al. [38] proposed a machine learning (ML) algorithm to provide prediction models for determining the seismic response, seismic performance curve and earthquake failure probability curve of brbf. Farzin Kazemi, Neda Asgarkhani, and Robert Jankowski [39] solved the problem of seismic probability and risk assessment of reinforced concrete shear walls (RCSWs) by introducing a stacked machine learning (stacked ML) model based on Bayesian optimization (BO), genetic algorithm (GA), particle swarm optimization (PSO), and gradient-based optimization (GBO) algorithms. The IDA curves (MIDA) and seismic probability curves of this model have a good curve-fitting ability.

The subsequent sections of this paper will be meticulously organized into three sections. Section 2 will thoroughly explore the distinctive characteristics of complex structures in the context of multiple failure modes, the methodology for adaptive sample selection, and the principle underlying the iterative AdaBoost algorithm. Additionally, it outlines a process for assessing the reliability of mechanical structures based on the AdaBoost surrogate model. The Section 3 validates the effectiveness and precision of the AdaBoost surrogate model in evaluating multi-failure mode complex structures through three illustrative examples and discusses their computational results. The Section 4 summarizes both the advantages and limitations of the AdaBoost surrogate model and establishes the applicable scope of this method.

2. Reliability Analysis Based on the AdaBoost Surrogate Model

2.1. Reliability Modeling of Complex Structures under Multi-Failure Mode

There are two primary reliability models for complex structures exhibiting multi-failure mode: the series system and the parallel system. Nevertheless, in the realm of practical engineering applications, complex structural systems frequently exhibit multiple failure modes, with the overall failure mode typically arising from the interactions among these failures. Particularly within intricate systems, the interrelationships between failure modes become progressively more complex, as each mode engages in reciprocal interactions with others.

Suppose that a problem contains m failure modes, the corresponding limit state equation is denoted by $g^{(k)}(x)=0(k=1,2,\dots ,m)$, and the corresponding failure domain is denoted by $D_f^{(k)}=\left\{g^{(k)}(x)\le 0\right\}(k=1,2,\dots ,m)$, where $x=\left\{x_1,x_2,\dots ,x_n\right\}$ represents an n-dimensional random variable.

When m failure modes are present in series, the relationship between the system’s failure domain, $D_f$, and the failure domain, $D_f^{(k)}$, of each individual mode can be expressed as follows:

$$D_f=\underset{k=1}{\overset{m}{{\displaystyle \cup }}}{D}_f^{(k)}$$

(1)

When m failure modes occur simultaneously, it is a parallel situation, and the relationship between the system’s failure domain, $D_f$, and failure domain, $D_f^{(k)}$, of each individual mode can be expressed as follows:

$$D_f=\underset{k=1}{\overset{m}{{\displaystyle \cap }}}{D}_f^{(k)}$$

(2)

2.2. Adaptive AdaBoost Algorithm

The adaptive AdaBoost algorithm initially employs an adaptive iteration method to obtain the optimal training sample set, which is as evenly distributed as possible on both sides of the failure curve, fully encompassing the information that describes the failure curve. By using the integration and iteration properties of the AdaBoost algorithm, a high-precision surrogate model for failure discrimination in complex structures under multi-failure modes can be achieved through simple binary classifier iteration (the dichotomy method).

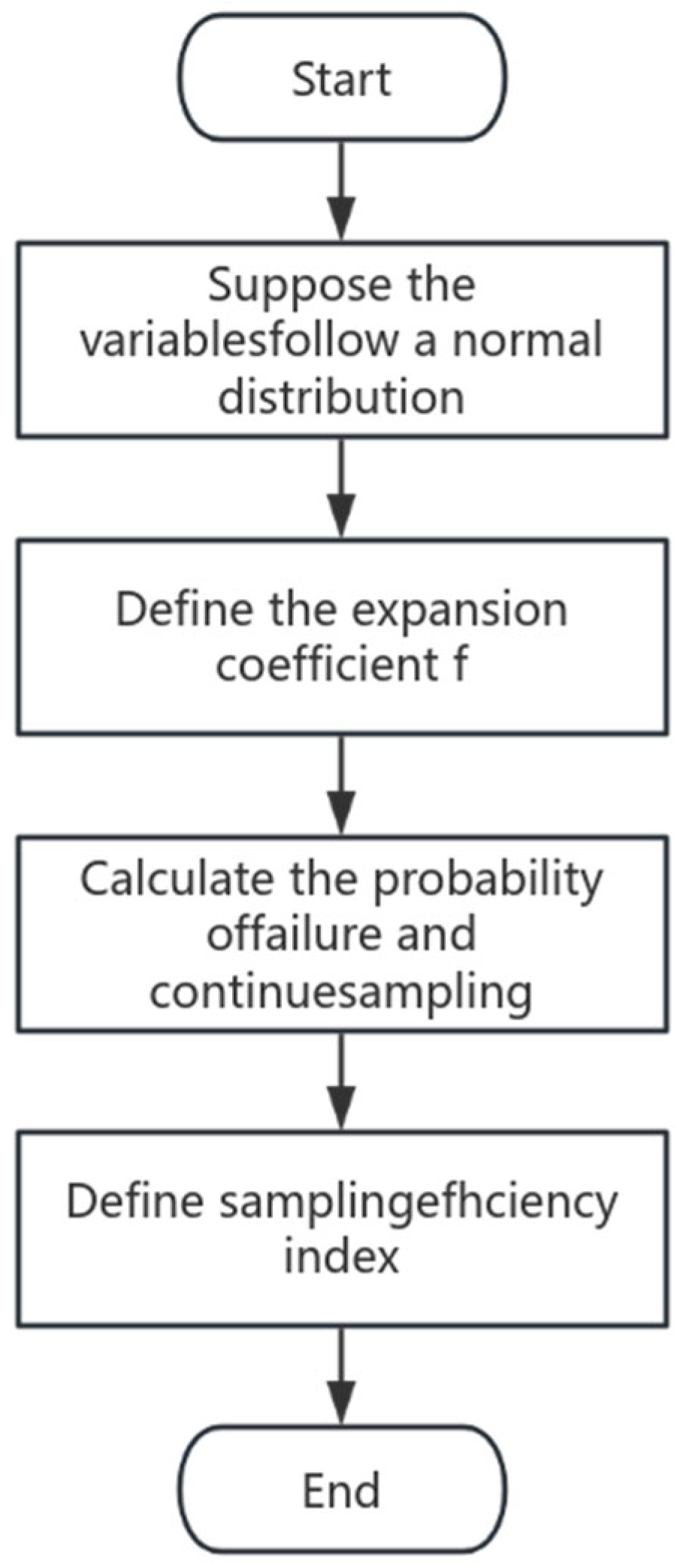
2.2.1. Adaptive Sampling

The idea of adaptive sampling is to determine the optimal design point through the iteration process and pre-sample the sample center in each iteration to obtain an optimal training sample set that is as evenly distributed as possible on both sides of the failure curve and fully contains the information of the failure curve. To swiftly ascertain the optimal design point, this study applied the extended sample variance and adaptive iteration method. The detailed steps of the proposed adaptive sampling method are outlined as follows:

(1)

It is presumed that the variables are mutually independent and follow a normal distribution, $x_i~N({\mu }_i,{\sigma }_i)(i=1,2,\dots ,n)$.

(2)

Define the expanded coefficient, f, and let $x_i~N({\mu }_i,f{\sigma }_i)(i=1,2,\dots ,n)$.

(3)

Employ Latin hypercube sampling to derive 200 sample points, and then bring them into the system model for discrimination and calculate failure probability ${\eta }_j(j=1,2,\dots ,m)$. Select the point ${\overline{x}}^{(j)}$ with the largest joint probability density from among the failure points; this point is taken as the sampling center for subsequent sampling.

(4)

Define a sampling efficiency index, ${\epsilon }_j=\left|0.5-{\eta }_j\right|$. The smaller the value of ${\epsilon }_j$, the closer the sampling center is to the optimal design point, and the failure probability approaches 50%.

(5)

When ${\epsilon }_j\le 0.1$, the loop comes to an end. The sampling center at this time is take as the new sampling center, and resampling is conducted using $x_i~N({\mu }_i,f{\sigma }_i)(i=1,2,\dots ,n)$.

The detailed flowchart illustrating the expanded sample variance and the adaptive iteration method is presented in Figure 1.

2.2.2. AdaBoost Algorithm

First, the AdaBoost algorithm builds the first simple classifier, h₁, based on the original data distribution. Then, Bootstrap produces T classifiers that are interconnected. Finally, these different classifiers are combined to form a stronger final classifier (strong classifier).

In theory, as long as each weak classifier’s classification ability is better than random guessing (a classification accuracy rate greater than 0.5), the error rate of the strong classifier will converge zero as the number of weak classifiers approaches infinity. Within the framework of the AdaBoost algorithm, different training sets are generated by adjusting the weights of each sample. At the beginning, the weight of each sample is the same, and basic classifier, $h_1(x)$, is trained under this sample distribution. The weights of the samples exhibiting poor $h_1(x)$ scores are elevated, while the weights of properly classified samples are decreased to highlight the incorrect samples. Meanwhile, $h_1(x)$ is assigned a weight according to its error, representing its importance; the lower the error rate, the greater the corresponding weight. The basic classifier is trained again using the new sample weight to obtain the basic classifier, $h_2(x)$, and its weight. Therefore, by analogy, after T rounds, T fundamental classifiers and their associated weights can be derived. Finally, T basic classifiers are added according to the previously calculated weights to obtain the final desired strong classifier.

Let us assume that the training set sample is denoted as $T=\left\{E_{11},E_{12},G_{12},G_{13},X_c,X_t,Y_c,Y_t,S_{12},S_{13},\mathrm{d}\right\}$, and the output weight of the training set in the k-th weak learner is $D(k)=(w_{k1},w_{k2},\dots w_{km});w_{1i}={\displaystyle \frac{1}{m}};i=1,2\dots m$.

Let us take a binary classification problem as an example. If the output is $\{0,1\}$, the weighted error rate of the k-th weak classifier, $G_k(x)$, on the training set is $e_k=P\left(G_k(x_i)\ne y_i\right)={\displaystyle \sum _{i=1}^m{w}_{ki}I(G_k(x_i)\ne y_i)}$.

The weight coefficient of the k-th weak classifier,$G_k(x)$, is denoted as ${\alpha }_k={\displaystyle \frac{1}{2}}\log {\displaystyle \frac{1-e_k}{e_k}}$. An increase in the classification error rate, $e_k$, is associated with a decrease in the corresponding weak coefficient, ${\alpha }_k$, of the classifier weight. Assuming that the sample set-weight coefficient for the k-th weak classifier is $D(k)=(w_{k1},w_{k2},\dots w_{km})$, then the sample set-weight coefficient of the corresponding k + 1 weak classifier is $w_{k+1,i}={\displaystyle \frac{w_{ki}}{Z_K}}\exp (-{\alpha }_k{y}_i{G}_k(x_i))$, where $Z_K$ represents a normalization factor, $Z_K={\displaystyle \sum _{i=1}^m{w}_{ki}\exp (-{\alpha }_k{y}_i{G}_k(x_i))}$. It is apparent from the $w_{k+1}$ calculation formula that if the i-th sample is classified incorrectly, $y_i{G}_k(x_i)<0$, resulting in the increase in the weight of the sample in the k + 1 weak classifier. Should the classification be deemed accurate, the weight in the k + 1 weak classifier decreases.

The weighted voting method is adopted for AdaBoost classification, and the ultimate strong classifier can be expressed as follows: $f(x)=sign({\displaystyle \sum _{k=1}^K{\alpha }_k{G}_k(x)})$.

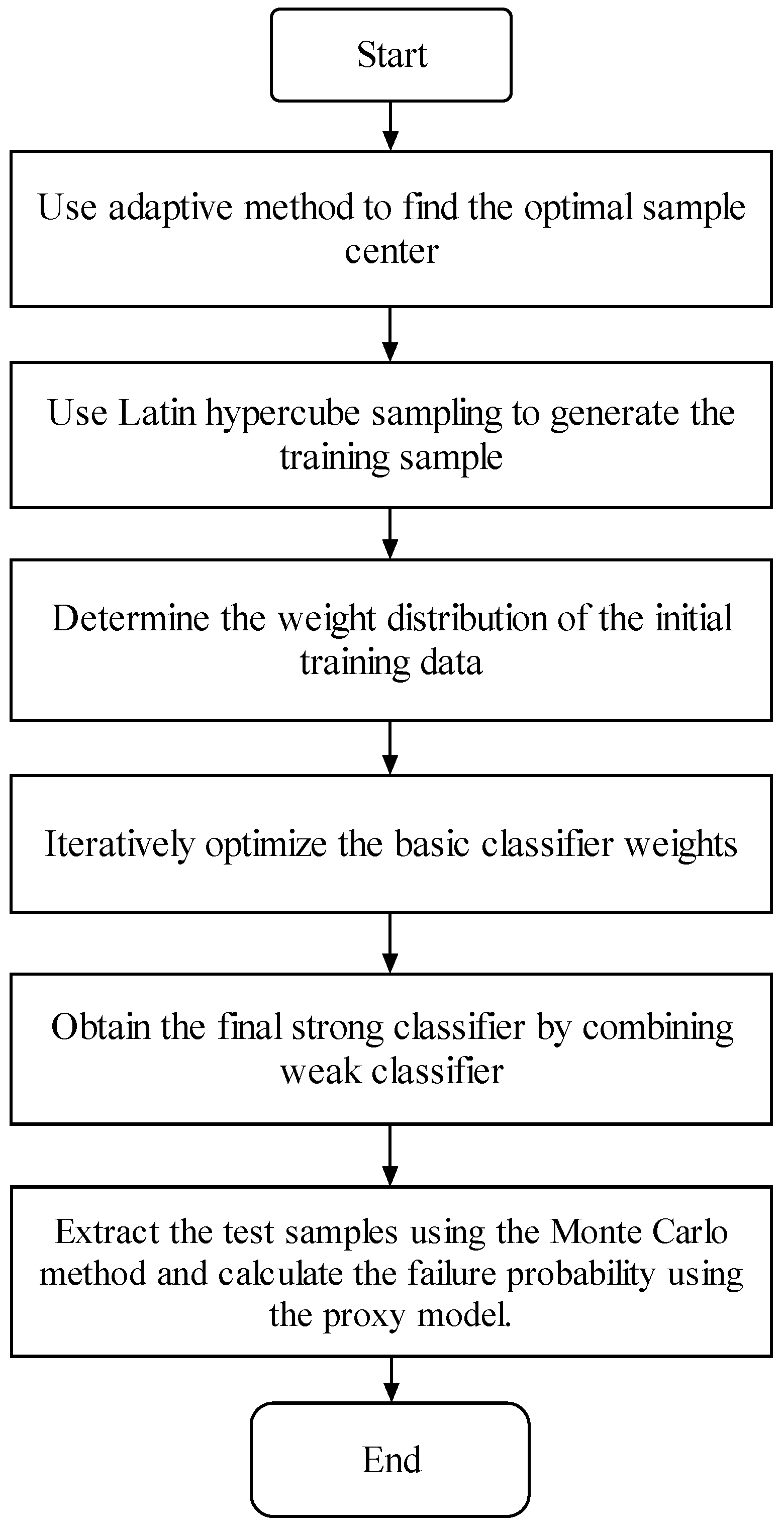
2.3. Reliability Analysis Model Based on the Adaptive AdaBoost Algorithm

The basic idea of a reliability analysis based on the adaptive AdaBoost algorithm involves employing an adaptive iterative method to find the optimal training sample set, as elaborated in Section 2.2.1. Then, a high-precision surrogate model for failure discrimination of complex structures under multiple failure modes is obtained through simple binary classifier iteration based on the integration and iteration characteristics to the AdaBoost algorithm, as discussed in Section 2.2.2. Finally, the Monte Carlo method is used to determine the failure probability. The detailed analytical procedures are delineated as follows:

(1)

Use the adaptive method to find the optimal sample center.

(2)

According to the sample center, use Latin hypercube sampling to generate training samples.

(3)

Initialize the weight distribution of the training data. Assign the same weight to each training sample as follows: $D_1=(w_{11},w_{12},\dots ,w_{1i},\dots ,w_{1N}),w_{1i}={\displaystyle \frac{1}{N}},i=1,2,\dots ,N$.

(4)

In the m-th iterations, obtain $G_m(x)$, which represents the current m-round iterative classifier; obtain $e_m$, denoting the present classification error; and obtain ${\alpha }_m$, which signifies the cumulative coefficient as elaborated below:

①

Obtain the basic classifier $G_m(x):x_i\to \left\{-1,+1\right\}$ by learning the training dataset with a weight distribution of $D_m$.

②

Calculate the classification error rate of $e_m$ for the training dataset:

$$e_m=P\left(G_m(x_i)\ne y_i\right)={\displaystyle \sum _{i=1}^N{w}_{mi}I(G_m(x_i)\ne y_i)}$$

(3)

③

Calculate the coefficient for $G_m(x)$, where ${\alpha }_m$ represents the importance of $G_m(x)$ in the final classifier:

$${\alpha }_m={\displaystyle \frac{1}{2}}\log {\displaystyle \frac{1-e_m}{e_m}}$$

(4)

It is evident from the preceding equation that $e_m\le {\displaystyle \frac{1}{2}}$ and ${\alpha }_m\ge 0$, and that ${\alpha }_m$ increases as $e_m$ decreases, thereby indicating that basic classifiers with lower classification error rates have a greater impact on the final strong classifier.

④

Update the weight distribution of the training dataset to obtain a new weight distribution for the subsequent interaction:

$$D_{m+1}=(w_{m+1,1},w_{m+1,2},\dots ,w_{m+1,\mathrm{i}},\dots ,w_{m+1,N})$$

(5)

$$w_{m+1,i}={\displaystyle \frac{w_{mi}}{Z_m}}\exp (-{\alpha }_m{y}_i{G}_m(x_i)),i=1,2,\dots ,N$$

(6)

where $Z_m={\displaystyle \sum _{i=1}^N{w}_{mi}\exp (-{\alpha }_m{y}_i{G}_m(x_i))}$.

As a result, the weights of samples misclassified by the fundamental classifier, $G_m(x)$, are augmented, whereas the weights of accurately classified samples are diminished. In this manner, the AdaBoost algorithm can concentrate on samples that are more challenging to differentiate.

(5)

Integrate the weak classifiers:

$$f(x)={\displaystyle \sum _{m=1}^M{\alpha }_m{G}_m(x)}$$

(7)

The ultimate strong classifier is denoted by

$$G(x)=sign(f(x))=sign({\displaystyle \sum _{m=1}^M{\alpha }_m{G}_m(x)})$$

(8)

(6)

Use the Monte Carlo method to calculate the failure probability based on the final strong classifier.

Figure 2 illustrates the flowchart of steps 1–6 for the reliability analysis of complex structures utilizing the adaptive AdaBoost algorithm proposed in this paper.

3. Examples

To verify the accuracy and efficiency of the proposed adaptive AdaBoost surrogate model, this section provides examples of mechanical structure reliability analysis under different failure functions, with the iteration number set to 200.

3.1. Parallel System

Consider a parallel system distinguished by two distinct failure modes, with the corresponding function articulated as follows.

$$y_1=x_1^2-x_2+2$$

(9)

$$y_2=-x_1^2+x_2-6$$

(10)

where $x_1$ and $x_2$ denote normally distributed random variables, specifically denoted as $x_1~N(4,1^2)$ and $x_2~N(3,{0.5}^2)$, respectively. The failure conditions of the system are defined by $y_1<0$ and $y_2<0$.

The proposed adaptive AdaBoost surrogate model is employed to evaluate the failure probability of the parallel system. The variation in error with respect to the number of iterations during the training process (resubstitution loss) is shown in Figure 2.

It can be discerned from Figure 3 that the adaptive AdaBoost surrogate model effectively simulates the failure surface of parallel systems. As the number of iterations escalates, the error of the agent model steadily diminishes and ultimately converges to zero.

The trained model is utilized to evaluate the failure probability, which is subsequently compared with the result obtained by using the conventional Monte Carlo method. The results are presented in

Table 1. Calculated failure probability of the parallel system.

Method	Sampling Frequency	Failure Probability	Relative Error
Monte Carlo method	106	4 × 10−5	/
Adaptive AdaBoost method	500	3.7 × 10−5	7.5%

, where it can be noted that the failure probability obtained derived from the adaptive AdaBoost method is 3.7 × 10⁻⁵, with a relative error of 7.5%, when compared to the conventional Monte Carlo method. This underscores the effectiveness of the proposed adaptive AdaBoost model. It is noteworthy that the conventional Monte Carlo method necessitated millions of samples, whereas the adaptive AdaBoost surrogate model required only 500 samples, leading to a substantial reduction in computation time and a marked enhancement in computational efficiency.

3.2. Series System

Consider a series structure system comprising two failure modes, with the corresponding function denoted as follows.

$$y_1=2x_1+2x_2-4.5x_4-100$$

(11)

$$y_2=x_1+x_2+2x_3-4.5x_4+380$$

(12)

where $x_1$, $x_2$, $x_3$, and $x_4$ are normal random variables, specifically denoted as $x_1~N(200,{30}^2)$, $x_2~N(200,{30}^2)$, $x_3~N(200,{30}^2)$, and $x_4~N(80,{15}^2)$, respectively. The failure conditions of the system are defined by $y_1<0$ or $y_2<0$.

The adaptive AdaBoost surrogate model is employed to assess the failure probability of the series system. The variation in error concerning the number of iterations throughout the training process (resubstitution loss) is illustrated in Figure 3.

As depicted in Figure 4, it is evident that with an increasing number of iterations, the error of the adaptive AdaBoost surrogate model gradually decreases and converges to zero, indicating its efficacy in failure discrimination for the series system.

The trained models are utilized to evaluate the failure probability, after which the results are compared with those derived from the conventional Monte Carlo method. The results are presented in

Table 2. Calculated failure probability of series system.

Method	Sampling Frequency	Failure Probability	Relative Error
Monte Carlo method	106	9.1 × 10−4	/
Adaptive AdaBoost method	300	9.6 × 10−4	5.49%

, with a relative error of 5.49% between the result obtained using the adaptive AdaBoost surrogate model and that obtained using conventional Monte Carlo methods. This illustrates the precision and substantiates the efficacy of the proposed method. In contrast to the traditional Monte Carlo method, which necessitated millions of samples, the adaptive AdaBoost surrogate model required only 300 samples, meaning that the sampling efficiency has been significantly improved and the computing time has been greatly shortened.

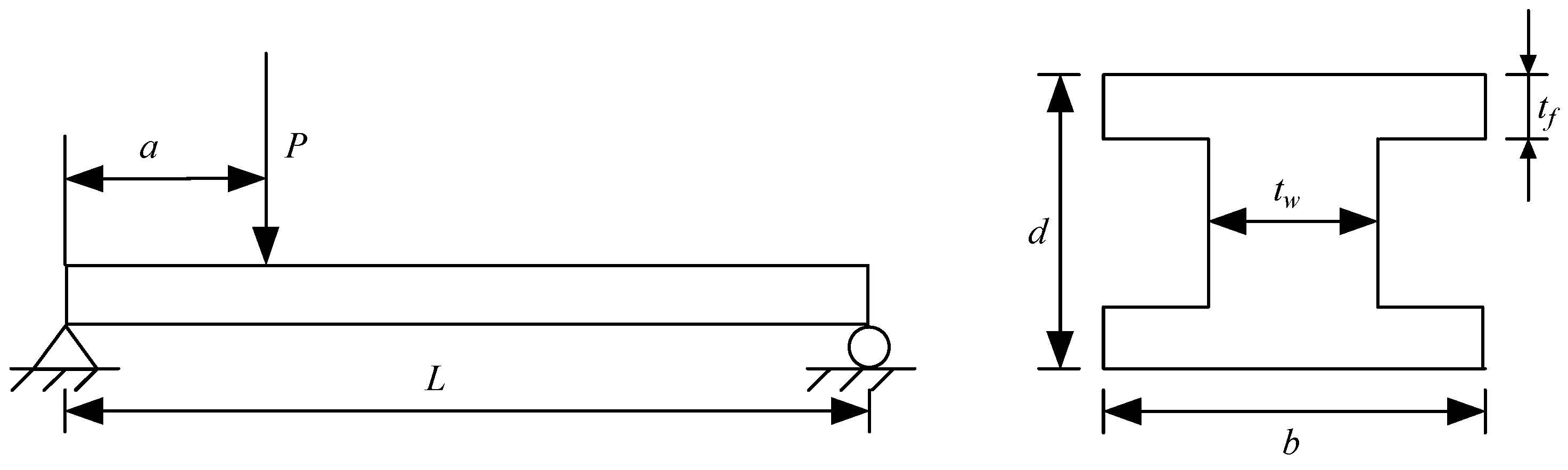
3.3. Engineering Example

Figure 5 shows an I-beam system with eight random input variables, $X=\left\{{d,b,t}_w{,t}_f,L,a,P,S\right\}$ [40]. The specific distribution is presented in

Table 3. Distribution of random variables of the I-beam system.

Variable	Mean Value	Standard Deviation	Distribution Type
$d/\mathrm{i}\mathrm{n}$	2.3	1/24	Normal
$b/\mathrm{i}\mathrm{n}$	2.3	1/24	Normal
$t_w/\mathrm{i}\mathrm{n}$	0.16	1/24	Normal
$t_f/\mathrm{i}\mathrm{n}$	0.26	1/24	Normal
$L/\mathrm{i}\mathrm{n}$	120	6	Normal
$a/\mathrm{i}\mathrm{n}$	72	6	Normal
$P/\mathrm{N}$	6070	200	Normal
$S/\mathrm{k}\mathrm{P}\mathrm{a}$	170,000	4760	Normal

. The response function of the I-beam system is given by

$$Y=g\left(X\right)=S-{\sigma }_{\mathit{max}}=S-{\displaystyle \frac{\mathit{Pa}\left(L-a\right)d}{2\mathit{LI}}}$$

(13)

where $S$ is the strength, ${\sigma }_{\mathit{max}}$ is the maximum stress, and $I={\displaystyle \frac{{\mathit{bd}}^3-\left({b-t}_w\right){\left({d-2t}_f\right)}^3}{12}}$.

The adaptive AdaBoost surrogate model is employed to obtain the failure probability of the I-beam system. The variation in the error with respect to the number of iterations during the training process (resubstitution loss) is shown in Figure 6.

As illustrated in Figure 5, it is evident that with an increasing number of iterations, the error of the adaptive AdaBoost surrogate model gradually decreases and converges to zero; this suggests that the surrogate model possesses a robust fitting capability.

The trained model is employed to ascertain the failure probability, which is subsequently compared with that determined using the conventional Monte Carlo method. The results are presented in

Table 4. Calculated failure probability of the I-beam system.

Method	Sampling Frequency	Failure Probability	Relative Error
Monte Carlo method	106	0.2074	/
Adaptive AdaBoost method	70	0.2041	1.59%

, in which the relative error between the results obtained from the adaptive AdaBoost surrogate model and those obtained from the conventional Monte Carlo method is 1.59%, satisfying accuracy requirements and demonstrating the effectiveness of the adaptive AdaBoost surrogate model. In comparison to the traditional Monte Carlo method, which necessitated millions of samples, only 70 samples are required by the adaptive AdaBoost surrogate model, indicating considerably improved sampling efficiency and a reduction in calculational time.

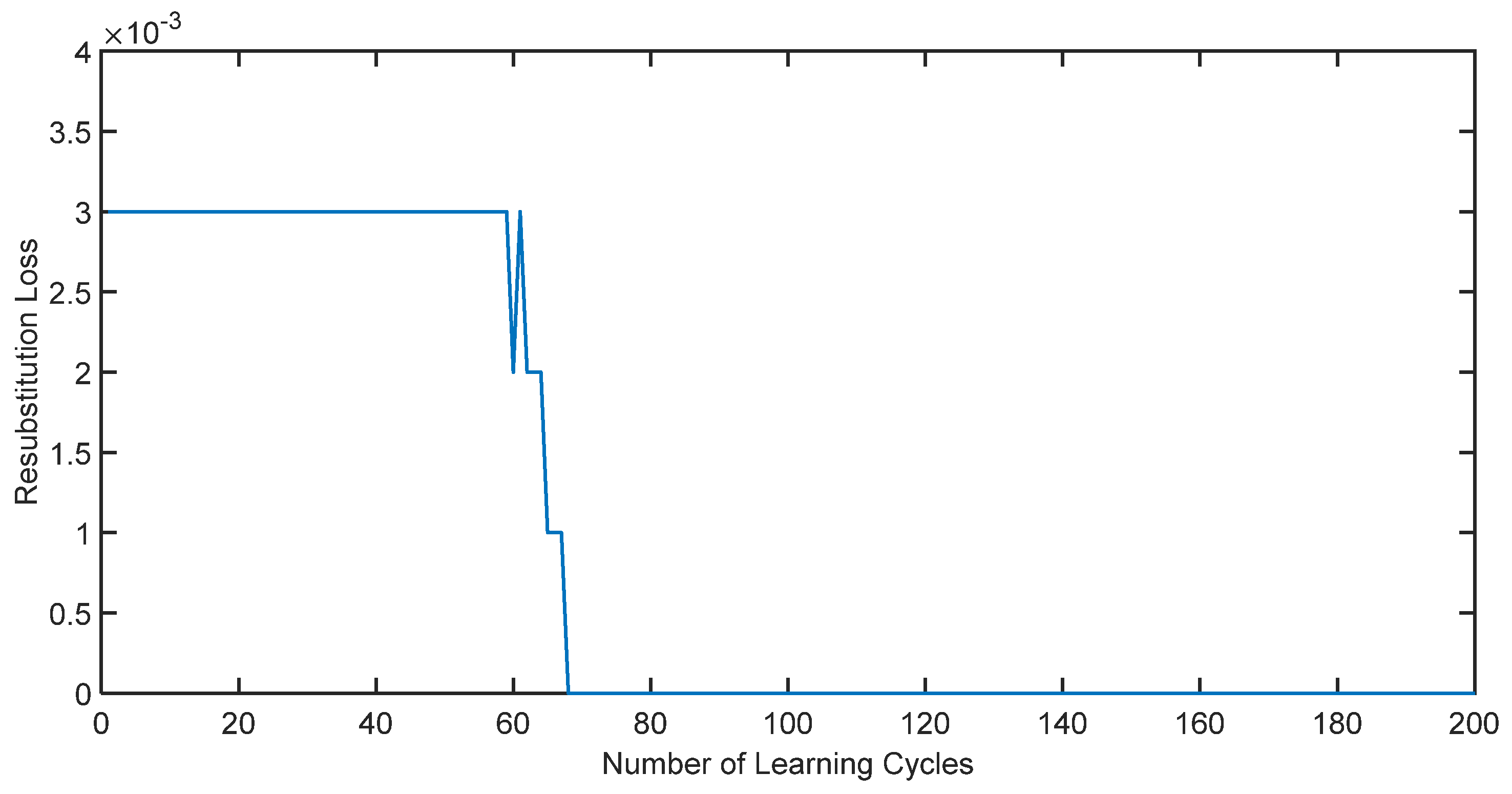
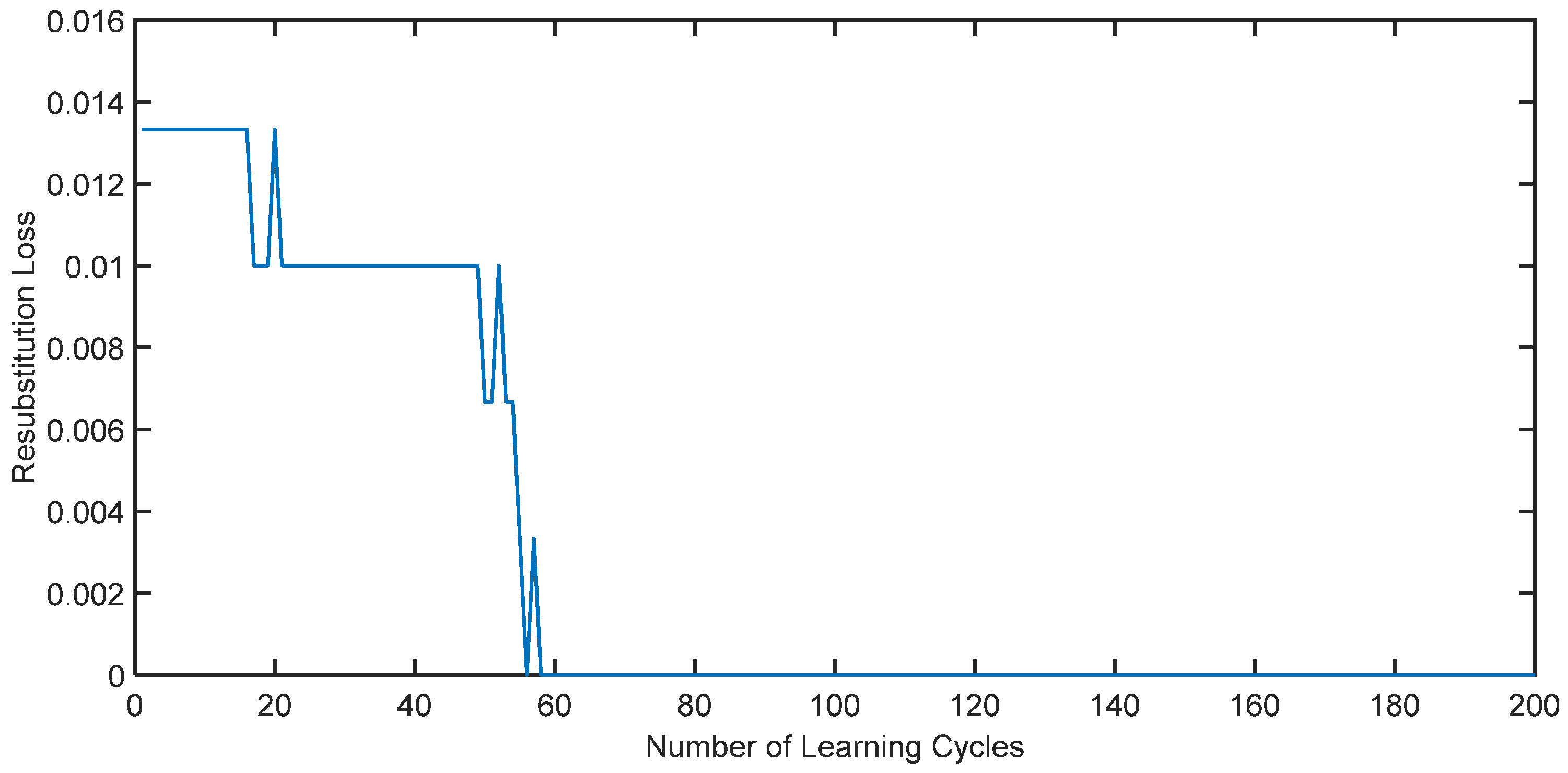
3.4. Analysis and Discussion

The previously mentioned examples illustrate that as the number of iterations escalates, the calculation error under the adaptive AdaBoost surrogate model converges to a minimum value for both parallel and series systems. This suggests that the AdaBoost surrogate model demonstrates an exceptional fitting performance and remarkable versatility in both parallel and series systems. Furthermore, when comparing the adaptive AdaBoost method with the Monte Carlo method, it is evident that the relative error between the failure probability derived from the adaptive AdaBoost alternative model method and that computed using the Monte Carlo method is smaller, aligning more closely with Monte Carlo simulation results, while significantly enhancing computational efficiency compared to traditional methods. Therefore, the accuracy of structural reliability calculated by the method proposed in this paper is higher than that of the traditional algorithm model, and calculation efficiency has been significantly enhanced, rendering it suitable for real engineering structures.

4. Conclusions

An adaptive AdaBoost algorithm is proposed to evaluate the reliability of multi-failure mode structures. This method shows excellent effectiveness in complex mechanical structures where explicit functions are difficult to establish. The optimal training sample set is obtained by the adaptive method, and then the AdaBoost algorithm is trained on this refined sample set. The generated proxy model not only meets the accuracy requirements, but also can better distinguish whether the target structure is invalid under the given parameters.

(1)

Compared with the traditional Monte Carlo method, this model significantly improves the computational efficiency and can accurately calculate the failure probability in a shorter time.

(2)

The method has good universality. Compared with the general alternative model, the adaptive AdaBoost algorithm proposed in this paper has the advantages of strong applicability, low dependence on the operator’s engineering experience, and high precision.

(3)

However, we must be aware that the studies conducted to date have some limitations. The adaptive AdaBoost algorithm proposed by us has not been applied to a multi-failure mode reliability analysis of more complex structures. More and more complex research scenarios put forward higher requirements and challenges for our proposed algorithms.

However, the method proposed in this paper is of great significance to the exploration of complex mechanical structures, which is helpful to improve the application level of mechanical structures and promote their wide application.