Adaptive Robust Control for Pump-Controlled Pitch Systems Facing Wind Speed and System Parameter Variability
Abstract
:1. Introduction
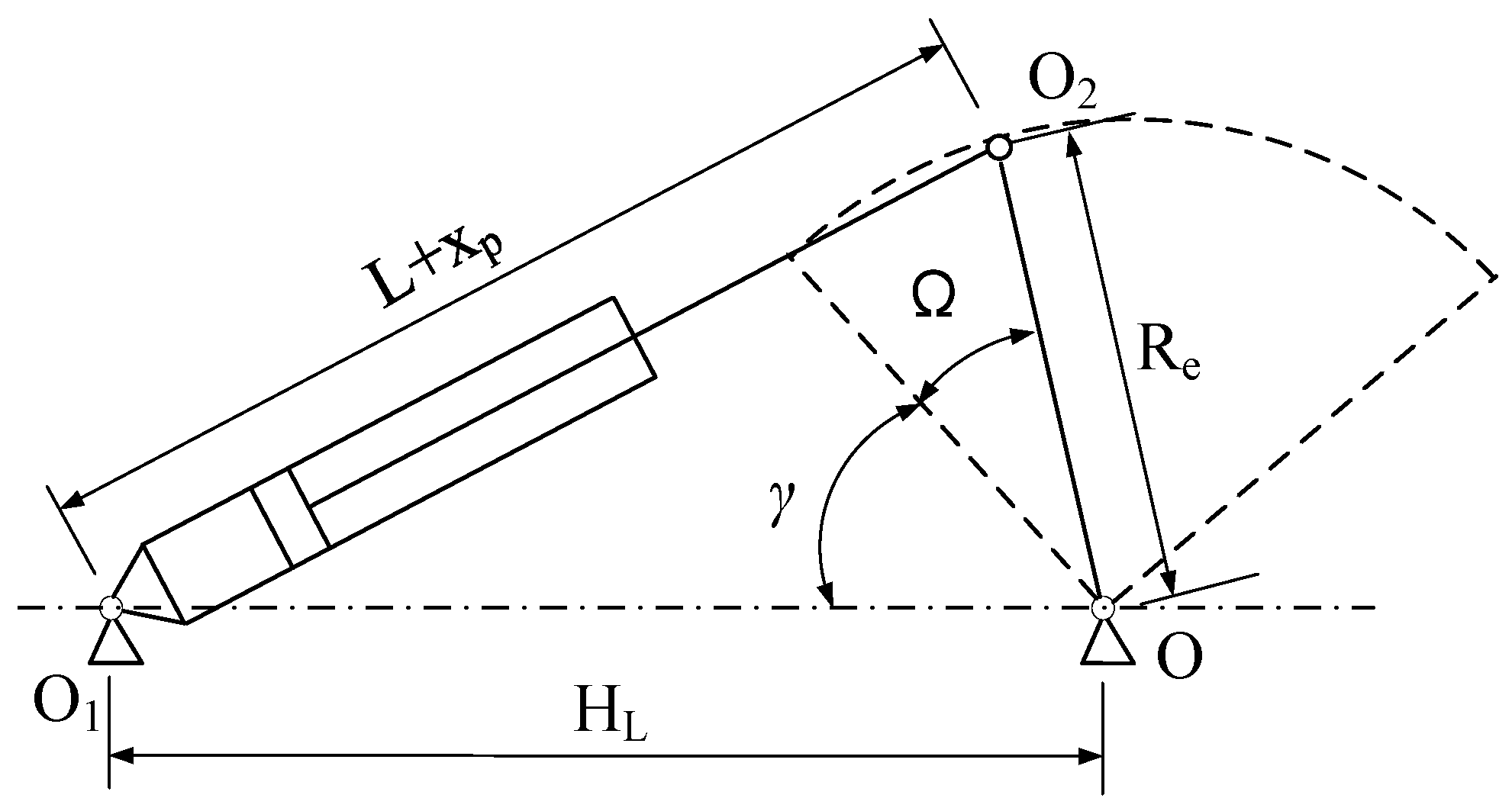
2. Pitch System Principles and Modeling
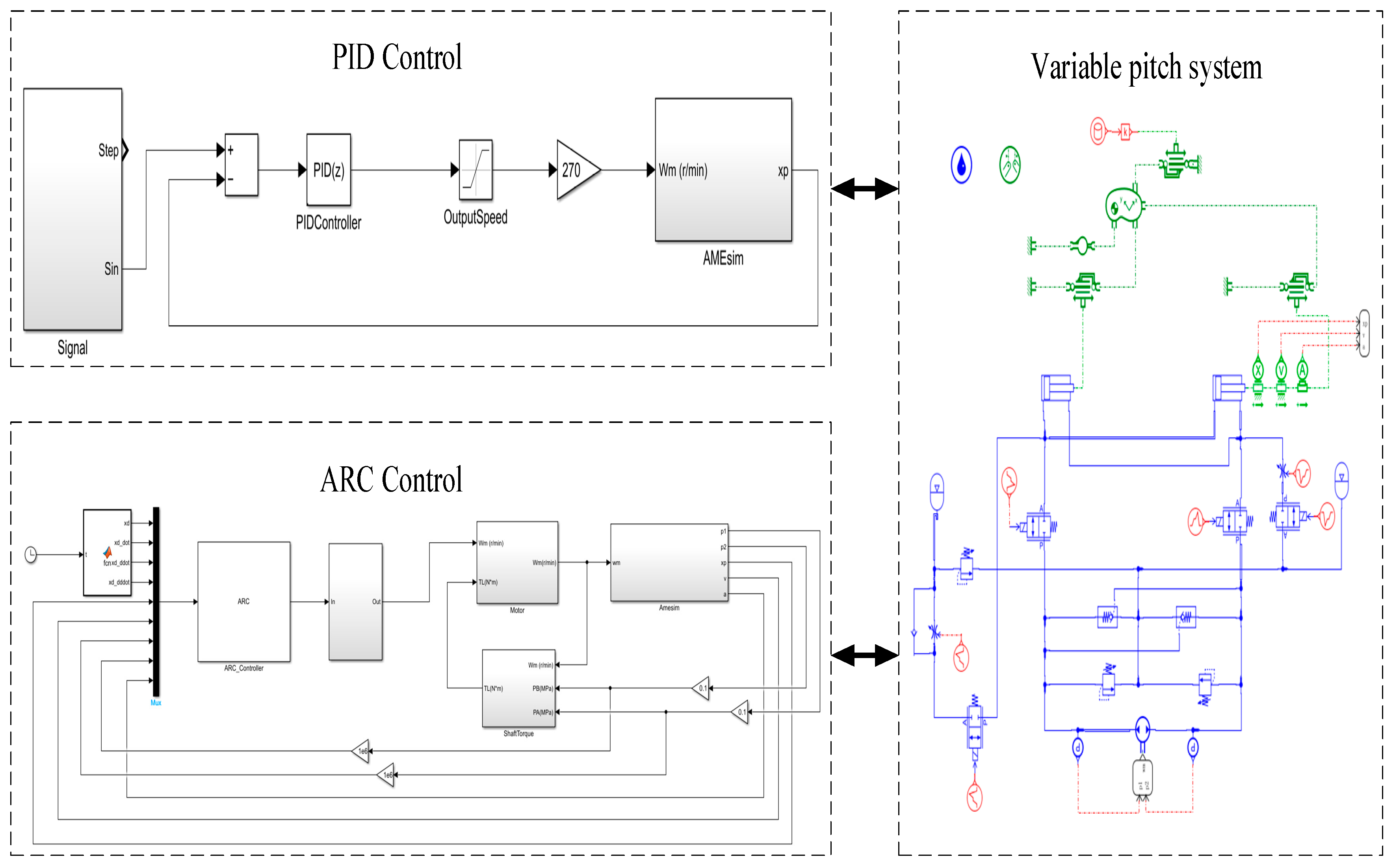
3. Controller Design
4. Experimental Results and Analysis
4.1. Simulation Results and Analysis
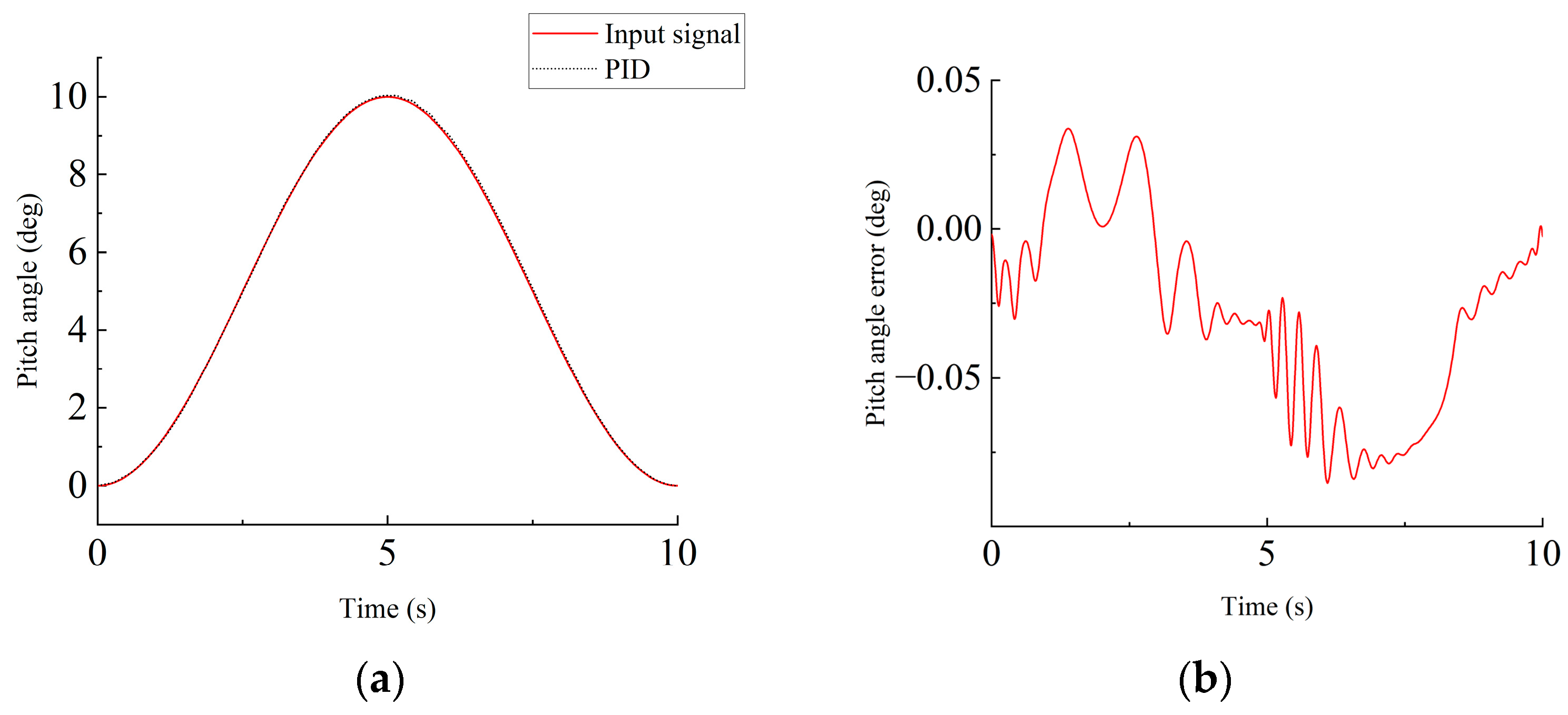
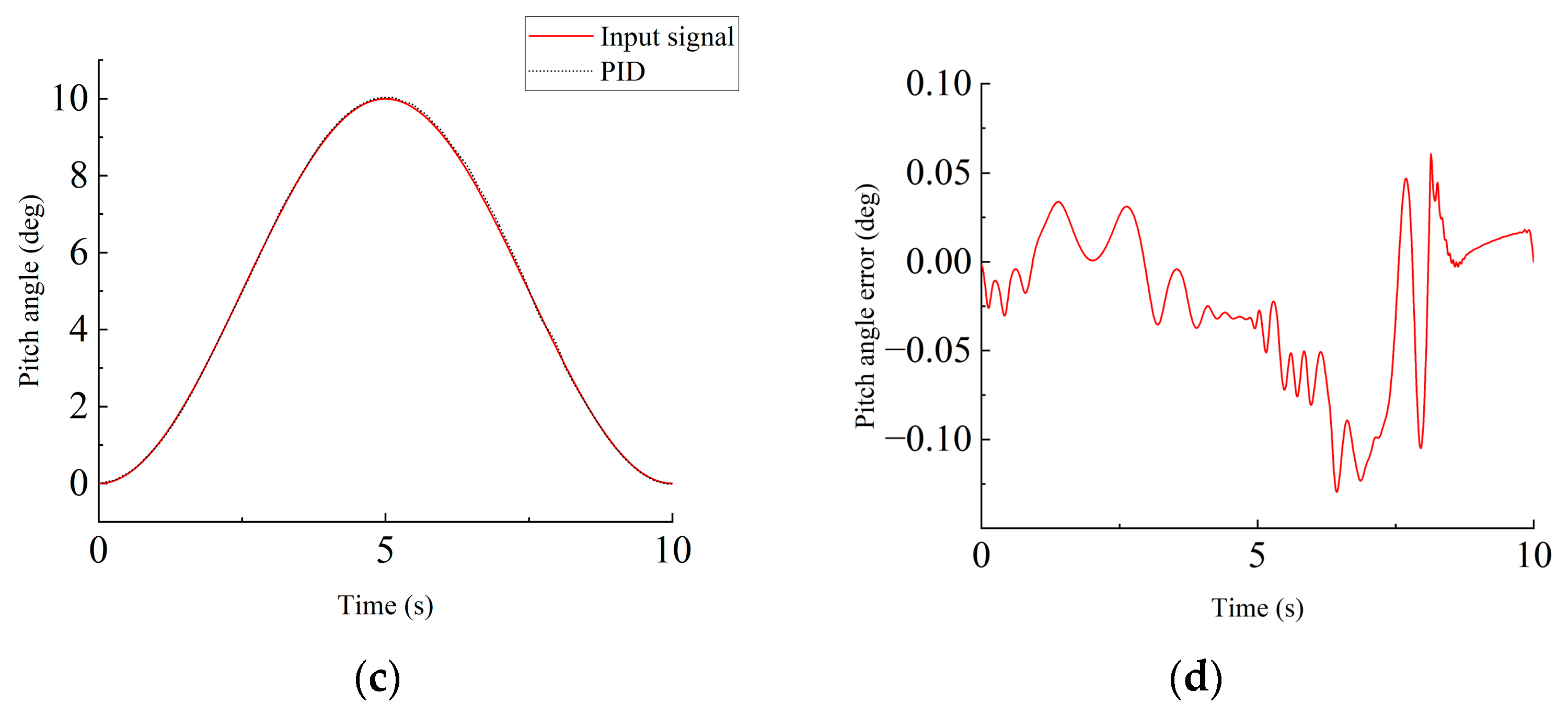
4.1.1. PID Controller Parameter Tuning
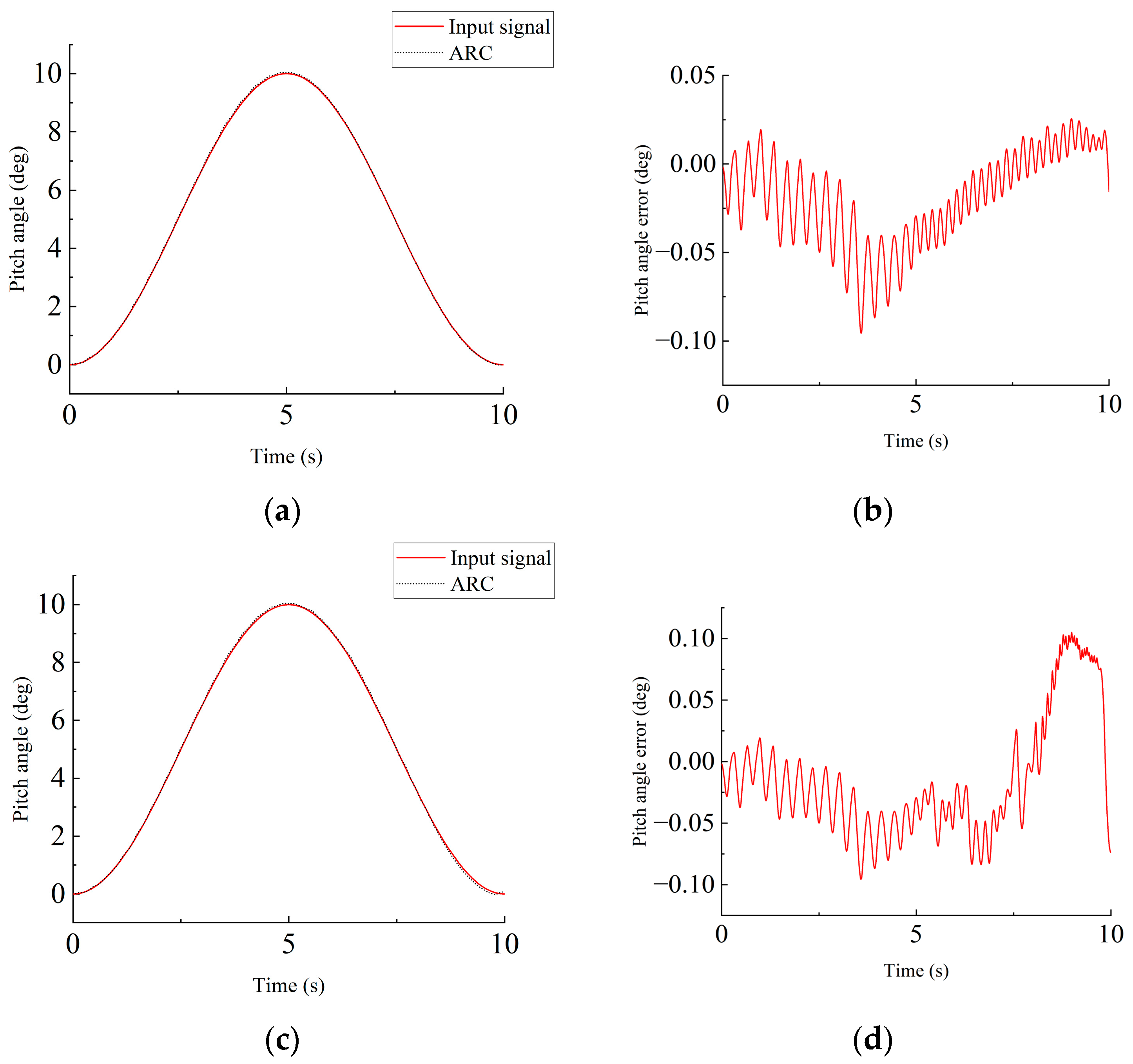
4.1.2. ARC Controller Parameter Tuning
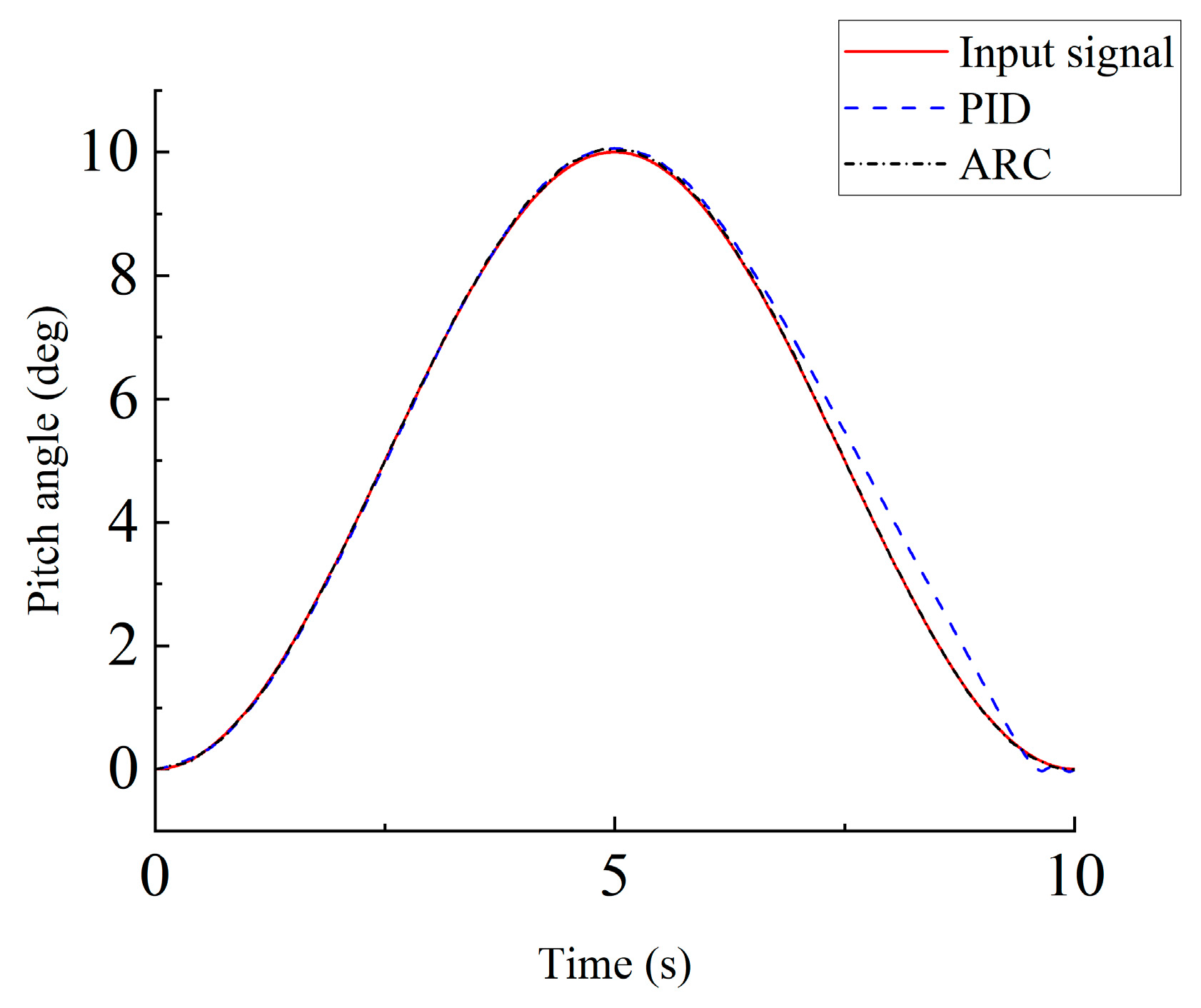
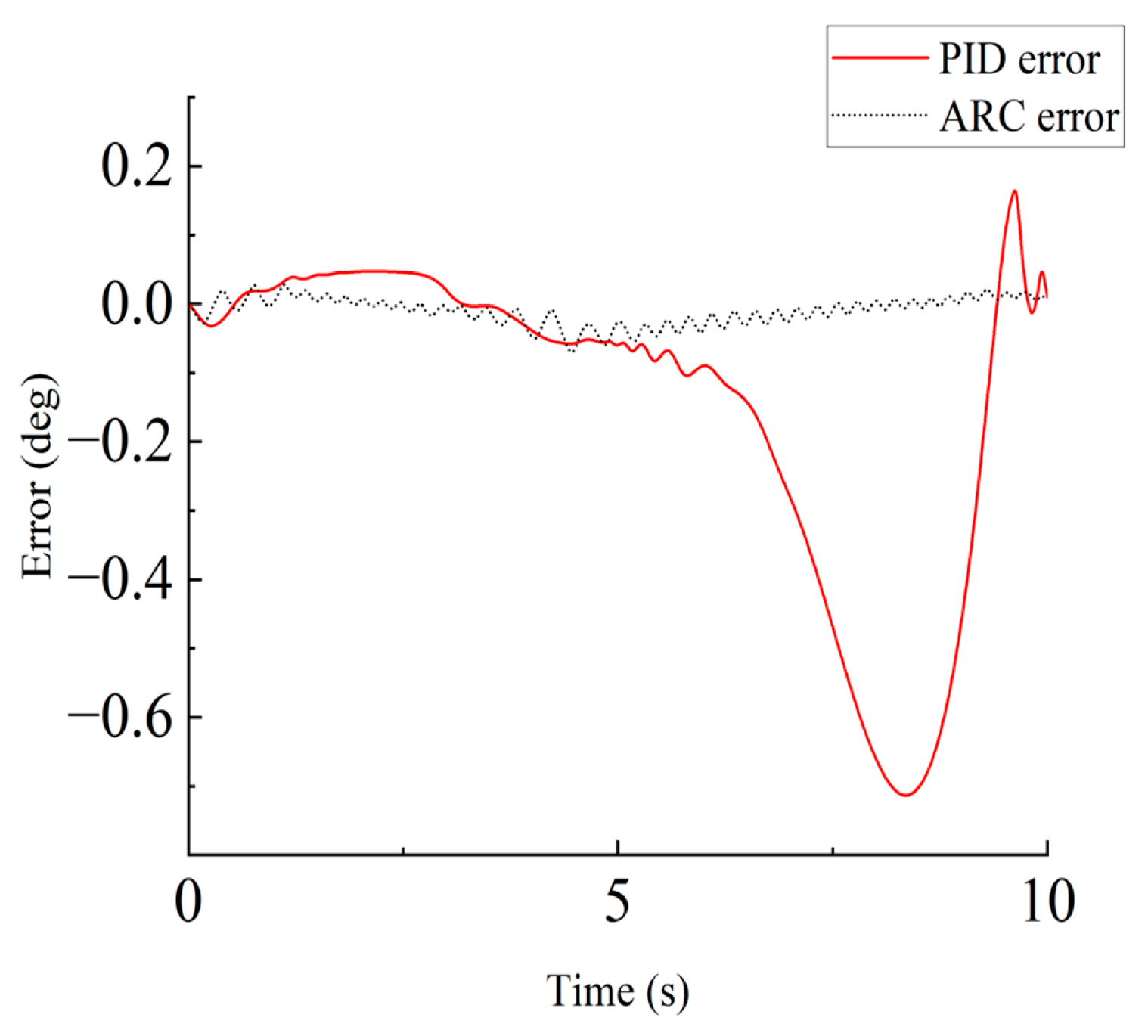
4.1.3. Robustness Analysis
4.2. Bench Test
5. Conclusions
- (1)
- The proposed mathematical model for pump-controlled pitch systems effectively integrates the angular dynamics of the pitch mechanism and hydraulic system characteristics. The model considers major nonlinear factors, system parameter uncertainties, and wind speed disturbance effects, providing a reliable theoretical foundation for controller design.
- (2)
- PSO was used to optimize both the PID and ARC parameters under wind speed disturbance conditions. With the obtained optimal parameter combinations, the PID and ARC controllers showed similar tracking performance for sinusoidal signals, with PID performing slightly better than ARC, indicating that PID control can outperform ARC under specific conditions.
- (3)
- The simulation results demonstrate that when system parameters change due to various factors, the ARC controller maintains a small tracking error below 0.15°, while the PID controller’s error exceeds 1.5°. The physical test bench results further confirm the practicality of this control strategy. During hydraulic cylinder reciprocating motion, especially in the retraction phase, the ARC controller shows excellent tracking performance with an error fluctuation range of approximately 0.1°, significantly outperforming the PID controller’s range of 0.7°. This indicates that the proposed control strategy can effectively handle nonlinear characteristics and uncertainties in actual systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.T.; Wang, X.Y.; Zhang, F.S.; Liu, H.W.; Lin, Y.G. Review of the application of hydraulic technology in wind turbine. Wind Energy 2020, 23, 1495–1522. [Google Scholar] [CrossRef]
- Liu, K.; Chen, W.; Chen, G.; Dai, D.; Ai, C.; Zhang, X.; Wang, X. Application and analysis of hydraulic wind power generation technology. Energy Strategy Rev. 2023, 48, 101117. [Google Scholar] [CrossRef]
- Petrovic, V.; Jelavic, M.; Baotic, M. MPC framework for constrained wind turbine individual pitch control. Wind Energy 2021, 24, 54–68. [Google Scholar] [CrossRef]
- Du, H.; Ding, K.Y.; Shi, J.J.; Feng, X.Y.; Guo, K.; Fang, J.H. High-gain observer-based pump/valve combined control for heavy vehicle electro-hydraulic servo steering system. Mechatronics 2022, 85, 15. [Google Scholar] [CrossRef]
- Helian, B.; Chen, Z.; Yao, B. Precision Motion Control of a Servomotor-Pump Direct-Drive Electrohydraulic System with a Nonlinear Pump Flow Mapping. IEEE Trans. Ind. Electron. 2020, 67, 8638–8648. [Google Scholar] [CrossRef]
- Shi, S.Y.; He, Z.L.; Zeng, D.B.; Huang, P.; Jin, G. Identification and Modeling of a Servo Pump-Controlled Hydraulic System. IEEE ASME Trans. Mechatron. 2024, 1–11. [Google Scholar] [CrossRef]
- Yan, G.; Jin, Z.; Zhang, T.; Zhang, C.; Ai, C.; Chen, G. Exploring the Essence of Servo Pump Control. Processes 2022, 10, 786. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.G.; Quan, L.; Zhang, H.J. Research on energy consumption of injection molding machine driven by five different types of electro-hydraulic power units. J. Clean Prod. 2020, 242, 11. [Google Scholar] [CrossRef]
- Karpenko, M. Aircraft Hydraulic Drive Energy Losses and Operation Delay Associated with the Pipeline and Fitting Connections. Aviation 2024, 28, 1–8. [Google Scholar] [CrossRef]
- Hagen, D.; Padovani, D.; Choux, M. A Comparison Study of a Novel Self-Contained Electro-Hydraulic Cylinder versus a Conventional Valve-Controlled Actuator-Part 2: Energy Efficiency. Actuators 2019, 8, 78. [Google Scholar] [CrossRef]
- Hati, S.K.; Mandal, N.P.; Sanyal, D. Energy-saving design of variable-displacement bi-directional pump-controlled electrohydraulic system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 1218–1236. [Google Scholar] [CrossRef]
- Skorek, G. Study of Losses and Energy Efficiency of Hydrostatic Drives with Hydraulic Cylinder. Pol. Marit. Res. 2018, 25, 114–128. [Google Scholar] [CrossRef]
- Qu, S.Y.; Fassbender, D.; Vacca, A.; Busquets, E. A high-efficient solution for electro-hydraulic actuators with energy regeneration capability. Energy 2021, 216, 16. [Google Scholar] [CrossRef]
- Bury, P.; Stosiak, M.; Urbanowicz, K.; Kodura, A.; Kubrak, M.; Malesinska, A. A Case Study of Open- and Closed-Loop Control of Hydrostatic Transmission with Proportional Valve Start-Up Process. Energies 2022, 15, 1860. [Google Scholar] [CrossRef]
- Helian, B.B.; Chen, Z.; Yao, B.; Lyu, L.T.; Li, C. Accurate Motion Control of a Direct-Drive Hydraulic System With an Adaptive Nonlinear Pump Flow Compensation. IEEE ASME Trans. Mechatron. 2021, 26, 2593–2603. [Google Scholar] [CrossRef]
- Wang, T.; Song, J.C. Clearance Nonlinear Control Method of Electro-Hydraulic Servo System Based on Hopfield Neural Network. Machines 2024, 12, 329. [Google Scholar] [CrossRef]
- Wang, W.B.; Liu, S.; Zhao, D.X. Low-Complexity Error-Surface Prescribed Performance Control for Nonlinear Uncertain Single-Rod Electro-Hydraulic System. IEEE Trans. Control Syst. Technol. 2024, 8, 2402–2409. [Google Scholar] [CrossRef]
- Zhao, W.; Ebbesen, M.K.; Hansen, M.R.; Andersen, T.O. Enabling Passive Load-Holding Function and System Pressures Control in a One-Motor-One-Pump Motor-Controlled Hydraulic Cylinder: Simulation Study. Energies 2024, 17, 2484. [Google Scholar] [CrossRef]
- Mohmmed, J.H.; Hassan, A.K.; Ali, M.; Kokz, S.; Mosa, M.H.; Kareem, A.K.; Zainulabdeen, A.A.; Feng, Z. Design of uncertain displacement controlled velocity control system for hydraulic actuator. Heliyon 2024, 10, 15. [Google Scholar] [CrossRef]
- Cecchin, L.; Frey, J.; Gering, S.; Manderla, M.; Trachte, A.; Diehl, M. Nonlinear Model Predictive Control for Efficient Control of Variable Speed Variable Displacement Pumps. In Proceedings of the 3rd Modeling, Estimation and Control Conference (MECC), Lake Tahoe, NV, USA, 2–5 October 2023; pp. 331–336. [Google Scholar]
- Nguyen, M.H.; Ahn, K.K. Extended Sliding Mode Observer-Based Output Feedback Control for Motion Tracking of Electro-Hydrostatic Actuators. Mathematics 2023, 11, 4324. [Google Scholar] [CrossRef]
- Elbeji, O.; Hannachi, M.; Benhamed, M.; Sbita, L. Pitch Angle Control of a Wind Turbine Conversion System at High Wind Speed. In Proceedings of the 2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 20–23 July 2020; pp. 819–823. [Google Scholar]
- Kim, D.; Lee, D. Hierarchical Fault-Tolerant Control using Model Predictive Control for Wind Turbine Pitch Actuator Faults. Energies 2019, 12, 3097. [Google Scholar] [CrossRef]
- Kamada, Y.; Maeda, T.; Takai, K.; Mizuno, S. Study on cyclic pitch control of HAWT by using instantaneous inflow observation. In Proceedings of the Conference on Science of Making Torque from Wind (TORQUE), Online, 28 September–2 October 2020. [Google Scholar]
- Salem, M.E.M.; El-Batsh, H.M.; El-Betar, A.A.; Attia, A.M.A. Application of Neural Network Fitting for Pitch Angle Control of Small Wind Turbines. In Proceedings of the 3rd IFAC Conference on Modelling, Identification and Control of Nonlinear Systems (MiCNON), Tokyo, Japan, 15–17 September 2021; pp. 185–190. [Google Scholar]
- Sierra-Garcia, J.E.; Santos, M. Neural networks and reinforcement learning in wind turbine control. Rev. Iberoam. Autom. Inform. Ind. 2021, 18, 327–335. [Google Scholar] [CrossRef]
- Xu, J.R.; Liu, Y.M. Voltage Flicker Mitigation Strategy Based on Individual Pitch Control of Wind Turbine. In Proceedings of the 13th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Beihai, China, 16–17 January 2021; pp. 459–462. [Google Scholar]
- Teferra, D.M.; Ngoo, L.M.H.; Nyakoe, G.N. A Fuzzy Controlled Pitch Angle in a Permanent Magnet Synchronous Generator Type Wind Energy Conversion System. In Proceedings of the 21st IEEE Mediterranean Electrotechnical Conference (IEEE MELECON), Palermo, Italy, 14–16 June 2022; pp. 324–329. [Google Scholar]
- Wang, X.; Zhou, J.S.; Qin, B.; Luo, Y.B.; Hu, C.J.; Pang, J.M. Individual Pitch Control of Wind Turbines Based on SVM Load Estimation and LIDAR Measurement. IEEE Access 2021, 9, 143913–143921. [Google Scholar] [CrossRef]
- Liu, J.P.; Nie, G.H. Variable Speed Control Analysis of Direct-Drive Wind Turbines Incorporating the Variable Gain Pitch Knowledge Identification Algorithm. Mob. Inf. Syst. 2022, 2022, 12. [Google Scholar] [CrossRef]



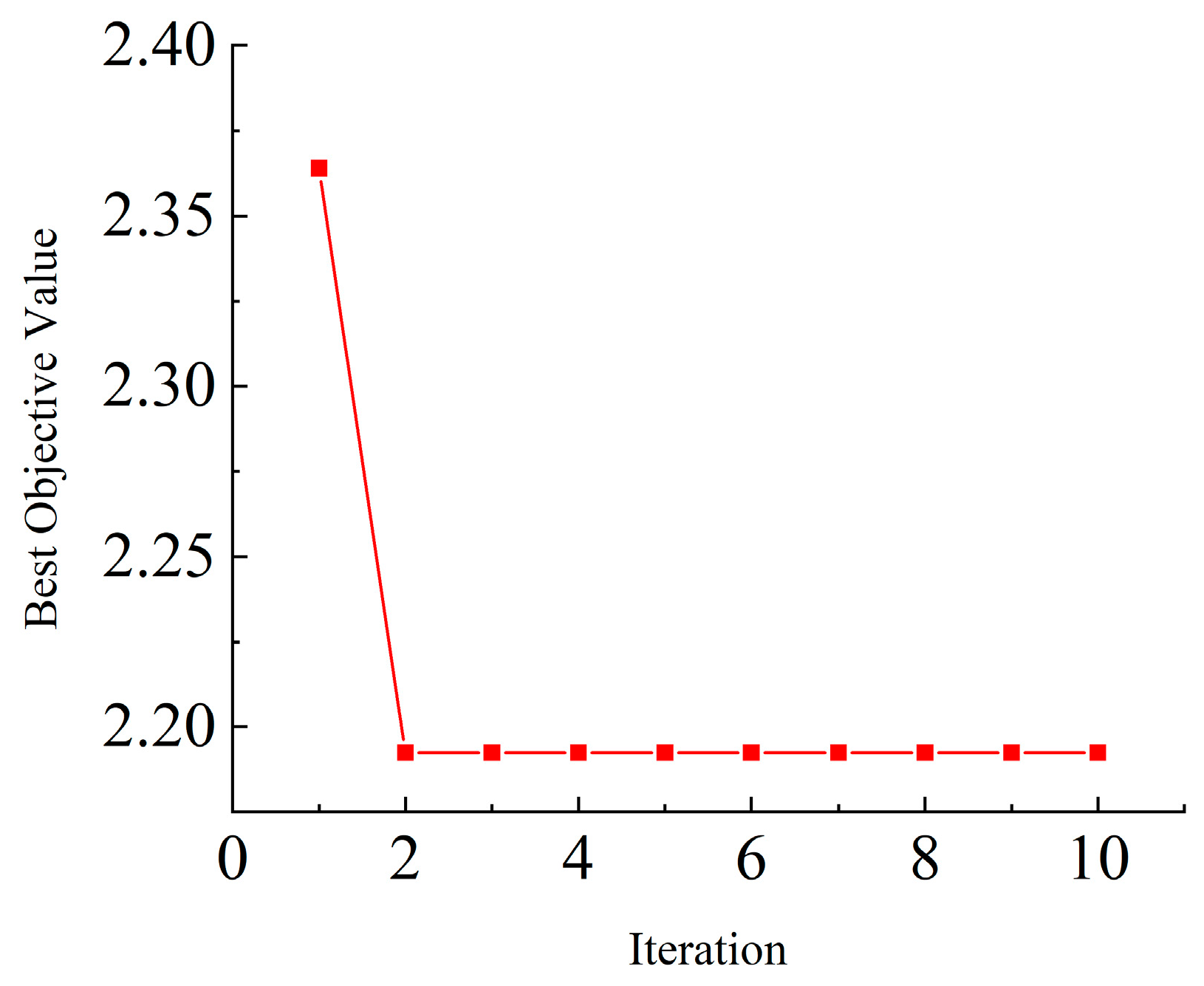



| kp | ki | kd | Cost |
|---|---|---|---|
| 7418.66 | 943.71 | 956.23 | 2.23 |
| 7282.47 | 973.19 | 1000 | 2.25 |
| 7388.91 | 924.47 | 972.03 | 2.25 |
| 7287.99 | 908.03 | 1000 | 2.26 |
| 7346.56 | 880.21 | 1000 | 2.27 |
| 7284.07 | 906.98 | 1000 | 2.28 |
| 7246.62 | 1000 | 961.29 | 2.28 |
| 7270.37 | 911.30 | 1000 | 2.29 |
| k1 | k2 | k3 | Cost |
|---|---|---|---|
| 289.41 | 144,353.04 | 744.41 | 2.29 |
| 170.85 | 141,003.76 | 676.88 | 2.30 |
| 252.89 | 140,169.72 | 10 | 2.37 |
| 218.52 | 144,235.10 | 1000 | 2.43 |
| 141.46 | 145,000 | 1000 | 2.47 |
| 148.04 | 143,786.98 | 847.09 | 2.53 |
| 300 | 143,518.45 | 1000 | 2.53 |
| 300 | 145,000 | 10 | 2.55 |
| Serial Number | Component Name | Manufacturer |
|---|---|---|
| 1 | Temperature Sensor | Zhuhong (Wuxi, China) |
| 2 | Pressure Sensor | Zhuhong |
| 3 | Relief Valve | SUN (Houston, TX, USA) |
| 4 | Two-Way Directional Valve | SUN |
| 5 | Throttle Valve | SUN |
| 6 | Accumulator | Liming (Zhoushan, China) |
| 7 | Check Valve | Huade (Beijing, China) |
| 8 | Displacement Sensor | Xiju (Wuhan, China) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Yu, B.; Wang, X.; Liu, Y.; Chen, G.; Liu, K.; Ai, C.; Wang, L. Adaptive Robust Control for Pump-Controlled Pitch Systems Facing Wind Speed and System Parameter Variability. Appl. Sci. 2024, 14, 10218. https://doi.org/10.3390/app142210218
Zhang T, Yu B, Wang X, Liu Y, Chen G, Liu K, Ai C, Wang L. Adaptive Robust Control for Pump-Controlled Pitch Systems Facing Wind Speed and System Parameter Variability. Applied Sciences. 2024; 14(22):10218. https://doi.org/10.3390/app142210218
Chicago/Turabian StyleZhang, Tiangui, Bo Yu, Xuewei Wang, Yinping Liu, Gexin Chen, Keyi Liu, Chao Ai, and Lihui Wang. 2024. "Adaptive Robust Control for Pump-Controlled Pitch Systems Facing Wind Speed and System Parameter Variability" Applied Sciences 14, no. 22: 10218. https://doi.org/10.3390/app142210218
APA StyleZhang, T., Yu, B., Wang, X., Liu, Y., Chen, G., Liu, K., Ai, C., & Wang, L. (2024). Adaptive Robust Control for Pump-Controlled Pitch Systems Facing Wind Speed and System Parameter Variability. Applied Sciences, 14(22), 10218. https://doi.org/10.3390/app142210218






