Next Article in Journal
Acoustic Applications of a Foamed Geopolymeric-Architected Metamaterial
Next Article in Special Issue
Floquet Modification of the Bandgaps and Energy Spectrum in Flat-Band Pseudospin-1 Dirac Materials
Previous Article in Journal
Effect of Time and Voltage on the Electrophoresis Deposition of Zinc Oxide Thin Films for Photovoltaic Applications
Previous Article in Special Issue
Recent Progress in Synthesis and Photonic Applications of Two-Dimensional Bismuthene
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 3
10.3390/app14031205
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characterization of Monovacancy Defects in Vanadium Diselenide Monolayer: A DFT Study

by
Andrey A. Kistanov
1,2
1
Institute for Metals Superplasticity Problems, Russian Academy of Sciences, 450001 Ufa, Russia
2
The Laboratory of Metals and Alloys Under Extreme Impacts, Ufa University of Science and Technology, 450076 Ufa, Russia
Appl. Sci. 2024, 14(3), 1205; https://doi.org/10.3390/app14031205
Submission received: 4 January 2024 / Revised: 24 January 2024 / Accepted: 30 January 2024 / Published: 31 January 2024
(This article belongs to the Special Issue Two-Dimensional (2D) Materials: Applications, Performance and Future Trends)
Browse Figures
Versions Notes

Abstract

:
Defects are an integral part of the structure of various two-dimensional materials (2D), including 2D transition-metal dichalcogenides. These defects usually govern their electronic properties. In this work, simulations based on the density functional theory are employed for a comprehensive characterization of typical point defects in the T–VSe2 and H–VSe2 monolayers. Specifically, Se and V monovacancy defects are studied. The formation of monovacancies in T–VSe2 and H–VSe2 monolayers are found to be less favorable than in other common transition-metal dichalcogenides. Meanwhile, Se and V monovacancy defects tune the electronic structure of the T–VSe2 and H–VSe2 monolayers significantly. The scanning tunneling microscopy simulated images obtained could facilitate the detection of monovacancies in T–VSe2 and H–VSe2 monolayers in experiments.

1. Introduction

Two-dimensional transition metal dichalcogenides (TMDs) are layered materials consisting of one layer of transition metal atoms, such as Mo, V, and W, that are stacked between two layers of chalcogen atoms (S, Se, or Te) [1]. There are some exceptions, such as M2×3 having 2:3 quintuple layers [2] and MX metal chalcogenides [3]. TMDs are used in various electronic, optoelectronic and energy devices, such as transistors [4,5,6], flexible and transparent displays [7,8], and sensors [9]. There are a large number of TMDs, such as molybdenum disulfide and tungsten disulfide [10]. They can be obtained through micromechanical design or through the chemical vapor deposition and chemical vapor transport approaches [11]. Two-dimensional TMDs have several stable polymorphs: the trigonal prismatic H phase, the octahedral T phase and the distorted octahedral atomic configurations (T′ phase or T″ phase) [12,13]. For example, 2D MoS2 has several polymorphs differing in the coordination of the Mo atom. The various phases of 2D MoS2 possess different fundamental properties. Two-dimensional MoS2 may show semiconducting, metallic or insulating behavior depending on the stacking of the S/Mo/S atomic planes [12]. It has been shown that controllable phase transformations in 2D TMDs are possible via electron beam [14], metal treatment [15] and laser irradiation [16].
Two-dimensional materials in which phase transition is associated with insignificant atomic structure rearrangement, not leading to a change in the material stoichiometry, have enhanced physical behavior. The energetics of the phase transitions in various 2D TMDs have been studied extensively, both experimentally and theoretically [17,18,19,20]. In the case of 2D MoS2, first-principles calculations have shown that it is unstable in the T phase [18] and spontaneously rearranges into the metastable T’ phase, while the metastable T’ phase transforms to the stable H phase after annealing, as was experimentally observed [21,22]. On the other hand, it is known that strong electron doping of the system can lead to phase transformations. It has been shown that strong n-type doping of 2D MoS2, induced by the alkali metal intercalation or by the electron transfer from the substrate to the MoS2, makes the T′ phase more energetically favorable than the H phase in 2D MoS2 [23,24,25,26,27,28]. In addition, the phase transition in 2D TMDs also occurs under in situ electron beam irradiation in the transmission electron microscope [29].
Vanadium diselenide (VSe2) is another member of the TMD family, with a trigonal T phase atomic configuration in the bulk form. It consists of layers of V atoms trapped between two layers of Se atoms, and these Se−V−Se layers are stacked in the (001) direction. Despite having a similar structure to MoS2, VSe2 exists only in the T phase, while MoS2 also exists in the H phase, with the Mo atoms in octahedral coordination with S atoms [30]. The phase transition from the T phase to the H phase in VSe2 can be realized via temperature control or applying strain, and the H phase of VSe2 is usually more stable up to high temperatures [31]. An extensive computation study has shown a comparison of the structural stability and properties of VSe2 in bulk, thin film, nanoribbon, monolayer and nanotube forms [32]. It has been shown that the VSe2 in all these forms is ferromagnetic, while exhibiting different electronic properties, such as a bulk and few-layer T phase and H phase. The VSe2 and a T phase VSe2 monolayer are metallic, while the H phase VSe2 monolayer is a semiconductor. Another theoretical study has demonstrated the thermodynamic stability of the H phase and T phase VSe2 monolayers and evaluated the phase transition temperature of 200 K, at which the phase transition between the H phase and T phase in the VSe2 monolayers occurs [30]. A thin film of VSe2 has been successfully synthesized by various approaches; for instance, an ultrathin VSe2 composed of four to eight layers has been synthesized via liquid exfoliation of a bulk VSe2 crystal in a formamide solvent [33]. A one-pot colloidal method has been applied to fabricate a 0.4 nm thick ultrathin VSe2 nanosheet consisting of five layers [34].
Similar to other 2D materials, 2D TMDs have a high surface-to-bulk ratio, and, as a consequence, there is a strong possibility of defects forming on their surface [35,36,37,38,39,40,41]. Native point defects may inevitably form in 2D TMDs under various production and usage conditions, for example, during the growth of 2D TMDs at relatively high temperatures. The concentration of defects in 2D materials also depends on the various growth and usage conditions, such as pressure, temperature, and environmental conditions [42,43,44]. Obviously, due to the reduced dimensionality of 2D TMDs, defects have a much stronger impact on their properties than the bulk TMDs [45]. It is well known that defects influence the optoelectronic and magnetic properties of 2D TMDs [46,47,48,49]. For instance, defects in 2D MoS2, such as vacancies, dislocations, and grain boundaries, reduce its charge carrier mobility [47]. On the other hand, the presence of a small concentration of defects in high-quality crystalline TMD samples can be desirable for their application. However, it is necessary to identify the type and concentration of defects in TMDs before their properties can be controlled via defect engineering. This is a non-trivial task; for example, scanning tunneling microscope techniques allow the spatial imaging, measurement, and manipulation of surfaces at the atomic level [50], while the use of a transmission electron microscope may damage ultrathin 2D samples [39,47]. Consequently, understanding the structure of defects is an important step in the understanding of their impact on various properties of 2D TMDs. Recently, a comprehensive analysis of defects in bilayer MoS2 at the atomic level using aberration-corrected transmission electron microscopy has shown that an increase in the concentration of the S vacancies leads to their aggregation into larger defect complexes, which, in turn, impacts the interlayer stacking in MoS2 [51]. The electron beam irradiation is an effective tool to control the spatial location and density of defects in layered materials [38,52]. For example, Lin et al. have proposed electron energy loss spectroscopy and scanning transmission electron microscopy techniques to assign types of impurities/defects in low-dimensional WS2 structures with different optical properties [53].
Computational studies play an important role in the study of defects in 2D TMDs. A systematic density functional theory (DFT)-based study has shown how to control the magnetic and electronic properties of the MoSe2 monolayer via the incorporation of point defects on its surface [54]. Another systematic investigation on vacancies in the MoSe2 monolayer by the scanning transmission electron microscope imaging and DFT-based simulations demonstrated that minimizing the concentration of antisite defects in the MoSe2 monolayer is needed for its application in electric transport devices, as the introduced antisite defects produce local magnetic moments in the MoSe2 monolayer [55]. A number of DFT-based simulations have also been used to identify the local defect states within the band gap of 2D TMDs obtained by scanning transmission electron microscopy [37,56,57,58]. First-principles calculations have demonstrated that the defect formation energy in a novel 2D PdSe2 is significantly lower than these in other 2D TMDs, which sheds light on the reason for the presence of a large number of Se defects in the PdSe2 monolayer obtained via the mechanical exfoliation [59]. DFT-based simulations have been utilized to show the fundamental role of defects in the fabrication of WSe2-based quantum emitters [60] and to explain the role of defects in the thermal conductivity of 2D WSe2 [61].
Despite the fact that defects in various 2D TMDs have been widely studied, there is still a niche in a systematic study of defects in a recently emerged VSe2 monolayer [62]. A deeper study for connecting the presence and type of defects in the VSe2 monolayer to its electronic characteristics at a mechanistic level is needed. To fulfil this scientific question, the most common native defects, chalogene and transition metal single vacancies, in the VSe2 monolayer are studied using DFT-based calculations.

2. Materials and Methods

DFT-based calculations were conducted in the Vienna Ab Initio Simulation Package (VASP). The valence electron and ionic core interactions were treated with the projector augmented wave (PAW) method. The generalized gradient approximation (GGA) with the Perdew−Burke−Ernzerhof (PBE) exchange–correlation density functional [63] was implemented for geometry optimization and electronic structure calculations. The Van der Waals interactions were treated with the Becke88 (optB88) optimization functional [64], as this functional is widely used to study the structure of defects in 2D materials [43,65]. Due to the consideration of systems based on transition metal state, spin-polarized DFT calculations were performed [66,67,68]. A cut-off energy of 400 eV was used to expand the wavefunctions. The 2D Brillouin zone integration was sampled by a 12 × 12 × 1 k-grid mesh for the unit cell structure optimization, while a 5 × 5 × 1 k-grid mesh was used for structure optimization and electronic property calculations of supercell systems. The proper choice of supercell size is essential to avoid possible inter-vacancy interactions in the replicated cells. In this work, to study defects in the VSe2 monolayer, a 5 × 5 supercell with a vacuum layer of a thickness larger than 20 Å was selected based on previous studies [69,70] to avoid inter-vacancy interactions. In the supercell systems optimization calculations, the atomic positions were freely optimized until the atomic force on each atom was smaller than 0.001 eV/Å. The defect migration energies Emigration were estimated following the climbing image−nudged elastic band (NEB) method [71].
The formation energy Eform of a particular defect was calculated as follows:
Eform= E(supercell with defect) − E(perfect supercell) + n µ(V) + n µ(Se)
where E(supercell with defect) is the energy of the supercell with a given defect, E(perfect supercell) is the energy of the perfect supercell, µ(V) and µ(Se) are the chemical potentials of V and Se atoms, respectively [72,73,74], and n = −1 corresponds to the case when the defect is a single vacancy.
The theory for simulating scanning tunneling microscopy imaging via DFT calculations is based on the Tersoff–Hamann approach [75,76], where the simulated STM image depends on the scanning distance between the surface of the sample and the tip. Equation (2) describes tunneling from the occupied states of the sample to the tip.
I   ( r ,   E )   ≈ ∫ E f E f + e V d E   n r , E ,
where the tunneling current I, which depends on the position of the tip r and the voltage applied V, can be found via the integrated local density of states.

3. Results

The top and side views of the unit cell of the optimized T–VSe2 and H–VSe2 monolayers are shown in Figure 1a,b, respectively. Both the T–VSe2 and H–VSe2 monolayers belong to the D3h point group symmetry. The optimized lattice constant is 2.90 Å for the T–VSe2 monolayer and 3.33 Å for the H–VSe2 monolayer. The Se−V bonds in the T–VSe2 and H–VSe2 monolayers are 2.49 Å and 2.50 Å, respectively, and the Se−Se bonds in T–VSe2 and H–VSe2 monolayers are 3.69 Å and 3.33 Å, respectively. The thickness of the T–VSe2 monolayer is 3.14 Å, while the thickness of the H–VSe2 monolayer is 3.20 Å. The obtained geometry and structural parameters of the considered T–VSe2 and H–VSe2 monolayers are in good agreement with previous works [32,77,78].
The electron localization function (ELF) can be defined as the probability of finding an electron pair in a space region. The value of the ELF ranges from 0 (a free electronic state) to 1 (perfect localization), representing the charge localization in real space [79]. The ELF for the T–VSe2 and H–VSe2 monolayers is analyzed and plotted in Figure 2a,d, respectively. The isosurface value of 0.7 is adopted in Figure 2. From Figure 2a,d it is seen that the electron localization basin is spherical and completely surrounds the respective atomic cores, suggesting an ionic type of bonding in the T–VSe2 and H–VSe2 monolayers, as it is expected in 2D TMDs [80]. The local density of states (LDOS) and band structure of the T–VSe2 and H–VSe2 monolayers are also analyzed and depicted in Figure 2b,c and e,f, respectively. The H (hexagonal symmetry) and T (trigonal symmetry) phases of VSe2 have substantially different electronic structures due to the difference in the structure symmetry [81]. According to Figure 2c, the T–VSe2 monolayer has no band gap, as has been reported previously [32]. From Figure 2f, it is seen that the H–VSe2 monolayer possesses a moderate direct band gap of ~0.2 eV, which is also consistent with previous DFT studies [77,82]. According to the LDOS plots in Figure 2b,e, the states in the vicinity of the Fermi level, in the case of the T–VSe2 monolayer, and valance bands minimum (VBM) and conduction bands maximum (CBM), in the case of the H–VSe2 monolayer, are mainly in the V d states.
The stability of the considered monovacancy defects in the T–VSe2 and H–VSe2 monolayers is evaluated based on their formation energy Eform and the energy needed for the migration of these defects Emigration. The calculated Eform for the monovacancy defects in the T–VSe2 monolayer and the Eform and Emigration for the monovacancy defects in the H–VSe2 monolayer are collected in Table 1. According to Table 1, the Eform of the VSe defect in the T–VSe2 and H–VSe2 monolayers are 5.31 eV and 5.60 eV, respectively. In turn, the Eform of the VV defect in the T–VSe2 and H–VSe2 monolayers are 10.08 eV and 13.03 eV, respectively. It should be noted that while the Eforms of a sulfur vacancy and molybdenum vacancy in a MoS2 monolayer are 2.12 eV and 6.20 eV [55], respectively, the selenide and palladium vacancies in a PdSe2 monolayer are lower than 1.82 eV and 1.84 eV [59], respectively. Therefore, the formation of the chalcogen vacancy and transition metal vacancies in VSe2 monolayers are less favorable than other common 2D TMDs. The migration process of the defects, which can tune the properties of 2D materials such as 2D TMDs, is also important to consider [83,84]. Despite H–VSe2 being usually more stable up to high temperatures, the phase transition between T–VSe2 and H–VSe2 could be realized via temperature control or applying strain [31]. Therefore, in this work, only the migration process of monovacancies in the T–VSe2 monolayer is considered. The migration process of the VSe and VV defects in the T–VSe2 monolayer, together with the calculated Emigration, are shown in Figure 3 and Figure 4.
The detailed pathway, including the initial state (IS), an intermediate transition state (TS), and the final state (FS) for the migration process of the VSe in the T–VSe2 monolayer, are presented in Figure 3a. According to Figure 3b and Table 1, the calculated energy barrier Emigration for the VSe in the T–VSe2 monolayer is 0.88 eV. Similarly, the detailed pathway, including the IS, an intermediate TS and the FS for the migration process of the VV in the T–VSe2 monolayer, are presented in Figure 4a. Based on Figure 4b and Table 1, the calculated Emigration is found to be 1.24 eV. It is seen that the formation and migration of the VV in the T–VSe2 monolayer are significantly less favorable than the formation and migration of the VSe.
It is well known that defects change the local electronic properties of 2D materials due to the breaking of their lattice periodicity [85]. Furthermore, the electronic structure of VSe- and VV-containing T–VSe2 and H–VSe2 monolayers are studied. Figure 5 shows the atomic structure (Figure 5a,d), LDOS (Figure 5b,e) and band structure (Figure 5c,f) plots for the T–VSe2 monolayer containing VSe and VV defects. It is found that the VSe and VV point defects tend to enhance the electron localization and, hence create a defect-induced localized state, as seen in the LDOS diagram of the T–VSe2 monolayer containing VSe and VV defects in Figure 5b.
Furthermore, significant changes in the local electronic properties of the H–VSe2 monolayer upon the introduction of monovacancies are found. Figure 6 shows the atomic structure (Figure 6a,d), LDOS (Figure 6b,e) and band structure (Figure 6c,f) plots for the H–VSe2 monolayer containing VSe and VV defects. Specifically, the presence of the VSe defect leads to a significant band redistribution and results in a semiconductor-to-metal transition (Figure 6c), with the defect-induced states appearing in the vicinity of the Fermi level and the conduction bands crossing the Fermi level. Interestingly, the presence of the VV defect leads to a significant downward shift of the VBM by ~0.15 eV and CBM by ~0.05 eV (Figure 6f). In addition, the conduction bands cross the Fermi level, which signifies a semiconductor-to-metal transition in the H–VSe2 monolayer containing the VV defect. These changes can be explained by the presence of dangling bonds in the core of the defect and the significant hybridization of states of the Se atoms in the core of the defect and neighboring V and Se atoms. Therefore, the VSe and VV defects in the T–VSe2 and H–VSe2 monolayers induce remarkable changes in their band diagram and, thus, can be detected via photoemission spectroscopy techniques [86].
Due to their outstanding functionality, 2D materials are widely applied in optoelectronic nanodevices [87,88,89]. Yet the functionality of 2D materials may be altered by defective engineering to facilitate their application [90]. In the case of TMDs, however, defect engineering plays an important role in the control of their electronic, optical, and magnetic properties, as well as surface chemical activity. For instance, the use of 2D TMD-based optoelectronic devices may be limited by the presence of chalogene monovacancies, as these vacancy sites function as non-radiative recombination centers for photoexcited carriers [91]. It is well-known that sulfur vacancies are the most energetically favorable among point defects in exfoliated TMD monolayers [47]. The results of this work are well in line with this theory, as the formation of the Se vacancy has been found to be the most energetically favorable in both the T–VSe2 and H–VSe2 monolayers. It has been shown earlier that chalogene monovacancies in 2D TMDs change their electronic structure by the formation of vacancy-induced localized electronic states [92]. These localized electronic states can increase the electrical conductivity of 2D TMDs through the hopping mechanism [93]. In the case of the T–VSe2 and H–VSe2 monolayers, the observed localized electronic states created by the VSe defect may also enhance electron transport and lead to a change of magnetic moment in them [72,94].
The STM images of perfect monovacancy-containing T–VSe2 and H–VSe2 monolayers are obtained to facilitate experimental observation of these point defects. STM images of the pristine and monovacancy-containing T–VSe2 and H–VSe2 monolayers are shown in Figure 7. The constant height tip position at 4 Å from the topmost Se atom is recorded in the image. This method is faster, despite being mainly useful for relatively smooth surfaces [42]. The STM image for the pristine T–VSe2 monolayer shows protrusions from the Se atoms and looks similar to the STM image of the VSe2 monolayer obtained previously in experiments and DFT simulations [72]. Specifically, the STM image of the T–VSe2 monolayer (Figure 7a) is identified as six Se atoms arranged in a hexagon and surrounded by one V atom, with these atoms Se atoms depicted as bright spots due to their small atomic number and the V atom as a dark spot due to its large atomic number [95]. The H–VSe2 monolayer (Figure 7b) is represented by three bright spots forming a triangle and one dark spot in the middle of that triangle [96]. The VSe defects (Figure 7c) in the T–VSe2 monolayer show STM images with three bright spots (Se atoms) forming a triangle with a dark area in the middle of that triangle. The VSe defects (Figure 7d) in the H–VSe2 monolayer are depicted as three blurred bright spots. The VV defects in the T–VSe2 monolayer (Figure 7e) are represented by five bright spots forming a pentagon with a dark area in the middle of that pentagon, while the VV defects in the H–VSe2 monolayer (Figure 7f) are represented by three bright blurred spots forming a triangle and located inside of a pentagon forming by another five bright spots. All the defects considered correlate with their corresponding atomic structures and are easy to recognize, as can be seen from the comparison of STM images in Figure 7 with the corresponding structures in Figure 2, Figure 5 and Figure 6.
Importantly, modern X-ray photoelectron and ultraviolet photoemission spectroscopy methods allow us to measure the density of states of the valence bands of nanostructures, which can be derived from the measured spectrum of the binding energy of a matter [97]. There are also experimental studies utilizing DFT-based simulations to detect structural defects in van der Waals crystals observed in STM images and ultraviolet photoemission spectra. Specifically, a redshift of the valence band maximum, because of the presence of a single tin defect observed in the ultraviolet photoemission spectra, has been mapped to an increased electronic state localization related to the defect states deep in the gap, as has been found in DFT calculated LDOS plots [98]. Very recently, a deep-level transient spectroscopy technique has been demonstrated for the non-destructive probe of point defects in layered TMDs. By using experimental STEM imaging and DFT calculations, it has been shown that it is possible to quantify the energy states of vacancy defects in a single-layer MoS2 [99]. Therefore, this study not only provides an atomic-scale characterization of point defects in terms of their effect on the electronic properties of the VSe2 monolayer but also facilitates their experimental identification.

4. Conclusions

In this work, monovacancy defects, such as the VSe and VV defects in the T–VSe2 and H–VSe2 monolayers, are studied. Specifically, their Eform and Emigration are calculated. It is predicted that the VSe and VV defects in the T–VSe2 monolayers have the Eform + Emigration of 6.19 eV and 11.32 eV, while even Eform of the VSe and VV defects in the H–VSe2 monolayer is higher and is equal to 5.60 eV and 13.03 eV. The results obtained suggest that the formation of monovacancy defects in the T–VSe2 and H–VSe2 monolayers is less favorable than in most other common 2D TMDs. It is also shown that the VSe and VV defects modulate the electronic structure of the T–VSe2 and H–VSe2 monolayers and, therefore, can be identified using photoemission spectroscopy methods. In addition, STM images of the VSe and VV defects in the T–VSe2 and H–VSe2 monolayers are presented to allow their identification in experiments.

Funding

The work was financially supported by the State Assignment of the IMSP RAS.

Data Availability Statement

Data available within the article.

Acknowledgments

The Author acknowledges the Joint Supercomputer Center of the Russian Academy of Sciences for computational resources.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
  2. Zhang, J.; Peng, Z.; Soni, A.; Zhao, Y.; Xiong, Y.; Peng, B.; Wang, J.; Dresselhaus, M.S.; Xiong, Q. Raman spectroscopy of few-quintuple layer topological insulator Bi2Se3 nanoplatelets. Nano Lett. 2011, 11, 2407–2414. [Google Scholar] [CrossRef] [PubMed]
  3. Zhou, X.; Cheng, J.; Zhou, Y.; Cao, T.; Hong, H.; Liao, Z.; Wu, S.; Peng, H.; Liu, K.; Yu, D. Strong second-harmonic generation in atomic layered GaSe. J. Am. Chem. Soc. 2015, 137, 7994–7997. [Google Scholar] [CrossRef] [PubMed]
  4. Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
  6. Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
  7. Bertolazzi, S.; Brivio, J.; Kis, A. Stretching and breaking of ultrathin MoS2. ACS Nano 2011, 5, 9703–9709. [Google Scholar] [CrossRef]
  8. Huang, S.; Ling, X.; Liang, L.; Kong, J.; Terrones, H.; Meunier, V.; Dresselhaus, M.S. Probing the interlayer coupling of twisted bilayer MoS2 using photoluminescence spectroscopy. Nano Lett. 2014, 14, 5500–5508. [Google Scholar] [CrossRef]
  9. Merki, D.; Hu, X. Recent developments of molybdenum and tungsten sulfides as hydrogen evolution catalysts. Energy Environ. Sci. 2011, 4, 3878–3888. [Google Scholar] [CrossRef]
  10. Ataca, C.; Şahin, H.; Ciraci, S. Stable, single-layer MX2 transition-metal oxides and dichalcogenides in a honeycomb-like structure. J. Phys. Chem. C 2012, 116, 8983–8999. [Google Scholar] [CrossRef]
  11. Yazyev, O.V.; Kis, A. MoS2 and semiconductors in the flatland. Mater. Today 2015, 18, 20–30. [Google Scholar] [CrossRef]
  12. Calandra, M. Chemically exfoliated single-layer MoS2: Stability, lattice dynamics, and catalytic adsorption from first principles. Phys. Rev. B 2013, 88, 245428. [Google Scholar] [CrossRef]
  13. Choe, D.-H.; Sung, H.-J.; Chang, K.J. Understanding topological phase transition in monolayer transition metal dichalcogenides. Phys. Rev. B Condens. Matter Mater. Phys. 2016, 93, 125109. [Google Scholar] [CrossRef]
  14. Lin, Y.-C.; Dumcenco, D.O.; Huang, Y.-S.; Suenaga, K. Atomic mechanism of the semiconducting-to-metallic phase transition in single-layered MoS2. Nat. Nanotechnol. 2014, 9, 391–396. [Google Scholar] [CrossRef] [PubMed]
  15. Kim, J.S.; Kim, J.; Zhao, J.; Kim, S.; Lee, J.H.; Jin, Y.; Choi, H.; Moon, B.H.; Bae, J.J.; Lee, Y.H.; et al. Electrical transport properties of polymorphic MoS2. ACS Nano 2016, 10, 7500–7506. [Google Scholar] [CrossRef] [PubMed]
  16. Cho, S.; Kim, S.; Kim, J.H.; Zhao, J.; Seok, J.; Keum, D.H.; Baik, J.; Choe, D.-H.; Chang, K.J.; Suenaga, K.; et al. Phase patterning for ohmic homojunction contact in MoTe2. Science 2015, 349, 625–628. [Google Scholar] [CrossRef] [PubMed]
  17. Zhang, C.; Kc, S.; Nie, Y.; Liang, C.; Vandenberghe, W.G.; Longo, R.C.; Zheng, Y.; Kong, F.; Hong, S.; Wallace, R.M.; et al. Charge mediated reversible metal-insulator transition in monolayer MoTe2 and WxMo1−xTe2 alloy. ACS Nano 2016, 10, 7370–7375. [Google Scholar] [CrossRef]
  18. Shirodkar, S.N.; Waghmare, U.V. Emergence of ferroelectricity at a metal-semiconductor transition in a 1T monolayer of MoS2. Phys. Rev. Lett. 2014, 112, 157601. [Google Scholar] [CrossRef]
  19. Rasmussen, F.A.; Thygesen, K.S. Computational 2D materials database: Electronic structure of transition-metal dichalcogenides and oxides. J. Phys. Chem. C 2015, 119, 13169–13183. [Google Scholar] [CrossRef]
  20. Pandey, M.; Bothra, P.; Pati, S.K. Phase transition of MoS2 bilayer structures. J. Phys. Chem. C 2016, 120, 3776–3780. [Google Scholar] [CrossRef]
  21. Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from chemically exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef]
  22. Guo, Y.; Sun, D.; Ouyang, B.; Raja, A.; Song, J.; Heinz, T.F.; Brus, L.E. Probing the dynamics of the metallic-to-semiconducting structural phase transformation in MoS2 crystals. Nano Lett. 2015, 15, 5081–5088. [Google Scholar] [CrossRef] [PubMed]
  23. Enyashin, A.N.; Yadgarov, L.; Houben, L.; Popov, I.; Weidenbach, M.; Tenne, R.; Bar-Sadan, M.; Seifert, G. New route for stabilization of 1T-WS2 and MoS2 phases. J. Phys. Chem. C 2011, 115, 24586–24591. [Google Scholar] [CrossRef]
  24. Enyashin, A.N.; Seifert, G. Density-functional study of LixMoS2 intercalates (0 ≤ x ≤ 1). Comput. Theor. Chem. 2012, 999, 13–20. [Google Scholar] [CrossRef]
  25. Kan, M.; Wang, J.Y.; Li, X.W.; Zhang, S.H.; Li, Y.W.; Kawazoe, Y.; Sun, Q.; Jena, P. Structures and phase transition of a MoS2 monolayer. J. Phys. Chem. C 2014, 118, 1515–1522. [Google Scholar] [CrossRef]
  26. Nasr Esfahani, D.; Leenaerts, O.; Sahin, H.; Partoens, B.; Peeters, F.M. Structural transitions in monolayer MoS2 by lithium adsorption. J. Phys. Chem. C 2015, 119, 10602–10609. [Google Scholar] [CrossRef]
  27. KC, S.; Zhang, C.; Hong, S.; Wallace, R.M.; Cho, K. Phase stability of transition metal dichalcogenide by competing ligand field stabilization and charge density wave. 2D Mater. 2015, 2, 035019. [Google Scholar] [CrossRef]
  28. Loh, T.A.; Chua, D.H. Origin of hybrid 1T- and 2H-WS2 ultrathin layers by pulsed laser deposition. J. Phys. Chem. C 2015, 119, 27496–27504. [Google Scholar] [CrossRef]
  29. Kretschmer, S.; Komsa, H.-P.; Bøggild, P.; Krasheninnikov, A.V. Structural transformations in two-dimensional transition-metal dichalcogenide MoS2 under an electron beam: Insights from first-principles calculations. J. Phys. Chem. Lett. 2017, 8, 3061–3067. [Google Scholar] [CrossRef]
  30. Zhang, H.; Sun, L.; Dai, Y.; Tong, C.; Han, X. Tunable electronic and magnetic properties from structure phase transition of layered vanadium diselenide. J. Wuhan Univ. Technol.-Mat. Sci. Ed. 2017, 32, 574–578. [Google Scholar] [CrossRef]
  31. Zhang, H.; Liuan, L.-M.; Lau, W.-M. Dimension-dependent phase transition and magnetic properties of VS2. J. Mater. Chem. A 2013, 1, 10821. [Google Scholar] [CrossRef]
  32. Li, F.; Tu, K.; Chen, Z. Versatile electronic properties of VSe2 bulk, few-layers, monolayer, nanoribbons, and nanotubes: A computational exploration. J. Phys. Chem. C 2014, 118, 21264–21274. [Google Scholar] [CrossRef]
  33. Xu, K.; Chen, P.; Li, X.; Wu, C.; Guo, Y.; Zhao, J.; Wu, X.; Xie, Y. Ultrathin nanosheets of vanadium diselenide: A metallic two- dimensional material with ferromagnetic charge-density-wave Behavior. Angew. Chem. Int. Ed. 2013, 52, 10477–10481. [Google Scholar] [CrossRef] [PubMed]
  34. Zhao, W.; Dong, B.; Guo, Z.; Su, G.; Gao, R.; Wang, W.; Cao, L. Colloidal synthesis of VSe2 single-layer nanosheets as novel electrocatalysts for the hydrogen evolution reaction. Chem. Commun. 2016, 52, 9228–9231. [Google Scholar] [CrossRef] [PubMed]
  35. Komsa, H.-P.; Kotakoski, J.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A.V. Two-dimensional transition metal dichalcogenides under electron irradiation: Defect production and doping. Phys. Rev. Lett. 2012, 109, 035503. [Google Scholar] [CrossRef] [PubMed]
  36. Saha, A.K.; Yoshiya, M. Native point defects in MoS2 and their influences on optical properties by first principles calculations. Phys. B 2018, 532, 184–194. [Google Scholar] [CrossRef]
  37. Chen, Y.; Huang, S.; Ji, X.; Adepalli, K.; Yin, K.; Ling, X.; Wang, X.; Xue, J.; Dresselhaus, M.; Kong, J.; et al. Tuning Electronic Structure of Single Layer MoS2 through Defect and Interface Engineering. ACS Nano 2018, 12, 2569–2579. [Google Scholar] [CrossRef] [PubMed]
  38. Lehnert, T.; Ghorbani-Asl, M.; Köster, J.; Lee, Z.; Krasheninnikov, A.V.; Kaiser, U. Electron-beam-driven structure evolution of single-layer MoTe2 for quantum devices. ACS Appl. Nano Mater. 2019, 2, 3262–3270. [Google Scholar] [CrossRef]
  39. Hasanian, M.; Mortazavi, B.; Ostadhossein, A.; Rabczuk, T.; van Duin, A.C.T. Hydrogenation and defect formation control the strength and ductility of MoS2 nanosheets: Reactive molecular dynamics simulation. Extreme Mech. Lett. 2018, 22, 157–164. [Google Scholar] [CrossRef]
  40. Horzum, S.; ÇakIr, D.; Suh, J.; Tongay, S.; Huang, Y.S.; Ho, C.H.; Wu, J.; Sahin, H.; Peeters, F.M. Formation and stability of point defects in monolayer rhenium disulfide. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 155433. [Google Scholar] [CrossRef]
  41. Mu, H.; Yu, W.; Yuan, J.; Lin, S.; Zhang, G. Interface and surface engineering of black phosphorus: A review for optoelectronic and photonic applications. Mater. Futures 2022, 1, 012301. [Google Scholar] [CrossRef]
  42. Kistanov, A.A.; Nikitenko, V.R.; Prezhdo, O.V. Point defects in two-dimensional γ-phosphorus carbide. J. Phys. Chem. Lett. 2021, 12, 620–626. [Google Scholar] [CrossRef] [PubMed]
  43. Kistanov, A.A.; Cai, Y.; Zhou, K.; Dmitriev, S.V.; Zhang, Y.W. Atomic-scale mechanisms of defect- and light-induced oxidation and degradation of InSe. J. Mater. Chem. C 2018, 6, 518–525. [Google Scholar] [CrossRef]
  44. Kistanov, A.A.; Shcherbinin, S.A.; Korznikova, E.A.; Prezhdo, O.V. Prediction and characterization of two-dimensional Zn2VN3. J. Phys. Chem. Lett. 2023, 14, 1148–1155. [Google Scholar] [CrossRef] [PubMed]
  45. Tsai, J.Y.; Pan, J.; Lin, H.; Bansil, A.; Yan, Q. Antisite defect qubits in monolayer transition metal dichalcogenides. Nat. Commun. 2022, 13, 492. [Google Scholar] [CrossRef] [PubMed]
  46. Lin, Y.-C.; Björkman, T.; Komsa, H.-P.; Teng, P.-Y.; Yeh, C.-H.; Huang, F.-S.; Lin, K.-H.; Jadczak, J.; Huang, Y.-S.; Chiu, P.-W.; et al. Three-fold rotational defects in two-dimensional transition metal dichalcogenides. Nat. Commun. 2015, 6, 6736. [Google Scholar] [CrossRef] [PubMed]
  47. Zhou, W.; Zou, X.; Najmaei, S.; Liu, Z.; Shi, Y.; Kong, J.; Lou, J.; Ajayan, P.M.; Yakobson, B.I.; Idrobo, J.C. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 2013, 13, 2615–2622. [Google Scholar] [CrossRef] [PubMed]
  48. Han, Y.; Hu, T.; Li, R.; Zhou, J.; Dong, J. Stabilities and electronic properties of monolayer MoS2 with one or two sulfur line vacancy defects. Phys. Chem. Chem. Phys. 2015, 17, 3813–3819. [Google Scholar] [CrossRef]
  49. Wang, S.; Lee, G.-D.; Lee, S.; Yoon, E.; Warner, J.H. Detailed atomic reconstruction of extended line defects in monolayer MoS2. ACS Nano 2016, 10, 5419–5430. [Google Scholar] [CrossRef]
  50. Xu, R.; Guo, J.; Mi, S.; Wen, H.; Pang, F.; Ji, W.; Cheng, Z. Advanced atomic force microscopies and their applications in two-dimensional materials: A review. Mater. Futures 2022, 1, 032302. [Google Scholar] [CrossRef]
  51. Zhou, S.; Wang, S.; Li, H.; Xu, W.; Gong, C.; Grossman, J.C.; Warner, J.H. Atomic structure and dynamics of defects in 2D MoS2 bilayers. ACS Omega 2017, 2, 3315–3324. [Google Scholar] [CrossRef]
  52. Dash, A.K.; Swaminathan, H.; Berger, E.; Mondal, M.; Lehenkari, T.; Prasad, P.R.; Watanabe, K.; Taniguchi, T.; Komsa, H.-P.; Singh, A. Evidence of defect formation in monolayer MoS2 at ultralow accelerating voltage electron irradiation. 2D Mater. 2023, 10, 035002. [Google Scholar] [CrossRef]
  53. Lin, Y.-C.; Li, S.; Komsa, H.-P.; Chang, L.-J.; Krasheninnikov, A.V.; Eda, G.; Suenaga, K. Revealing the atomic defects of WS2 governing its distinct optical emissions. Adv. Funct. Mater. 2018, 28, 1704210. [Google Scholar] [CrossRef]
  54. Lin, Z.; Yan, H.; Liu, J.; An, Y. Defects engineering monolayer MoSe2 magnetic states for 2D spintronic device. J. Alloys Compd. 2019, 774, 160–167. [Google Scholar] [CrossRef]
  55. Hong, J.; Hu, Z.; Probert, M.; Li, K.; Lv, D.; Yang, X.; Gu, L.; Mao, N.; Feng, Q.; Xie, L.; et al. Exploring atomic defects in molybdenum disulphide monolayers. Nat. Commun. 2015, 6, 6293. [Google Scholar] [CrossRef] [PubMed]
  56. Houssa, M.; Iordanidou, K.; Pourtois, G.; Afanas’ev, V.V.; Stesmans, A. Point defects in MoS2: Comparison between first-principles simulations and electron spin resonance experiments. Appl. Surf. Sci. 2017, 416, 853–857. [Google Scholar] [CrossRef]
  57. Zheng, Y.J.; Chen, Y.; Huang, Y.L.; Gogoi, P.K.; Li, M.-Y.; Li, L.-J.; Trevisanutto, P.E.; Wang, Q.; Pennycook, S.J.; Wee, A.T.S.; et al. Point defects and localized excitons in 2D WSe2. ACS Nano 2019, 13, 6050–6059. [Google Scholar] [CrossRef]
  58. Blades, W.H.; Frady, N.J.; Litwin, P.M.; McDonnell, S.J.; Reinke, P. Thermally induced defects on WSe2. J. Phys. Chem. C 2020, 124, 15337–15346. [Google Scholar] [CrossRef]
  59. Kuklin, A.V.; Begunovich, L.V.; Gao, L.; Zhang, H.; Ågren, H. Point and complex defects in monolayer PdSe2: Evolution of electronic structure and emergence of magnetism. Phys. Rev. B 2021, 104, 134109. [Google Scholar] [CrossRef]
  60. Parto, K.; Azzam, S.I.; Banerjee, K.; Moody, G. Defect and strain engineering of monolayer WSe2 enables site-controlled single-photon emission up to 150 K. Nat. Commun. 2021, 12, 3585. [Google Scholar] [CrossRef]
  61. Wang, Y.; Zhang, X. On the role of crystal defects on the lattice thermal conductivity of monolayer WSe2 (P63/mmc) thermoelectric materials by DFT calculation. Superlattices Microstruct. 2021, 160, 107057. [Google Scholar] [CrossRef]
  62. Wang, S.; Wang, R.; Wang, L.; Chang, J. Fabrication and thermoelectric properties of bulk VSe2 with layered structure. Solid State Commun. 2020, 318, 113983. [Google Scholar] [CrossRef]
  63. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
  64. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
  65. To, J.; Sokol, A.A.; French, S.A.; Kaltsoyannis, N.; Catlow, C.R.A. Hole localization in defects in silica materials. J. Chem. Phys. 2005, 122, 144704. [Google Scholar] [CrossRef] [PubMed]
  66. Li, W.; Zhou, L.; Prezhdo, O.V.; Akimov, A.V. Spin–orbit interactions greatly accelerate nonradiative dynamics in lead halide perovskites. ACS Energy Lett. 2018, 3, 2159–2166. [Google Scholar] [CrossRef]
  67. von Barth, U.; Hedin, L. A local exchange-correlation potential for the spin polarized case: I. J. Phys. C 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
  68. Pant, M.M.; Rajagopal, A.K. Theory of in homogeneous magnetic electron gas. Solid State Commun. 1972, 10, 1157–1160. [Google Scholar] [CrossRef]
  69. Akkoush, A.; Litman, Y.; Rossi, M. A hybrid-density functional theory study of intrinsic point defects in MX2 (M = Mo, W.; X = S, Se) monolayers. Phys. Status Solidi A 2024, 221, 2300180. [Google Scholar] [CrossRef]
  70. Sanyal, G.; Kaur, S.P.; Rout, C.S.; Chakraborty, B. Defect-engineering of 2D dichalcogenide VSe2 to enhance ammonia sensing: Acumens from DFT calculations. Biosensors 2023, 13, 257. [Google Scholar] [CrossRef]
  71. Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  72. Kezilebieke, S.; Huda, M.N.; Dreher, P.; Manninen, I.; Zhou, Y.; Sainio, J.; Mansell, R.; Ugeda, M.M.; van Dijken, S.; Komsa, H.-P.; et al. Electronic and magnetic characterization of epitaxial VSe2 monolayers on superconducting NbSe2. Commun. Phys. 2020, 3, 116. [Google Scholar] [CrossRef]
  73. Komsa, H.-P.; Rantala, T.T.; Pasquerello, A. Finite-size supercell correction schemes for charged defect calculations. Phys. Rev. B 2012, 86, 045112. [Google Scholar] [CrossRef]
  74. Zhou, X.; He, S.; Marian, J. Vacancy energetics and diffusivities in the equiatomic multielement Nb-Mo-Ta-W alloy. Materials 2022, 15, 5468. [Google Scholar] [CrossRef] [PubMed]
  75. Tersoff, J.; Hamann, D.R. Theory and application for the scanning tunneling microscope. Phys. Rev. Lett. 1983, 50, 1998. [Google Scholar] [CrossRef]
  76. Tománek, D.; Louie, S.G. First-principles calculation of highly asymmetric structure in scanning-tunneling-microscopy images of graphite. Phys. Rev. B 1988, 37, 8327. [Google Scholar] [CrossRef] [PubMed]
  77. Liu, J.; Hou, W.-J.; Cheng, C.; Fu, H.-X.; Sun, J.-T.; Meng, S. Intrinsic valley polarization of magnetic VSe2 monolayers. J. Phys. Condens. Matter 2017, 29, 255501. [Google Scholar] [CrossRef] [PubMed]
  78. Chua, R.; Henke, J.; Saha, S.; Huang, Y.; Gou, J.; He, X.; Das, T.; van Wezel, J.; Soumyanarayanan, A.; Wee, A.T.S. Coexisting charge-ordered states with distinct driving mechanisms in monolayer VSe2. ACS Nano 2022, 16, 783–791. [Google Scholar] [CrossRef]
  79. Kistanov, A.A.; Cai, Y.; Zhou, K.; Srikanth, N.; Dmitriev, S.V.; Zhang, Y.-W. Exploring the charge localization and band gap opening of borophene: A first-principles study. Nanoscale 2018, 10, 1403–1410. [Google Scholar] [CrossRef]
  80. Thanh, V.V.; Van, N.D.; Truong, D.V.; Saito, R.; Hung, N.T. First-principles study of mechanical, electronic and optical properties of Janus structure in transition metal dichalcogenides. Appl. Surf. Sci. 2020, 526, 146730. [Google Scholar] [CrossRef]
  81. Tang, Q.; Jiang, D. Stabilization and band-gap tuning of the 1T-MoS2 monolayer by covalent functionalization. Chem. Mater. 2015, 27, 3743–3748. [Google Scholar] [CrossRef]
  82. Fuh, H.R.; Chang, C.R.; Wang, Y.K.; Evans, R.F.L.; Chantrell, R.W.; Jeng, H.-T. Newtype single-layer magnetic semiconductor in transition-metal dichalcogenides VX2 (X = S, Se and Te). Sci. Rep. 2016, 6, 32625. [Google Scholar] [CrossRef]
  83. Huang, P.; Lukin, R.; Faleev, M.; Kazeev, N.; Al-Maeeni, A.R.; Andreeva, D.V.; Ustyuzhanin, A.; Tormasov, A.; Castro Neto, A.H.; Novoselov, K.S. Unveiling the complex structure-property correlation of defects in 2D materials based on high throughput datasets. npj 2D Mater. Appl. 2023, 7, 6. [Google Scholar] [CrossRef]
  84. Komsa, H.-P.; Krasheninnikov, A.V. Physics and theory of defects in 2D materials: The role of reduced dimensionality. In Materials Today, Defects in Two-Dimensional Materials; Addou, R., Colombo, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 7–41. [Google Scholar] [CrossRef]
  85. Cai, Y.; Zhou, H.; Zhang, G.; Zhang, Y.-W. Modulating carrier density and transport properties of MoS2 by organic molecular doping and defect engineering. Chem. Mater. 2016, 28, 8611–8621. [Google Scholar] [CrossRef]
  86. Hamer, M.J.; Zultak, J.; Tyurnina, A.V.; Zólyomi, V.; Terry, D.; Barinov, A.; Garner, A.; Donoghue, J.; Rooney, A.P.; Kandyba, V.; et al. Indirect to direct gap crossover in two dimensional InSe revealed by angle-resolved photoemission spectroscopy. ACS Nano 2019, 13, 2136–2142. [Google Scholar] [CrossRef] [PubMed]
  87. Su, Z.; Zhao, Y.; Huang, Y.; Xu, C.; Yang, X.; Wang, B.; Xu, B.; Xu, S.; Bai, G. Light-driven soft actuator based on graphene and WSe2 nanosheets composite for multimodal motion and remote manipulation. Nano Res. 2023, 16, 1313–1319. [Google Scholar] [CrossRef]
  88. Gong, Y.; Xu, Z.-Q.; Li, D.; Zhang, J.; Aharonovich, I.; Zhang, Y. Two-dimensional hexagonal boron nitride for building next-generation energy-efficient devices. ACS Energy Lett. 2021, 6, 985–996. [Google Scholar] [CrossRef]
  89. Lei, Y.; Zhang, T.; Lin, Y.-C.; Granzier-Nakajima, T.; Bepete, G.; Kowalczyk, D.A.; Lin, Z.; Zhou, D.; Schranghamer, T.F.; Dodda, A.; et al. Graphene and beyond: Recent advances in two-dimensional materials synthesis, properties, and devices. ACS Nanosci. Au 2022, 2, 450–485. [Google Scholar] [CrossRef]
  90. Lin, Z.; Carvalho, B.R.; Kahn, E.; Lv, R.; Rao, R.; Terrones, H.; Pimenta, M.A.; Terrones, M. Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 2016, 3, 022002. [Google Scholar] [CrossRef]
  91. Homan, S.B.; Sangwan, V.K.; Balla, I.; Bergeron, H.; Weiss, E.A.; Hersam, M.C. Ultrafast exciton dissociation and long-lived charge separation in a photovoltaic pentacene–MoS2 van der Waals heterojunction. Nano Lett. 2017, 17, 164–169. [Google Scholar] [CrossRef]
  92. Kirubasankar, B.; Won, Y.S.; Adofo, L.A.; Choi, S.H.; Kim, S.M.; Kim, K.K. Atomic and structural modifications of two-dimensional transition metal dichalcogenides for various advanced applications. Chem. Sci. 2022, 13, 7707–7738. [Google Scholar] [CrossRef]
  93. Tran, T.T.; Wong-Leung, J.; Smillie, L.A.; Hallén, A.; Grimaldi, M.G.; Williams, J.S. High hole mobility and non-localized states in amorphous germanium. APL Mater. 2023, 11, 041115. [Google Scholar] [CrossRef]
  94. Pushkarev, G.V.; Mazurenko, V.G.; Mazurenko, V.V.; Boukhvalov, D.W. Structural phase transitions in VSe2: Energetics, electronic structure and magnetism. Phys. Chem. Chem. Phys. 2019, 21, 22647–22653. [Google Scholar] [CrossRef] [PubMed]
  95. Zhang, Z.; Niu, J.; Yang, P.; Gong, Y.; Ji, Q.; Shi, J.; Fang, Q.; Jiang, S.; Li, H.; Zhou, X.; et al. Vanadium diselenide single crystals: Van der Waals epitaxial growth of 2D metallic vanadium diselenide single crystals and their extra-high electrical conductivity. Adv. Mater. 2017, 29, 1702359. [Google Scholar] [CrossRef] [PubMed]
  96. Su, J.W.; Wang, M.S.; Li, Y.; Wang, F.K.; Chen, Q.; Luo, P.; Han, J.B.; Wang, S.; Li, H.Q.; Zhai, T.Y. Sub-millimeter-scale monolayer p-type H-phase VS2. Adv. Funct. Mater. 2020, 30, 2000240. [Google Scholar] [CrossRef]
  97. Whitten, E. Ultraviolet photoelectron spectroscopy: Practical aspects and best practices. Appl. Surf. Sci. Adv. 2023, 13, 100384. [Google Scholar] [CrossRef]
  98. Yesilpinar, D.; Vondráček, M.; Čermák, P.; Mönig, H.; Kopeček, J.; Caha, O.; Carva, K.; Drašar, Č.; Honolka, J. Defect pairing in Fe-doped SnS van der Waals crystals: A photoemission and scanning tunneling microscopy study. Nanoscale 2023, 15, 13110. [Google Scholar] [CrossRef] [PubMed]
  99. Zhao, Y.; Tripathi, M.; Čerņevičs, K.; Avsar, A.; Ji, H.G.; Marin, J.F.G.; Cheon, C.-Y.; Wang, Z.; Yazyev, O.V.; Kis, A. Electrical spectroscopy of defect states and their hybridization in monolayer MoS2. Nat. Commun. 2023, 14, 44. [Google Scholar] [CrossRef]
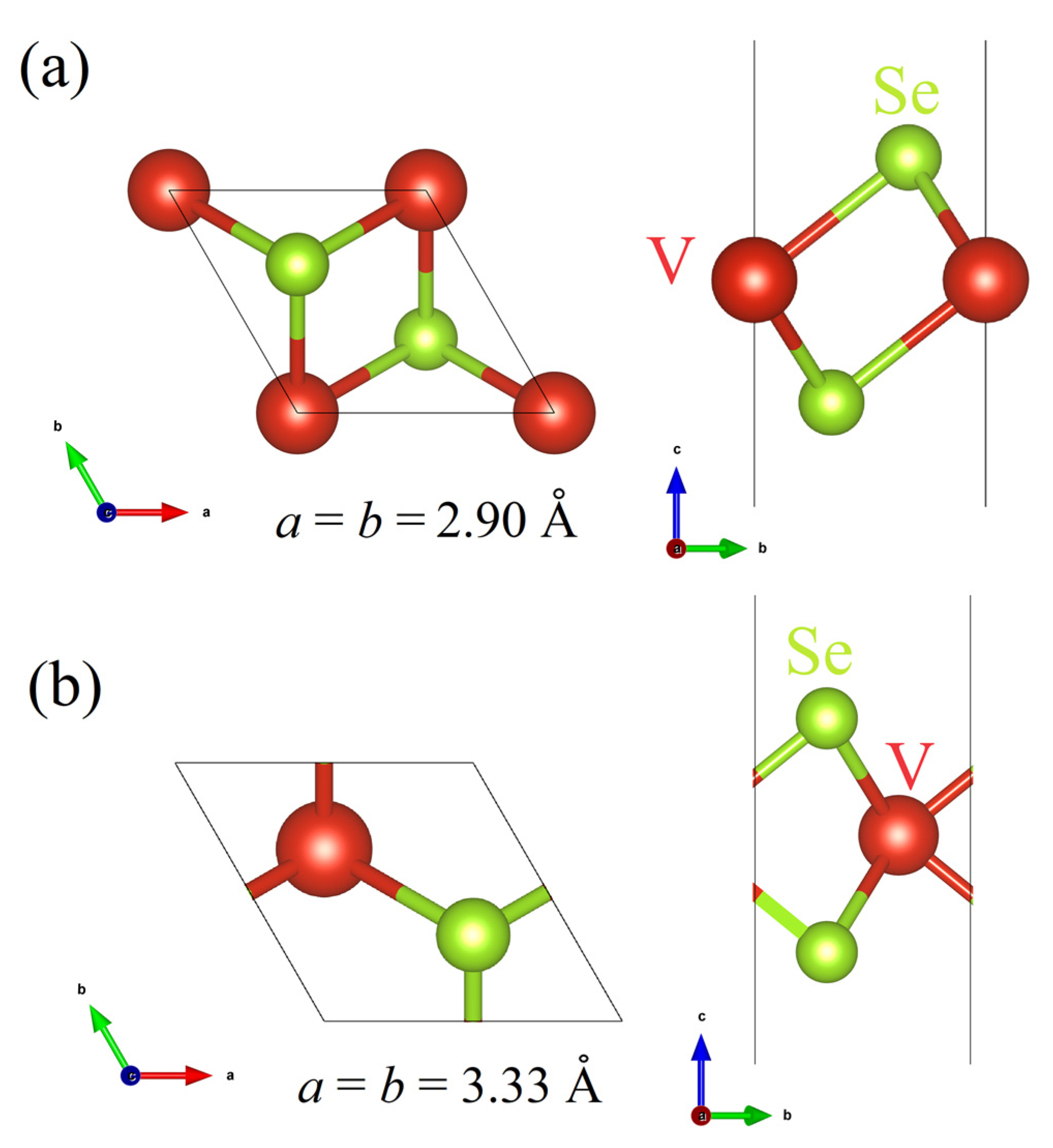
Applsci 14 01205 g001
Figure 1. The optimized unit cell structure of the T–VSe2 (a) and H–VSe2 (b) monolayers.
Figure 1. The optimized unit cell structure of the T–VSe2 (a) and H–VSe2 (b) monolayers.
Applsci 14 01205 g001
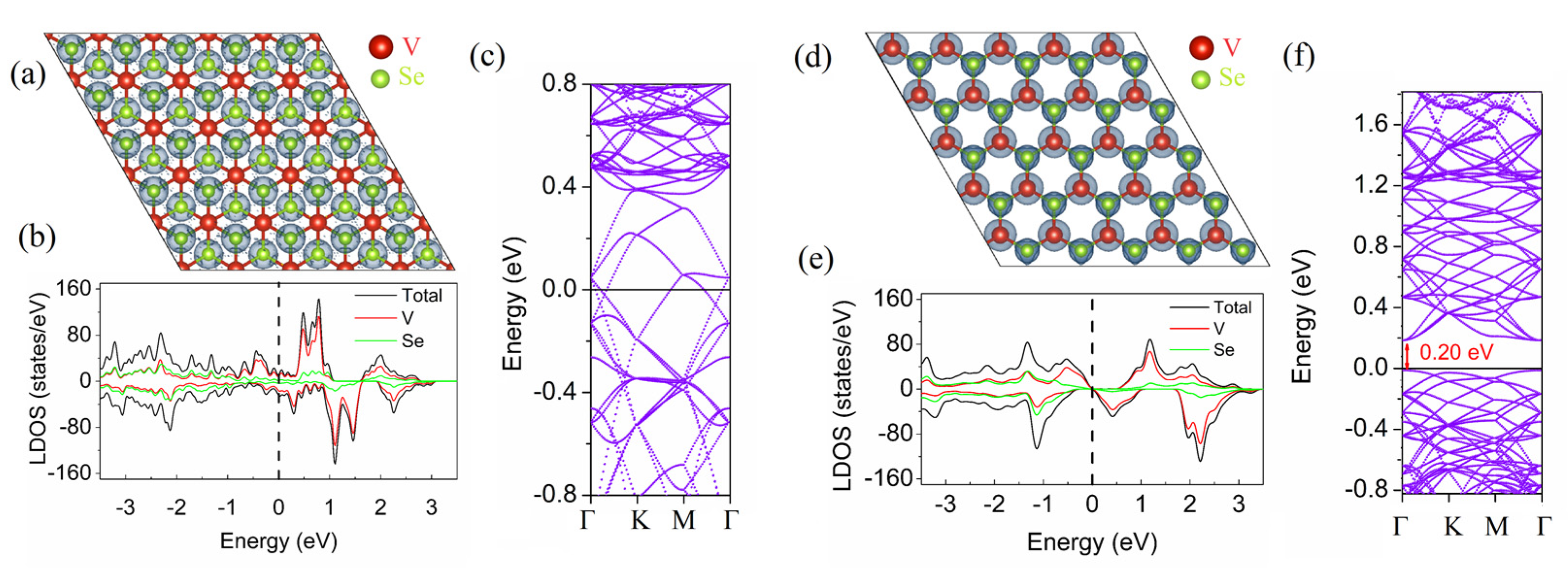
Applsci 14 01205 g002
Figure 2. The 5 × 5 supercell structure combined with the electron localization function (a,d), the local density of states (b,e) and band structure (c,f) of the T–VSe2 and H–VSe2 monolayers, respectively.
Figure 2. The 5 × 5 supercell structure combined with the electron localization function (a,d), the local density of states (b,e) and band structure (c,f) of the T–VSe2 and H–VSe2 monolayers, respectively.
Applsci 14 01205 g002
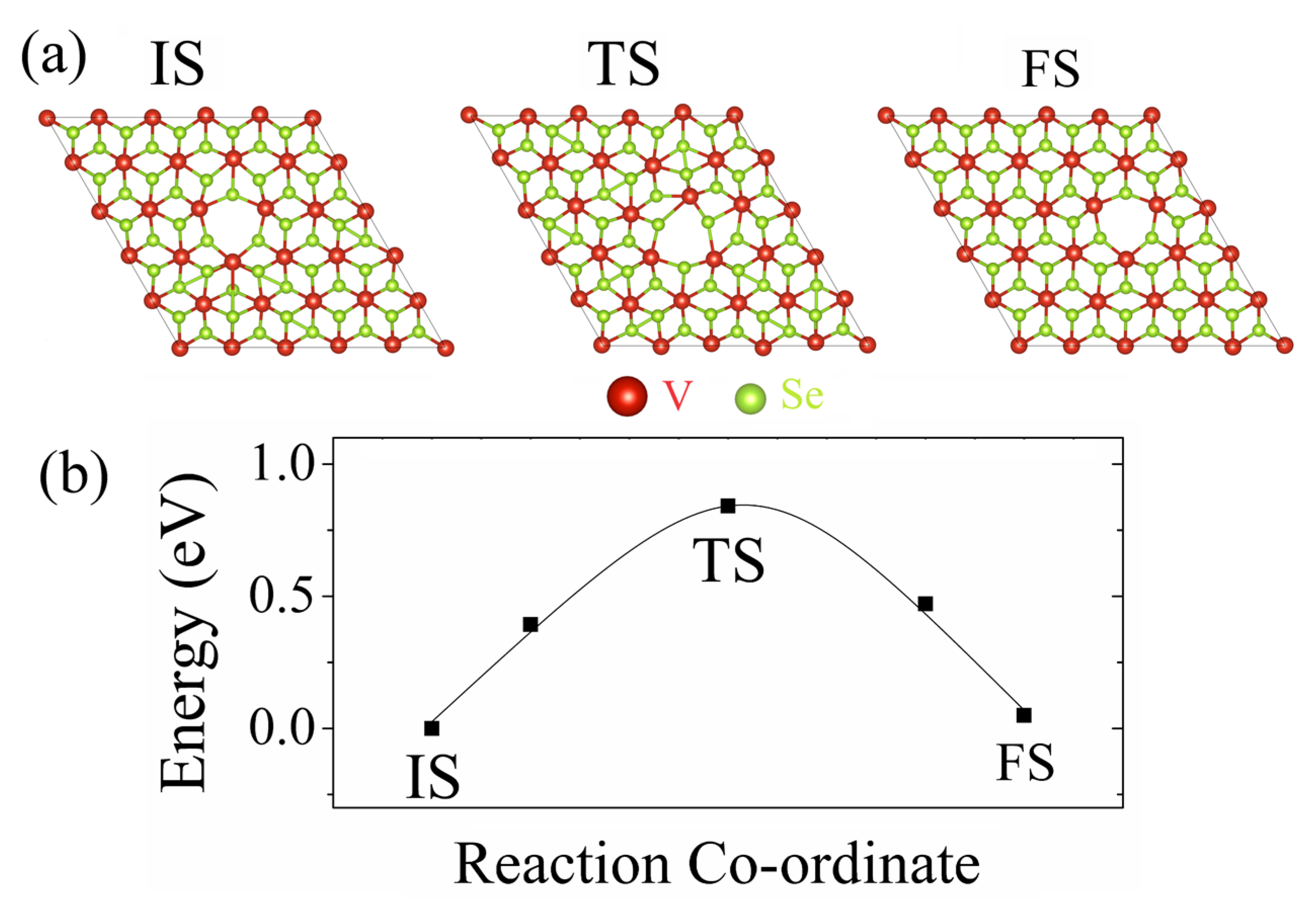
Applsci 14 01205 g003
Figure 3. The illustration of the migration process of the VSe in the T–VSe2 monolayer (a). Energetic profiles of the reaction pathway obtained from NEB calculations (b).
Figure 3. The illustration of the migration process of the VSe in the T–VSe2 monolayer (a). Energetic profiles of the reaction pathway obtained from NEB calculations (b).
Applsci 14 01205 g003
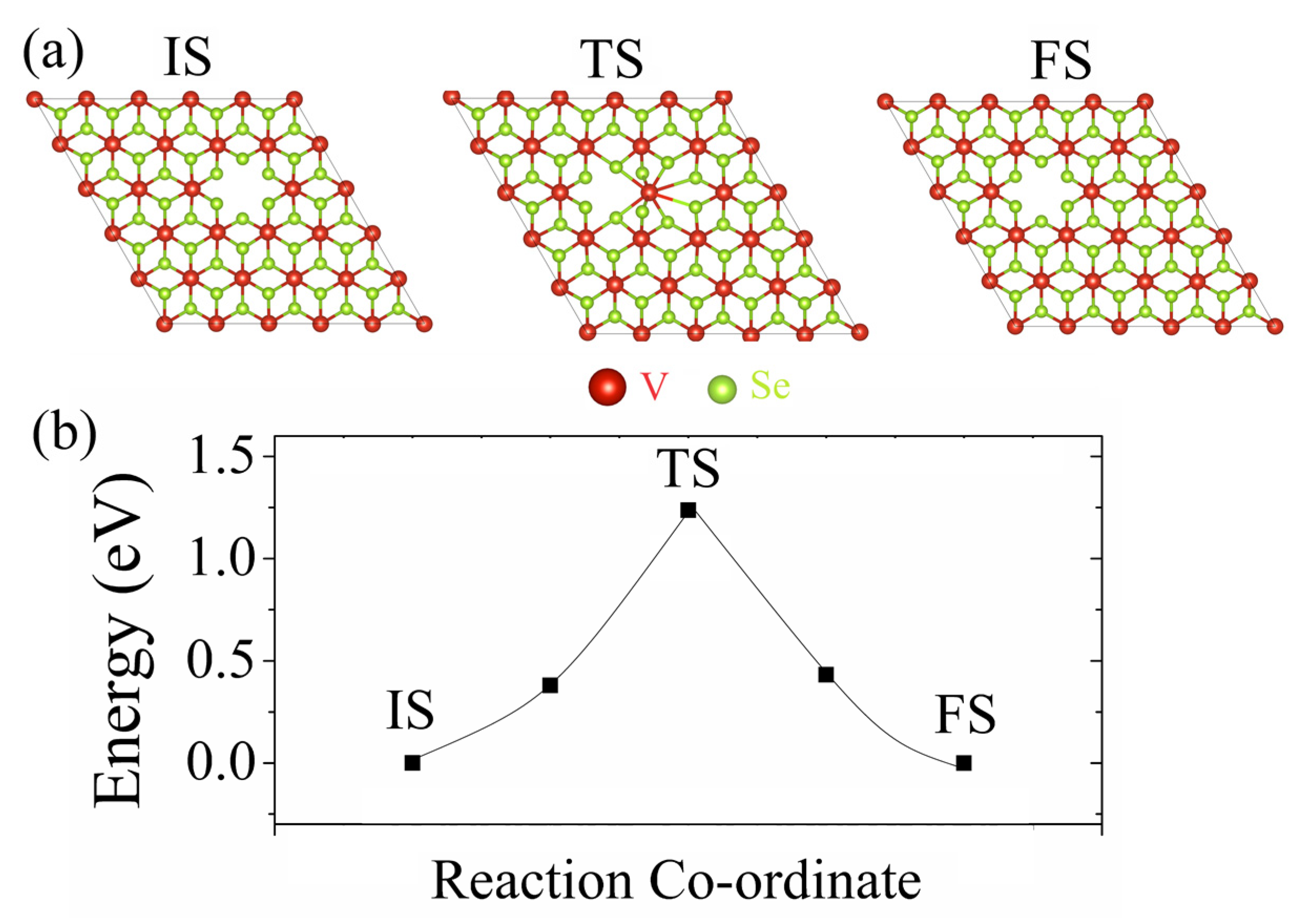
Applsci 14 01205 g004
Figure 4. The illustration of the migration process of the VV in the T–VSe2 monolayer (a). Energetic profiles of the reaction pathway obtained from NEB calculations (b).
Figure 4. The illustration of the migration process of the VV in the T–VSe2 monolayer (a). Energetic profiles of the reaction pathway obtained from NEB calculations (b).
Applsci 14 01205 g004
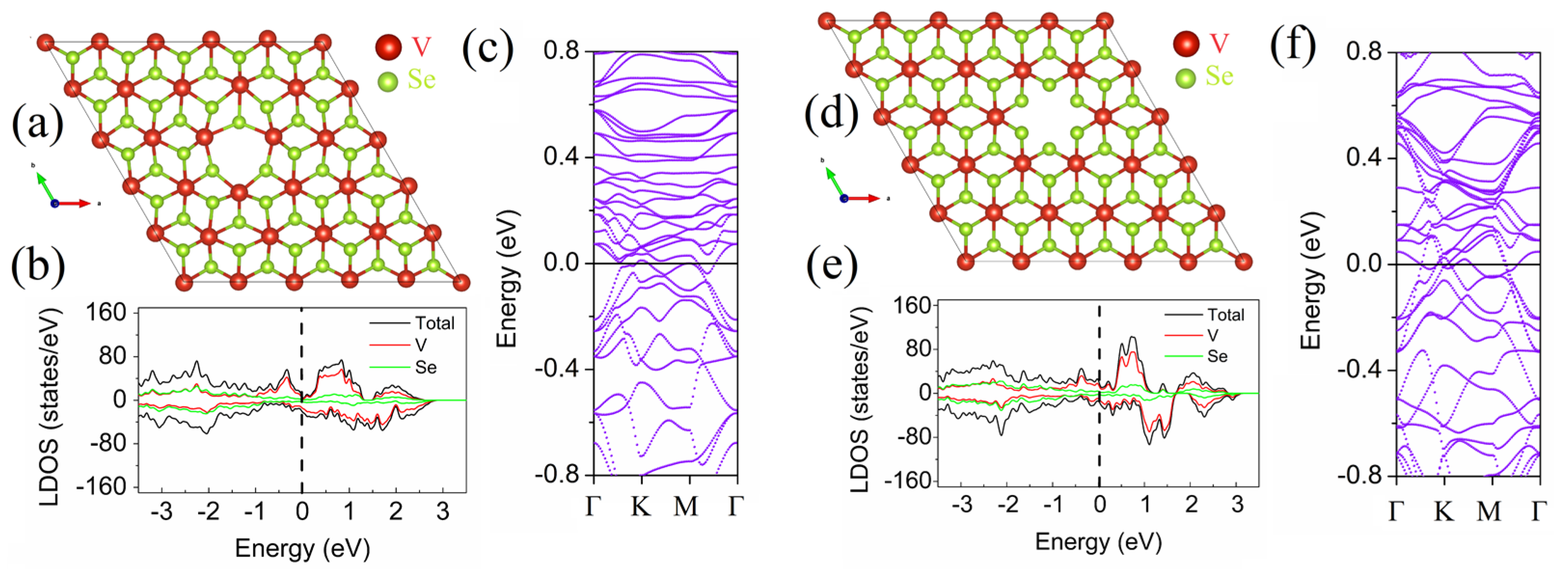
Applsci 14 01205 g005
Figure 5. The atomic structure of the 5 × 5 supercell structure (a,d), the local density of states (b,e) and band structure (c,f) of the T–VSe2 monolayer containing VSe and VV defects, respectively.
Figure 5. The atomic structure of the 5 × 5 supercell structure (a,d), the local density of states (b,e) and band structure (c,f) of the T–VSe2 monolayer containing VSe and VV defects, respectively.
Applsci 14 01205 g005
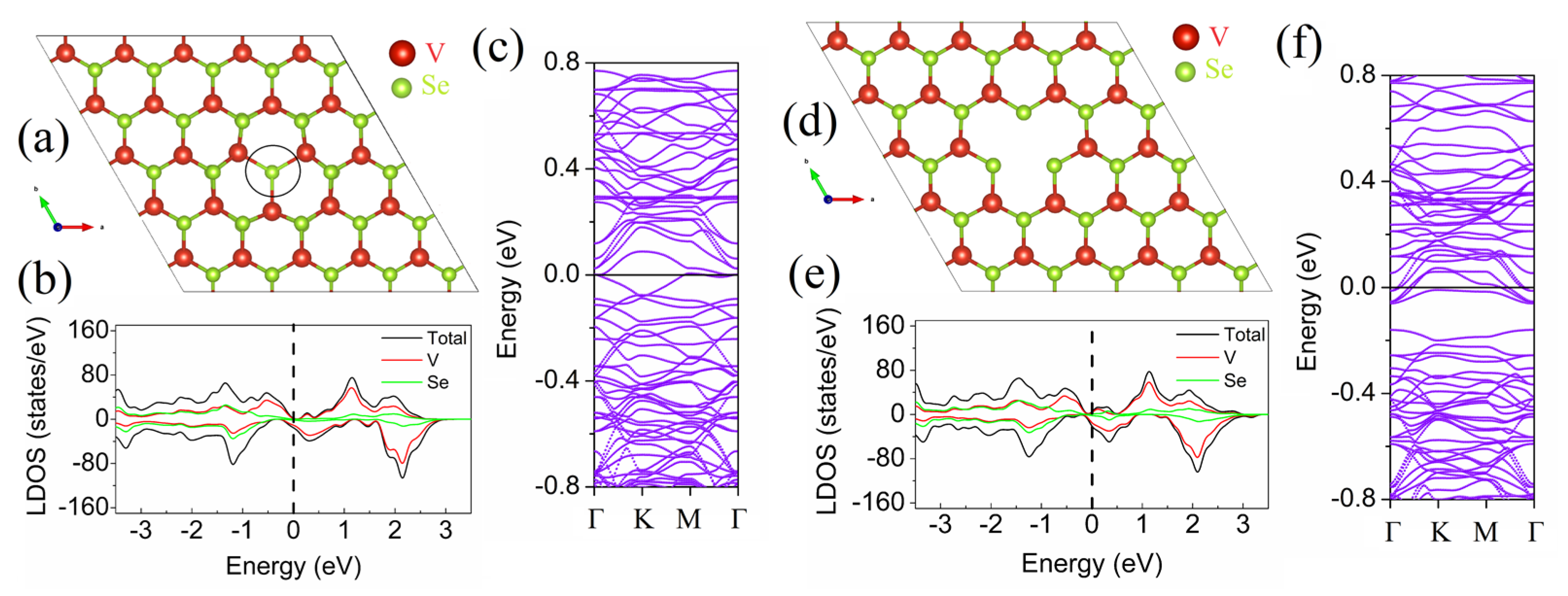
Applsci 14 01205 g006
Figure 6. Atomic structure of the 5 × 5 supercell structure (a,d), the local density of states (b,e) and band structure (c,f) of the H–VSe2 monolayer containing VSe (marked by the black circle) and VV defects, respectively.
Figure 6. Atomic structure of the 5 × 5 supercell structure (a,d), the local density of states (b,e) and band structure (c,f) of the H–VSe2 monolayer containing VSe (marked by the black circle) and VV defects, respectively.
Applsci 14 01205 g006
Applsci 14 01205 g007
Figure 7. STM images of the 5 × 5 supercell structure (a,b) pristine, (c,d) VSe-containing, and (e,f) VV-containing the T–VSe2 and H–VSe2 monolayers, respectively.
Figure 7. STM images of the 5 × 5 supercell structure (a,b) pristine, (c,d) VSe-containing, and (e,f) VV-containing the T–VSe2 and H–VSe2 monolayers, respectively.
Applsci 14 01205 g007
Table 1. Eform and Emigration for the monovacancy defects in T–VSe2 and H-VSe2.
Table 1. Eform and Emigration for the monovacancy defects in T–VSe2 and H-VSe2.
DefectEform, eVEmigration, eVEform + Emigration, eV
T–VSe2 VSe5.310.886.19
T–VSe2 VV10.081.2411.32
H–VSe2 VSe5.60--
H–VSe2 VV13.03--
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kistanov, A.A. Characterization of Monovacancy Defects in Vanadium Diselenide Monolayer: A DFT Study. Appl. Sci. 2024, 14, 1205. https://doi.org/10.3390/app14031205

AMA Style

Kistanov AA. Characterization of Monovacancy Defects in Vanadium Diselenide Monolayer: A DFT Study. Applied Sciences. 2024; 14(3):1205. https://doi.org/10.3390/app14031205

Chicago/Turabian Style

Kistanov, Andrey A. 2024. "Characterization of Monovacancy Defects in Vanadium Diselenide Monolayer: A DFT Study" Applied Sciences 14, no. 3: 1205. https://doi.org/10.3390/app14031205

APA Style

Kistanov, A. A. (2024). Characterization of Monovacancy Defects in Vanadium Diselenide Monolayer: A DFT Study. Applied Sciences, 14(3), 1205. https://doi.org/10.3390/app14031205

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop