Performance Assessment and Optimization of the Ultra-High Speed Air Compressor in Hydrogen Fuel Cell Vehicles
Abstract
1. Introduction
2. Methodology
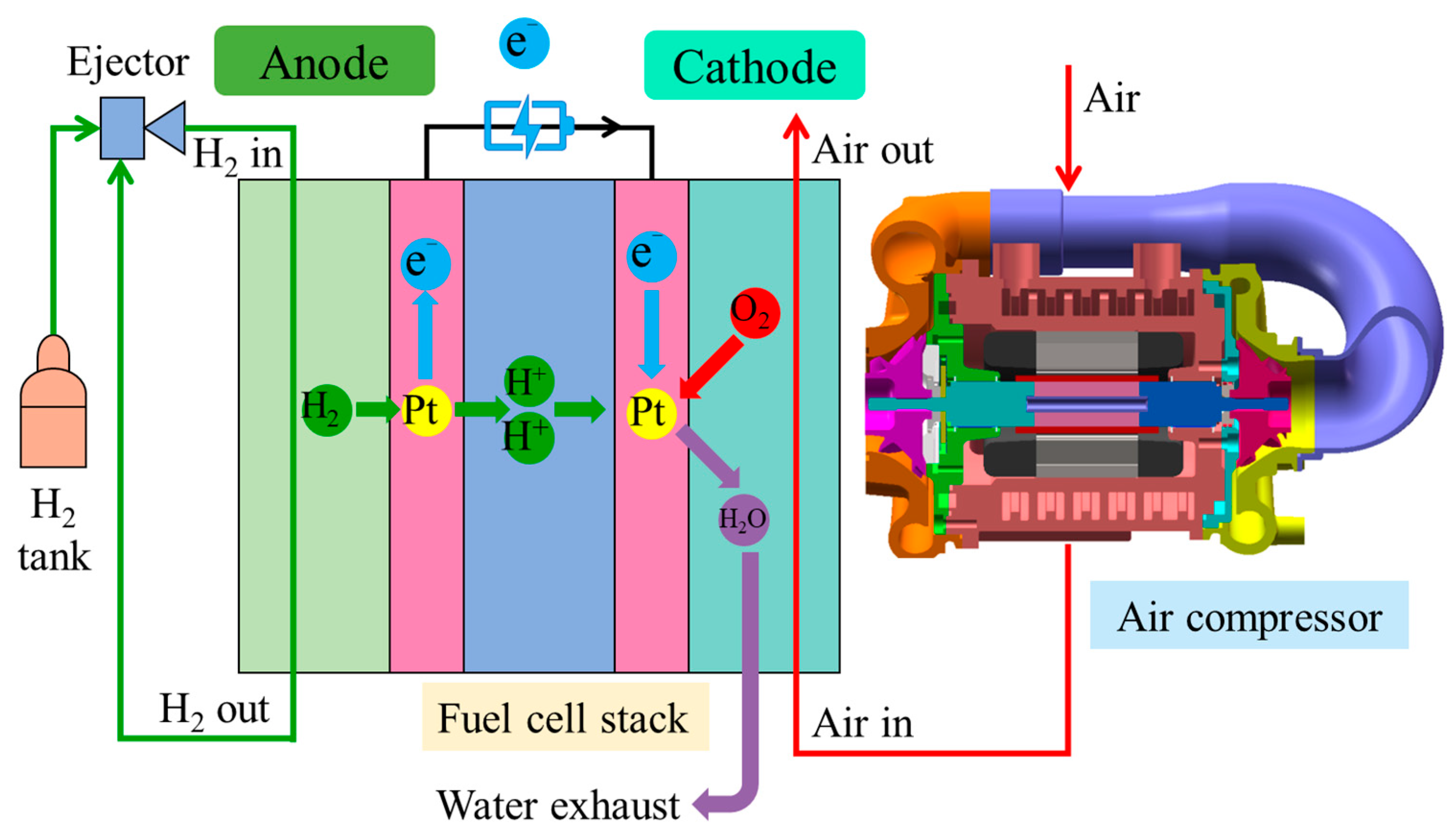
2.1. Air Compressors in HFCVs
2.2. Content and Methodologies Employed in the Research
3. Experimental Bench and Theoretical Model
3.1. Experimental Bench
3.1.1. Experimental Setup
3.1.2. Theoretical Calculation of Air Compressor
3.2. Theoretical Model
3.2.1. Global Sensitivity Analysis
3.2.2. Initial Sample and Multi-Objective Optimization
4. Results and Discussions
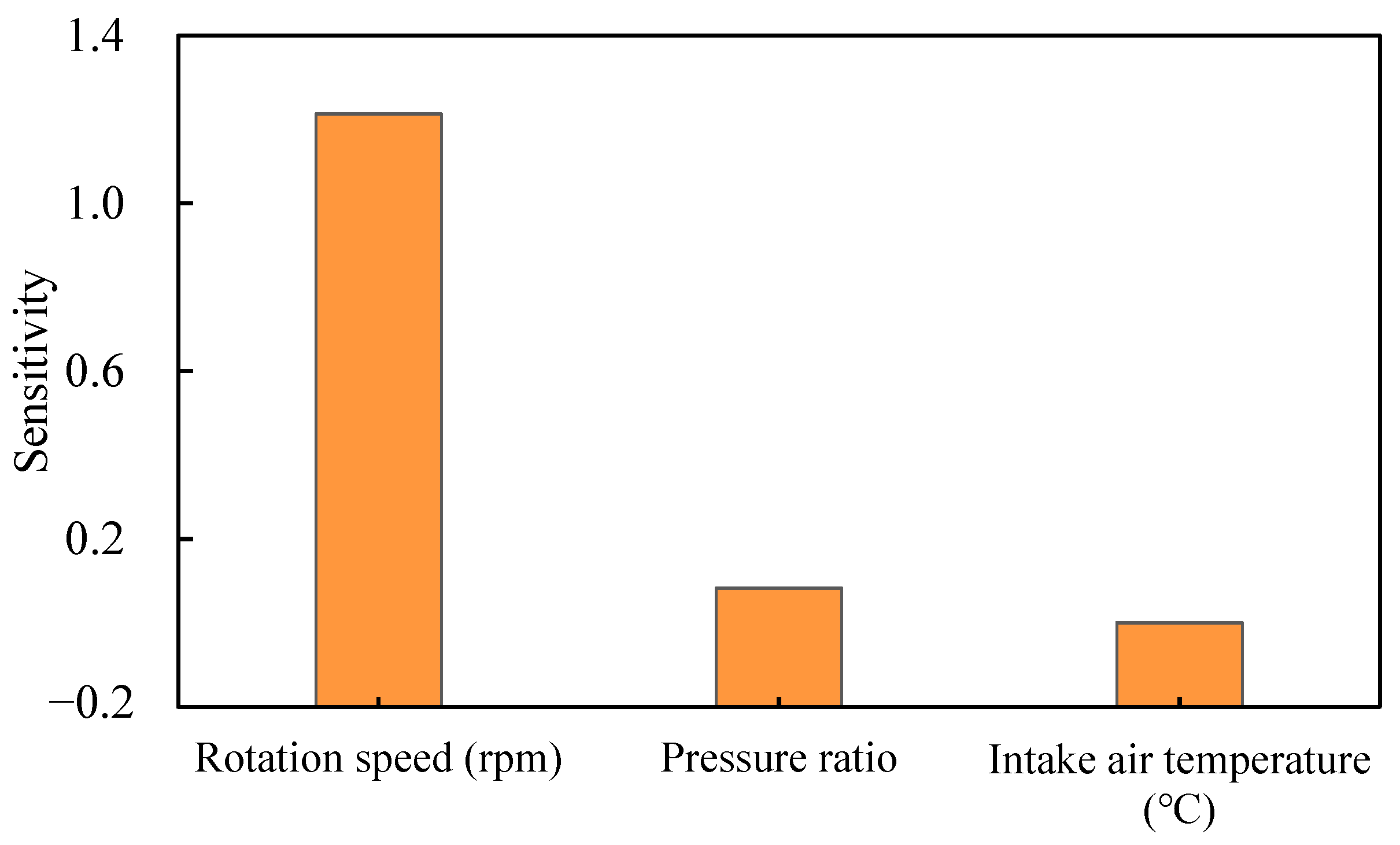
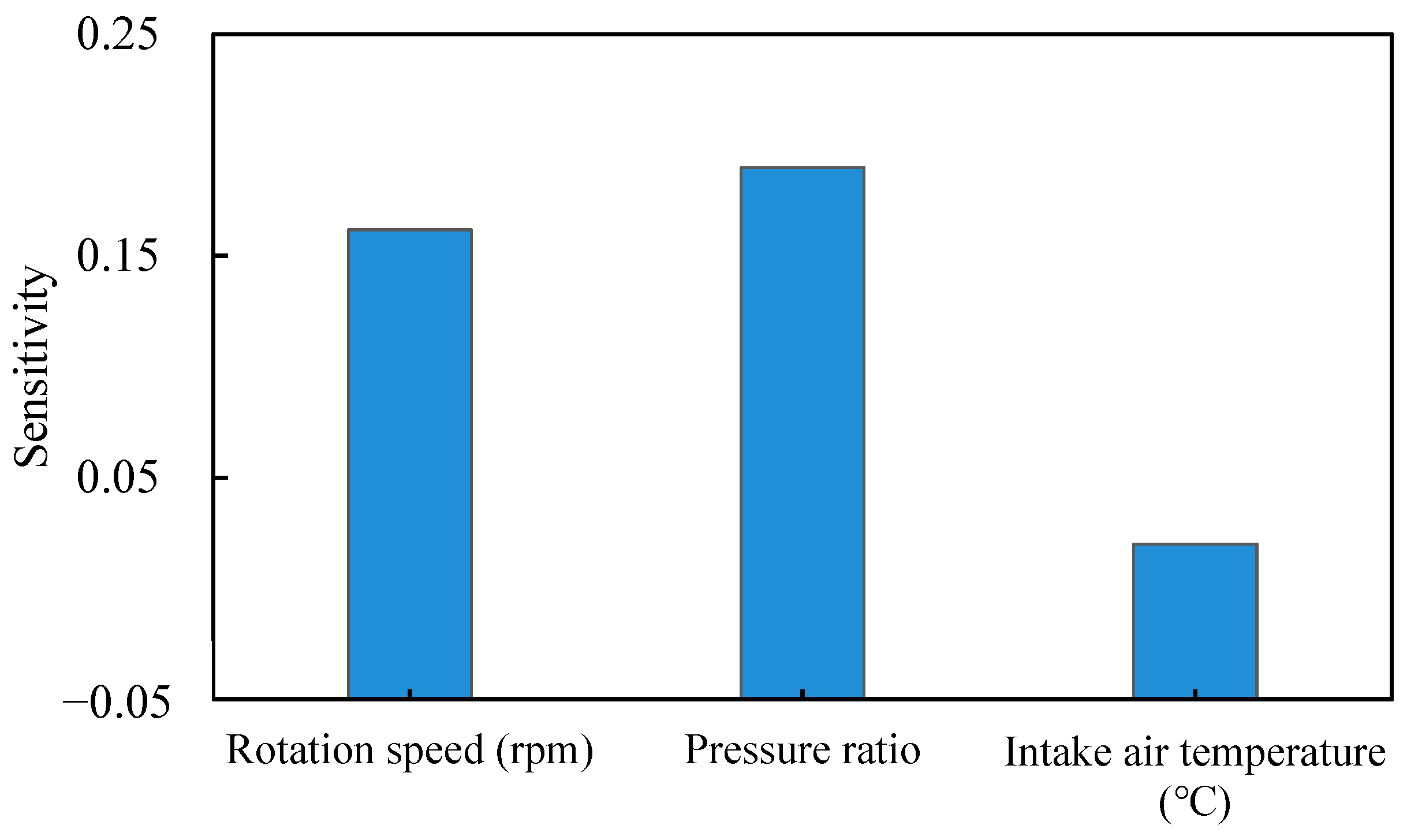
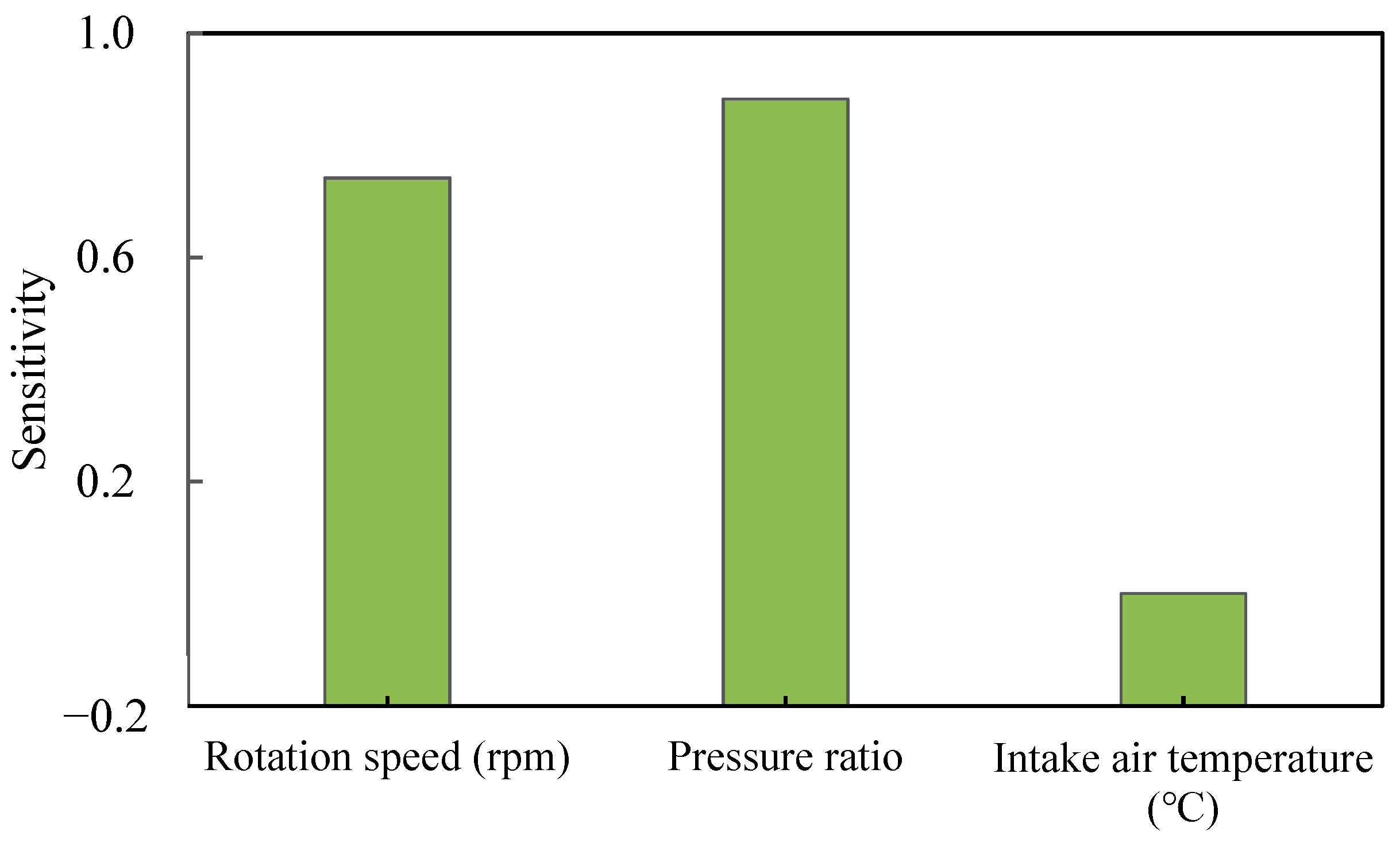
4.1. Sensitivity Analysis
4.2. Impact of Operational Parameters on the Performance of the Air Compressor
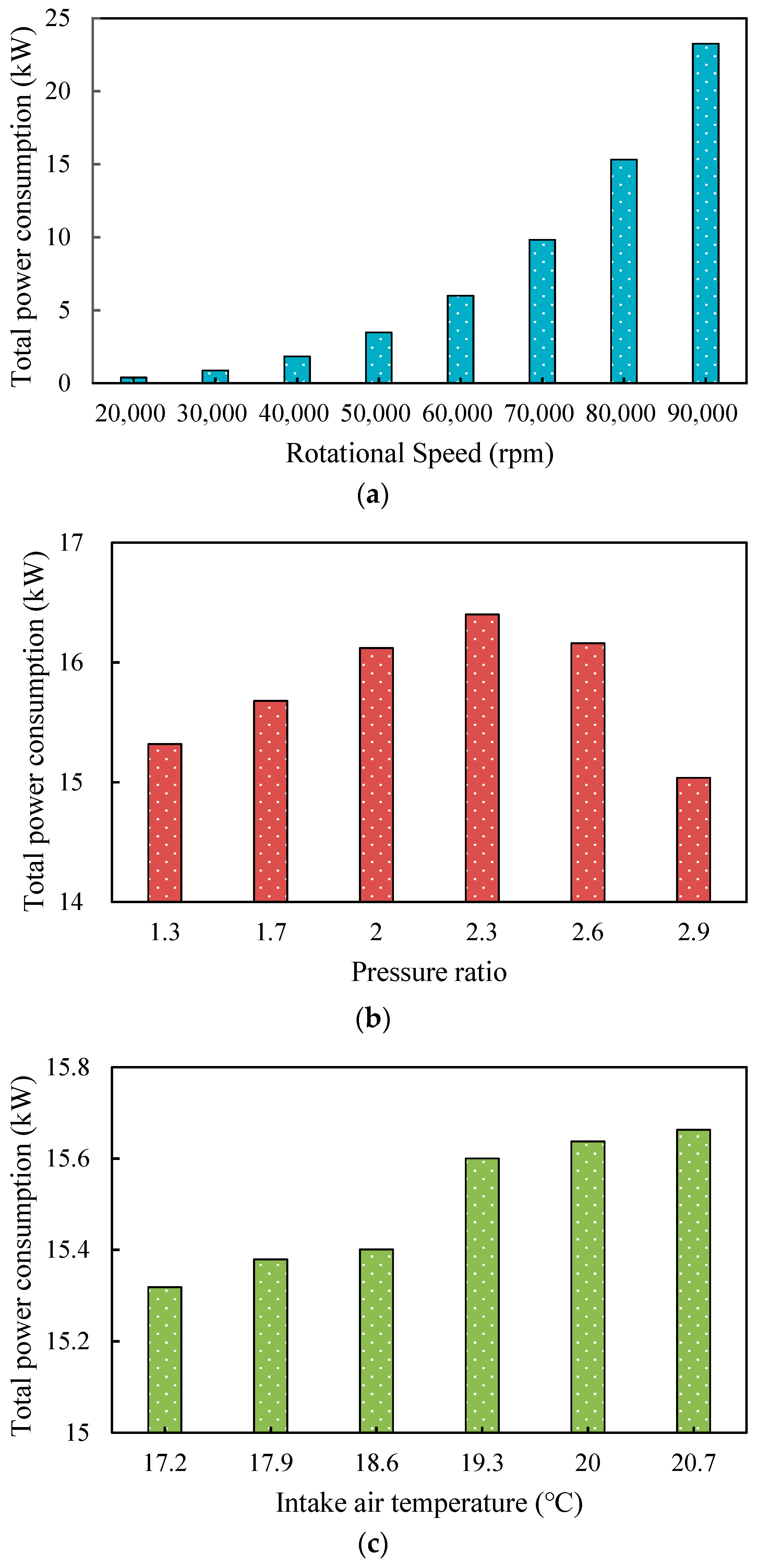
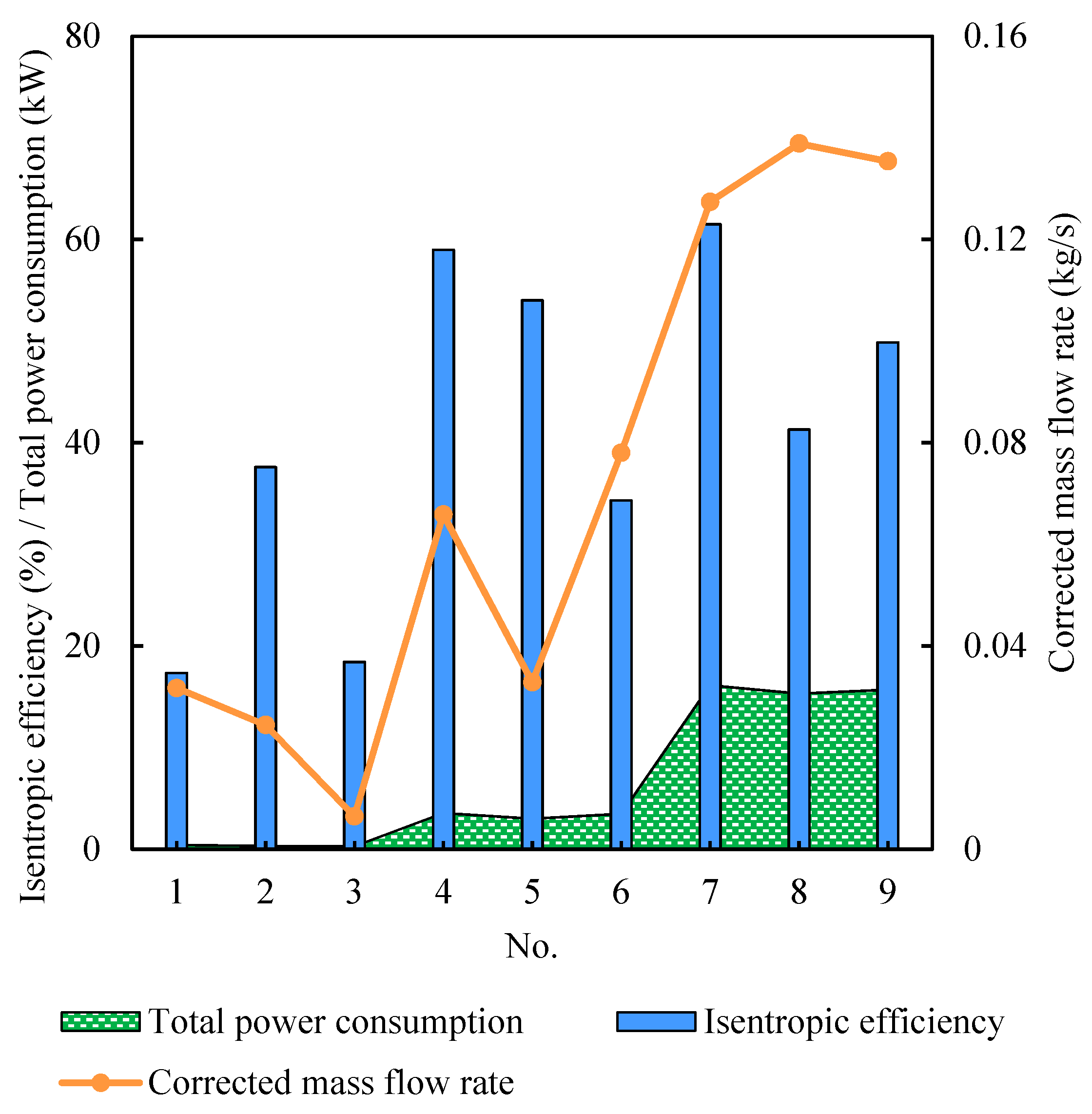
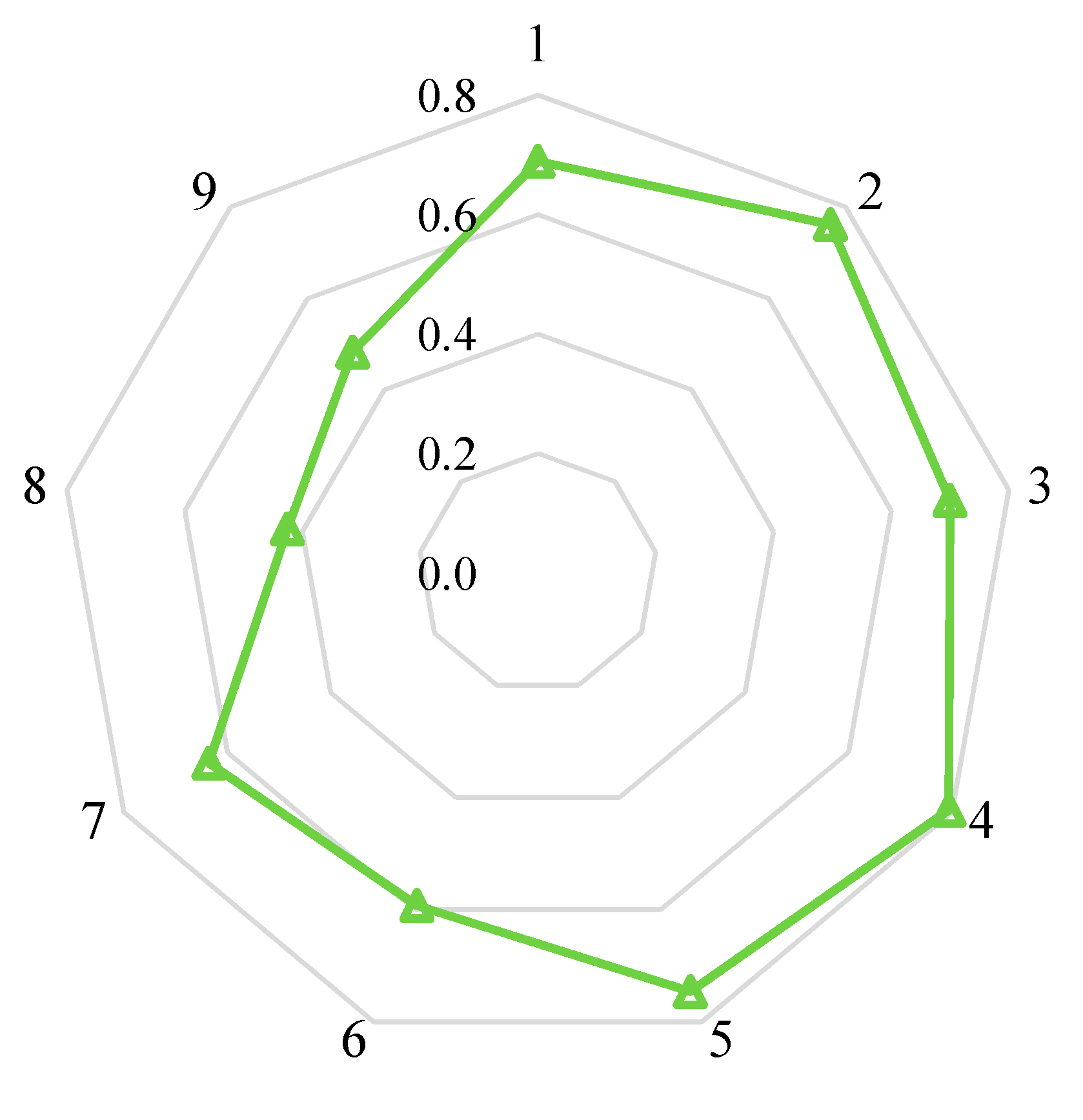
4.2.1. Total Power Consumption
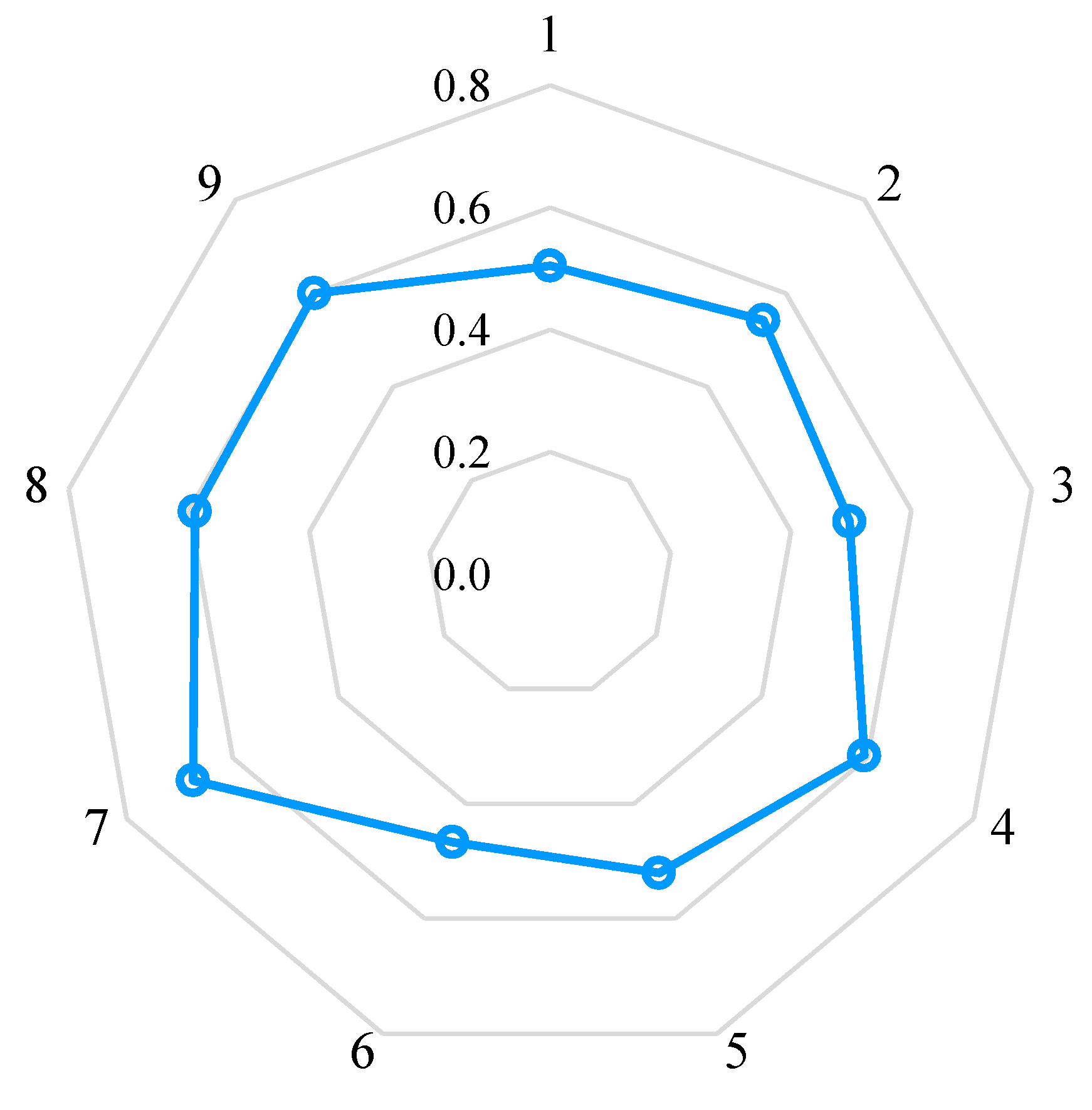
4.2.2. Isentropic Efficiency
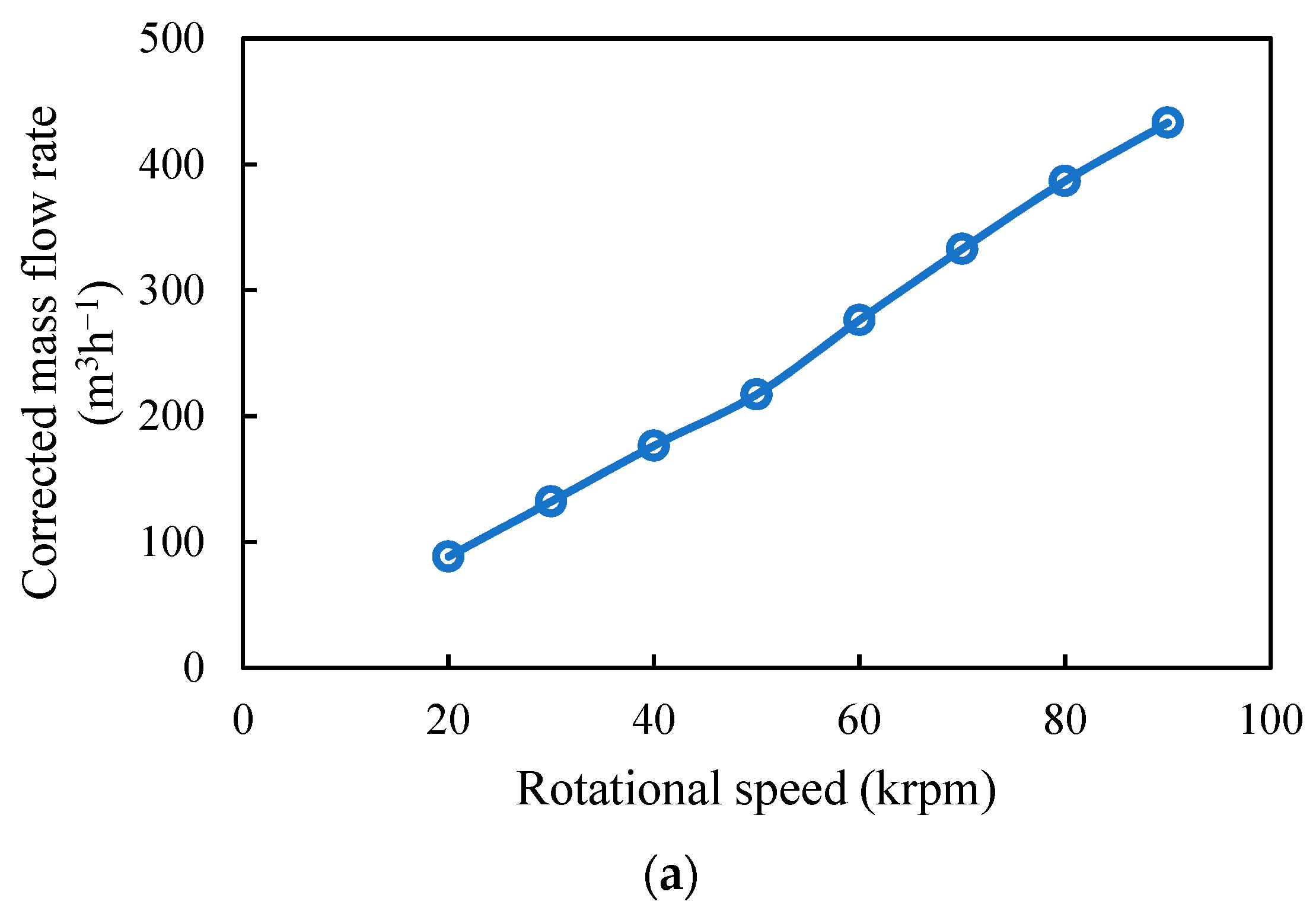
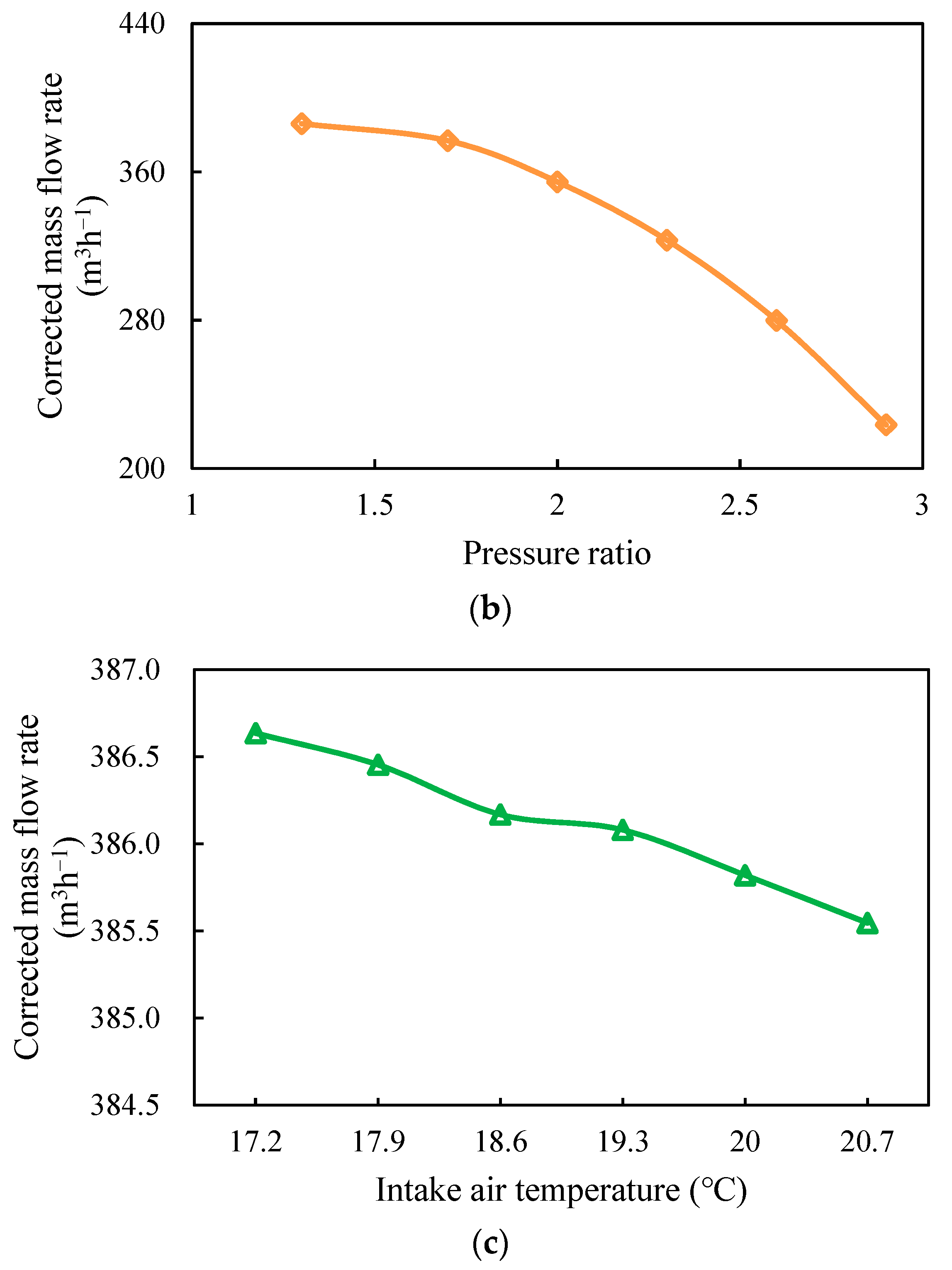
4.2.3. Corrected Mass flow Rate
4.3. Results of Multi-Objective Optimization
4.3.1. Initial Sample
4.3.2. Multi-Objective Optimization Results
4.4. Optimal Combination Verification
4.5. Constraints and Future Investigations
5. Conclusions
- The rotational speed exhibits the highest sensitivity to total energy consumption, while the pressure ratio showcases the most prominent sensitivity towards the isentropic efficiency and mass flow rate. Conversely, the impact of the intake temperature on energy consumption, efficiency, and flow rate is minimal.
- The total power consumption increases with higher rotational speed and inlet temperature. Notably, with an increase in the pressure ratio, total power consumption initially rises before decreasing. Isentropic efficiency increases with higher values of rotational speed, pressure ratio, and intake temperature. As rotational speed increases, mass flow rate increases. However, with an increase in the pressure ratio and intake temperature, the mass flow rate decreases.
- Considering high efficiency and low energy consumption, the optimal combination of operational parameters is a rotational speed of 50,000 rpm, a pressure ratio of 1.4, and an intake temperature of 18.3 °C. At these optimal operational parameters, the isentropic efficiency improved by 42.18%, while power consumption decreased by 44.92%.
- Considering the high mass flow rate and low energy consumption, the optimal combination of operational parameters is a rotational speed of 80,000 rpm, a pressure ratio of 1.0, and an intake temperature of 18.8 °C. At these optimal operational parameters, the mass flow rate increased by 95.1%.
- When considering a high flow rate, high efficiency, and low energy consumption simultaneously, the optimal combination of operational parameters is a rotational speed of 80,000 rpm, a pressure ratio of 1.8, and an intake temperature of 18.3 °C. Compared to the average values, at half the increase in power consumption, the mass flow rate increased by 78.88%, and the isentropic efficiency increased by 48.23%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Rensburg, T.M.; Brennan, N.; Howard, A. Tourist preferences for fuel cell vehicle rental: Going green with hydrogen on the island of tenerife. Int. J. Hydrogen Energy 2023, 48, 29350–29366. [Google Scholar] [CrossRef]
- Nanmaran, R.; Mageswari, M.; Srimathi, S.; Ganesh Raja, G.; Al Obaid, S.; Ali Alharbi, S.; Elumalai, P.; Thanigaivel, S. Mathematical modelling of hydrogen transportation from reservoir tank to hydrogen fuel cell electric vehicle (fcev) tank. Fuel 2024, 361, 130725. [Google Scholar] [CrossRef]
- Park, S.; Lee, S. Theoretical analysis for improving the efficiency of ht-pemfc through unreacted hydrogen circulation. Appl. Sci. 2023, 13, 9292. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, W.; Li, S.; Xu, M.; Huang, W.; Qin, Z. Finite element analysis and optimization of hydrogen fuel cell city bus body frame structure. Appl. Sci. 2023, 13, 10964. [Google Scholar] [CrossRef]
- Mori, M.; Iribarren, D.; Cren, J.; Cor, E.; Lotrič, A.; Gramc, J.; Drobnič, B.; Rey, L.; Campos-Carriedo, F.; Puig-Samper, G.; et al. Life cycle sustainability assessment of a proton exchange membrane fuel cell technology for ecodesign purposes. Int. J. Hydrogen Energy 2023, 48, 39673–39689. [Google Scholar] [CrossRef]
- Akimoto, Y.; Shibata, M.; Tsuzuki, Y.; Okajima, K.; Suzuki, S. In-situ onboard evaluation and control of proton exchange membrane fuel cells using magnetic sensors. Appl. Energy 2023, 351, 121873. [Google Scholar] [CrossRef]
- Thounthong, P.; Mungporn, P.; Guilbert, D.; Takorabet, N.; Pierfederici, S.; Nahid-Mobarakeh, B.; Hu, Y.; Bizon, N.; Huangfu, Y.; Kumam, P. Design and control of multiphase interleaved boost converters-based on differential flatness theory for pem fuel cell multi-stack applications. Int. J. Electr. Power 2021, 124, 106346. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, H.; Lin, Z.; Zhu, Z.; Wang, H.; Yuan, Y. Experimental study of the thermal and power performances of a proton exchange membrane fuel cell stack affected by the coolant temperature. Appl. Therm. Eng. 2023, 225, 120211. [Google Scholar] [CrossRef]
- Deng, B.; Zhang, X.; Yin, C.; Luo, Y.; Tang, H. Improving a fuel cell system’s thermal management by optimizing thermal control with the particle swarm optimization algorithm and an artificial neural network. Appl. Sci. 2023, 13, 12895. [Google Scholar] [CrossRef]
- Pourrahmani, H.; Van Herle, J. Evaluation criterion of proton exchange membrane (ecpem) fuel cells considering inserted porous media inside the gas flow channel. Appl. Therm. Eng. 2022, 203, 117952. [Google Scholar] [CrossRef]
- Hu, D.; Liu, J.; Yi, F.; Yang, Q.; Zhou, J. Enhancing heat dissipation to improve efficiency of two-stage electric air compressor for fuel cell vehicle. Energy Convers. Manag. 2022, 251, 115007. [Google Scholar] [CrossRef]
- Hu, C.; Geng, K.; Yang, C.; Zhou, M.; Chen, H. Thermodynamics investigation and spike-stall identification based on energy loss of centrifugal compressor. Int. J. Heat Mass. Tran. 2021, 166, 120693. [Google Scholar] [CrossRef]
- Ahsan, N.; Al Rashid, A.; Zaidi, A.A.; Imran, R.; Abdul Qadir, S. Performance analysis of hydrogen fuel cell with two-stage turbo compressor for automotive applications. Energy Rep. 2021, 7, 2635–2646. [Google Scholar] [CrossRef]
- Li, Z.; Han, G.; Lu, X.; Huang, E.; Zhao, S. Improving the operating range using a centrifugal compressor with a tandem impeller. Aerosp. Sci. Technol. 2020, 96, 105548. [Google Scholar] [CrossRef]
- Sun, J.; Zuo, Z.; Liang, Q.; Zhou, X.; Guo, W.; Chen, H. Theoretical and experimental study on effects of humidity on centrifugal compressor performance. Appl. Therm. Eng. 2020, 174, 115300. [Google Scholar] [CrossRef]
- Zhao, D.; Xu, L.; Huangfu, Y.; Dou, M.; Liu, J. Semi-physical modeling and control of a centrifugal compressor for the air feeding of a pem fuel cell. Energy Convers. Manag. 2017, 154, 380–386. [Google Scholar] [CrossRef]
- Wan, Y.; Guan, J.; Xu, S. Improved empirical parameters design method for centrifugal compressor in pem fuel cell vehicle application. Int. J. Hydrogen Energy 2017, 42, 5590–5605. [Google Scholar] [CrossRef]
- Mirzaee, S.; Zheng, X.; Lin, Y. Improvement in the stability of a turbocharger centrifugal compressor by tip leakage control. Proceedings of the Institution of Mechanical Engineers. Part D J. Automob. Eng. 2017, 231, 700–714. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Ding, Y.; Deng, H.; Chen, W. Modeling and control of an air supply system for a heavy duty pemfc engine. Int. J. Hydrogen Energy 2016, 41, 16230–16239. [Google Scholar] [CrossRef]
- Fang, X.; Chen, W.; Zhou, Z.; Xu, Y. Empirical models for efficiency and mass flow rate of centrifugal compressors. Int. J. Refrig. 2014, 41, 190–199. [Google Scholar] [CrossRef]
- Zhao, D.; Zheng, Q.; Gao, F.; Bouquain, D.; Dou, M.; Miraoui, A. Disturbance decoupling control of an ultra-high speed centrifugal compressor for the air management of fuel cell systems. Int. J. Hydrogen Energy 2014, 39, 1788–1798. [Google Scholar] [CrossRef]
- Cho, J.; Song, S. Prediction of hydrogen-added combustion process in t-gdi engine using artificial neural network. Appl. Therm. Eng. 2020, 181, 115974. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A. Sensitivity analysis of an environmental model: An application of different analysis methods. Reliab. Eng. Syst. Safe 1997, 57, 49–69. [Google Scholar] [CrossRef]
- Petersen, S.; Kristensen, M.H.; Knudsen, M.D. Prerequisites for reliable sensitivity analysis of a high fidelity building energy model. Energy Build. 2019, 183, 1–16. [Google Scholar] [CrossRef]
- Liu, L.; Ao, T.; Zhou, L.; Takeuchi, K.; Gusyev, M.; Zhang, X.; Wang, W.; Ren, Y. Comprehensive evaluation of parameter importance and optimization based on the integrated sensitivity analysis system: A case study of the btop model in the upper min river basin, china. J. Hydrol. 2022, 610, 127819. [Google Scholar] [CrossRef]
- Xiong, F.; Wei, B.; Xu, F. Identification of arch dam mechanical parameters based on sensitivity analysis and hooke–jeeves algorithm optimization. Structures 2022, 46, 88–98. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Z.; Zhang, J.; Peng, X.; Feng, J. Performances investigation and multi-objective optimization of gas foil bearings in hydrogen fuel cell vehicles. Int. J. Energy Res. 2022, 46, 18849–18865. [Google Scholar] [CrossRef]
- Wang, P.; Meng, P.; Zhai, J.; Zhu, Z. A hybrid method using experiment design and grey relational analysis for multiple criteria decision making problems. Knowl.-Based Syst. 2013, 53, 100–107. [Google Scholar] [CrossRef]
- Zheng, G.; Jing, Y.; Huang, H.; Gao, Y. Application of improved grey relational projection method to evaluate sustainable building envelope performance. Appl. Energy 2010, 87, 710–720. [Google Scholar] [CrossRef]
- Kuo, Y.; Yang, T.; Huang, G. The use of grey relational analysis in solving multiple attribute decision-making problems. Comput. Ind. Eng. 2008, 55, 80–93. [Google Scholar] [CrossRef]
- Schröter, J.; Graf, T.; Frank, D.; Bauer, C.; Kallo, J.; Willich, C. Influence of pressure losses on compressor performance in a pressurized fuel cell air supply system for airplane applications. Int. J. Hydrogen Energy 2021, 46, 21151–21159. [Google Scholar] [CrossRef]
- Yang, H.; Xu, Z.; Shi, Y.; Tang, W.; Liu, C.; Yunusa-Kaltungo, A.; Cui, H. Multi-objective optimization designs of phase change material-enhanced building using the integration of the stacking model and nsga-iii algorithm. J. Energy Storage 2023, 68, 107807. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, J.; Zhang, Q.; Peng, X. Performance prediction and evaluation of the scroll-type hydrogen pump for fcvs based on cfd–taguchi method. Int. J. Hydrogen Energy 2019, 44, 15333–15343. [Google Scholar] [CrossRef]
- Sabarish, K.V.; Parvati, T.S. An experimental investigation on l9 orthogonal array with various concrete materials. Mater. Today Proc. 2021, 37, 3045–3050. [Google Scholar] [CrossRef]
- Zhu, H.; Liao, Q.; Qu, B.; Hu, L.; Wang, H.; Gao, R.; Zhang, Y. Relationship between the main functional groups and complex permittivity in pre-oxidised lignite at terahertz frequencies based on grey correlation analysis. Energy 2023, 278, 127821. [Google Scholar] [CrossRef]


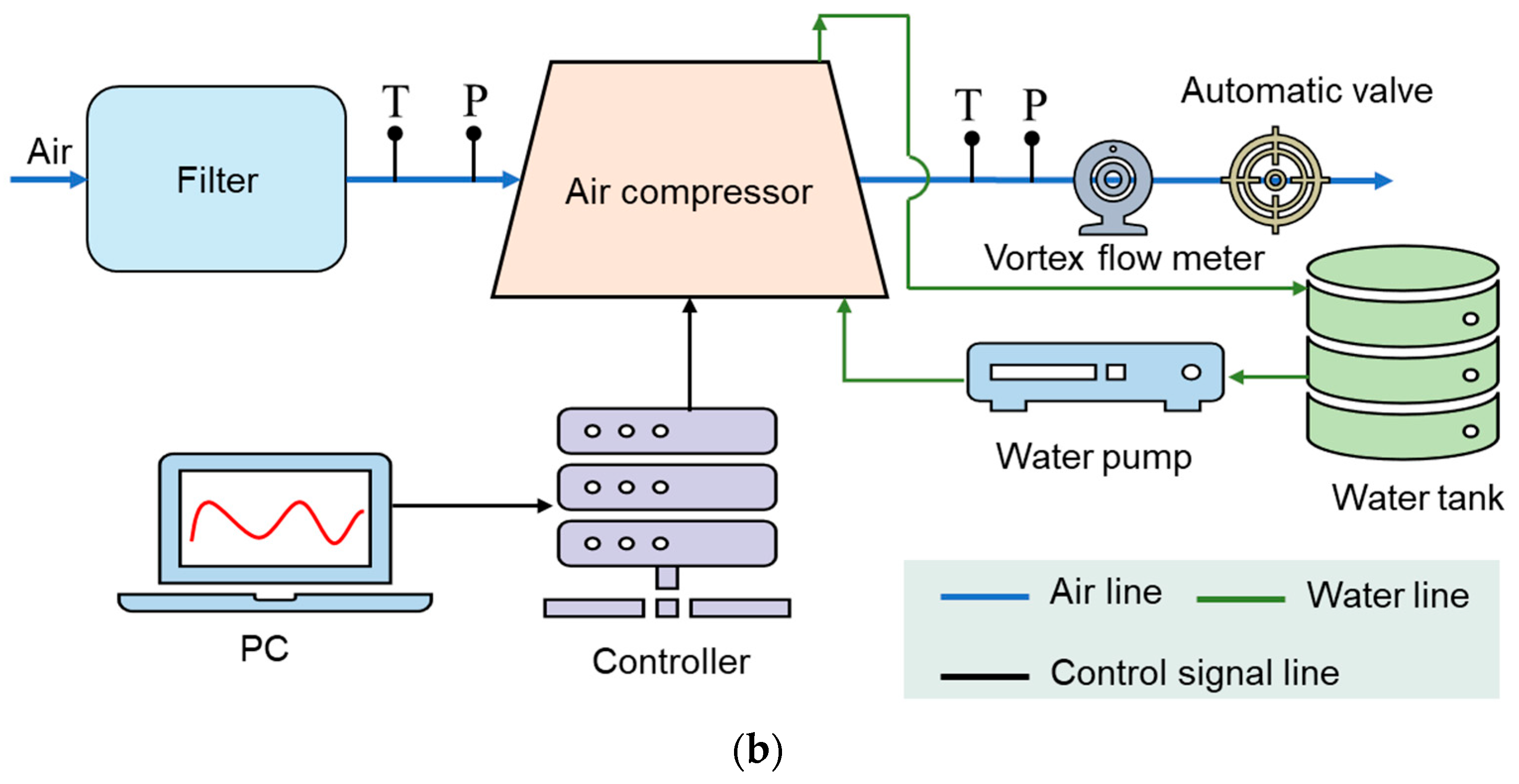



| No. | Equipment and Appliances | Limit | Precision |
|---|---|---|---|
| 1 | Filter | ≥0.003 µm | / |
| 2 | Centrifugal compressor | 20,000–90,000 rpm, 0.01–0.162 kg/s | / |
| 3 | Compressor controller | 180–445 VDC | ±200 rpm |
| 4 | DC power cabinet | 500 V | ±1% |
| 5 | Automatic valve | 0–1 | / |
| 6 | Temperature transducer | 300 °C | ±1 °C |
| 7 | Pressure transducer | 0.6 MPa | ±0.2% |
| 8 | Vortex flow meter | 30–500 m3/h | ±1% |
| Factors | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Rotational speed/rpm | 20,000 | 50,000 | 80,000 |
| Intake air temperature/°C | 18.3 | 18.8 | 19.3 |
| Pressure ratio | 1.0 | 1.4 | 1.8 |
| No. | Operational Parameters | ||
|---|---|---|---|
| Rotational Speed/rpm | Intake Air Temperature/°C | Pressure Ratio | |
| 1 | 20,000 | 18.3 | 1.0 |
| 2 | 20,000 | 18.8 | 1.4 |
| 3 | 20,000 | 19.3 | 1.8 |
| 4 | 50,000 | 18.3 | 1.4 |
| 5 | 50,000 | 18.8 | 1.8 |
| 6 | 50,000 | 19.3 | 1.0 |
| 7 | 80,000 | 18.3 | 1.8 |
| 8 | 80,000 | 18.8 | 1.0 |
| 9 | 80,000 | 19.3 | 1.4 |
| Weight | Optimization A | Optimization B | Optimization C |
|---|---|---|---|
| Total power consumption ↓ | 0.45 | 0.48 | 0.35 |
| Isentropic efficiency ↑ | 0.55 | 0 | 0.35 |
| Corrected mass flow rate ↑ | 0 | 0.52 | 0.30 |
| Optimal combination | No. 4 | No. 8 | No. 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, T.; Peng, X. Performance Assessment and Optimization of the Ultra-High Speed Air Compressor in Hydrogen Fuel Cell Vehicles. Appl. Sci. 2024, 14, 1232. https://doi.org/10.3390/app14031232
Shi T, Peng X. Performance Assessment and Optimization of the Ultra-High Speed Air Compressor in Hydrogen Fuel Cell Vehicles. Applied Sciences. 2024; 14(3):1232. https://doi.org/10.3390/app14031232
Chicago/Turabian StyleShi, Ting, and Xueyuan Peng. 2024. "Performance Assessment and Optimization of the Ultra-High Speed Air Compressor in Hydrogen Fuel Cell Vehicles" Applied Sciences 14, no. 3: 1232. https://doi.org/10.3390/app14031232
APA StyleShi, T., & Peng, X. (2024). Performance Assessment and Optimization of the Ultra-High Speed Air Compressor in Hydrogen Fuel Cell Vehicles. Applied Sciences, 14(3), 1232. https://doi.org/10.3390/app14031232






