Abstract
Large-scale low Earth orbit (LEO) remote satellite constellations have become a brand new, massive source of space data. Federated learning (FL) is considered a promising distributed machine learning technology that can communicate optimally using these data. However, when applying FL in satellite networks, it is necessary to consider the unique challenges brought by satellite networks, which include satellite communication, computational ability, and the interaction relationship between clients and servers. This study focuses on the siting of parameter servers (PSs), whether terrestrial or extraterrestrial, and explores the challenges of implementing a satellite federated learning (SFL) algorithm equipped with client selection (CS). We proposed an index called “client affinity” to measure the contribution of the client to the global model, and a CS algorithm was designed in this way. A series of experiments have indicated the advantage of our SFL paradigm—that satellites function as the PS—and the availability of our CS algorithm. Our method can halve the convergence time of both FedSat and FedSpace, and improve the precision of the models by up to 80%.
1. Introduction
As a resurgence in the space industry, the declining cost of producing and launching nanosatellites has stimulated exponential growth in low Earth orbit (LEO) constellations over the past two decades [1,2]. The volume of space-native raw data increases exponentially with constellation size, and due to the bandwidth constraints of the satellite–ground link, timely downloads of all the updated data are not achievable [3]. Therefore, as a distinctive distributed learning method, federated learning (FL) [4,5,6] holds immense potential for broad deployment in satellites. This system avoids transmitting training data between satellites, thereby preserving the data security of satellite data [7] and reducing costly traffic in satellite communication [8,9,10].
In traditional Earth observation missions, the ground users must wait for all satellites to send back data, typically requiring two to three days [11]. In contrast, FL can harness the local computational resources of satellites to decentralize the model training tasks among them, thereby eliminating the need for data transmission to ground stations (GSs) or other satellites [12].
FL has been widely used in terrestrial networks, where the Google team has developed a basic FL algorithm called FedAvg [13]. Chen et al. [14] applied this to the LEO constellation to verify the effectiveness of SFL. However, as a synchronous approach, FedAvg forces all satellites to complete local training and transmit their parameters to servers in a global training round, resulting in several days to converge a model. Therefore, Razmi et al. [15] applied an asynchronous approach and proposed FedSat, where servers no longer need to wait for parameters from all satellites before starting the next round of training. Although the asynchronous-based approach has some benefits, it can also lead to a new problem: model aging, because a few satellites fall too far behind the global rounds. Then, So et al. [16] proposed the FedSpace algorithm, which balances the idle connections of satellites and the obsolescence of local models. They calculated the variable satellite connectivity based on the satellite orbits and Earth’s rotation to determine the global model aggregate schedule. On this basis, Razmi et al. [17] proposed FedISL, which uses inter-satellite links to reduce the delay of FL. Furthermore, they considered whether satellites can complete local model training during the communication window and designed a scheduling algorithm, FedSatSchedule [18]. Due to the intermittent connectivity between satellites and GSs, stale gradients and unstable learning in SFL are challenges. Hence, Wu et al. [19] proposed FedGSM, a novel asynchronous FL algorithm that introduces a compensation mechanism to mitigate gradient staleness.
The introduction of FL to satellite networks has brought many new opportunities. For example, Al-Hawawreh et al. [20] proposed a new FL-assisted distributed intrusion detection system using a mesh satellite net to protect autonomous vehicles. Li et al. [21] developed a FL module for multi-satellite, multi-modality in-orbit data fusion, which compressed communication costs by a factor of 4 and significantly reduced the training time by 48.4 min (15.18%). Salim et al. [22] proposed a novel threat detection FL model for proactively identifying intrusions in satellite communication networks. This model utilizes decentralized on-device data while preserving data privacy.
However, the applications of FL in satellite networks still face many unique challenges. The mobility of satellites usually makes satellite communication unstable, which relies on the predictability of satellite visits to create a system design [23]. One limitation of LEO satellites is their brief visibility period with GSs. While their orbit period typically ranges from 90 to 120 min, they are only in direct contact with a GS for 5 to 20 min per orbit [19]. Moreover, failures from the network, hardware, software, etc., make SFL face more challenges than terrestrial FL [12].
It is necessary for FL to make a client selection (CS), and this problem in terrestrial networks has been fully studied [24]. However, to the best of our knowledge, this was lacking in satellite networks. This problem needs to consider the orbital characteristics of the client satellites, data value, computing capabilities, etc., to improve the performance of the model in satellite federated learning (SFL).
In this paper, we firstly investigate the characteristics of satellites links, and discuss the positioning of a parameter server (PS) in two distinct scenarios: deployment at a GS and deployment on an LEO satellite. Secondly, we consider these specific attributes of satellites in the context of SFL, and propose an index called “client affinity” for client satellites to gauge their contribution to the global model. Finally, we validated the efficacy of our methods by conducting experiments based on two benchmark methods—FedSat [15] and FedSpace [16].
The contributions of this paper can be summarized as follows:
- We demonstrate a SFL paradigm where LEO satellites act as PSs, and conduct simulations based on a constellation of 120 low-orbit satellites.
- We demonstrate in detail the communication and mobility models of SFL, and model the CS problem in SFL as a 0–1 knapsack problem.
- We establish a model quality evaluation function for client satellites, and use affinity to describe the contribution of the client to global training. Then, we combine client access and communication to establish a CS mechanism.
- Simulation results are presented which verify that the proposed method can effectively improve the convergence speed and accuracy of the model in SFL.
2. Motivation
In this section, we demonstrate how SFL performance can be improved when the LEO satellite plays the role of the PS. One of the benefits of LEO satellites is their short orbital period. For example, the period of a satellite in a circular orbit with an altitude of 500 km is approximately one hour. However, the restricted communication range between the GSs and satellites inherently limits the access time. The communication window between an LEO satellite and a GS is typically only a few minutes long.
We simulated a LEO satellite constellation with a total of 120 satellites. We separately counted the number and duration of accesses for the two cases: an LEO satellite as the PS and a GS as the PS. We constructed Walker delta constellations at three different orbital heights of 400 km, 500 km, and 600 km, whose inclinations are 40°, 45°, and 50°, respectively. At each height, five orbits were placed, each with eight satellites.
In the satellite-to-ground scenario (a GS as the PS), we placed a GS at a location in Shanghai, China, and counted the number and duration of all 120 satellites’ visits to the GS within 24 h. In the satellite-to-satellite scenario (an LEO satellite as the PS), we monitored visit numbers and durations from other satellites to the PS.
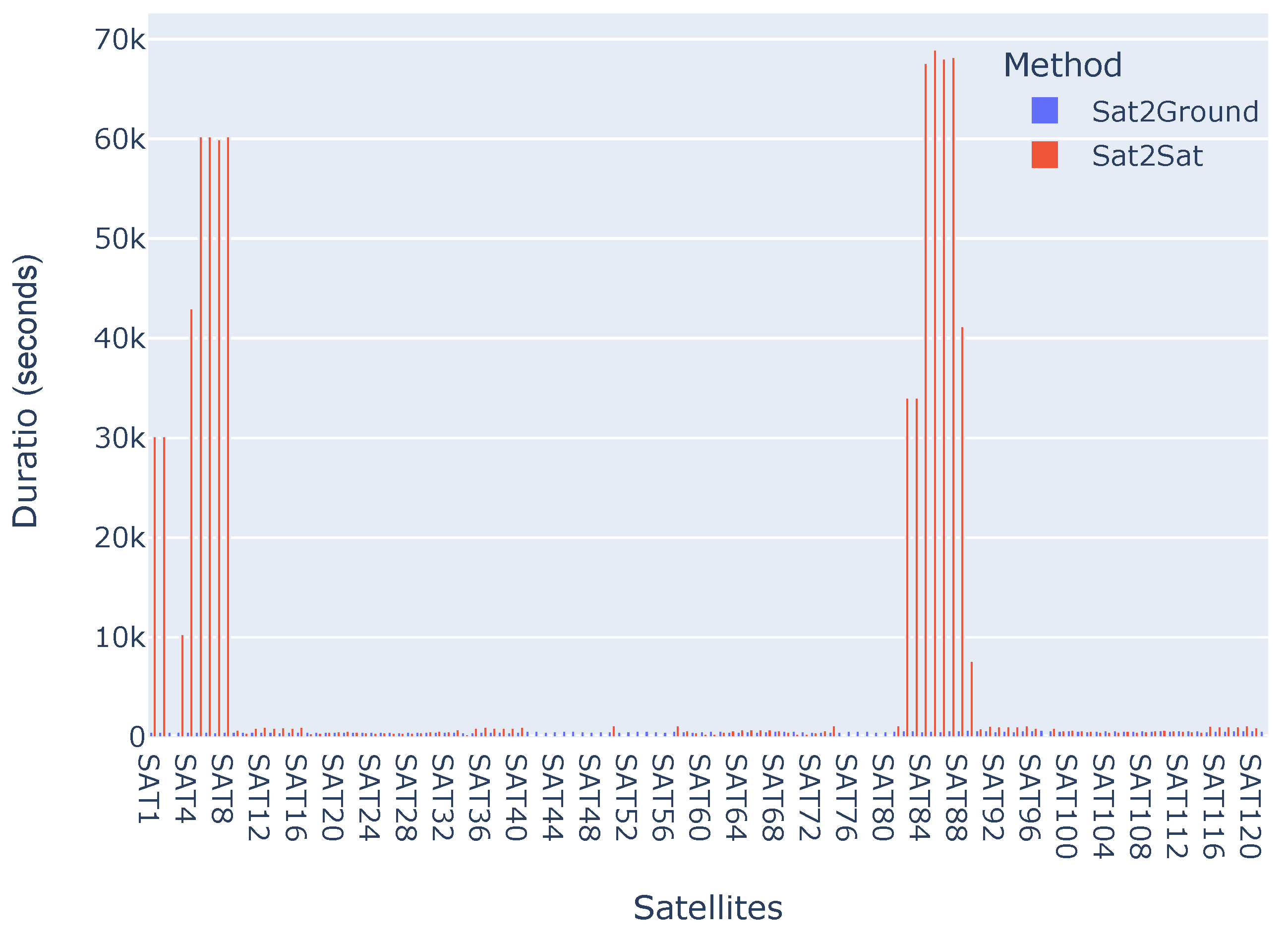
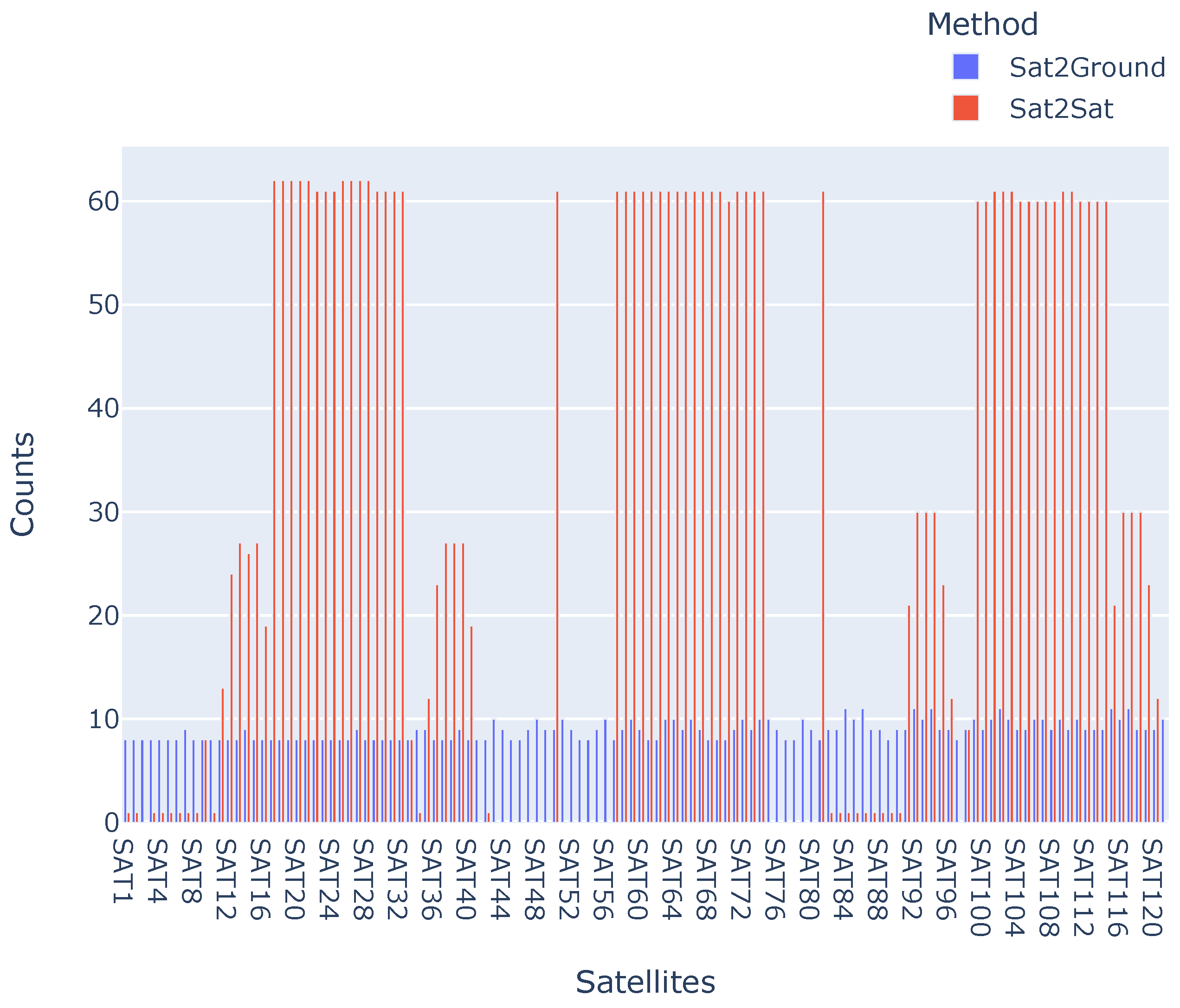
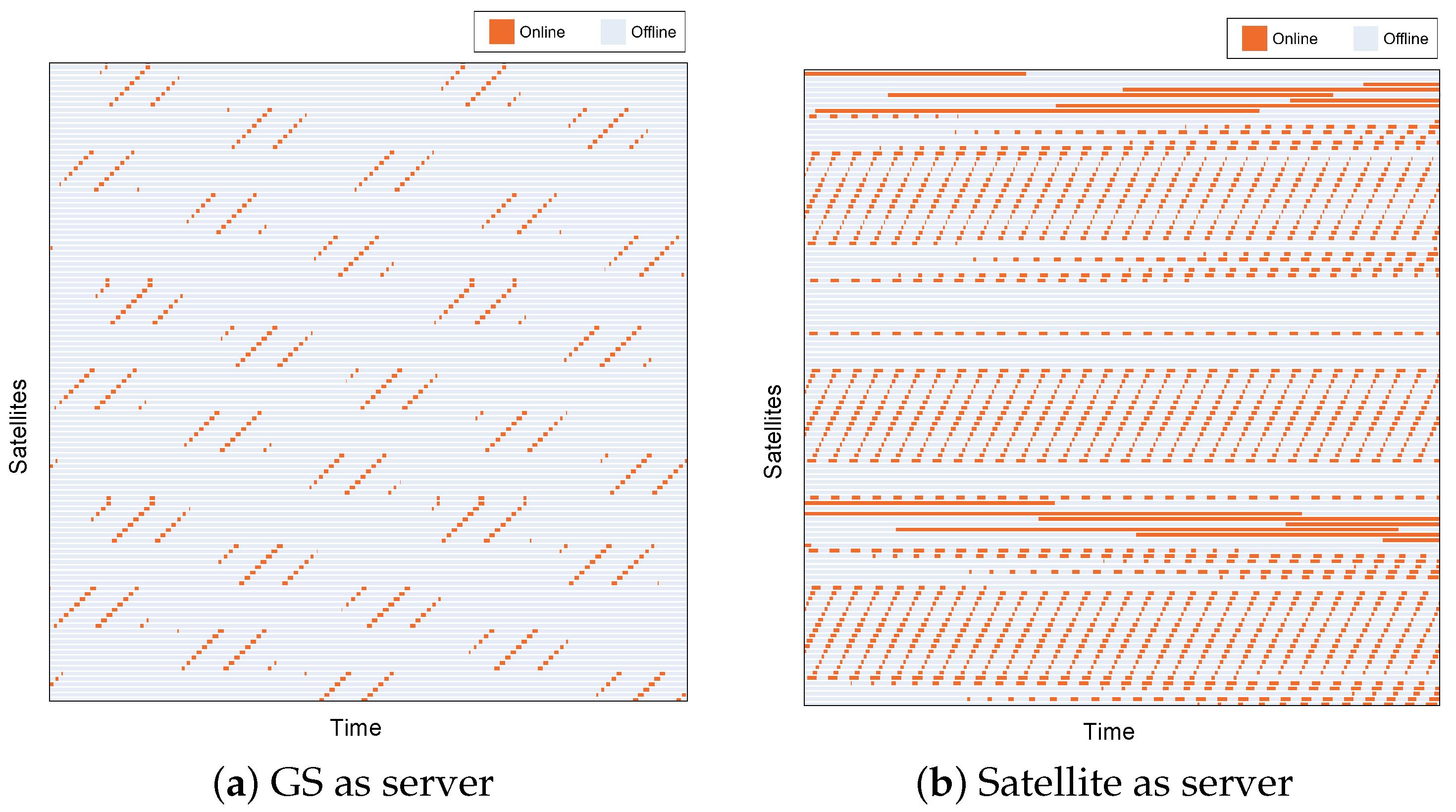
As Figure 1 shows, although the PS satellite cannot access all other satellites, some of them can establish a very long communication window with the PS, which is difficult for GSs to achieve. The statistical results show that the average access duration when the satellite is the PS is 6571.9 s, while it is only 555.3 s for the GS. Similarly, Figure 2 shows the number of times the satellite accesses when the GS and the satellite, respectively, are the PSs. When a GS is the PS, each satellite has a relatively equal chance of access, but the access frequency is much lower than when the satellite is the PS. Specifically, when the PS is a satellite, the average number of accesses is 30, while for the GS it is only 8. Furthermore, Figure 3 illustrates the numbers, durations, and temporal relationships of accesses between the clients and the PS. When a GS is the PS, the access in different satellites has no significant differences. However, when a satellite is the PS, some satellites can establish a stable and continuous connection, while others can access the server intermittently, and still others cannot access the server during the simulation period.
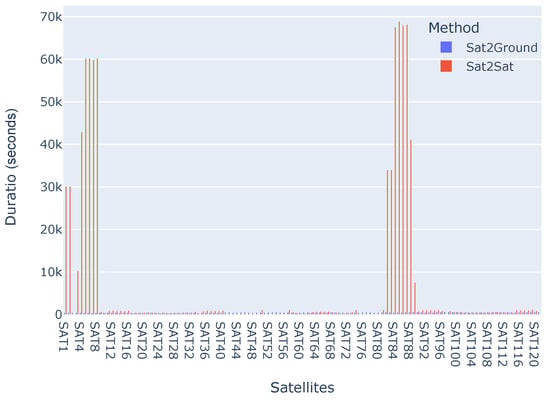
Figure 1.
Comparison of the duration of satellites-to-ground and satellites-to-satellites visits.
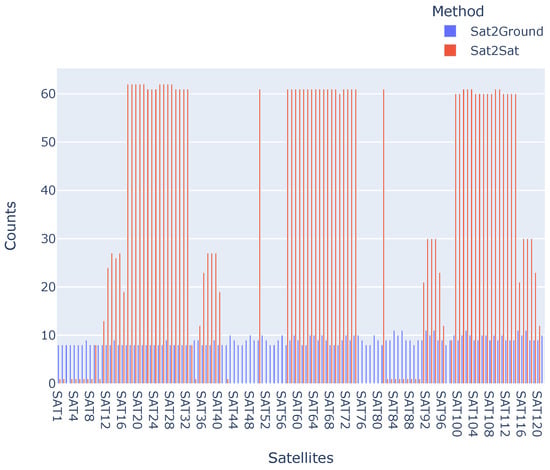
Figure 2.
Comparison of the number of satellites-to-ground and satellites-to-satellites visits.
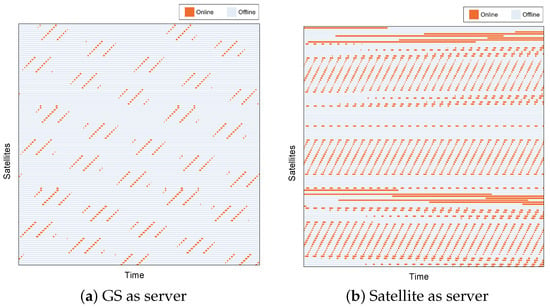
Figure 3.
The access comparison between the satellite and GS acts as the PS. The horizontal axis represents the simulation time, and each horizontal line on the vertical axis represents the status of the connection between the client satellites and the PS.
In summary, in FL, we hope that clients have longer connection windows and more frequent access to the PS, but the accessibility performance in the satellite–ground scenario is far less than in the satellite–satellite scenario. Moreover, the revisit time of some satellites is too long in both the satellite–ground and satellite–satellite scenarios, which produces performance loss in both synchronous SFL and asynchronous SFL. Therefore, it is necessary to filtrate clients to improve the overall training performance.
3. System Model
This section begins with the model assumptions and, secondly, the communication model is introduced. Then, an overview of the general framework of FL algorithms is given. Finally, we introduce the CS in SFL.
3.1. Model Assumption
Our study focuses on comparing the SFL performance between a GS as the PS and an LEO satellite as the PS, verifying the effectiveness of CS for SFL. We ignore some conditions and constraints, differing from real physical systems. Therefore, we list our assumptions in our model as follows:
- (1)
- All satellites are run in the standard circular orbits and ignore perturbation.
- (2)
- We exclude the potential effects of the harsh space environment on satellites, such as satellite failures caused by cosmic rays. We assume that the satellite’s communication and computing will not be adversely affected.
- (3)
- Inter-satellite links and ground–satellite links share the same communication channel model, which ignores most of the complex effects such as atmospheric absorption, antenna misalignment, and Doppler shift.
- (4)
- The queuing delay in communication is ignored.
- (5)
- The computation ability is constant for a satellite; it is not affected by radiation, overheat, low power, etc.
- (6)
- All satellites’ hardware remain healthy, and always have enough energy to complete communication and computation tasks.
- (7)
- The time the PS takes to make decisions is ignored.
- (8)
- When the link is established, the communication parameters remain stable.
- (9)
- The PS knows all the clients’ orbit information, and can forecast their position during the whole simulation.
3.2. Coverage and Access Time Model
3.2.1. Satellites to GS
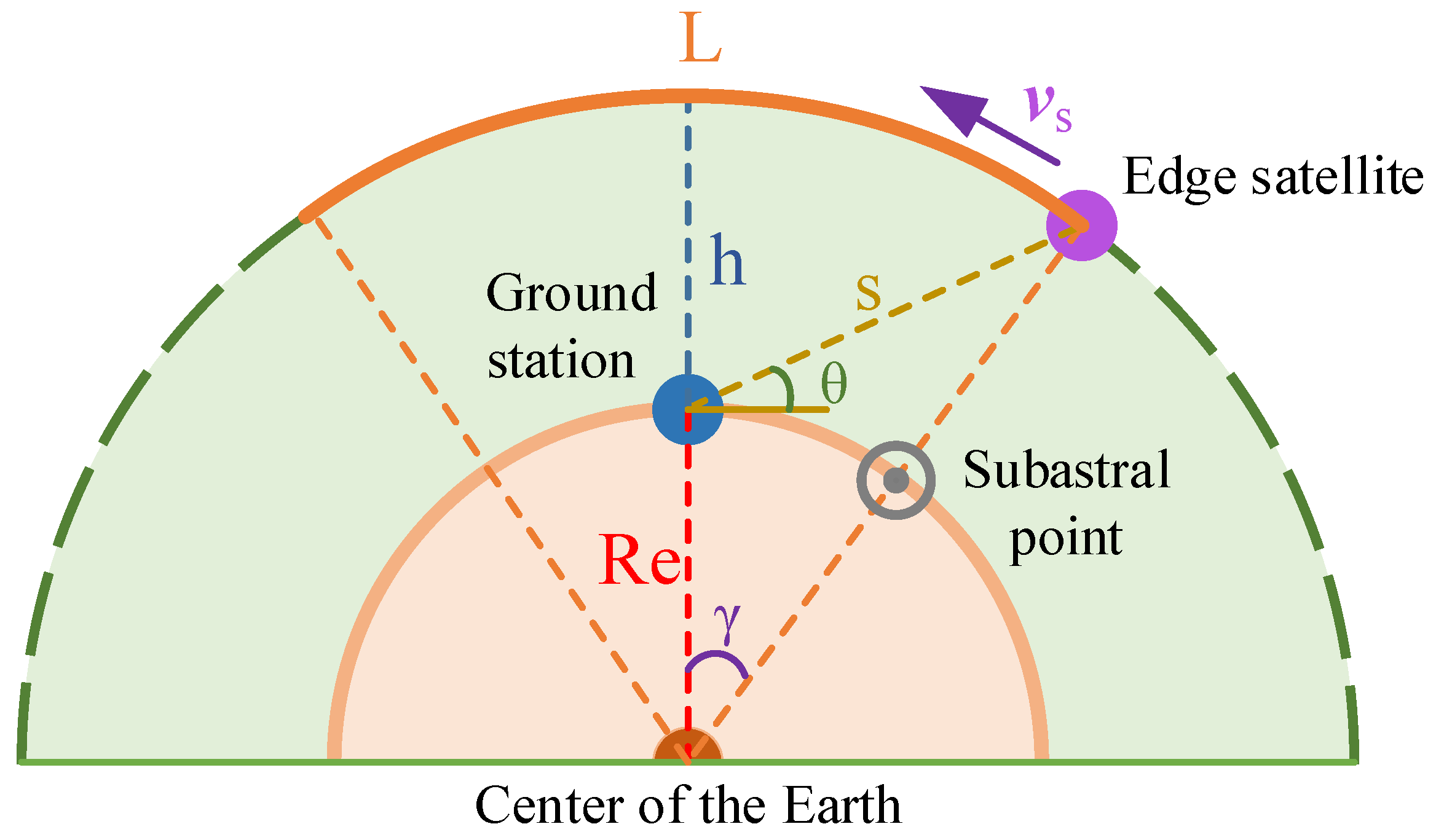
Figure 4 explains the space geometric relationship between LEO satellites and the GS [25], where L is the arc length that the GS can communicate with a satellite, and is the satellite’s speed (uniform on the circle orbit). Then, we have the visibility time T between the GS and a satellite:
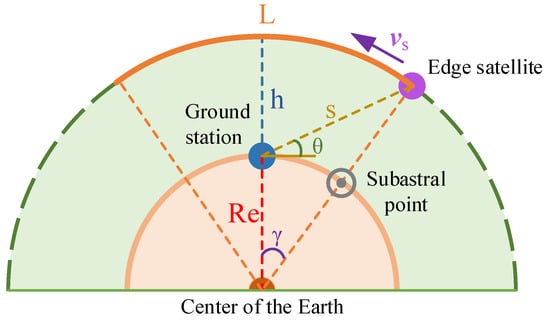
Figure 4.
Space geometric relationship between the LEO satellite and the GS [25].
In addition, and L can be calculated as follows:
where = 3.986013 km3/s2 is the Kepler constant, km is the earth’s radius, and h is the distance between the orbit plane and the Earth’s surface.
3.2.2. Satellites to Satellites
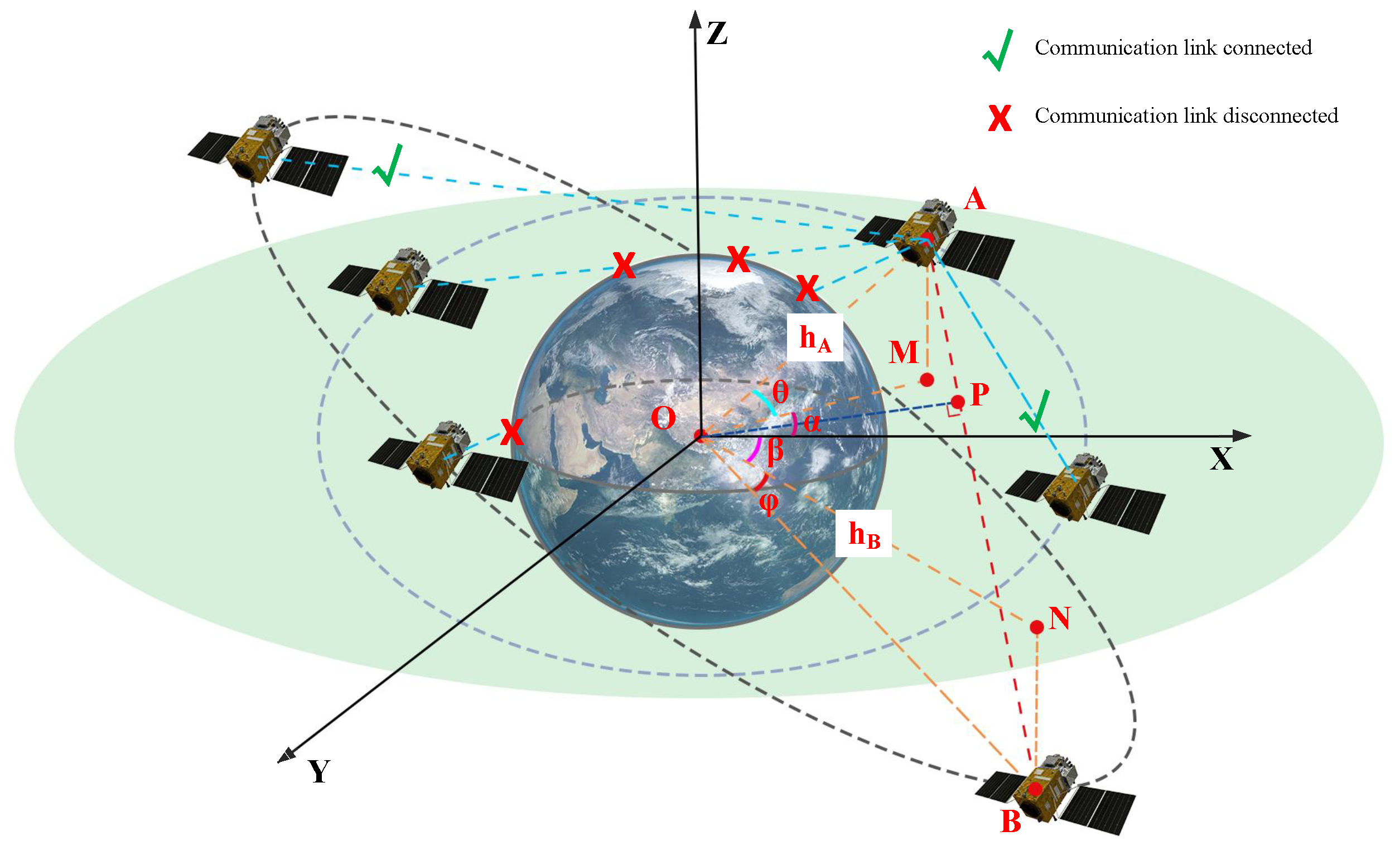
As Figure 5 shows, we assume that two satellites can communicate with each other only if the line connecting them is not obstructed by the Earth. Then, we demonstrate how to calculate the visibility between satellites. A space Cartesian coordinate system is established with the Earth’s center as the origin, the line connecting the South and North poles as the Z-axis, and the X-axis pointing to the 0° longitude line. We assume that the orbit inclination of satellite A is and B is , and that the orbit heights are and , respectively. At a certain moment, the projection points of satellites A and B on the plane where the Earth’s equator is located are M and N, respectively. Then, we set and to express and . It is worth noting that and are constant because they are orbit inclinations, while the and are parameters that change uniformly over time. Hence, we can obtain the coordinates of these two satellites:
and the minimum distance between origin point O and line can be expressed by , which is perpendicular from point O to line and can be calculated as follows:
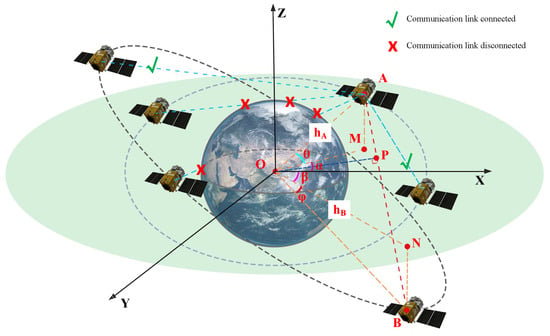
Figure 5.
Space geometric relationship between the LEO satellites in circle orbit.
Finally, we can determine whether the link is obstructed by the earth based on the comparison of and :
3.3. Communication Model
In the simulation, we only consider a set of clients with only one server (a GS or an LEO satellite). In our model, the satellites use wide beams in the Ka band (receiver between 20.1–21.2 GHz and transmitter between 29.9–31 GHz [26]) for inter-satellite communication. Mutual interference exists because the PS receives multiple clients at the same time. Considering large-scale fading and shadowed-Rician fading [27], we denote the channel power gain from client i to the server as . Hence, the transmission rate for parameter aggregation can be calculated as follows:
where B is the available spectrum bandwidth, is the transmit power of client i, and is the additive white Gaussian noise (AWGN) power.
Factually, the satellite communication model is more complex and there are differences between satellite-to-GS and satellite-to-satellite. However, in this simulation, we ignore many of the communication details such as atmospheric absorption loss and antenna pointing loss [28]. We only give a rough model, since the amount of data we are transmitting is not large and communication has a relatively minor impact on overall performance.
4. Algorithm
In this section, we explain the algorithm flow of SFL and introduce the method of CS.
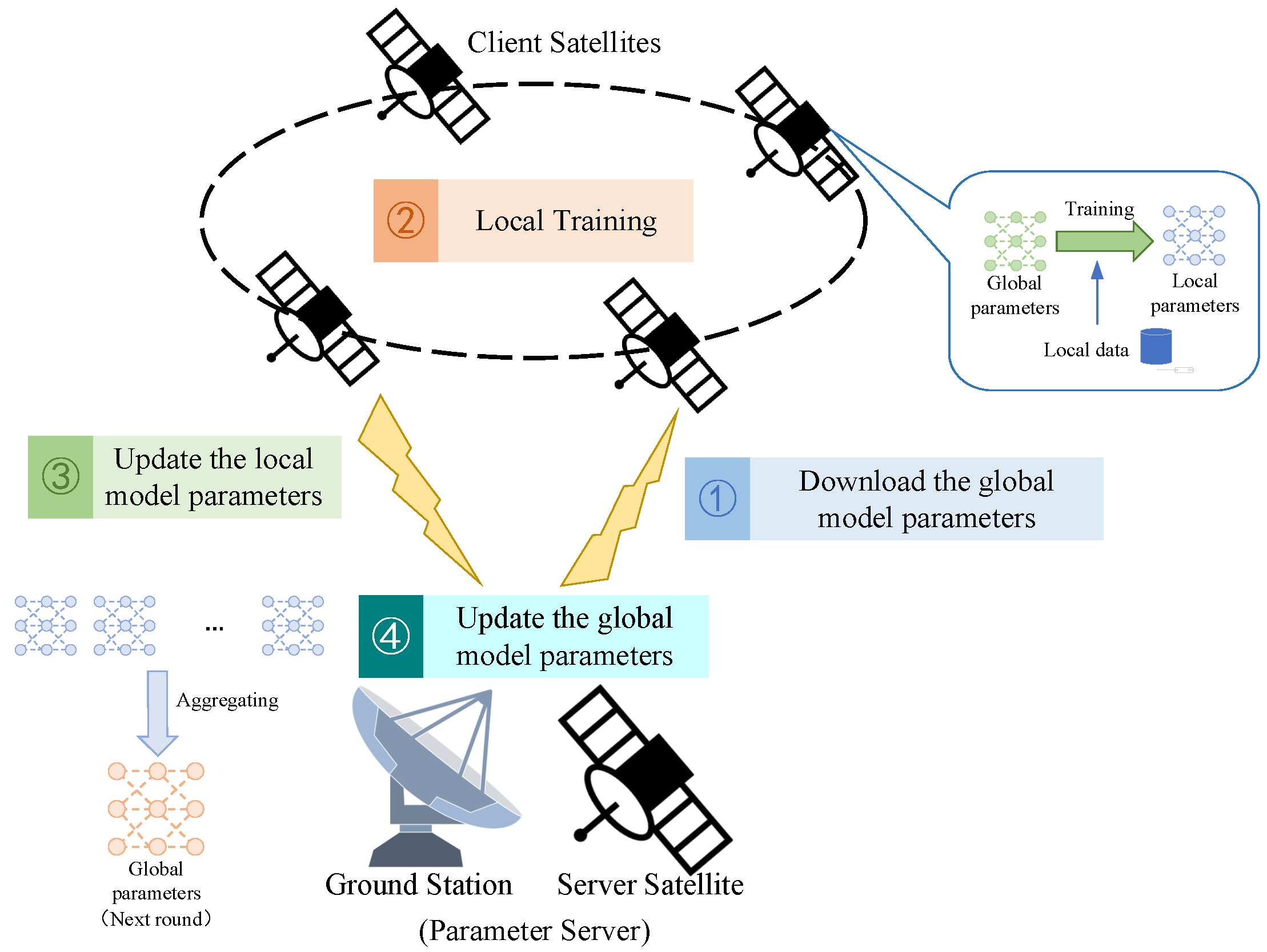
4.1. Federated Learning
As Figure 6 shows, we consider a PS with N satellite clients. A typical implementation of federate learning is FedAvg [13]; the PS will randomly choose K clients from to participate in training, which is denoted as set . The parameters of the global model are aggregated by these clients. Every client has a local dataset , where is the sample data and is the label data, and the size of is . For a client that can participate in the learning, the loss function can be denoted as , where is the model parameter.
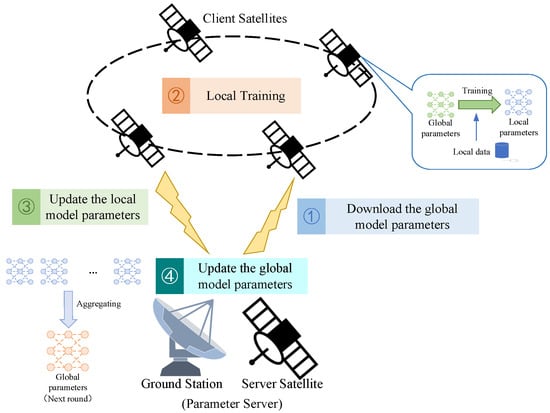
Figure 6.
Architecture of SFL.
The goal of FL is finding the that can minimize the global average loss, and the optimization function is given by
where the D is the data size of the total dataset. For client k, it updates the model parameters by stochastic gradient descent:
where is the learning rate.
The PS aggregates the parameters and updates the global model from clients by
The pseudo-code of FedAvg is given in Algorithm 1.
| Algorithm 1 FedAvg [13]. The chosen K clients are indexed by k; B is the local minibatch size and E is the number of local epochs |
Server Process
|
4.2. Client Selection
We design a CS algorithm for SFL. We evaluate a client from the delay (which includes the communication delay and computational time cost), orbit characteristics, and data quality. These data can be provided directly in the form of hyper-parameters or calculated through a program. For example, the communication and computational ability is represented by channel rate and CPU frequency, respectively. They can be assigned reasonable values directly in the simulation. In this paper, we gave each client a random value range from 1 Gbytes/s to 10 Gbytes/s. The orbit characteristics include the satellites’ position, direction, and velocity, all of which can be computed easily by STK. Data quality is a unique designed index in this study, and it is also a variate that is evaluated and updated in every round of training.
4.2.1. Delay
We set as the computation capability of satellite k [29]. If the client is selected, it will obtain the global model parameter from the PS. We denote W as the data size of the parameter that client k downloads from the PS, and as the size of the updated parameter uploaded to the PS. After finishing the local computing, the new local model parameter is sent to the server. The time cost of this process consists of the propagation delay, the transmission delay, and the computing delay, which can be calculated by
where is the distance from the client to the server, and m/s is the speed of light; is the required CPU cycles of one round of local training.
If the PS is the GS, can be calculated by
or if the PS is the satellite, is , which can be calculated by Equations (4) and (5).
Hence, the time cost of a round training process in FL, that consists of a K client and one server, can be expressed as:
where is the computation ability of the PS, and is the number of CPU cycles required for the average size of each parameter datum to aggregate.
4.2.2. Orbit Characteristic
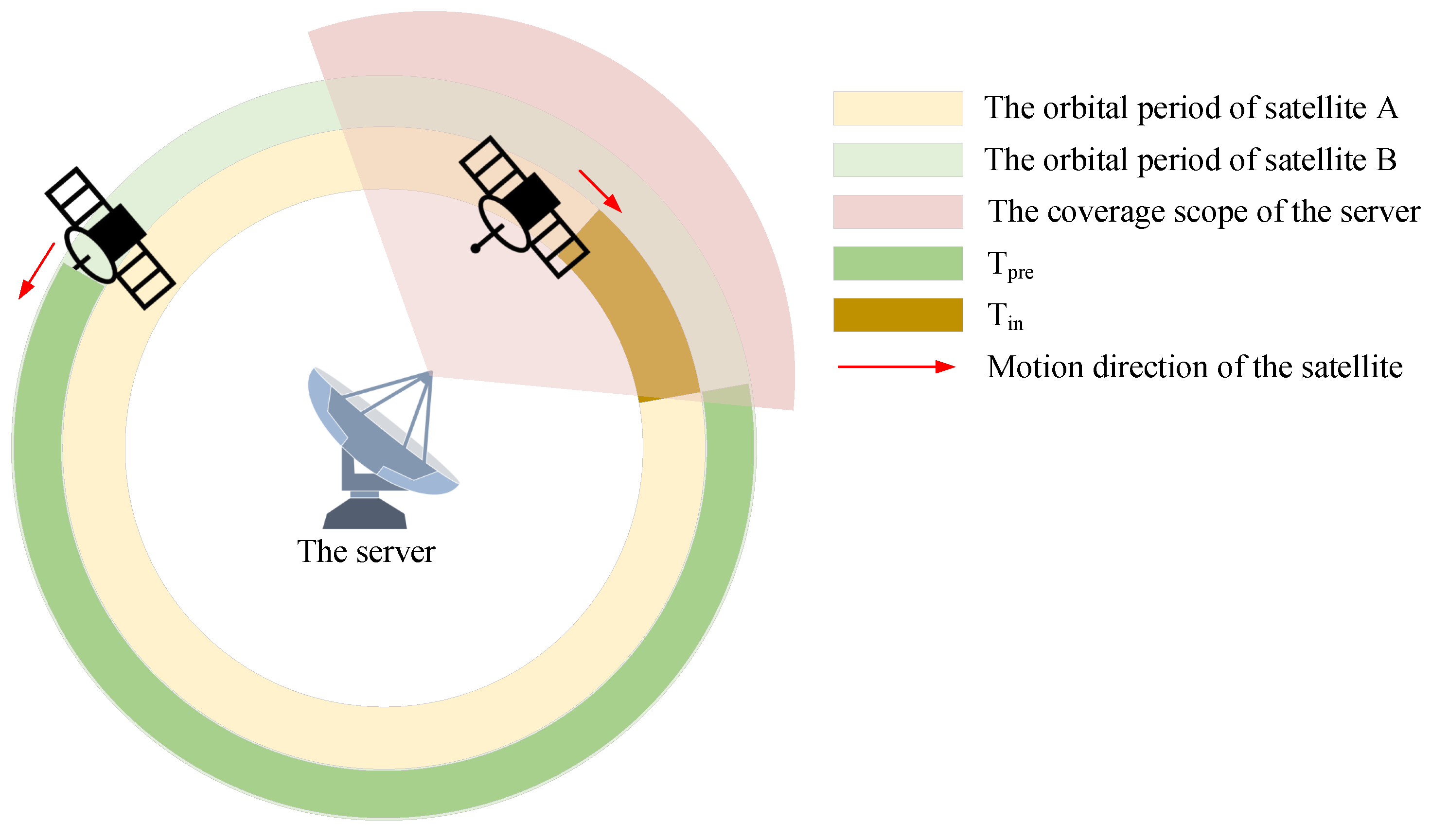
Unlike FL on the ground, one of the challenges of SFL is the orbital characteristics of satellites. In CS methods that do not consider orbital characteristics, it is highly likely that client satellites will disconnect from the server after completing local training, resulting in client resource waste. In extreme cases, the PS may not have immediate access to any available client satellites for some time, thereby being unable to distribute the global model immediately. In such cases, it is necessary to consider the orbital characteristics in CS.
According to Section 3.2, we can calculate the duration of satellite access. Actually, we can assign the task of orbit simulation to the Systems Tool Kit (STK) (https://www.ansys.com/products/missions/ansys-stk, accessed on 1 December 2023), a professional satellite-to-simulation tool. We can easily obtain the status of any satellite by this simulator. As shown in Figure 7, a satellite could be in two statuses; one is that it has time left to connect to the PS, and the other is that it has been connected, but has time left to disconnect. In addition, once the client connects to the PS, will refresh as the remaining time until the next server access.
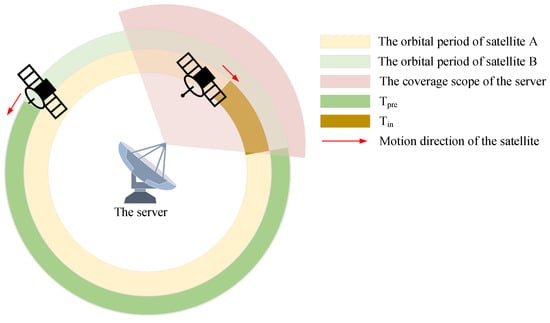
Figure 7.
Two statuses between the client satellite and the server.
We represent the maximum duration for a satellite to access the server at once as , and denote as the time that the PS will wait for the client. Then, we have according to Algorithm 2, where expresses that the client is unusable.
| Algorithm 2 Calculate |
|
4.2.3. Data Quality
Ensuring data quality poses challenges in FL because of the diverse range of client devices. Randomly selecting clients as a strategy could result in global model deterioration as a result of the inclusion of poor data samples, leading to sluggish convergence or even failure to converge.
We propose a method for measuring the degree of anomaly in local models and determine the affinity of clients to assess the quality of data maintained by them. In doing so, we consider the impact of local data when designing the CS mechanism.
This method determines whether the client’s data have deteriorated the global model by comparing the distance from the updated local model to the global model, and other clients’ models. We define the abnormality of the model as for client k in global round t:
where is the proportionality factor, a hyper-parameter that can adjusted according to need.
We evaluate the quality of the client’s data according to its historical performance, and determine the client affinity to indicate the impact of the client’s data on the global model during the training process. For a selected client k, its can be calculated as follows:
4.2.4. Optimization Model
We have proposed the optimization object of CS towards SFL:
We cannot exclude the possibility of having no eligible clients at one moment. Therefore, in the constraints, we allow K equal to 0, which means the server will keep waiting until a suitable client becomes available. In addition, we set a threshold for the total waiting time, which is a hyper-parameter that will be manually adjusted based on the experimental results.
The above problem can be regarded as a 0-1 knapsack combinatorial optimization problem, where the capacity of the knapsack is , the weight of the item i is denoted by , and its value is denoted by . Then, we can solve the optimal CS problem by using Algorithm 3:
| Algorithm 3 CS algorithm based on 0-1 knapsack problem |
|
5. Simulation
We simulated an LEO constellation with 120 satellites by STK, and imported the information on links between clients and PS as a JSON file. Hence, our program checked the connections between clients and the PS every time slot (0.1 s) based the JSON file, so we can know which clients were connected to the PS at any time. Then, we compared the SFL between satellite-to-ground and inter-satellite communication, and validated effectiveness of our CS algorithm.
5.1. LEO Constellation
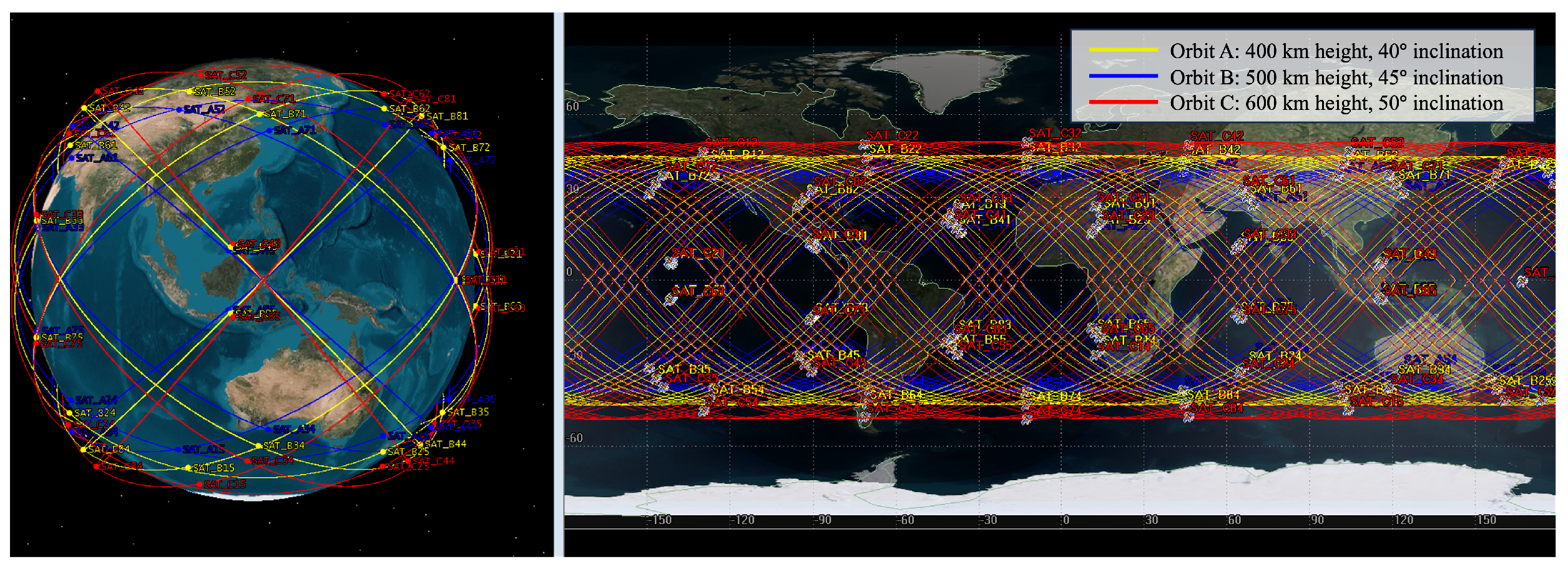
We consider an LEO Walker constellation consisting of 120 satellites, distributed at 400 km, 500 km, and 600 km, respectively. Five orbital planes are evenly deployed at each altitude, with each orbital plane having eight satellites. The details of constellation simulation parameters are listed in Table 1, and the results of the Walker configuration constellation simulated using the STK based on these parameters are shown in Figure 8.

Table 1.
The constellation simulation parameters.
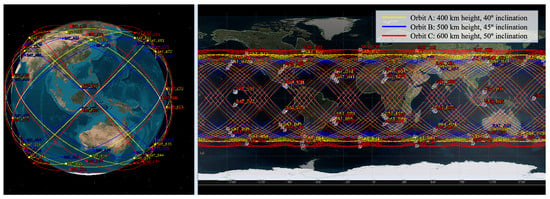
Figure 8.
The simulated constellation with 120 satellites.
In the simulation, we established a GS in Shanghai, situated at latitude 31.25° and longitude 121.48°, to serve as the ground PS. Additionally, we selected a satellite orbiting at an altitude of 500 km to serve as the space PS.
5.2. Experimental Environment, Datasets, and Hyper-Parameters
The construction and simulation of constellations in this study were carried out using STK 12.2 and Python 3.9, and client access times (start and end) were obtained via the generation of files in JSON format. We built the SFL using Python 3.9, Pytorch 2.0 with CUDA 11.7. The experiment was executed on a personal computer equipped with Windows 11-64 bit system (Microsoft, Washington, DC, USA), and 64 GB of memory, a 36-thread Intel-i9-10980XE CPU (Intel, Shanghai, China), and an NVIDIA RTX 3090 graphics card (ASUS, Taipei, China) with 24 GB of memory.
The ResNet-50 [30] model was applied as the backbone network in this experiment, which consists of five stages each with a convolution and identity block. Each convolution block has three convolution layers and each identity block also has three convolution layers. The ResNet-50 has over 23 million trainable parameters, which is challenging to train but is capable of providing highly accurate results.
The Fashion-MINIST [31] and CIFAR-100 [32] datasets were applied during the experimental phase. Fashion-MINIST is a dataset comprising 28 × 28 grayscale images of 70,000 fashion products from 10 categories, with 7000 images per category, whose training set has 60,000 images and the test set has 10,000 images. CIFAR-100 has 100 classes containing 600 images each and there are 500 training images and 100 testing images per class, which include animals, foods, vehicles, flowers, etc.
In the experiment, the training set was randomly distributed across the clients after being shuffled, and an overlap coefficient was set to allow for the possibility of identical data among different clients. The test set was deployed on the server side for evaluating the aggregated model. The term signifies that all clients possessed identical datasets, whereas implies that no client datasets overlapped. In one of our experiments, the was set at 0.2, indicating that each client contained 20% of the data common to one or more other clients.
We have established 5 epochs for local training and a total of 200 epochs for global training. When clients have finished the five epochs of local learning, they immediately send their results to the PS. For model evaluation, the ratio coefficient was set to 0.2. In a single-round of training, the maximum number of client systems that can be selected is capped at 40. On the client side, there were three rounds of localized training, with the learning rate being fixed at and the batch size configured to 32.
5.3. Experiment Results
We measured the accuracy and convergence speed in different scenarios, that is, we compared the impact of server deployment on the GS or the satellite, and FedSat [15] and FedSpace [16] were applied as two benchmark methods. We compared the impact of CS mechanisms on these SFL methods.
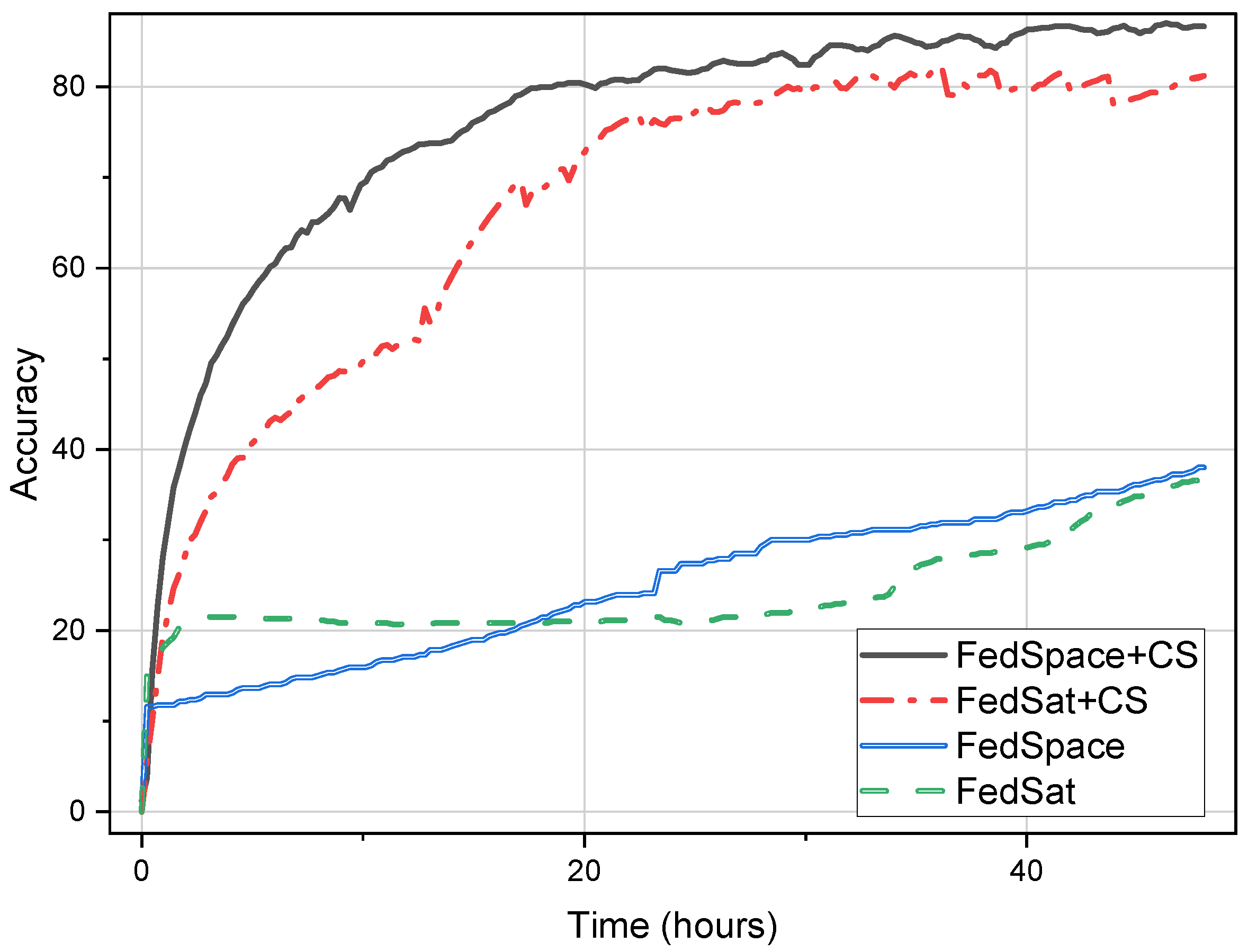
Firstly, we considered the impact of the CS mechanism on both methods when the PS is located is the GS. As shown in Figure 9, in 200 rounds of iterations, the algorithms equipped with a CS mechanism not only exhibited a faster convergence speed but also significantly improved the accuracy of the model. Amid the stringent visitation conditions, both FedSpace and FedSat, devoid of CS, faced arduous endeavors in reaching model convergence within a span of 48 h. Consequently, the final precision obtained stood at 38.4% and 37.5% for each, respectively. Fortunately, the CS mitigated this situation and significantly improved the convergence speed and accuracy rate; both methods achieved more than 80% model accuracy within 48 h.
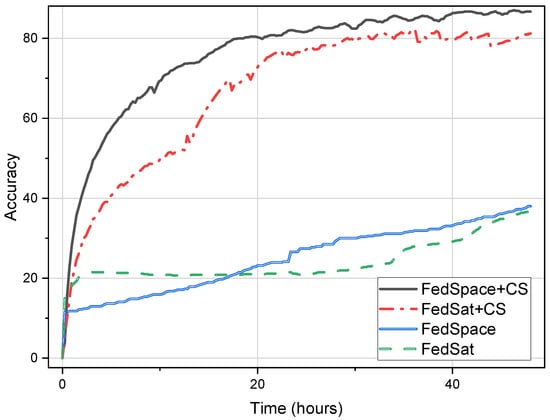
Figure 9.
The result of experiment in satellite–GS scenario with Fashion-MINIST.
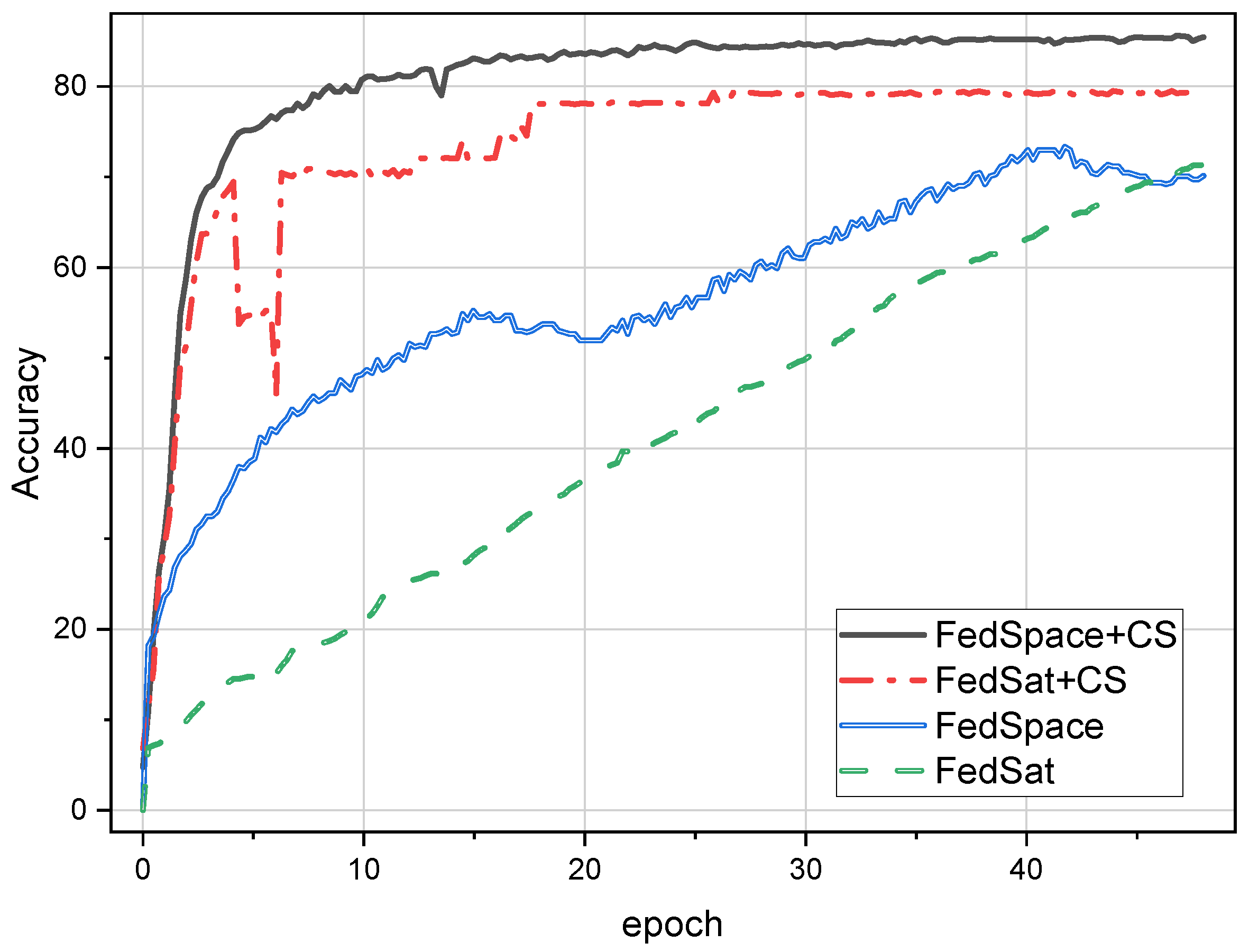
What we wanted to illustrate next is that, in SFL, deploying the PS on the satellite is a better choice. We used the same training parameters and configurations as on the GS, but changed the location of the PS to a satellite at a height of 500 km. As shown in Figure 10, the benchmark method significantly improved the convergence speed and accuracy rate. This reveals the potential of inter-satellite FL. Compared to the traditional methods, we achieved more than a 30% improvement in accuracy. Moreover, using CS can shorten the model convergence time to less than 16 h, with FedSpace achieving an accuracy of 85.5% and FedSat achieving an accuracy of 79.8%. A detailed comparison of the results is shown in Table 2.
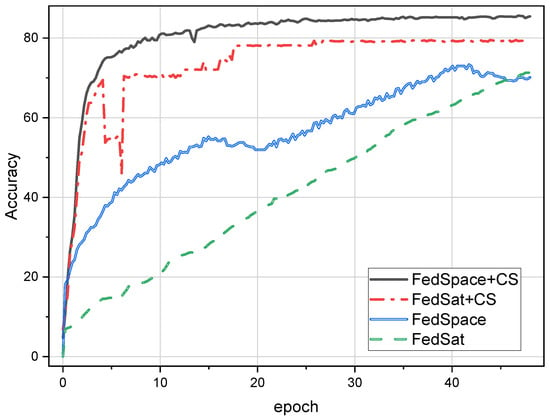
Figure 10.
The result of experiment in inter-satellites scenario with Fashion-MINIST.

Table 2.
Comparison of experimental results (Fashion-MINIST).
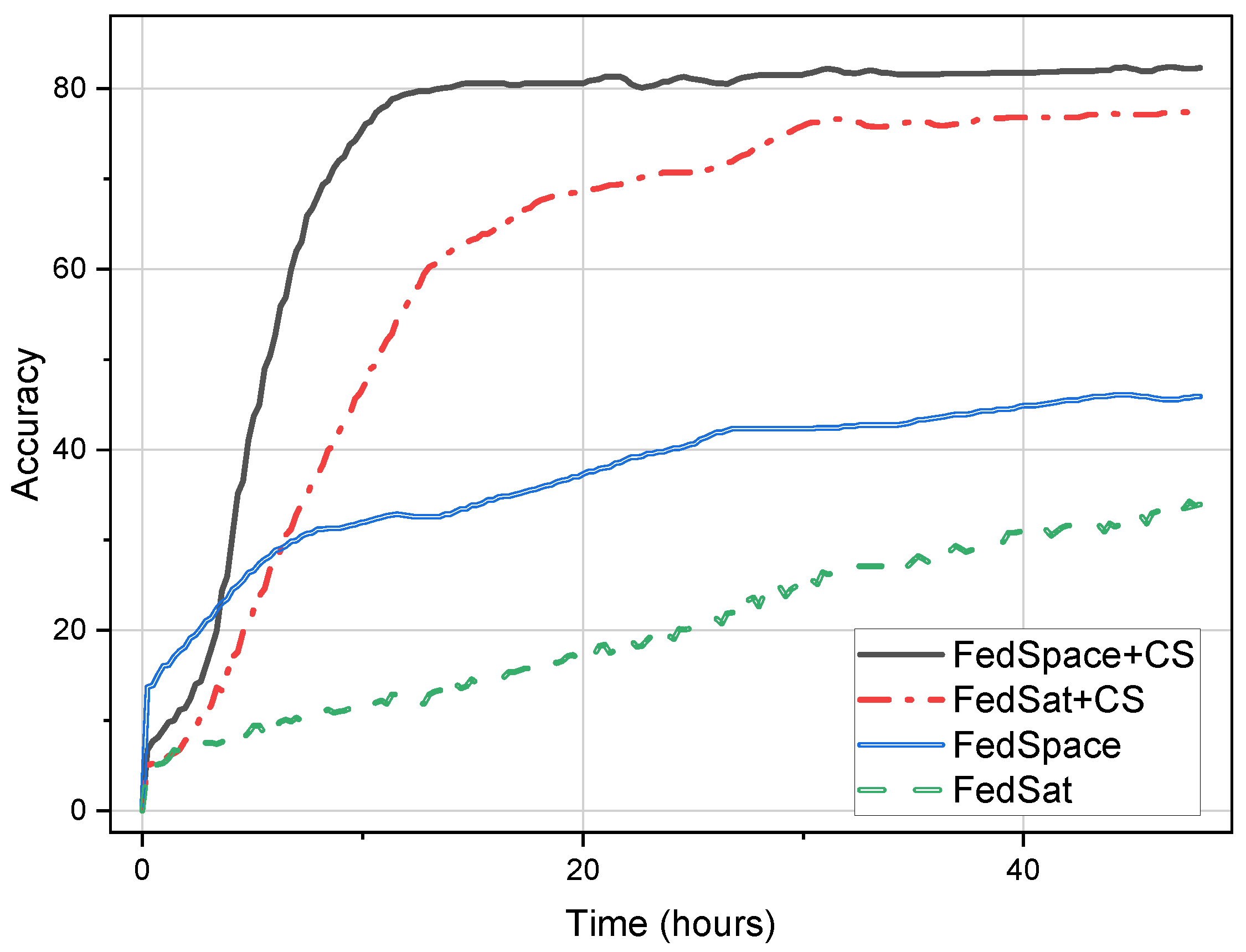
We attempted to further validate the effectiveness of the algorithm on the CIFAR-100 dataset. As shown in Figure 11, although the increase in dataset variety indeed presents challenges for satellite federal learning, our method was still able to achieve convergence within 24 h and attain accuracies of 82.3% and 77.4%.
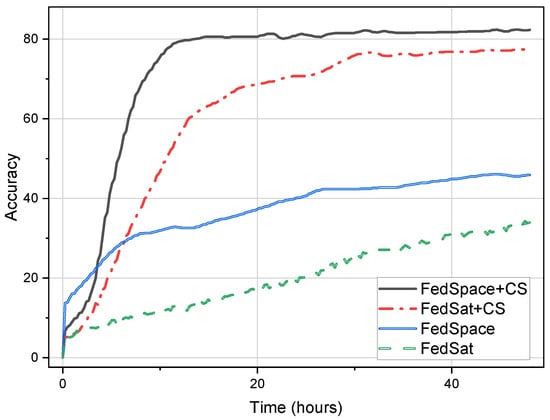
Figure 11.
The result of experiment in inter-satellites scenario with CIFAR-100.
6. Conclusions
Federated learning (FL) is a communication-efficient machine learning framework that is well-suited for satellite applications, where communication capabilities are often limited. Additionally, satellite data transmission via wireless broadcasting inherently poses privacy and security risks. FL, however, has strong privacy protection capabilities, which can help to ensure the privacy of remote sensing data. This study investigates the positioning of parameter servers (PSs) and the problem of client selection (CS) within the context of satellite federated learning (SFL). We examined and contrasted the access times and duration from client satellites to both the ground station (GS) and the server satellite. It has been observed that a satellite, when functioning as a PS, possesses a better ability to receive client parameters within its field of view compared to a GS. Both the communication and mobility models for SFL were demonstrated. The CS is modeled as a 0–1 knapsack problem to be solved. A comparative analysis with two benchmark methods, FedSat and FedSpace, was conducted to establish the advancements of inter-satellite FL. Then, Fashion-MINIST and CIFAR-100 were applied as datasets to test the models. Notably, the experimental results indicate that the CS mechanism can expedite the convergence speed of SFL up to 12 h, and it achieved an accuracy surpassing 80%.
We have not yet conducted experiments in a larger-scale constellation. In fact, future constellations may expand to the scale of tens of thousands of low Earth orbit (LEO) satellites, such as Starlink (https://www.starlink.com/, accessed on 1 December 2023). Therefore, the CS mechanism proposed in this paper may bring about very high computational overheads in the large-scale constellation scenario. This is a problem worth studying in future work. At the same time, we used a general dataset in the simulation. In the real satellite scenario, the remote sensing data of satellites may be different. The impact of the long-tail distribution of data on SFL and client selection has not yet been considered. In the future, we will explore more diverse paradigms of SFL for applications, as well as consider more comprehensive CS mechanisms.
Author Contributions
Conceptualization, C.W. and Z.Y.; methodology, C.G.; software, C.W. and S.H.; validation, C.W. and Z.Y.; formal analysis, C.G.; investigation, C.W. and S.H.; resources, Z.Y. and C.G.; data curation, C.W.; writing—original draft preparation, C.W. and S.H.; writing—review and editing, C.G.; visualization, C.W. and S.H.; supervision, C.G.; project administration, C.W.; funding acquisition, C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Shanghai Rising-Star Program under Grant No. 19QA140800, the Youth Innovation Promotion Association for CAS under Grant No. 2019292, and the Hong Kong, Macau, and Taiwan Science and Technology Cooperation Project in the “Science and Technology Innovation Plan Of Shanghai Science and Technology Commission” under Grant No. 23510760200.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data such as code are not publicly available due to privacy concerns. The datasets were derived from source in public domain: CIFAR-100 (https://www.cs.toronto.edu/~kriz/cifar.html) and Fashion-MNIST (https://www.kaggle.com/datasets/zalando-research/fashionmnist).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| N | The number of clients |
| The set of all clients | |
| K | The number of clients chosen |
| The chosen set of clients | |
| L | The arc length that GS can communicate with a satellite |
| The satellite’s speed | |
| T | The visible time between GS and a satellite |
| Kepler constant | |
| Earth’s radius | |
| h | The distance between the orbit plane and Earth’s surface |
| The satellite’s depression angle | |
| B | The available spectrum bandwidth |
| The transmission rate of the client i | |
| The channel power of the client i | |
| The channel power gain of the client i | |
| The AWGN power | |
| The sample data of the client k | |
| The label data of the client k | |
| The model parameter of the client k in t-th round training | |
| The loss function of the client k | |
| D | The size of the total dataset with all clients |
| The size of the dataset in the client k | |
| The dataset of the client k | |
| The computation ability of the client k | |
| W | The data size of global model parameters |
| The data size of local model parameters for the client k | |
| The distance between the client and the server | |
| c | The speed of light |
| The abnormality of the model; the required CPU cycles for client k to train a round | |
| The abnormality of the local model for client k in round i | |
| The affinity of the client k in round i | |
| The threshold of the total waiting time for all selected clients. |
References
- Sanad, I.; Vali, Z.; Michelson, D.G. Statistical Classification of Remote Sensing Satellite Constellations. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, Y.; Xue, C.; Xue, Z.; Cai, H. LEO Mega Constellations: Review of Development, Impact, Surveillance, and Governance. Space Sci. Technol. 2022, 2022, 9865174. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q. Satellite Computing: Vision and Challenges. IEEE Internet Things J. 2023, 10, 22514–22529. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, Q. Joint Resource Allocation and Learning Optimization for UAV-Assisted Federated Learning. Appl. Sci. 2023, 13, 3771. [Google Scholar] [CrossRef]
- Asad, M.; Shaukat, S.; Javanmardi, E.; Nakazato, J.; Tsukada, M. A Comprehensive Survey on Privacy-Preserving Techniques in Federated Recommendation Systems. Appl. Sci. 2023, 13, 6201. [Google Scholar] [CrossRef]
- Cao, H.; Feng, W.; He, J.; Liu, S. Decentralized Federated Learning for Secure Space-Terrestrial Communication With Intelligent Reflecting Surface. IEEE Wirel. Commun. Lett. 2023, 12, 2083–2087. [Google Scholar] [CrossRef]
- Zhu, J.; Wu, J.; Bashir, A.K.; Pan, Q.; Yang, W. Privacy-Preserving Federated Learning of Remote Sensing Image Classification With Dishonest Majority. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4685–4698. [Google Scholar] [CrossRef]
- Hassan, S.S.; Majeed, U.; Han, Z.; Hong, C.S. SFL-LEO: Secure Federated Learning Computation Based on LEO Satellites for 6G Non-Terrestrial Networks. In Proceedings of the NOMS 2023–2023 IEEE/IFIP Network Operations and Management Symposium, Miami, FL, USA, 8–12 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Elmahallawy, M.; Luo, T. Optimizing Federated Learning in LEO Satellite Constellations via Intra-Plane Model Propagation and Sink Satellite Scheduling. In Proceedings of the ICC 2023-IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 3444–3449. [Google Scholar] [CrossRef]
- Carlos, E.A.; Pinard, R.; Hassani, M. Over-the-Air Federated Learning in Satellite systems. arXiv 2023, arXiv:2306.02996. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q.; Xu, M.; Ma, X.; Zhou, A.; Sun, Q. Tiansuan constellation: An open research platform. In Proceedings of the IEEE International Conference on Edge Computing (EDGE), IEEE, Chicago, IL, USA, 5–10 September 2021; pp. 94–101. [Google Scholar] [CrossRef]
- Matthiesen, B.; Razmi, N.; Leyva-Mayorga, I.; Dekorsy, A.; Popovski, P. Federated Learning in Satellite Constellations. IEEE Netw. 2023, 1–16. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, M.; Pang, Z. Satellite-based computing networks with federated learning. IEEE Wirel. Commun. 2022, 29, 78–84. [Google Scholar] [CrossRef]
- Razmi, N.; Matthiesen, B.; Dekorsy, A.; Popovski, P. Ground-assisted federated learning in LEO satellite constellations. IEEE Wirel. Commun. Lett. 2022, 11, 717–721. [Google Scholar] [CrossRef]
- So, J.; Hsieh, K.; Arzani, B.; Noghabi, S.; Avestimehr, S.; Chandra, R. Fedspace: An efficient federated learning framework at satellites and ground stations. arXiv 2022, arXiv:2202.01267. [Google Scholar] [CrossRef]
- Razmi, N.; Matthiesen, B.; Dekorsy, A.; Popovski, P. On-board federated learning for dense LEO constellations. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 4715–4720. [Google Scholar] [CrossRef]
- Razmi, N.; Matthiesen, B.; Dekorsy, A.; Popovski, P. Scheduling for Ground-Assisted Federated Learning in LEO Satellite Constellations. In Proceedings of the 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; pp. 1102–1106. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, J. FedGSM: Efficient Federated Learning for LEO Constellations with Gradient Staleness Mitigation. In Proceedings of the IEEE 24th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Shanghai, China, 25–28 September 2023; pp. 356–360. [Google Scholar] [CrossRef]
- Al-Hawawreh, M.; Hossain, M.S. Federated Learning-assisted Distributed Intrusion Detection Using Mesh Satellite Nets for Autonomous Vehicle Protection. IEEE Trans. Consum. Electron. 2023, 1–9. [Google Scholar] [CrossRef]
- Li, D.; Xie, W.; Li, Y.; Fang, L. FedFusion: Manifold-Driven Federated Learning for Multi-Satellite and Multi-Modality Fusion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5500813. [Google Scholar] [CrossRef]
- Salim, S.; Moustafa, N.; Hassanian, M.; Ormod, D.; Slay, J. Deep Federated Learning-Based Threat Detection Model for Extreme Satellite Communications. IEEE Internet Things J. 2023, 11, 3853–3867. [Google Scholar] [CrossRef]
- Razmi, N.; Matthiesen, B.; Dekorsy, A.; Popovski, P. On-board federated learning for satellite clusters with inter-satellite links. arXiv 2023, arXiv:2307.08346. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Gao, G.; Zhang, M.; Liu, X. Client Selection in Federated Learning: Principles, Challenges, and Opportunities. IEEE Internet Things J. 2023, 10, 21811–21819. [Google Scholar] [CrossRef]
- Tang, Q.; Fei, Z.; Li, B.; Han, Z. Computation Offloading in LEO Satellite Networks With Hybrid Cloud and Edge Computing. IEEE Internet Things J. 2021, 8, 9164–9176. [Google Scholar] [CrossRef]
- Venugopal, D.; Muthugadahalli, C.; KS, M.; Narayanan, K. Ka band satellite communication systems—Applications and configurations. In Proceedings of the 66th International Astronautical Congress (IAC 2015), Jerusalem, Israel, 12–16 October 2015; pp. 12–16. [Google Scholar]
- Abdi, A.; Lau, W.C.; Alouini, M.S.; Kaveh, M. A new simple model for land mobile satellite channels: First-and second-order statistics. IEEE Trans. Wirel. Commun. 2003, 2, 519–528. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Guvenc, I. On Modeling Satellite-to-Ground Path-Loss in Urban Environments. IEEE Commun. Lett. 2021, 25, 696–700. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, S.; Yang, P.; Alhussein, O.; Zhuang, W.; Shen, X.S. Software Defined Space-Air-Ground Integrated Vehicular Networks: Challenges and Solutions. IEEE Commun. Mag. 2017, 55, 101–109. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Technical Report. Toronto, ON, Canada. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 1 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).