Abstract
Mixnets are an instrument to achieve anonymity. They are generally a sequence of servers that apply a cryptographic process and a permutation to a batch of user messages. Most use asymmetric cryptography, with the high computational cost that this entails. The main objective of this study is to reduce delay in mixnet nodes. In this sense, this paper presents a new scheme that is based only on symmetric cryptography. The novelty of this scheme is the use of binary graphs built by mixnet nodes. The root node collects user keys and labels without knowing their owners. After feeding each node by its graph, they can establish a random permutation and relate their keys to the incoming batch positions through labels. The differences with previous symmetric schemes are that users do not need long headers and nodes avoid the searching process. The outcomes are security and efficiency improvements. As far as we know, it is the fastest mixnet system. Therefore, it is appropriate for high-throughput applications like national polls (many users) or debates (many messages).
1. Introduction
Anonymity is a service required in several applications like e-voting, journalism, surveys, etc. Additionally, it is a desirable feature in order to mitigate the threats of communications surveillance. For these reasons, many anonymous communication systems have been proposed [1,2]. These can be classified by their strategies [3].
One of them is to build a broadcast channel where all users participate. These schemes are known as DC-nets (Dinning Cryptographers Network) [4] and have some variants, such as Dissent (Dining Cryptographers Shuffled Send Network) [5] or BAR (Broadcast Anonymous Routing) [6]. These protocols offer a high level of privacy, but they lack flexibility, require all participants’ cooperation, and allow only one user to communicate in one protocol round, which implies low throughput.
Another technique is hiding the transmission path by multiple hops. For example, Tor (The Onion Router) [7], Herd [8], Hornet [9], TresMep (Tracking-resistant Communication Mechanism with Dynamic Paths) [10], Misty Clouds [11], dPHI (dependable Path-HIdden lightweight anonymity protocol) [12], and Nym [13] belong to this category. These onion routing systems are suitable for low-latency communications in environments where messages arrive at different times in an almost constant flow. Nevertheless, they are vulnerable to traffic analysis [14,15] and attacks from adversary nodes [16,17].
The third approach is the use of mixnets. They are sequences of nodes that work with batches of messages. Each node makes a cryptographic operation and shuffles the batch, thus breaking the relationship between incoming and outgoing messages [18]. Mixnets have evolved and diversified widely in recent years. They started with [19], where users have to encrypt their messages with the public keys of the nodes. Then, each one decrypts the batch with its private key. These were followed by the so-called “encryption mixnets” [20]. Taking advantage of the properties of the ElGamal cryptosystem, this new category provides greater privacy and less delay for users and nodes.
An effort to improve efficiency is the combination of asymmetric and symmetric encryption. This gave rise to hybrid mixnets [21,22,23]. Instead of encrypting the entire message with public keys, what is encrypted with these is a symmetric one. Then, the message encrypted with the latter is appended. This solution reduces the high computational effort of asymmetric encryption to the few bits of a symmetric key. However, this does not bypass exponential calculations and must add symmetric decryption to the process.
A better idea is cMIX (fixed cascade mixnet), proposed in [24], where operations in users and nodes are reduced to a set of modular multiplications. Although the latency in the production phase is small, each message must traverse the mixnet twice. Moreover, it requires a precomputation phase where a set of asymmetric cryptographic operations must be carried out. Another solution is the use of alternative encryption methods like lattice-based ones [25], which can be six times faster than traditional mixnets [26]. However, these methods are relatively new and require deeper research [27,28].
The first pure symmetric mixnet was SEBM (Symmetric-Key-Encryption-Based Mixnet) [29], improved with ESEBM (Enhanced SEBM) [30]. In these schemes, nodes generate keys and an identifier linked to it in an internal table. These values are propagated, shuffled, and blinded from the last node in a predefined sequence to the first one, which delivers them to users. Then, users send their encrypted messages to the mixnet, which is composed in another different sequence. There is no need for asymmetric operations in any step, which provides this scheme the highest speed. However, each message entails a vector of identifiers that must be found in a table at each step. Moreover, depending on the place each node occupies in the mixnet, several vulnerabilities arise. Some of them could be exploited by just one adversary.
The purpose of this work has been overcoming the drawbacks of ESEBM and improving its throughput. In this regard, the new scheme presented here, called binary-tree-fed mixnets or BTFM, does not require any identifiers and eliminates the need of searching in tables. The outcome is a faster mixnet without overloading messages with superfluous headers. Additionally, it can stand with a higher number of adversaries. The major contribution is a starting phase where keys are established by means of a binary graph. Then, the production phase is faster than in any other mixnet. This new idea of working with binary graphs solves the problem of how to share keys anonymously without using asymmetric encryption and is a new tool to apply independently in other contexts.
In summary, the main contributions of this paper are
- A new tool for sharing keys anonymously without asymmetric encryption. Users can send keys or messages to a server while preserving their privacy. This is achieved using a binary graph where only permutations and XOR operations are required.
- The development of a new mixnet scheme, BTFM, which is based solely on symmetric encryption. Its main attributes are improvements in performance and security.
- The discovery of some vulnerabilities in a previous symmetric encryption mixnet scheme, ESEBM.
- A security study of BTFM, where the minimum threshold of adversaries necessary to violate privacy is determined.
- The comparison of BTFM with previous schemes, carried out through a series of experiments.
The paper is structured as follows. The next section is devoted to ESEBM, describes it, and shows some vulnerabilities. Then, BTFM is detailed in Section 3. The security analysis follows in Section 4. Section 5 shows and discusses the results of some experiments. The last section presents our conclusions.
2. Vulnerabilities of ESEBM
ESEBM is an evolution of SEBM [29] and is explained in detail in [30]. To date, no weaknesses in its security have been published. This is precisely the objective of this section. In this mixnet, nodes form groups to generate concealing patterns that are delivered to users. Figure 1 shows an example of an ESEBM mixnet with nine nodes. They form three groups labeled as , and C. Notice that members of these groups are scattered in the mixnet. The only rule is that priority in the group must be respected on the mixnet.
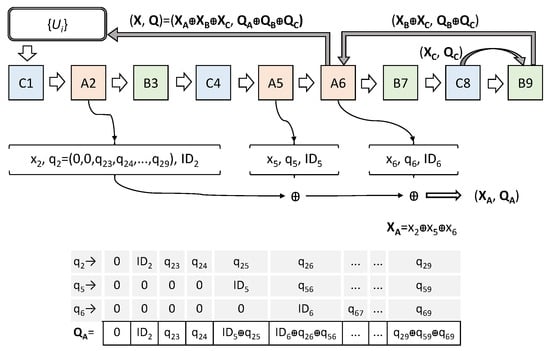
Figure 1.
Example of ESEBM. Mixnet of 9 servers distributed in three groups. Each node builds its concealing patterns and , which are stored in a table with an identifier . Then, they are combined by groups (like for group A), and then by mixnet (), which are sent to users.
Concealing patterns are random numbers intended to hide user messages. These concealing patterns are built by XORing binary strings generated by each node. Users encrypt their messages by an XOR operation with the patterns and send the result to the first node of the mixnet. Then, each node of the mixnet must remove its binary string. For each node to know which string to apply to which message, it needs a separate identifier. These identifiers could be used to trace senders and therefore must be hidden too. This is the purpose of vector q in Figure 1.
In ESEBM, each node generates a binary string ( in node ), a vector (), and an identifier (). These values are stored in a table. Then, inside each group, this tuple is passed to the next node, which performs an XOR operation and sends the result to the next one, and so on until reaching the last node of the group (). This one, the collector node, obtains two values: the aggregated keys () and the concealed identifiers (vector ).
Each collector node (, , and ) shuffles many pairs obtained this way. Then, the batch is passed from collector node to collector node, creating an XOR operation. The last node, (), the delivery node, delivers the result to users, which is
When a user sends a message m to the mixnet, it follows the format . The first node of the mixnet, , recognizes the identifier , which is disclosed in the first position of Q. It must be in its table, in the same row as and . Then, creates an XOR operation with these values. The result is an encrypted message without the string and a vector Q without the concealing values of . The next node will find its identifier unveiled and will create the same process. At the end, all the strings will be removed and the message shown in plain text.
The only node that knows the complete key X and the user is the delivery node (). In order to prevent that, the user sends blinding factors to each member of this last group. These factors () are combined with the strings by each node ( for in the example). Therefore, the user receives the pair , where B is an XOR of blinding factors to be removed by the user before sending m. The delivery node can store in its internal table the aggregated key of the remaining groups () and the user but cannot know its group key (). Collector nodes can store its keys (pair for node ; pair for node ). With this scheme, there are feasible attacks such as the following:
- Collusion of last group with the first node of the mixnet. If all members of the last group ( and ) reveal their passwords () to the last member (), the latter will have the password of its group () and also that of the rest of the groups (). That is, it has the complete key. It also knows which user it gave that key to; that is, it has the link with the user. Therefore, it is able to decrypt any message of this user delivered to the first member of the mixnet. In the example (Figure 1), it means a collusion of four nodes: , and .
- Collusion of the delivery node with the remaining nodes in the mixnet. The delivery node () can associate its key and ID with the receiving user. This node, by passing the message through it, can therefore identify the user and transmit this knowledge to the following nodes. The last one reveals the message in plain text and it will know its author. This case corresponds with the collusion of four nodes in the example: , and .
- Collusion of the delivery node, the nodes of the groups that have performed a partial decryption, and nodes in between. The delivery node knows the full key of the remaining groups (). When the message arrives within the mixnet (to ), its key () is applied and the message is clean of the keys of the last group (), but it may already have the keys of some nodes of the following groups applied ( from from , and from ). These nodes can collude and share these keys with the delivery node, but it also needs to know where the message is within the batch. Namely, the permutations of previous nodes are also required. (If any of the following groups have already fully operated on the mixnet, then only collusion from the collector node of that group would be required.) For this example, it means a collusion of the following six nodes: , and .
- Collusion of collection nodes. The delivery node can relate the user to the message. If all collection nodes collaborate, they can know the aggregate key of each group for that message. From the added key, they can know their particular key. The last member of the mixnet, who is necessarily a group leader, will know the author when he has to use that key. In the example, only three nodes are required: , and .
ESEBM does not establish how many groups to define and how to scatter groups in the mixnet. Therefore, each vulnerability requires more or fewer adversaries depending on this distribution. Table 1 shows the list of vulnerabilities with the adversaries required in each one. The last two columns depict the maximum and minimum number of adversaries needed in each attack considering the best and worst distribution for each case. Notice that two vulnerabilities requires only one adversary in the worst case (delivery node at the end in type 2 and last group placed at the beginning in type 3). This problem is solved in the new scheme.

Table 1.
Adversaries required in ESEBM for n nodes = k groups × m members.
3. Binary-Tree-Fed Mixnets
The new mixnet scheme, BTFM, is detailed below. With the intention of facilitating its understanding, first, an example is shown and then the formal description of the method is undertaken.
3.1. Overview
The presented scheme consists of three stages. The first one allows mix nodes to share secret keys with users but preserve privacy. The second stage configures a fixed permutation on each node of the mixnet. The last stage is the production mode, where users can continuously send messages.
In the first stage, each node is placed at the root of a binary node tree. For each root, the remaining nodes form the branches of the tree. Each user links with each node of the last level (nodes without children), called leaf nodes. Through those links, users send fragments of a key and a label they want to share with the root node. Therefore, each leaf node has a key fragment but needs all the other nodes to unveil the key. All the leaf nodes agree on a permutation and shuffle their fragments with it. Each pair of leaf nodes delivers the batch to its parent node in the next level. Each parent node creates an XOR operation with the key fragments at the same position of the batch. In this level, all the nodes agree on a permutation, which is applied to the result. The process is repeated in each level. When it reaches the root node, all the fragments will build the complete key.
Figure 2 shows a case of a mixnet of seven nodes in which a generic user is feeding with a key and a label node G. This couple is divided into four parts: and . User sends to node A the couple , to node B the couple , and similarly to nodes C and D. Notice that, at this moment, only a collusion of and D is able to unveil the key . These four nodes agree on the permutation . The four nodes create this permutation for the batch of all users including and deliver the result to the parent node. In the case of nodes A and B, the parent node is E, which receives the two batches and creates an XOR operation. As the permutation is the same, the first two fragments of the user key will be at the same position in its batch and E will compute . Nodes E and F agree on a permutation: . Both of them shuffle their results following it. Then, the result reaches node G, which will be able to build the complete couple , that is, .
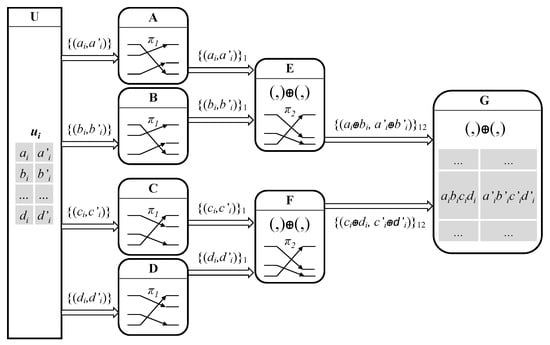
Figure 2.
Each user shares a pair label–key with a node G by means of binary trees. Key is composed of XORing , and ; label , and .
In the second stage, each user sends a vector with the encrypted labels. In the example of Figure 2, it is , assuming that the mixnet sequence is . Each node chooses a permutation and sets it. Each node receives a batch of vectors whose first element is a label stored in the previous stage. This process can be observed in Figure 3. Then, each node finds the label in its table and links the corresponding key to the input position of the batch. Next, it removes its label from the vector and applies this key to the remaining values, which is sent to the next node. In the example, B receives . Then, at each position i of the batch, it looks for in its table and finds in the same row. Now, B knows which key to apply to which incoming batch position in the next stage. This node then removes key from each element of the label vector, performs its permutation, and sends to the following node (C). When this stage ends, nodes have set an unknown permutation and associated keys that are shared only with users. Then, in the third stage, users only perform an XOR operation of any message with the key and send it to the mixnet.
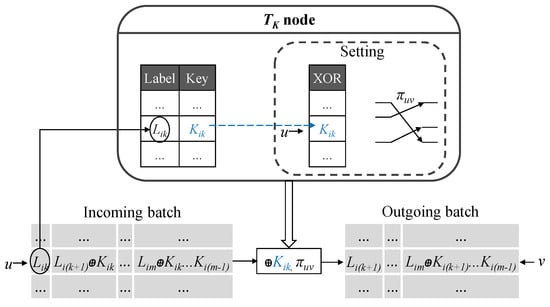
Figure 3.
Setting stage: user keys () are linked to the incoming batch positions (u) and a random permutation ( is established).
3.2. Formal Description
Let be a set of n users. Let be a set of nodes. The elements of these sets can establish communication links among them. The scheme follows three stages:
- STAGE 1: FEEDING. The value k is computed from . That is, k is the highest number that accomplishes . Then, each user generates random numbers per node. A half builds the keys with each node: , where corresponds to different nodes and . The other half are fragments of the labels: . Next, for each node , a perfect binary tree of k levels is established by selecting other nodes randomly until the tree is completed. Nodes collaborate to ensure this randomness against adversaries [31]. The tree is a subset of T with elements, where is the root at the first level. Each node of the tree has two children nodes, occupying the next level. The exception is at the last level, which has nodes that have no children. To these leaf nodes, each user sends the pair , where corresponds to each leaf node. All the nodes in the same level agree on a random permutation . Nodes at the last level receive the pairs from users in a batch. Next, they create the same permutation and send the result to their parent node. From the level to the root, each node creates an XOR operation between the pairs received in the same position of the batches. Then, they create the permutation of their level and send the result to their parent node. The root node creates the XOR operation to obtain the pair , which is stored in a table.
- STAGE 2: SETTING. A random sequence of defines the mixnet. Users send to the first node the vector . Each node of the mixnet looks for the first element of the vector in its table, where it must be next to the key . Then, it removes the first element of the vector and applies XOR to the remaining elements with . Next, the node establishes a permutation on the input batch and sends the result. From now on, the key will be applied with any value that comes in the same batch position.
- STAGE 3: MIXING. Users compute . Then, they can anonymously publish any message by sending to the first node of the mixnet. The first node processes the batch of encrypted messages, which will remove its partial key . The next nodes do the same until the last one, which shows a batch of decrypted messages.
4. Security Analysis
The nodes of any mixnet can collude among themselves and/or with some users to break the anonymity of others. This section studies this problem. Firstly, some hypotheses are established regarding the limits of these adversaries. Based on these, the strength of the system is determined, indicating the minimum number of conspirators to violate it. Finally, the properties of this scheme are reviewed.
4.1. Security Model
In order to obtain a security measure of the scheme, some starting assumptions must be established:
- The bit length of keys () and labels () is large enough to reduce the probability of guessing them from their XOR encryption forms to a negligible value.
- Peer-to-peer communications are safe; in other words, adversaries cannot prevent (DoS), decrypt (confidentiality), impersonate (authentication), or tamper with (integrity) these communications.
- Adversaries can only gather information from their role in the process or from other adversaries.
4.2. Analysis
The objective of adversaries is to link the decrypted message with its author. If the first node is an adversary, it will only need the key because it knows the sender. If the last node is an adversary, it will only need the authorship because the message is decrypted. Intermediate nodes will need the two kinds of information.
Definition 1.
“Binary-tree cut” is defined as a set of nodes of which at least one participates in any connected path between root and leaves.
Proposition 1.
The nodes capable of learning user keys must necessarily constitute a cut.
Proof.
The information needed to deduce the key is initially the set of fragments. All the leaf nodes could reconstruct the key, and it is also true that the set defined by them is a cut. If instead of the initial fragments any aggregation of them is available, it can also be reconstructed as long as all the fragments have participated. For a fragment not to have participated, it must happen that, on the path that joins it to the root, there is no node of the cut, which is precisely the definition of cut. □
Figure 4 shows two examples of binary-tree cuts. Although being a cut is a necessary condition, it is not sufficient. Notice that the cut in Figure 4a has no node of the third level ; therefore, the elements of the cut are unaware of the permutation carried out at said level and cannot associate the keys to the users. However, the cut in Figure 4b is capable.
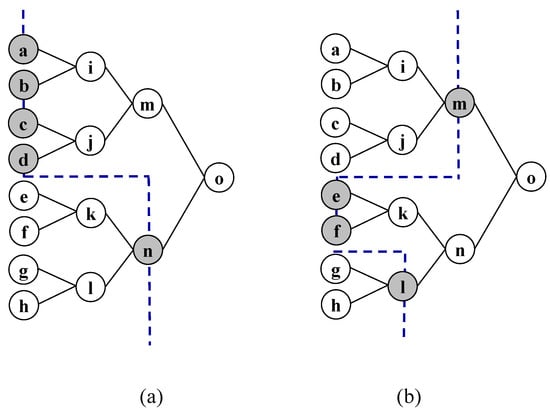
Figure 4.
Binary-tree cuts: (a) permutation of third level (node i) is not known for the cut, so they cannot build the key; (b) cut able to break privacy.
Proposition 2.
For a cut to reveal the keys and associate them with their users, it must have at least one node at each level between the level of the leaves and the lowest level (closest to the root) of the cut.
Proof.
To construct the keys, in addition to the fragments or aggregations of these, the permutations carried out on them must be known. Only the nodes at each level know their permutation. That is, the collaboration of at least one of the nodes at each level is needed between the extreme nodes of the cut. If the top of the cut is a level that does not correspond to the leaf nodes, then a batch of keys can be obtained, but they cannot be associated with users. The first permutation is only known to the leaf nodes. Therefore, it is necessary to incorporate the information of all the permutations from these to the cut. □
Theorem 1.
The minimum number of adversaries to learn keys in a binary tree of k levels is k.
Proof.
Given Proposition 1, the minimum number of levels of a cut capable of revealing the keys would be the one constituted by the leaf nodes, whose number is . Furthermore, it is the only cut possible with this single level given Proposition 2. The fragment information that exists in two leaf nodes is obtained aggregated in their parent nodes. Therefore, if we now consider a cut that includes the next level, each pair of leaf nodes can be replaced by its parent node by reducing the cut by one. It is not possible to conduct it with all of them because at least one leaf node must remain to report the permutation of its level. In this way, different cuts of size can be established, that is, the nodes of the next level plus a leaf node. This number would be the minimum because with one less node there would always be a lack of information.
Now consider a cut A that reaches level r formed by a sequence of nodes from a leaf node to r (minimum number of nodes to know all the permutations) and the rest of the nodes of level r (those that make up the minimum number to build the keys). That is, (for example, nodes , and n in Figure 4 for the case and ). Suppose there is a cut B with a smaller number of nodes (). This cut B must necessarily exclude nodes from cut A as it is smaller in number. If the excluded node is one of level r, then it must be replaced with any combination of its descendants, a number never less than two. Therefore, for this change to allow the size of B to be reduced, the level would have to be decreased, thus reducing the number of nodes necessary to know the permutations. However, reducing a level implies multiplying by two the minimum number of nodes necessary to know the key (those of the level) while only reducing those necessary to know the permutation by one unit. Therefore, B can never be less than A. Its size, , reaches the minimum value for ; that is, the root node is enough to know the key to which any sequence up to a leaf node must be added. Therefore, there is one node per level. □
This result can be applied to labels as they follow the same process as keys. At the second stage, the mixnet is constituted with a random sequence of all the nodes. Then, each node chooses a random permutation to apply to the batches. Users then send their encrypted labels to the mixnet. Nodes learn the position to apply each key through the labels. If a node knows the owner of a key (for example, when this node is the root node in a successful attack of k adversaries on stage 1), it can identify the owner of any message when it reaches that node and share that information with the following node. However, this node cannot disclose the message without the remaining keys. Therefore, any successful collusion in stage 2 will need the collaboration of all the existing nodes between this attacking node and the end of the mixnet. The easiest case is when the attacking node is precisely the last in the mixnet. In this case, no additional node is required for the attacker and therefore no more adversaries than k are needed. In stage 3, the same reasoning can be applied as in stage 2 since it is very similar (messages are encrypted instead of labels). Thus, the minimum number of adversaries to break privacy is, again, k.
4.3. Properties
Mixnets are usually compared based on a number of commonly known features [2]. The main one is anonymity, and both schemes (ESEBM and BTFM) provide it. However, ESEBM shows cases (2 and 3 in Table 1) where only one adversary can break privacy. In comparison, BTFM offers a higher minimum adversary threshold (). On the other hand, it is enough to have a single honest node in asymmetric mixnets to ensure privacy.
When considering the other characteristics, there are some that no symmetric mixnet can meet. As far as we know, verifiability, robustness, and fault tolerance can only be accomplished by asymmetric encryption techniques. Nevertheless, scalability, throughput, and latency are vastly surpassed by symmetric mixnets, as indicated in experiments. In this area, BTFM shows better results than ESEBM, especially when processing huge amounts of messages, as described in the next section.
5. Results and Discussion
This section describes a series of experiments aimed at assessing the differences regarding BTFM with other schemes. Firstly, it is compared with asymmetric systems (RSA and cMIX) and then with ESEBM. The first graph meets the objective of contextualizing purely symmetric systems with respect to traditional schemes (RSA), including one of the most advanced in terms of speed, such as cMIX. The following charts show cases in which BTFM and ESEBM clearly differ in delay and header size.
The following results have been obtained using a CPU i5-3230M, at 2.6 GHz and 16 GB of RAM. The software has been developed on Java 1.8.0_121 in a Windows 10 OS. The message length has been chosen to be 1024 bits. It must be the same for any key. However, for labels ( in ESEBM and in BFTM), an integer (32 bits) has been selected. Network delays are not considered. With this scenario, a mixnet of ten nodes throws an average node delay shown in Figure 5. The batch size varies from 1000 to 10,000 users. Each line corresponds to one of the four schemes: a decryption mixnet based on RSA, cMIX (modular products), ESEBM, and BTFM. As can be seen, symmetric mixnets are very similar with the lowest latency. However, RSA and cMIX present a significantly higher delay. In fact, for 10,000 users, RSA is 91 times slower than BTFM, cMIX 30 times, and ESEBM 1.6 times.
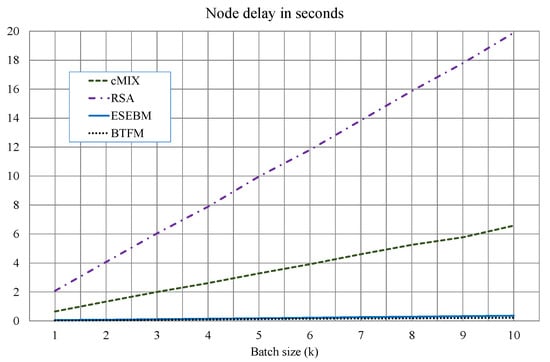
Figure 5.
Node delay comparison among RSA, cMIX, ESEBM, and BTFM mixnets.
In order to appreciate the differences between BTFM and ESEBM, the batch size must be increased. The considerable reduction offered by BTFM can be seen in Figure 6. In the first case (100 K users), BTFM takes almost half (50.8%) the time of ESBM. This difference increases as the number of users grows, to the point that with 550 K users it reaches 23.6%. That is, BTFM is 4.2 times faster than ESEBM in this case. A deeper look reveals that the XORing time is very reduced in both schemes (4.2% of total time in BTFM and 1.6% in ESEBM). Permutation and serialization operations are the most time-consuming.
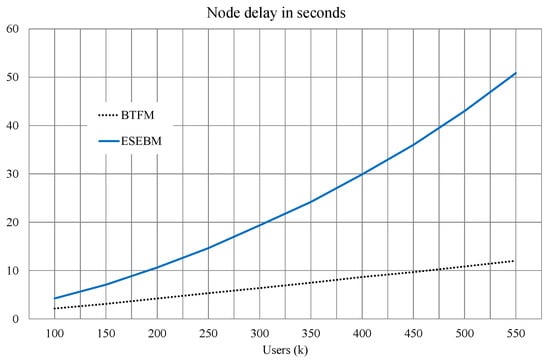
Figure 6.
Delay in an ESEBM node (continuous line) and in a BTFM node (dots).
In ESEBM, the batch size is significantly larger than in BTFM because a label vector proportional to the size of the mixnet must be added. Figure 7 shows this exceedance of the BTFM batch in two ways: megabytes in columns and percentages in a line. The mixnet size, from 10 nodes to 100, is represented on the abscissa. In ordinates, the same number represents the percentage and the overload megabytes. This chart corresponds to 250 K users. However, if the number of users with the same mixnet size is varied, horizontal lines are observed. That is, the percentage that represents the excess of the batch size remains constant with respect to users. Regarding the nodes, the worst case (100 nodes) presents an overload of 100.1 MB (39.6%).
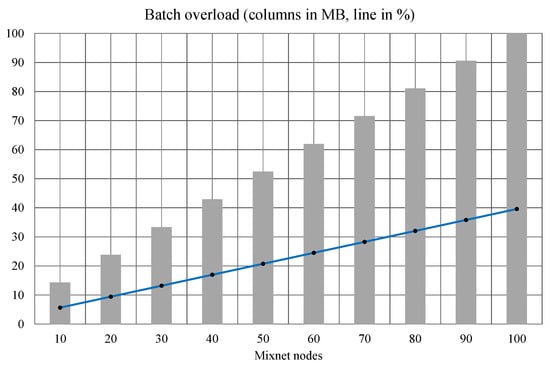
Figure 7.
Excedance of an ESEBM batch over BTFM.
Overall, in light of these experiments, the performance of BTFM stands out from other systems. It is overwhelmingly superior to asymmetric encryption systems (up to 30 times faster), it slightly improves ESEBM in low-demand environments (batches of 10.000 users), and clearly surpasses it when demand increases (doubles it from 100,000 users). Furthermore, messages do not increase in size by aggregating headers as in ESEBM, which implies a reduction in the time to send batches between nodes.
6. Conclusions
This section offers an overview of this work. The main contributions are reviewed, the advantages and limitations of this new scheme are highlighted, and future lines of research are discussed.
In the context prior to this article, ESEBM was the fastest mixnet to date. It represented a qualitative leap over previous schemes by reducing the computing time in the nodes by two orders of magnitude. Its greatest merit is perhaps to have demonstrated that it is possible to do without asymmetric encryption. However, ESEBM has certain weaknesses and needs to use long message headers. The challenge driving this work was to further improve performance by leveraging the pure symmetric encryption approach. The solution comes from two simple ideas: fragmenting the keys to hide them from the nodes (stage 1) and using labels to enable free permutation in stage 2. The former originated the key sending method of the binary graph, and the latter enables the nodes to reduce the operations to be performed to a minimum (stage 3), thus maximizing their performance.
Among the contributions, the new technique of sending keys through a binary graph from stage 1 stands out. Through this, a set of entities can establish a symmetric key with another anonymously, all this using only XOR operations and permutations. Although it has been applied to mixnets, it could be used in other environments. For example, a group of authorized users could establish label–key pairs in this way with a server. They could then contact it using any anonymous channel [1]. By identifying themselves only with the tag and demonstrating knowledge of the key, the server would know that they belong to the authorized group but would not be able to identify any user in particular. From here, users could interact anonymously and securely with the server. This technique would be similar to blind signature but with the advantage of requiring less computational cost and without the weakness inherent to any asymmetric key cryptosystem.
The main contribution is BTFM. It is a new mixnet scheme inside a very rare category, symmetric encryption mixnets, which includes only two more: SEBM and ESEBM. While these types of mixnets lack robustness, fault tolerance, and verifiability, they instead offer a qualitative leap in performance, reducing delay. In this respect, BTFM shows better rates than ESEBM (4 times faster). The reason is that BTFM minimizes the processing of each node. As far as we know, there is no mixnet faster than BTFM.
This new scheme can be used in any scenario where a mixnet is the solution. Nevertheless, the requisite of a complex starting phase leads to environments where the same users send messages continuously, like in forums or meetings. In this context, using the same key multiple times could be a weakness when just an XOR operation is performed. However, the same scheme is valid with other symmetric encryption algorithms like AES (Advanced Encryption Standard) in the production phase. Other applications appropriate for BTFM are those requiring high throughput, such as elections or nationwide surveys.
Another contribution of this article has been the revelation of ESEBM vulnerabilities. A comparison with BTFM yields a tougher constraint on adversaries being successful. Therefore, BTFM improves ESEBM in speed and security. The drawback is that BTFM must be applied to batches of users acting at the same time. ESEBM can better deal with an asynchronous demand. For both, it remains an open question to provide verifiability and robustness to overcome traditional schemes. In this sense, it would be interesting as a line of research to study the combination with asymmetric encryption techniques only for verifiability, trying to maintain the same performance when all nodes are honest. Another challenge for future work is to increase the minimum threshold of adversaries to break anonymity.
Author Contributions
Conceptualization, D.A.L.-G.; Methodology, D.A.L.-G.; Literature review, D.A.L.-G., J.P.T., D.V. and M.S.-R.; Software, D.A.L.-G., J.P.T., D.V. and M.S.-R.; Validation, J.P.T., D.V. and M.S.-R.; Writing—original draft preparation, D.A.L.-G.; writing—review and editing, D.A.L.-G., J.P.T., D.V. and M.S.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Datasets at https://www.uhu.es/diego.lopez/research/dataBTFM.xls (accessed on 21 December 2023).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shirazi, F.; Simeonovski, M.; Asghar, M.R.; Backes, M.; Diaz, C. A survey on routing in anonymous communication protocols. ACM Comput. Surv. (CSUR) 2018, 51, 1–39. [Google Scholar] [CrossRef]
- He, Y.; Zhang, M.; Yang, X.; Luo, J.; Chen, Y. A Survey of Privacy Protection and Network Security in User On-Demand Anonymous Communication. IEEE Access 2020, 8, 54856–54871. [Google Scholar] [CrossRef]
- Ren, J.; Wu, J. Survey on anonymous communications in computer networks. Comput. Commun. 2010, 33, 420–431. [Google Scholar] [CrossRef]
- Chaum, D. The dining cryptographers problem: Unconditional sender and recipient untraceability. J. Cryptol. 1988, 1, 65–75. [Google Scholar] [CrossRef]
- Corrigan-Gibbs, H.; Ford, B. Dissent: Accountable anonymous group messaging. In Proceedings of the 17th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 4–8 October 2010; pp. 340–350. [Google Scholar]
- Kotzanikolaou, P.; Chatzisofroniou, G.; Burmester, M. Broadcast anonymous routing (bar): Scalable real-time anonymous communication. Int. J. Inf. Secur. 2017, 16, 313–326. [Google Scholar] [CrossRef]
- Dingledine, R.; Mathewson, N.; Syverson, P.F. Tor: The second-generation onion router. USENIX Secur. Symp. 2004, 4, 303–320. [Google Scholar]
- Blond, S.L.; Choffnes, D.; Caldwell, W.; Druschel, P.; Merritt, N. Herd: A scalable, traffic analysis resistant anonymity network for voip systems. In Proceedings of the 2015 ACM Conference on Special Interest Group on Data Communication, London, UK, 17–21 August 2015; pp. 639–652. [Google Scholar]
- Chen, C.; Asoni, D.E.; Barrera, D.; Danezis, G.; Perrig, A. Hornet: High-speed onion routing at the network layer. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1441–1454. [Google Scholar]
- Tian, C.; Zhang, Y.; Yin, T.; Tuo, Y.; Ge, R. Achieving dynamic communication path for anti-tracking network. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Al-Muhtadi, J.; Qiang, M.; Saleem, K.; AlMusallam, M.; Rodrigues, J.J. Misty clouds—A layered cloud platform for online user anonymity in Social Internet of Things. Future Gener. Comput. Syst. 2019, 92, 812–820. [Google Scholar] [CrossRef]
- Alexander, B.; Becker, G.T. dPHI: An improved high-speed network-layer anonymity protocol. Proc. Priv. Enhancing Technol. 2020, 3, 304–326. [Google Scholar]
- Kramer, A.; Rezabek, F.; von Seck, R. Recent Advancements in Privacy Preserving Network Layer Approaches. In Proceedings of the Seminar Innovative Internet Technologies and Mobile Communications (IITM); Winter Semester 2022/2023. Chair of Network Architectures and Services (NET 2023-06-1); Technical University of Munich: Munich, Germany, 2023; pp. 19–24. [Google Scholar]
- Montieri, A.; Ciuonzo, D.; Aceto, G.; Pescapé, A. Anonymity services tor, i2p, jondonym: Classifying in the dark (web). IEEE Trans. Dependable Secure Comput. 2018, 17, 662–675. [Google Scholar] [CrossRef]
- Kwon, A.; AlSabah, M.; Lazar, D.; Dacier, M.; Devadas, S. Circuit fingerprinting attacks: Passive deanonymization of tor hidden services. In Proceedings of the 24th USENIX Security Symposium (USENIX Security 15), Washington, DC, USA, 12–14 August 2015; pp. 287–302. [Google Scholar]
- Evans, N.S.; Dingledine, R.; Grothoff, C. A practical congestion attack on tor using long paths. In Proceedings of the 18th USENIX Security Symposium (USENIX Security 09), Montreal, QC, Canada, 10–12 August 2009; pp. 33–50. [Google Scholar]
- Winter, P.; Ensafi, R.; Loesing, K.; Feamster, N. Identifying and characterizing sybils in the tor network. In Proceedings of the 25th USENIX Security Symposium (USENIX Security 16), Austin, TX, USA, 10–12 August 2016; pp. 1169–1185. [Google Scholar]
- Sampigethaya, K.; Poovendran, R. A survey on mix networks and their secure applications. Proc. IEEE 2006, 94, 2142–2181. [Google Scholar] [CrossRef]
- Chaum, D. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 1981, 24, 84–88. [Google Scholar] [CrossRef]
- Park, C.; Itoh, K.; Kurosawa, K. Efficient anonymous channel and all/nothing election scheme. In Advances in Cryptology—EUROCRYPT’93: Workshop on the Theory and Application of Cryptographic Techniques Lofthus, Norway, 23–27 May 1993 Proceedings 12; Springer: Berlin/Heidelberg, Germany, 1994; pp. 248–259. [Google Scholar]
- Goldschlag, D.; Reed, M.; Syverson, P. Hiding routing information. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 1996; pp. 137–150. [Google Scholar]
- Jakobsson, M.; Juels, A. An optimally robust hybrid mix network. In Proceedings of the Twentieth Annual ACM Symposium on Principles of Distributed Computing, Newport, RI, USA, 26–29 August 2001; pp. 284–292. [Google Scholar]
- Huszti, A.; Kovács, Z. Bilinear pairing-based hybrid mixnet with anonymity revocation. In Proceedings of the 2015 International Conference on Information Systems Security and Privacy (ICISSP), Angers, France, 9–11 February 2015; pp. 238–245. [Google Scholar]
- Chaum, D.; Das, D.; Javani, F.; Kate, A.; Krasnova, A.; De Ruiter, J.; Sherman, A.T. cMix: Mixing with minimal real-time asymmetric cryptographic operations. In Applied Cryptography and Network Security: 15th International Conference, ACNS 2017, Kanazawa, Japan, 10–12 July 2017, Proceedings 15; Springer: Berlin/Heidelberg, Germany, 2017; pp. 557–578. [Google Scholar]
- Aranha, D.F.; Baum, C.; Gjøsteen, K.; Silde, T. Verifiable mix-nets and distributed decryption for voting from lattice-based assumptions. In Proceedings of the 2023 ACM SIGSAC Conference on Computer and Communications Security, Copenhagen, Denmark, 26–30 November 2023; pp. 1467–1481. [Google Scholar]
- Ahmad, K.; Kamal, A.; Ahmad, K.A.B.; Khari, M.; Crespo, R.G. Fast hybrid-MixNet for security and privacy using NTRU algorithm. J. Inf. Secur. Appl. 2021, 60, 102872. [Google Scholar] [CrossRef]
- Rabas, T.; Bucek, J.; Lórencz, R. SPA Attack on NTRU Protected Implementation with Sparse Representation of Private Key. In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 23), Lisbon, Portugal, 22–24 February 2023; pp. 135–143. [Google Scholar]
- Esser, A.; May, A.; Verbel, J.; Wen, W. Partial key exposure attacks on BIKE, Rainbow and NTRU. In Proceedings of the 42nd Annual International Cryptology Conference, Santa Barbara, CA, USA, 13–18 August 2022; Springer: Cham, Switzerland, 2022; pp. 346–375. [Google Scholar]
- Tamura, S.; Kouro, K.; Sasatani, M.; Alam, K.M.R.; Haddad, H.A. An information system platform for anonymous product recycling. J. Softw. 2008, 3, 46–56. [Google Scholar] [CrossRef]
- Haddad, H.; Tamura, S.; Taniguchi, S.; Yanase, T. Development of anonymous networks based on symmetric key encryptions. J. Netw. 2011, 6, 1533. [Google Scholar] [CrossRef]
- Awerbuch, B.; Scheideler, C. Robust random number generation for peer-to-peer systems. Theor. Comput. Sci. 2009, 410, 453–466. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).