Stable Rules Definition for Fuzzy TS Speed Controller Implemented for BLDC Motor
Abstract
1. Introduction
2. Description of the Speed Control Algorithm
2.1. Fuzzy Controller Applied in the Control Structure
- The mechanical part does not include nonlinearities (e.g., friction torque and backlash).
- The elasticity of the shaft is omitted.
- The optimal tuning of the internal part is ensured (the dynamic response of the electromagnetic torque after the reference signal from the speed controller).
- The fast processing and measurement of the state variables.
- The relation between the total time constant of the torque control loop and , due to the modern switches used in specialized power electronic devices and modern control techniques [51], can be defined as follows:
- The omission of the influence of disturbances in the power electronic devices.
2.2. Fuzzy Speed Controller
If input1 is … and input2 is …, then the output is…,
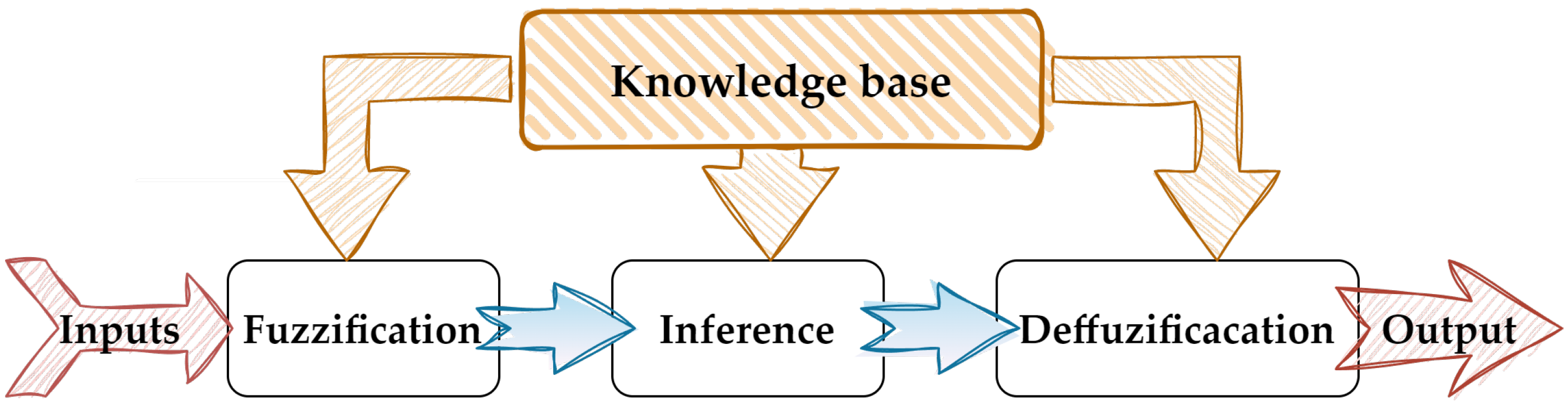
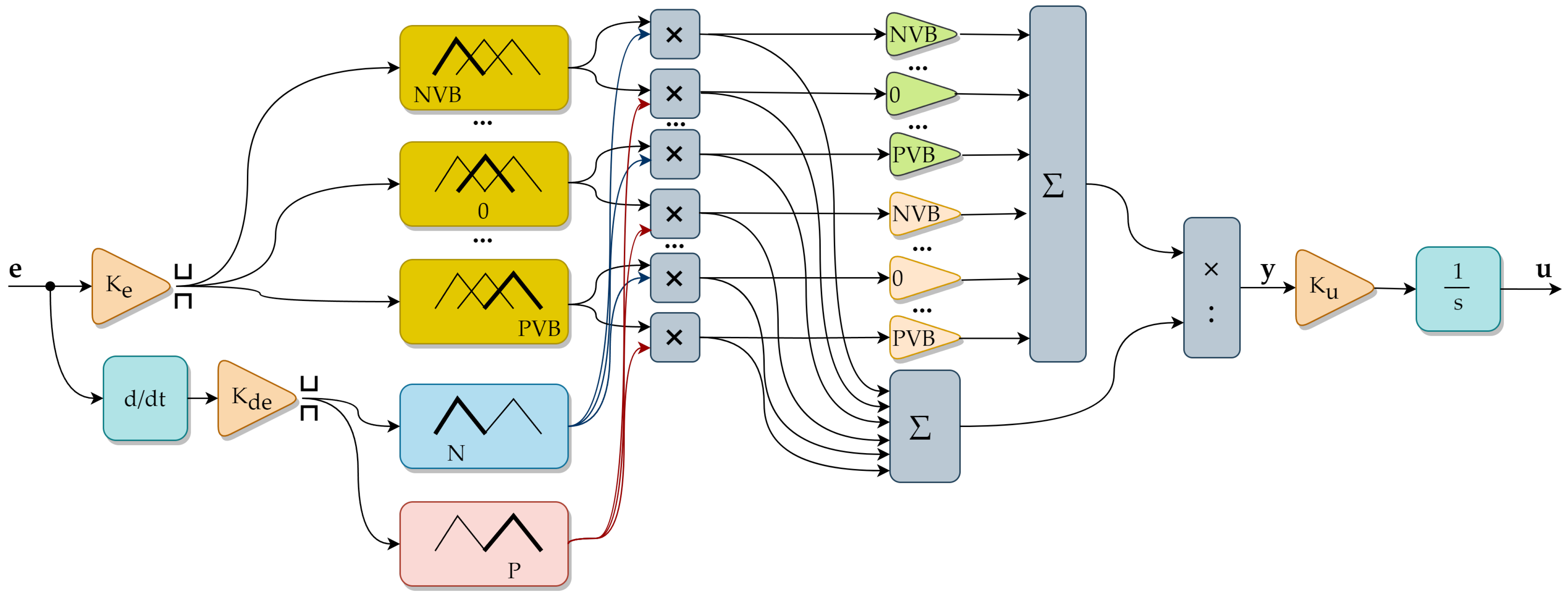
- where the considered variables are not given as crisp values, but rather as fuzzy labels. The next step of the fuzzy controller data processing is defuzzification, the process of translating a fuzzy conclusion into a crisp output value. Different defuzzification methods can be found in the literature [52]. The commonly used singleton method utilizes weights placed at the peak coordinates of the membership functions. In comparison to Mamdami reasoning, the Takagi–Sugeno (T-S) model applies a different structure for the inference block. The fuzzified inputs are compiled with functions, resulting in a crisp output. The T-S fuzzy system is very efficient, and hardware implementation in programable devices seems to be easier. It was applied in tests described later on in this paper. A schematic representing the fuzzy logic controller is presented in Figure 4.
2.3. Fuzzy Rules Definition
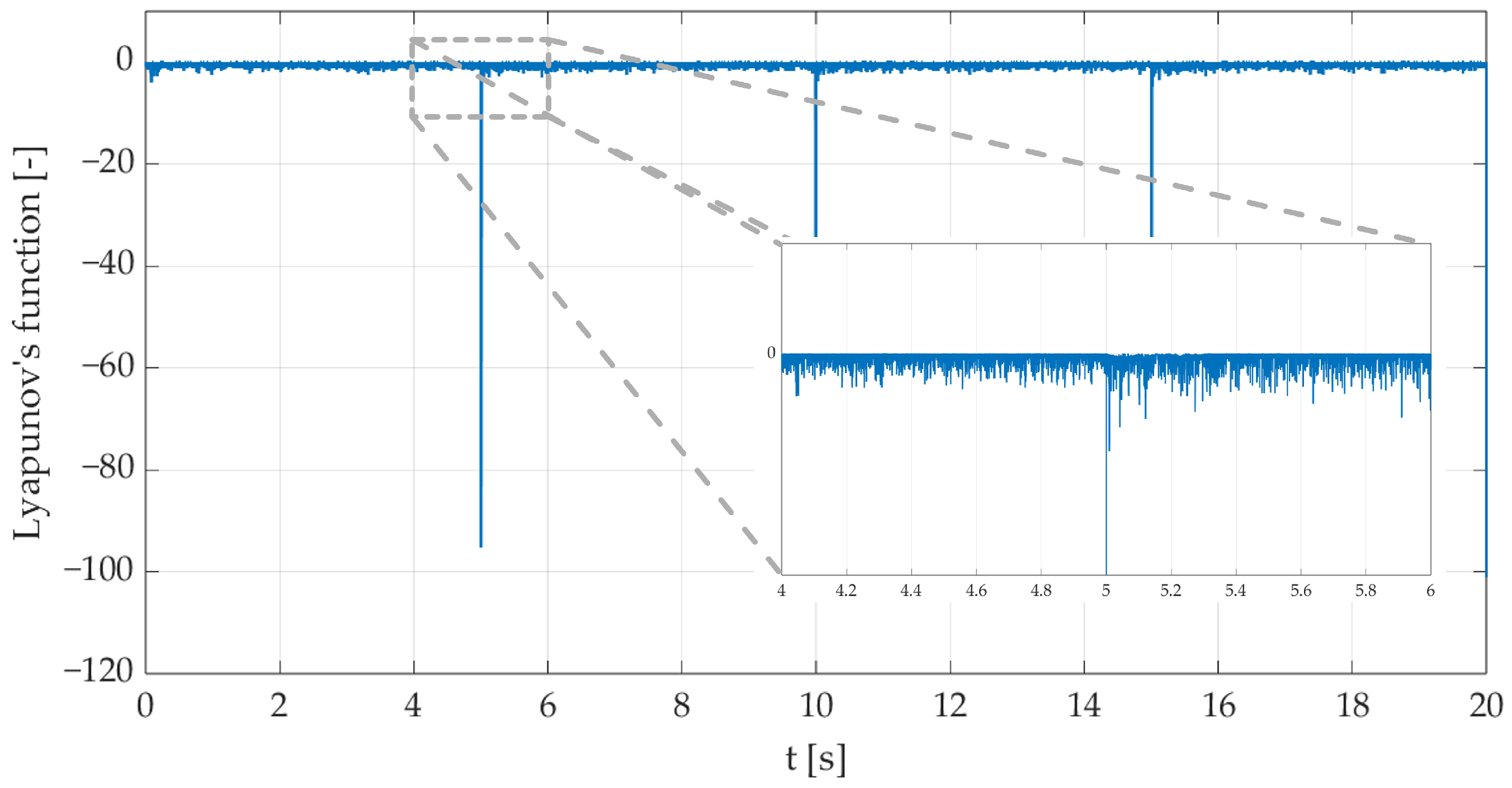
- For the stability considerations, the two-element positive-definite Lyapunov candidate function was chosen (7):
Let ; then, the condition in (15) is true if . This is always true for and .
- This is a trivial relation but not the only possible combination. Depending on the size of the knowledge base and the resolution of the membership function, more detailed rules could be defined. The following statement can also be considered:
Let ; then, the requirement in (15) is fulfilled if , which is true for , , and .
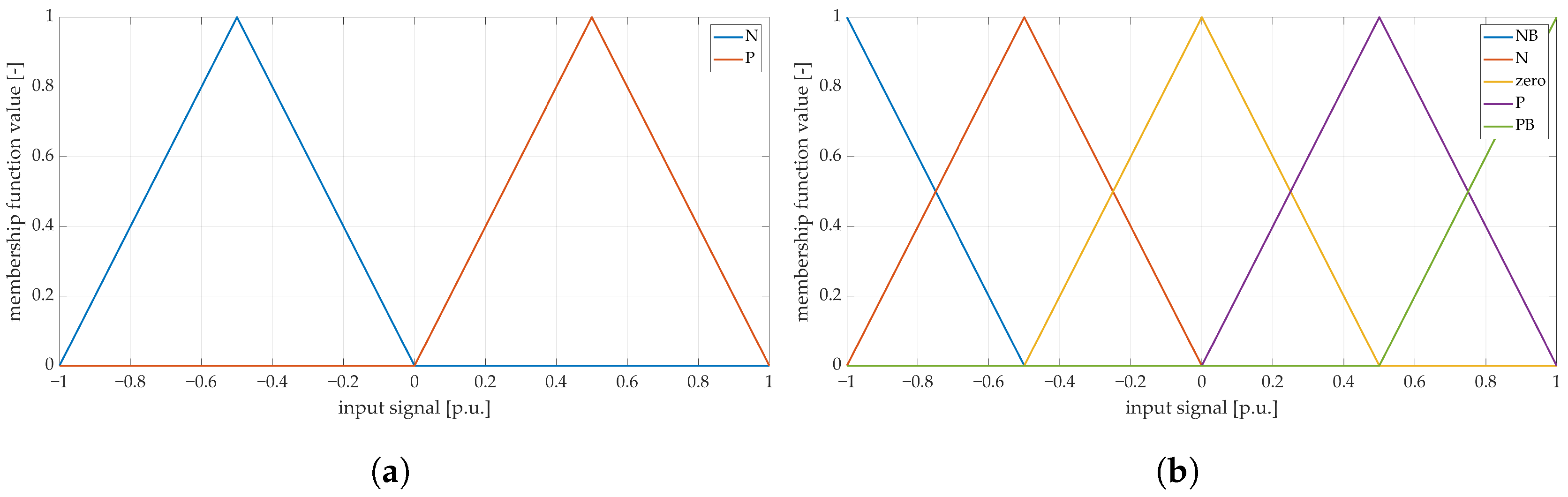
- Based on a similar analysis, more rules can be defined, and the control surface can be achieved (Figure 5). It can be noted that an offset of at least a single linguistic label should be present between the values of and . For the membership functions presented in Figure 6, the stable control rules are gathered in Table 1.
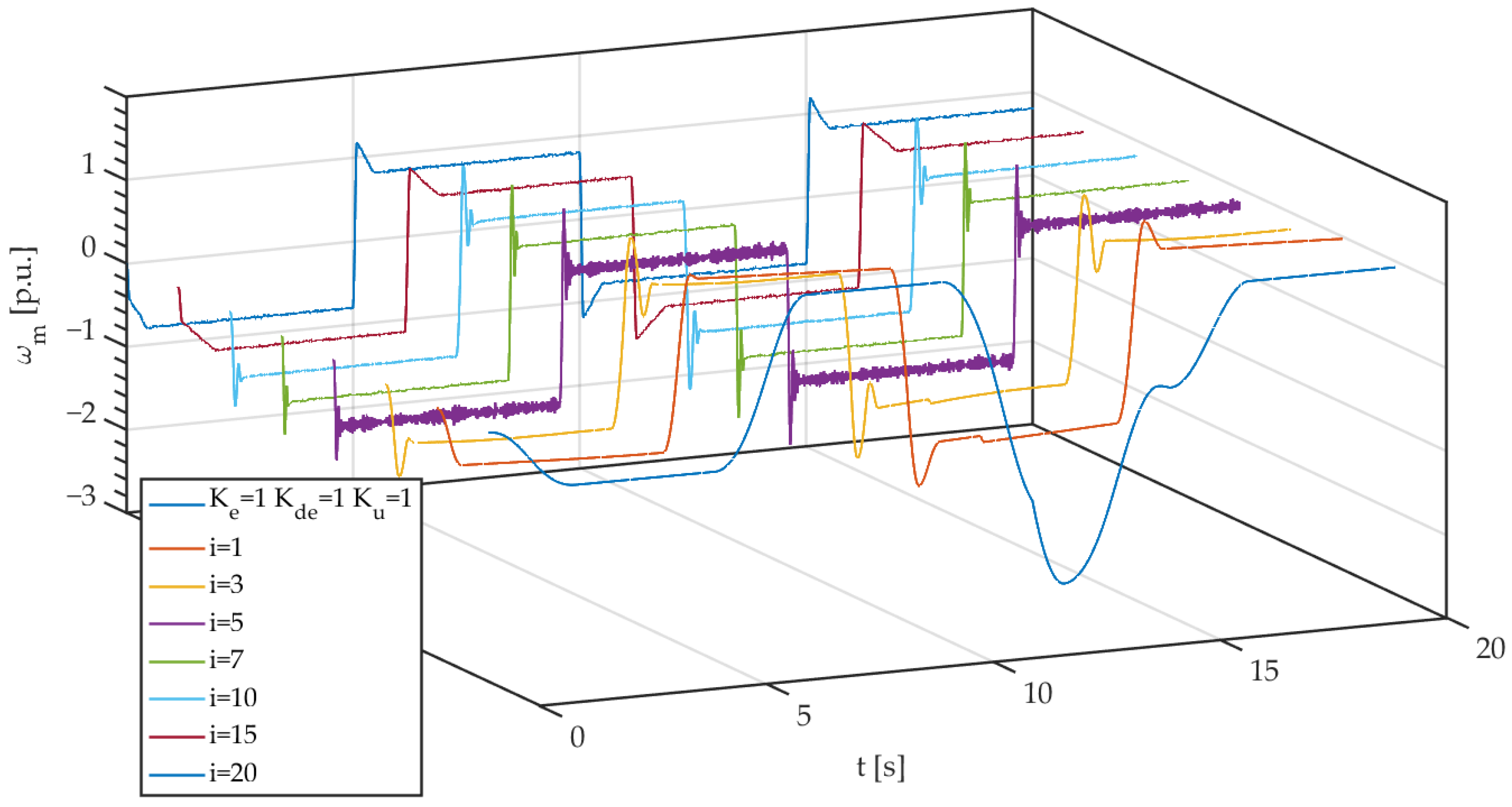
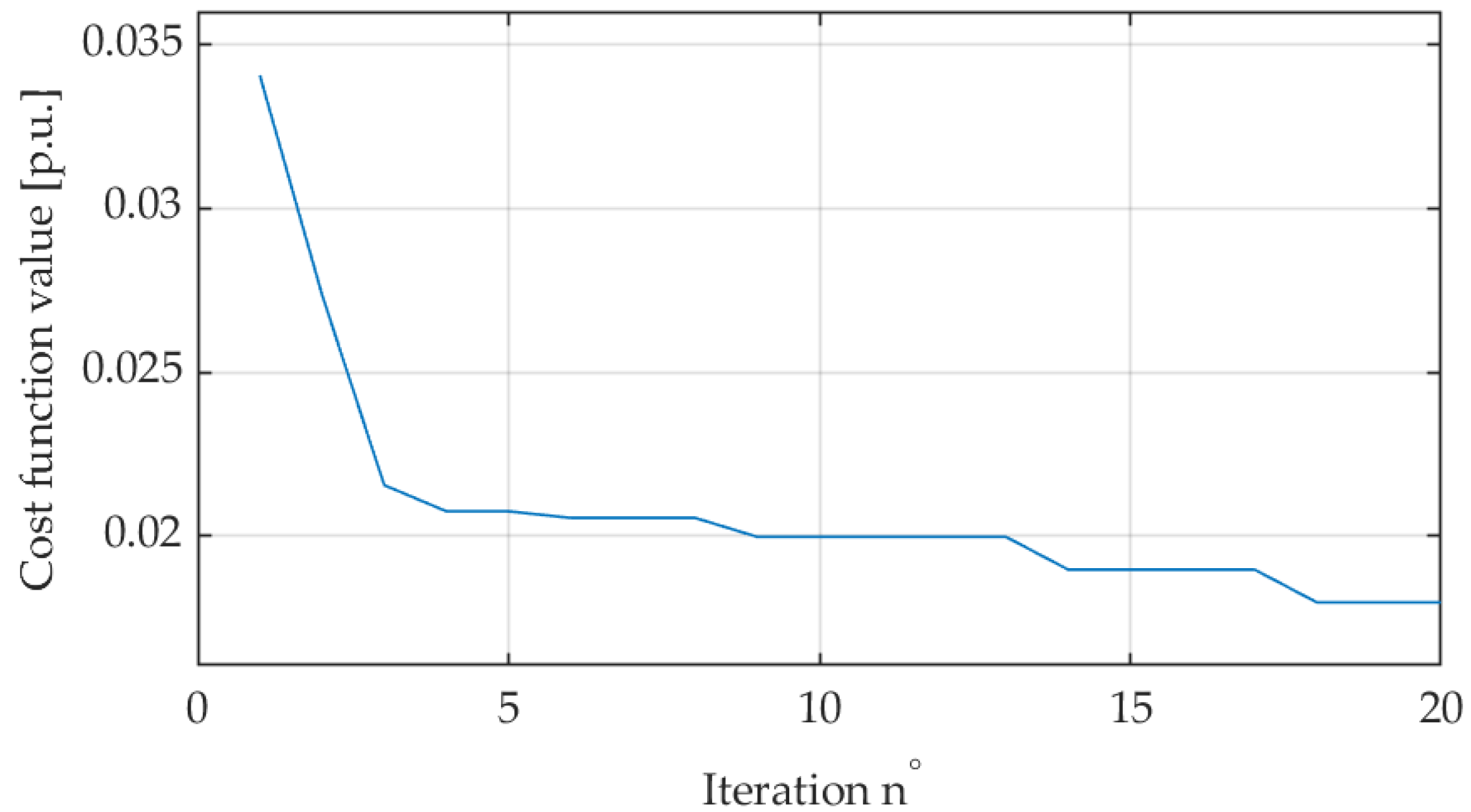
2.4. Bio-Inspired Optimization of the Fuzzy Speed Controller Using the Chameleon Swarm Algorithm
- Search for prey;
- Eye rotation to locate prey;
- Prey capture.
3. Simulation Results
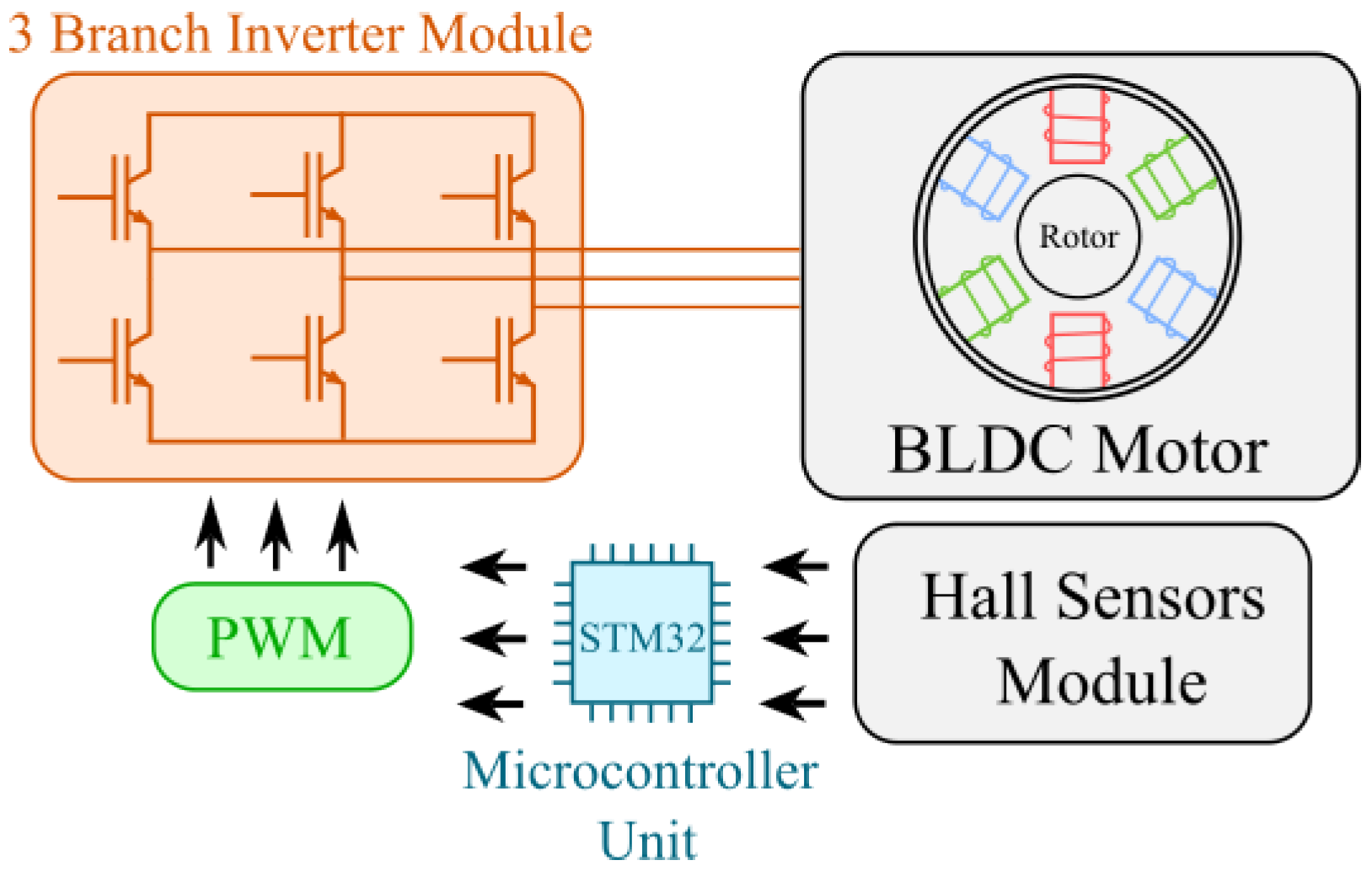
4. Hardware Construction and Tests of the Stable Fuzzy Speed Controller
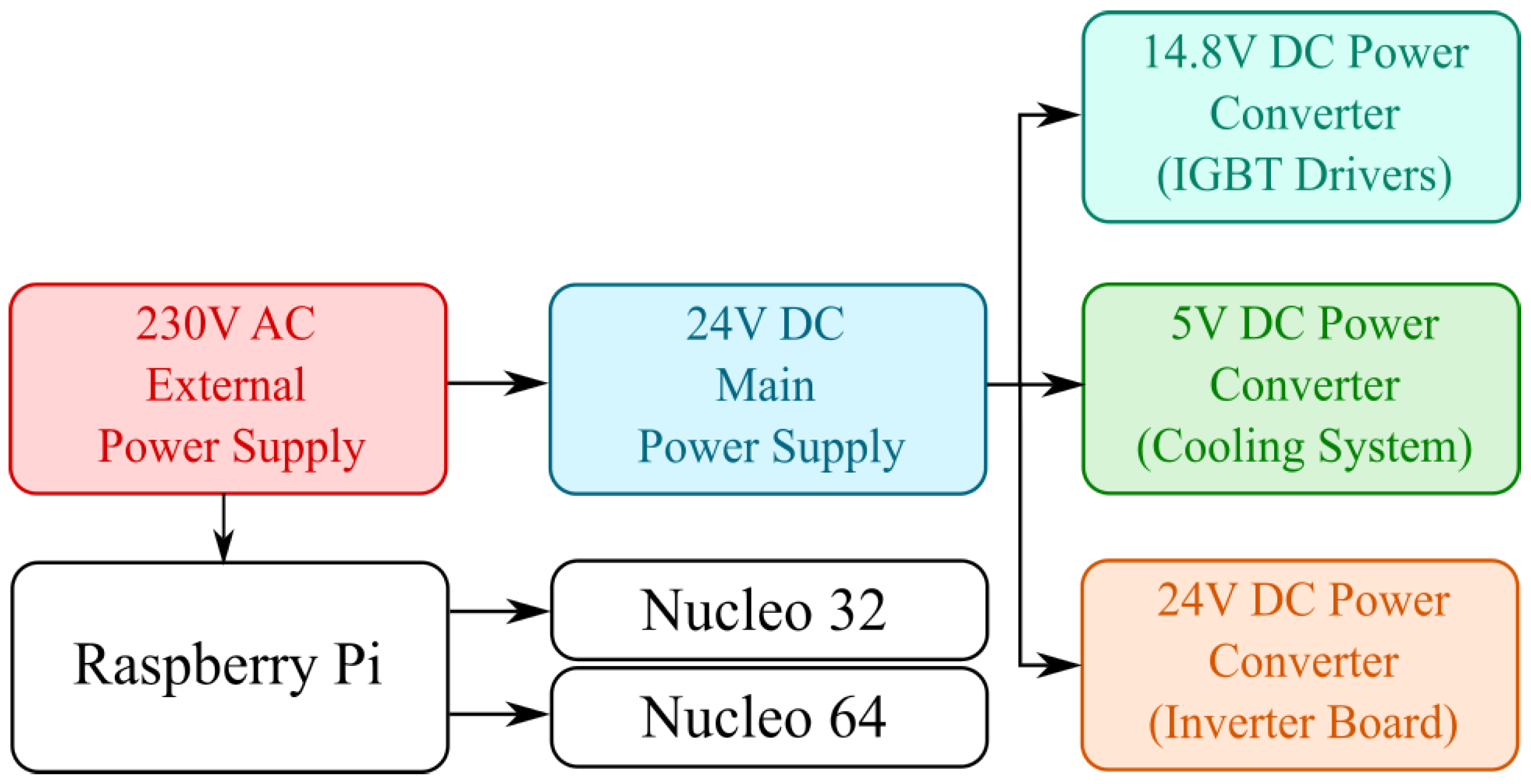
4.1. The Design of the Control and Power System
4.2. Power Module
4.3. Cabinet
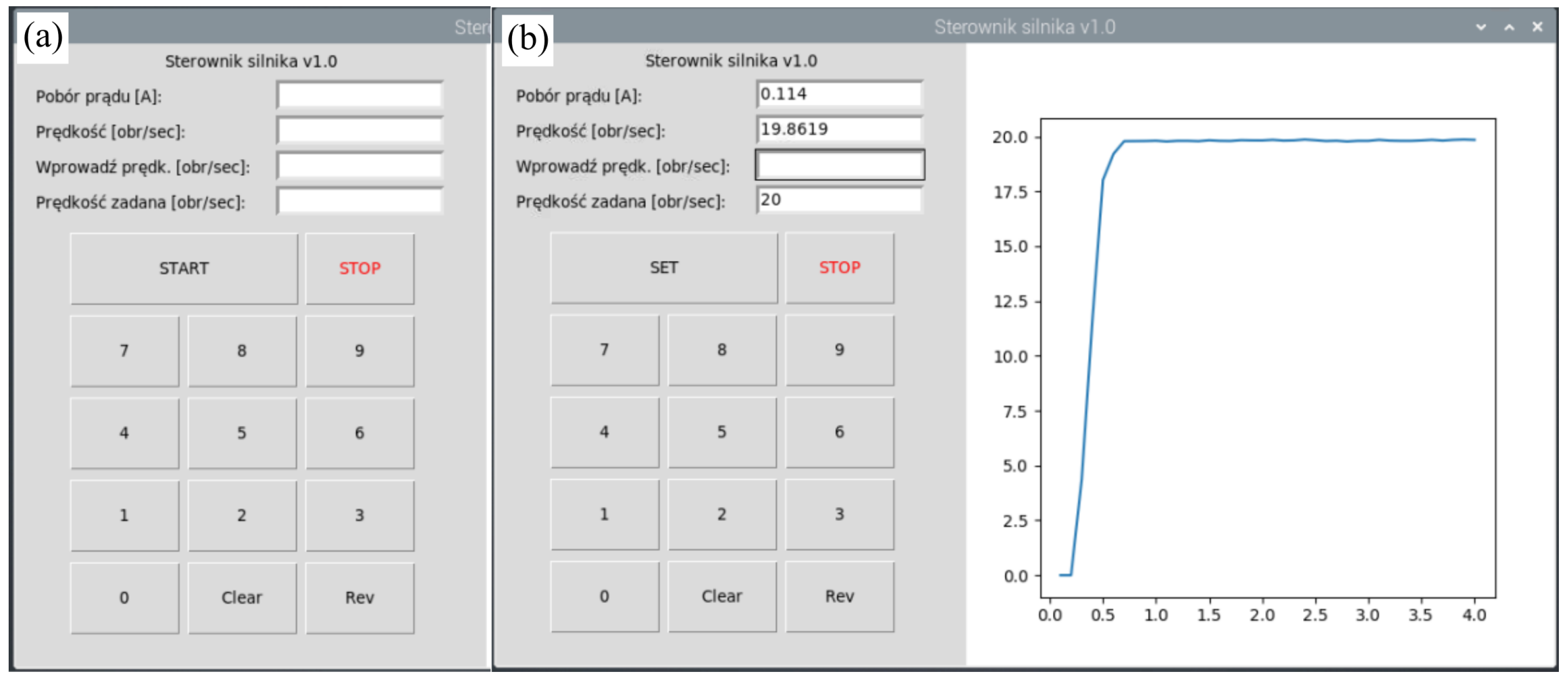
4.4. Control Panel—The Python Application
4.5. Encoder
4.6. BLDC Motor
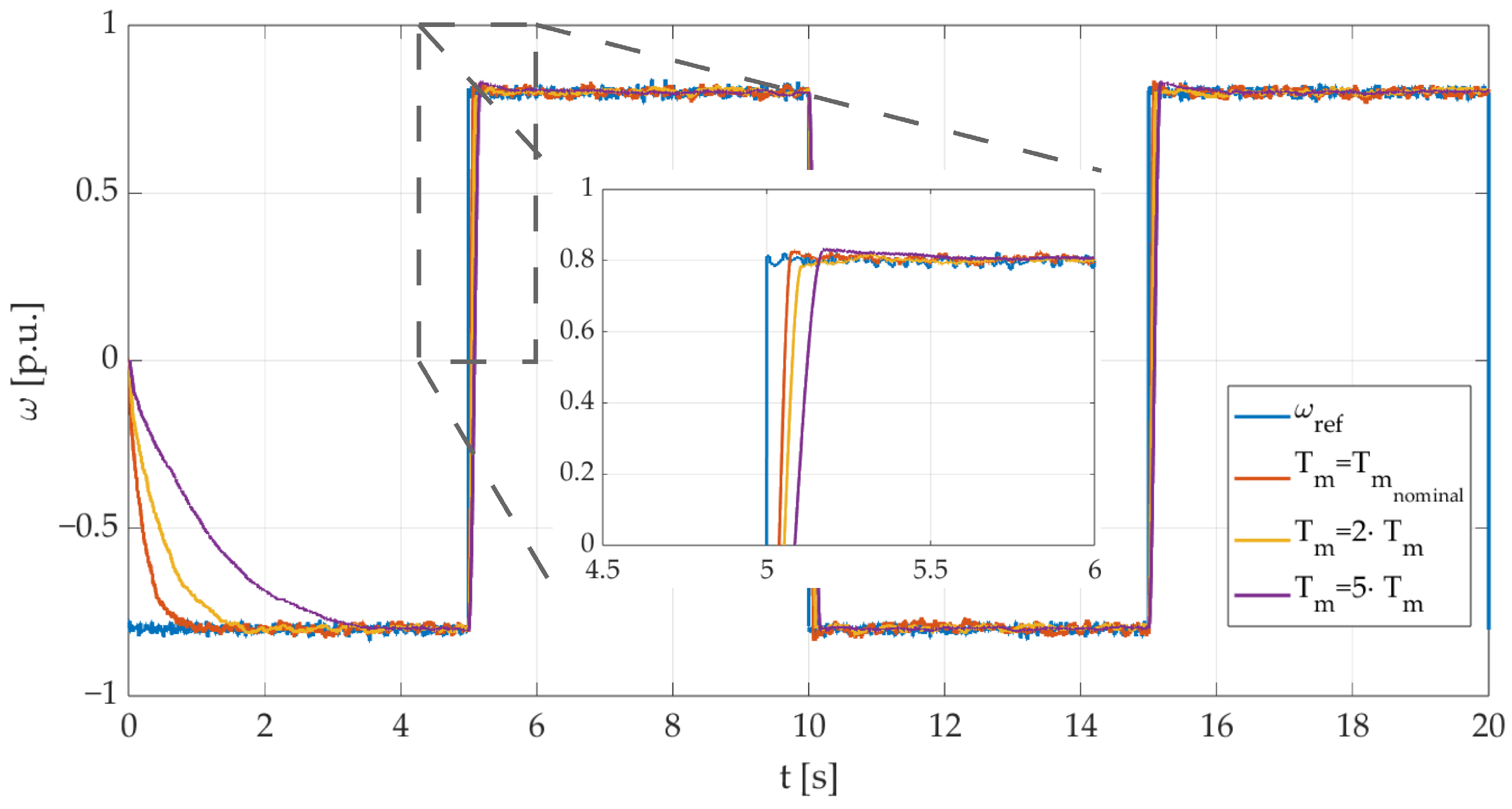
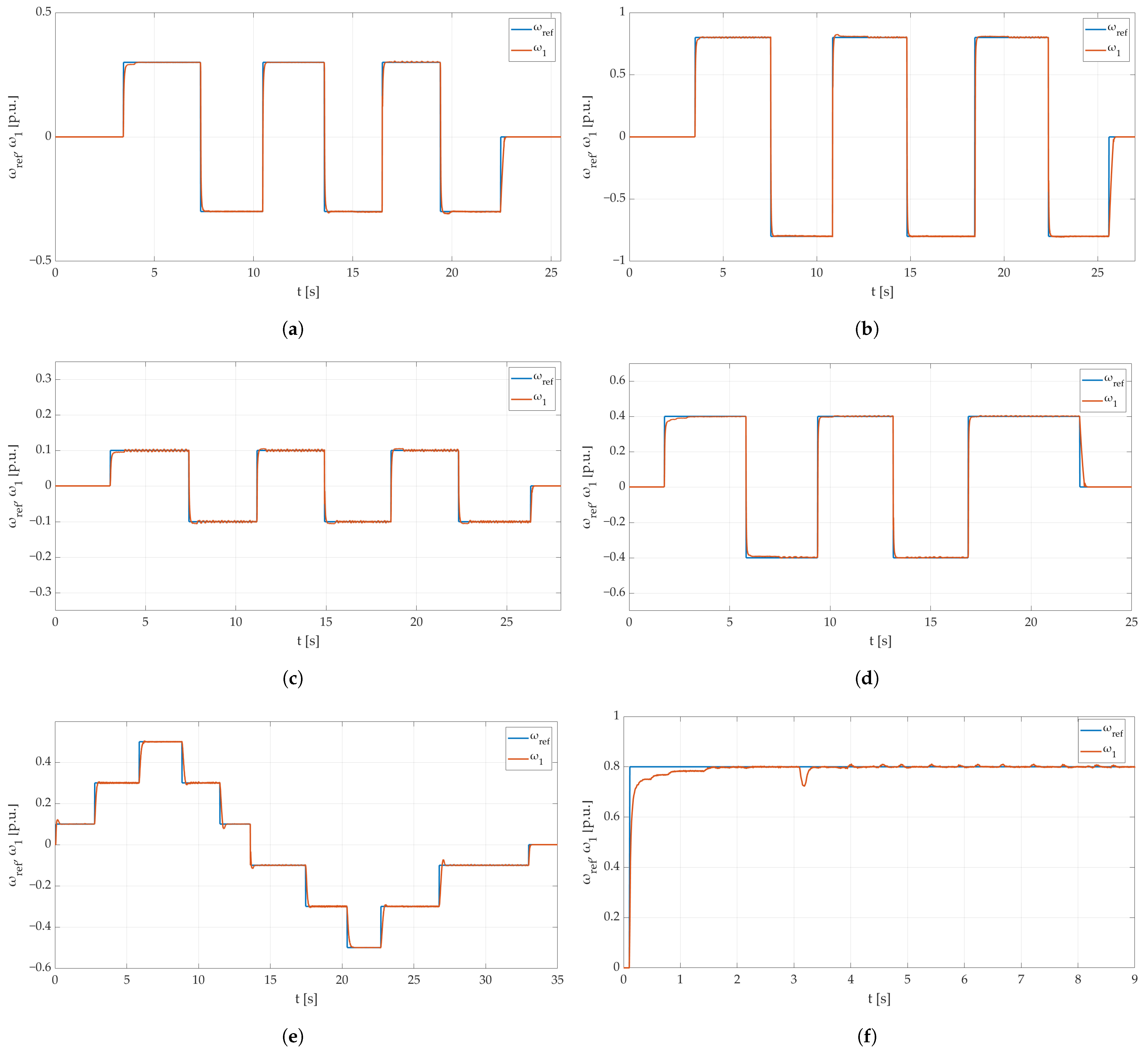
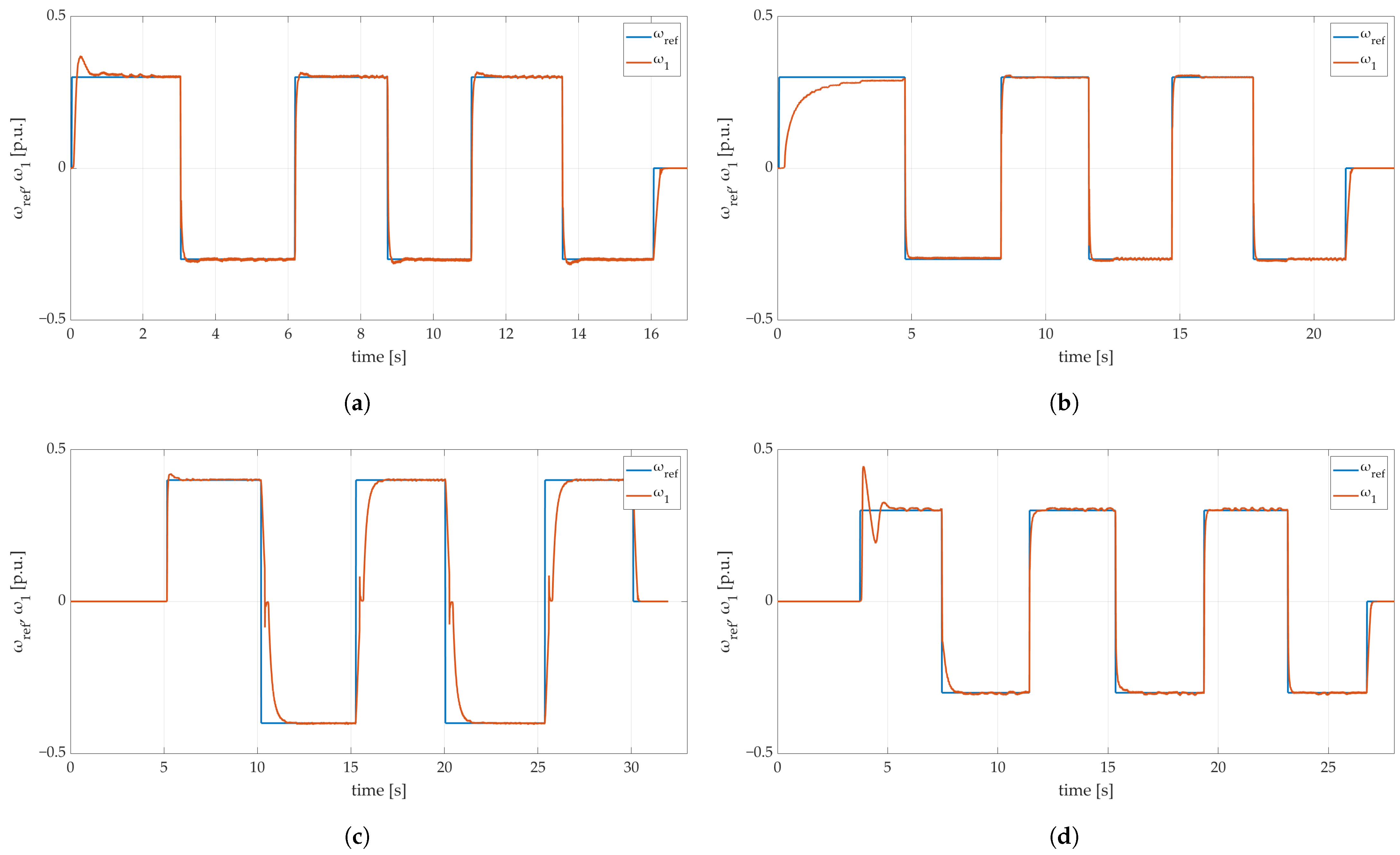
4.7. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| BLDC | Brushless DC motor |
| CSA | Chameleon Swarm Algorithm |
| HMI | Human–machine interface |
| HVAC | Heating, ventilation, and air conditioning |
| IGBT | Insulated-gate bipolar transistor |
| PPR | Pulses per revolution |
| PWM | Pulse width modulation |
| RAM | Random-access memory |
References
- Buettner, M.A.; Monzen, N.; Hackl, C.M. Artificial Neural Network Based Optimal Feedforward Torque Control of Interior Permanent Magnet Synchronous Machines: A Feasibility Study and Comparison with the State-of-the-Art. Energies 2022, 15, 1838. [Google Scholar] [CrossRef]
- Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Grey Wolf Optimizer in Design Process of the Recurrent Wavelet Neural Controller Applied for Two-Mass System. Electronics 2022, 11, 177. [Google Scholar] [CrossRef]
- Hoai, H.K.; Chen, S.C.; Chang, C.F. Realization of the Neural Fuzzy Controller for the Sensorless PMSM Drive Control System. Electronics 2020, 9, 1371. [Google Scholar] [CrossRef]
- Stanislawski, R.; Tapamo, J.R.; Kaminski, M. A Hybrid Adaptive Controller Applied for Oscillating System. Energies 2022, 15, 6265. [Google Scholar] [CrossRef]
- Pajchrowski, T.; Siwek, P.; Wojcik, A. Application of the Reinforced Learning Method for adaptive electric drive control with variable parameters. In Proceedings of the IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 687–694. [Google Scholar] [CrossRef]
- Malarczyk, M.; Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Electric Drive with an Adaptive Controller and Wireless Communication System. Future Internet 2023, 15, 49. [Google Scholar] [CrossRef]
- Glowacz, A. Thermographic Fault Diagnosis of Shaft of BLDC Motor. Sensors 2022, 22, 8537. [Google Scholar] [CrossRef]
- Yurchenko, V.; Pikalov, V.; Belokopytov, R.; Boykov, A.; Drapak, K. Electric Drive Modernization by Replacing Brushed DC Motor with Permanent Magnet Synchronous Motor in Rehabilitation Robotic System. In Proceedings of the 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 9–11 November 2022; pp. 509–513. [Google Scholar] [CrossRef]
- Yen, S.H.; Tang, P.C.; Lin, Y.C.; Lin, C.Y. A Sensorless and Low-Gain Brushless DC Motor Controller Using a Simplified Dynamic Force Compensator for Robot Arm Application. Sensors 2019, 19, 3171. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Tian, J.; Yang, B.; Liu, M.; Gu, B.; Yin, Z.; Yin, L.; Zheng, W. A Novel Architecture of a Six Degrees of Freedom Parallel Platform. Electronics 2023, 12, 1774. [Google Scholar] [CrossRef]
- Suganthi, P.; Nagapavithra, S.; Umamaheswari, S. Modeling and simulation of closed loop speed control for BLDC motor. In Proceedings of the Conference on Emerging Devices and Smart Systems (ICEDSS), Mallasamudram, India, 3–4 March 2017; pp. 229–233. [Google Scholar] [CrossRef]
- Sakunthala, S.; Kiranmayi, R.; Mandadi, P.N. A study on industrial motor drives: Comparison and applications of PMSM and BLDC motor drives. In Proceedings of the International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 537–540. [Google Scholar] [CrossRef]
- Khambhadiya, H.; Dhaneria, A. Sensorless Control Method of 3-Phase BLDC Motor Through Back-EMF Observer. In Proceedings of the International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Sreeram, K. Design of Fuzzy Logic Controller for Speed Control of Sensorless BLDC Motor Drive. In Proceedings of the International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 18–24. [Google Scholar] [CrossRef]
- Ahsan, M.; Abbas, K.; Zahid, A.; Farooq, A.; Mashhood Murtaza, S. Modification of a toy helicopter into a highly cost effective, semi-autonomous, reconnaissance unmanned aerial vehicle. In Proceedings of the International Conference of Robotics and Artificial Intelligence, Rawalpindi, Pakistan, 22–23 October 2012; pp. 49–54. [Google Scholar] [CrossRef]
- Kudelina, K.; Asad, B.; Vaimann, T.; Belahcen, A.; Rassõlkin, A.; Kallaste, A.; Lukichev, D.V. Bearing Fault Analysis of BLDC Motor for Electric Scooter Application. Designs 2020, 4, 42. [Google Scholar] [CrossRef]
- Chen, C.-H.; Cheng, M.-Y. Implementation of a Highly Reliable Hybrid Electric Scooter Drive. IEEE Trans. Ind. Electron. 2007, 54, 2462–2473. [Google Scholar] [CrossRef]
- Rowe, A.; Sen Gupta, G.; Demidenko, S. Instrumentation and control of a high power BLDC motor for small vehicle applications. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria, 13–16 May 2012; pp. 559–564. [Google Scholar] [CrossRef]
- Shao, J. An Improved Microcontroller-Based Sensorless Brushless DC (BLDC) Motor Drive for Automotive Applications. IEEE Trans. Ind. Appl. 2006, 42, 1216–1221. [Google Scholar] [CrossRef]
- Vishnu Sidharthan, P.; Kashyap, Y. Brushless DC Hub Motor Drive Control for Electric Vehicle Applications. In Proceedings of the 1st International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 448–453. [Google Scholar] [CrossRef]
- Arifiyan, D.; Riyadi, S. Hardware Implementation of Sensorless BLDC Motor Control To Expand Speed Range. In Proceedings of the International Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 21–22 September 2019; pp. 476–481. [Google Scholar] [CrossRef]
- Ctibor, J.; Vorel, P.; Knobloch, J.; Pazdera, I. BLDC Motor Control with Cascade Structure Utilizing ARM MCU. In Proceedings of the International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 61–65. [Google Scholar] [CrossRef]
- Ning, Z.; Chen, L.; Luo, J.; Qi, L. Research on Hardware Controller of BLDC Motor Rehabilitation Robot Based on STM32. In Proceedings of the CIBDA 2022: 3rd International Conference on Computer Information and Big Data Applications, Wuhan, China, 25–27 March 2022; pp. 1–5. [Google Scholar]
- Primiceri, P.; Visconti, P.; Melpignano, A.; Colleoni, G.; Vilei, A. Hardware and software solution developed in ARM mbed environment for driving and controlling DC brushless motors based on ST X-NUCLEO development boards. Int. J. Smart Sens. Intell. Syst. 2016, 9, 1534–1562. [Google Scholar] [CrossRef]
- Joo, J.-H.; Kim, D.-H.; Sim, D.-S.; Choi, J.-K. Design of a DSP controller and driver for the power-by-wire driving system with BLDC servo motor pump. In Proceedings of the 8th Electrical Engineering/ Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand—Conference 2011, Khon Kaen, Thailand, 17–19 May 2011; pp. 573–576. [Google Scholar] [CrossRef]
- Wu, H.-C.; Wen, M.-Y.; Wong, C.-C. Speed control of BLDC motors using hall effect sensors based on DSP. In Proceedings of the International Conference on System Science and Engineering (ICSSE), Puli, Taiwan, 7–9 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Nair, A. Design and development of a TMS320F2812 DSP controller based PM BLDC motor drive. In Proceedings of the International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 776–780. [Google Scholar]
- Mihalache, G.; Ioan, A.-D. FPGA Implementation of BLDC Motor Driver with Hall Sensor Feedback. In Proceedings of the International Conference and Exposition on Electrical And Power Engineering (EPE), Iasi, Romania, 18–19 October 2018; pp. 0624–0629. [Google Scholar] [CrossRef]
- Pindoriya, R.M.; Rajendran, S.; Chauhan, P.J. Field programmable gate array based speed control of BLDC motor. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Schulte, T.; Bracker, J. Real-time simulation of BLDC motors for hardware-in-the-loop applications incorporating sensorless control. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2195–2200. [Google Scholar] [CrossRef]
- Rubaai, A.; Young, P. Hardware/Software Implementation of Fuzzy-Neural-Network Self-Learning Control Methods for Brushless DC Motor Drives. IEEE Trans. Ind. Appl. 2016, 52, 414–424. [Google Scholar] [CrossRef]
- Kumar, K.; Yadav, A.S.; Yadav, A.; Mehdi, A.; Pal, A.; Fouad, L. Speed Analysis of BLDC Motor by Implementation of Fuzzy Logic Based PID Controller. In Proceedings of the 3rd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 12–13 May 2023; pp. 1980–1985. [Google Scholar] [CrossRef]
- Arulmozhiyal, R. Design and Implementation of Fuzzy PID controller for BLDC motor using FPGA. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Mathew, T.; Sam, C.A. Closed loop control of BLDC motor using a fuzzy logic controller and single current sensor. In Proceedings of the International Conference on Advanced Computing and Communication Systems, Coimbatore, India, 19–21 December 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Rajan, A.A.; Raj, R.D.; Vasantharathna, S. Fuzzy based reconfigurable controller for BLDC motor. In Proceedings of the 2nd International conference on Computing, Communication and Networking Technologies, Karur, India, 29–31 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Kumbasar, T.; Hagras, H. A Type-2 Fuzzy Cascade Control Architecture for Mobile Robots. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 3226–3231. [Google Scholar] [CrossRef]
- Siong, T.C.; Ismail, B.; Siraj, S.F.; Mohammed, M.F.; Tajuddin, M.F.N. Implementation of Fuzzy Logic controller for permanent magnet brushless DC motor drives. In Proceedings of the IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 462–467. [Google Scholar] [CrossRef]
- Derugo, P.; Szabat, K.; Pajchrowski, T.; Zawirski, K. Fuzzy Adaptive Type II Controller for Two-Mass System. Energies 2022, 15, 419. [Google Scholar] [CrossRef]
- Asere, H.; Lei, C.; Jia, R. Cruise Control Design Using Fuzzy Logic Controller. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2210–2215. [Google Scholar] [CrossRef]
- Nagadurga, T.; Devarapalli, R.; Knypiński, Ł. Comparison of Meta-Heuristic Optimization Algorithms for Global Maximum Power Point Tracking of Partially Shaded Solar Photovoltaic Systems. Algorithms 2023, 16, 376. [Google Scholar] [CrossRef]
- Priyadarshini, J.; Premalatha, M.; Cep, R.; Jayasudha, M.; Kalita, K. Analyzing Physics-Inspired Metaheuristic Algorithms in Feature Selection with K-Nearest-Neighbor. Appl. Sci. 2023, 13, 906. [Google Scholar] [CrossRef]
- Alehin, R.A.; Kubarkov, Y.P.; Zakamov, D.V.; Umyarov, D.V. Overview of metaheuristic optimization techniques applied to solving power engineering problems. Tech. Sci. Ser. 2019, 27, 6–19. [Google Scholar] [CrossRef]
- Vais, R.; Sahay, K.; Chiranjeevi, T.; Devarapalli, R.; Knypiński, Ł. Parameter Extraction of Solar Photovoltaic Modules Using a Novel Bio-Inspired Swarm Intelligence Optimisation Algorithm. Sustainability 2023, 15, 8407. [Google Scholar] [CrossRef]
- Soler-Dominguez, A.; Juan, A.A.; Kizys, R. A Survey on Financial Applications of Metaheuristics. ACM Comput. Surv. 2018, 50, 15. [Google Scholar] [CrossRef]
- Kaur, S.; Kumar, Y.; Koul, A.; Kumar Kamboj, S. A Systematic Review on Metaheuristic Optimization Techniques for Feature Selections in Disease Diagnosis: Open Issues and Challenges. Arch. Comput. Methods Eng. 2023, 30, 1863–1895. [Google Scholar] [CrossRef]
- Dhawan, S.; Gupta, R.; Rana, A.; Sharma, S. Various Swarm Optimization Algorithms: Review, Challenges, and Opportunities. In Soft Computing for Intelligent Systems. Algorithms for Intelligent Systems; Marriwala, N., Tripathi, C.C., Jain, S., Mathapathi, S., Eds.; Springer: Singapore, 2021. [Google Scholar]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Carev, V.; Roháč, J.; Šipoš, M.; Schmirler, M. A Multilayer Brushless DC Motor for Heavy Lift Drones. Energies 2021, 14, 2504. [Google Scholar] [CrossRef]
- Zaharia, S.M.; Pop, M.A.; Buican, G.R.; Chicos, L.A.; Stamate, V.M.; Pascariu, I.S.; Lancea, C. Design and Testing of Brushless DC Motor Components of A6 Steel Additively Manufactured by Selective Laser Sintering. Aerospace 2023, 10, 60. [Google Scholar] [CrossRef]
- Vanus, J.; Bilik, P. Research on Micro-Mobility with a Focus on Electric Scooters within Smart Cities. World Electr. Veh. J. 2022, 13, 176. [Google Scholar] [CrossRef]
- Kim, H.J.; Park, H.S.; Kim, J.M. Expansion of Operating Speed Range of High-Speed BLDC Motor Using Hybrid PWM Switching Method Considering Dead Time. Energies 2020, 13, 5212. [Google Scholar] [CrossRef]
- Dumitrescu, C.; Ciotirnae, P.; Vizitiu, C. Fuzzy Logic for Intelligent Control System Using Soft Computing Applications. Sensors 2021, 21, 2617. [Google Scholar] [CrossRef] [PubMed]
- Zahreddine, Z. Symmetric Properties of Routh–Hurwitz and Schur–Cohn Stability Criteria. Symmetry 2022, 14, 603. [Google Scholar] [CrossRef]
- Frutos, P.; Ladoux, P.; Roux, N.; Larrazabal, I.; Guerrero, J.M.; Briz, F. Low Frequency Stability of AC Railway Traction Power Systems: Analysis of the Influence of Traction Unit Parameters. Electronics 2022, 11, 1593. [Google Scholar] [CrossRef]
- Taieb, A.; Salhi, H.; Chaari, A. Adaptive TS fuzzy MPC based on Particle Swarm Optimization-Cuckoo Search algorithm. ISA Trans. 2022, 131, 598–609. [Google Scholar] [CrossRef]
- Precup, R.E.; Tomescu, M.L.; Preitl, S. Fuzzy Logic Control System Stability Analysis Based on Lyapunov’s Direct Method. J. Comput. Commun. Control 2009, 4, 415–426. [Google Scholar] [CrossRef]
- Voloşencu, C. Stability Analysis of Systems with Fuzzy PI Controllers Applied to Electric Drives. Mathematics 2021, 9, 1246. [Google Scholar] [CrossRef]
- Castillo, O.; Aguilar, L.; Cázarez, N.; Cárdenas, S. Systematic design of a stable type-2 fuzzy logic controller. J. Appl. Soft Comput. 2008, 8, 1274–1279. [Google Scholar] [CrossRef]
- Kos, T.; Huba, M.; Vrančić, D. Parametric and Nonparametric PI Controller Tuning Method for Integrating Processes Based on Magnitude Optimum. Appl. Sci. 2020, 10, 1443. [Google Scholar] [CrossRef]
- Feng, W.; Bai, J.; Zhang, Z.; Zhang, J. A Composite Variable Structure PI Controller for Sensorless Speed Control Systems of IPMSM. Energies 2022, 15, 8292. [Google Scholar] [CrossRef]
- Szczepanski, R.; Kaminski, M.; Tarczewski, T. Auto-Tuning Process of State Feedback Speed Controller Applied for Two-Mass System. Energies 2020, 13, 3067. [Google Scholar] [CrossRef]
- Morar, D.; Mihaly, V.; Şuşcă, M.; Dobra, P. Cascade Control for Two-Axis Position Mechatronic Systems. Fractal Fract. 2023, 7, 122. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration Suppression in Two-Mass Drive System Using PI Speed Controller and Additional Feedbacks-Comparative Study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Zawirski, K.; Nowopolski, K.; Siwek, P. Application of Cuckoo Search Algorithm for Speed Control Optimization in Two-Sided Electrical Drive. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018; pp. 651–656. [Google Scholar] [CrossRef]
- Lotfi, C.; Youcef, Z.; Marwa, A.; Schulte, H.; Riad, B.; El-Arkam, M. Optimization of a Speed Controller of a DFIM with Metaheuristic Algorithms. Eng. Proc. 2023, 29, 29013. [Google Scholar] [CrossRef]
- Rodríguez-Molina, A.; Gabriel Villarreal-Cervantes, M.; Aldape-Pérez, M. An adaptive control study for a DC motor using meta-heuristic algorithms. IFACPapersOnLine 2017, 50, 13114–13120. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Dafinescu, V. Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 2021, 9, 2335. [Google Scholar] [CrossRef]
- Safi, S.A.; Castillo, P.A.; Faris, H. Cost-Sensitive Metaheuristic Optimization-Based Neural Network with Ensemble Learning for Financial Distress Prediction. Appl. Sci. 2022, 12, 6918. [Google Scholar] [CrossRef]
- Vasiliadis, V.; Dounias, G. Applications of Nature-Inspired Intelligence in Finance. In Proceedings of the 2007 IFIP International Conference on Artificial Intelligence Applications and Innovations, Athens, Greece, 19–21 September 2007; pp. 187–194. [Google Scholar] [CrossRef]
- Santos, E.S.d.; Nunes, M.V.A.; Nascimento, M.H.R.; Leite, J.C. Rational Application of Electric Power Production Optimization through Metaheuristics Algorithm. Energies 2022, 15, 3253. [Google Scholar] [CrossRef]
- Chicco, G.; Mazza, A. Metaheuristic Optimization of Power and Energy Systems: Underlying Principles and Main Issues of the ‘Rush to Heuristics’. Energies 2020, 13, 5097. [Google Scholar] [CrossRef]
- Cao, T.S.; Nguyen, T.T.T.; Nguyen, V.S.; Truong, V.H.; Nguyen, H.H. Performance of Six Metaheuristic Algorithms for Multi-Objective Optimization of Nonlinear Inelastic Steel Trusses. Buildings 2023, 13, 868. [Google Scholar] [CrossRef]
- Braik, M.S. Chameleon Swarm Algorithm: A bio-inspired optimizer for solving engineering design problems. Expert Syst. Appl. 2021, 174, 114685. [Google Scholar] [CrossRef]
- Uluslu, A. Chameleon Swarm Algorithm assisted optimization of U-slot patch antenna for quad-band applications. IEEE Access 2022, 10, 74152–74163. [Google Scholar] [CrossRef]
- Sun, Y.; Cheng, Y.; Liu, T.; Huang, Q.; Guo, J.; Jin, W. Research on Signal Detection of OFDM Systems Based on the LSTM Network Optimized by the Improved Chameleon Swarm Algorithm. Mathematics 2023, 11, 1989. [Google Scholar] [CrossRef]
- Hamza, M.A.; Al-Otaibi, S.; Althahabi, S.; Alzahrani, J.S.; Mohamed, A.; Motwakel, A.; Zamani, A.S.; Eldesouki, M.I. Improved Chameleon Swarm Optimization-Based Load Scheduling for IoT-Enabled Cloud Environment. Comput. Syst. Sci. Eng. 2023, 46, 1371–1383. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, L.; Han, X.; Wang, Y.; Zhang, Y.; Jia, Z. Adaptive Density Spatial Clustering Method Fusing Chameleon Swarm Algorithm. Entropy 2023, 25, 782. [Google Scholar] [CrossRef]
- Malarczyk, M.; Kaminski, M.; Szrek, J. Metaheuristic Approach to Synthesis of Suspension System of Mobile Robot for Mining Infrastructure Inspection. Sensors 2022, 22, 8839. [Google Scholar] [CrossRef]
- Tarchała, G.; Orłowska-Kowalska, T. Discrete Sliding Mode Speed Control of Induction Motor Using Time-Varying Switching Line. Electronics 2020, 9, 185. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Wu, C.; Cui, Z.; Niu, C. A new lightweight deep neural network for surface scratch detection. Int. J. Adv. Manuf. Technol. 2022, 123, 1999–2015. [Google Scholar] [CrossRef]
- Khaing, C.C.; Thein, T.L.L. Prediction of Rainfall Based on Deep Learning and Internet of Things to Prevent Landslide. In Proceedings of the IEEE 9th Global Conference on Consumer Electronics (GCCE), Kobe, Japan, 13–16 October 2020; pp. 190–191. [Google Scholar] [CrossRef]








| e | u | |
|---|---|---|
| N | PB | PB |
| N | P | PB |
| N | PB | P |
| N | P | P |
| N | PB | N |
| N | P | 0 |
| N | PB | 0 |
| N | 0 | PB |
| N | 0 | P |
| N | 0 | 0 |
| N | N | PB |
| P | N | N |
| P | N | NB |
| P | NB | N |
| P | NB | NB |
| P | 0 | N |
| P | 0 | NB |
| P | NB | 0 |
| P | N | 0 |
| P | NB | P |
| P | P | NB |
| Parameter | Lower Boundary | Upper Boundary |
|---|---|---|
| 0.001 | 10 | |
| 0.001 | 10 | |
| 0.001 | 1000 |
| Parameter | Value |
|---|---|
| 0.001 s | |
| 0.016 s | |
| 0.001 s |
| Device | Raspberry Pi 4B | STM32 Nucleo 64 | STM32 Nucleo 32 |
|---|---|---|---|
| Power consumption | 15 W | <1 W | <1 W |
| Core | Chipset Broadcom BCM2711 with 64-bit Quad-Core ARM-8 Cortex A-72 CPU | ARM Cortex M4 | ARM Cortex M4 |
| Clock rate | 1.5 GHz | 180 MHz | 80 MHz |
| User memory size | External SD memory | 512 kB | 256 kB |
| RAM | 2 GB (up to 8 GB, depending on version) | 128 kB | 64 kB |
| Parameter | Value |
|---|---|
| Model | 42BLF01 |
| Number of Poles | 8 |
| Rated voltage | 24 V |
| Rated speed | 4000 rpm |
| Rated current | 1.9 A |
| Maximum power | 26 W |
| Maximum torque | 0.18 Nm |
| Back-EMF | 3.7 V/kRPM |
| Torque constant | 0.035 Nm/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarczyk, G.; Malarczyk, M.; Ferreira, D.D.; Kaminski, M. Stable Rules Definition for Fuzzy TS Speed Controller Implemented for BLDC Motor. Appl. Sci. 2024, 14, 982. https://doi.org/10.3390/app14030982
Kaczmarczyk G, Malarczyk M, Ferreira DD, Kaminski M. Stable Rules Definition for Fuzzy TS Speed Controller Implemented for BLDC Motor. Applied Sciences. 2024; 14(3):982. https://doi.org/10.3390/app14030982
Chicago/Turabian StyleKaczmarczyk, Grzegorz, Mateusz Malarczyk, Danton Diego Ferreira, and Marcin Kaminski. 2024. "Stable Rules Definition for Fuzzy TS Speed Controller Implemented for BLDC Motor" Applied Sciences 14, no. 3: 982. https://doi.org/10.3390/app14030982
APA StyleKaczmarczyk, G., Malarczyk, M., Ferreira, D. D., & Kaminski, M. (2024). Stable Rules Definition for Fuzzy TS Speed Controller Implemented for BLDC Motor. Applied Sciences, 14(3), 982. https://doi.org/10.3390/app14030982






