A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka
Abstract
1. Introduction
1.1. Background
1.2. Related Work
2. Materials and Methods
2.1. Proposed Methodology
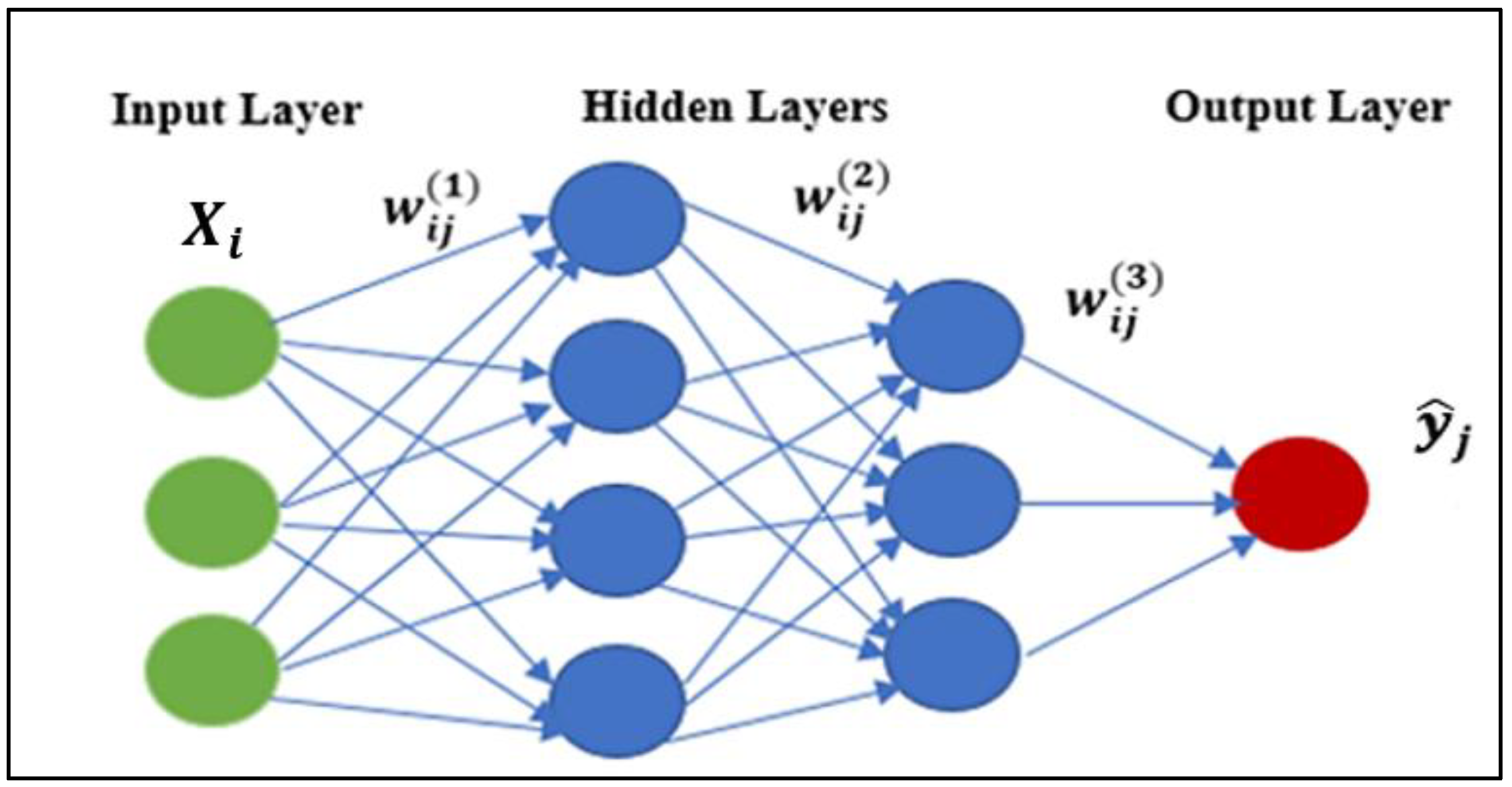
2.1.1. Multi-Layer Perceptron Neural Network
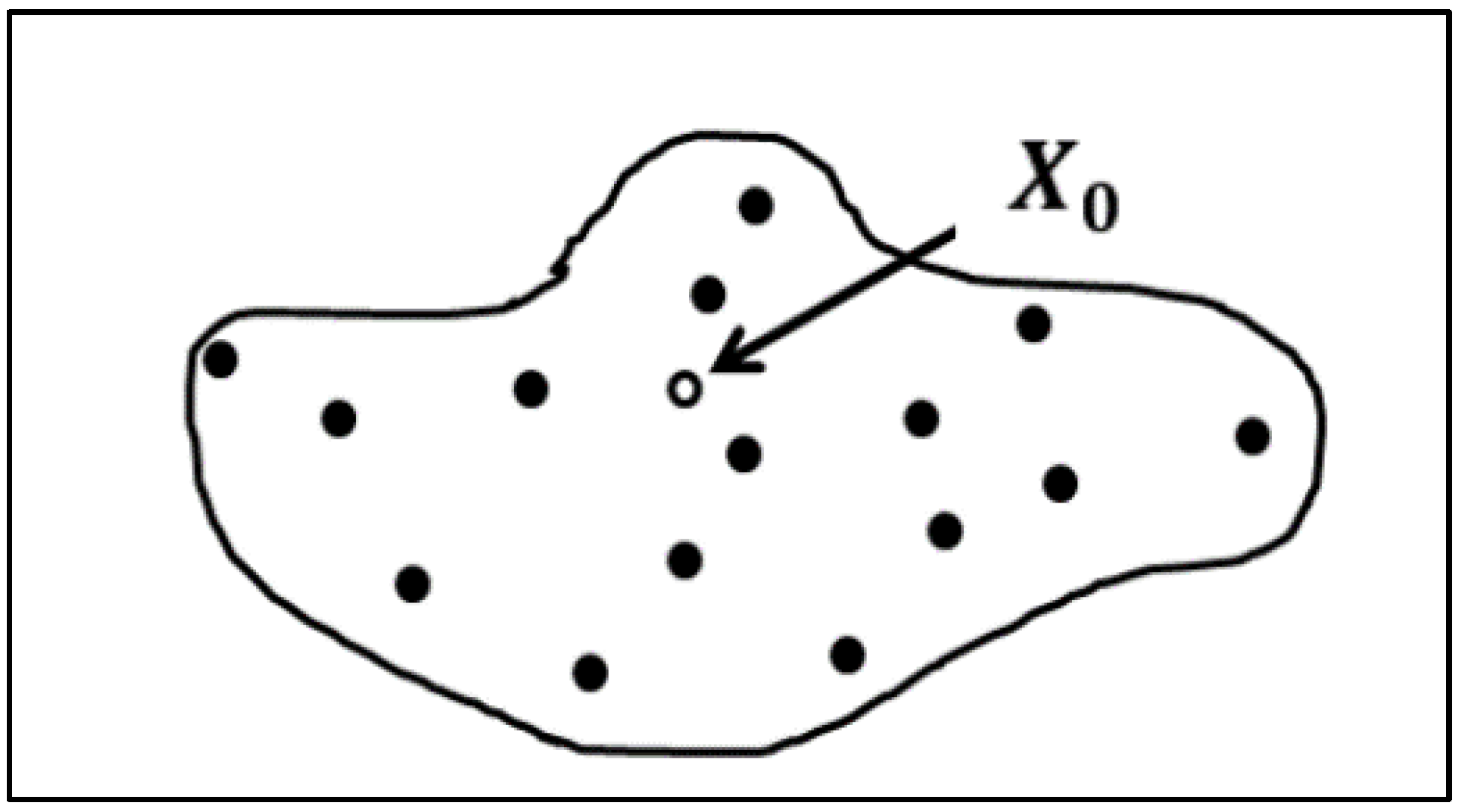
2.1.2. Spatial Kriging
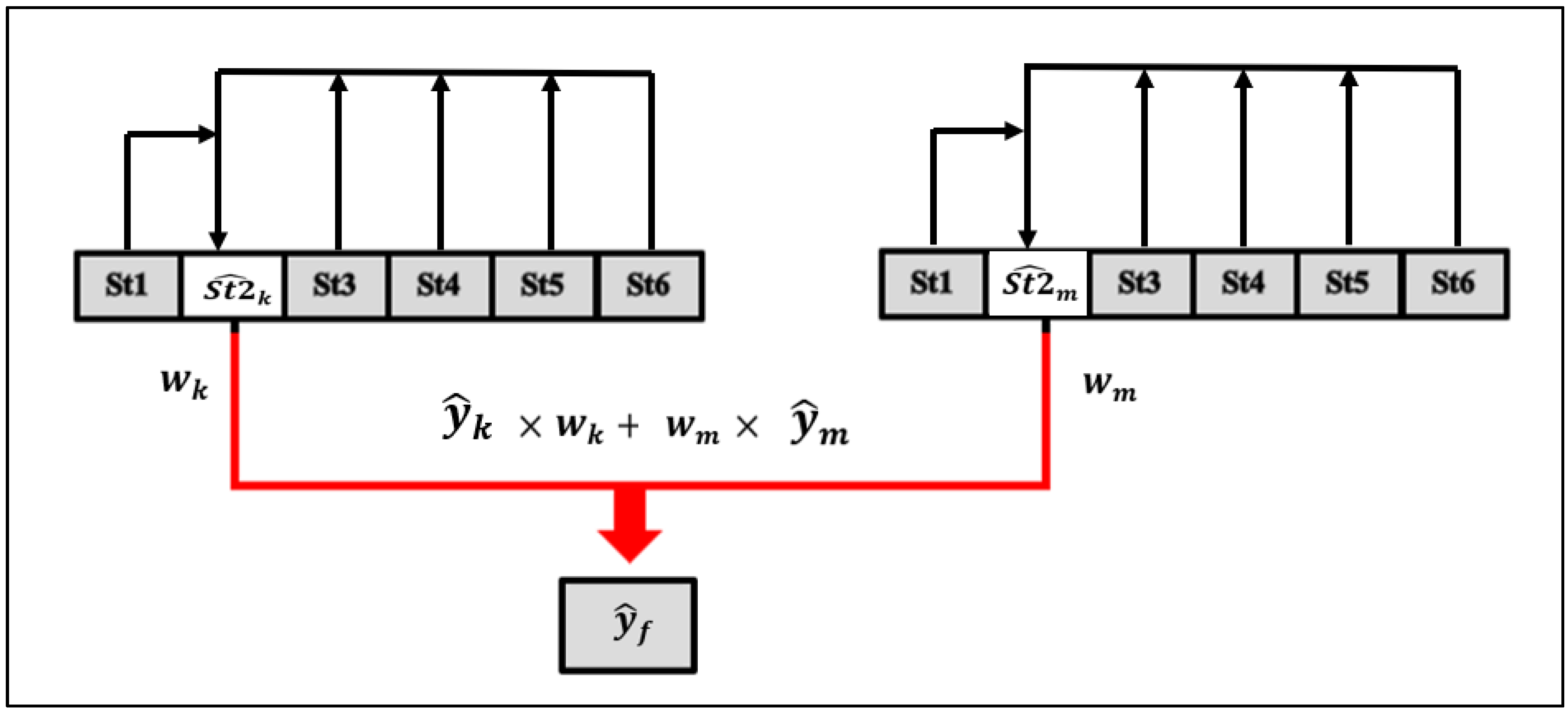
2.1.3. Hybrid Model for Missing Value Estimation
2.1.4. Spatiotemporal Kriging
2.1.5. Model Evaluation
2.2. Description of Data
3. Results and Discussion
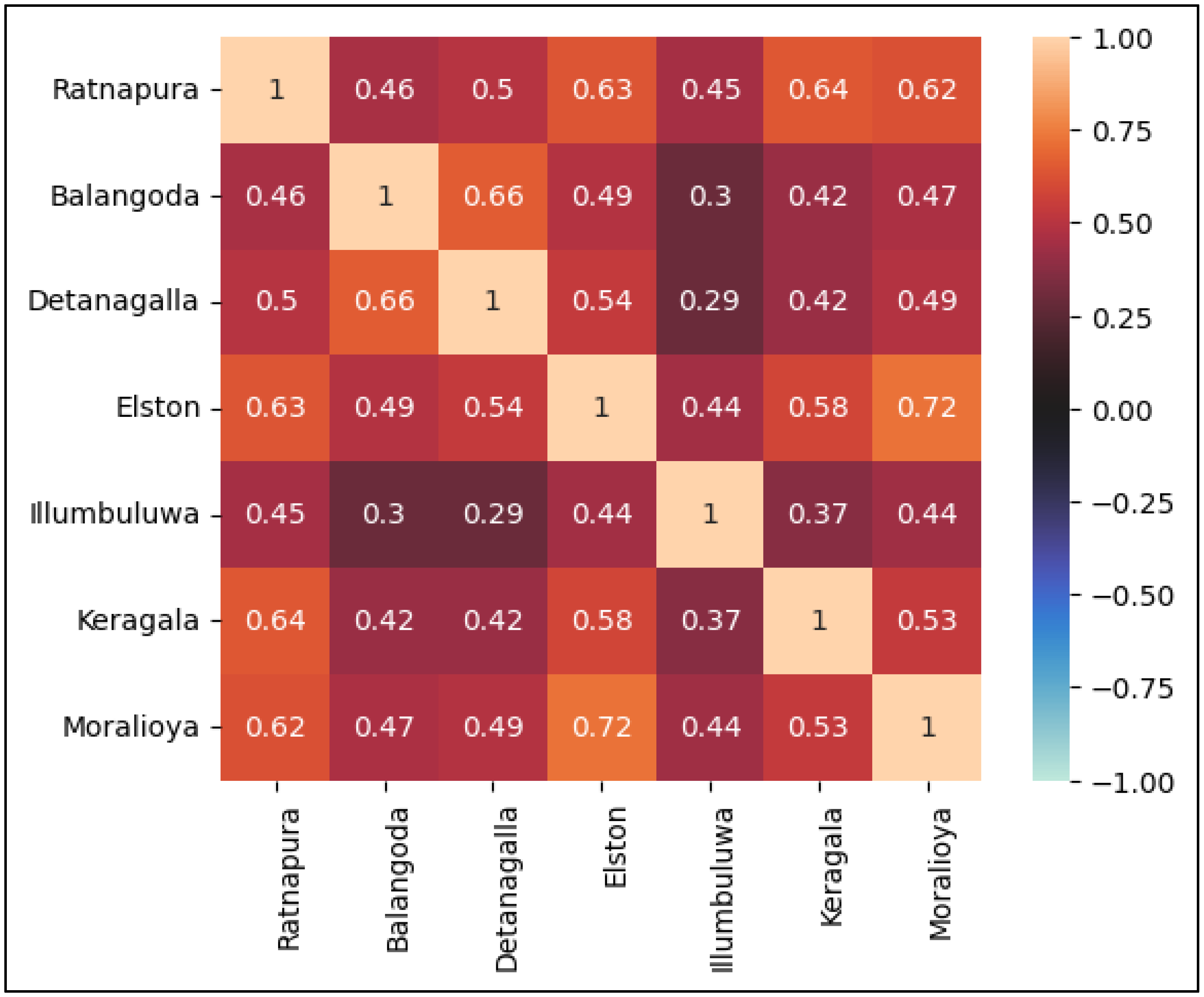
3.1. Preliminary Analysis
3.2. The Hybrid Model Formation
- (a)
- From the original data set, three complete subsets (with no missing cases for all the stations) were selected. Consequently, subsets from the years 2015, 2016, and 2019 were selected.
- (b)
- Consecutive missing periods were artificially created randomly within the three subsets to capture the missing pattern of the original data set.
- (c)
- The spatial kriging and MLP were applied to estimate the missing cases.
- (d)
- Those estimated rainfall values were combined to form a single data set of 120 estimated rainfall values.
- (e)
- Then, from the final data set mentioned in (d), 100 simple random samples (with replacement) with a moderate sample size of 60 were drawn.
- (f)
- For each sample, the optimal values of two weights, and were calculated by applying Equations (11) and (12) as described in Section 2.1.3. The procedure resulted in 100 optimal pairs of weights.
- (g)
- Then, the first optimal weight pair was used to calculate the weighted estimates () of the rest of the samples (99). For each sample, the RMSE values (including the first sample considered) were calculated. Using these RMSE values, the average RMSE was computed.
- (h)
- Likewise, steps (a) to (g) were repeated using the second optimal weight pair, then third optimal weight pair, and so on.
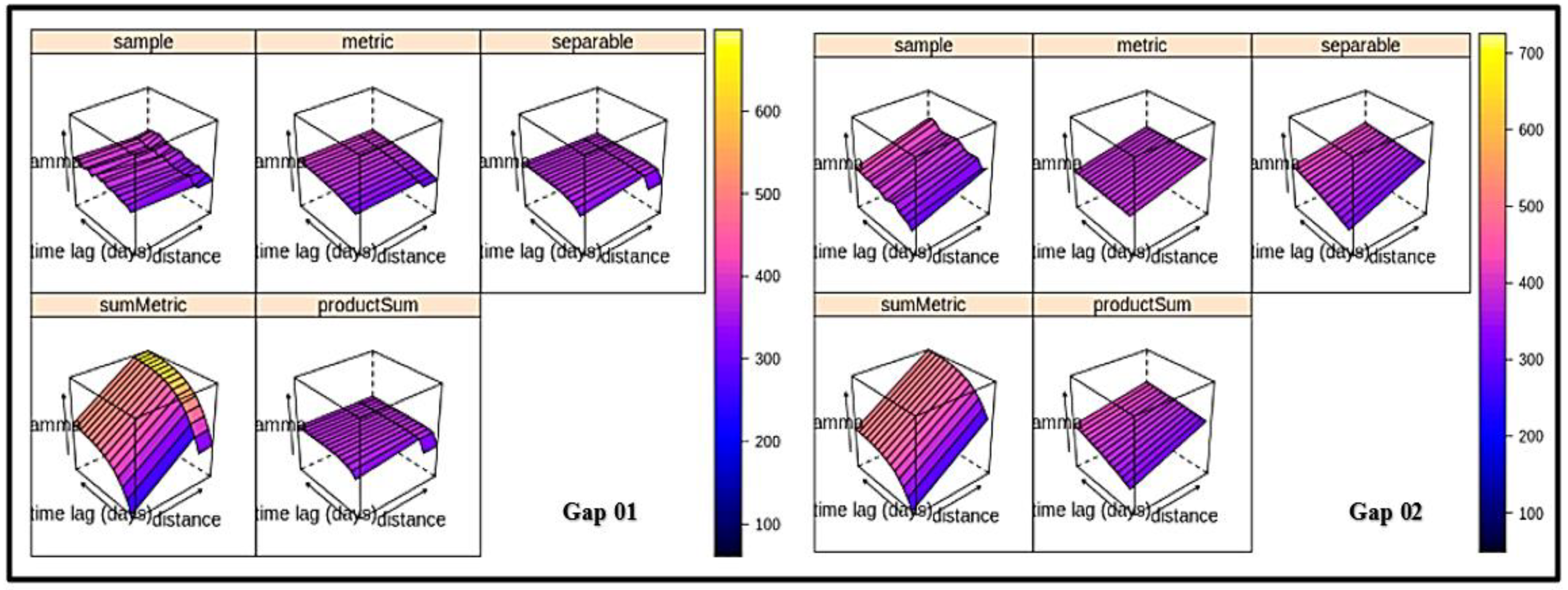
3.3. The Spatiotemporal Kriging Model (SPTK Model)
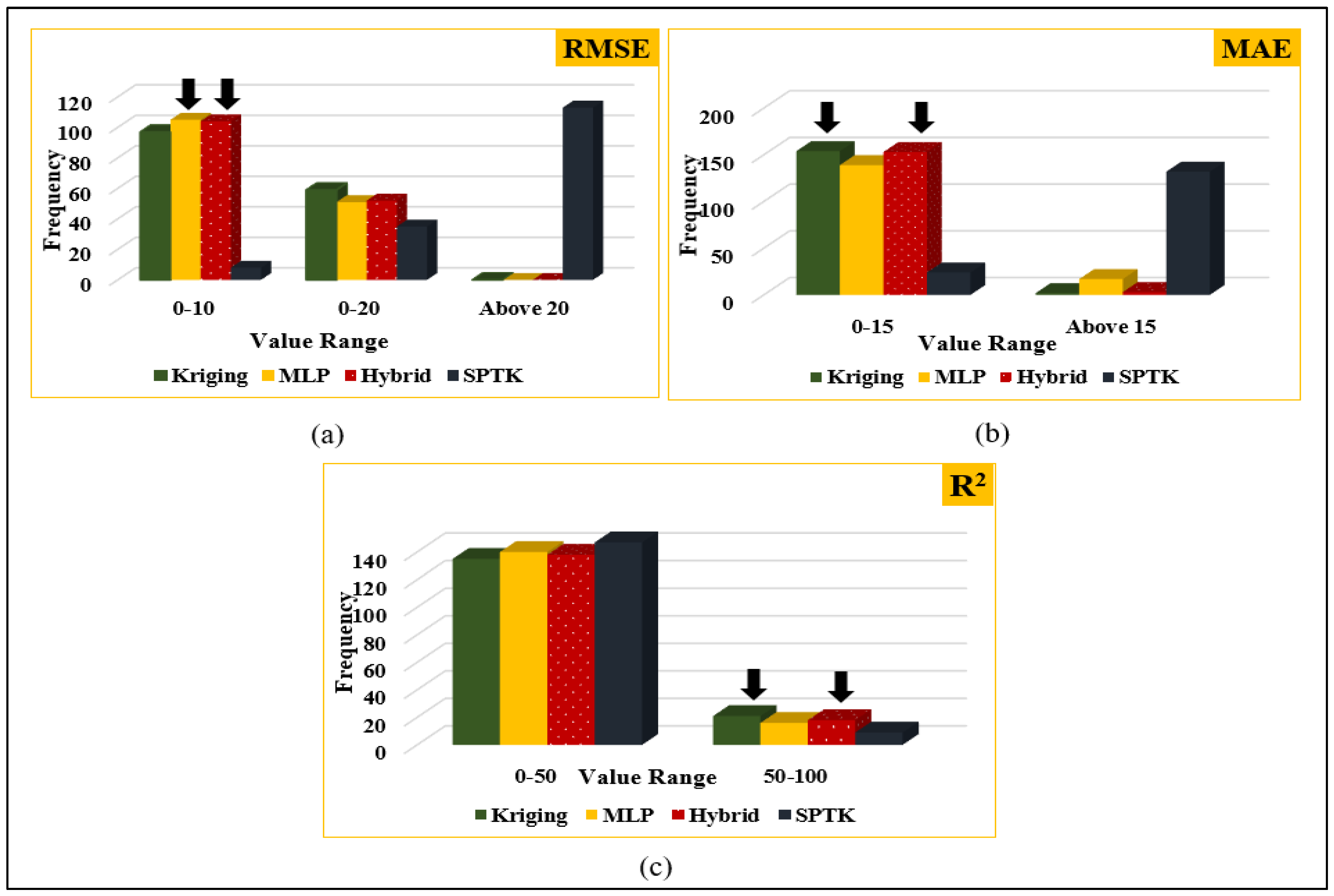
3.4. Model Evaluation
3.4.1. Model Evaluation along with Actual Missing Data
3.4.2. Model Evaluation on Artificially Generated Missing Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mital, U.; Dwivedi, D.; Brown, J.B.; Faybishenko, B.; Painter, S.L.; Steefel, C.I. Sequential Imputation of Missing Spatio-Temporal Precipitation Data Using Random Forests. Front. Water 2020, 2, 20. [Google Scholar] [CrossRef]
- Asadi, R.; Regan, A. A convolution recurrent autoencoder for spatio-temporal missing data imputation. arXiv 2019, arXiv:1904.12413. [Google Scholar]
- Soley-Bori, M. Dealing with Missing Data: Key Assumptions and Methods for Applied Analysis; Boston University: Boston, MA, USA, 2013; Volume 4, pp. 1–19. [Google Scholar]
- Yang, H.; Yang, J.; Han, L.; Liu, X.; Pu, L.; Chin, S.; Hwang, H. A Kriging based spatiotemporal approach for traffic volume data imputation. PLoS ONE. 2018, 13, e0195957. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A. A New Approach to Spatio-Temporal Kriging and Its Applications. Master’s Thesis, Ohio State University, OhioLINK Electronic Theses and Dissertations Center, Columbus, OH, USA, 2011. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=osu1306871646 (accessed on 18 November 2023).
- Aguilera, H.; Guardiola-Albert, C.; Hidalgo, C.S. Estimating extremely large amounts of missing precipitation data. J. Hydroinformatics 2020, 22, 578–592. [Google Scholar] [CrossRef]
- Feng, L.; Nowak, G.; O’Neill, T.J.; Welsh, A. CUTOFF: A spatio-temporal imputation method. J. Hydrol. 2014, 519, 3591–3605. [Google Scholar] [CrossRef]
- Hettiarachchi, P. Inundation Maps of the Kalu Ganga Basin during the Flood in May 2003; Department of Irrigation: Colombo, Sri Lanka, 2013. [Google Scholar]
- Nandalal, K.D.W. Use of a hydrodynamic model to forecast floods of Kalu River in Sri Lanka. J. Flood Risk Manag. 2009, 2, 151–158. [Google Scholar] [CrossRef]
- Rafii, F.; Kechadi, T. Collection of historical weather data: Issues with missing values. In Proceedings of the 4th International Conference on Smart City Applications (SCA’19), Casablanca, Morocco, 2–4 October 2019. [Google Scholar]
- Burhanuddin, A.; Zahrah, S.N.; Deni, S.; Ramli, N.M. Imputation of Missing Rainfall Data Using Revised Normal Ratio Method. Adv. Sci. Lett. 2017, 23, 10981–10985. [Google Scholar] [CrossRef]
- Jahan, F.; Sinha, N.; Rahman, M.; Rahman, M.M.; Mondal, M.S.; Islam, M. Comparison of Missing Value Estimation Techniques in Rainfall Data of Bangladesh. Theor. Appl. Climatol. 2019, 136, 1–17. [Google Scholar] [CrossRef]
- Ahmad, R.; Noor, F.; Zakaria, R.; Azman, M.A. Estimation of missing rainfall data using spatial interpolation and imputation methods. AIP Conf. Proc. 2015, 1643, 42–48. [Google Scholar] [CrossRef]
- Gad, I.; Doreswamy, H.; Manjunatha, B. A robust deep learning model for missing value imputation in big NCDC dataset. Iran J. Comput. Sci. 2021, 4, 67–84. [Google Scholar] [CrossRef]
- Afrifa-Yamoah, E.; Mueller, U.; Taylor, S.; Fisher, A. Missing data imputation of high-resolution temporal climate time series data. Meteorol. Appl. 2020, 27, e1873. [Google Scholar] [CrossRef]
- Nassir, S.; Badr, A.; Mousa, W. Estimation the Missing Data of Meteorological Variables in Different Iraqi Cities By using ARIMA Model. Iraqi J. Sci. 2018, 59, 792–801. [Google Scholar]
- Medeiros, E.; De Lima, R.; Olinda, R.; Santos, C. Modeling Spatiotemporal Rainfall Variability in Paraíba, Brazil. Water 2019, 11, 1843. [Google Scholar] [CrossRef]
- Cuenca, J.; Correa-Flórez, C.; Patino, D.; Vuelvas, J. Spatio-Temporal Kriging Based Economic Dispatch Problem Including Wind Uncertainty. Energies. 2020, 13, 6419. [Google Scholar] [CrossRef]
- Duan, Y.; Lv, Y.; Liu, Y. An efficient realization of deep learning for traffic data imputation. Transp. Res. Part C Emerg. Technol. 2016, 72, 168–181. [Google Scholar] [CrossRef]
- Zoest, V.V.; Osei, F.; Hoek, G.; Stein, A. Spatio-temporal regression Kriging for modelling urban NO2 concentrations Spatio-temporal regression Kriging for modelling urban NO2 concentrations. Int. J. Geogr. Inf. Sci. 2019, 34, 851–865. [Google Scholar] [CrossRef]
- Bae, B.; Kim, H.; Lim, H.; Liu, Y.; Han, L.; Freeze, P. Missing data imputation for traffic flow speed using spatio-temporal cokriging. Transp. Res. Part C Emerg. Technol. 2018, 88, 124–139. [Google Scholar] [CrossRef]
- Srinivasan, B.; Duraiswami, R.; Murtugudde, R. Efficient Kriging for real-time spatio-temporal interpolation. In Proceedings of the 20th Conference on Probability and Statistics in the Atmospheric Sciences, Atlanta, Georgia, 18–21 January 2010; p. 228. [Google Scholar]
- Abirami, S.P.; Chitra, P. Chapter Fourteen-Energy-efficient edge based real-time healthcare support system. Adv. Comput. 2020, 117, 339–368. [Google Scholar]
- Orhan, U.; Hekim, M.; Ozer, M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model. Expert Syst. Appl. 2011, 38, 13475–13481. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Grosse, R. Lecture 5: Multilayer Perceptrons. 2018. Available online: https://www.cs.toronto.edu/~rgrosse/courses/csc321_2018/readings/L05%20Multilayer%20Perceptrons.pdf (accessed on 16 January 2022).
- Zhou, Y.; Guan, Z.; Ji, P.; Wang, X. Drug Abuse Prediction Model Based on Relevance Analysis. In Data Processing Techniques and Applications for Cyber-Physical Systems (DPTA 2019)–Advances in Intelligent Systems and Computing; Huang, C., Chan, Y.W., Yen, N., Eds.; Springer: Singapore, 2020; Volume 1088. [Google Scholar] [CrossRef]
- Jeewanthi, P.W.; Wijesuriya, W.; Liyanarachchi, L.A.T.S.; Gunatathne, L.H.P. Appropriate conventional methods forestimating missing precipitation values in Sri Lanka. J. Agric. Value Addit. 2023, 5, 45–53. [Google Scholar] [CrossRef]



| Sub Station | Missing Count | Missing Percentage |
|---|---|---|
| St1_Bal | 32 | 1.75 |
| St2_Det | 1 | 0.05 |
| St3_Els | 519 | 28.42 |
| St4_Ill | 491 | 26.89 |
| St5_Ker | 123 | 6.74 |
| St6_Mor | 183 | 10.02 |
| St7_Niv | 1249 | 68.4 |
| St8_Uli | 1343 | 73.55 |
| Parameters | Value |
|---|---|
| Activation function | ReLU |
| Epochs | 80 |
| Number of hidden layers | 1 |
| Number of neurons in hidden layer | 20 |
| Batch size | 72 |
| Learning rate | 0.01 |
| Optimizer | Adam |
| Loss Function | MAE |
| Gap no | Metric | Separable | SumMetric | Product Sum |
|---|---|---|---|---|
| 1 | 13.79 | 23.16 | 64.75 | 23.33 |
| 2 | 38.56 | 22.871 | 52.43 | 22.868 |
| 3 | 15.46 | 16.19 | 31.14 | 16.25 |
| 4 | 30.31 | 30.86 | 71.54 | 30.82 |
| 5 | 136.15 | 132.79 | 128.77 | 132.79 |
| 6 | 17.53 | 10.03 | 31.8 | 9.99 |
| 7 | 11.02 | 9.67 | 9.13 | 9.66 |
| 8 | 88.75 | 89.13 | 110.29 | 89.28 |
| 9 | 21.58 | 21.95 | 41.33 | 22.13 |
| 10 | 81.02 | 81.03 | 118.85 | 81.04 |
| 11 | 34.95 | 13.54 | 58.8 | 13.63 |
| Method | Spatial Kriging | MLP | Hybrid | SPTK |
|---|---|---|---|---|
| RMSE | 12.76 | 11.68 | 10.72 | 15.97 |
| MAE | 7.12 | 4.01 | 5.12 | 10.25 |
| R2 | 13% | 3% | 13% | 0% |
| Number Stations with Missing Observations (M) | Number of Combinations (of Stations) |
|---|---|
| 01 | 6C1 = 6 |
| 02 | 6C2 = 15 |
| 03 | 6C3 = 20 |
| 04 | 6C4 = 15 |
| Total number of data sets | 56 |
| Method | Kriging | MLP | Hybrid | SPTK |
|---|---|---|---|---|
| No. of times that each approach produced best results (as a percentage with respect to the sum of trials) | 30 | 20 | 41 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saubhagya, S.; Tilakaratne, C.; Lakraj, P.; Mammadov, M. A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka. Appl. Sci. 2024, 14, 999. https://doi.org/10.3390/app14030999
Saubhagya S, Tilakaratne C, Lakraj P, Mammadov M. A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka. Applied Sciences. 2024; 14(3):999. https://doi.org/10.3390/app14030999
Chicago/Turabian StyleSaubhagya, Shanthi, Chandima Tilakaratne, Pemantha Lakraj, and Musa Mammadov. 2024. "A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka" Applied Sciences 14, no. 3: 999. https://doi.org/10.3390/app14030999
APA StyleSaubhagya, S., Tilakaratne, C., Lakraj, P., & Mammadov, M. (2024). A Novel Hybrid Spatiotemporal Missing Value Imputation Approach for Rainfall Data: An Application to the Ratnapura Area, Sri Lanka. Applied Sciences, 14(3), 999. https://doi.org/10.3390/app14030999






