Optimization of DLTS Hinges for the Assembly of the Solar Arrays of a Communication CubeSat
Abstract
:1. Introduction
2. Methodology
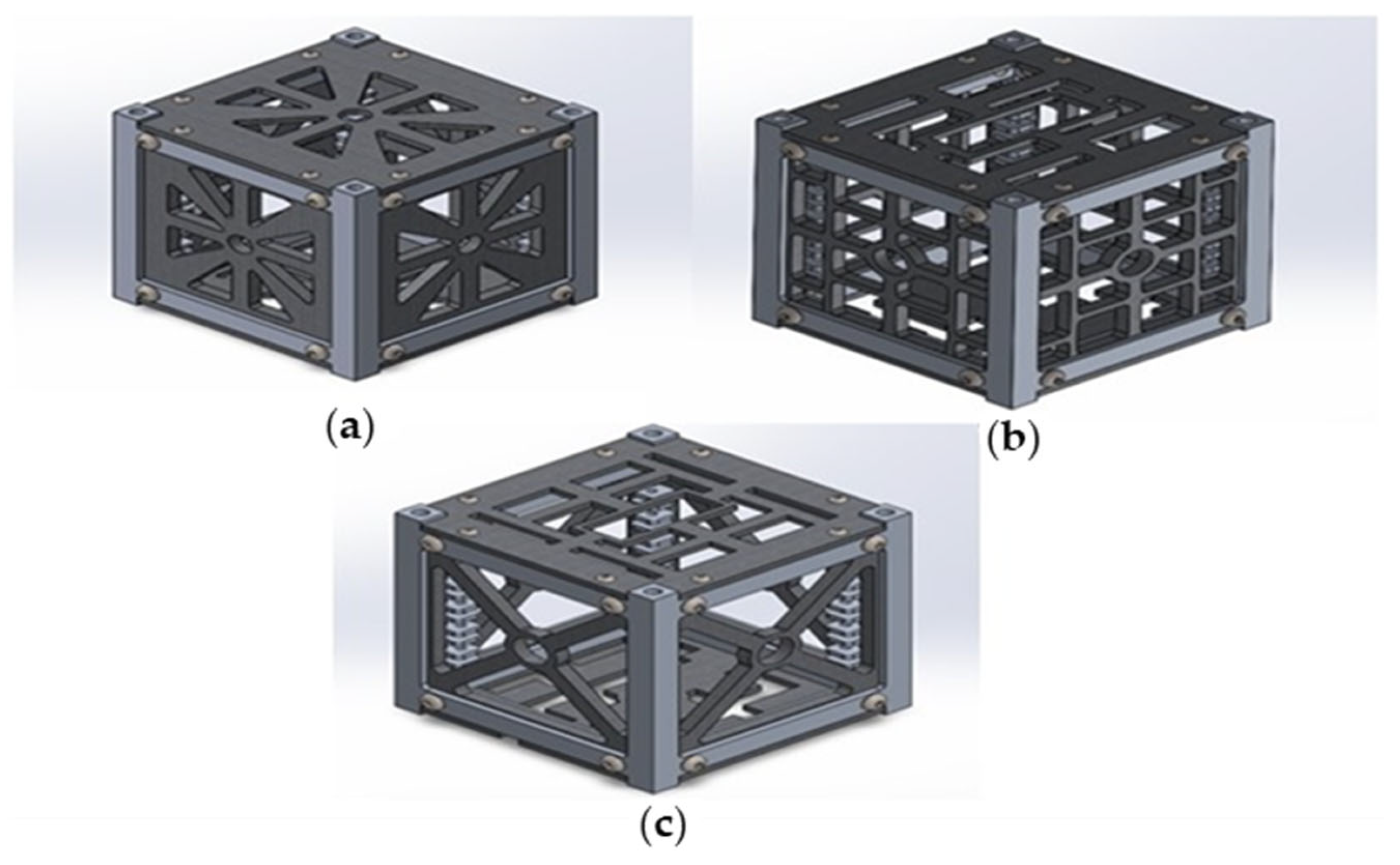
2.1. General Design Objectives of CubeSat
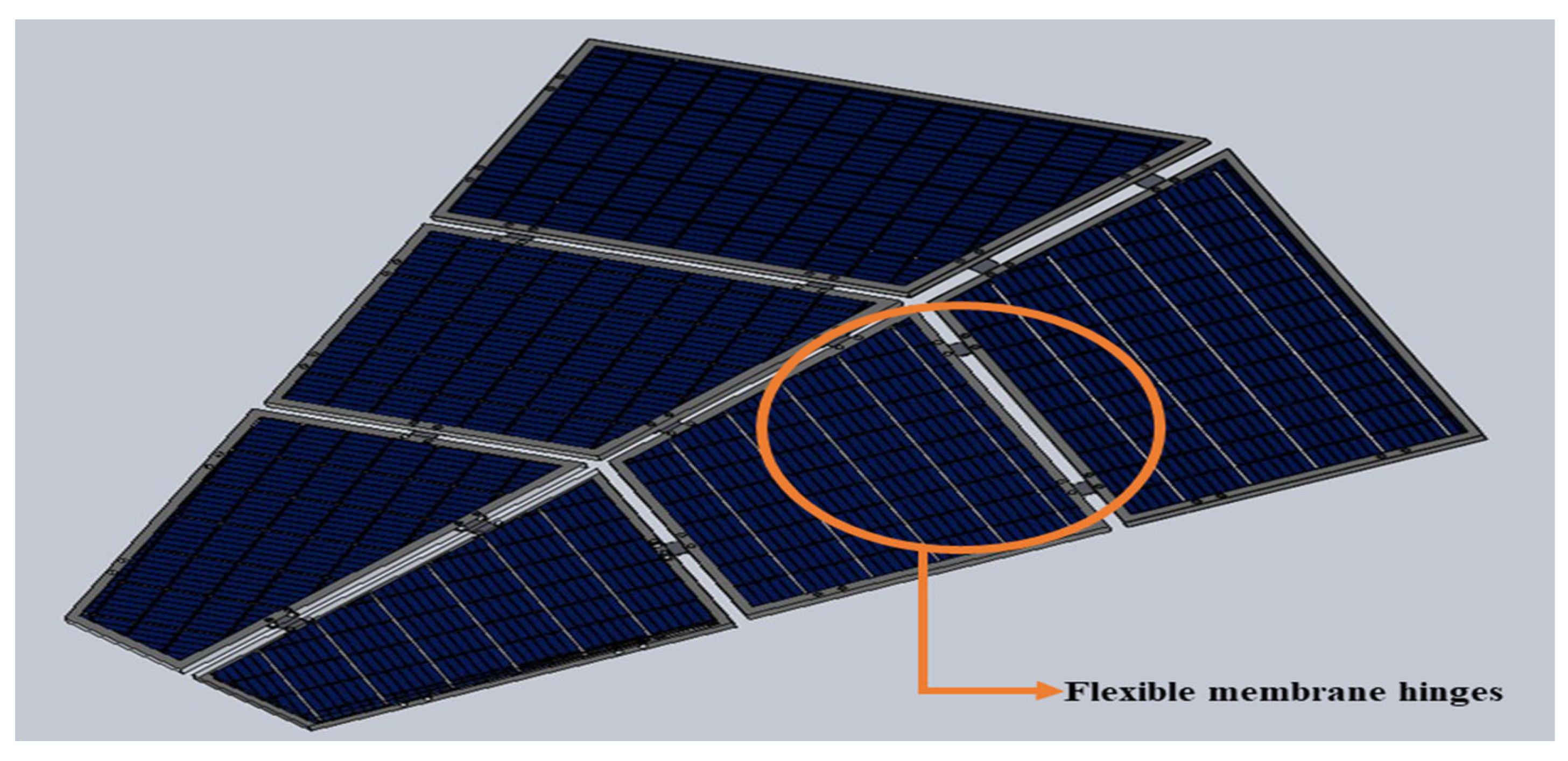
2.2. Design of Double-Layer Tape Spring (DLTS) Hinge (Coupling Mechanism)
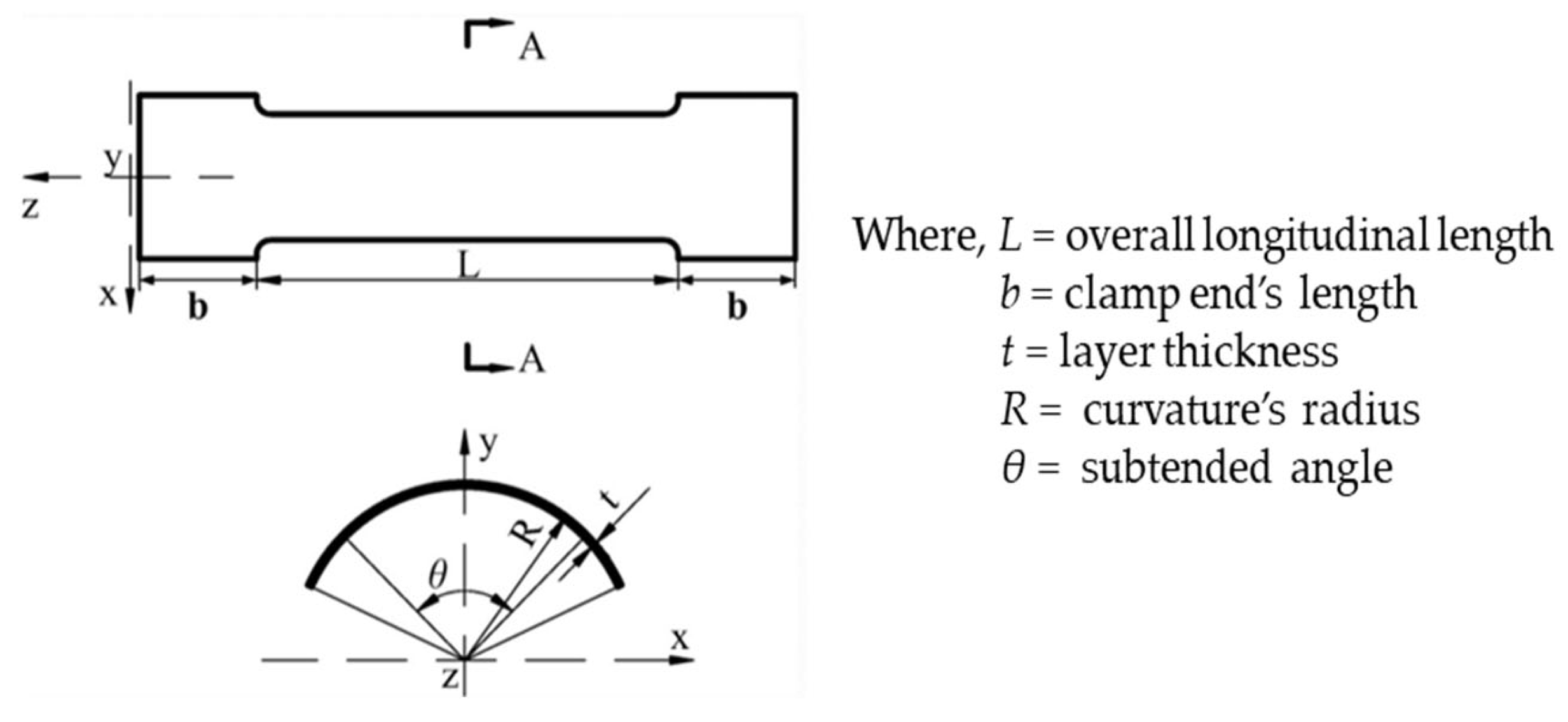
2.2.1. Thickness Accommodation Technique
2.2.2. Double-Layer Tape Spring Hinge/DLTS
3. Computational Modeling
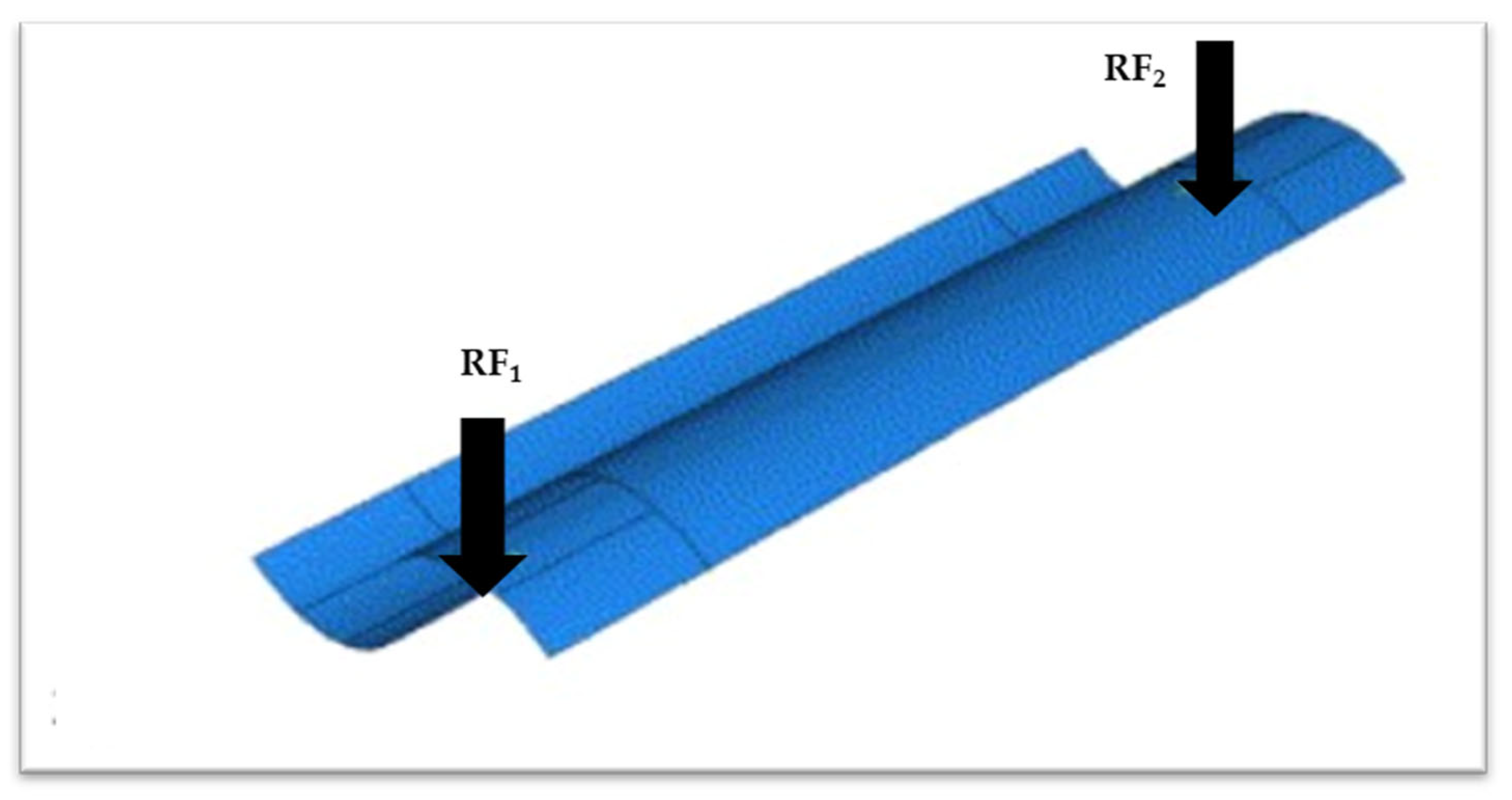
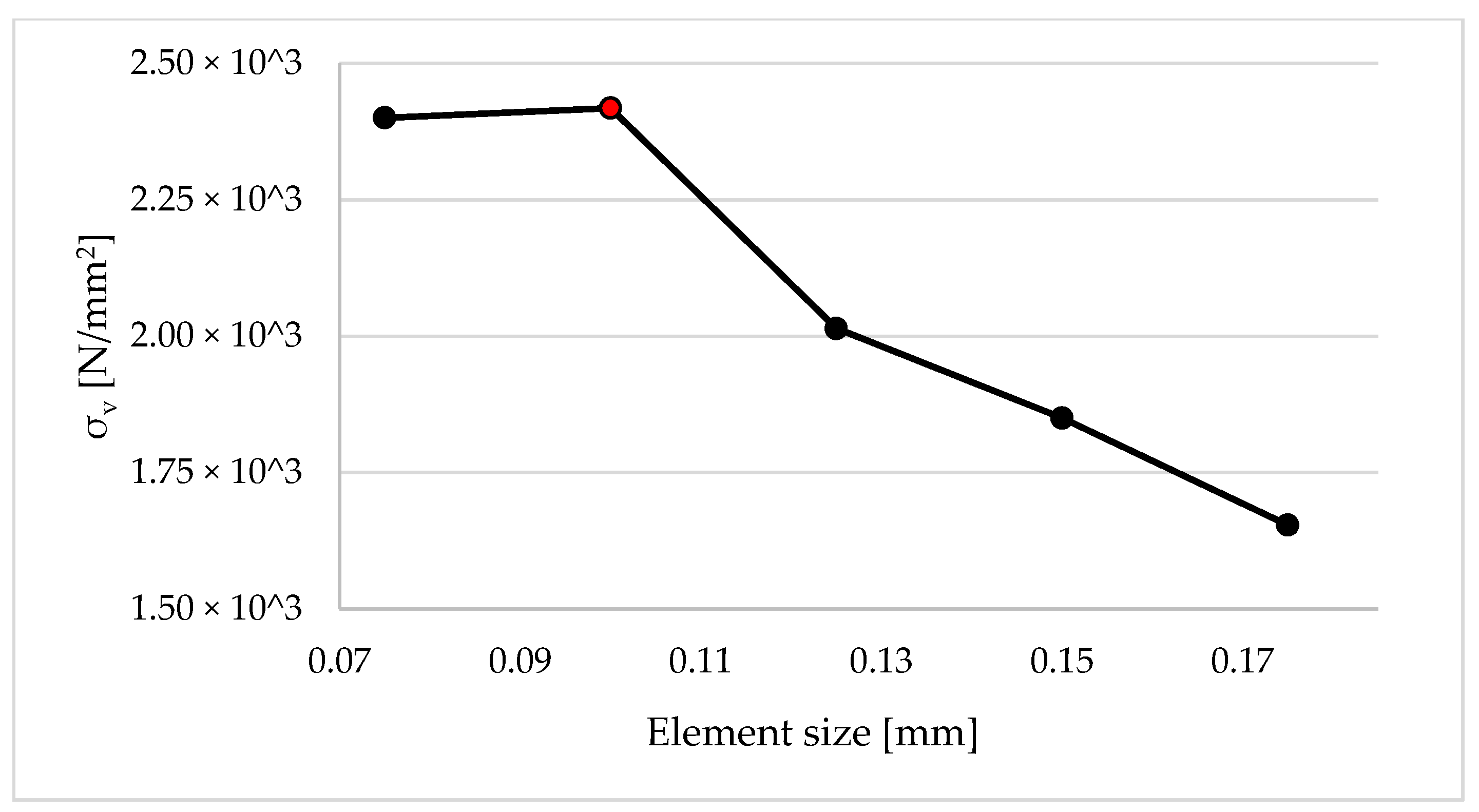
3.1. Generation of Finite Element Model
3.2. Static versus Quasi-Static Simulation
4. Results and Discussion
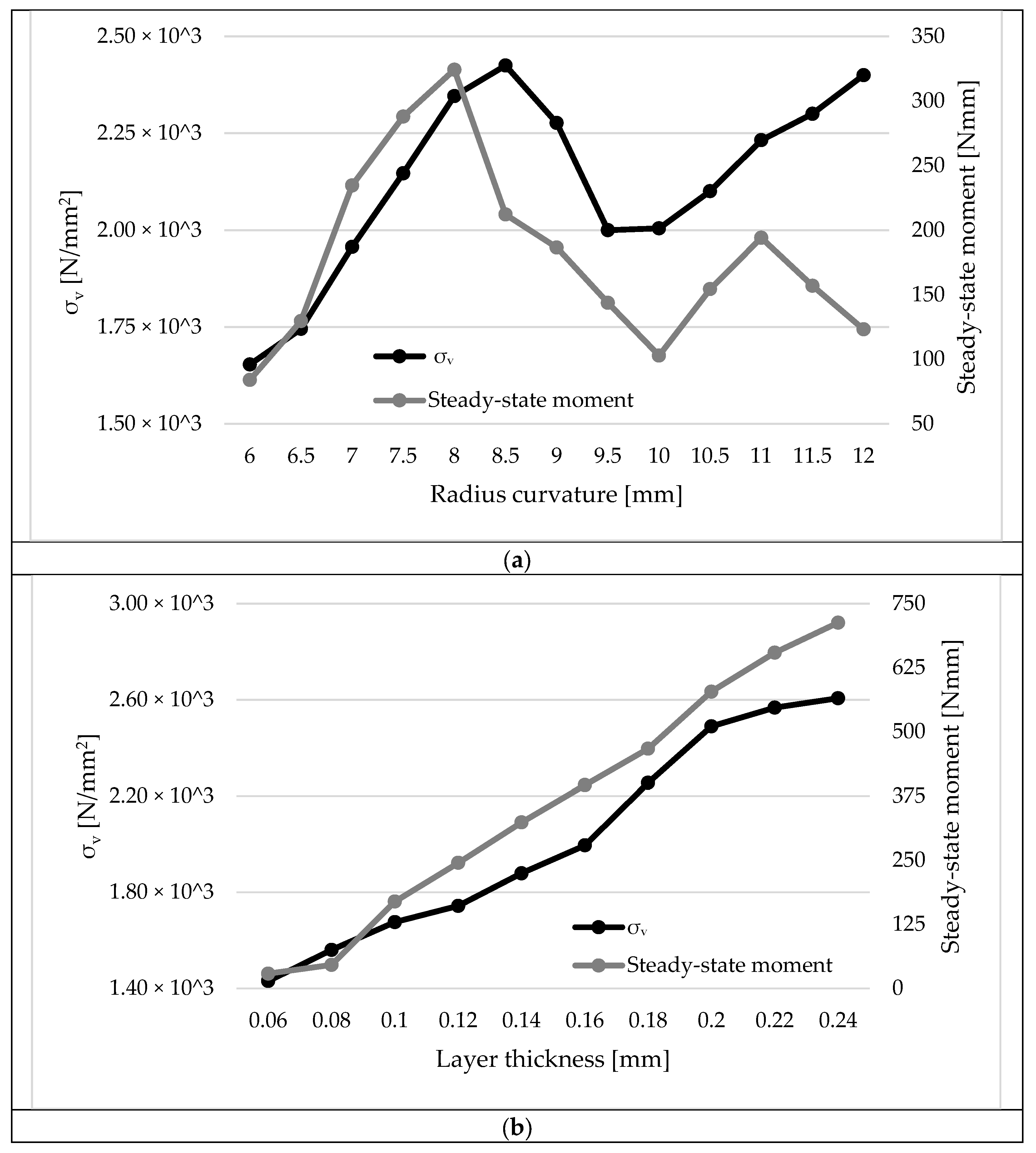
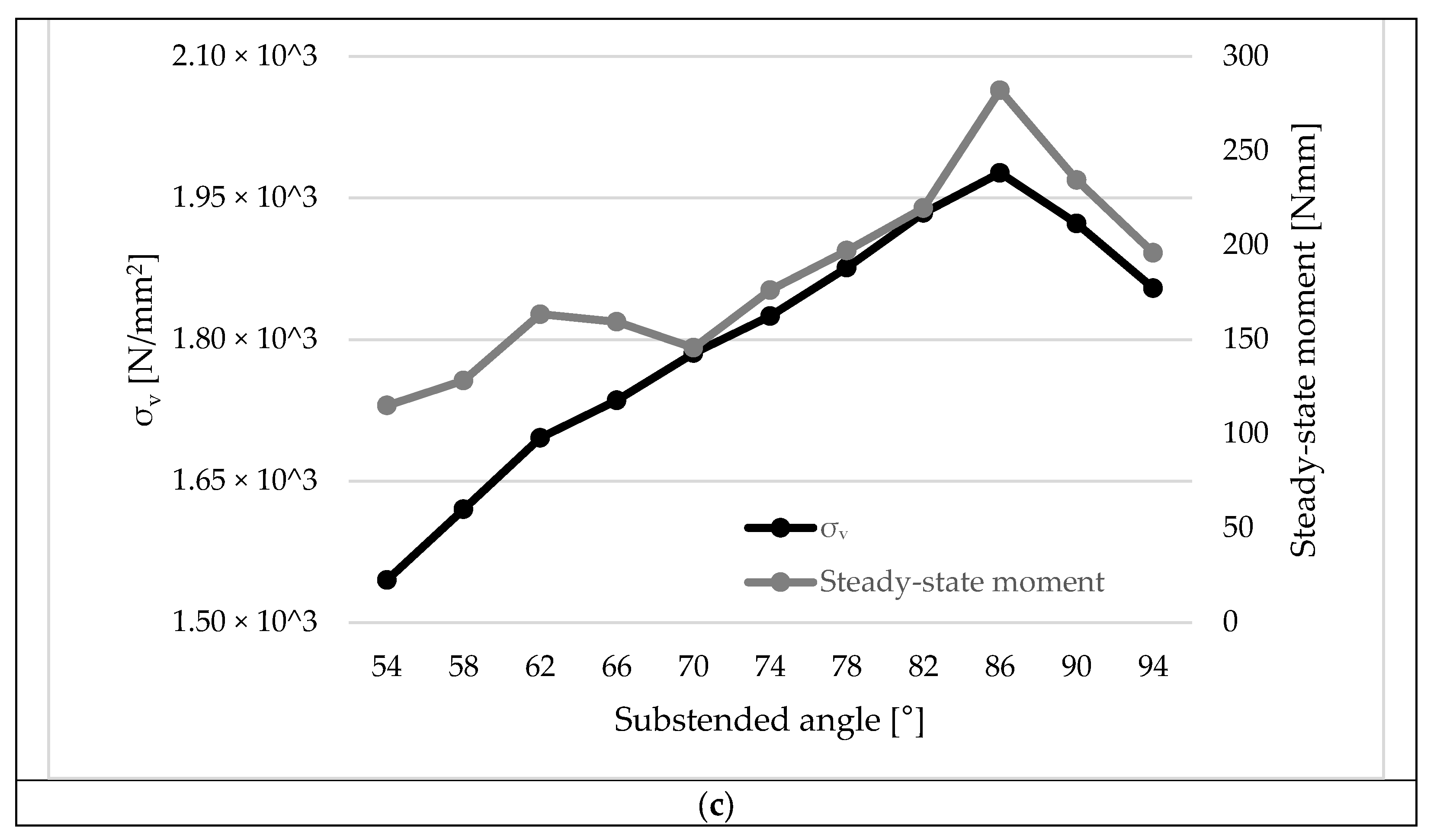
4.1. Parametric Analysis
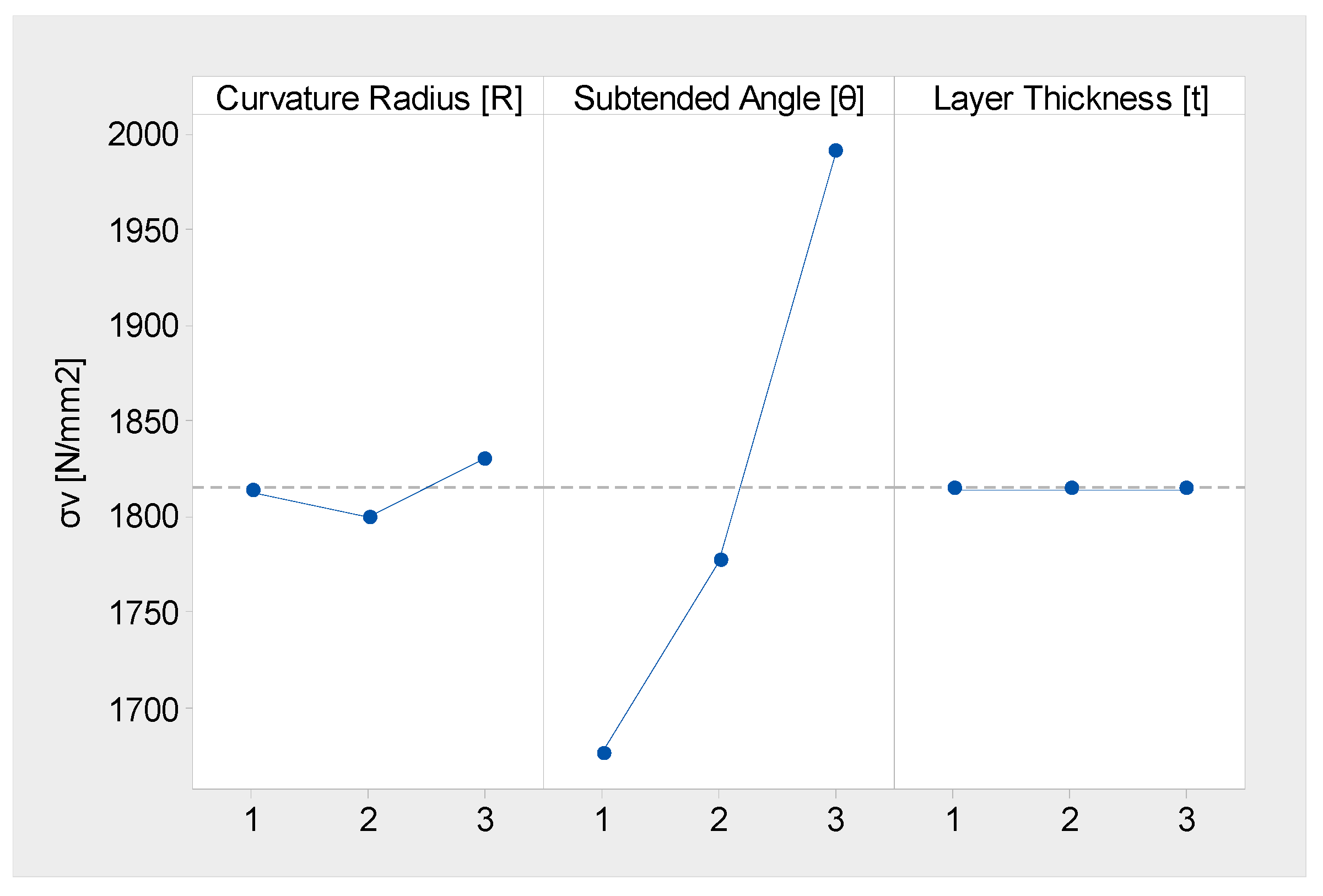
4.2. Optimization Analysis—Taguchi Model
4.2.1. Main Effects and Predicted Results for σv
4.2.2. Main Effects and Predicted Results for Steady-State Moment
4.2.3. Interaction Optimization Results for σv and Steady-State Moment
- It is possible to achieve a low σv with a reduced subtended angle (<1.5°) and a curvature radius between 1.5 and 2.25 mm (Figure 10a).
- Similarly, a low σv can be achieved with a subtended Angle (<1.5°) and a layer thickness between 1.75 and 2.75 mm (Figure 10b).
- A layer thickness between 1.75 and 2.5 mm and a curvature radius of 1.5–2.0 mm results in a low σv (Figure 10c).
- It is possible to achieve a low moment with a reduced subtended angle (<1.2°) and a curvature radius between 1.25 and 2.0 mm (Figure 10d).
- A low σv can also be achieved with an angle of 1.5° and a layer thickness between 1.75 and 2.2 mm (Figure 10e).
- A layer thickness between 1.75 and 2.25 mm and a curvature radius of 1.25–2.0 mm results in a low σv (Figure 10f).
4.3. Optimization Analysis—RSM Model
- Ms = steady-state moment of DLTS hinge
- σmax = maximum σv in stowed state
- = lower limit of the critical design parameter
- = upper limit of the critical design parameter
- n = number of total critical design parameters
- F(x) = estimation of the function’s true response
- a = undetermined parameters
- = response of sample point with ith terms (FEA)
- = mean response
- yi = response of sample point with ith terms (MATLAB)
- m = number of design points
- N = number of basic functions
5. Conclusions
- The predicted lowest σv and steady-state moment were estimated to be 1661 N/mm2 and 133.9 N/mm by setting an R of 6.0 mm, a θ of 60°, and a t of 0.1 mm, utilizing the RSM model.
- Optimization was achieved by keeping σv below 1700 N/mm2 and the steady-state moment below 150 N/mm2.
- Consequently, the optimum parameters of t, R, and θ were determined to be between 1.75 and 2.25 mm, 1.50 and 2.0 mm, and 1 and 1.2°, respectively.
- A safe limit of maximum σv was determined for the avoidance of permanent deformation and degradation of the DLTS hinge, which could not exceed the 2.43 × 103 N/mm2 value.
- Following this, the accuracy criterion for the max σv and steady-state moment yielding value was satisfied by determining the percentage difference between R2 and for the two responses.
- Subsequently, the optimum values of the t and θ parameters were 2.90 mm and 1.35°, with a max σv of 1.49 × 103 N/mm2 and steady-state moment of 145.76 Nmm.
- The design goal of the DLTS hinges was to accommodate the thickness of the flasher pattern and rotate 90°. The optimum values of t and θ achieved this with a reduced σv to the system, and hence, sufficient stability of the DLTS hinges was accomplished to ensure safe launch conditions, withstand the harsh environmental conditions, rotate appropriately the solar panels for the obtainment of power, and expand the life service of the whole system.
- Future research investigations will require a life cycle assessment and on-site validation, with a focus on the deformation and degradation of DLTS hinges. Additionally, multi-layer tape spring hinges combined with different CubeSat solar array origami patterns are of interest.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jacobs, M.; Selva, D. A CubeSat catalog design tool for a multi-agent architecture development framework. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–10. [Google Scholar]
- Levchenko, I.; Bazaka, K.; Ding, Y.; Raitses, Y.; Mazouffre, S.; Henning, T.; Klar, P.J.; Shinohara, S.; Schein, J.; Garrigues, L.; et al. Space micropropulsion systems for Cubesats and small satellites: From proximate targets to furthermost frontiers. Appl. Phys. Rev. 2018, 5, 011104. [Google Scholar] [CrossRef]
- Popescu, O. Power Budgets for CubeSat Radios to Support Ground Communications and Inter-Satellite Links. IEEE Access 2017, 5, 12618–12625. [Google Scholar] [CrossRef]
- Swartwout, M. The first one hundred CubeSats: A statistical look. J. Small Satell. 2013, 2, 213–233. [Google Scholar]
- Poghosyan, A.; Golkar, A. CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions. Prog. Aerosp. Sci. 2017, 88, 59–83. [Google Scholar] [CrossRef]
- Xilun, D.I.; Xin, L.I.; Kun, X.U.; Qiaolong, Y.A.; Hailing, P.U. Study on the behavior of solar array deployment with root hinge drive assembly. Chin. J. Aeronaut. 2012, 25, 276–284. [Google Scholar]
- Oh, H.-U.; Park, T. Experimental feasibility study of concentrating photovoltaic power system for cubesat applications. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1942–1949. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Wang, C.; Huang, W. Effects of torque spring, CCL and latch mechanism on dynamic response of planar solar arrays with multiple clearance joints. Acta Astronaut. 2017, 132, 243–255. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Huang, W. Rigid-flexible-thermal analysis of planar composite solar array with clearance joint considering tor-sional spring, latch mechanism and attitude controller. Nonlinear Dyn. 2019, 96, 2031–2053. [Google Scholar] [CrossRef]
- Solís-Santomé, A.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Torres-San Miguel, C.R.; Hernández-Gómez, J.J.; Medina-Sánchez, I.; Couder-Castañeda, C.; Grageda-Arellano, J.I.; Urriolagoitia-Calderón, G. Conceptual design and finite element method valida-tion of a new type of self-locking hinge for deployable CubeSat solar panels. Adv. Mech. Eng. 2019, 11, 1687814018823116. [Google Scholar] [CrossRef]
- Soykasap, Ö. Analysis of tape spring hinges. Int. J. Mech. Sci. 2007, 49, 853–860. [Google Scholar] [CrossRef]
- Mansfield, E.H. Large-deflexion torsion and flexure of initially curved strips. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1973, 334, 279–298. [Google Scholar] [CrossRef]
- Seffen, K.; You, Z.; Pellegrino, S. Folding and deployment of curved tape springs. Int. J. Mech. Sci. 2000, 42, 2055–2073. [Google Scholar] [CrossRef]
- Yuanyuan, L.I.; Meng, L.I.; Yufei, L.I.; Xinyu, G.E.; Chengbo, C.U. Parameter optimization for torsion spring of deployable solar array system with multiple clearance joints considering rigid–flexible coupling dynamics. Chin. J. Aeronaut. 2022, 35, 509–524. [Google Scholar]
- Yee, J.C. Thin CFRP Composite Deployable Structures. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2006. [Google Scholar]
- Mallikarachchi, H.M. Thin-Walled Composite Deployable Booms with Tape-Spring Hinges. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2011. [Google Scholar]
- Fernandes, P.; Pinto, R.; Correia, N. Design and optimization of self-deployable damage tolerant composite structures: A review. Compos. Part B Eng. 2021, 221, 109029. [Google Scholar] [CrossRef]
- Yang, H.; Liu, R.; Wang, Y.; Deng, Z.; Guo, H. Experiment and multiobjective optimization design of tape-spring hinges. Struct. Multidiscip. Optim. 2015, 51, 1373–1384. [Google Scholar] [CrossRef]
- Sibalija, T.V.; Majstorovic, V.D. An integrated approach to optimise parameter design of multi-response processes based on Taguchi method and artificial intelligence. J. Intell. Manuf. 2012, 23, 1511–1528. [Google Scholar] [CrossRef]
- Asiltürk, I.; Neşeli, S. Multi response optimisation of CNC turning parameters via Taguchi method-based response surface analysis. Measurement 2012, 45, 785–794. [Google Scholar] [CrossRef]
- Bolanos, D.S. Selecting and Optimizing Origami-Based Patterns for Deployable Space Systems. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2022. [Google Scholar]
- Lang, R.J.; Tolman, K.A.; Crampton, E.B.; Magleby, S.P.; Howell, L.L. A review of thickness-accommodation techniques in origami-inspired engineering. Appl. Mech. Rev. 2018, 70, 010805. [Google Scholar] [CrossRef]
- Tolman, K.A.; Lang, R.J.; Magleby, S.P.; Howell, L.L. Split-vertex technique for thickness-accommodation in origami-based mechanisms. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OI, USA, 6–9 August 2017; Volume 58189, p. V05BT08A054. [Google Scholar]
- Ye, H.; Zhang, Y.; Yang, Q.; Xiao, Y.; Grandhi, R.V.; Fischer, C.C. Optimal design of a three tape-spring hinge deployable space structure using an experimentally validated physics-based model. Struct. Multidiscip. Optim. 2017, 56, 973–989. [Google Scholar] [CrossRef]
- Wilson, L.; Gdoutos, E.E.; Pellegrino, S. Tension-Stabilized Coiling of Isotropic Tape Springs. Int. J. Solids Struct. 2020, 188, 103–117. [Google Scholar] [CrossRef]
- Jin, H.; Jia, Q.; An, N.; Zhao, G.; Ma, X.; Zhou, J. Surrogate modeling accelerated shape optimization of deployable composite tape-spring hinges. AIAA J. 2022, 60, 5942–5953. [Google Scholar] [CrossRef]



| Experiment | Radius Curvature [mm] | Subtended Angle [°] | Layer Thickness [mm] |
|---|---|---|---|
| 1 | 5.5 | 60 | 0.10 |
| 2 | 5.5 | 65 | 0.15 |
| 3 | 5.5 | 70 | 0.20 |
| 4 | 6.0 | 60 | 0.10 |
| 5 | 6.0 | 65 | 0.15 |
| 6 | 6.0 | 70 | 0.20 |
| 7 | 6.5 | 60 | 0.10 |
| 8 | 6.5 | 65 | 0.15 |
| 9 | 6.5 | 70 | 0.20 |
| Descriptive Statistics | Mean | SE Mean | StDev |
|---|---|---|---|
| 1814.6 | 46.6 | 139.9 | |
| Level | Curvature Radius [R] | Subtended Angle [θ] | Layer Thickness [t] |
| 1 | 1813 N/mm2 | 1676 N/mm2 | 1815 N/mm2 |
| 2 | 1800 N/mm2 | 1777 N/mm2 | 1815 N/mm2 |
| 3 | 1830 N/mm2 | 1991 N/mm2 | 1815 N/mm2 |
| Difference (δ) | 31 N/mm2 | 315 N/mm2 | 0 N/mm2 |
| Rank importance | 2 | 1 | 3 |
| Prediction | 1661 N/mm2 (lowest σv) | ||
| Descriptive Statistics | Mean | SE Mean | StDev |
|---|---|---|---|
| 209.4 | 19.7 | 59.1 | |
| Level | Curvature Radius [R] | Subtended Angle [θ] | Layer Thickness [t] |
| 1 | 206.9 [N/mm] | 140.3 [N/mm] | 209.4 [N/mm] |
| 2 | 203.1 [N/mm] | 212.2 [N/mm] | 209.4 [N/mm] |
| 3 | 218.3 [N/mm] | 275.7 [N/mm] | 209.4 [N/mm] |
| Difference (δ) | 15.2 [N/mm] | 135.4 [N/mm] | 0.0 [N/mm] |
| Rank importance | 2 | 1 | 3 |
| Prediction | 133.9 N/mm (lowest steady-state moment) | ||
| Design | Layer Thickness, t (mm) | Subtended Angle, θ (°) | σv (N/mm2) | Steady-State Moment (Nmm) |
|---|---|---|---|---|
| Optimal | 2.90 | 1.35 | 1493.87 | 145.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsouli, A.; Griffiths, C.A.; Langford, E.H. Optimization of DLTS Hinges for the Assembly of the Solar Arrays of a Communication CubeSat. Appl. Sci. 2024, 14, 1350. https://doi.org/10.3390/app14041350
Katsouli A, Griffiths CA, Langford EH. Optimization of DLTS Hinges for the Assembly of the Solar Arrays of a Communication CubeSat. Applied Sciences. 2024; 14(4):1350. https://doi.org/10.3390/app14041350
Chicago/Turabian StyleKatsouli, Aikaterini, Christian Andrew Griffiths, and Euan H. Langford. 2024. "Optimization of DLTS Hinges for the Assembly of the Solar Arrays of a Communication CubeSat" Applied Sciences 14, no. 4: 1350. https://doi.org/10.3390/app14041350
APA StyleKatsouli, A., Griffiths, C. A., & Langford, E. H. (2024). Optimization of DLTS Hinges for the Assembly of the Solar Arrays of a Communication CubeSat. Applied Sciences, 14(4), 1350. https://doi.org/10.3390/app14041350







