Minimizing the Limitations in Improving Historical Aerial Photographs with Super-Resolution Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Minimizing the Restrictions
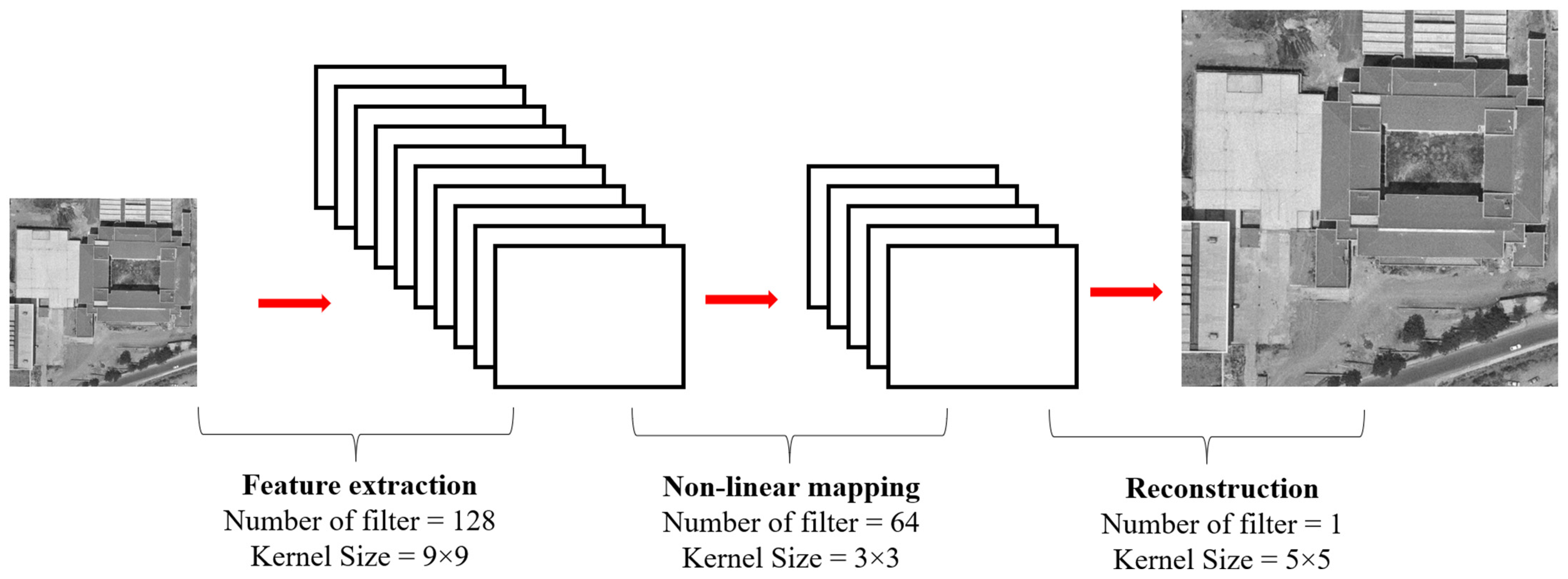
2.3. Super-Resolution Implementation
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anwar, S.; Khan, S.; Barnes, N. A deep journey into super-resolution: A survey. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Li, K.; Yang, S.; Dong, R.; Wang, X.; Huang, J. Survey of single image super-resolution reconstruction. IET Image Process. 2020, 14, 2273–2290. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef]
- Ooi, Y.K.; Ibrahim, H. Deep learning algorithms for single image super-resolution: A systematic review. Electronics 2021, 10, 867. [Google Scholar] [CrossRef]
- Ha, V.K.; Ren, J.C.; Xu, X.Y.; Zhao, S.; Xie, G.; Masero, V.; Hussain, A. Deep learning based single image super-resolution: A survey. Int. J. Autom. Comput. 2019, 16, 413–426. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar] [CrossRef]
- Caballero, J.; Ledig, C.; Aitken, A.; Acosta, A.; Totz, J.; Wang, Z.; Shi, W. Real-time video super-resolution with spatio-temporal networks and motion compensation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Lan, R.; Sun, L.; Liu, Z.; Lu, H.; Su, Z.; Pang, C.; Luo, X. Cascading and enhanced residual networks for accurate single-image super-resolution. IEEE Trans. Cybern. 2021, 51, 115–125. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Wei, W.; Yongbin, J.; Yanhong, L.; Ji, L.; Xin, W.; Tong, Z. An advanced deep residual dense network (DRDN) approach for image super-resolution. Int. J. Comput. Intell. Syst. 2019, 12, 1592–1601. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar] [CrossRef]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Kim, S.; Jun, D.; Kim, B.-G.; Lee, H.; Rhee, E. Single image super-resolution method using CNN-Based lightweight neural networks. Appl. Sci. 2021, 11, 1092. [Google Scholar] [CrossRef]
- Gendy, G.; He, G.; Sabor, N. Lightweight image super-resolution based on deep learning: State-of-the-art and future directions. Inf. Fusion 2023, 94, 284–310. [Google Scholar] [CrossRef]
- Anwar, S.; Barnes, N. Densely residual laplacian super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1192–1204. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. NTIRE 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Mla, M. Low-complexity single-image super resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth-Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Benecki, P.; Kawulok, M.; Kostrzewa, D.; Skonieczny, L. Evaluating super-resolution reconstruction of satellite images. Acta Astronaut. 2018, 153, 15–25. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Mahapatra, D.; Bozorgtabar, B.; Garnavi, R. Image super-resolution using progressive generative adversarial networks for medical image analysis. Comput. Med. Imaging Graph. 2019, 71, 30–39. [Google Scholar] [CrossRef]
- Xia, G.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A benchmark data set for performance evaluation of aerial scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Zou, Q.; Ni, L.; Zhang, T.; Wang, Q. Deep learning based feature selection for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2321–2325. [Google Scholar] [CrossRef]
- Dai, D.; Yang, W. Satellite image classification via two-layer sparse coding with biased image representation. IEEE Geosci. Remote Sens. Lett. 2010, 8, 173–176. [Google Scholar] [CrossRef]
- Deeba, F.; Dharejo, F.A.; Zhou, Y.; Ghaffar, A.; Memon, M.H.; Kun, S. Single image super-resolution with application to remote-sensing image. In Proceedings of the Global Conference on Wireless and Optical Technologies, Malaga, Spain, 6–8 October 2020. [Google Scholar] [CrossRef]
- Panagiotopoulou, A.; Grammatikopoulos, L.; El Saer, A.; Petsa, E.; Charou, E.; Ragia, L.; Karras, G. Super-resolution tech-niques in photogrammetric 3D reconstruction from close-range UAV imagery. Heritage 2023, 6, 2701–2715. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Liebel, L.; Korner, M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B3, 883–890. [Google Scholar] [CrossRef]
- Huang, N.; Yang, Y.; Liu, J.; Gu, X.; Cai, H. Single-image super-resolution for remote sensing data using deep residual-learning neural network. In Proceedings of the International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017. [Google Scholar] [CrossRef]
- Ren, C.; He, X.; Qing, L.; Wu, Y.; Pu, Y. Remote sensing image recovery via enhanced residual learning and dual-luminance scheme. Knowl.-Based Syst. 2021, 222, 107013. [Google Scholar] [CrossRef]
- Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat super-resolution enhancement using convolution neural networks and Sentinel-2 for training. Remote Sens. 2018, 10, 394. [Google Scholar] [CrossRef]
- Shermeyer, J.; Van Etten, A. The effects of super-resolution on object detection performance in satellite imagery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar] [CrossRef]
- Wang, X.; Yi, J.; Guo, J.; Song, Y.; Lyu, J.; Xu, J.; Yan, W.; Zhao, J.; Cai, Q.; Min, H. A review of image super-resolution approaches based on deep learning and applications in remote sensing. Remote Sens. 2022, 14, 5423. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Ozturk, O.; Isik, M.S.; Kada, M.; Seker, D.Z. Improving road segmentation by combining satellite images and LiDAR data with a feature-wise fusion strategy. Appl. Sci. 2023, 13, 6161. [Google Scholar] [CrossRef]
- Keshk, H.M.; Abdel-Aziem, M.; Ali, A.S.; Assal, M.A. Performance evaluation of quality measurement for super-resolution satellite images. In Proceedings of the Science and Information Conference, London, UK, 27–29 August 2014. [Google Scholar] [CrossRef]
- Girod, B. What’s wrong with mean-squared error? In Digital Images and Human Vision; MIT Press: London, UK, 1993; pp. 207–220. [Google Scholar]
- Naidu, V.P.S. Discrete cosine transform-based image fusion. J. Commun. Navig. Signal Process. 2012, 1, 35–45. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Greeshma, M.S.; Bindu, V.R. Super-resolution quality criterion (SRQC): A super-resolution image quality assessment metric. Multimed. Tools Appl. 2020, 79, 35125–35146. [Google Scholar] [CrossRef]
- Medda, A.; DeBrunner, V. Color image quality index based on the UIQI. In Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation, Denver, CO, USA, 26–28 March 2006. [Google Scholar] [CrossRef]
- Goudail, F.; Réfrégier, P.; Delyon, G. Bhattacharyya distance as a contrast parameter for statistical processing of noisy optical images. J. Opt. Soc. Am. A 2004, 21, 1231–1240. [Google Scholar] [CrossRef]


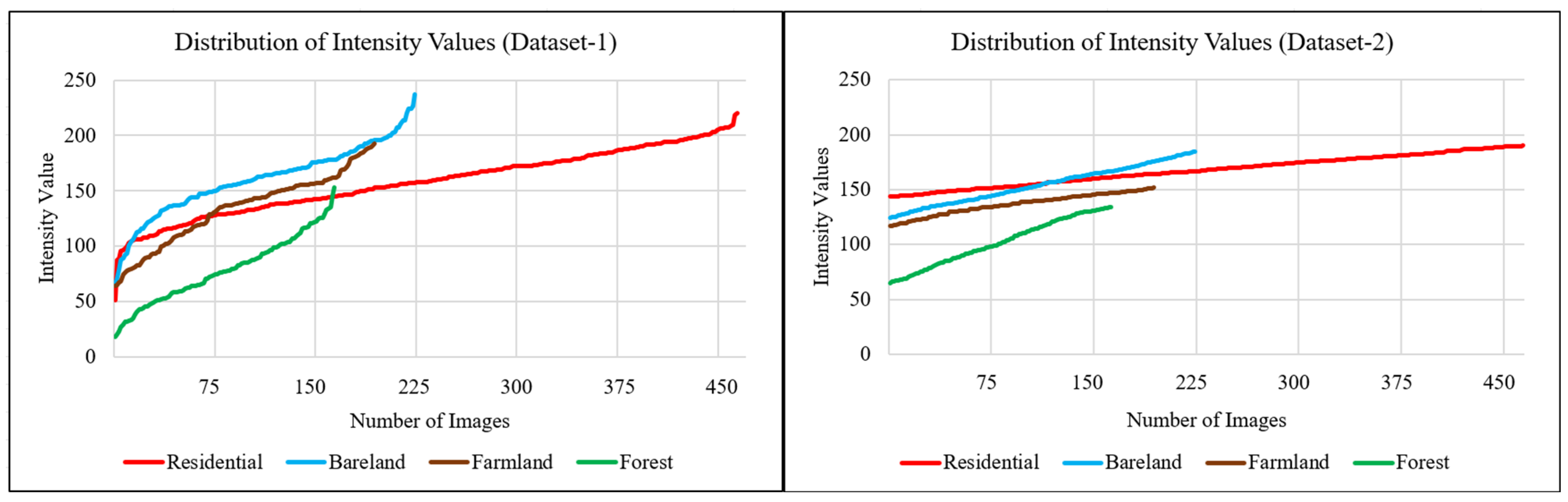


| Quality Metric | Dataset-1 | Dataset-2 |
|---|---|---|
| RMSE | 5.46 | 5.87 |
| PSNR | 33.40 | 32.80 |
| SSIM | 0.8714 | 0.8604 |
| UIQI | 0.9143 | 0.9070 |
| BHATTACHARYYA | 0.023 | 0.026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Incekara, A.H.; Alganci, U.; Arslan, O.; Seker, D.Z. Minimizing the Limitations in Improving Historical Aerial Photographs with Super-Resolution Technique. Appl. Sci. 2024, 14, 1495. https://doi.org/10.3390/app14041495
Incekara AH, Alganci U, Arslan O, Seker DZ. Minimizing the Limitations in Improving Historical Aerial Photographs with Super-Resolution Technique. Applied Sciences. 2024; 14(4):1495. https://doi.org/10.3390/app14041495
Chicago/Turabian StyleIncekara, Abdullah Harun, Ugur Alganci, Ozan Arslan, and Dursun Zafer Seker. 2024. "Minimizing the Limitations in Improving Historical Aerial Photographs with Super-Resolution Technique" Applied Sciences 14, no. 4: 1495. https://doi.org/10.3390/app14041495
APA StyleIncekara, A. H., Alganci, U., Arslan, O., & Seker, D. Z. (2024). Minimizing the Limitations in Improving Historical Aerial Photographs with Super-Resolution Technique. Applied Sciences, 14(4), 1495. https://doi.org/10.3390/app14041495









