Research on Energy Absorption Characteristics of Polypropylene Foam Concrete Buffer Layer in High Ground Stress Soft Rock Tunnel
Abstract
:1. Introduction
2. Development of EPP Concrete
2.1. EPP Particle Modification Test
2.2. Specimen Development
- (1)
- Development of EPP concrete specimens with different EPP particle contents
- (2)
- Development of laminated specimens
3. Physical and Mechanical Properties Test of EPP Concrete Specimens
3.1. Uniaxial Compression Test
3.2. Axial Compression Deformation Test
3.3. Splitting Compressive Test
3.4. Confined Uniaxial Compression Test
3.5. Confined Uniaxial Compression Test of Laminated Specimens
4. Analysis of Mechanical Properties and Energy Absorption Performance of Confined Compression
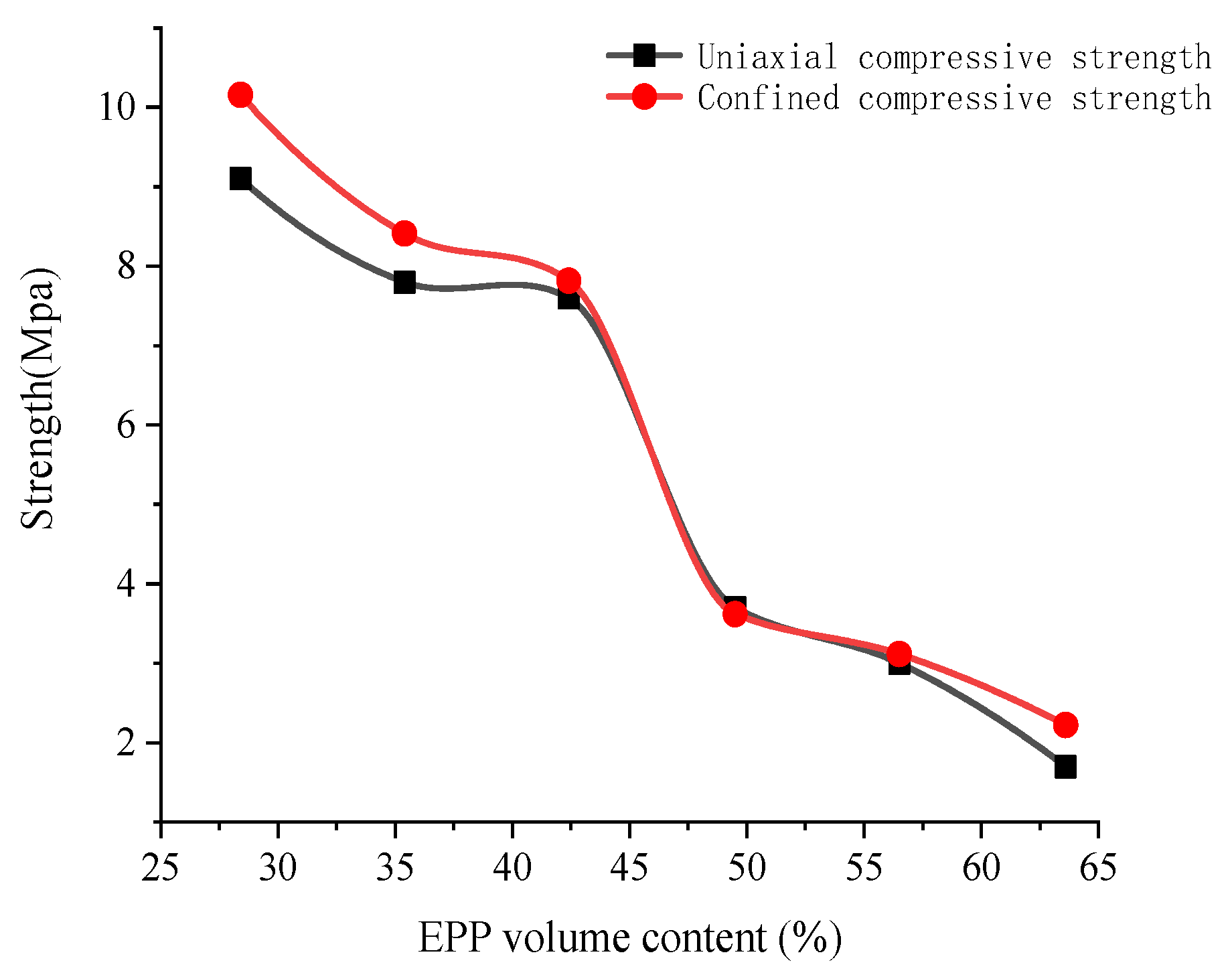
4.1. Confined Compressive Strength Analysis
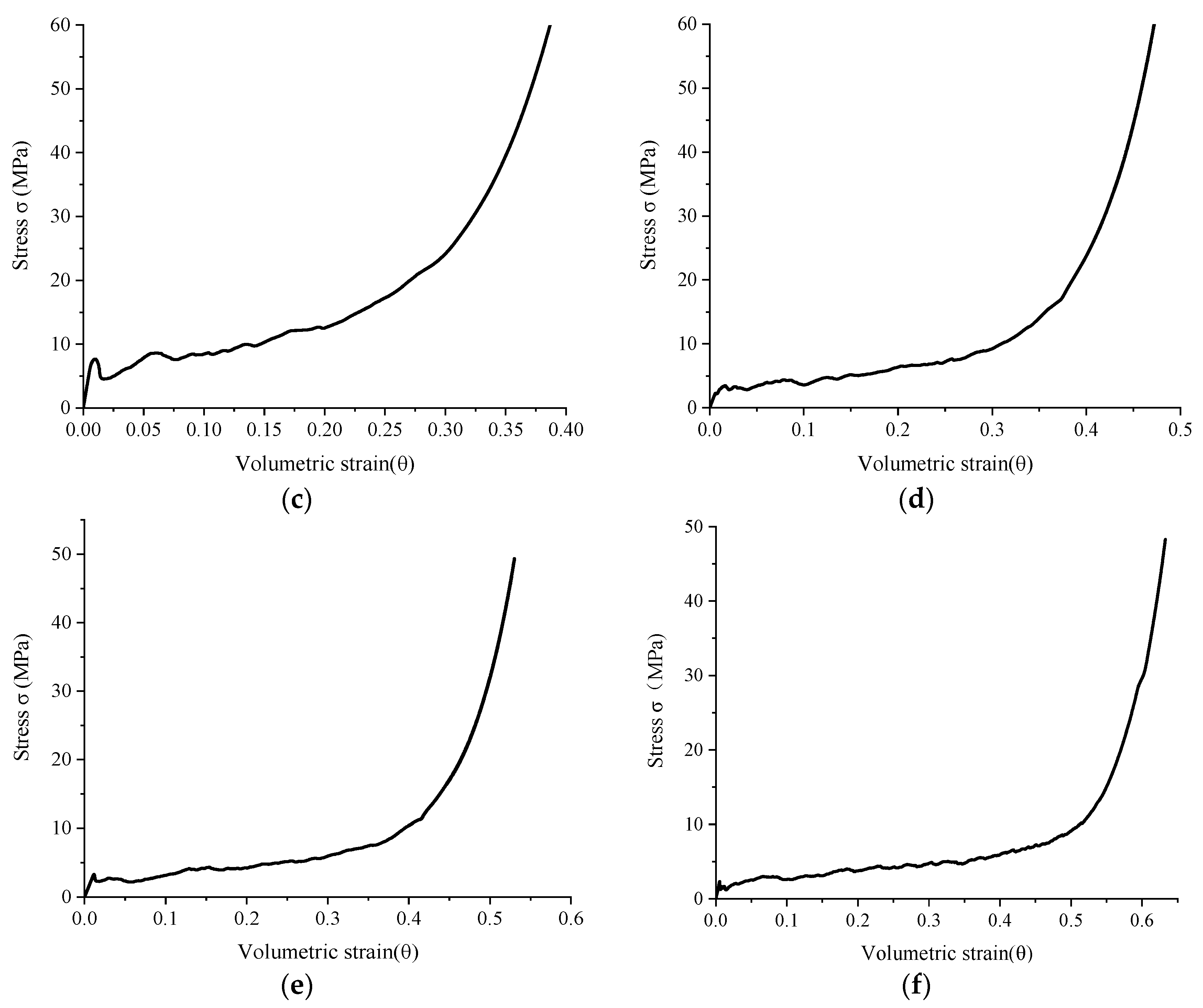
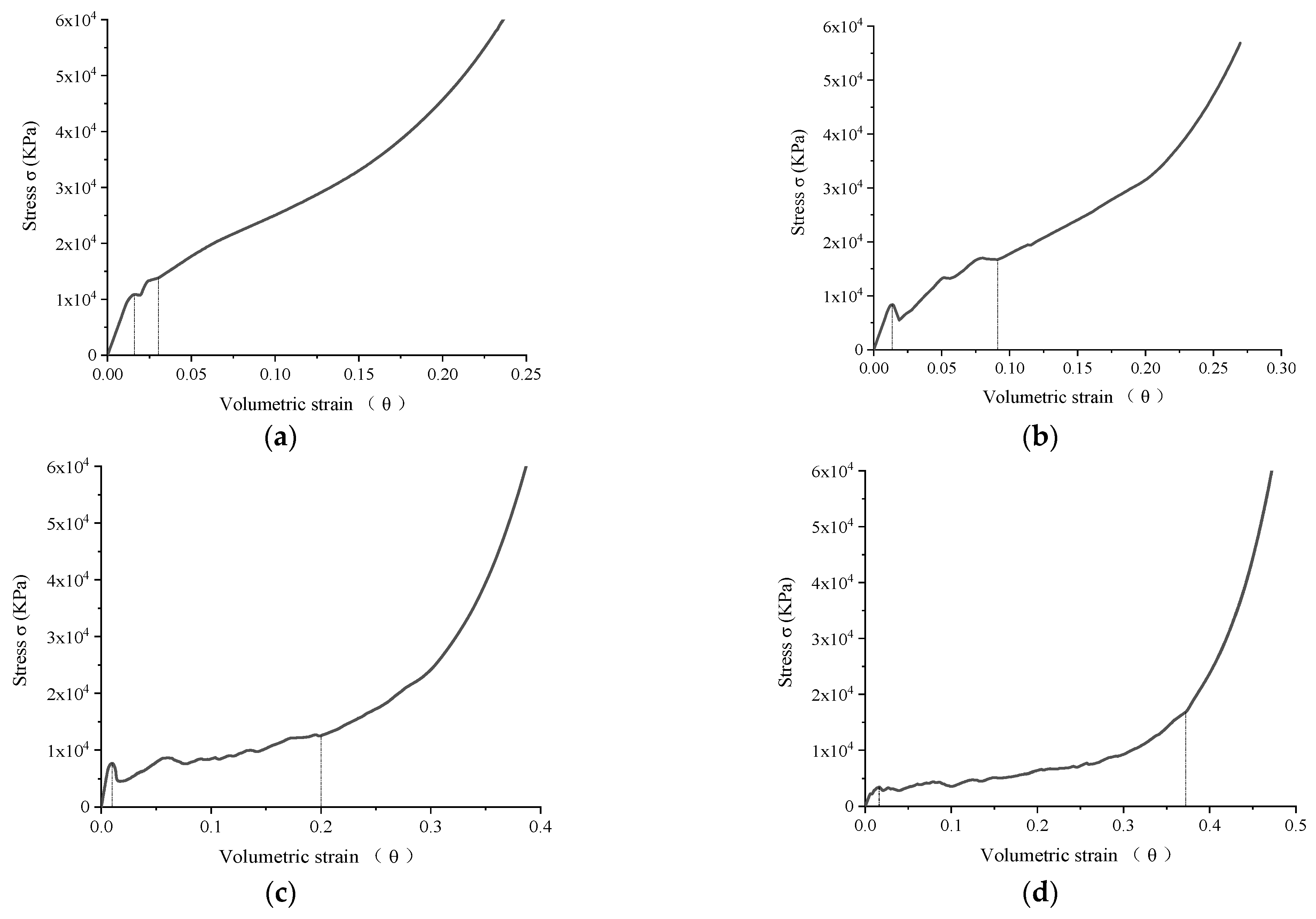
4.2. Stress–Strain Curve Analysis
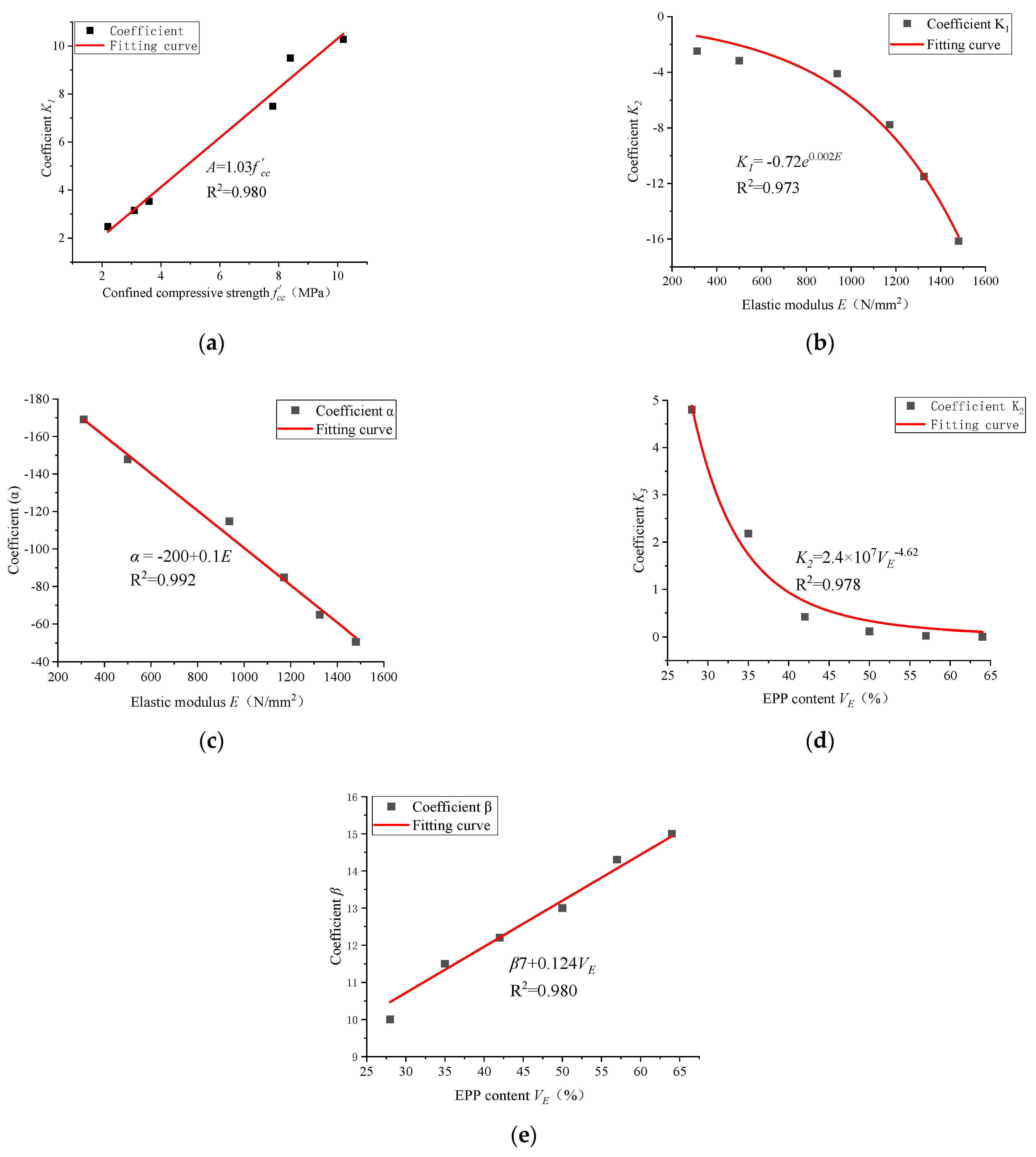
4.3. Constitutive Relation of EPP Concrete under Confined Compression
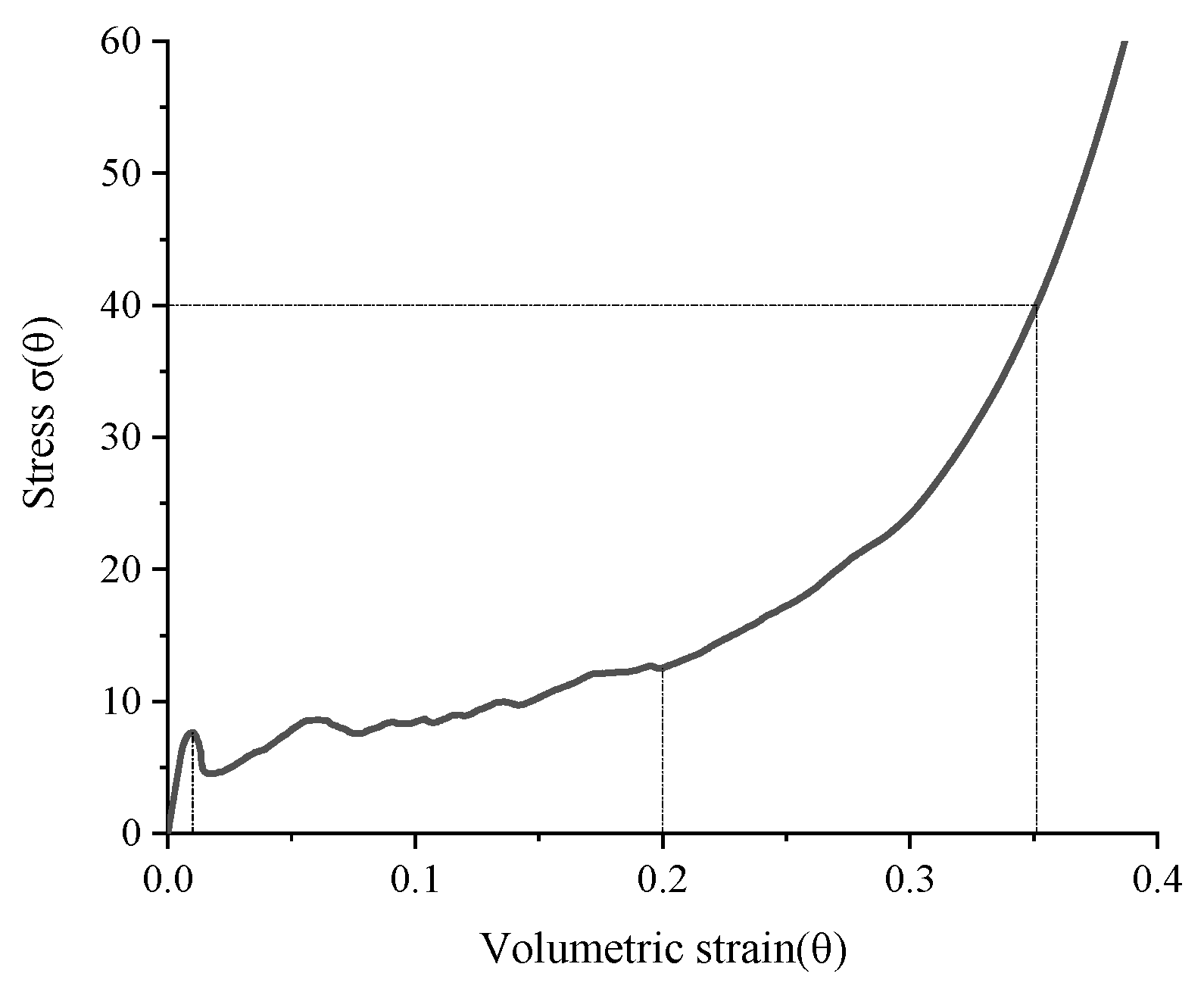
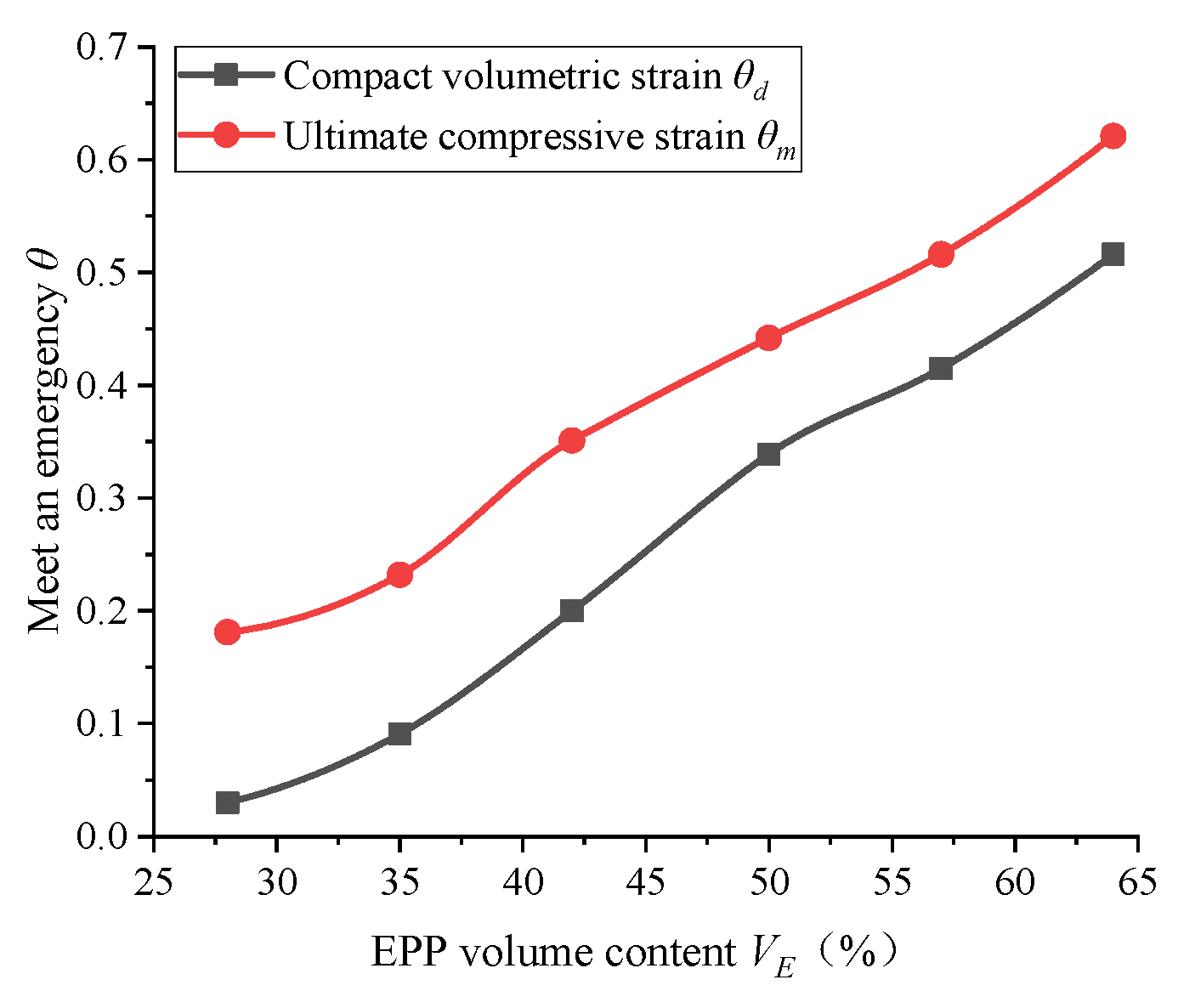
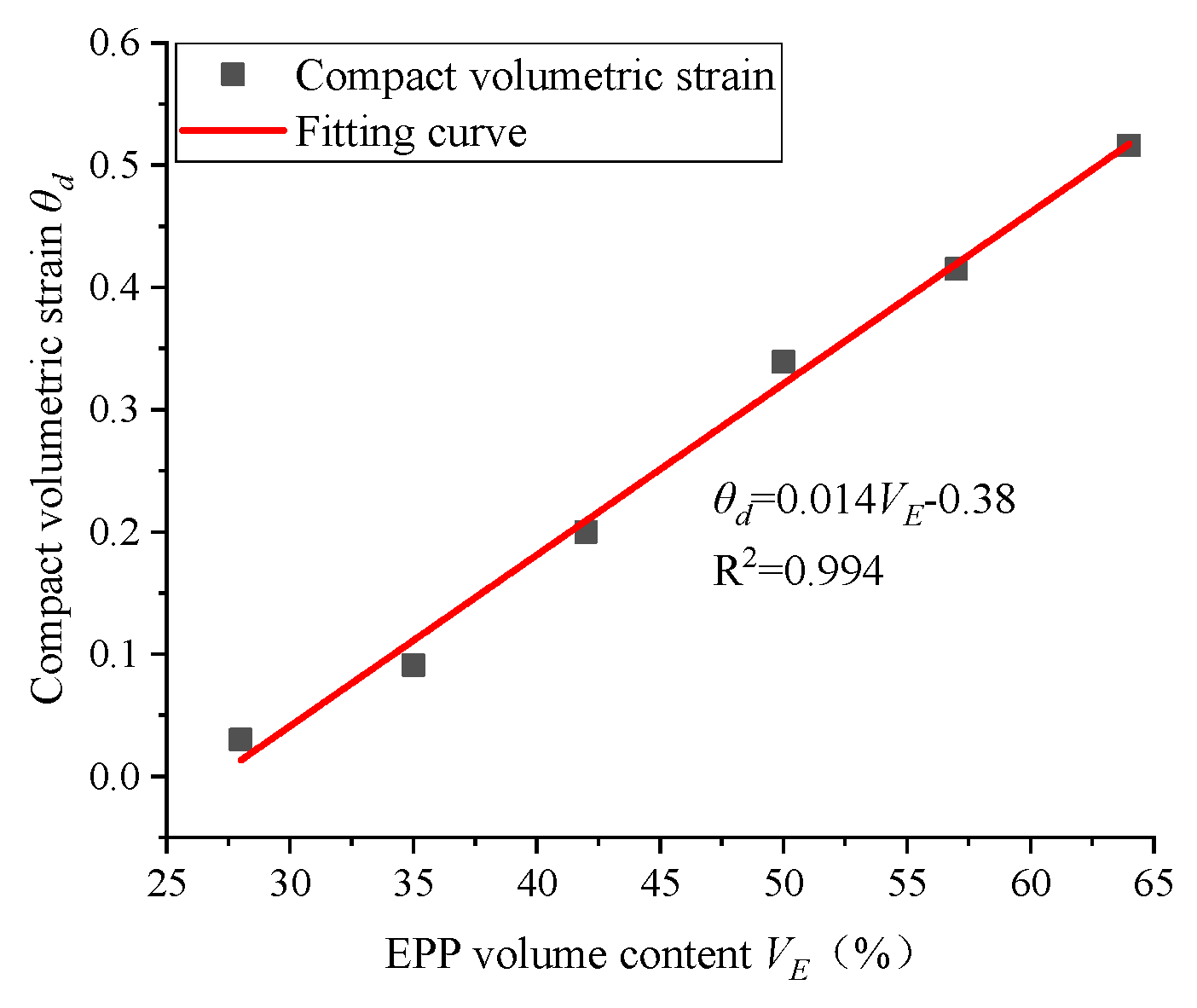
4.4. Analysis of Volume Strain and Compressibility
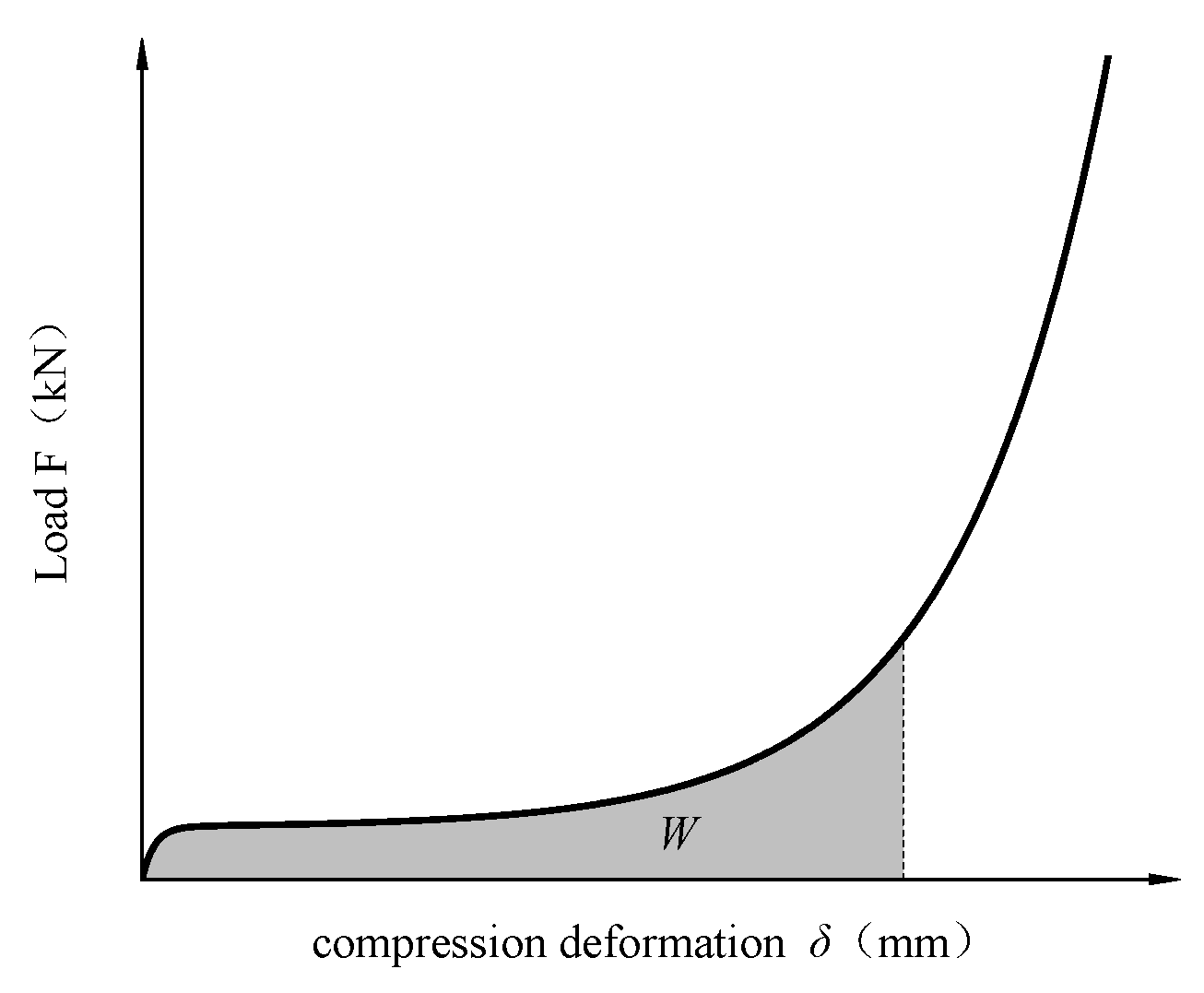
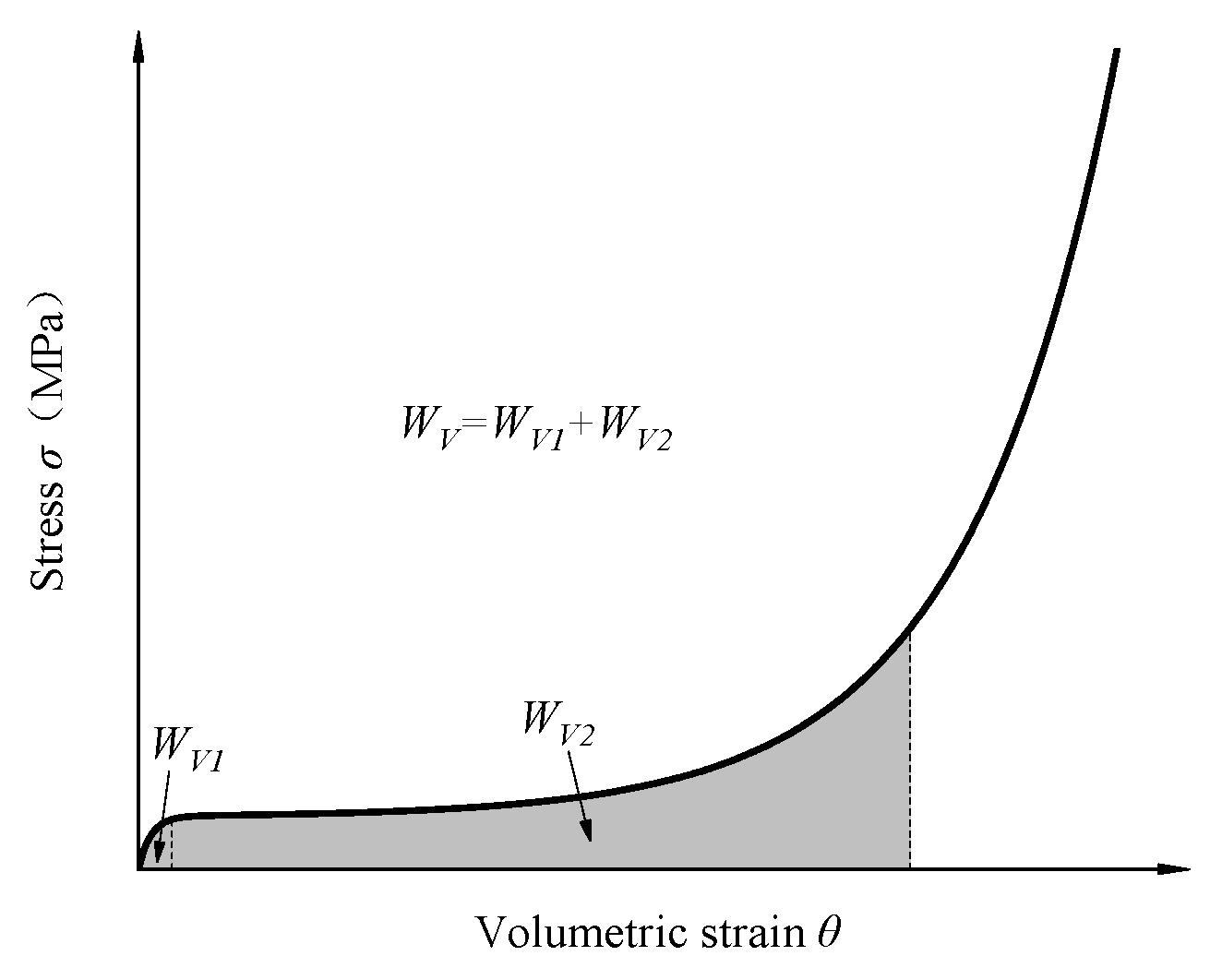
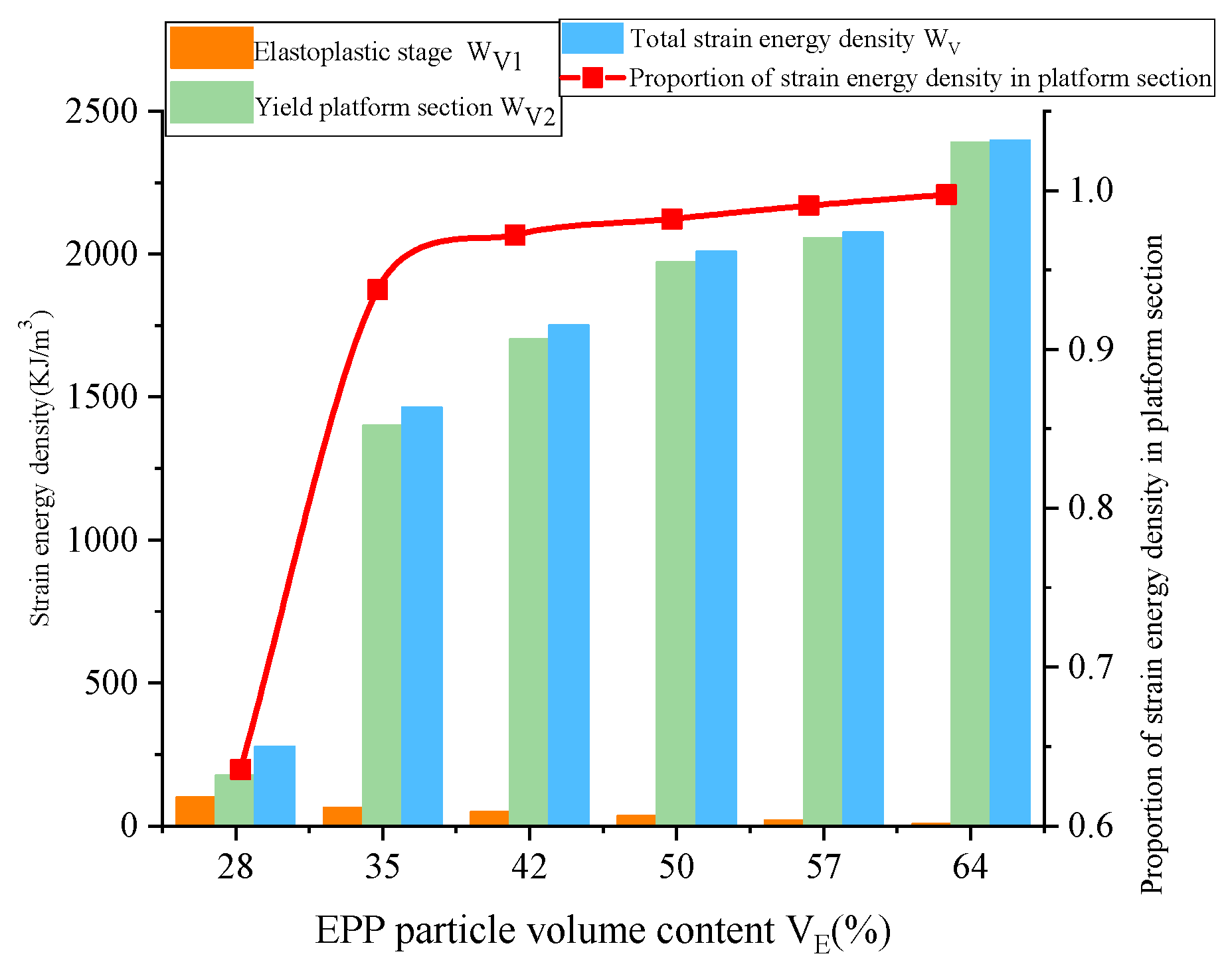
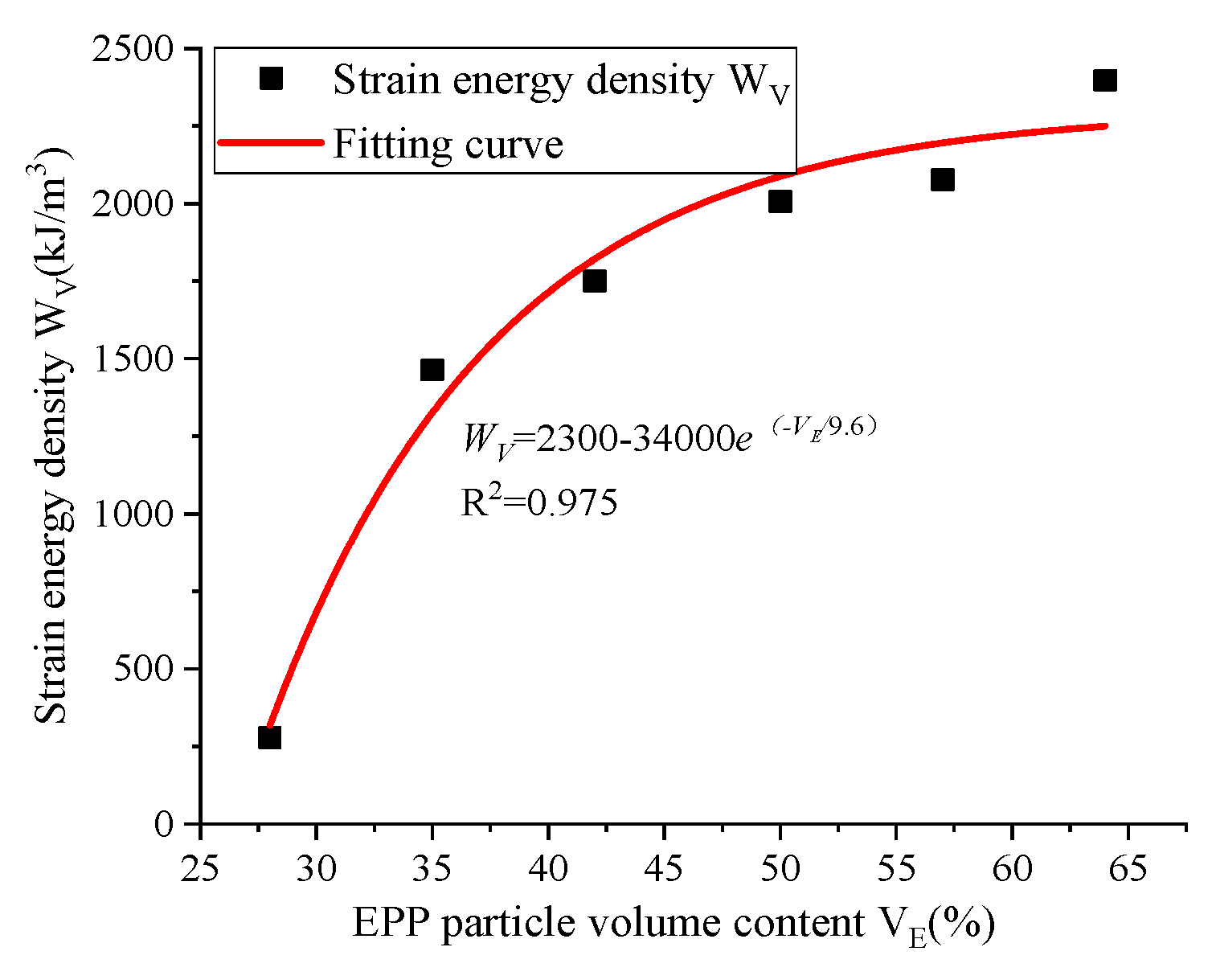
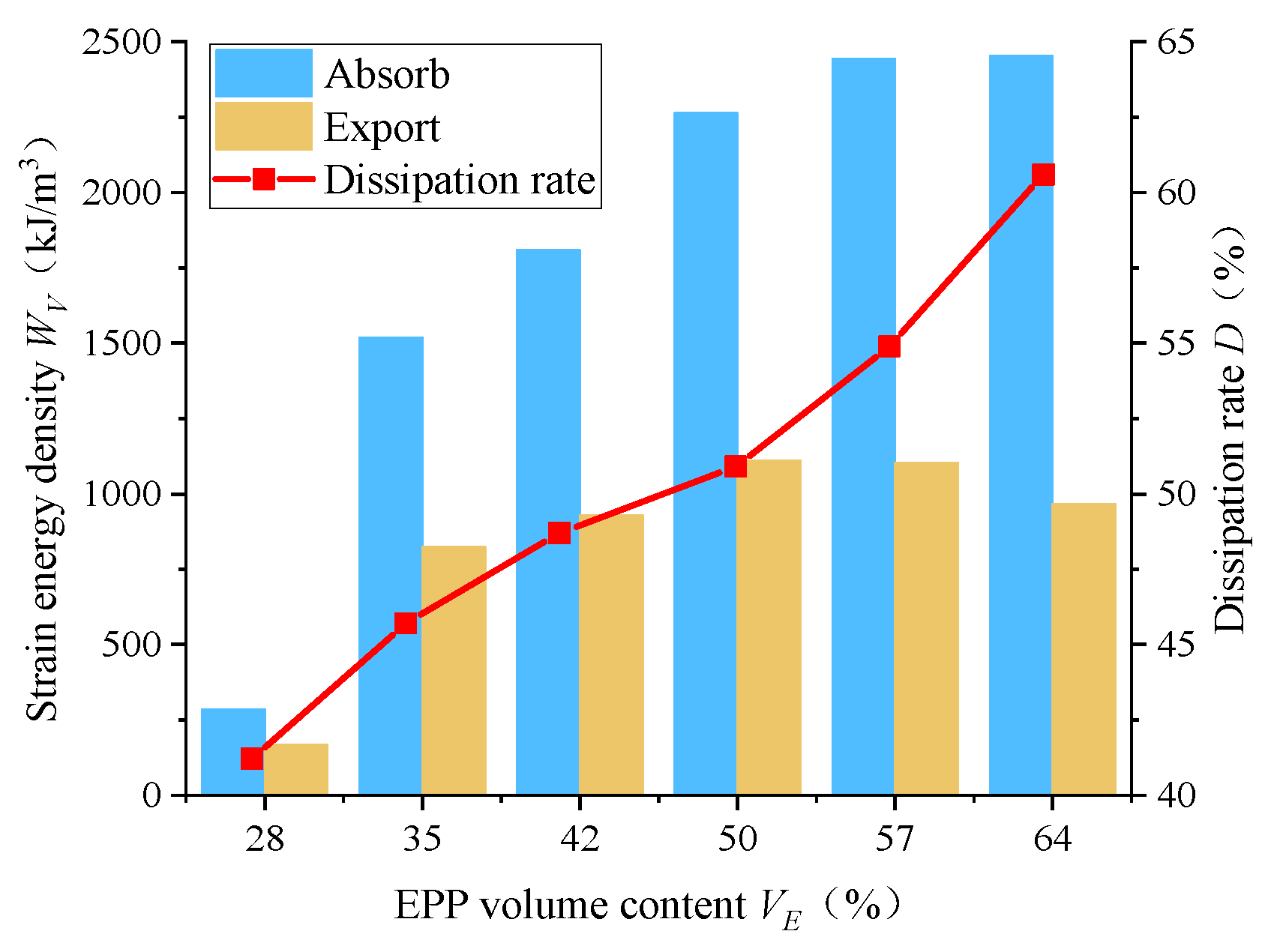
4.5. Analysis of Energy Absorption Performance
5. Energy Absorption Performance of Laminated Specimens under Confined Compression
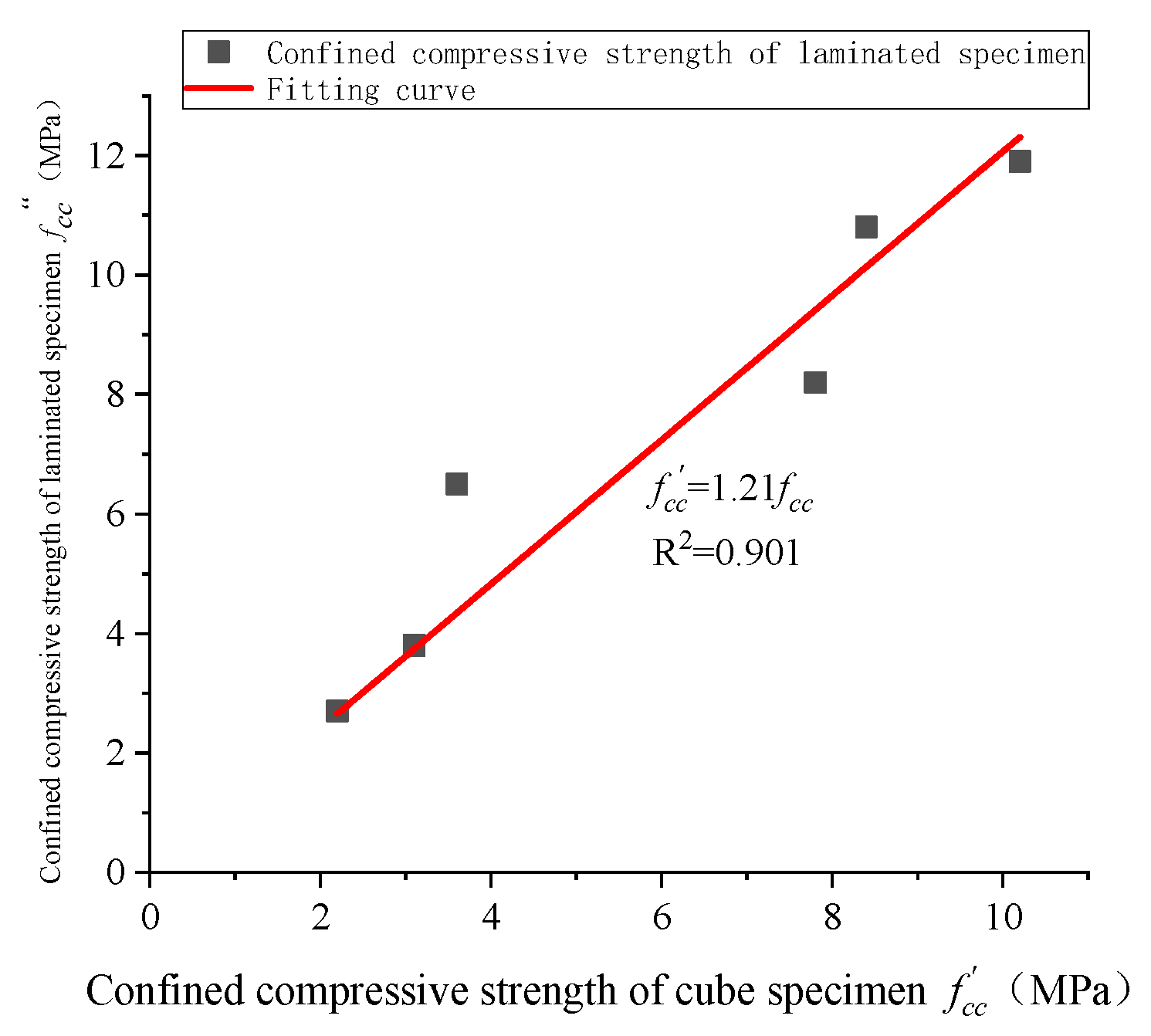
5.1. Confined Compressive Strength Analysis
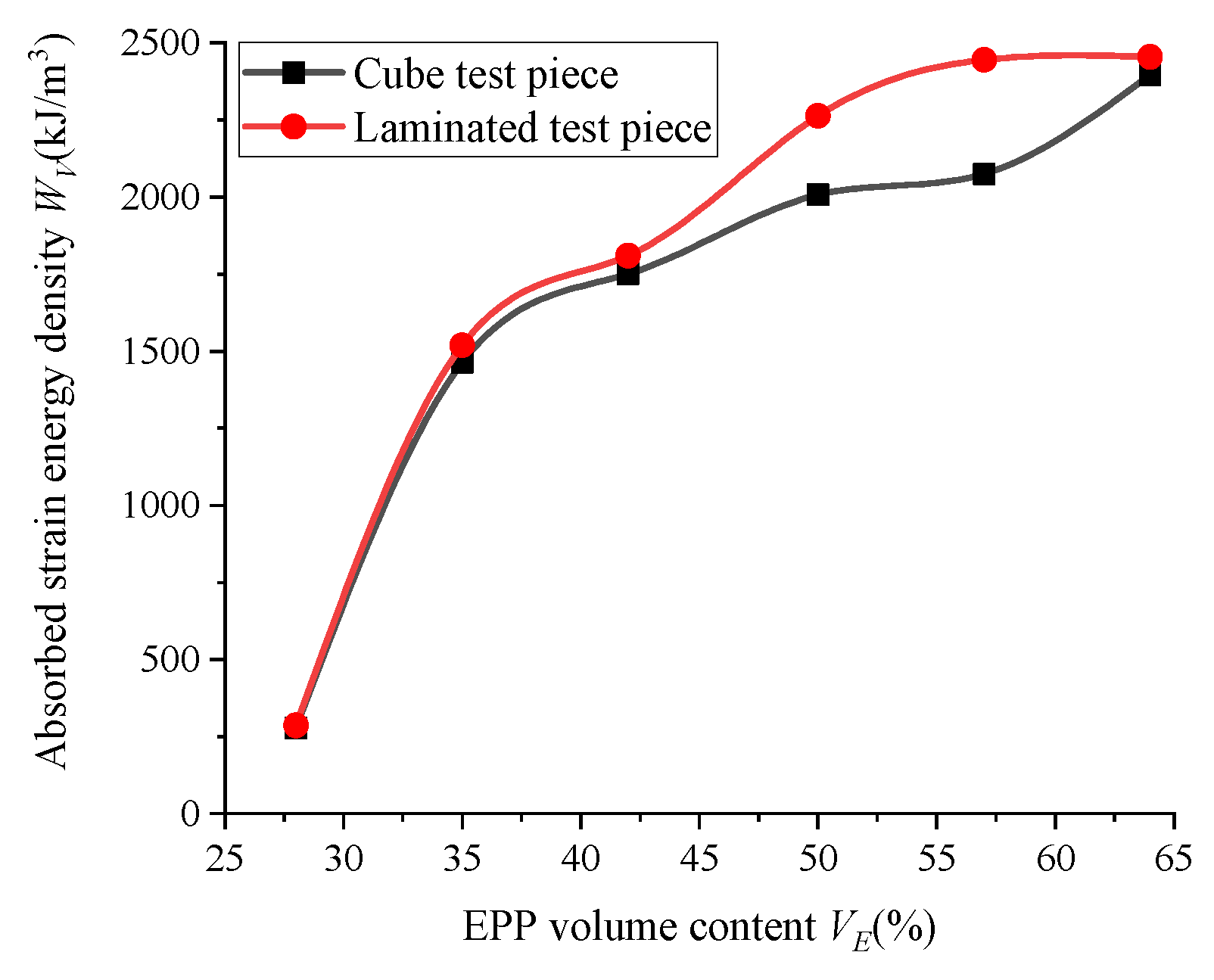
5.2. Energy Absorption Performance of Composite Specimen
6. Conclusions
- (1)
- The increase in the EPP particle volume content decreases the strength parameters of the EPP concrete. This is while the elastic modulus and Poisson’s ratio of the concrete decrease with an increase in the EPP particle volume content;
- (2)
- Good compression and energy absorption performance are exhibited by the EPP concrete under limited compression conditions;
- (3)
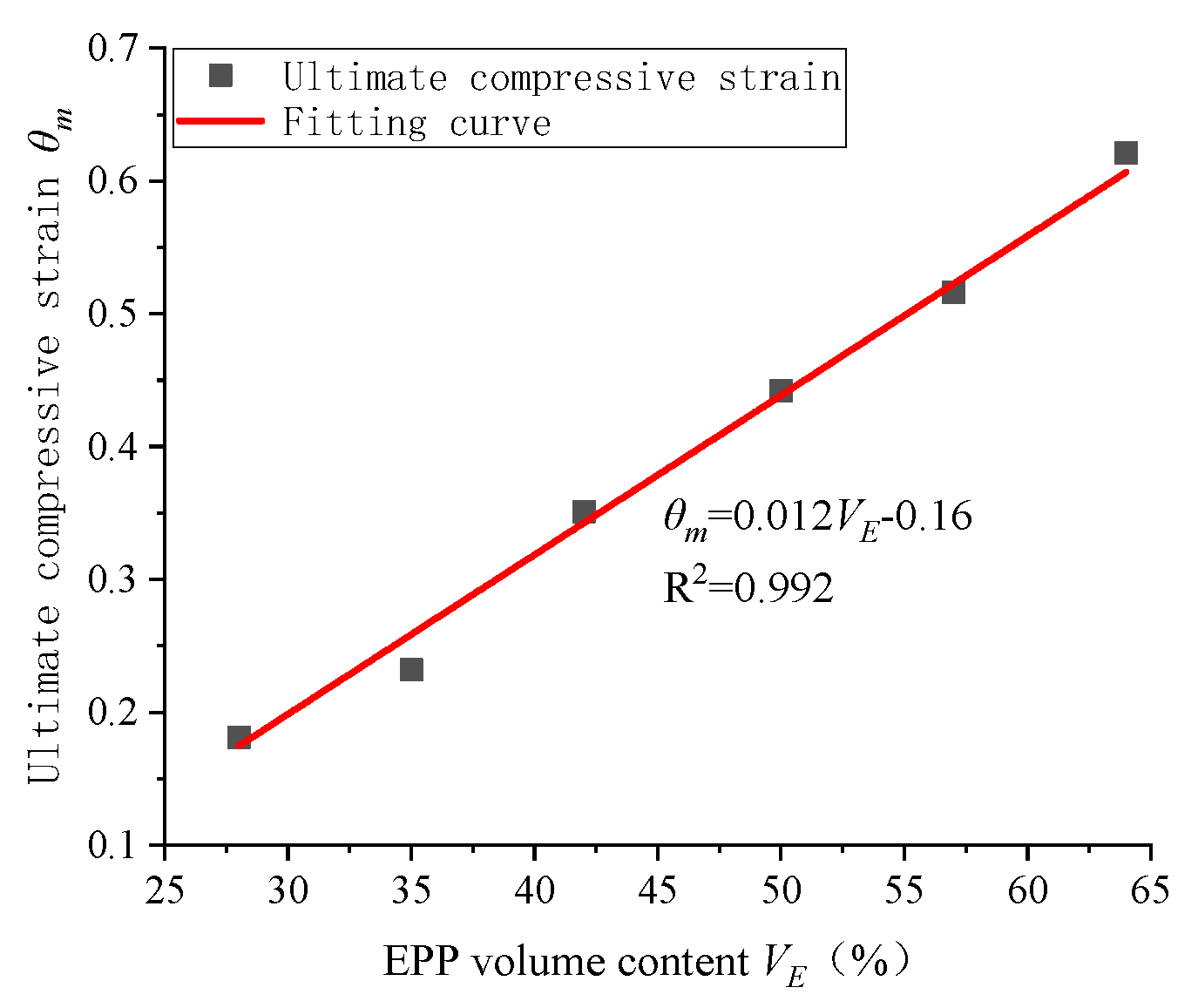
- The compressive performance of the EPP concrete can be reflected by dense volume strain index θd;
- (4)
- An increase in the EPP particle content results in an increase in the strain energy density. Moreover, the group with the highest EPP particle content (64%) presents the highest strain energy density (2396.5 kJ/m3). Also, the ratio of the concentration to the total strain energy in the compression platform section also increases, indicating the energy absorption characteristics of the EPP concrete to be determined by the internal pores;
- (5)
- Similar to the axial compressive strength, the compressive strength of the composite specimen depends on the strength of the EPP concrete layer. Furthermore, the strength of the composite specimens is not only influenced by the content of the EPP particles but is greatly related to the aspect ratio of the EPP concrete layer;
- (6)
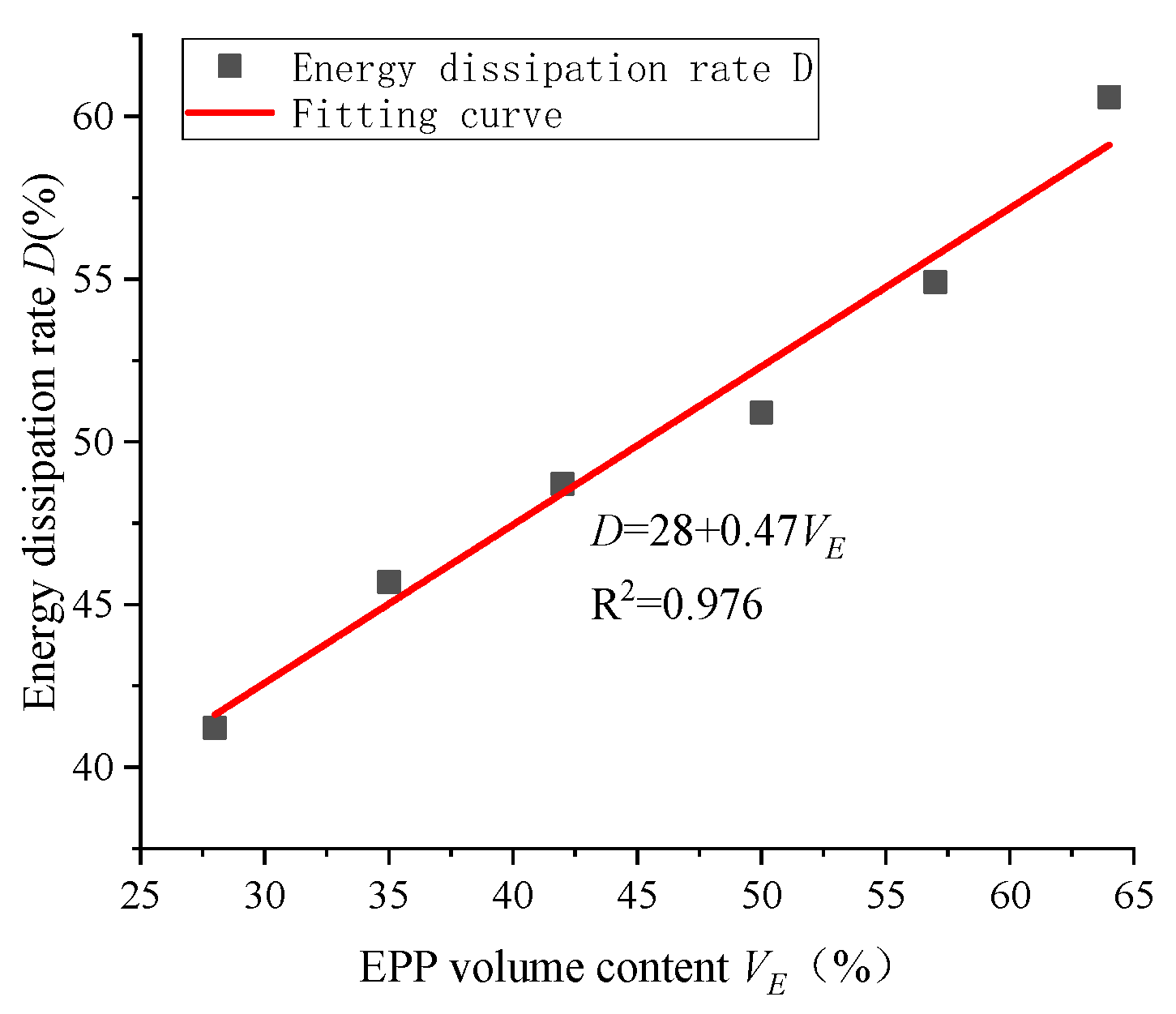
- The higher content of EPP particles results in a higher rate of energy dissipation. Moreover, the energy dissipation rate of the group with the highest EPP particle content (64%) is 60.6%, which approximately varies linearly with the EPP particle content.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Z.; Yang, Y.; Pan, C. Determination of the parameters of rock viscoelastic creep model and analysis of parameter Degradation. Sci. Rep. 2023, 13, 5739. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhou, H.; Zhang, S.; Jiang, S.; Yang, L. A nonlinear creep model for surrounding rocks of tunnels based on kinetic energy theorem. J. Rock Mech. Geotech. Eng. 2023, 15, 363–374. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Li, H.; Wang, Z.; Shi, X.; Chen, X.; Lu, Q. Experimental Study on the Infuence of Temperature on Rock Salt Creep. Rock Mech. Rock Eng. 2023, 56, 3499–3518. [Google Scholar] [CrossRef]
- Fahimifar, A.; Tehrani, F.M.; Hedayat, A.; Vakilzadeh, A. Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field. Tunn. Undergr. Space Technol. 2010, 25, 297–304. [Google Scholar] [CrossRef]
- Spyridis, P.; Konstantis, S.; Gakis, A. Performance indicator of tunnel linings under geotechnical uncertainty. Geomech. Tunn. 2016, 9, 158–164. [Google Scholar] [CrossRef]
- Ren, H.-G.; Tan, Z.-Y.; Feng, P.-X. Back Analysis of In-Situ Stress under Complicated Geological Conditions Based on Function Superposition of Multiple Regressions. In Proceedings of the 5th International Conference on Mechanics and Mechatronics (ICMM 2017), Tokyo, Japan, 20–22 January 2017. [Google Scholar] [CrossRef]
- Han, C.L.; Wang, F.; Li, G. Study on deformation characteristics and multi-layer initial support control of large-section soft rock tunnel. Highway 2021, 66, 335–339. [Google Scholar]
- Yang, Y.; Tan, Z.-S.; Xue, J.; Li, S.-T. Study on the Supporting Performance of High-strength Steel Grille Arch in Soft and Broken Surrounding Rock of Highway Tunnel. China J. Highw. Transp. 2020, 33, 125–134. [Google Scholar]
- Liu, D.; Zuo, J.; Wang, J.; Zhang, T.; Liu, H. Large deformation mechanism and concrete-filled steel tubular support control technology of soft rock roadway-A case study. Eng. Fail. Anal. 2020, 116, 104721. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, W.; Duan, D. Using Energy-Absorbing Dampers to Solve the Problem of Large Deformation in Soft-Rock Tunnels: A Case Study. Energies 2022, 15, 1916. [Google Scholar] [CrossRef]
- Castiglioni, A.; Castellani, L.; Cuder, G.; Comba, S. Relevant Materials Parameters in Cushioning for EPS Foams. Colloids Surf. A Physicochem. Eng. Asp. 2017, 534, 71–77. [Google Scholar] [CrossRef]
- Sahu, S.S.; Gandhi, I.S.R.; Khwairakpam, S. State-of-the-art review on the characteristics of surfactants and foam from foam concrete perspective. J. Inst. Eng. Ser. A 2018, 99, 391–405. [Google Scholar] [CrossRef]
- Li, H.-N.; Liu, P.-F.; Li, C.; Li, G.; Zhang, H. Experimental research on dynamic mechanical properties of metal tailings porous concrete. Constr. Build. Mater. 2019, 213, 20–31. [Google Scholar] [CrossRef]
- Thienel, K.C.; Haller, T.; Beuntner, N. Lightweight Concrete-From Basics to Innovations. Materials 2020, 13, 1120. [Google Scholar] [CrossRef] [PubMed]
- Ma, W. Dynamic impact properties of lightweight aggregate concrete based on different loading systems. Silic. Bull. 2019, 38, 974–982. [Google Scholar]
- Medher, A.H.; Al-Hadithi, A.I.; Hilal, N. The Possibility of Producing Self-Compacting Lightweight Concrete by Using Expanded Polystyrene Beads as Coarse Aggregate. Arab. J. Sci. Eng. 2020, 46, 4253–4270. [Google Scholar] [CrossRef]
- Jose, S.K.; Soman, M.; Evangeline, Y.S. Influence of mixture composition on the properties of foamed concrete. Mater. Today Proc. 2020, 42, 399–404. [Google Scholar] [CrossRef]
- Rapaka, S.D.; Pandey, M.; Annabattula, R.K. Effect of defects on the dynamic compressive behavior of cellular solids. Int. J. Mech. Sci. 2020, 170, 105365. [Google Scholar] [CrossRef]
- Tian, X.; Li, Q.; Lu, Z.; Wang, Z. Experimental study of blast mitigation by foamed concrete. Int. J. Prot. Struct. 2016, 8, 1–14. [Google Scholar] [CrossRef]
- Hu, X.-Y.; He, C.; Lai, X.-H.; Walton, G.; Xu, G.-W. Study on the interaction between squeezing ground and yielding supports with different yielding materials. Tunn. Undergr. Space Technol. 2020, 97, 103242. [Google Scholar] [CrossRef]






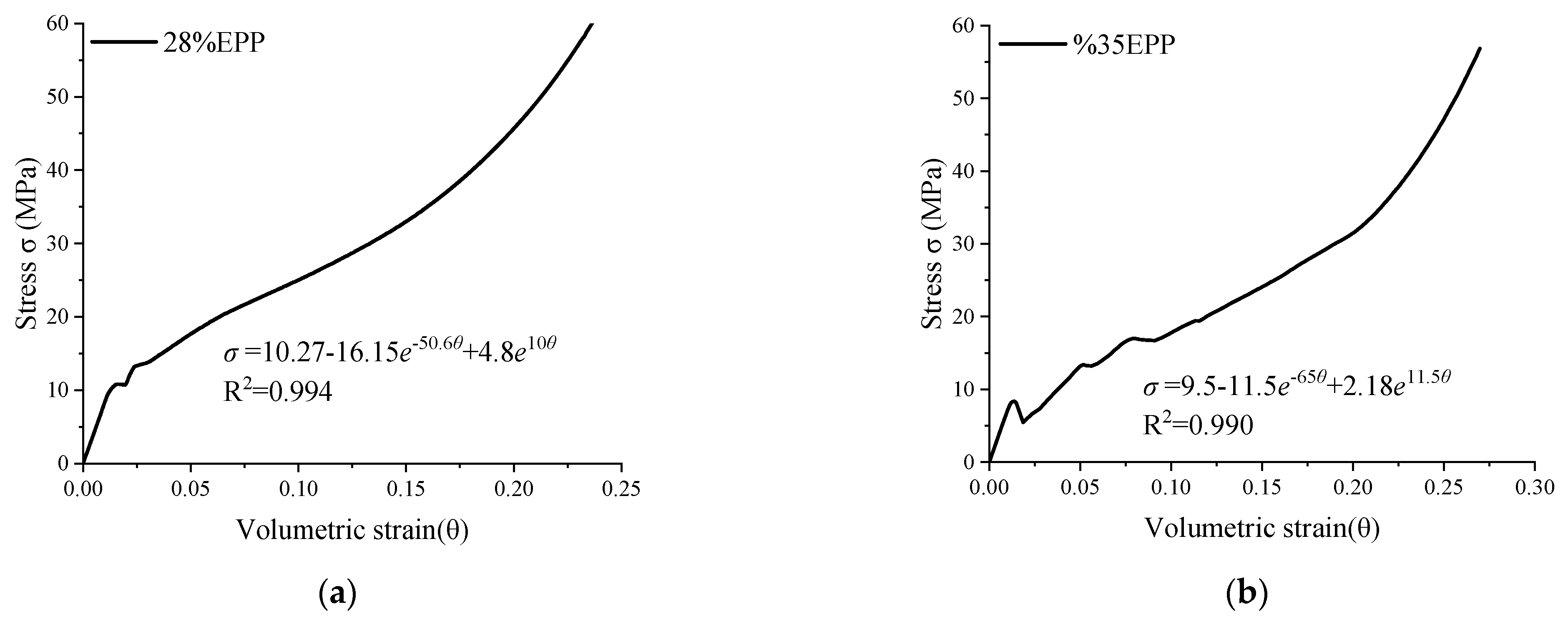
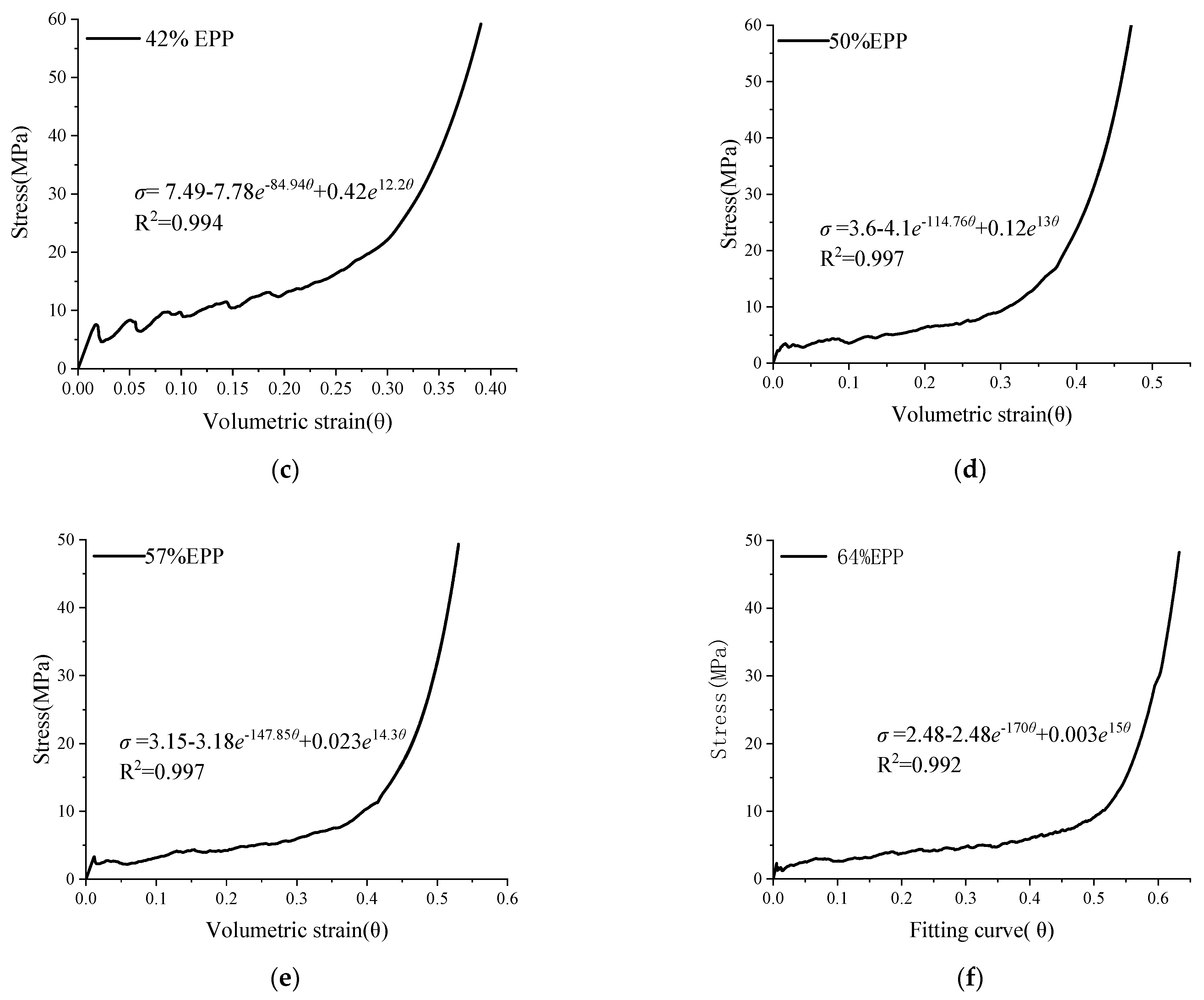







| Water Cement Ratio (kg/m3) | Cement (kg/m3) | Sand (kg/m3) | Broken Stone (kg/m3) | Water (kg/m3) | Water Reducing Agent (kg/m3) |
|---|---|---|---|---|---|
| 0.44 | 457 | 936 | 766 | 201 | 4.6 |
| Number | Cement (kg/m3) | Water (kg/m3) | Broken Stone (kg/m3) | Sand (kg/m3) | Sand Replacement Rate | EPP (kg/m3) | Water Reducing Agent (kg/m3) | Porosity |
|---|---|---|---|---|---|---|---|---|
| A1 | 457 | 201 | 0 | 936 | 0 | 5.67 | 4.6 | 28% |
| A2 | 457 | 201 | 0 | 748.8 | 20% | 7.078 | 4.6 | 35% |
| A3 | 457 | 201 | 0 | 561.6 | 40% | 8.486 | 4.6 | 42% |
| A4 | 457 | 201 | 0 | 374.4 | 60% | 9.894 | 4.6 | 50% |
| A5 | 457 | 201 | 0 | 187.2 | 80% | 11.302 | 4.6 | 57% |
| A6 | 457 | 201 | 0 | 0 | 100% | 12.71 | 4.6 | 64% |
| Number | EPP Volume Content | K1 | K2 | α | K3 | β | R2 |
|---|---|---|---|---|---|---|---|
| A1 | 28% | 10.27 | −16.15 | −50.6 | 4.8 | 10 | 0.994 |
| A2 | 35% | 9.5 | −11.5 | −65 | 2.18 | 11.5 | 0.990 |
| A3 | 42% | 7.49 | −7.78 | −84.94 | 0.42 | 12.2 | 0.994 |
| A4 | 50% | 3.6 | −4.1 | −114.76 | 0.12 | 13 | 0.997 |
| A5 | 57% | 3.15 | −3.18 | −147.85 | 0.023 | 14.3 | 0.997 |
| A6 | 64% | 2.48 | −2.48 | −170 | 0.003 | 15 | 0.992 |
| Number | EPP Volume Content VE | Compressive Failure Strain θcc | Dense Volume Strain θd | Ultimate Compressive Strain θm |
|---|---|---|---|---|
| A1 | 28% | 0.016 | 0.030 | 0.181 |
| A2 | 35% | 0.014 | 0.091 | 0.232 |
| A3 | 42% | 0.010 | 0.200 | 0.351 |
| A4 | 50% | 0.016 | 0.339 | 0.442 |
| A5 | 57% | 0.012 | 0.415 | 0.516 |
| A6 | 64% | 0.005 | 0.516 | 0.621 |
| Number | EPP Volume Content VE | Elastic-Plastic Segment WV1 (kJ/m3) | Compression Platform Section WV2 (kJ/m3) | Total Strain Energy Density WV (kJ/m3) |
|---|---|---|---|---|
| A1 | 28% | 101.1 | 176.3 | 277.4 |
| A2 | 35% | 63.7 | 955.3 | 1463.6 |
| A3 | 42% | 49.1 | 1701.8 | 1750.9 |
| A4 | 50% | 36.0 | 1971.9 | 2007.8 |
| A5 | 57% | 19.8 | 2055.6 | 2075.4 |
| A6 | 64% | 6.4 | 2390.1 | 2396.5 |
| Number | EPP Volume Content VE | Confined Compressive Strength (MPa) | Confined Compressive Strength Value f″cc (MPa) | ||
|---|---|---|---|---|---|
| B1 | 28% | 11.2 | 18.9 | 11.9 | 11.9 |
| B2 | 35% | 8.5 | 10.8 | 13.4 | 10.8 |
| B3 | 42% | 7.8 | 8.0 | 8.7 | 8.2 |
| B4 | 50% | 6.7 | 6.4 | 6.5 | 6.5 |
| B5 | 57% | 3.4 | 4.2 | 3.8 | 3.8 |
| B6 | 64% | 2.7 | 2.7 | 2.2 | 2.7 |
| Number | EPP Volume Content VE | Absorbed Strain Energy Density WV (kJ/m3) | Output Strain Energy Density WO (kJ/m3) | Energy Dissipation Rate D |
|---|---|---|---|---|
| B1 | 28% | 285.9 | 167.9 | 41.3% |
| B2 | 35% | 1519.5 | 824.5 | 45.7% |
| B3 | 42% | 1810.3 | 929.4 | 48.7% |
| B4 | 50% | 3234.0 | 1587.6 | 50.9% |
| B5 | 57% | 2445.2 | 1102.2 | 54.9% |
| B6 | 64% | 2454.6 | 966.2 | 60.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jili, C.; Lu, J.; Lu, H.; Miao, Z. Research on Energy Absorption Characteristics of Polypropylene Foam Concrete Buffer Layer in High Ground Stress Soft Rock Tunnel. Appl. Sci. 2024, 14, 1544. https://doi.org/10.3390/app14041544
Jili C, Lu J, Lu H, Miao Z. Research on Energy Absorption Characteristics of Polypropylene Foam Concrete Buffer Layer in High Ground Stress Soft Rock Tunnel. Applied Sciences. 2024; 14(4):1544. https://doi.org/10.3390/app14041544
Chicago/Turabian StyleJili, Ciqie, Junfu Lu, Hanyu Lu, and Zhihao Miao. 2024. "Research on Energy Absorption Characteristics of Polypropylene Foam Concrete Buffer Layer in High Ground Stress Soft Rock Tunnel" Applied Sciences 14, no. 4: 1544. https://doi.org/10.3390/app14041544
APA StyleJili, C., Lu, J., Lu, H., & Miao, Z. (2024). Research on Energy Absorption Characteristics of Polypropylene Foam Concrete Buffer Layer in High Ground Stress Soft Rock Tunnel. Applied Sciences, 14(4), 1544. https://doi.org/10.3390/app14041544





