An Interval-Valued Intuitionistic Fuzzy Bow-Tie Model (IVIF-BT) for the Effectiveness Evaluation of Safety Barriers in Natural Gas Storage Tank
Abstract
1. Introduction
2. Preliminaries
2.1. Safety Barriers
- Barrier systems: physical and/or non-physical means;
- Barrier functions: for prevention, control, or mitigation;
- Barrier objects: undesired events or accidents.
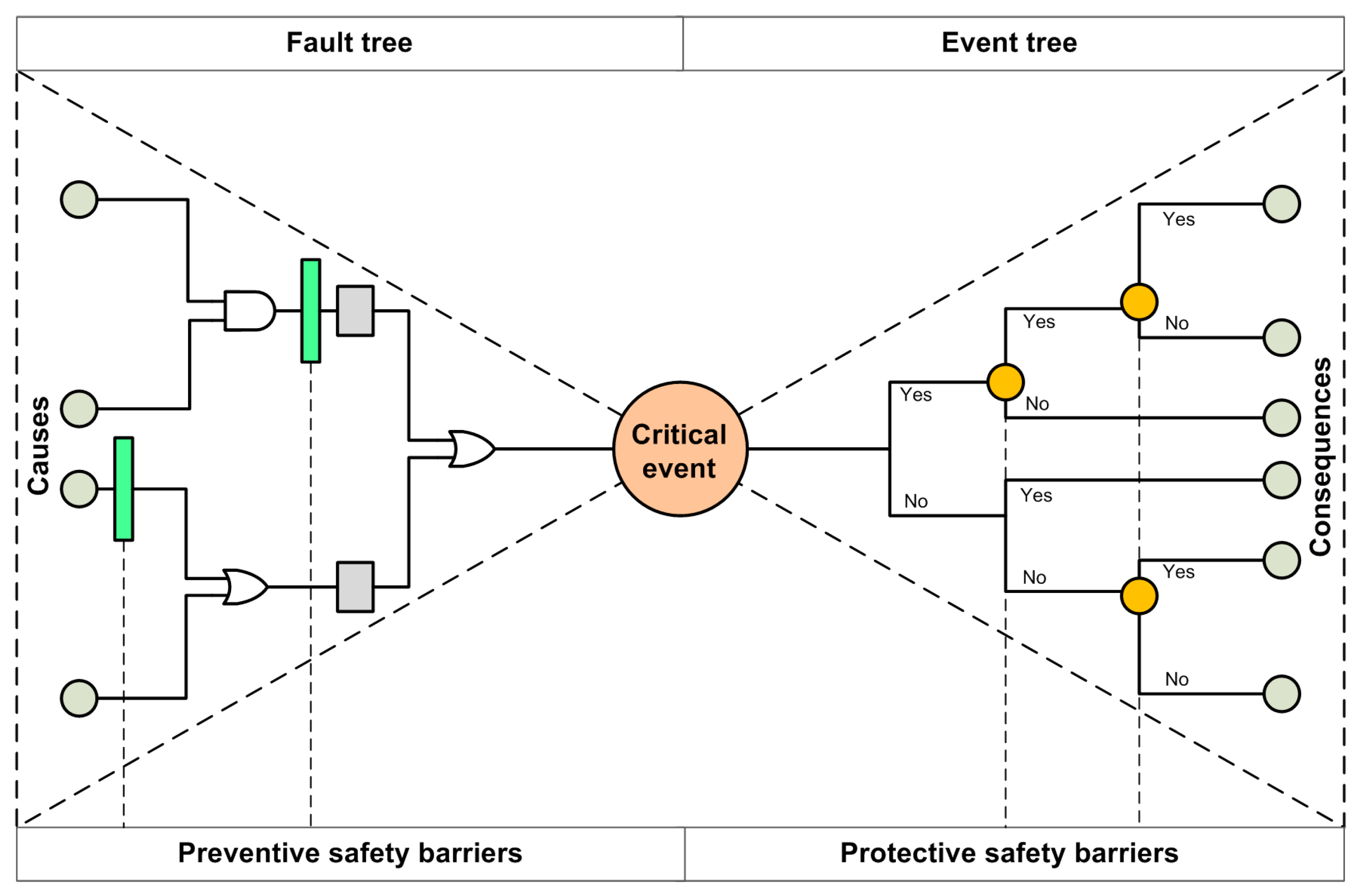
2.2. Bow-Tie Model with Safety Barriers
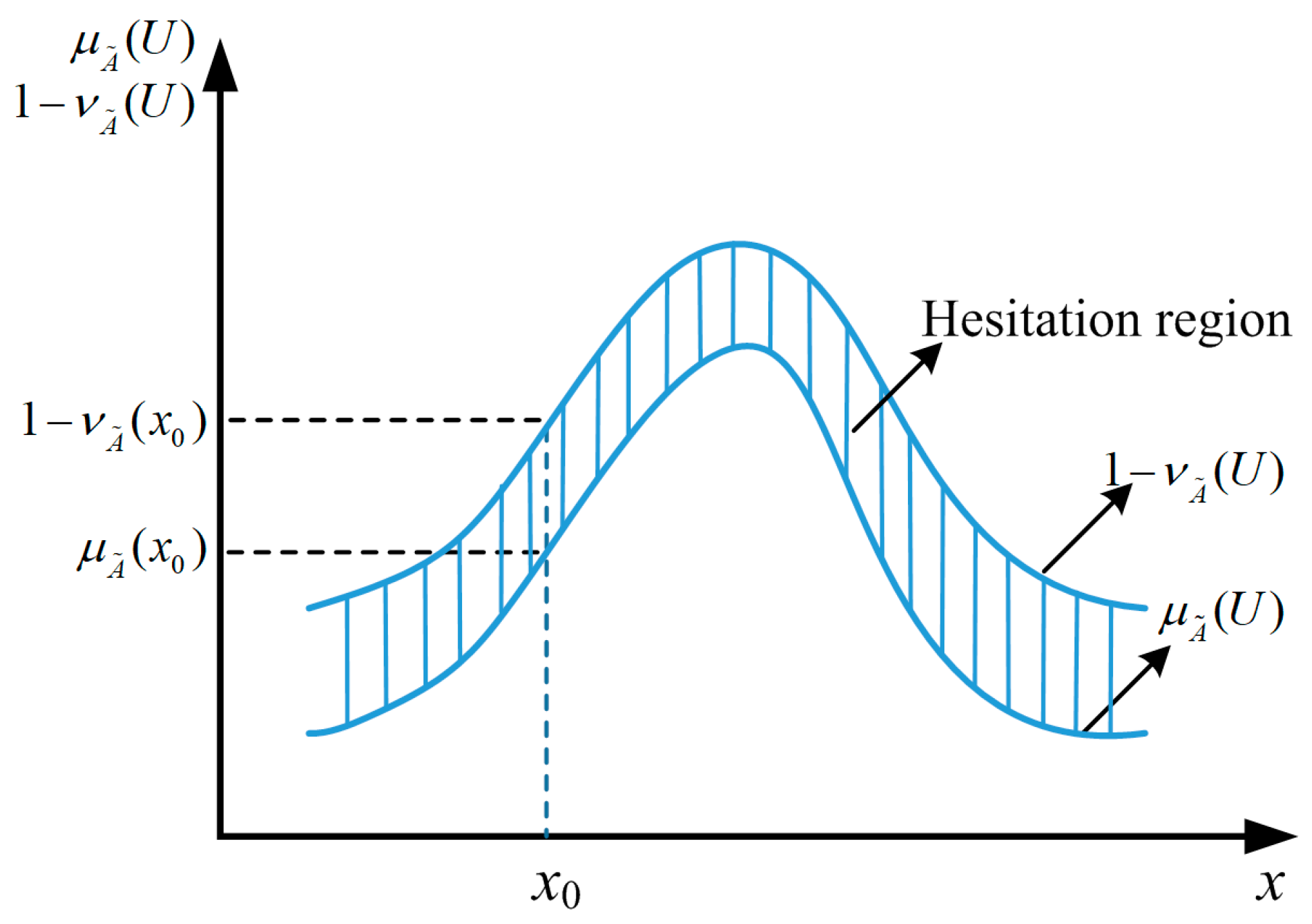
2.3. Interval-Valued Intuitionistic Fuzzy Set
2.3.1. Fuzzy Set and IFS
2.3.2. IVIFS and IVIFNs
- (1)
- Closure Property: , , , , and are also interval-value intuitionistic fuzzy numbers;
- (2)
- Commutative law: , ;
- (3)
- Associative law: , ;
- (4)
- Distributive law: , .
3. Proposed Effectiveness Evaluation Method of Safety Barrier
3.1. Preparatory Work
3.1.1. Identify the System to Be Evaluated
3.1.2. Form an Expert Group and Assign Weights to Experts
3.1.3. Construct the Bow-Tie Model with Safety Barriers
3.2. System Failure Probability Analysis
3.2.1. Determine the Possibility of Each Basic Event in FT via IVIFNs
3.2.2. Determine the Effect of Preventive Safety Barriers on Associated Events via IVIFNs
3.2.3. Compute the Probability of the Critical Event with and/or without Preventive Safety Barriers
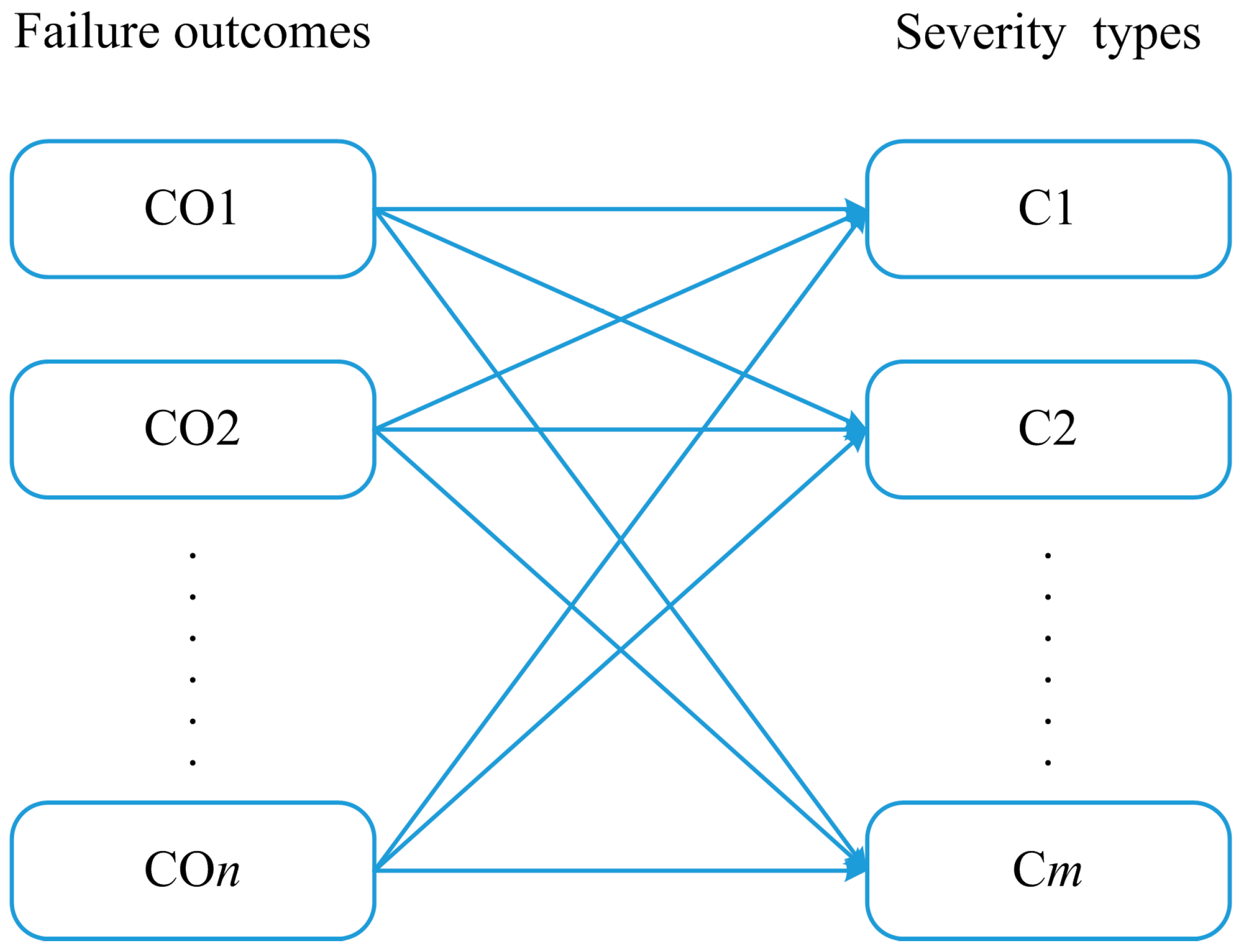
3.3. System Failure Consequence Analysis
3.3.1. Determine Severity Types of Failure Outcomes and Their Weights Using IVIF-AHP
3.3.2. Determine the Severity Index of Each Failure Outcome
3.3.3. Determine the Possibilities of the Conditioning Events in ET via IVIFNs
3.3.4. Determine the Effect of Protective Safety Barriers on Associated Events via IVIFNs
3.3.5. Compute the Failure Consequence Severity without Protective Safety Barriers
3.3.6. Compute the Failure Consequence Severity Considering Protective Safety Barriers
3.4. Safety Barrier Analysis
3.4.1. Compute the Failure Risk of the System without Safety Barriers
3.4.2. Compute the Failure Risk of the System Considering Different Safety Barriers
3.4.3. Compute the Effectiveness of Each Safety Barrier and Rank Safety Barriers
3.4.4. Compute the Effectiveness of Various Combinations of Safety Barriers
3.4.5. Determine the Optimal Configuration of Safety Barriers for Future Plan
4. Case Study
4.1. Case Information
4.2. Construction of the Bow-Tie Model for Describing the Failure of Storage Tank
4.3. Expert Group Formation
4.4. System Failure Probability Analysis
4.4.1. Determination of the Possibilities of Basic Events
4.4.2. Computation of the Probability of the Critical Event with/without Preventive Safety Barriers
4.5. System Failure Consequence Analysis
4.5.1. Determination of the Type of Failure Consequence and Their Weights
4.5.2. Determination of the Severity Index of Each Failure Outcome
4.5.3. Determination of the Possibilities of Conditioning Events with/without Safety Barriers
4.5.4. Computation of the Failure Consequence Severity with/without Safety Barriers
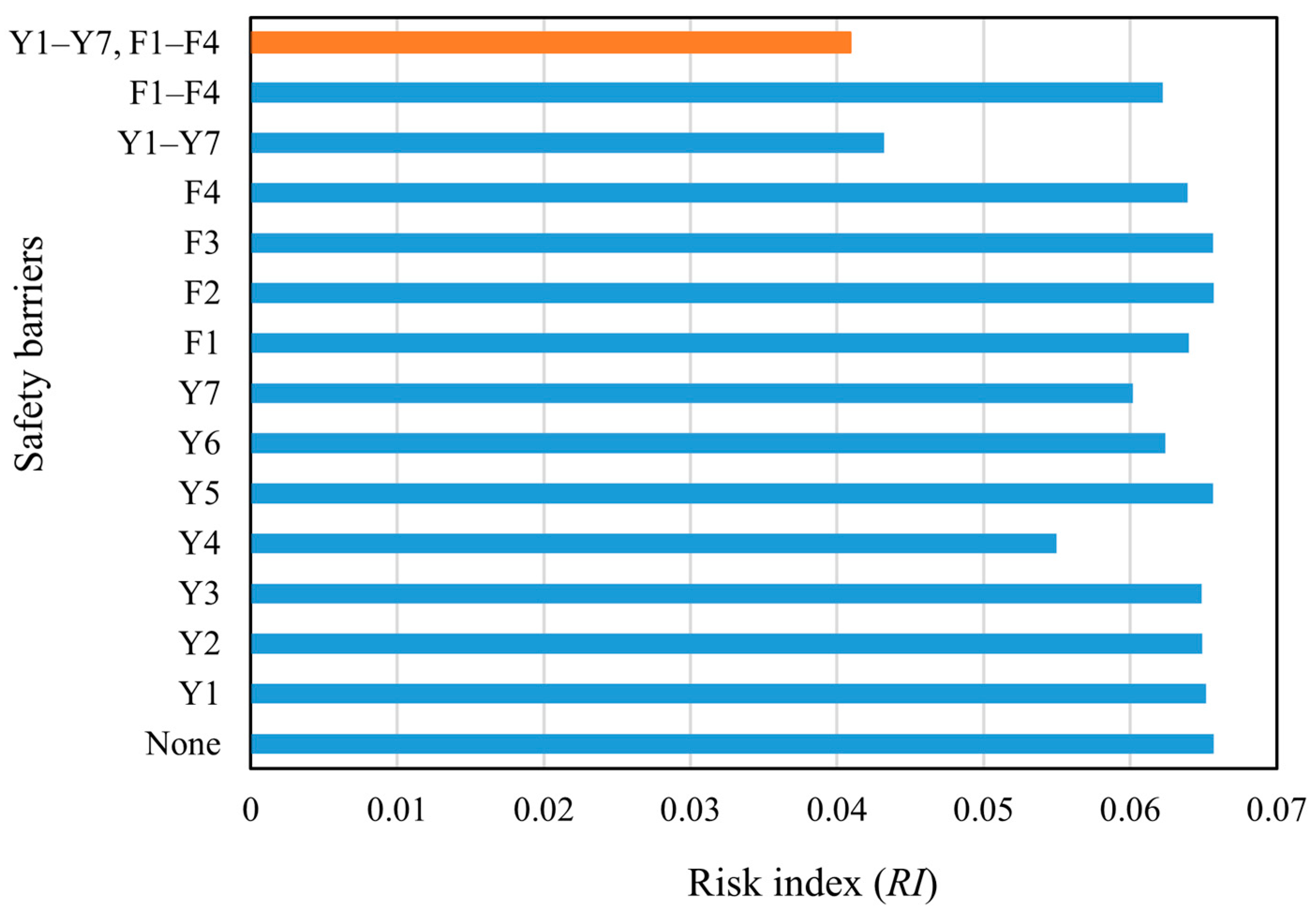
4.6. Computation of the Failure Risk and Effectiveness with/without Safety Barriers
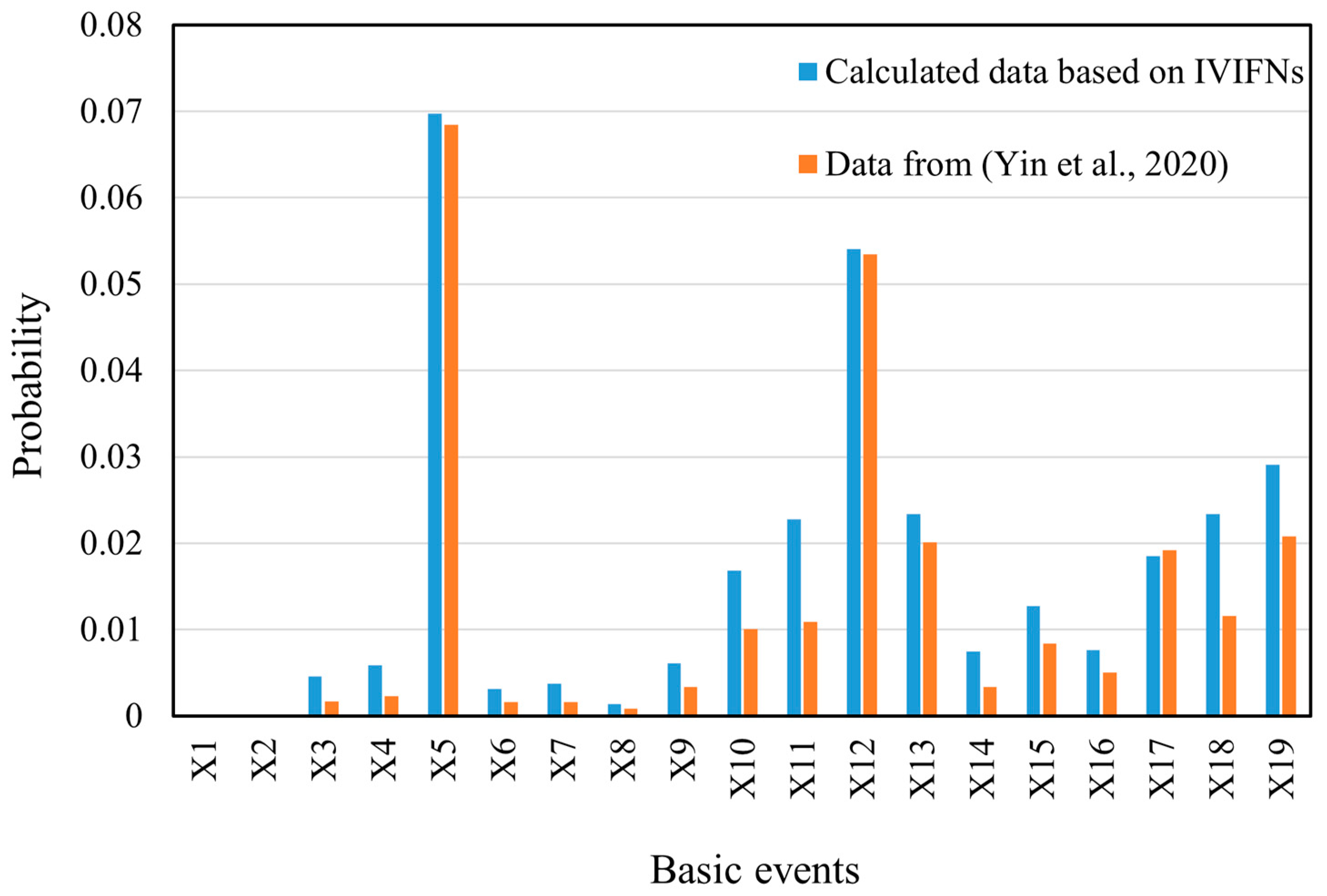
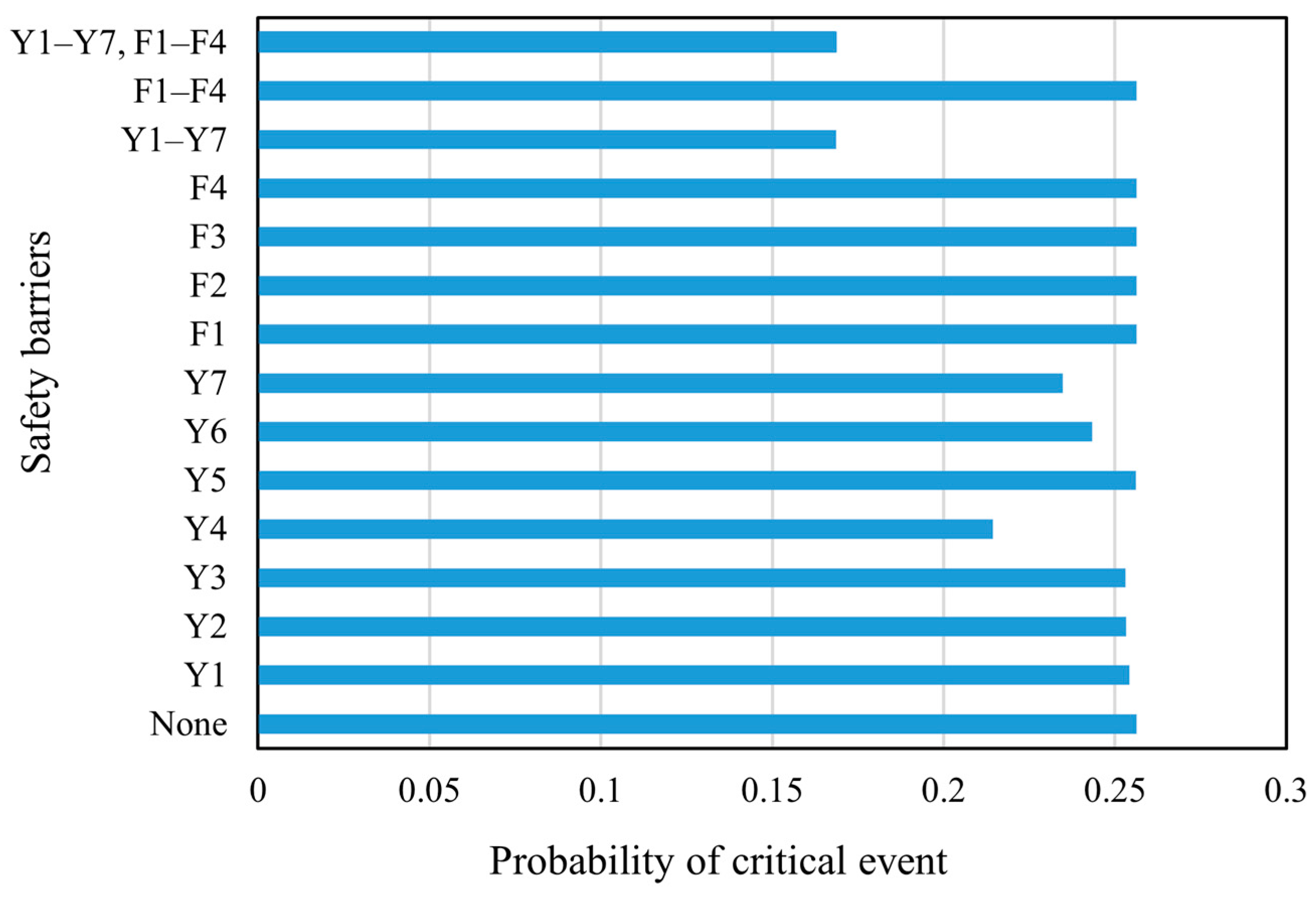
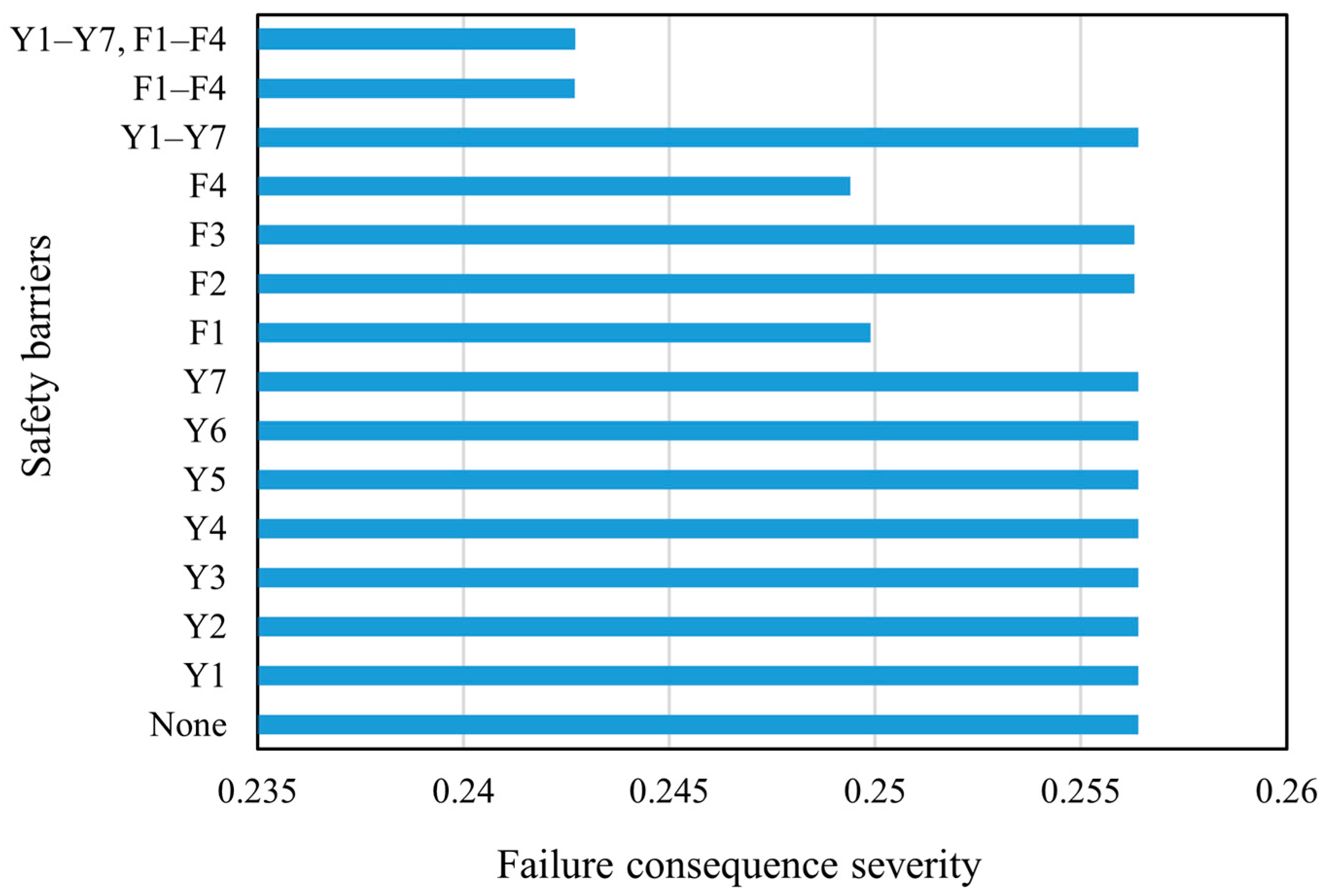
4.7. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reason, J.; Hollnagel, E.; Pariès, J. Revisiting the “Swiss Cheese” Model of Accidents. J. Clin. Eng. 2006, 27, 110–115. [Google Scholar]
- Duijm, N.J. Safety-Barrier Diagrams as a Safety Management Tool. Reliab. Eng. Syst. Saf. 2009, 94, 332–341. [Google Scholar] [CrossRef]
- Aven, T.; Sklet, S.; Vinnem, J.E. Barrier and Operational Risk Analysis of Hydrocarbon Releases (BORA-Release): Part I. Method Description. J. Hazard. Mater. 2006, 137, 681–691. [Google Scholar] [CrossRef]
- Center of Chemical Process Safety. Layer of Protection Analysis: Simplified Process Risk Assessment; Center of Chemical Process Safety: New York, NY, USA, 2010. [Google Scholar]
- Center of Chemical Process Safety. Guidelines for Chemical Process Quantitative Risk Analysis; Center of Chemical Process Safety: New York, NY, USA, 2000. [Google Scholar]
- Leveson, N.G.; Stolzy, J.L. Safety Analysis Using Petri Nets. IEEE Trans. Softw. Eng. 1987, SE-13, 386–397. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- de Dianous, V.; Fiévez, C. ARAMIS Project: A More Explicit Demonstration of Risk Control through the Use of Bow–Tie Diagrams and the Evaluation of Safety Barrier Performance. J. Hazard. Mater. 2006, 130, 220–233. [Google Scholar] [CrossRef]
- Yazdi, M.; Kabir, S.; Walker, M. Uncertainty Handling in Fault Tree Based Risk Assessment: State of the Art and Future Perspectives. Process Saf. Environ. Prot. 2019, 131, 89–104. [Google Scholar] [CrossRef]
- Ferdous, R.; Khan, F.; Sadiq, R.; Amyotte, P.; Veitch, B. Analyzing System Safety and Risks under Uncertainty Using a Bow-Tie Diagram: An Innovative Approach. Process Saf. Environ. Prot. 2013, 91, 1–18. [Google Scholar] [CrossRef]
- Aqlan, F.; Mustafa Ali, E. Integrating Lean Principles and Fuzzy Bow-Tie Analysis for Risk Assessment in Chemical Industry. J. Loss Prev. Process Ind. 2014, 29, 39–48. [Google Scholar] [CrossRef]
- Wang, D.; Liang, P.; Yu, Y.; Fu, X.; Hu, L. An Integrated Methodology for Assessing Accident Probability of Natural Gas Distribution Station with Data Uncertainty. J. Loss Prev. Process Ind. 2019, 62, 103941. [Google Scholar] [CrossRef]
- Yazdi, M.; Hafezi, P.; Abbassi, R. A Methodology for Enhancing the Reliability of Expert System Applications in Probabilistic Risk Assessment. J. Loss Prev. Process Ind. 2019, 58, 51–59. [Google Scholar] [CrossRef]
- Arici, S.S.; Akyuz, E.; Arslan, O. Application of Fuzzy Bow-Tie Risk Analysis to Maritime Transportation: The Case of Ship Collision during the STS Operation. Ocean Eng. 2020, 217, 107960. [Google Scholar] [CrossRef]
- Das, S.; Garg, A.; Maiti, J.; Krishna, O.B.; Thakkar, J.J.; Gangwar, R.K. A Comprehensive Methodology for Quantification of Bow-Tie under Type II Fuzzy Data. Appl. Soft Comput. 2021, 103, 107148. [Google Scholar] [CrossRef]
- Elidolu, G.; Akyuz, E.; Arslan, O.; Arslanoğlu, Y. Quantitative Failure Analysis for Static Electricity-Related Explosion and Fire Accidents on Tanker Vessels under Fuzzy Bow-Tie CREAM Approach. Eng. Fail. Anal. 2022, 131, 105917. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L.; Gao, Z.; Li, S.; Gao, Y. Fault Tree Analysis Combined with Quantitative Analysis for High-Speed Railway Accidents. Saf. Sci. 2015, 79, 344–357. [Google Scholar] [CrossRef]
- Guo, J. A Risk Assessment Approach for Failure Mode and Effects Analysis Based on Intuitionistic Fuzzy Sets and Evidence Theory. J. Intell. Fuzzy Syst. 2016, 30, 869–881. [Google Scholar] [CrossRef]
- Yazdi, M. Risk Assessment Based on Novel Intuitionistic Fuzzy-Hybrid-Modified TOPSIS Approach. Saf. Sci. 2018, 110, 438–448. [Google Scholar] [CrossRef]
- Yazdi, M.; Nedjati, A.; Abbassi, R. Fuzzy Dynamic Risk-Based Maintenance Investment Optimization for Offshore Process Facilities. J. Loss Prev. Process Ind. 2019, 57, 194–207. [Google Scholar] [CrossRef]
- Viegas, R.A.; da Silva Mota, F.D.A.; Costa, A.P.C.S.; dos Santos, F.F.P. A Multi-Criteria-Based Hazard and Operability Analysis for Process Safety. Process Saf. Environ. Prot. 2020, 144, 310–321. [Google Scholar] [CrossRef]
- Kaushik, M.; Kumar, M. An Integrated Approach of Intuitionistic Fuzzy Fault Tree and Bayesian Network Analysis Applicable to Risk Analysis of Ship Mooring Operations. Ocean Eng. 2023, 269, 113411. [Google Scholar] [CrossRef]
- Wang, L.-E.; Liu, H.-C.; Quan, M.-Y. Evaluating the Risk of Failure Modes with a Hybrid MCDM Model under Interval-Valued Intuitionistic Fuzzy Environments. Comput. Ind. Eng. 2016, 102, 175–185. [Google Scholar] [CrossRef]
- Liu, H.-C.; You, J.-X.; Duan, C.-Y. An Integrated Approach for Failure Mode and Effect Analysis under Interval-Valued Intuitionistic Fuzzy Environment. Int. J. Prod. Econ. 2019, 207, 163–172. [Google Scholar] [CrossRef]
- Huang, G.; Xiao, L.; Zhang, G. Improved Failure Mode and Effect Analysis with Interval-Valued Intuitionistic Fuzzy Rough Number Theory. Eng. Appl. Artif. Intell. 2020, 95, 103856. [Google Scholar] [CrossRef]
- Huang, G.; Xiao, L. Failure Mode and Effect Analysis: An Interval-Valued Intuitionistic Fuzzy Cloud Theory-Based Method. Appl. Soft Comput. 2021, 98, 106834. [Google Scholar] [CrossRef]
- Sklet, S. Safety Barriers: Definition, Classification, and Performance. J. Loss Prev. Process Ind. 2006, 19, 494–506. [Google Scholar] [CrossRef]
- International Organization for Standardization. Petroleum and Natural Gas Industries Offshore Production Installations Major Accident Hazard Management during the Design of New Installations; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Landucci, G.; Argenti, F.; Spadoni, G.; Cozzani, V. Domino Effect Frequency Assessment: The Role of Safety Barriers. J. Loss Prev. Process Ind. 2016, 44, 706–717. [Google Scholar] [CrossRef]
- Guldenmund, F.; Hale, A.R.; Goossens, L.H.J.; Betten, J.; Duijm, N.J. The Development of an Audit Technique to Assess the Quality of Safety Barrier Management. J. Hazard. Mater. 2006, 130, 234–241. [Google Scholar] [CrossRef]
- Holland, P. Chapter Three—Blowout Barriers and Analyses. In Offshore Blowouts; Holland, P., Ed.; Gulf Professional Publishing: Burlington, NJ, USA, 1997; pp. 17–32. [Google Scholar]
- Petroleum Safety Authority. Guidelines to Regulations Relating to Management in the Petroleum Activities (The Management Regulations); Petroleum Safety Authority: Stavanger, Norway, 2002.
- Hollnagel, E. Barriers and Accident Prevention; Routledge: London, UK, 2004. [Google Scholar]
- Kang, J.; Zhang, J.; Gao, J. Analysis of the Safety Barrier Function: Accidents Caused by the Failure of Safety Barriers and Quantitative Evaluation of Their Performance. J. Loss Prev. Process Ind. 2016, 43, 361–371. [Google Scholar] [CrossRef]
- Lauridsen, O.; Lootz, E.; Husebo, T.; Ersdal, G. Barrier Management and the Interaction between Technical, Operational and Organisational Barrier Elements; SPE: Stavanger, Norway, 2016; p. D011S010R001. [Google Scholar]
- Khakzad, N.; Landucci, G.; Reniers, G. Application of Graph Theory to Cost-Effective Fire Protection of Chemical Plants during Domino Effects: Cost-Effective Fire Protection of Chemical Plants. Risk Anal. 2017, 37, 1652–1667. [Google Scholar] [CrossRef]
- Delvosalle, C.; Fievez, C.; Pipart, A.; Debray, B. ARAMIS Project: A Comprehensive Methodology for the Identification of Reference Accident Scenarios in Process Industries. J. Hazard. Mater. 2006, 130, 200–219. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Li, D.-F. Extension Principles for Interval-Valued Intuitionistic Fuzzy Sets and Algebraic Operations. Fuzzy Optim. Decis. Mak. 2011, 10, 45–58. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, X. Intuitionistic Fuzzy Information Aggregation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Oztaysi, B.; Onar, S.C.; Goztepe, K.; Kahraman, C. Evaluation of Research Proposals for Grant Funding Using Interval-Valued Intuitionistic Fuzzy Sets. Soft Comput. 2017, 21, 1203–1218. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Kar, S.; Pamučar, D. An Extension of the CODAS Approach Using Interval-Valued Intuitionistic Fuzzy Set for Sustainable Material Selection in Construction Projects with Incomplete Weight Information. Symmetry 2019, 11, 393. [Google Scholar] [CrossRef]
- Karaşan, A.; Kahraman, C. A Novel Intuitionistic Fuzzy DEMATEL—ANP—TOPSIS Integrated Methodology for Freight Village Location Selection. J. Intell. Fuzzy Syst. 2019, 36, 1335–1352. [Google Scholar] [CrossRef]
- Bellamy, L.J.; Ale, B.J.M.; Geyer, T.A.W.; Goossens, L.H.J.; Hale, A.R.; Oh, J.; Mud, M.; Bloemhof, A.; Papazoglou, I.A.; Whiston, J.Y. Storybuilder—A Tool for the Analysis of Accident Reports. Reliab. Eng. Syst. Saf. 2007, 92, 735–744. [Google Scholar] [CrossRef]
- Onar, S.C.; Oztaysi, B.; Otay, İ.; Kahraman, C. Multi-Expert Wind Energy Technology Selection Using Interval-Valued Intuitionistic Fuzzy Sets. Energy 2015, 90, 274–285. [Google Scholar] [CrossRef]
- Onisawa, T. An Approach to Human Reliability in Man-Machine Systems Using Error Possibility. Fuzzy Sets Syst. 1988, 27, 87–103. [Google Scholar] [CrossRef]
- Abdullah, L.; Najib, L. A New Preference Scale Mcdm Method Based on Interval-Valued Intuitionistic Fuzzy Sets and the Analytic Hierarchy Process. Soft Comput. 2016, 20, 511–523. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Havle, C.A. Intuitionistic Fuzzy AHP Based Strategic Analysis of Service Quality in Digital Hospitality Industry. IFAC Pap. 2019, 52, 1687–1692. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria Fuzzy Decision-Making Method Using Entropy Weights-Based Correlation Coefficients of Interval-Valued Intuitionistic Fuzzy Sets. Appl. Math. Model. 2010, 34, 3864–3870. [Google Scholar] [CrossRef]
- Yin, H.; Liu, C.; Wu, W.; Song, K.; Liu, D.; Dan, Y. Safety Assessment of Natural Gas Storage Tank Using Similarity Aggregation Method Based Fuzzy Fault Tree Analysis (SAM-FFTA) Approach. J. Loss Prev. Process Ind. 2020, 66, 104159. [Google Scholar] [CrossRef]
- Yin, H.; Liu, C.; Wu, W.; Song, K.; Dan, Y.; Cheng, G. An Integrated Framework for Criticality Evaluation of Oil & Gas Pipelines Based on Fuzzy Logic Inference and Machine Learning. J. Nat. Gas Sci. Eng. 2021, 96, 104264. [Google Scholar]




| Classification Principle | Classification | Description | Examples | References |
|---|---|---|---|---|
| Barrier functions in accident management and emergency response |
|
|
| [29] |
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
| Barrier functions and purposes in safety management |
|
|
| [28] |
|
|
| ||
| Barrier functions and implementation method in safety management |
|
|
| [4] |
|
|
| ||
| Barrier functions and implementation method in safety management |
|
|
| [30] |
|
|
| ||
|
|
| ||
| Barrier types and characteristics |
|
|
| [31] |
|
|
| ||
|
|
| ||
|
|
| ||
| Barrier properties and implementation method |
|
|
| [32] |
|
|
| ||
|
|
| ||
|
|
| ||
| Barrier elements |
|
|
| [33] |
|
|
| ||
| Barrier elements (further divided in the category of non-physical barriers) |
|
|
| [34] |
|
|
| ||
|
|
| ||
|
|
| ||
| Barrier movement characteristics |
|
|
| [32] |
|
|
| ||
| Barrier implementation subjects or source |
|
|
| [35] |
|
|
| ||
|
|
| ||
| Barrier properties and implementation method |
|
|
| [36] |
|
|
| ||
|
|
| ||
|
|
| ||
| Barrier lifespan (durability and lifespan of the barriers) |
|
|
| [34] |
|
|
|
| Criterion | Classification | Score |
|---|---|---|
| Work experience (Q1) | >30 years | 4 |
| 21–30 years | 3 | |
| 11–20 years | 2 | |
| <10 years | 1 | |
| Education level (Q2) | Doctor’s | 4 |
| Master’s | 3 | |
| Bachelor’s | 2 | |
| Technical school | 1 | |
| Professional relevance (Q3) | Completely related | 4 |
| Basically related | 3 | |
| Basically irrelevant | 2 | |
| Completely irrelevant | 1 | |
| Professional title (Q4) | Senior | 4 |
| Deputy senior | 3 | |
| Intermediate | 2 | |
| Primary | 1 |
| Linguistic Terms | Abbreviation | IVIFNs |
|---|---|---|
| Absolutely Low | AL | ([0, 0.2], [0.5, 0.8]) |
| Very Low | VL | ([0.1, 0.3], [0.4, 0.7]) |
| Low | L | ([0.2, 0.4], [0.3, 0.6]) |
| Medium Low | ML | ([0.3, 0.5], [0.2, 0.5]) |
| Medium | M | ([0.4, 0.6], [0.2, 0.4]) |
| Medium High | MH | ([0.5, 0.7], [0.1, 0.3]) |
| High | H | ([0.6, 0.8], [0, 0.2]) |
| Very High | VH | ([0.7, 0.9], [0, 0.1]) |
| Absolutely High | AH | ([0.8, 1.0], [0, 0]) |
| Preference in Pairwise Comparison | Notation | AHP Preference Number | IVIFNs |
|---|---|---|---|
| Equally Important | EI | 1 | ([0.38, 0.42], [0.22, 0.58]) |
| Equally Very Important | EVI | 2 | ([0.29, 0.41], [0.12, 0.58]) |
| Moderately Important | MI | 3 | ([0.10, 0.43], [0.03, 0.57]) |
| Moderately More Important | MMI | 4 | ([0.03, 0.47], [0.03, 0.53]) |
| Strongly Important | SI | 5 | ([0.13, 0.53], [0.07, 0.47]) |
| Strongly More Important | SMI | 6 | ([0.32, 0.62], [0.08, 0.38]) |
| Very Strongly More Important | VSMI | 7 | ([0.52, 0.72], [0.08, 0.28]) |
| Extremely Strong Important | ESI | 8 | ([0.75, 0.85], [0.05, 0.15]) |
| Extremely More Important | EMI | 9 | ([1.00, 1.00], [0.00, 0.00]) |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.0 | 0.0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Symbol | Content | Symbol | Content |
|---|---|---|---|
| X1 | Geological factors | M3 | Equipment reasons |
| X2 | Environmental factors | M4 | Natural factors |
| X3 | Failure to standardize operation according to requirements | M5 | Non-natural factors |
| X4 | Daily inspections do not meet the requirements | M6 | Main equipment |
| X5 | Mechanical breakdown | M7 | Others |
| X6 | Installation failure | M8 | Design reasons |
| X7 | Design specification failure | M9 | Processing problem |
| X8 | Unreasonable layout | M10 | Material reasons |
| X9 | Foundation subsidence or displacement | M11 | Instrument problem |
| X10 | Weld defect | M12 | Corrosion |
| X11 | Failure to finish processing as required | M13 | External corrosion |
| X12 | Deformation/breakage | EV1 | Generate an open flame |
| X13 | Internal corrosion occurred | EV2 | Forming steam clouds |
| X14 | Damage of coating | EV3 | Limited space |
| X15 | External environment meets corrosion standards | EV4 | Delayed ignition |
| X16 | Failure of other fittings | CO1 | Jet fire |
| X17 | No alarm/indicator light | CO2 | Vapor cloud explosion |
| X18 | Other failures in the instrument system | CO3 | Poisoning |
| X19 | Instrument system open circuit | CO4 | Flash fire |
| M1 | Natural gas leakage | CO5 | Natural gas dispersion |
| M2 | Third-party sabotage | CO6 | Deflagration |
| Symbol | Description | Safety Barrier Type |
|---|---|---|
| Y1 | Personnel operation and safety training | Preventive safety barriers |
| Y2 | Using a checklist to establish complete and strict specifications and requirements for daily inspection work | |
| Y3 | Regular detection of tank subsidence height and ground soil condition | |
| Y4 | Regular detection of deformation or damage in the storage tank | |
| Y5 | Regular detection of the complete length of the surface coating | |
| Y6 | Regular maintenance of safety alarm system equipment | |
| Y7 | Installation and regular maintenance of safety electrical equipment | |
| F1 | Fire source detection and alarm device | Protective safety barriers |
| F2 | Storage tank pressure detection | |
| F3 | Gas concentration detection instrument | |
| F4 | Fire alarm and extinguishing system |
| Number | Work Experience (Year) | Education Level | Professional Relevance | Professional Title | Weight (λi) |
|---|---|---|---|---|---|
| 1 | 21 | Master’s | Basically related | Senior | 0.382 |
| 2 | 4 | PhD | Basically related | Deputy senior | 0.324 |
| 3 | 11 | Master’s | Basically irrelevant | Deputy senior | 0.294 |
| Basic Events | Expert No.1 | Expert No.2 | Expert No.3 | Basic Events | Expert No.1 | Expert No.2 | Expert No.3 |
|---|---|---|---|---|---|---|---|
| X1 | AL | VL | AL | X14 | MH | M | MH |
| X2 | VL | VL | VL | X15 | H | MH | MH |
| X3 | M | M | M | X16 | MH | MH | M |
| X4 | M | MH | M | X17 | VH | H | M |
| X5 | AH | AH | VH | X18 | MH | VH | VH |
| X6 | M | ML | ML | X19 | VH | VH | H |
| X7 | M | ML | M | X3-Y1 | ML | ML | L |
| X8 | L | L | ML | X4-Y2 | L | ML | ML |
| X9 | MH | M | M | X9-Y3 | ML | L | ML |
| X10 | H | M | VH | X12-Y4 | L | VL | L |
| X11 | H | VH | H | X14-Y5 | L | L | ML |
| X12 | VH | AH | H | X17-Y6 | ML | L | L |
| X13 | MH | VH | VH | X19-Y7 | L | ML | VL |
| Basic Events | Expert No.1 | Expert No.2 | Expert No.3 | Aggregation Value |
|---|---|---|---|---|
| X1 | ([0, 0.2], [0.5, 0.8]) | ([0.1, 0.3], [0.4, 0.7]) | ([0, 0.2], [0.5, 0.8]) | ([0.0335, 0.2339], [0.4651, 0.7661]) |
| X2 | ([0.1, 0.3], [0.4, 0.7]) | ([0.1, 0.3], [0.4, 0.7]) | ([0.1, 0.3], [0.4, 0.7]) | ([0.1, 0.3], [0.4, 0.7]) |
| X3 | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) |
| X4 | ([0.4, 0.6], [0.2, 0.4]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4344, 0.6356], [0.1598, 0.3644]) |
| X5 | ([0.8, 1], [0, 0]) | ([0.8, 1], [0, 0]) | ([0.7, 0.9], [0, 0.1]) | ([0.7747, 1], [0, 0]) |
| X6 | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.3400, 0.5409], [0.2, 0.4591]) |
| X7 | ([0.4, 0.6], [0.2, 0.4]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.3693, 0.5700], [0.2, 0.4230]) |
| X8 | ([0.2, 0.4], [0.3, 0.6]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.2308, 0.4313], [0.2663, 0.5687]) |
| X9 | ([0.5, 0.7], [0.1, 0.3]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4404, 0.6416], [0.1535, 0.3584]) |
| X10 | ([0.6, 0.8], [0, 0.2]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.7, 0.9], [0, 0.1]) | ([0.5808, 0.7958], [0, 0.2042]) |
| X11 | ([0.6, 0.8], [0, 0.2]) | ([0.7, 0.9], [0, 0.1]) | ([0.6, 0.8], [0, 0.2]) | ([0.6356, 0.8402], [0, 0.1598]) |
| X12 | ([0.7, 0.9], [0, 0.1]) | ([0.8, 1], [0, 0]) | ([0.6, 0.8], [0, 0.2]) | ([0.7137, 1], [0, 0]) |
| X13 | ([0.5, 0.7], [0.1, 0.3]) | ([0.7, 0.9], [0, 0.1]) | ([0.7, 0.9], [0, 0.1]) | ([0.6354, 0.8479], [0, 0.1521]) |
| X14 | ([0.5, 0.7], [0.1, 0.3]) | ([0.6, 0.8], [0, 0.2]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.4695, 0.6707], [0.1252, 0.3293]) |
| X15 | ([0.6, 0.8], [0, 0.2]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.5409, 0.7430], [0, 0.2570]) |
| X16 | ([0.5, 0.7], [0.1, 0.3]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4725, 0.6735], [0.1226, 0.3265]) |
| X17 | ([0.7, 0.9], [0, 0.1]) | ([0.6, 0.8], [0, 0.2]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.5963, 0.8118], [0, 0.1882]) |
| X18 | ([0.5, 0.7], [0.1, 0.3]) | ([0.7, 0.9], [0, 0.1]) | ([0.7, 0.9], [0, 0.1]) | ([0.6354, 0.8479], [0, 0.1521]) |
| X19 | ([0.7, 0.9], [0, 0.1]) | ([0.7, 0.9], [0, 0.1]) | ([0.6, 0.8], [0, 0.2]) | ([0.6735, 0.8774], [0, 0.1226]) |
| X3-Y1 | ([0.3, 0.5], [0.2, 0.5]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.2720, 0.4725], [0.2253, 0.5275]) |
| X4-Y2 | ([0.2, 0.4], [0.3, 0.6]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.2634, 0.4639], [0.2335, 0.5361]) |
| X9-Y3 | ([0.3, 0.5], [0.2, 0.5]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.2691, 0.4696], [0.2281, 0.5304]) |
| X12-Y4 | ([0.2, 0.4], [0.3, 0.6]) | ([0.1, 0.3], [0.4, 0.7]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.1689, 0.3693], [0.3293, 0.6307]) |
| X14-Y5 | ([0.2, 0.4], [0.3, 0.6]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.2308, 0.4313], [0.2663, 0.5687]) |
| X17-Y6 | ([0.3, 0.5], [0.2, 0.5]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.2398, 0.4404], [0.2570, 0.5596]) |
| X19-Y7 | ([0.2, 0.4], [0.3, 0.6]) | ([0.3, 0.5], [0.2, 0.5]) | ([0.1, 0.3], [0.4, 0.7]) | ([0.2069, 0.4082], [0.2863, 0.5918]) |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | EI | 1/MMI | MI | SMI |
| C2 | MMI | EI | SI | VSMI |
| C3 | 1/MI | 1/SI | EI | SMI |
| C4 | 1/SMI | 1/VSMI | 1/SMI | EI |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | EI | 1/SMI | MI | SI |
| C2 | SMI | EI | VSMI | ESI |
| C3 | 1/MI | 1/VSMI | EI | EVI |
| C4 | 1/SI | 1/ESI | 1/EVI | EI |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | EI | 1/SI | EVI | SMI |
| C2 | SI | EI | SMI | VSMI |
| C3 | 1/EVI | 1/SMI | EI | MMI |
| C4 | 1/SMI | 1/VSMI | 1/MMI | EI |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | ([0.38, 0.42], [0.22, 0.58]) | ([0.03, 0.57], [0.03, 0.47]) | ([0.10, 0.43], [0.03, 0.57]) | ([0.32, 0.62], [0.08, 0.38]) |
| C2 | ([0.03, 0.47], [0.03, 0.57]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.13, 0.53], [0.07, 0.47]) | ([0.52, 0.72], [0.08, 0.28]) |
| C3 | ([0.03, 0.57], [0.10, 0.43]) | ([0.07, 0.47], [0.13, 0.53]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.32, 0.62], [0.08, 0.38]) |
| C4 | ([0.08, 0.38], [0.32, 0.62]) | ([0.08, 0.28], [0.52, 0.72]) | ([0.08, 0.38], [0.32, 0.62]) | ([0.38, 0.42], [0.22, 0.58]) |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | ([0.38, 0.42], [0.22, 0.58]) | ([0.08, 0.38], [0.32, 0.62]) | ([0.10, 0.43], [0.03, 0.57]) | ([0.13, 0.53], [0.07, 0.47]) |
| C2 | ([0.32, 0.62], [0.08, 0.38]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.52, 0.72], [0.08, 0.28]) | ([0.75, 0.85], [0.05, 0.15]) |
| C3 | ([0.03, 0.57], [0.10, 0.43]) | ([0.08, 0.28], [0.52, 0.72]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.29, 0.41], [0.12, 0.58]) |
| C4 | ([0.07, 0.47], [0.13, 0.53]) | ([0.05, 0.15], [0.75, 0.85]) | ([0.12, 0.58], [0.29, 0.41]) | ([0.38, 0.42], [0.22, 0.58]) |
| Cm | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | ([0.38, 0.42], [0.22, 0.58]) | ([0.07, 0.47], [0.13, 0.53]) | ([0.29, 0.41], [0.12, 0.58]) | ([0.32, 0.62], [0.08, 0.38]) |
| C2 | ([0.13, 0.53], [0.07, 0.47]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.32, 0.62], [0.08, 0.38]) | ([0.52, 0.72], [0.08, 0.28]) |
| C3 | ([0.12, 0.58], [0.29, 0.41]) | ([0.08, 0.38], [0.32, 0.62]) | ([0.38, 0.42], [0.22, 0.58]) | ([0.03, 0.47], [0.03, 0.53]) |
| C4 | ([0.08, 0.38], [0.32, 0.62]) | ([0.08, 0.28], [0.52, 0.72]) | ([0.03, 0.57], [0.03, 0.47]) | ([0.38, 0.42], [0.22, 0.58]) |
| Failure Outcomes | Expert No.1 | Expert No.2 | Expert No.3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | |
| CO1 | H | VH | H | H | H | VH | H | H | H | H | H | VH |
| CO2 | VH | VH | VH | VH | VH | H | H | VH | VH | H | VH | H |
| CO3 | L | M | L | VL | L | L | L | VL | VL | M | L | VL |
| CO4 | H | H | H | H | H | VH | M | VH | M | H | H | H |
| CO5 | VL | VL | VL | L | L | VL | VL | VL | VL | VL | VL | VL |
| CO6 | VH | VH | VH | VH | VH | VH | VH | VH | VH | VH | VH | VH |
| Failure Outcomes | Severity Index (SI) | Failure Outcomes | Severity Index (SI) |
|---|---|---|---|
| CO1 | ([0.6194, 0.8226], [0, 0.1774]) | CO4 | ([0.5937, 0.8012], [0, 0.1988]) |
| CO2 | ([0.6876, 0.88897], [0, 0.1103]) | CO5 | ([0.1169, 0.3172], [0.3819, 0.6828]) |
| CO3 | ([0.2189, 0.4218], [0.3002, 0.5782]) | CO6 | ([0.7, 0.9], [0, 0.1]) |
| Conditioning Events | Expert No.1 | Expert No.2 | Expert No.3 | Conditioning Events | Expert No.1 | Expert No.2 | Expert No.3 |
|---|---|---|---|---|---|---|---|
| EV1 | H | H | MH | EV1-F1 | ML | L | L |
| EV2 | H | VH | VH | EV2-F2 | MH | M | M |
| EV3 | H | H | VH | EV3-F3 | M | M | M |
| EV4 | H | H | H | EV4-F4 | ML | M | L |
| Conditioning Events | Expert No.1 | Expert No.2 | Expert No.3 | Aggregation Value |
|---|---|---|---|---|
| EV1 | ([0.6, 0.8], [0, 0.2]) | ([0.6, 0.8], [0, 0.2]) | ([0.5, 0.7], [0.1, 0.3]) | ([0.5729, 07747], [0, 0.2253]) |
| EV2 | ([0.6, 0.8], [0, 0.2]) | ([0.7, 0.9], [0, 0.1]) | ([0.7, 0.9], [0, 0.1]) | ([0.6652, 0.8697], [0, 0.1303]) |
| EV3 | ([0.6, 0.8], [0, 0.2]) | ([0.6, 0.8], [0, 0.2]) | ([0.7, 0.9], [0, 0.1]) | ([0.6324, 0.8369], [0, 0.1631]) |
| EV4 | ([0.6, 0.8], [0, 0.2]) | ([0.6, 0.8], [0, 0.2]) | ([0.6, 0.8], [0, 0.2]) | ([0.6, 0.8], [0, 0.2]) |
| EV1-F1 | ([0.3, 0.5], [0.2, 0.5]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.2398, 0.4404], [0.2570, 0.5596]) |
| EV2-F2 | ([0.5, 0.7], [0.1, 0.3]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4404, 0.6416], [0.1535, 0.3584]) |
| EV3-F3 | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) |
| EV4-F4 | ([0.3, 0.5], [0.2, 0.5]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.2, 0.4], [0.3, 0.6]) | ([0.3074, 0.5093], [0.2253, 0.4907]) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yin, H.; Zhang, Y.; Li, X.; Li, Y.; Gong, X.; Wu, W. An Interval-Valued Intuitionistic Fuzzy Bow-Tie Model (IVIF-BT) for the Effectiveness Evaluation of Safety Barriers in Natural Gas Storage Tank. Appl. Sci. 2024, 14, 1586. https://doi.org/10.3390/app14041586
Liu J, Yin H, Zhang Y, Li X, Li Y, Gong X, Wu W. An Interval-Valued Intuitionistic Fuzzy Bow-Tie Model (IVIF-BT) for the Effectiveness Evaluation of Safety Barriers in Natural Gas Storage Tank. Applied Sciences. 2024; 14(4):1586. https://doi.org/10.3390/app14041586
Chicago/Turabian StyleLiu, Jiawei, Hailong Yin, Yixin Zhang, Xiufeng Li, Yongquan Li, Xueru Gong, and Wei Wu. 2024. "An Interval-Valued Intuitionistic Fuzzy Bow-Tie Model (IVIF-BT) for the Effectiveness Evaluation of Safety Barriers in Natural Gas Storage Tank" Applied Sciences 14, no. 4: 1586. https://doi.org/10.3390/app14041586
APA StyleLiu, J., Yin, H., Zhang, Y., Li, X., Li, Y., Gong, X., & Wu, W. (2024). An Interval-Valued Intuitionistic Fuzzy Bow-Tie Model (IVIF-BT) for the Effectiveness Evaluation of Safety Barriers in Natural Gas Storage Tank. Applied Sciences, 14(4), 1586. https://doi.org/10.3390/app14041586






