Stability Analysis of the Exploitation System with Room and Pillar by Analytical Methods
Abstract
:1. Introduction
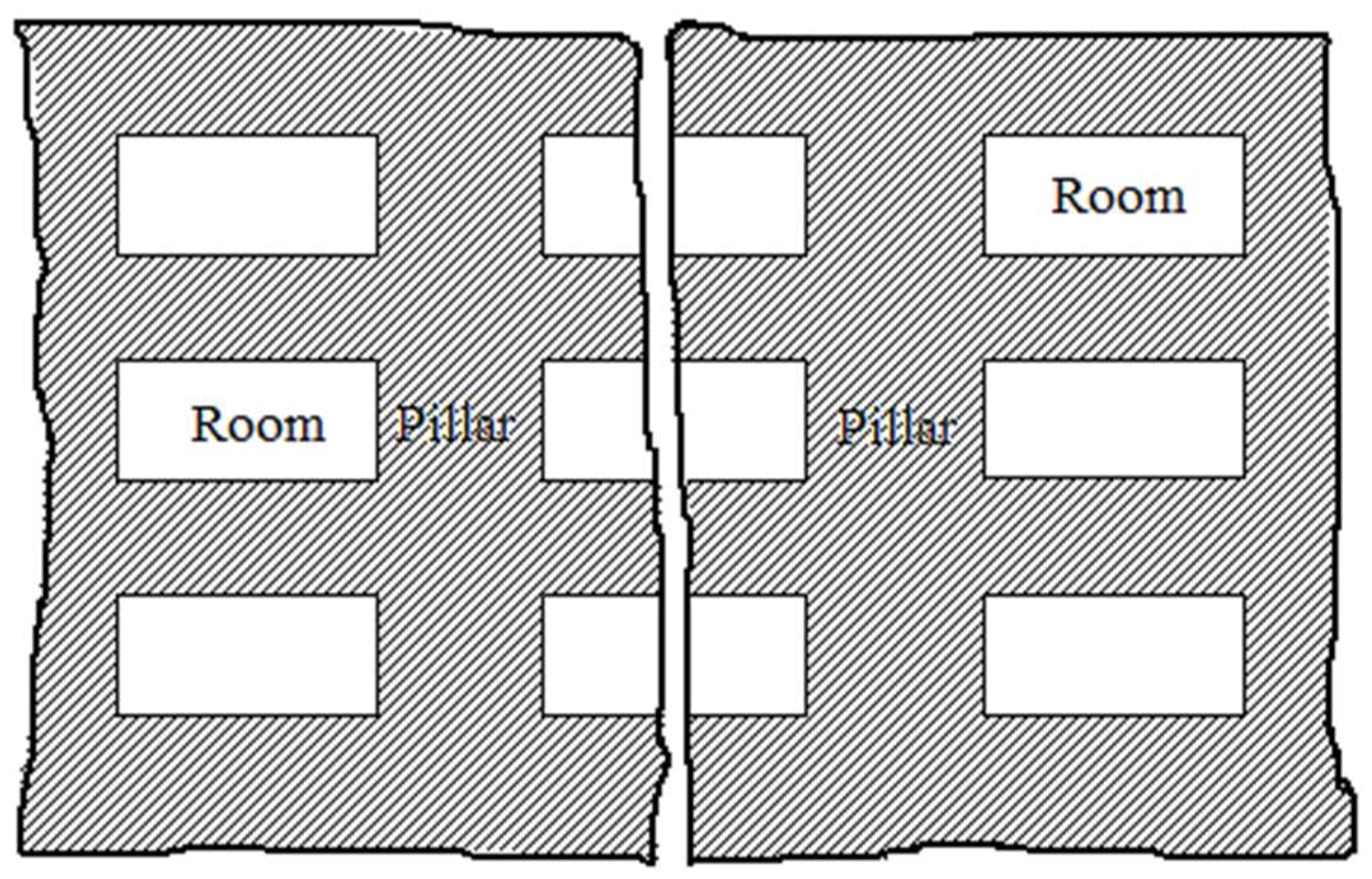
2. Geomechanical, Technical, and Mining Considerations
3. Methods
3.1. Stability Analysis of a Rock Salt Mining System with Rooms and Pillars Based on the Limit Equilibrium Theory
3.2. Stability Analysis of the Rooms and Pillars Exploitation System through Analytical Method
3.2.1. Analytical Model for Assessing the Stress State in the Pillar Based on the Principles and Theories of the Mechanics of the Continuous Medium
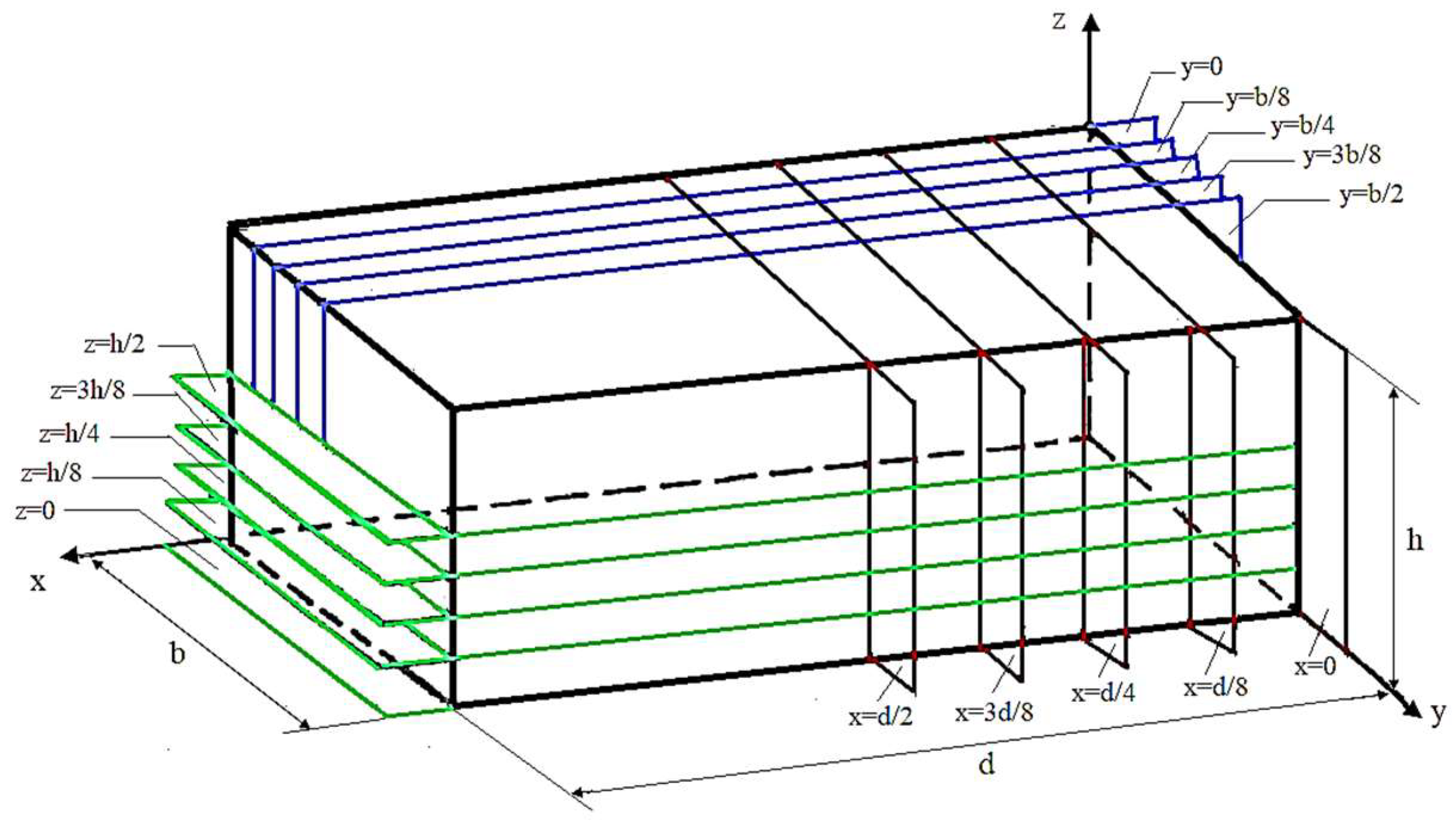
3.2.2. Analytical Model for Assessing the Stress State of Pillar and Floor Based on the Principle of Complex Variables
- evaluation of boundary conditions:
- -
- at the surface of the massif, the normal and tangential stresses are zero, which means that for Y = H, it follows that σz = τx z = 0, and −∞ < x < ∞;
- -
- at the contact of the floor with the pillar, for Y = 0 (Figure 4), the following conditions are valid:
- and the equilibrium equations based on the principle of Cauchy–Riemann, obtaining:
4. Results
4.1. Stability Analysis of a Rock Salt Mining System with Rooms and Pillars Based on the Limit Equilibrium Theory
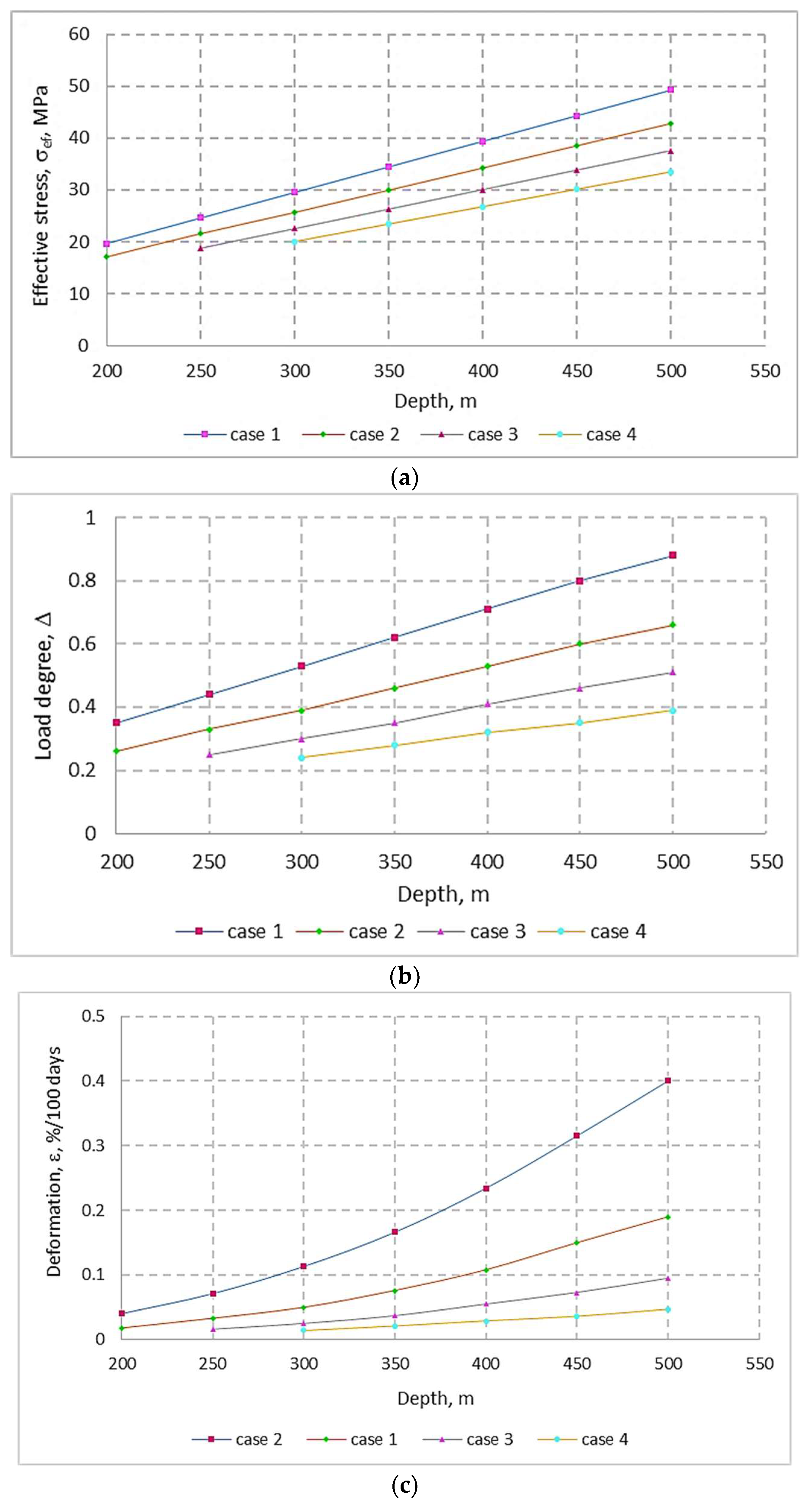
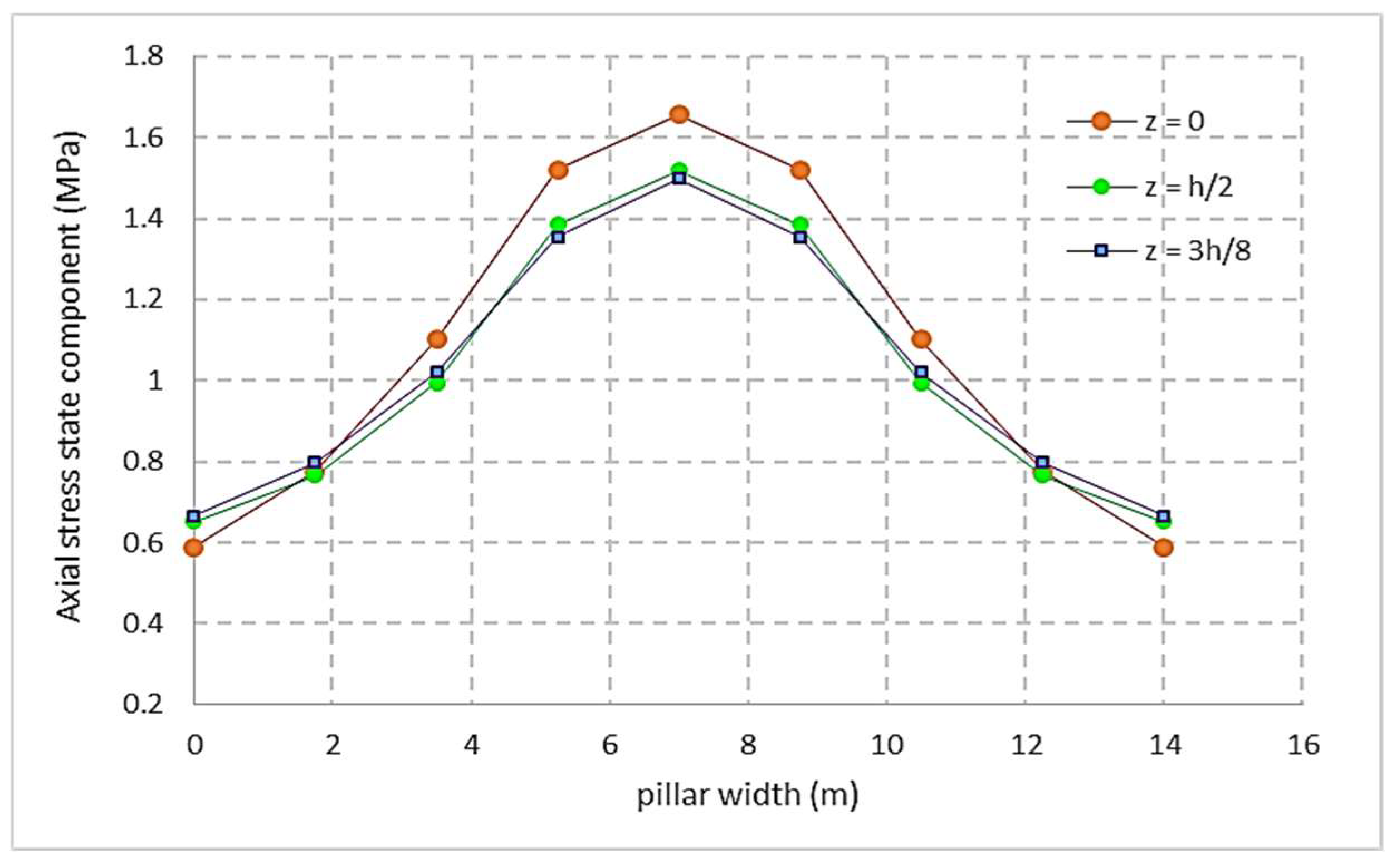
4.2. Stress State in the Pillar Based on the Principles and Theories of the Mechanics of the Continuous Medium
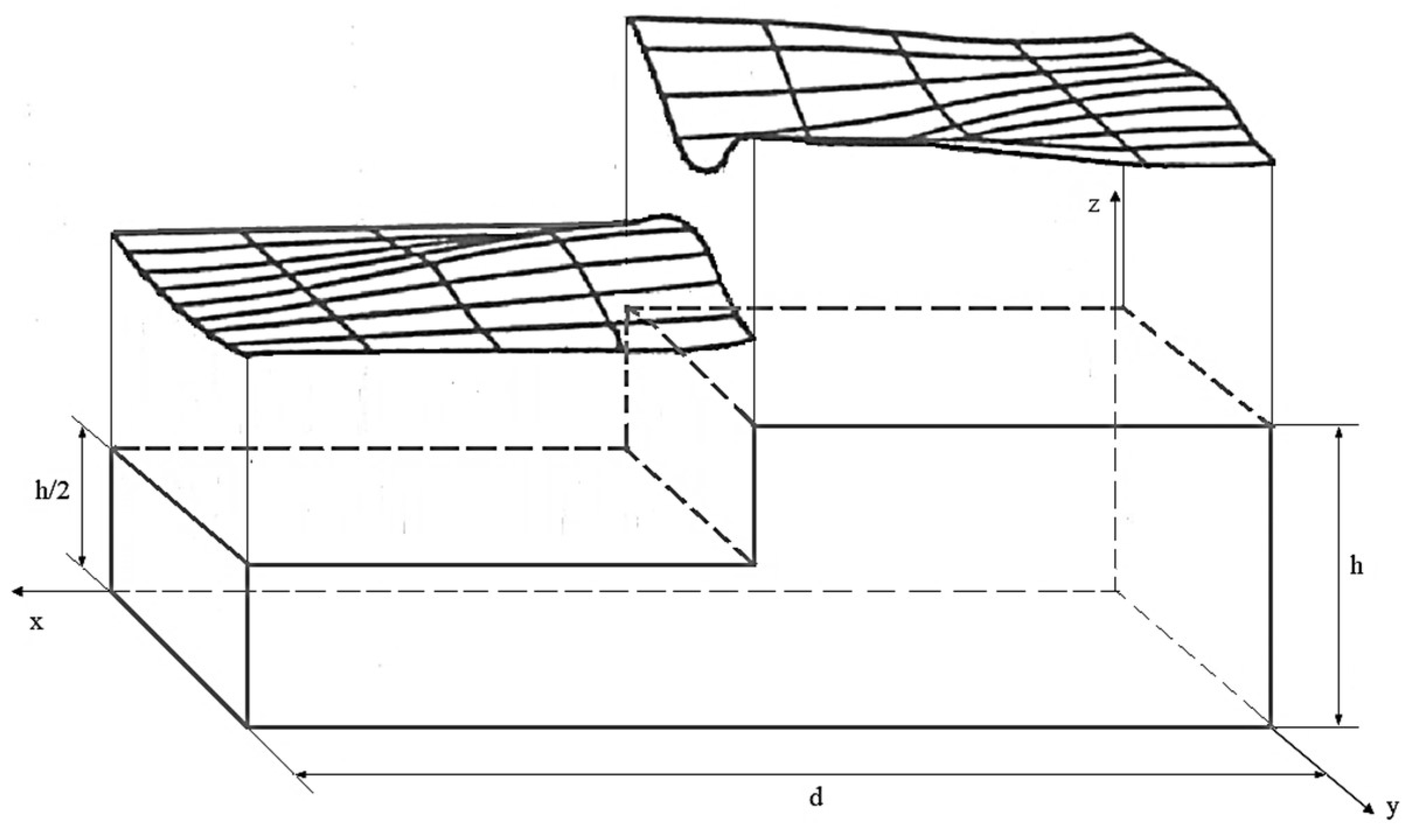
4.3. Stress State of Pillar and Floor Based on the Principle of Complex Variables
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Wang, Z.; Zheng, Y.; Duan, P.; Ding, S. Study on tri-axial creep experiment and constitutive relation of different rock salt. Saf. Sci. 2012, 50, 801–805. [Google Scholar] [CrossRef]
- Chu, Z.; Wu, Z.; Liu, Q.; Liu, B.; Sun, J. Analytical solution for lined circular tunnels in deep viscoelastic Burgers rock considering the longitudinal discontinuous excavation and sequential installation of liners. J. Eng. Mech. 2021, 147, 04021009. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Wang, L.; Zhang, K.; Daemen, J.J.K.; Liu, W. Time-dependent subsidence prediction model and influence factor analysis for underground gas storages in bedded salt formations. Eng. Geol. 2015, 187, 156–169. [Google Scholar] [CrossRef]
- Toderaş, M. Analysis the natural stress state of salt massive from Praid Mine, Romania. In Proceedings of the 15th International Multidisciplinary Scientific Geo-Conference & EXPO SGEM 2015 Modern Management of Mine Producing, Geology and Environmental Protection, Albena, Bulgaria, 18–24 June 2015; Volume 3, pp. 73–80. [Google Scholar]
- Li, Z.J. Analysis and Application of Pillar Stability of Deep Salt Rock Gas Storage; Shandong University: Jinan, China, 2018. [Google Scholar]
- Fu, X.F. Stability analysis of Huangchang salt cavern underground gas storage in Jianghan Basin. J. Shanxi Datong Univ. (Nat. Sci. Ed.) 2020, 36, 73–75. [Google Scholar]
- Habibi, R. An investigation into design concepts, design methods and stability criteria of salt caverns. Oil Gas Sci. Technol.—Rev. IFP Energ. Nouv. 2019, 74, 14. [Google Scholar] [CrossRef]
- Ma, H.; Wei, X.; Shi, X.; Liang, X.; Bai, W.; Ge, L. Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage. Energies 2022, 15, 7570. [Google Scholar] [CrossRef]
- Jeremic, M.L. Rock Mechanics in Salt Mining; A. A. Balkema: Rotterdam, The Netherlands, 1994; p. 530. [Google Scholar]
- Junthong, P.; Khamrat, S.; Sartkaew, S.; Fuenkajorn, K. Determination of time-dependent strengths of salt pillars based on strain energy principle. Int. J. Min. Sci. Technol. 2019, 29, 273–279. [Google Scholar] [CrossRef]
- Toderas, M. The Octahedral Concept and Cubic Triaxiality in Assessment of Secondary Stress State. Min. Miner. Depos. 2020, 14, 81–90. [Google Scholar] [CrossRef]
- Toderaș, M.; Iosif, C. The Interaction Principle in the Assessment of Pillars’ Secondary Stress-Deformation State. Min. Rev. 2023, 29, 14–25. [Google Scholar] [CrossRef]
- Majeed, Y.; Abbas, N.; Emad, M.Z. Stability evaluation of room-and-pillar rock salt mines by using a flat jack technique—A case study. J. South. Afr. Inst. Min. Metall. 2023, 123, 287–298. [Google Scholar] [CrossRef]
- Berest, P.; Brouard, B.; Feuga, B.; Karimi-Jafari, M. The 1873 collapse of the Saint-Maximilien panel at the Varangeville salt mine. Int. J. Rock Mech. Min. Sci. 2008, 45, 1025–1043. [Google Scholar] [CrossRef]
- Qin, X.S.; Cao, H.; Guo, L.J. Sensitivity analysis of factors influencing pillar stability in the deep stope of underground salt mine. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 022002. [Google Scholar] [CrossRef]
- Zhang, S.Z. Analysis of the Roof-Pillar Stability of the 1# Copper Mine with the Room-Pillar Method in the Dahongshan Iron Mine; Kunming University of Science and Technology: Kunming, China, 2014. [Google Scholar]
- Singh, A.; Kumar, C.; Kannan, L.G.; Rao, K.S.; Ramanathan, A. Estimation of Creep Parameters of Rock Salt from Uniaxial Compression Tests. Int. J. Rock Mech. Min. Sci. 2018, 107, 243–248. [Google Scholar] [CrossRef]
- Laouafa, F.; Ghoreychi, M. Contribution to improve pillar analysis in abandoned room and pillar salt mines. In Proceedings of the Symposium Post Mining 2005, Nancy, France, 16–18 November 2005. [Google Scholar]
- Onica, I.; Cozma, E.; Marica, D.P. Stability Analysis of the Rock Salt Rooms and Pillars of the Ocnele Mari Saline with the Aid of the 2d Finite Element Modelling. Ann. Univ. Petrosani Min. Eng. 2011, 12, 7–17. [Google Scholar]
- Esterhuizen, G.S.; Tyrna, P.L.; Murphy, M.M. A Case Study of the Collapse of Slender Pillars Affected by Through-Going Discontinuities at a Limestone Mine in Pennsylvania. Rock Mech. Rock Eng. 2019, 52, 4941–4952. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.-Y.; Li, W.-C.; Liu, Y.-X.; Jiang, Y.-D. Numerical simulation of surface movement laws under different unconsolidated layers thickness. Trans. Nonferrous Met. Soc. China 2011, 21, 599–603. [Google Scholar] [CrossRef]
- Poulsen, B.A.; Shen, B. Subsidence risk assessment of decommissioned bord-and-pillar collieries. Int. J. Rock Mech. Min. Sci. 2013, 60, 312–320. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, S.; Zhao, F. Study on the mechanics and micro/macroeconomics of multiple strip-shaped pillar recovery. Arch. Min. Sci. 2020, 65, 19–33. [Google Scholar]
- Afshin, M.; Javad, G. Stability Analysis and Feasibility of Pillar Recovery Inextraction Workplace of Salt Rockmining at Ghaplogh Region at Khoy. Indian J. Fundam. Appl. Life Sci. 2015, 5, 823–837. Available online: www.cibtech.org/sp.ed/jls/2015/03/jls.htm (accessed on 17 September 2023).
- Wu, A.-X.; Huang, M.-Q.; Han, B.; Wang, Y.-M.; Yu, S.-F.; Miao, X.-X. Orthogonal design and numerical simulation of room and pillar configurations in fractured stopes. J. Cent. South Univ. 2014, 21, 3338–3344. [Google Scholar] [CrossRef]
- Stamatiu, M. Problema Dimensiunii Stâlpilor la Minele de Sare Din România; Editura Academiei: Bucharest, Romania, 1959. [Google Scholar]
- Hunsche, U. Results and interpretation of creep experiments on rock salt. In Proceedings of the First Conference on the Mecanical Behaviour of Salt, State College, PA, USA, 9–11 November 1981. [Google Scholar]
- Thorel, L.; Ghoreychi, M. Rock salt damage—Experimental results and interpretation. In Proceedings of the Mechanical Behavior of Salt: 3rd Conference, Palaiseau, France, 14–16 September 1993; Ghoreychi, M., Berest, P., Hardy, H., Jr., Langer, M., Eds.; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1996; pp. 175–189. [Google Scholar]
- Vouille, G.; Bergues, J.; Durup, J.G.; You, T. Study of the stability of caverns in rock salt created by solution mining proposal for a new design criterion. In Proceedings of the Third Conference on the Mechanical Behavior of Salt, Palaiseau, France, 14–16 September 1993; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1996; pp. 427–444. [Google Scholar]
- Nguyen-Minh, D.; Quintanilha de Menezes, E. Incompressible numerical modeling for long term convergence evaluation of underground works in salt. In Proceedings of the Third Conference on the Mechanical Behavior of Salt, Palaiseau, France, 14–16 September 1993; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1996; pp. 523–531. [Google Scholar]
- Wang, F.; Chen, J. Reasonable coal pillar design and remote control mining technology for highwall residual coal resources. R. Soc. Open Sci. 2019, 6, 181817. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Yue, Z.Q.; Tham, L.G.; Zhu, H.H. Pillar design by combining finite element methods, neural networks and reliability: A case study of the Fenghuangshan copper mine, China. Int. J. Rock Mech. Min. Sci. 2003, 40, 585–599. [Google Scholar] [CrossRef]
- Julien, M.R.; Foerch, R.; Aubertin, M.; Cailletaud, G. Some aspects of numerical implementation of SUVIC-D. In Proceedings of the Fourth Conference on the Mechanical Behavior of Salt, Montreal, QC, Canada, 17–18 June 1996; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1998; pp. 389–402. [Google Scholar]
- Munson, D.E.; Wawersik, W.R. Constitutive modeling of salt behavior-State of the technology. In Proceedings of the Seventh International Congess on Rock Mechanics, Aachen, Germany, 16–20 September 1991; A. A. Balkema: Rotterdam, The Netherlands, 1993; Volume 3, pp. 1797–1810. [Google Scholar]
- Massier, D. Rate type constitutive equations with applications to the calculus of the stress state and of the displacement field around cavities in rock salt. In Proceedings of the Third Conference on the Mechanical Behavior of Salt, Palaiseau, France, 14–16 September 1993; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1996; pp. 545–558. [Google Scholar]
- Zhou, H.; Jia, Y.; Shao, J.F. A unified elastic-plastic and viscoplastic damage for quasi-brittle rocks. Int. J. Rock Mech. Min. Sci. 2008, 43, 1237–1251. [Google Scholar] [CrossRef]
- Mahdi, S.; Charlie, C.L. A numerical study of stress changes in barrier pillars and a border area in a longwall coal mine. Int. J. Coal Geol. 2013, 106, 39–47. [Google Scholar]
- Liedtke, L.; Meister, D. Stability Analysis of Underground Structures in Rock Salt Utilizing Laboratory and In-Situ testing and Numerical Calculations, Manchester, England. 4–5 October 1982. [Google Scholar]
- Menzel, W.; Schreiner, W. Rock Mechanical Observations and Results in the Construction of Salt Caverns in Salt Deposits in Central Germany and Their use as Underground Storages, Hannover, Germany. 26–28 September 1994. [Google Scholar]
- Li, Y.; Liu, L.; Zhang, J.; Liu, C.; Zhang, M.; Wang, X. Stability Analysis of Underground Pillar Supporting System under Different Disturbed Stresses. Geofluids 2021, 2021, 6634673. [Google Scholar] [CrossRef]
- Parfenov, V.I.; Bochkareva, R.V.; Shafarenko, E.M.; Sohranskij, V.B. Influence of Stress-Strain State Change of Rock Salt Shielding Properties, Rome, Italy. 4–7 October 1998. [Google Scholar]
- Toderas, M.; Danciu, C.; Nistor, C.; Badulescu, C. In situ studies to estimate the stress state in pillars, from salt mine Praid. In Proceedings of the 11th International Multidisciplinary Scientific Geo-Conference & EXPO SGEM, Albena, Bulgaria, 20–25 June 2011; Volume 1, pp. 513–520. [Google Scholar]
- Todorescu, A. Reologia Rocilor cu Aplicaţii în Minerit; Editura Tehnică: Bucureşti, Romania, 1986. [Google Scholar]
- Todorescu, A. Mecanica Rocilor în Minerit; Editura Tehnică: Bucureşti, Romania, 1982. [Google Scholar]
- Hirian, C.; Todorescu, A.; Gaiducov, V.; Arad, V.; Toderaş, M. Assessment of pillar dimension between rooms for the room—Pillars exploitation. Method based on laboratory trials in Romania salt. In Proceedings of the 5th Conference “Mechanical Behavior of Salt”, Bucharest, Romania, 9–11 August 1999. [Google Scholar]
- Georgescu, M.; Hirian, C.; Toderaş, M. Dimensioning of the strenght elements (pillar—Ceilings) afferent to the +190 m and +190 m levels from Praid salt mine. Environnement friendly policy in mining activities. In Proceedings of the First International Seminar ECOMINING—EUROPE IN 21st CENTURY, Sovata & Praid Salt Mine, Sovata, Romania, 27–29 October 2005; Editura Estfalia: Bucharest, Romania, 2005; pp. 97–102, ISBN 973-7681-03-7. [Google Scholar]
- Stamatiu, M. Mecanica Rocilor; Editura Didactică şi Pedagogică: Bucureşti, Romania, 1962. [Google Scholar]
- Mushelisvili, N.I. N Ecotorîe Osnovnîe Zadaci Matematiceskoi Teorii Uprugosti; Izd. AN URSS: Moscva, Russia, 1954. [Google Scholar]
- Laouafa, F.; Ghoreychi, M. Analysis of failure in a salt room and pillar mine. In Proceedings of the 3rd International Symposium on Mine Safety Science and Engineering (ISMS 2016), Montreal, QC, Canada, 13–19 August 2016; pp. 108–113. [Google Scholar]





| λ = h/b | Coefficient | Ration h/Day | |||||
|---|---|---|---|---|---|---|---|
| 0.01 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | ||
| 0.1 | A0 | −21.31 | −25.76 | −24.64 | −23.44 | −22.61 | −22.07 |
| B0 | −28.40 | −20.14 | −13.71 | −8.94 | −5.81 | −3.85 | |
| C0 | −220.91 | 46.09 | 12.49 | 5.68 | 3.23 | 2.09 | |
| 0.5 | A0 | −11.13 | −10.99 | −10.46 | −9.89 | −9.55 | −9.38 |
| B0 | −25.48 | −20.41 | −12.92 | −8.00 | −5.04 | −3.25 | |
| C0 | 8.88 | 6.26 | 2.93 | 1.48 | 0.93 | 0.66 | |
| 1 | A0 | −3.90 | −3.71 | 3.39 | −3.13 | −2.96 | −2.86 |
| B0 | −23.29 | −19.02 | −12.08 | −7.29 | −4.50 | −2.86 | |
| C0 | 2.23 | 1.74 | 0.95 | 0.46 | 0.22 | 0.12 | |
| 2 | A0 | −0.74 | −0.67 | −0.55 | −0.46 | −0.42 | −0.40 |
| B0 | −22.25 | −18.40 | −11.89 | −7.21 | −4.43 | −2.81 | |
| C0 | 0.56 | 0.46 | 0.28 | 0.16 | 0.09 | 0.05 | |
| 3 | A0 | −0.24 | −0.20 | −0.14 | −0.10 | −0.08 | −0.07 |
| B0 | −22.05 | −18.30 | −11.91 | −7.28 | −4.50 | −87 | |
| C0 | 0.25 | 0.21 | 0.13 | 0.08 | 0.05 | 0.03 | |
| Pillar Width (m) | Pillar Height (m) | Apparent Specific Weight, γa × 104 (N/m3) | Depth H, (m) | Elasticity Modulus of the Salt, E (MPa) | Poisson’s Coefficient, μ |
|---|---|---|---|---|---|
| 14 | 8 | 2.2 | 100 | 726 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toderas, M. Stability Analysis of the Exploitation System with Room and Pillar by Analytical Methods. Appl. Sci. 2024, 14, 1827. https://doi.org/10.3390/app14051827
Toderas M. Stability Analysis of the Exploitation System with Room and Pillar by Analytical Methods. Applied Sciences. 2024; 14(5):1827. https://doi.org/10.3390/app14051827
Chicago/Turabian StyleToderas, Mihaela. 2024. "Stability Analysis of the Exploitation System with Room and Pillar by Analytical Methods" Applied Sciences 14, no. 5: 1827. https://doi.org/10.3390/app14051827
APA StyleToderas, M. (2024). Stability Analysis of the Exploitation System with Room and Pillar by Analytical Methods. Applied Sciences, 14(5), 1827. https://doi.org/10.3390/app14051827






