Optimal Global Positioning System/European Geostationary Navigation Overlay Service Positioning Model Using Smartphone

Abstract

The potential for the use of smartphones in GNSSs (Global Navigation Satellite Systems) positioning has increased in recent years due to the emergence of the ability of Android-based devices used to process raw satellite data. This paper presents the results of a study on the use of SBAS data transmitted by the EGNOS (European Geostationary Navigation Overlay Service) system in GNSS positioning using a Xiaomi Mi8 smartphone. Raw data recorded at a fixed point were used in post-processing calculations in GPS/EGNOS positioning by determining the coordinates for every second of a session of about 5 h and comparing the results to those obtained with a Septentrio AsteRx2 GNSS receiver operating at the same time at a distance of about 3 m. The calculations were performed using the assumptions of the GNSS/SBAS positioning algorithms, which were modified with carrier-phase smoothed code observations and the content of the corrections transmitted by EGNOS.

1. Introduction

The main purpose of SBASs (Satellite-Based Augmentation Systems) is to support civil aviation tasks. However, due to their ability to improve the quality parameters of GNSS positioning, they can also have other applications [1,2,3,4]. The operation of SBAS systems relies on the use of geostationary satellites to transmit correction data and other information that can improve GNSS positioning. EGNOS is a European system based on the transmission of data using three geostationary satellites. In addition to EGNOS, the main SBAS group includes the US WAAS (Wide Area Augmentation System), Russia’s SDCM (System of Differential Correction and Monitoring), Japan’s MSAS (Multi-functional Satellite Augmentation System), India’s GAGAN (GPS-Aided Geosynchronous Augmented Navigation System), China’s Beidou SBAS BDSBAS, and Australia’s SouthPAN (Southern Positioning Augmentation Network) [5]. With real-time transmitted data, EGNOS can significantly improve the accuracy of autonomous positioning using code-based observations [6,7,8]. Depending on the observation conditions and measurement equipment, real-time accuracy of several tens of centimetres can be achieved. In [9], EGNOS was used to integrate a measurement system with INS (Inertial Navigation System) for autonomous ships in Inland Waterways. In turn, Ref. [10] investigated the impact of using EGNOS for Remotely Piloted Aircraft System (RPAS) positioning.

In 2016, a smartphone with the ability to record raw GNSS data using the Android Nougat operating system was made available for the first time [11,12]. Over time, the capabilities were increased in terms of the types of observations that could be recorded, starting with GPS data at L1 frequency. In 2018, a Xiaomi Mi8 smartphone running on the Broadcom BCM47755 GNSS chipset was made available to users, characterised by the ability to record full GNSS observations including L5 GPS, QZSS frequencies, and E5a Galileo [13,14]. Today, many mobile devices offer similar capabilities.

A significant problem with recording raw GNSS data with smartphones is duty cycling, which is a process during which the smartphone’s chipset runs in discontinuous mode. This results in a saving in battery consumption, but at the same time activates cycle slips during positioning. In paper [15], the results of the effect of duty cycling on GNSS code and phase observations were presented. Currently offered Android-based mobile devices are very often not using duty cycling, as is the case for the Xiaomi Mi8.

The ability of smartphones to record raw GNSS data has led to a great number of application uses. The paper [16] presents the use of raw GNSS data acquired with a smartphone for geophysical applications. The paper [17] presents the possibilities of using raw GNSS data in SPP (single-point positioning) and PPP (precise point positioning) using a smartphone. Raw satellite observations acquired with a smartphone are also being investigated for new concepts in RTK (real-time kinematic) positioning technology [18], as well as anti-spoofing and anti-jamming solutions [19].

The paper [20] presents the results of horizontal single-point positioning for smartphone measurements based on raw GNSS data and frequency E5. The root mean square error of these measurements was at the level of 4.57 m. The paper [21] presents the results of a multi-GNSS single-frequency (L1/E1/B1/G1) positioning solution obtained by Huawei P30 with a horizontal RMS of 3.24 m. On the other hand, the use of raw GNSS data on smartphones for DGNSS positioning can yield accuracy results of 1.5 m [22].

According to [23], by augmenting smartphone positioning with EGNOS and DGNSS corrections, it is possible to obtain a horizontal accuracy of better than 1 m with 95% availability. In [24], the possibility of SBAS single-frequency multiple-constellation positioning using raw GNSS data acquired with a smartphone was investigated obtaining a horizontal RMS of 1.30 m and a vertical RMS of 2.06 m. The use of smartphones in GNSS/SBAS positioning could have interesting results using DFMC (dual-frequency multi-constellation SBAS). It is envisaged that DFMC will be able to support SBAS positioning with four GNSS systems by 2025 [25,26,27].

The motivation for this article is the dynamic development of applications related to the use of raw GNSS data acquired with smartphones. Given the limitations on the amount and type of data that can be processed by smartphones, we decided to see how modifications to the basic GPS/EGNOS algorithm could possibly improve autonomous positioning. The aim of this paper is to investigate the feasibility of a modified satellite positioning algorithm using a smartphone and data associated with GPS and EGNOS. During the calculations, the effects of carrier-phase smoothed code observations, correction components determined using EGNOS, and modifying the observation weighting model were analysed.

The remainder of the article presents the research methodology and related issues, followed by the results of the fieldwork and conclusions.

2. Materials and Methods

Positioning using SBAS is achieved by implementing corrections to the mathematical model of positioning. In SBAS systems, data related to long-term correction, fast correction, ionospheric delay and tropospheric delay, among others, are transmitted to improve positioning quality. The corrected pseudorange determined in SBAS systems can be written with the general formula [28,29]:

$$P_{corr}=P_{meas}+R{C}_{fast}+{RC}_{clock}-R{C}_{iono}+R{C}_{tropo}$$

(1)

where

$P_{corr}$ is the corrected pseudorange based on SBAS data;

$P_{meas}$is the pseudorange as measured by the receiver;

${RC}_{fast}$is the fast correction;

$R{C}_{clock}$is the clock correction;

$R{C}_{iono}$ is the ionospheric correction;

$R{C}_{tropo}$ is the tropospheric correction.

Short-term corrections are used to correct rapid changes in ephemeris errors and clock errors [30]. They are applied in all positioning modes of air operations using SBAS with an interval of no more than 60 s. Fast corrections for a given epoch can be calculated according to the formula:

$${RC}_{fast}\left(t\right)=PRC\left(1\right)+RRC\left(t_1\right)(t-t_1)$$

(2)

where

${RC}_{fast}$ is the total fast correction,

$PRC$ is the pseudorange correction,

$RRC$ is the range rate correction,

$t$ is the user time,

$t_1$ is the application time of the most up-to-date fast correction.

Range rate corrections are not transmitted by SBAS systems, but calculated at receiver algorithm level:

$$RRC(t_1)=\frac{PRC\left(t_1\right)-PRC\left(t_0\right)}{t_1-t_0}$$

(3)

where

$t_0$ is the time of application of the recently received fast correction.

The use of raw GNSS data in smartphone-based positioning puts some strain on the computing resources of Android-based devices. The use of fast corrections in the GNSS receiver algorithm significantly consumes the bandwidth of transmitted messages [24].

Long-term corrections are used to correct infrequent changes in ephemeris errors and clock errors of GPS satellites [30]. Data on the parameters of the satellites’ orbits and information on the coefficients are transmitted to determine the values of the clock corrections. Some of the correction data are applied to the calculated satellite positions and velocity, while the remaining data are applied to the pseudorange measurements. Corrections to satellite positions are calculated using linear interpolation and applied to satellite positions according to the following formulas:

$$DX\left(t\right)=DX+{DX}_{ROC}(t-t_V)$$

(4)

$$DY\left(t\right)=DY+{DY}_{ROC}(t-t_V)$$

(5)

$$DZ\left(t\right)=DZ+{DZ}_{ROC}(t-t_V)$$

(6)

where

$DX\left(t\right)$, $DY\left(t\right)$, $DZ\left(t\right)$ are the current corrections for satellite position;

$DX$, $DY$, $DZ$ are the corrections to satellite positions transmitted as part of slow corrections;

${DX}_{ROC}$, ${DY}_{ROC}$, ${DZ}_{ROC}$ are transmitted adjustments to velocity;

$t$ is the user time;

$t_V$ is the application time of transmitted corrections to velocity.

Slow corrections related to satellite clocks are determined by the following formula:

$$R{C}_{clock}=\left[\delta a_{f0}+\delta a_{f1}\left(t-t_0\right)\right]c$$

(7)

where

$R{C}_{clock}$ is the resulting correction of the satellite clock;

$\delta a_{f0}$, $\delta a_{f1}$ are clock correction parameters provided in EGNOS system messages;

$t$ is the user time;

$t_0$ is the time of application of clock correction parameters;

$c$ is the speed of propagation of an electromagnetic wave in a vacuum.

Standard satellite clock corrections determined for absolute GNSS positioning and additional clock corrections determined based on the SBAS model are calculated independently. Applying them to GNSS/SBAS positioning is also carried out independently.

The impact of the ionospheric correction on GNSS/SBAS positioning has been the subject of many scientific studies [31,32,33,34,35,36]. According to [30], its value is determined by either an SBAS model or a classical model based on the Klobuchar algorithm. Scientific publications show better positioning results when using a model based on data transmitted by EGNOS.

The ionospheric slant delay $R{C}_{iono}$ determined according to the model used in EGNOS (based on four-point interpolation), can be determined by the following formula [30]:

$$R{C}_{iono}=-F_{pp}{\tau }_{vpp}({\lambda }_{pp},{\varphi }_{pp})$$

(8)

where

$F_{pp}$ is a coefficient that changes vertical delay to slant;

${\tau }_{vpp}$ is the vertical ionospheric delay for IPP;

${\lambda }_{pp},{\varphi }_{pp}$ are IPP coordinates.

$F_{pp}$ and ${\tau }_{vpp}$ can be determined from the following formulae:

$$F_{pp}={\left[1-{\left(\frac{R_{e}cosE}{R_e+h_I}\right)}^2\right]}^{-\frac{1}{2}}$$

(9)

$${\tau }_{vpp}=\sum _{i=1}^4{W}_i(x_{pp},y_{pp}){\tau }_{vi}$$

(10)

where

$R_e$ is the Earth’s radius;

$E$ is the elevation of the satellite;

$h_I$ is the altitude at which the highest electron density occurs (350 km);

${\tau }_{vi}$ are vertical delays for four gridpoints, transmitted by EGNOS;

$W_i\left(x_{pp},y_{pp}\right)$ is the weighing function.

SBAS systems use averaged and seasonal atmospheric data determined for a specific day and user position to determine the tropospheric correction. The model is based on tropospheric delay values towards the zenith, determined based on five meteorological parameters: pressure, temperature, water vapour pressure, rate of change of temperature, and rate of change of water vapour pressure. Their values are made available from meteorological data mainly from North American centres.

The influence of tropospheric refraction on GPS/EGNOS positioning results is determined individually for the receiver location (without using EGNOS transmitted data).

According to [30], the tropospheric delay ${TC}_i$ for satellite i takes the following form:

$${TC}_i=-(d_{hyd}+d_{wet})·m\left({El}_i\right)$$

(11)

where

$d_{hyd}, d_{wet}\left(\mathrm{m}\right)$ are estimated signal delays for a satellite at zenith, determined from receiver altitude, pressure, temperature, water vapour pressure, rate of change of temperature, and rate of change of water vapour pressure,

$m\left({El}_i\right)$ is the mapping function that transforms the delay based on the satellite’s current horizontal altitude $({El}_i$).

Previous studies on the quality of the tropospheric EGNOS model have shown very good correlation with the Saastamoinen model, which is considered to accurately represent the local state of the troposphere [37].

The use of smoothing according to the Hutch filter of carrier-phase smoothed code observations in GPS/EGNOS positioning before applying EGNOS corrections can reduce the noise level [30,38]:

$${PR}_k^S=\alpha {PR}_{k-1}^C+\left(1-\alpha \right)⟦{PR}_{k-1}^P+\frac{\lambda }{2\pi }({PR}_k^P-{PR}_{k-1}^P)⟧$$

(12)

$$\alpha =\frac{dt}{T}$$

(13)

where

${PR}_k^S$ is the smoothed pseudorange code;

${PR}_{k-1}^C$ is the code pseudorange in the epoch $k$;

${PR}_k^P$ is the pseudorange distance in the epoch $k$;

$\lambda$ is the wavelength of GPS carrier frequency at L₁;

$T$ is the smoothing constant;

$dt$ is the sampling interval.

Data acquired with a Xiaomi Mi 8 smartphone (Xiaomi Corporation, Beijing, China) operating in duty cycling off mode were used for the study. Satellite observations were recorded on 25 April 2020 between 7:00 and 12:00 GPS time with an interval of 1 s in the vicinity of the city of Olsztyn in the north-eastern part of Poland. Measurements were taken at a fixed point over which a Xiaomi Mi8 smartphone was mounted on a tripod. At a distance of approximately 3 m, data were collected simultaneously using a Septentrio AsteRx2 receiver (Septentrio, Leuven, Belgium), which was equipped with a geodesic-grade antenna that has a uniform quasi-hemispherical gain pattern, right-handed circular polarisation, and a stable phase centre (Figure 1). The collected raw observational data were computed in gLAB v5.5.0 software and using proprietary computational scripts [39,40].

In the first stage of development, GPS/EGNOS positions were determined in post-processing mode by modifying the assumptions related to the carrier-phase smoothing of code observations. The official recommendations of the Minimum Operational Performance Standards assume that a satellite of any GNSS system can be included in the calculation if it has reached a steady state, i.e., if code observations from that satellite have been smoothed by carrier-phase observations for at least 6 min. The smoothing window associated with smoothing observations is defined as the product of the number of samples accepted for the calculation and the interval of the measurement data. This is related to restrictive aviation applications, which may not translate into validity for use in smartphone-based positioning on the Earth’s surface. By multiplying the data recording interval and the number of samples accepted for calculation, the smoothing window used in GPS/EGNOS positioning can be obtained. A strictly defined minimum of uninterrupted epochs for smoothing the code pseudorange with carrier-phase observations is required for aeronautical applications based on [30]. Since we are not concerned with aeronautical positioning, for research purposes related to GPS/EGNOS positioning with a smartphone, several computational variants related to smoothing window and steady state were performed.

3. Results

Data associated with the Mi8 smartphone were recalculated in GPS/EGNOS mode according to [30], with the following variations: smoothing window—10 s, smoothing window—20 s, smoothing window—30 s, no smoothing.

Each of these options has sub-options: excluding satellites before reaching a steady state at 1 s, excluding satellites before reaching a steady state at 60 s, excluding satellites before reaching a steady state at 180 s, and excluding satellites before reaching steady state at 360 s.

Figure 2 and Figure 3 show the results of the smoothing window and steady-state analysis of GPS/EGNOS positioning using an Mi8 smartphone compared to GPS/EGNOS positioning using a Septentrio AsteRx2 receiver. The horizontal positioning error (HPE) and vertical positioning error (VPE) values were calculated. Different colours indicate the number of individual solutions with similar values, so one can deduce which error values occurred most often in the calculations.

Already, using the results presented in Figure 2, we can deduce that for the Mi8 smartphone, the best accuracy obtained both horizontally and vertically is characterised by a steady state of 60 s and a smoothing window of 20 s. The numerical values of the accuracy analysis presented in

Table 1. Numerical values of the accuracy analysis performed for the Xiaomi Mi8 smartphone with varying steady states and smoothing windows.

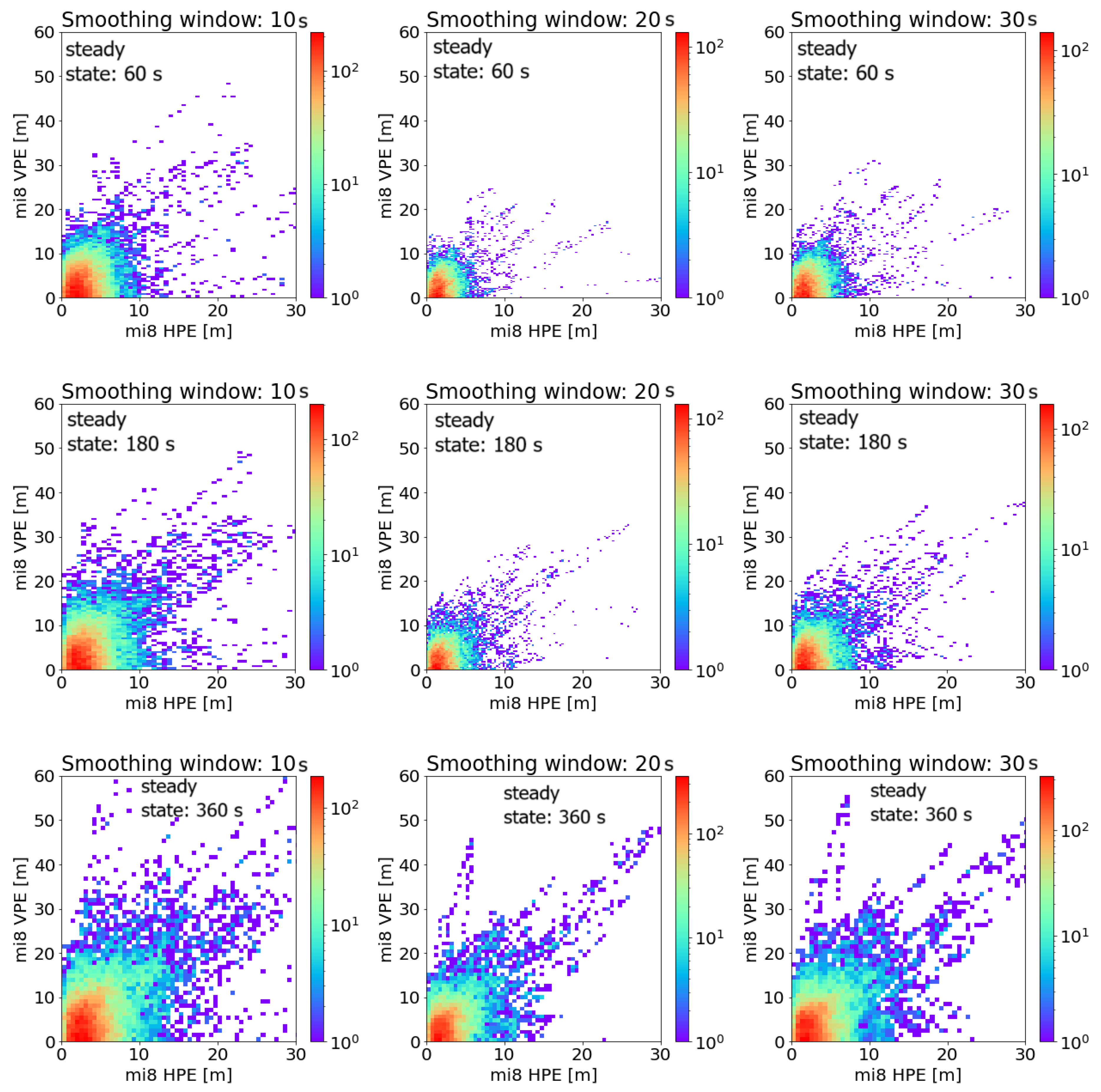
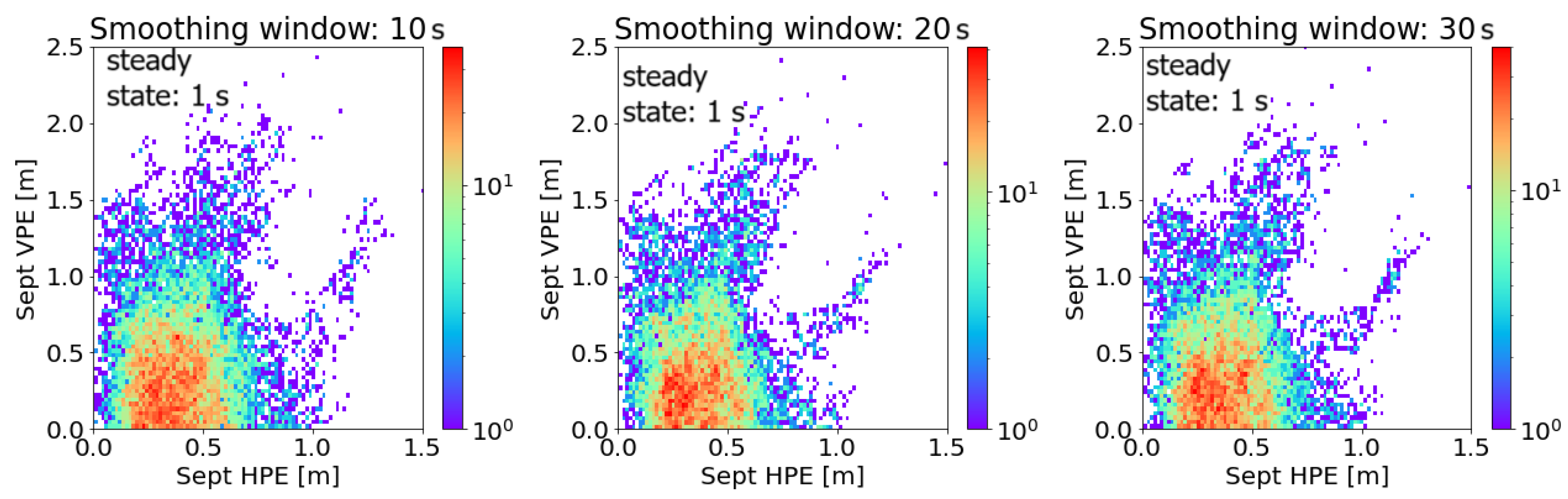
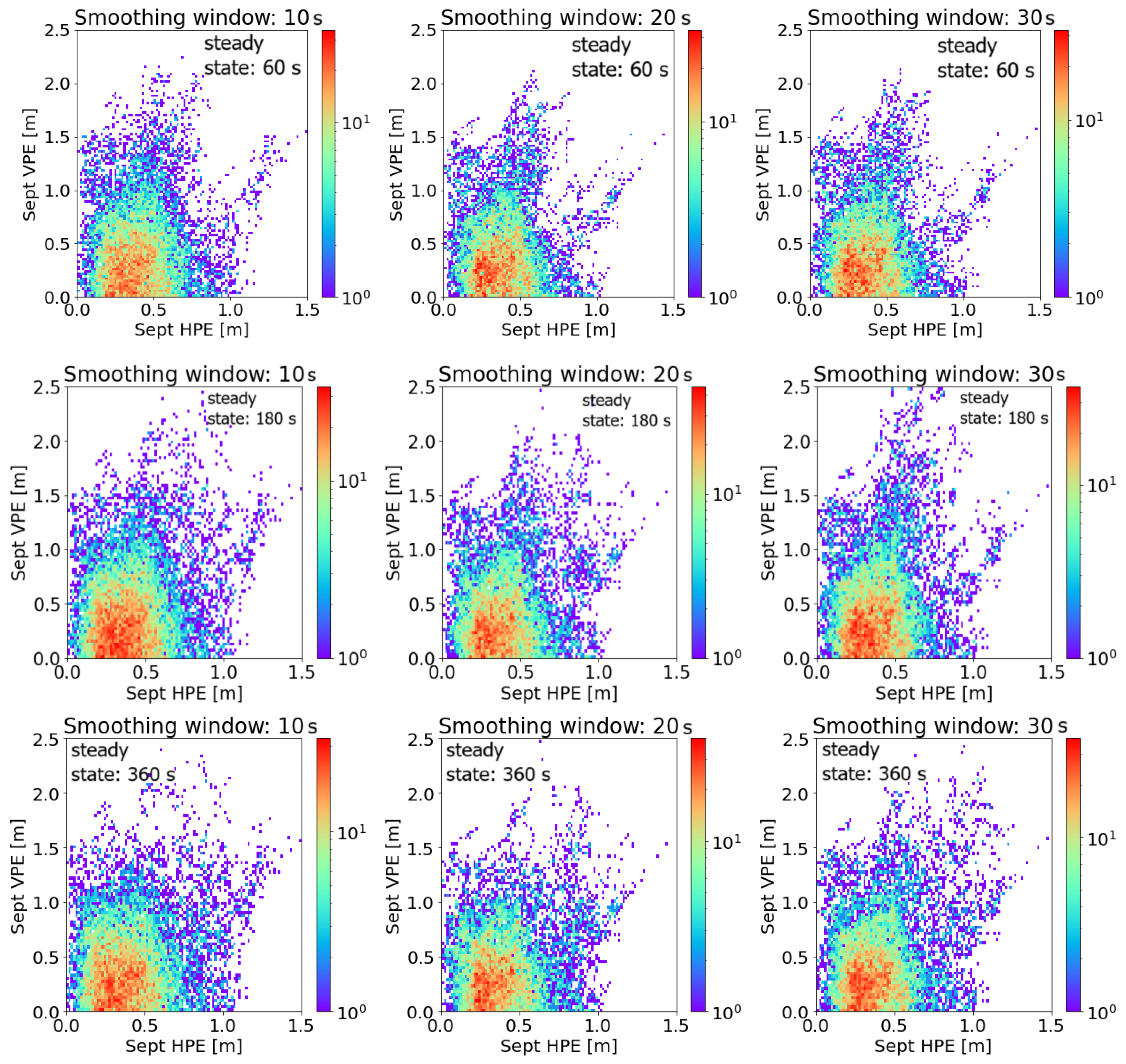
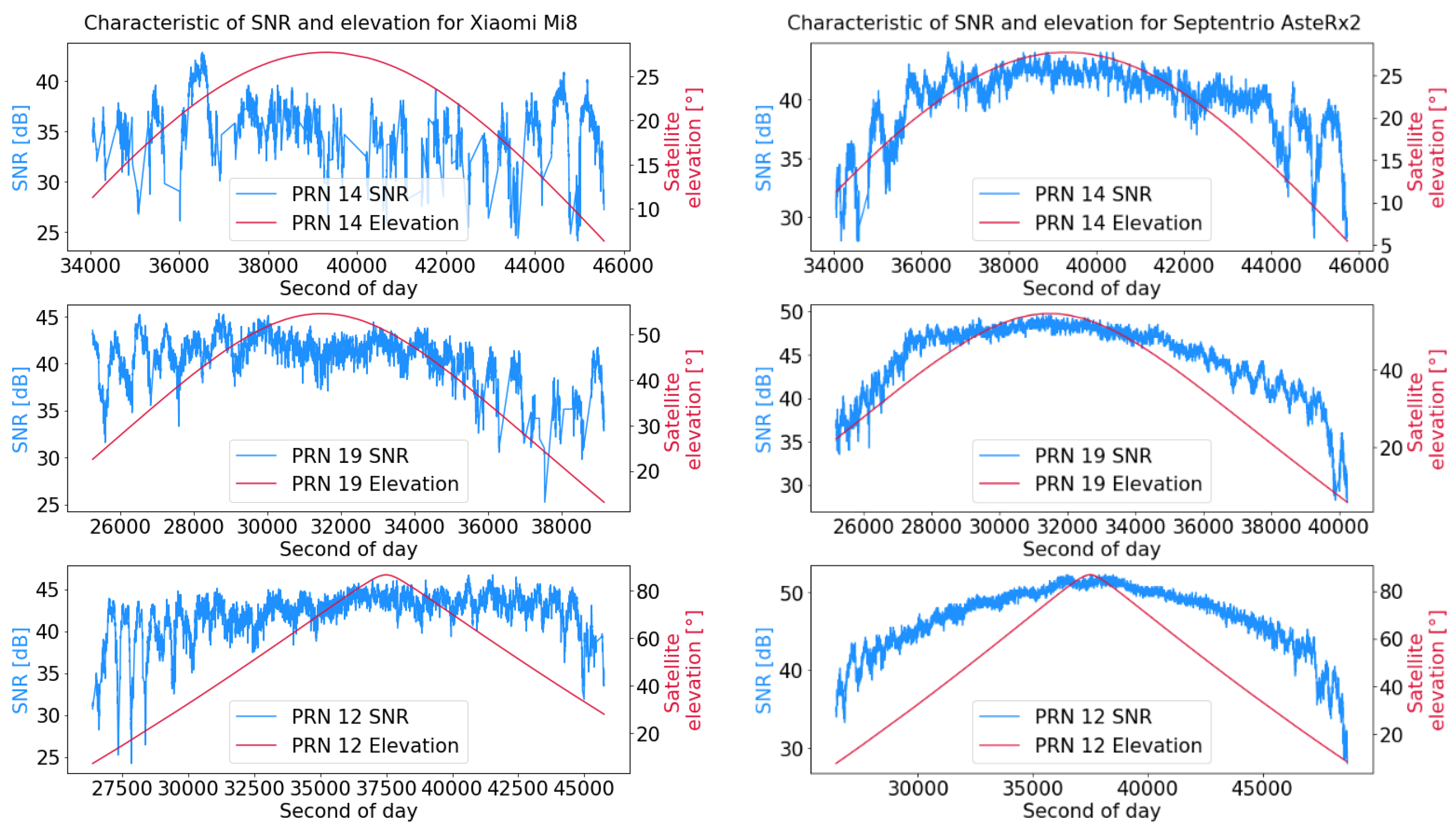
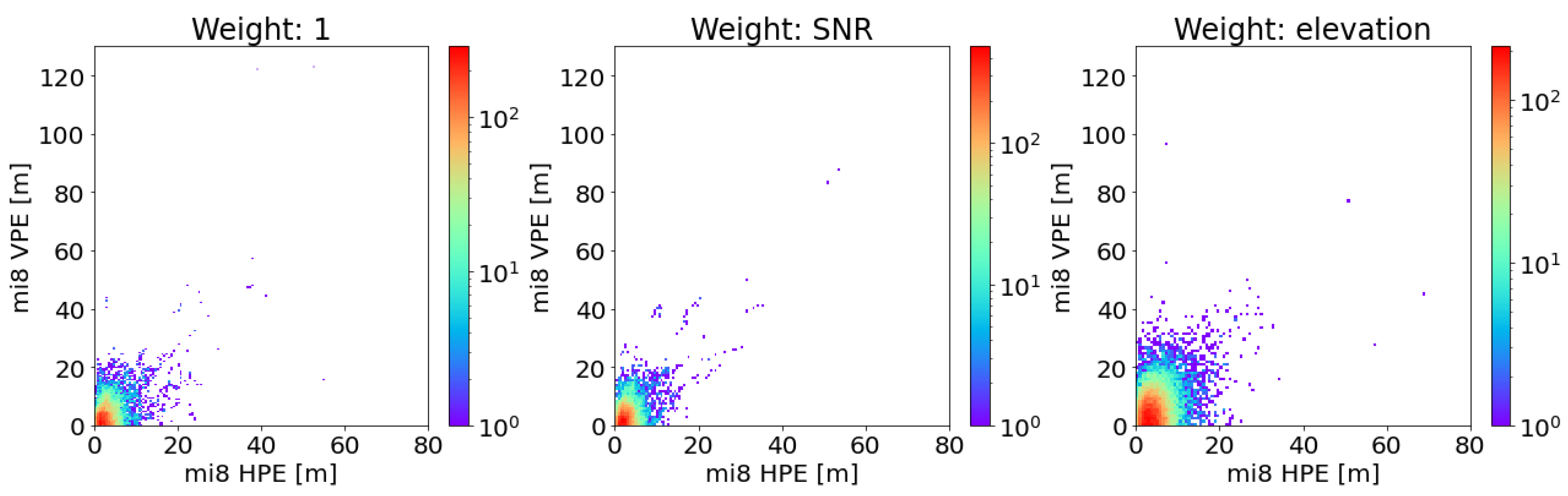
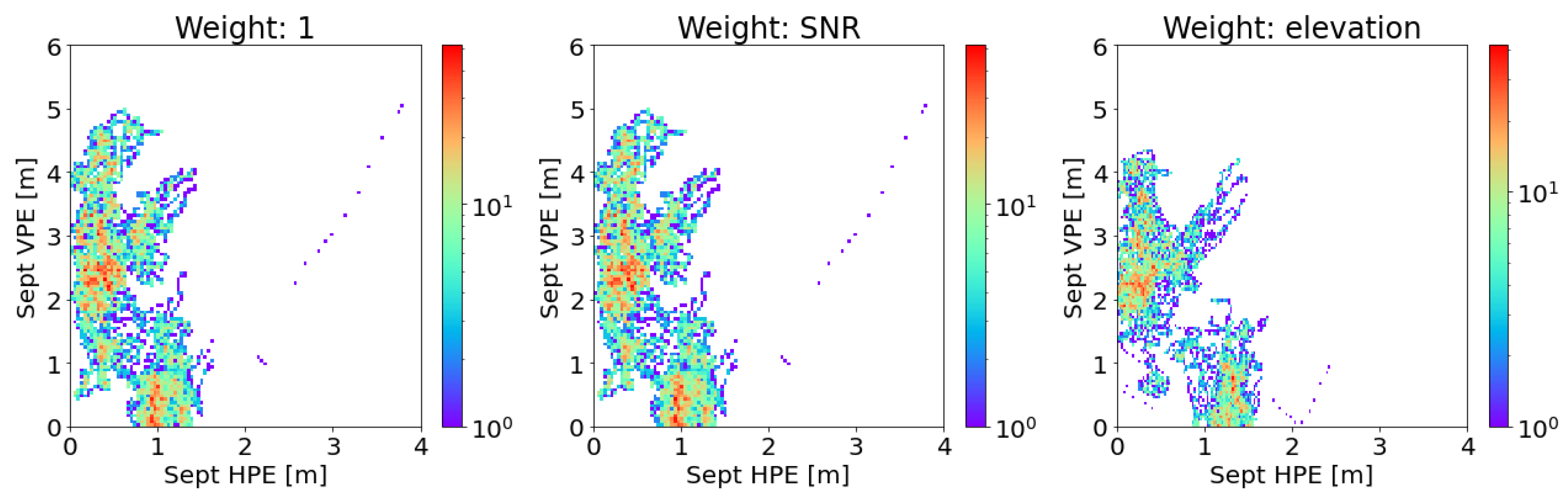
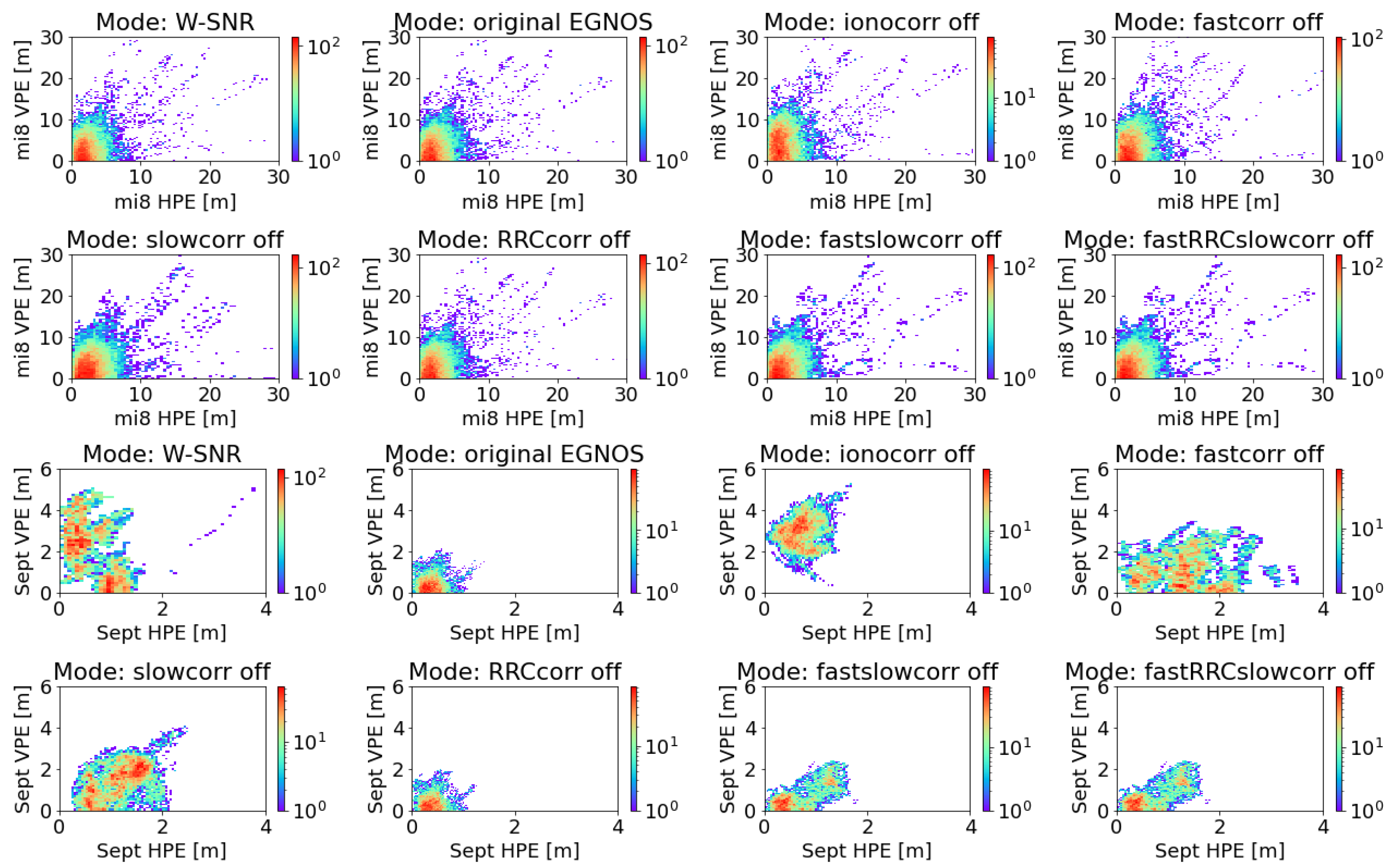
Smoothing Window [s]	Steady State [s]	HPEmean [m]	HPEstd [m]	HPEmax [m]	VPEmean [m]	VPEstd [m]	VPEmax [m]
10	1	3.16	2.55	26.56	4.67	4.41	60.46
	60	3.23	2.85	57.05	4.52	4.22	48.37
	180	4.01	3.87	64.24	5.73	5.58	51.58
	360	4.74	5.42	86.87	22.21	46.78	171.00
20	1	2.84	2.46	26.25	4.25	4.23	59.31
	60	2.24	1.95	30.62	3.27	2.78	24.48
	180	3.12	2.84	40.65	4.47	4.27	39.29
	360	4.06	4.20	60.89	6.27	7.12	106.42
30	1	2.68	2.45	26.03	4.05	4.16	58.94
	60	2.59	2.22	33.49	3.70	3.25	30.84
	180	2.66	2.39	27.02	3.81	3.58	32.71
	360	3.48	3.66	50.00	5.41	6.21	86.42
No smoothing	-	4.47	3.01	43.04	6.38	5.32	64.95

show that indeed, for both horizontal and vertical analysis, the best results of the mean positioning errors, their standard deviation, as well as the VPE_max were obtained for a steady state of 60 s and a smoothing window of 20 (HPE_mean = 2.24 m, HPE_std = 1.95 m, VPE_mean = 3.27 m, VPE_std = 2.78 m, VPE_max = 24.48). However, the best results of maximum horizontal error values were obtained for a steady state of 1 s and a smoothing window of 30 s, where HPE_max = 26.03 m. In further analyses, a steady state of 60 s and a smoothing window of 20 s were assumed to be the best pairing among the analysed variants and were included in further analyses as a positioning variant using the Xiaomi Mi8 GPS/EGNOS smartphone.

In the case of the results obtained for the Septentrio AsteRx2 receiver presented in Figure 3, the differences obtained between the variants are not so noticeable, but the analysis of the numerical results obtained also identifies a steady state of 60 s and a smoothing window of 20 s as being optimal (HPE_mean = 0.38 m, HPE_std = 0.17 m, HPE_max = 1.48 m, VPE_mean = 0.50 m, VPE_std = 0.43 m, VPE_max = 2.19 m). Compared to the results obtained for the smartphone, this variant performs much better, which is understandable due to the different GNSS chipsets and antennas used in these two measuring devices.

Figure 4 compares the best GPS/EGNOS positioning result with smoothing (steady state of 60 s and a smoothing window of 20 s) with the solution without smoothing code observations. It can be seen that the vertical and horizontal accuracy results are significantly better for the solution based on smoothing (according to Table 1: for the no-smoothing variant, HPE_mean = 4.47 m, HPE_std = 3.01 m, HPE_max = 43.03 m, VPE_mean = 6.38 m, VPE_std = 5.32 m, VPE_max = 64.95 m). Also noticeable in Figure 4 is the significant improvement in vertical positioning accuracy when using carrier-phase smoothed code observation. In the case of the analysis performed for the Septentrio AsteRx2 receiver, similar conclusions were also drawn (for the no-smoothing variant, HPE_mean = 0.44 m, HPE_std = 0.23 m, HPE_max = 1.89 m, VPE_mean = 0.58 m, VPE_std = 0.50 m, VPE_max = 3.77 m).

The next stage of the research was to analyse the use of different observation weighting strategies in the observation model. The Xiaomi Mi 8 device is equipped with a Broadcom chipset, BCM4775, GLL ver. 107.20.22 414037, characterised by dual-frequency (E1/L1 + E5/L5) satellite observation capabilities. The quality of GNSS positioning using smartphones is highly dependent on the antenna design these devices are equipped with [26,41,42,43]. Smartphone GNSS antennas are characterised by low gain and low multipath resistance [44,45]. As a rule, mobile devices are equipped with either omnidirectional linearly or elliptically polarised antennas due to the theoretically differently oriented smartphone performing the positioning [46].

When using more advanced GNSS receivers and their antennas, the signal-to-noise ratio increases with increasing elevation, whereas this relationship cannot be observed for smartphone devices [47]. Therefore, for calculations related to data acquired with a smartphone, a signal-to-noise ratio-dependent weighting model is preferred to one related to satellite elevation [48].

The study analysed the impact of the type of observation weighting within the autonomous positioning model using a Xiaomi Mi8 smartphone (Formula (14)). Values of standard deviation are equal to 1 ($\sigma =1$), dependent on satellite elevation and dependent on the value of the signal-to-noise ratio.

$$W=\frac{1}{{\sigma }^2}$$

(14)

In the case of the option of adopting a satellite elevation-dependent standard deviation value, it takes the following form:

$$\sigma =a+b·e^{(-E/c)}$$

(15)

where

$E$ is the satellite elevation.

According to [30], $a=0.13 \mathrm{m},b=0.53 \mathrm{m},c=10°$.

A variant taking the value of the standard deviation depending on the signal-to-noise ratio’s standard deviation takes the following form:

$$\sigma =a+b·{10}^{(-SNR/10)}$$

(16)

where

$SNR$ is the signal-to-noise ratio for pseudorange measurement.

In the case of positioning using SBAS systems, according to [30], the calculation associated with the $\sigma$ takes the following form:

$${\sigma }_i^2={\sigma }_{i,flt}^2+{\sigma }_{i, UIRE}^2+{\sigma }_{i,air}^2+{\sigma }_{i, tropo}^2$$

(17)

where

${\sigma }_i^2$ is the variance of pseudorange measurement;

${\sigma }_{i,flt}^2$ is the variance of rapid and long-term adjustments;

${\sigma }_{i, UIRE}^2$ is the ionospheric delay variance;

${\sigma }_{i,air}^2$ is the variance associated with the operation of the GNSS receiver;

${\sigma }_{i, tropo}^2$ is the tropospheric delay variance.

Figure 5 shows the SNR (signal-to-noise ratio) and elevation values of sample satellites associated with observations acquired with a Xiaomi Mi8 smartphone and a Septentrio AsteRx2 receiver. For the Mi8 smartphone, it can be seen that there is no correlation between satellite elevation and SNR, which cannot be inferred for the data presented for the AsteRx2 receiver. The impact of SNR on smartphone positioning is considered in further analyses related to autonomous positioning and GPS/EGNOS.

Figure 6 shows the results of autonomous positioning smoothed by phase observations in post-processing mode using a Xiaomi Mi8 smartphone and a Septentrio AsteRx2 receiver and considering different variants of observation weighting (i.e., weight equal to 1, weight dependent on satellite elevation, and weight dependent on SNR). For the Mi8 smartphone and the variant weighting equal to 1, the results were HPE_mean = 3.22 m, HPE_std = 2.66 m, HPE_max = 55.08 m, VPE_mean = 4.39 m, VPE_std = 4.29 m, and VPE_max = 123.29 m. The variant taking the weighting of observations according to SNR for the Mi8 smartphone presents the best results in this analysis: HPE_mean = 2.72 m, HPE_std = 2.18 m, HPE_max = 53.56 m, VPE_mean = 3.90 m, VPE_std = 3.82 m, and VPE_max = 88.14 m. In contrast, in the case of the Mi8 smartphone, the variant for the observation weight depending on the satellite elevation gave worse results: HPE_mean = 4.70 m, HPE_std = 3.72 m, HPE_max = 69.07 m, VPE_mean = 6.58 m, VPE_std = 5.63 m, and VPE_max = 96.68 m. For the Septentrio AsteRx2 receiver, the results of various variants are not as significantly different. The smallest maximum error of horizontal and vertical positioning was obtained for the variant based on the weight depending on the elevation of the satellite (HPE_max = 2.44 m, VPE_max = 4.35 m). On the other hand, variants based on weighting equal to 1 and dependent on SNR obtained the best results for HPE_mean, VPE_mean, HPE_std, and VPE_std (see

Table 2. Numerical values of the accuracy analysis performed for GPS autonomous positioning with carrier-phase smoothed code observations for the Xiaomi Mi8 smartphone and the Septentrio AsteRx2 receiver with different variants of observation weighting. All values are expressed in meters.

Receiver	Weighting Variant	HPEmean	HPEstd	HPEmax	VPEmean	VPEstd	VPEmax
Xiaomi Mi8	1	3.22	2.66	55.08	4.39	4.29	123.29
	SNR	2.72	2.18	53.56	3.90	3.82	88.14
	elevation	4.70	3.72	69.08	6.58	5.63	96.68
Septentrio AsteRx2	1	0.64	0.37	3.81	2.20	1.26	5.06
	SNR	0.62	0.37	3.81	2.15	1.29	5.06
	elevation	0.66	0.47	2.44	2.07	1.11	4.35

).

4. Discussion

Table 3. Numerical values of the accuracy analysis performed for positioning with the Xiaomi Mi8 smartphone: autonomous GPS (SNR-dependent observation weighting); GPS/EGNOS with a smoothing window of 20 s and a steady state of 60 s (SNR-dependent observation weighting); and GPS/EGNOS with a smoothing window of 20 s and a steady state of 60 s (standard EGNOS weighting model). All values are expressed in meters.

Receiver	Positioning Variant	HPEmean	HPEstd	HPEmax	VPEmean	VPEstd	VPEmax
Xiaomi Mi8	GPS autonomous (weight: SNR)	2.72	2.18	53.56	3.90	3.82	88.14
	GPS/EGNOS, smoothing window: 20 s; steady state: 60 s (weight: SNR)	2.59	2.24	33.26	3.65	3.25	30.83
	GPS/EGNOS, smoothing window: 20 s; steady state: 60 s (standard EGNOS weighting model)	2.24	1.95	30.62	3.27	2.78	24.48

summarises the results of the accuracy analysis for three positioning variants with the Xiaomi Mi8 smartphone: autonomous GPS (SNR-dependent observation weighting); GPS/EGNOS with a smoothing window of 20 and steady state of 60 s (SNR-dependent observation weighting); and GPS/EGNOS with a smoothing window of 20 s and a steady state of 60 s (standard EGNOS weighting model). The results clarify that the GPS/EGNOS variant with the EGNOS weighting model presents the best accuracy, which may indicate a fairly good adaptation of the component observation weights to the performance of the Mi8 smartphone positioning model. Also noteworthy are the vertical results, which have a lower maximum error than the horizontal analysis. The GSP/EGNOS variant with the standard weighting model obtained the following results: HPE_mean = 2.24 m, HPE_std = 1.95 m, HPE_max = 30.62 m, VPE_mean = 3.27 m, VPE_std = 2.78 m, and VPE_max = 24.48 m.

The final part of the study analyses the possibility of manipulating the components of the pseudorange correction that is applied in the GPS/EGNOS positioning algorithm. This analysis aims to test the feasibility of reducing the amount of correction data applied to the smartphone, which is necessary to achieve accuracy close to the GPS/EGNOS variant. Figure 7 and

Table 4. Numerical values of the accuracy analysis performed for GPS/EGNOS positioning with a Xiaomi Mi8 smartphone and Septentrio AsteRx2 receiver in different variants. All values are expressed in meters.

Receiver	Variant	HPEmean	HPEstd	HPEmax	VPEmean	VPEstd	VPEmax
Xiaomi Mi8	W: SNR	2.59	2.24	33.26	3.65	3.25	30.83
	Original EGNOS	2.24	1.95	30.62	3.27	2.78	24.48
	Iono correction off	2.64	2.25	30.68	5.00	3.69	32.10
	Fast correction off	2.80	2.31	32.88	4.18	3.54	30.51
	Slow correction off	3.09	2.57	43.93	3.66	3.29	39.03
	RRC off	2.59	2.22	33.49	3.70	3.25	30.84
	Fast and slow correction off	2.80	2.45	38.97	3.73	3.35	38.70
	Fast, RRC, slow correction off	2.80	2.45	38.97	3.73	3.35	38.70
Septentrio AsteRx2	IN: SNR	0.62	0.37	3.81	2.15	1.29	5.06
	Original EGNOS	0.39	0.18	1.48	0.45	0.36	2.13
	Iono correction off	0.73	0.26	1.70	2.87	0.67	5.25
	Fast correction off	1.30	0.61	3.53	1.12	0.76	3.47
	Slow correction off	1.17	0.44	2.50	1.43	0.76	4.09
	RRC off	0.39	0.18	1.24	0.45	0.36	1.97
	Fast and slow correction off	0.74	0.42	1.81	0.73	0.56	2.37
	Fast, RRC, slow correction off	0.74	0.42	1.81	0.73	0.56	2.37

show that horizontally, the variants with RRC (range rate correction) off and Iono correction off perform well, while vertically, only the variant with RRC off produces good results. It is noteworthy that the lack of ionospheric correction has a significant impact on the mean vertical accuracy and standard deviation (VPE_mean = 5.00 m, VPE_std = 3.69 m). The largest maximum vertical positioning error is presented by the slow-correction-off variant (VPE_max = 39.03). For the horizontal analysis, the slow-correction-off variant (HPE_mean = 3.09 m, HPE_std = 2.57 m, HPE_max = 43.93 m) was unequivocally the worst. For the Septentrio receiver, it is clear that the RRC-off variant is characterised by results close to the original EGNOS solution (HPE_mean = 0.39 m, HPE_std = 0.18 m, HPE_max = 1.24 m, VPE_mean = 0.45 m, VPE_std = 0.36 m, VPE_max = 1.97 m). For both the Mi8 smartphone and the Septentrio receiver, the SNR-dependent weighting variant performs moderately well for both horizontal and vertical positioning.

5. Conclusions

The intention of the analyses presented here was to indicate possible modifications to the standard GPS/EGNOS algorithm, with a view to using it in its most optimal form in smartphone-type mobile devices. The results obtained indicate the use of steady-state values other than those recommended for aeronautical purposes related to the smoothing of observations. The smoothing of code observations alone for mobile devices has a positive impact on the quality of positioning. For autonomous positioning, the signal-to-noise-related weighting model gives better accuracy results than the satellite elevation-related observation weighting model. However, in the case of positioning using SBAS data, the EGNOS weighting model performs best. Interfering with the components of the corrections to the pseudorange indicated that in order to process fewer data, it is possible to dispense with range rate corrections without degrading positioning accuracy. In the case of vertical positioning, the use of ionospheric corrections is of great importance for accuracy.