Damage Characteristics and Dynamic Response of RC Shells Subjected to Underwater Shock Wave
Abstract
:1. Introduction
2. Materials and Validation of the Numerical Simulation
2.1. The Equation of State of the Explosive
2.2. The Equation of State of the Water
2.3. The Equation of State of the Air
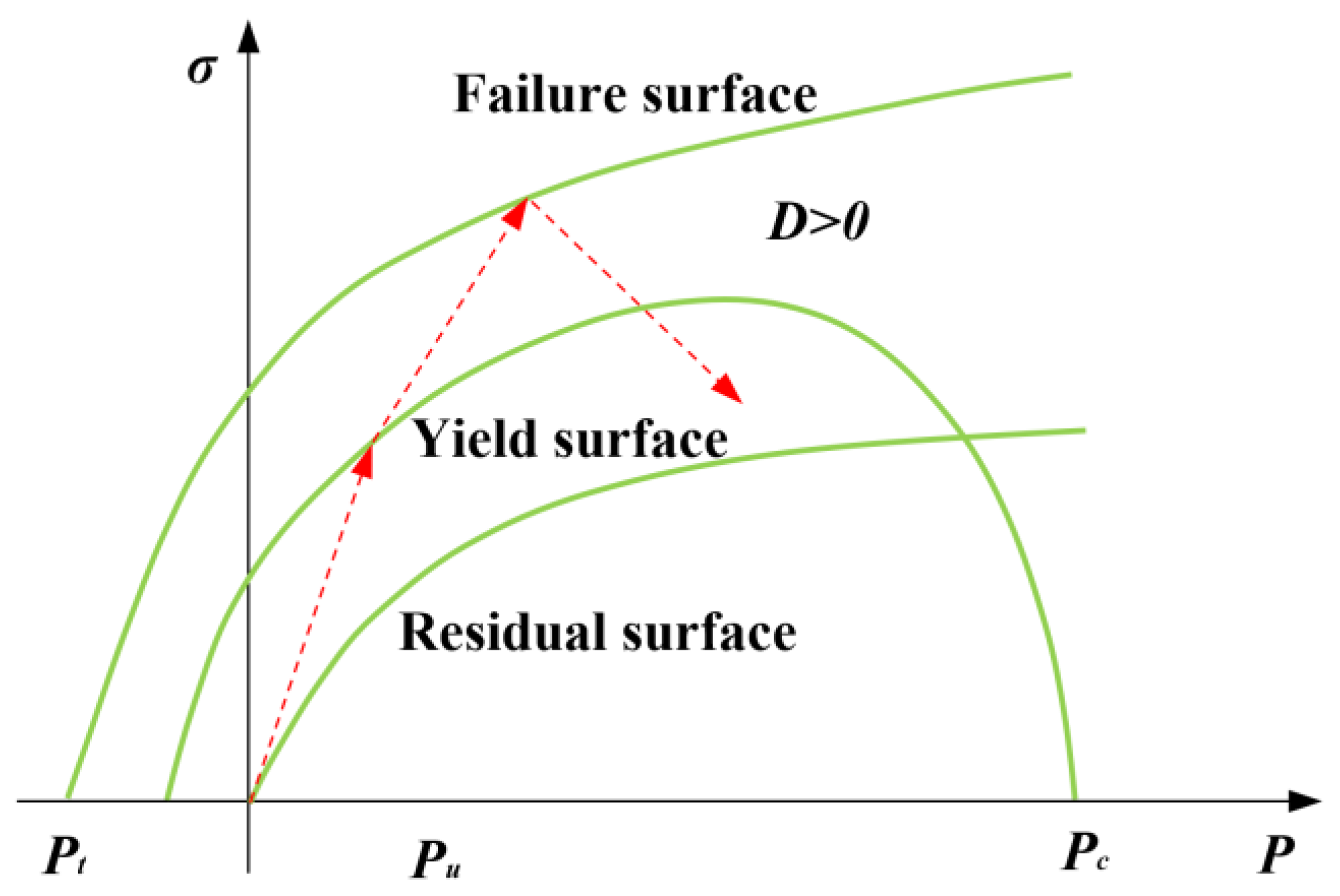
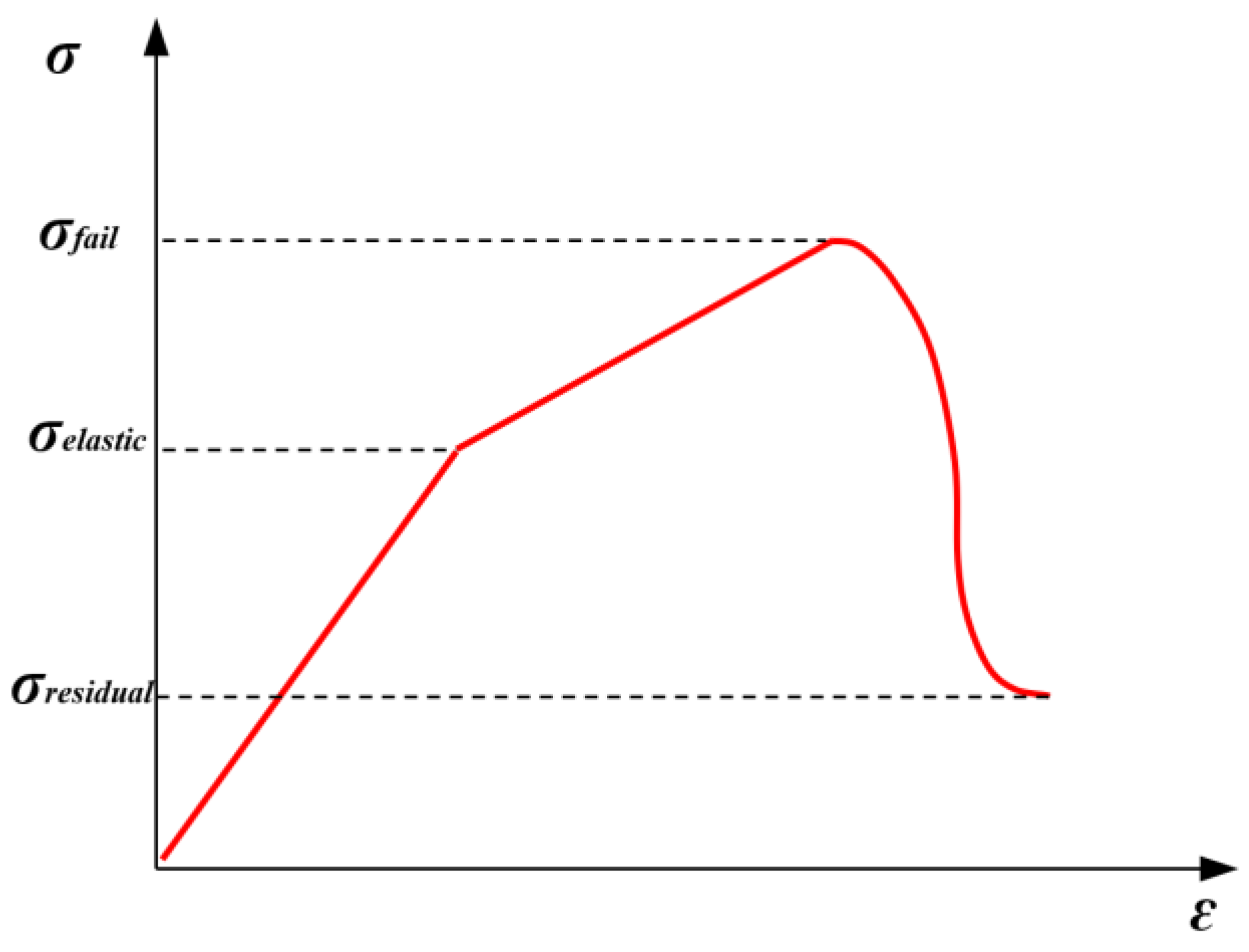
2.4. The Material Model of the Concrete
2.5. The Material Model of the Rebar
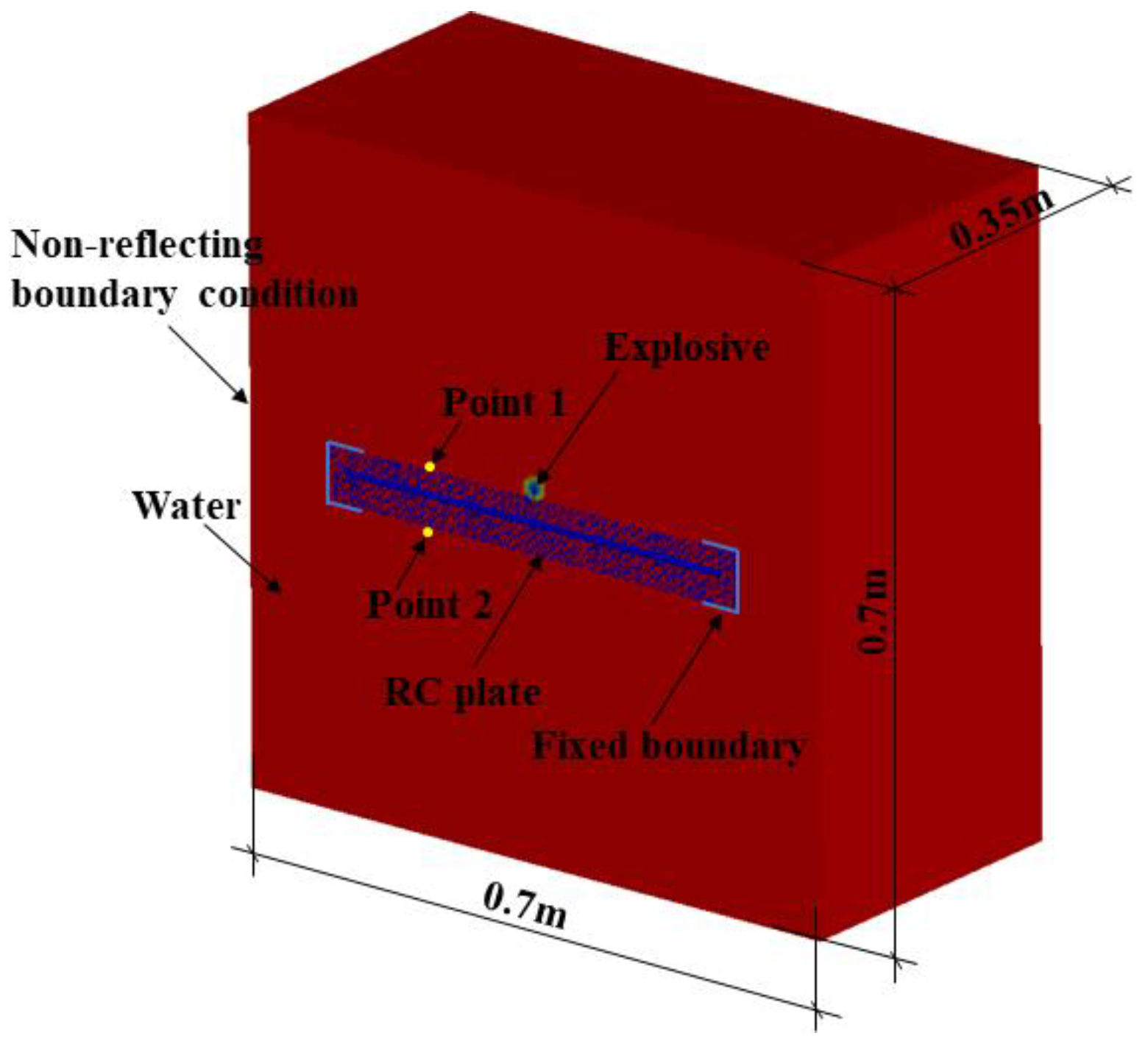
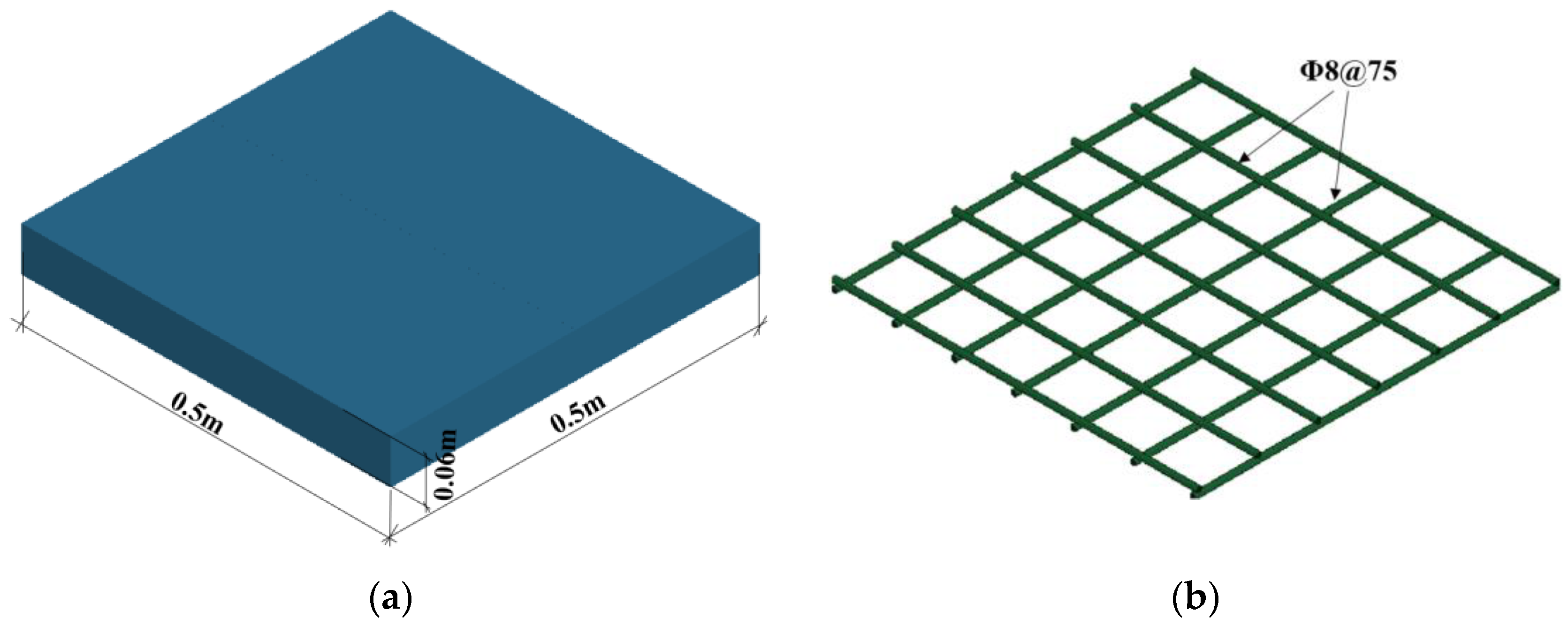
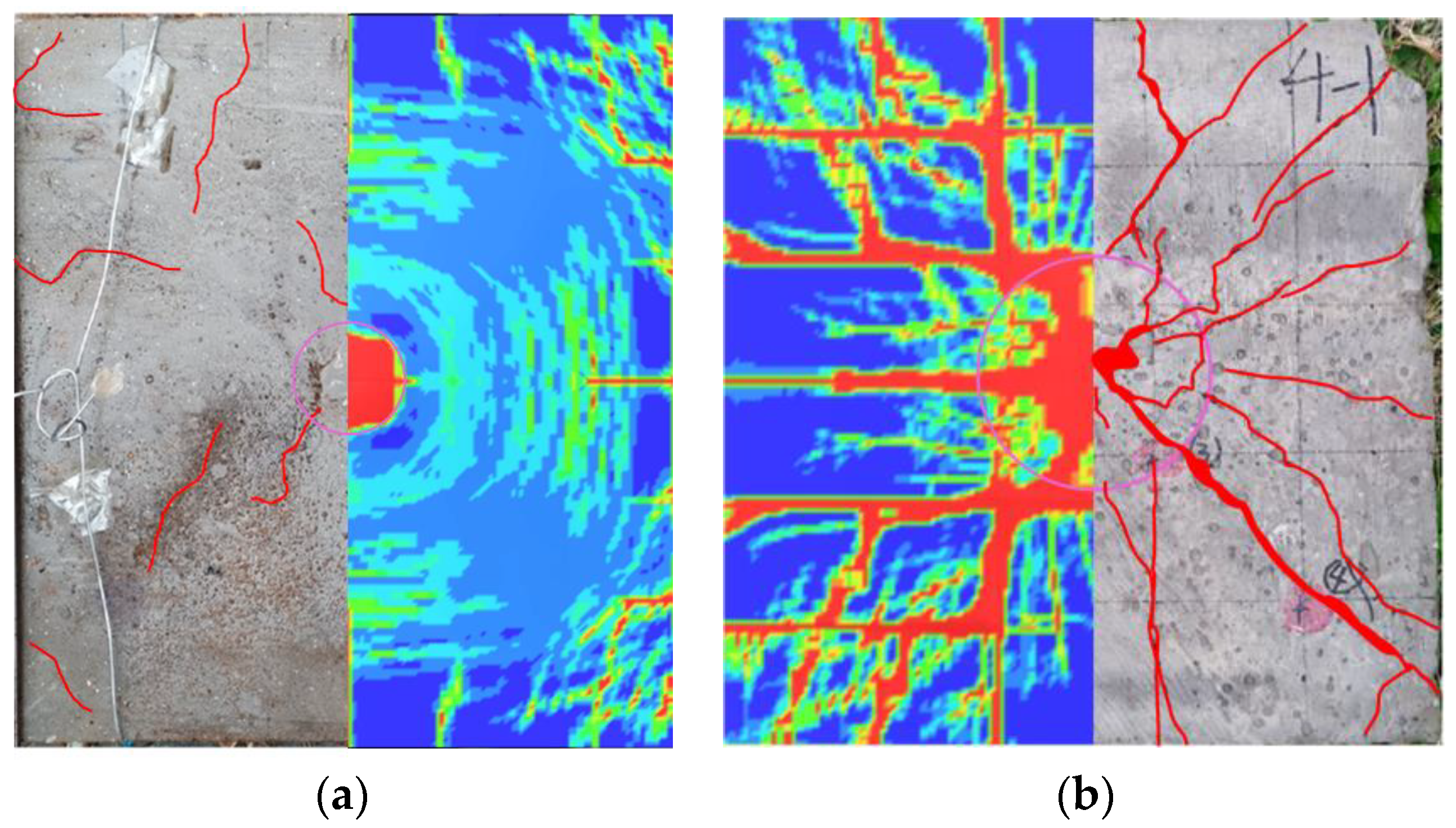
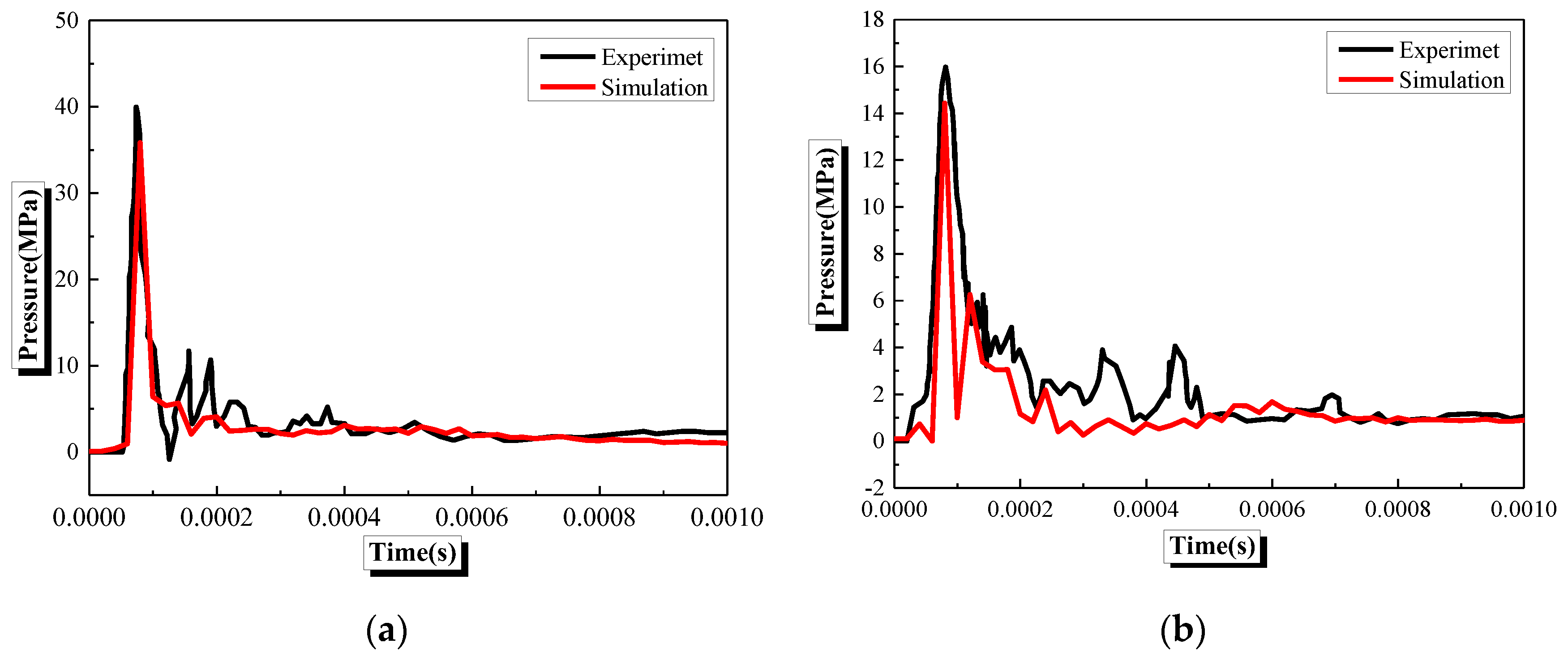
3. Validation of the Numerical Simulation
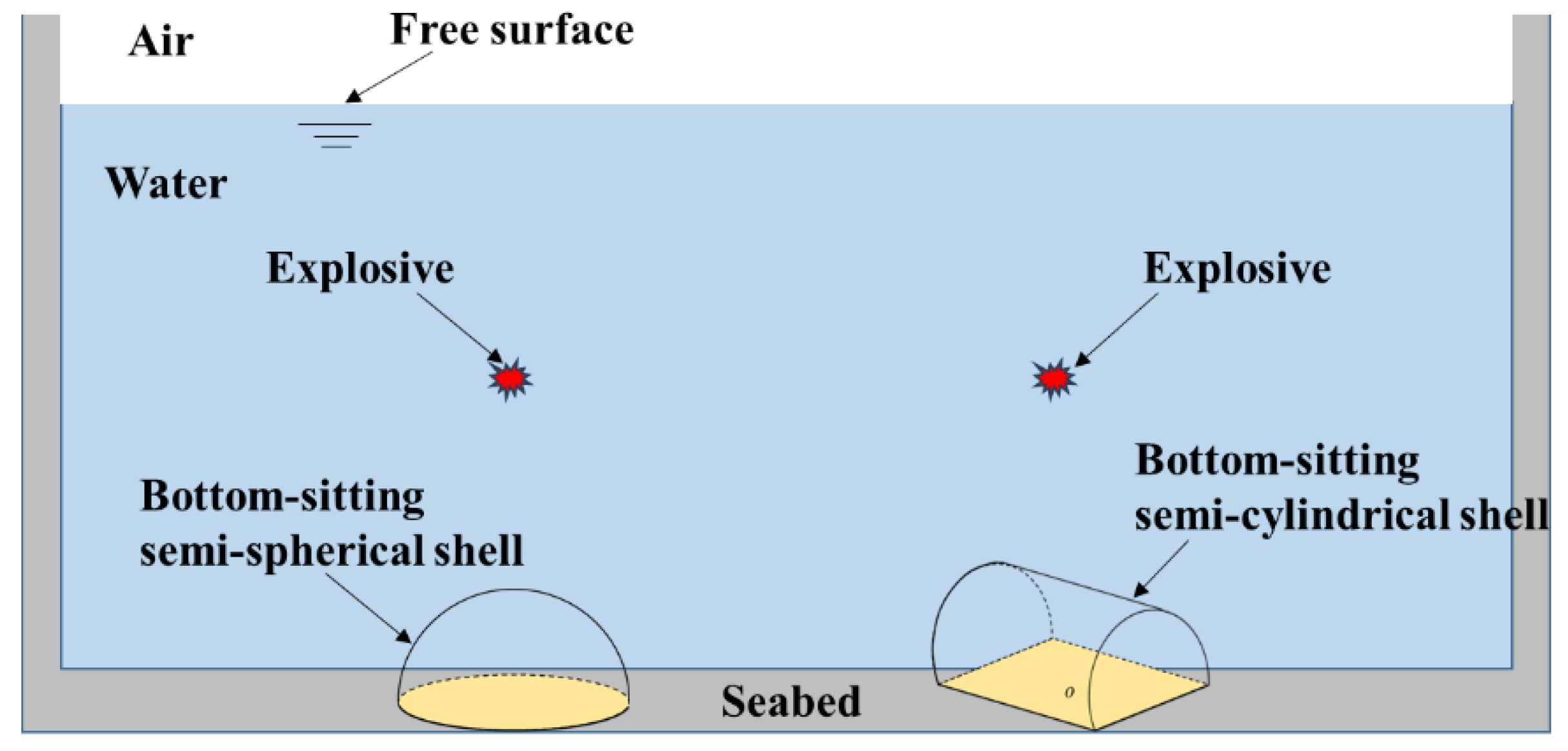
4. Numerical Investigation
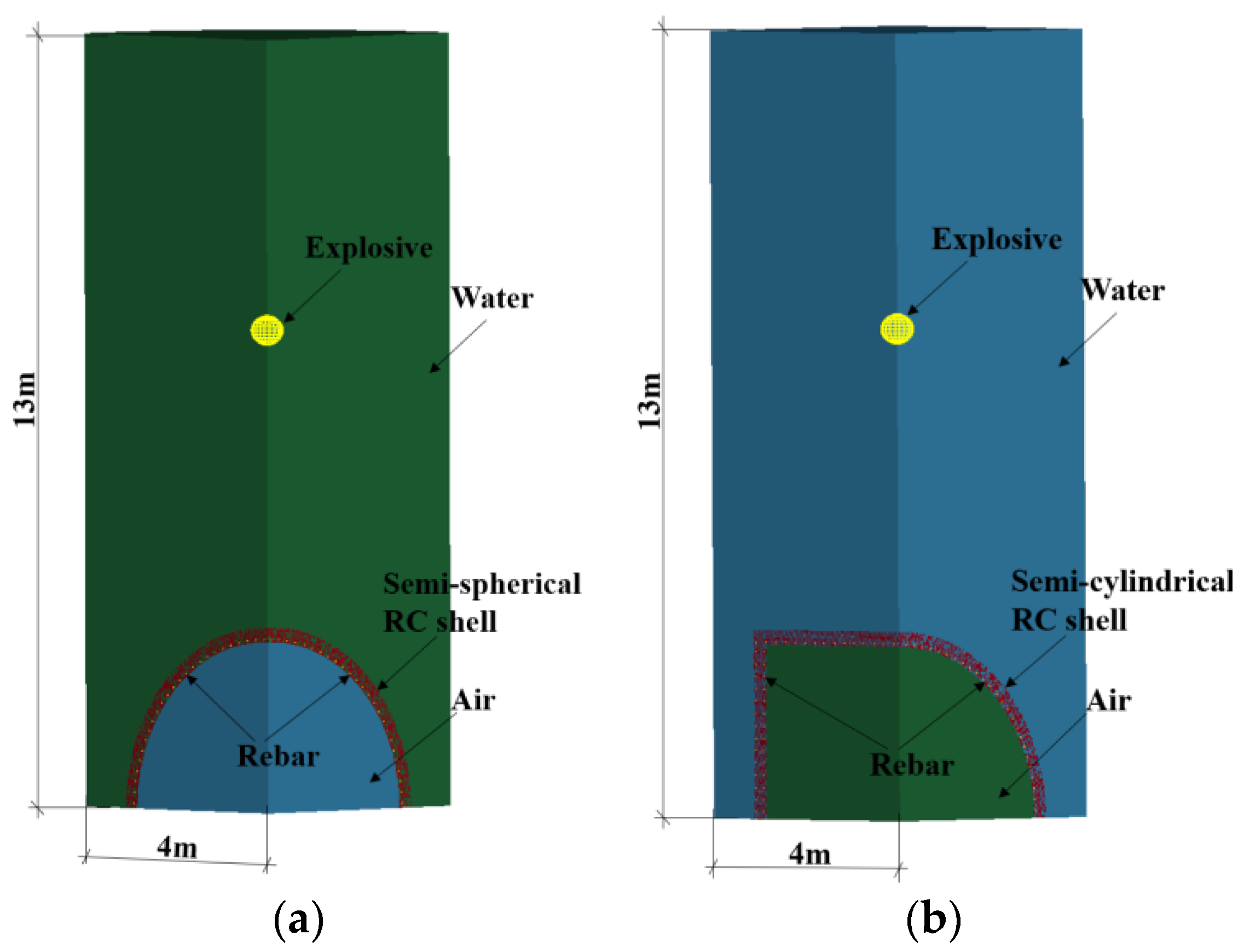
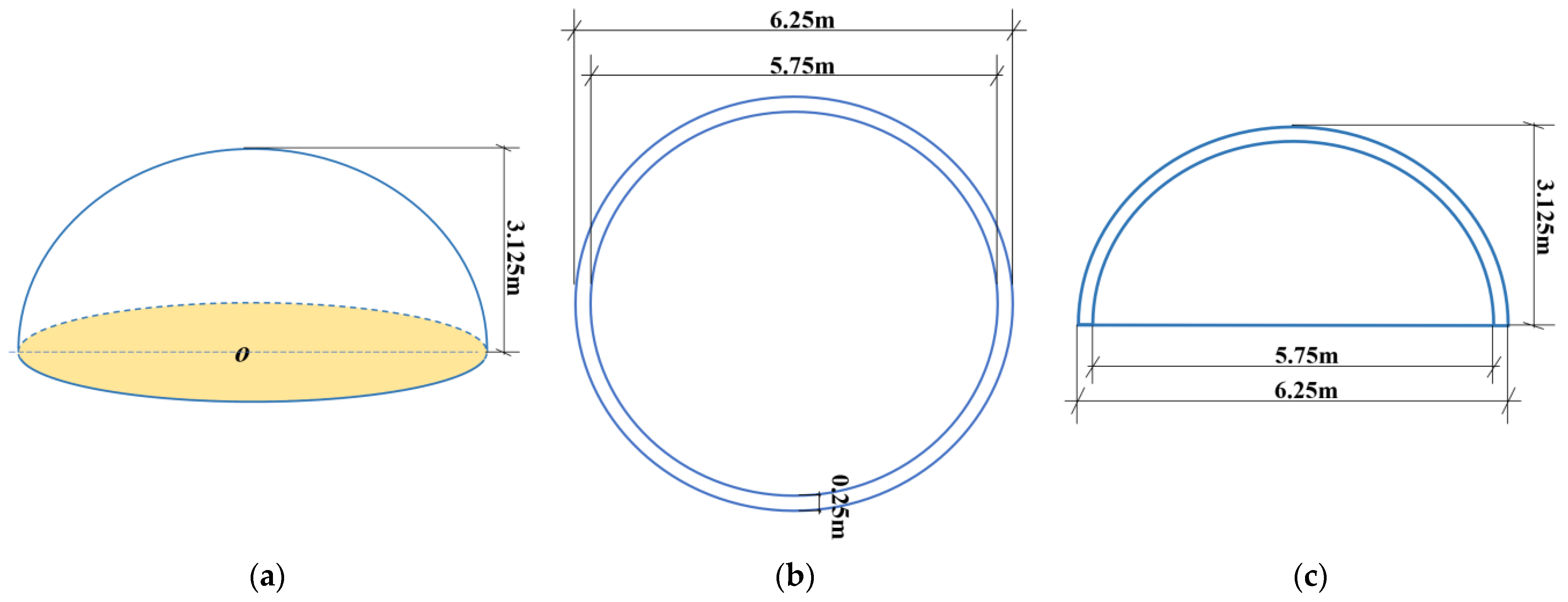
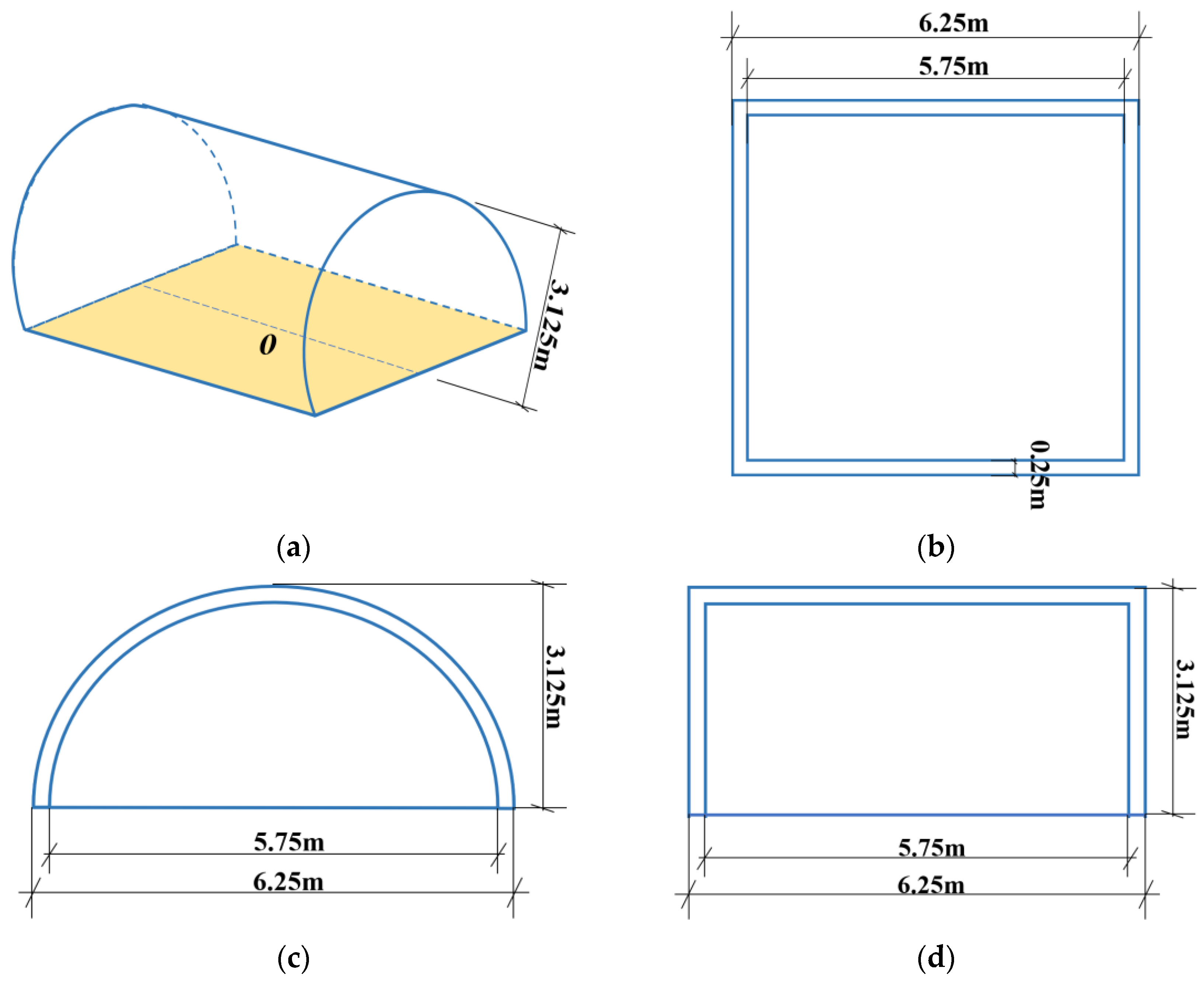
4.1. Numerical Model
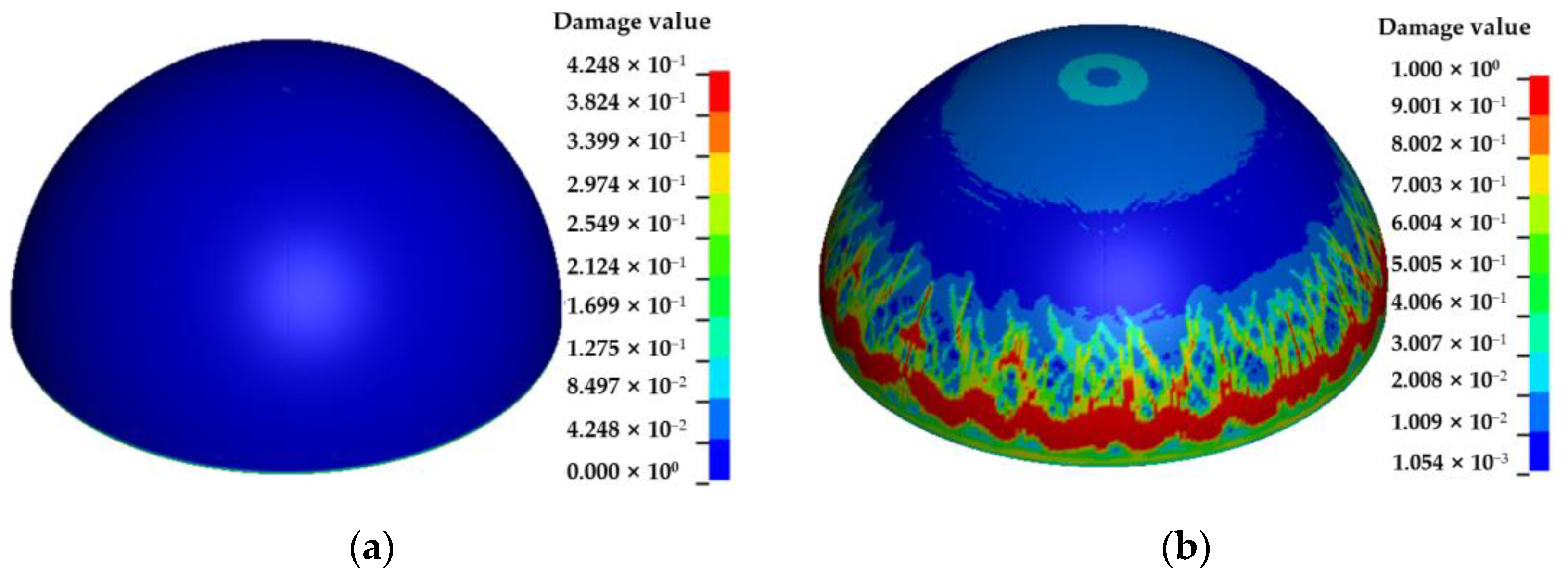
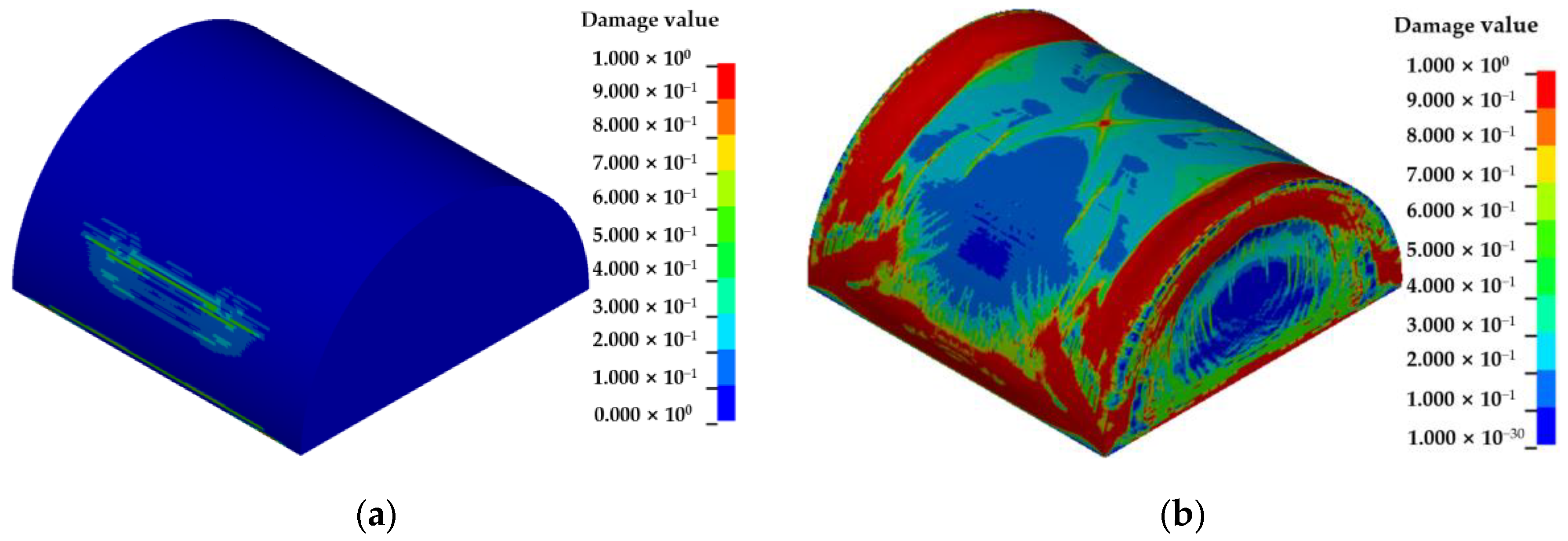
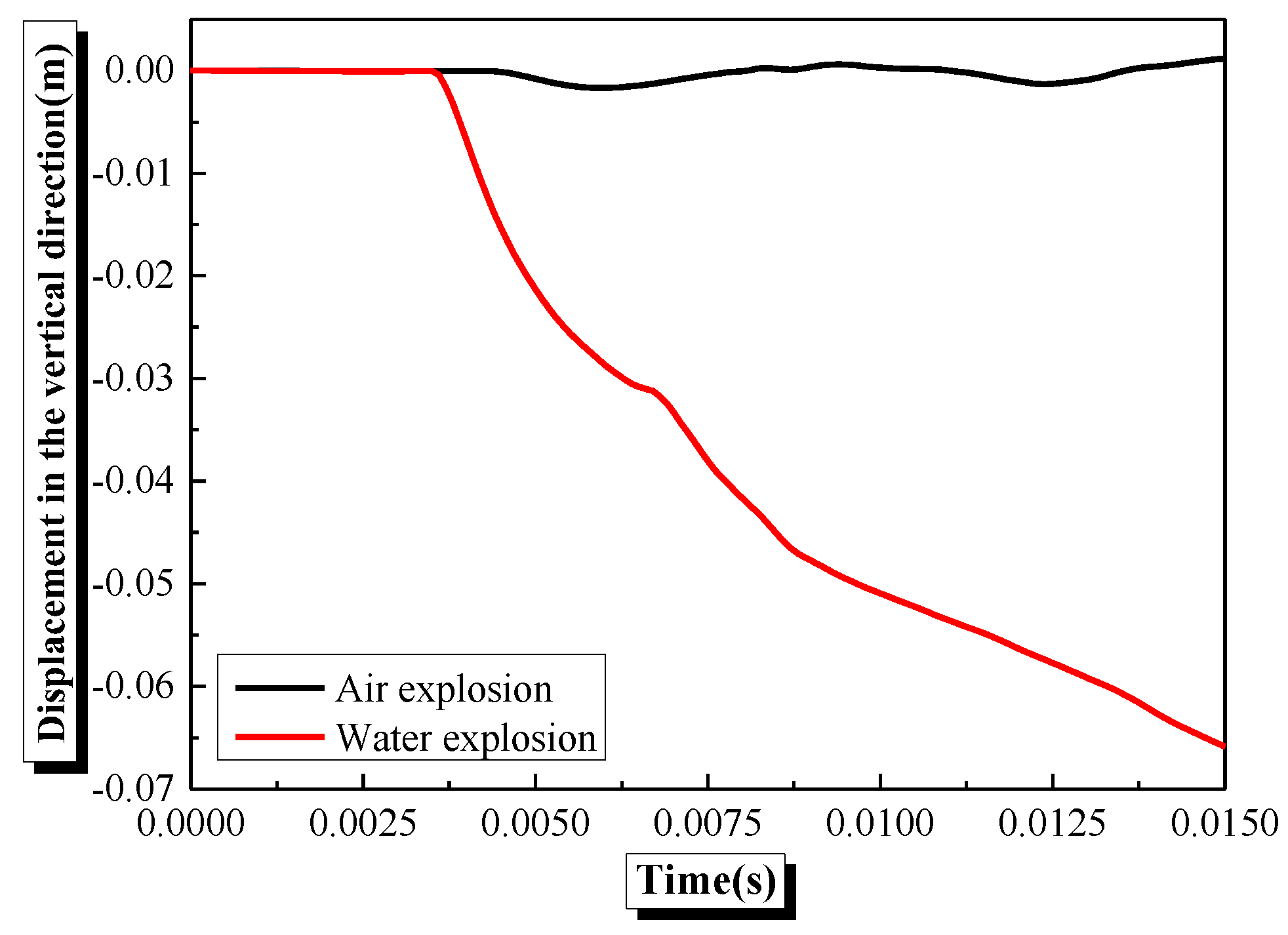
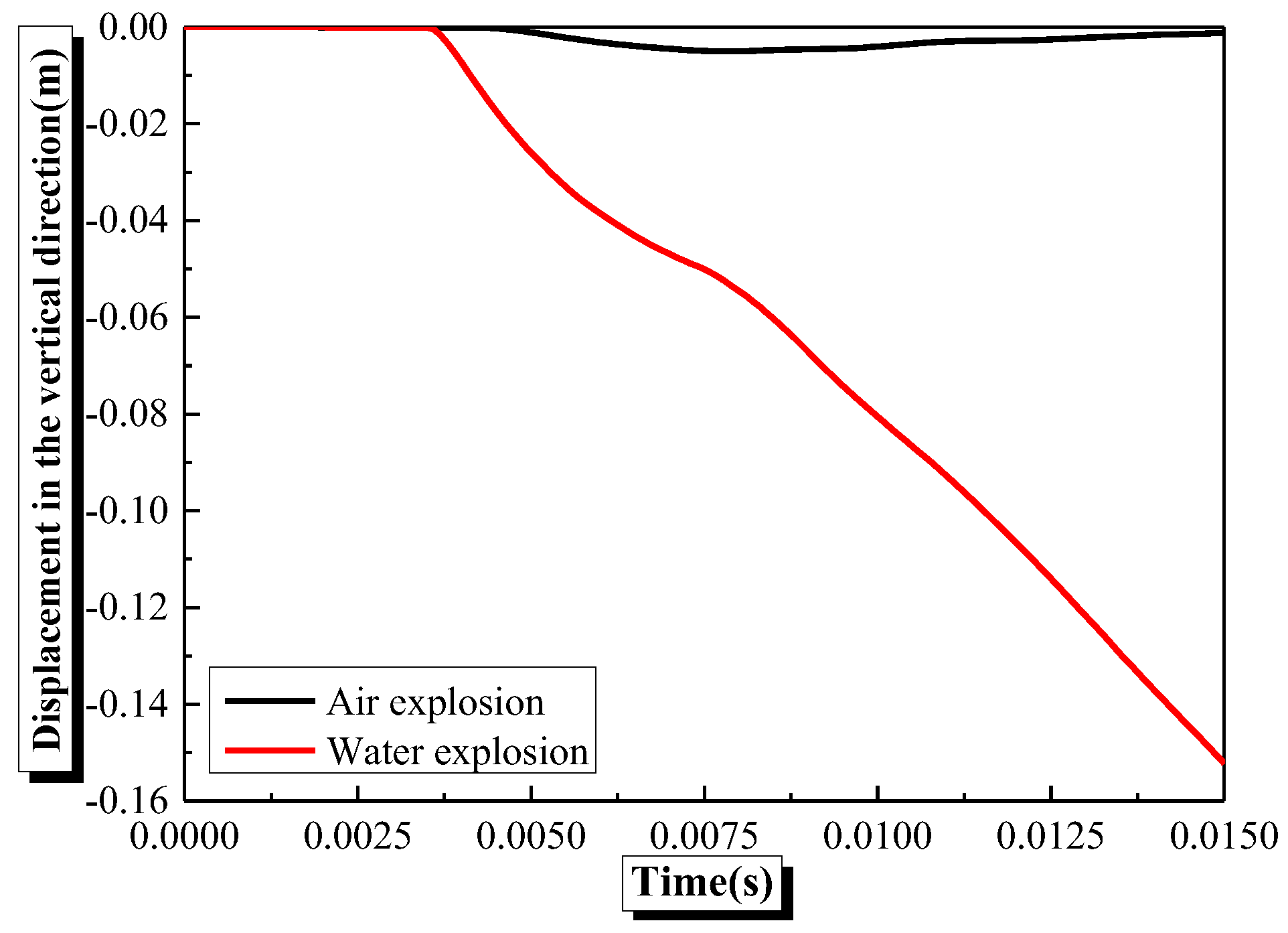
4.2. Effects of Shock Wave Transmission Medium on the Damage Characteristics and Dynamic Response of Semi-Spherical and Semi-Cylindrical Bottom-Sitting RC Shells
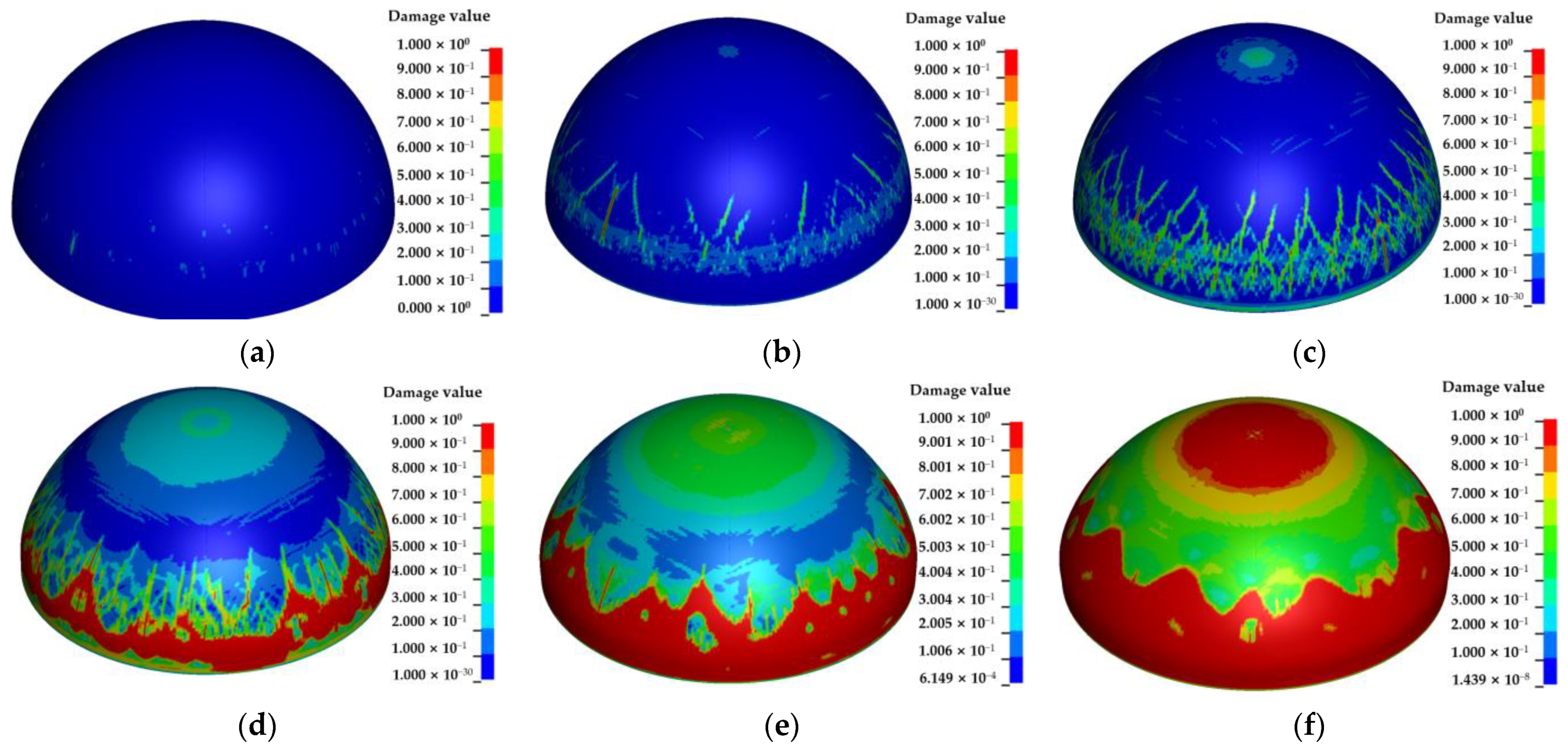
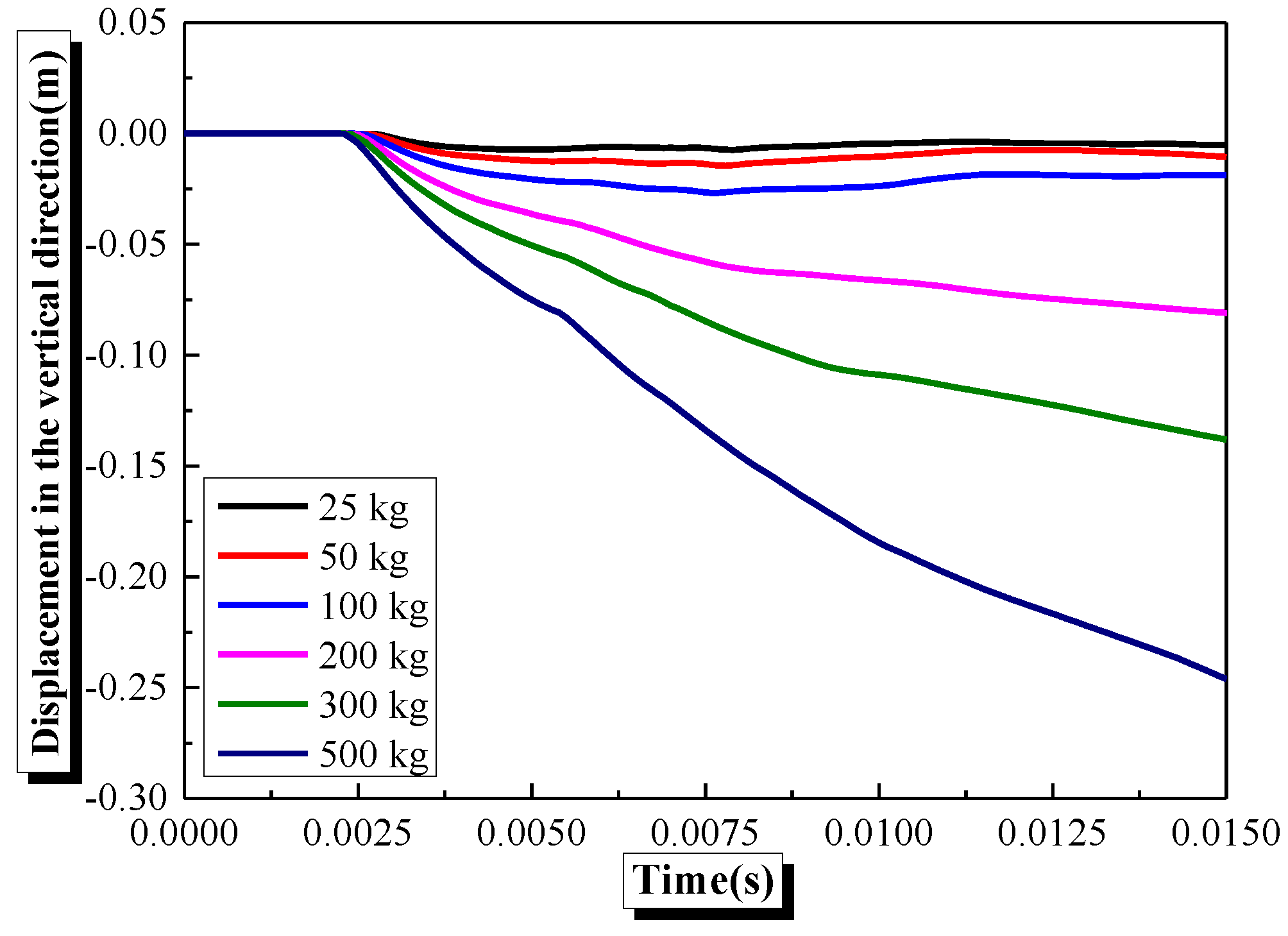
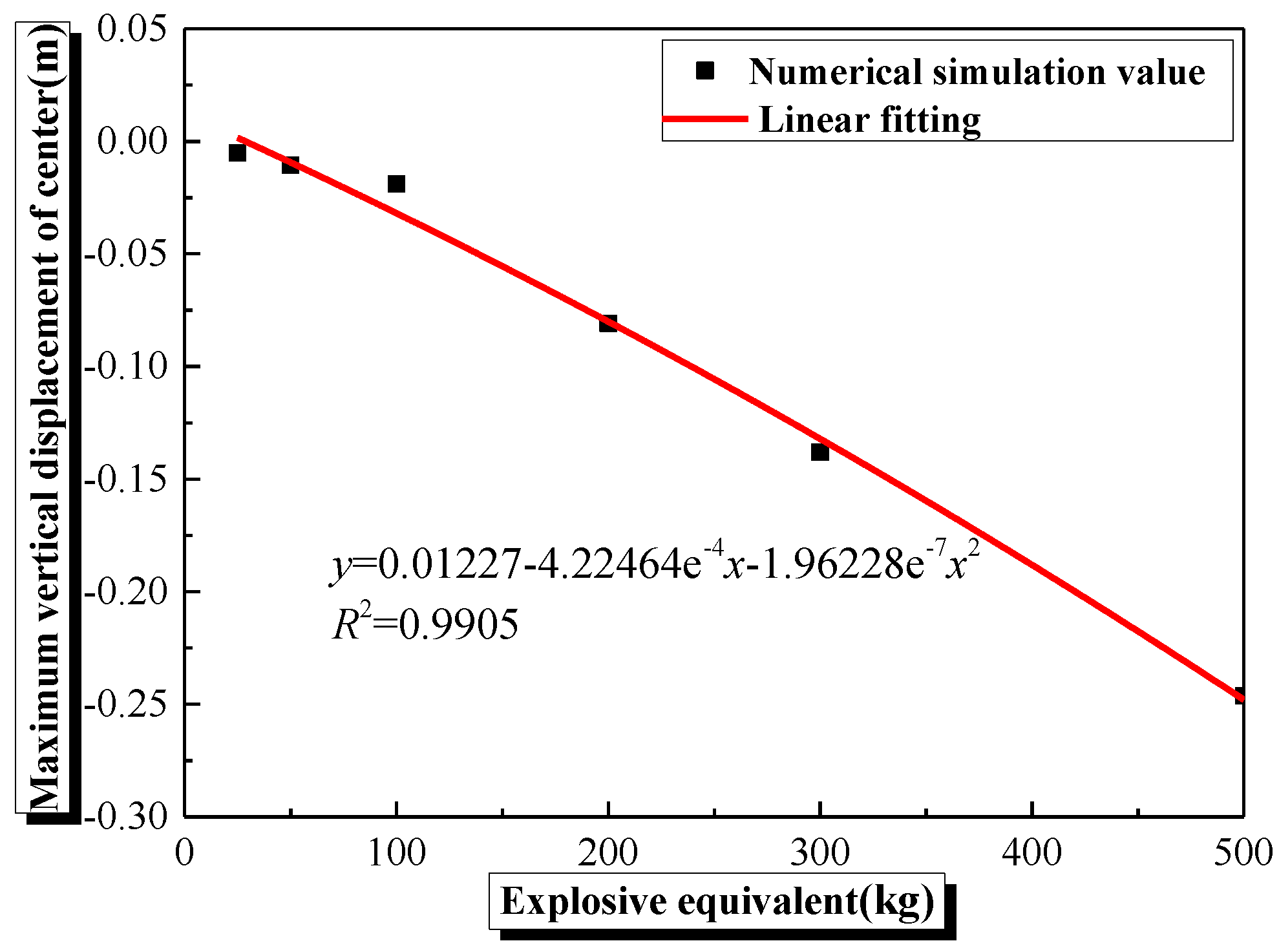
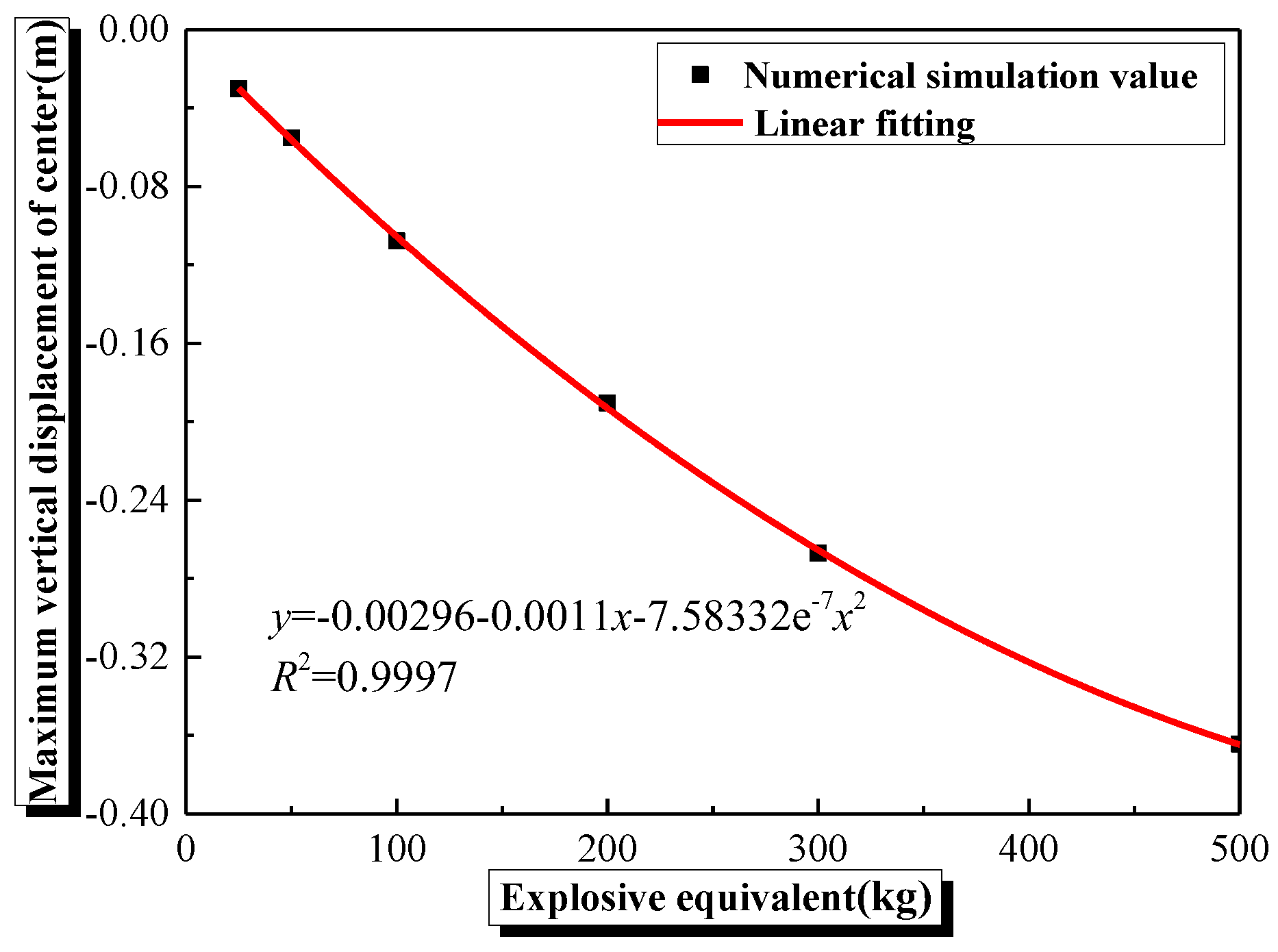
4.3. Effects of Explosive Equivalent on the Damage Characteristics and Dynamic Response of Semi-Spherical and Semi-Cylindrical Bottom-Sitting RC Shells
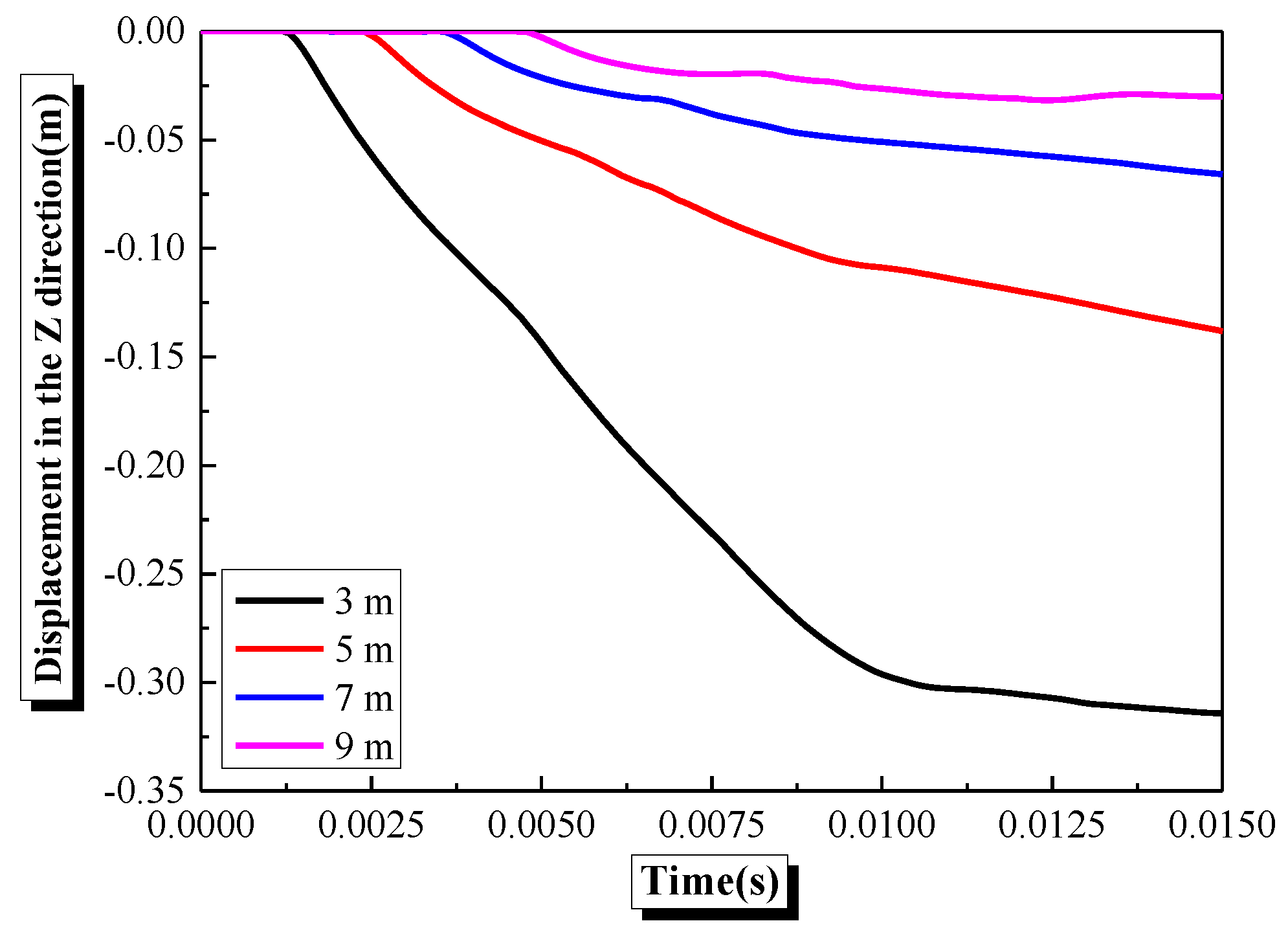
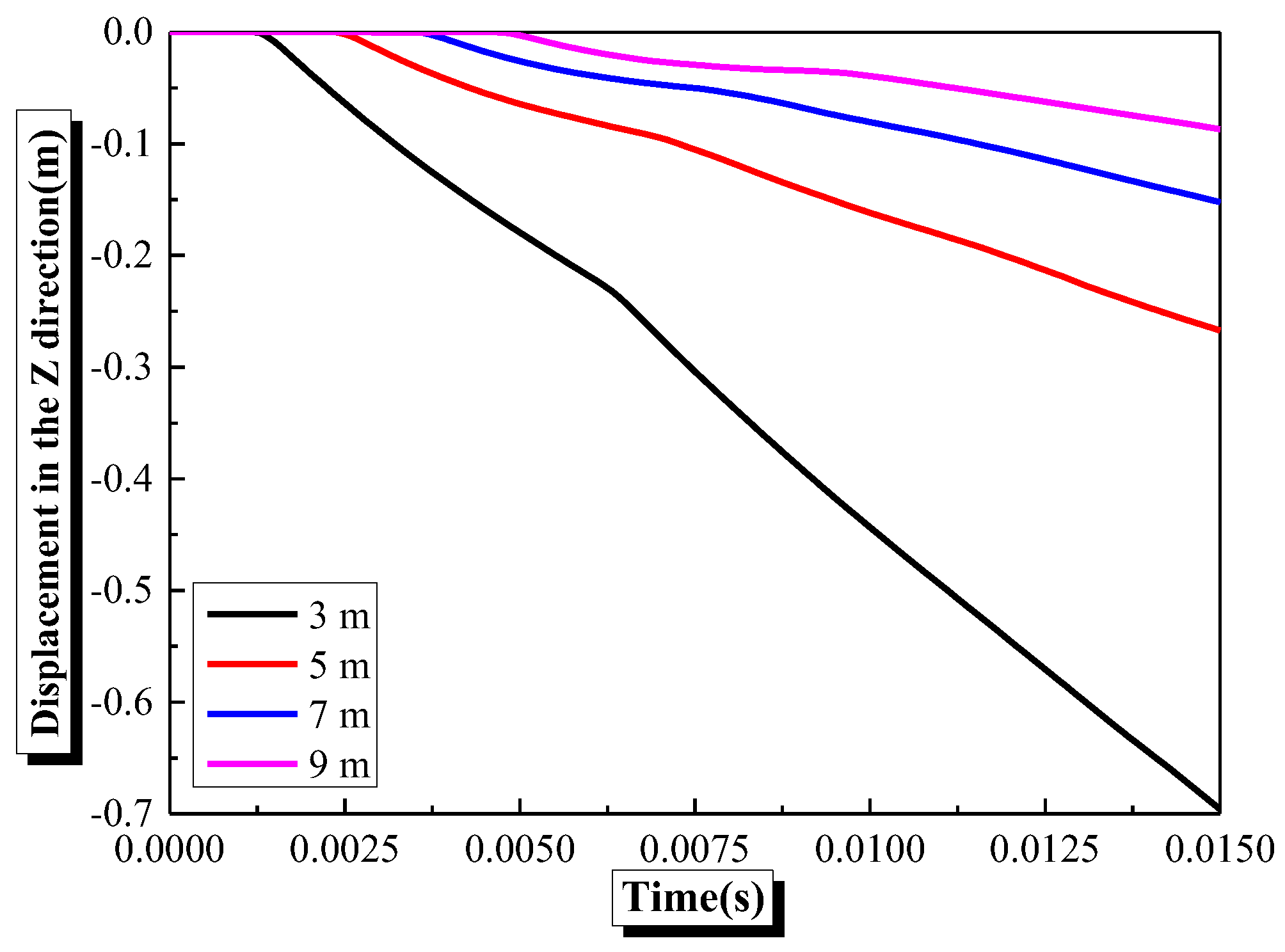
4.4. Effects of Explosive Distance on the Damage Characteristics and Dynamic Response of Semi-Spherical and Semi-Cylindrical Bottom-Sitting RC Shells
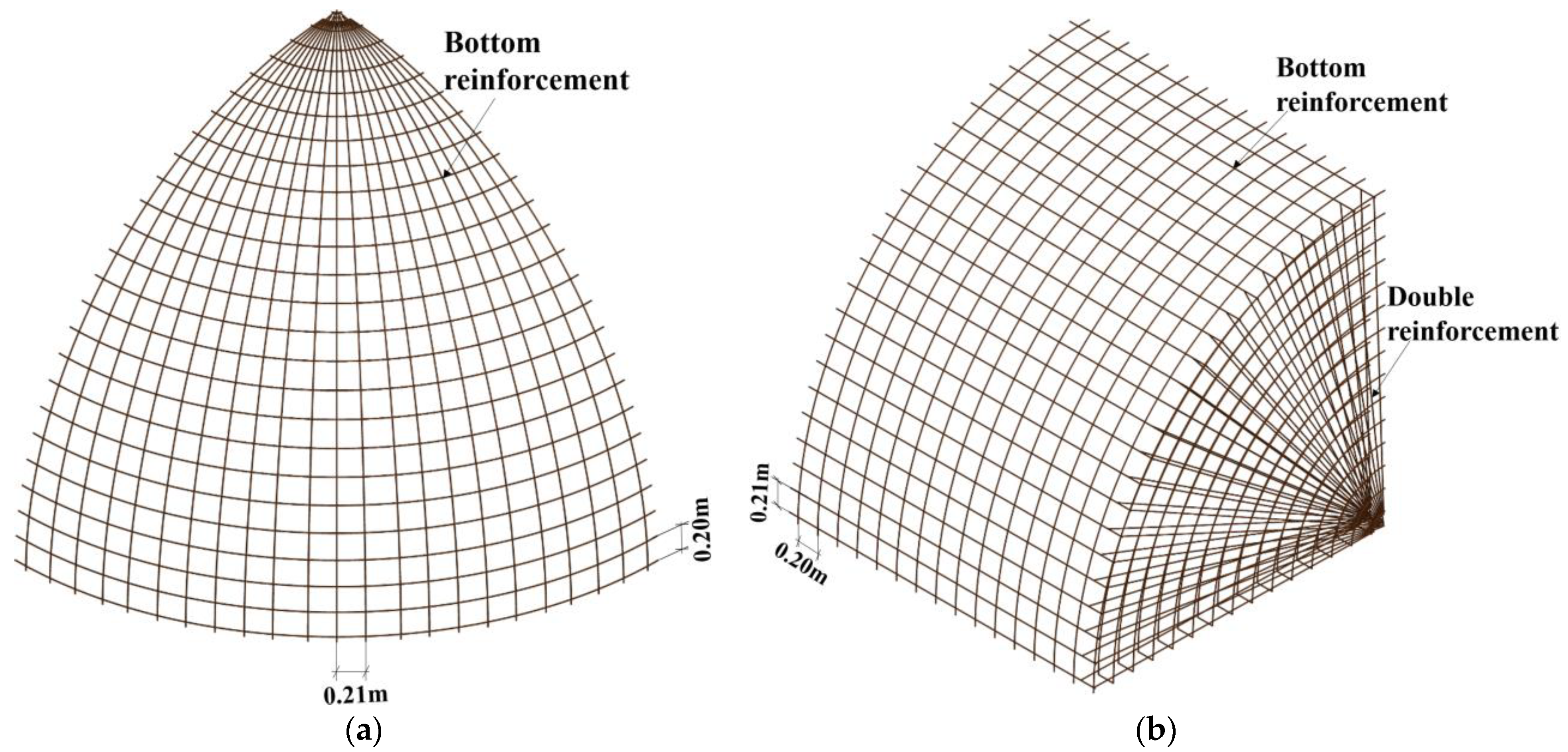
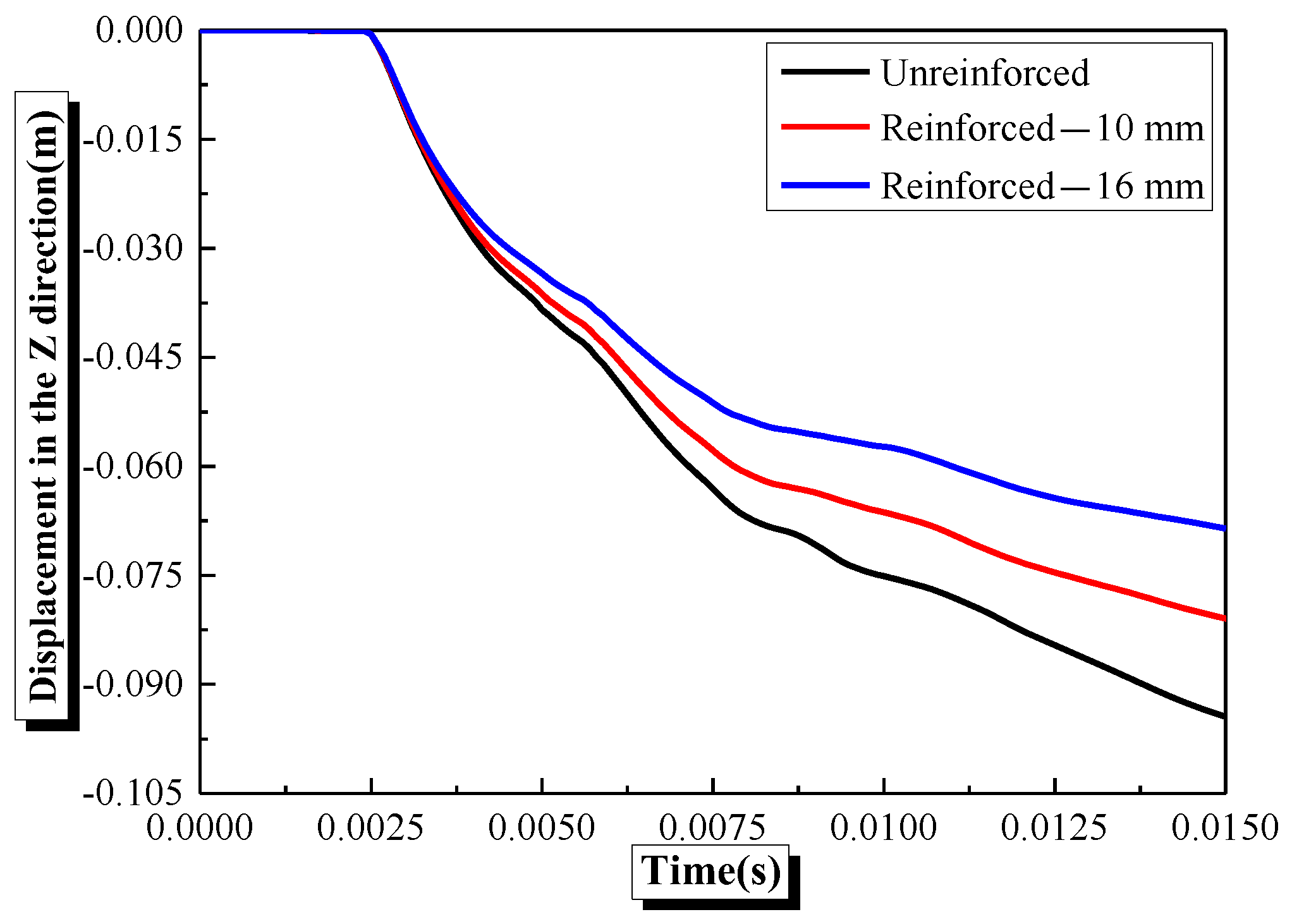
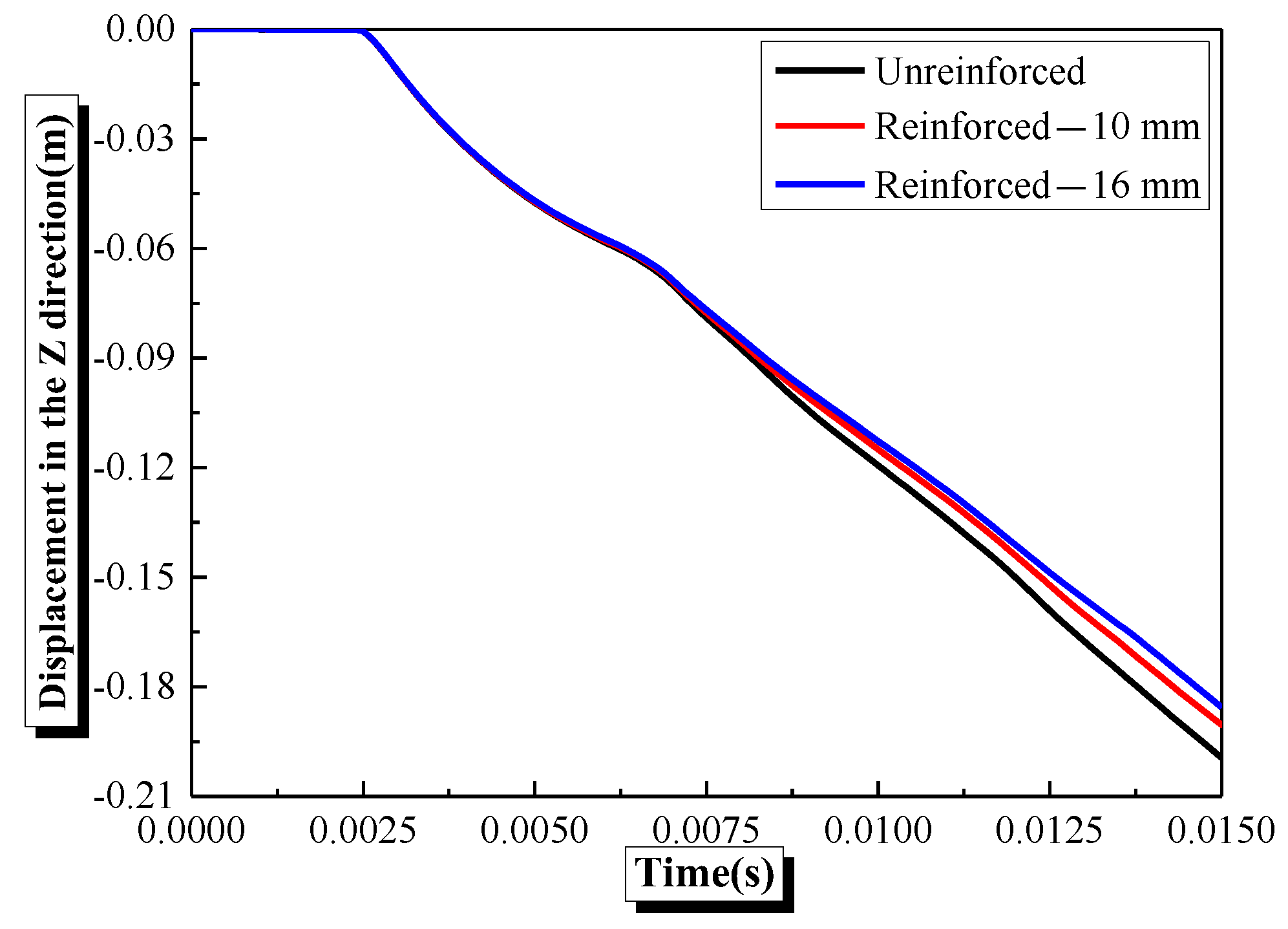
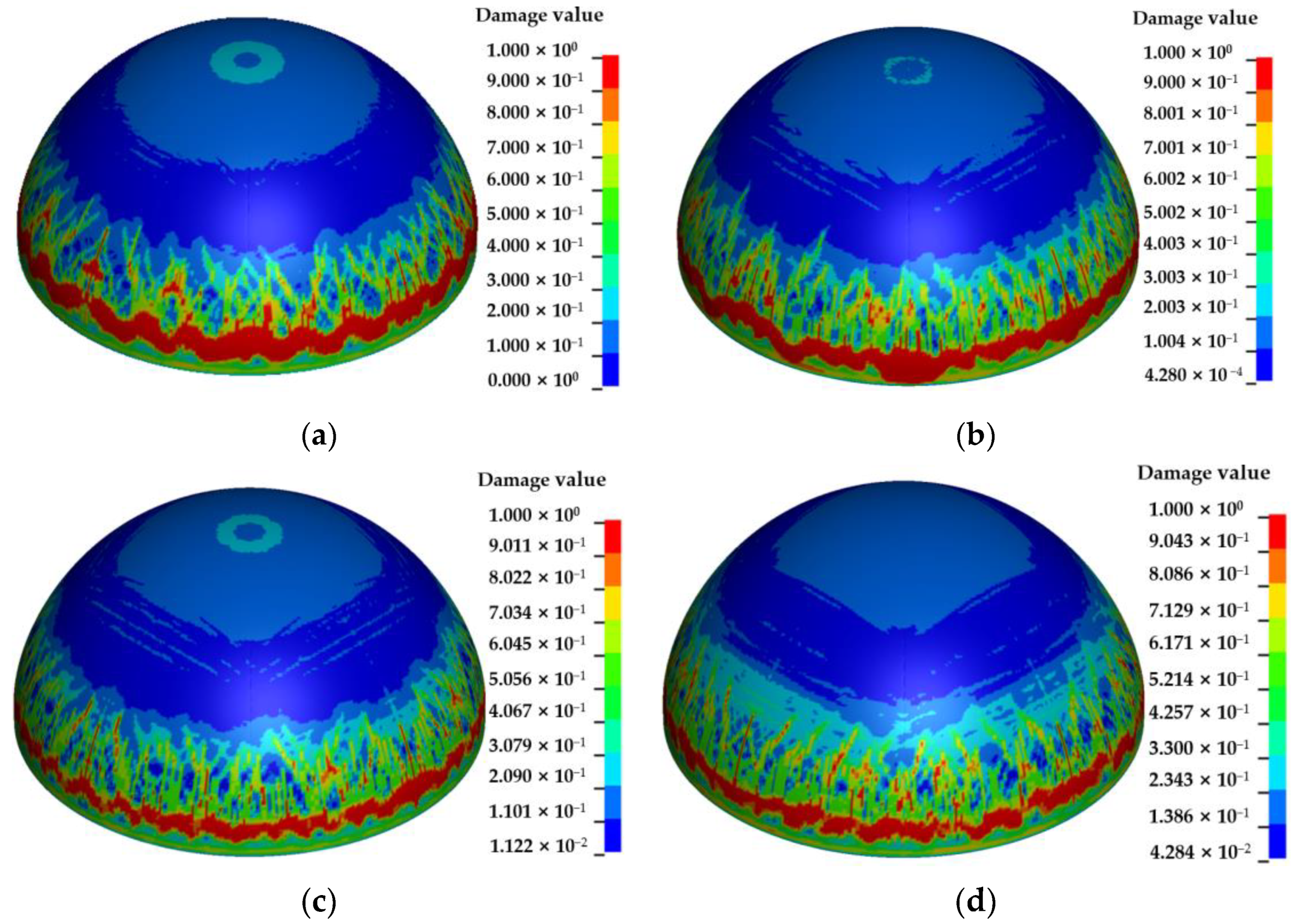
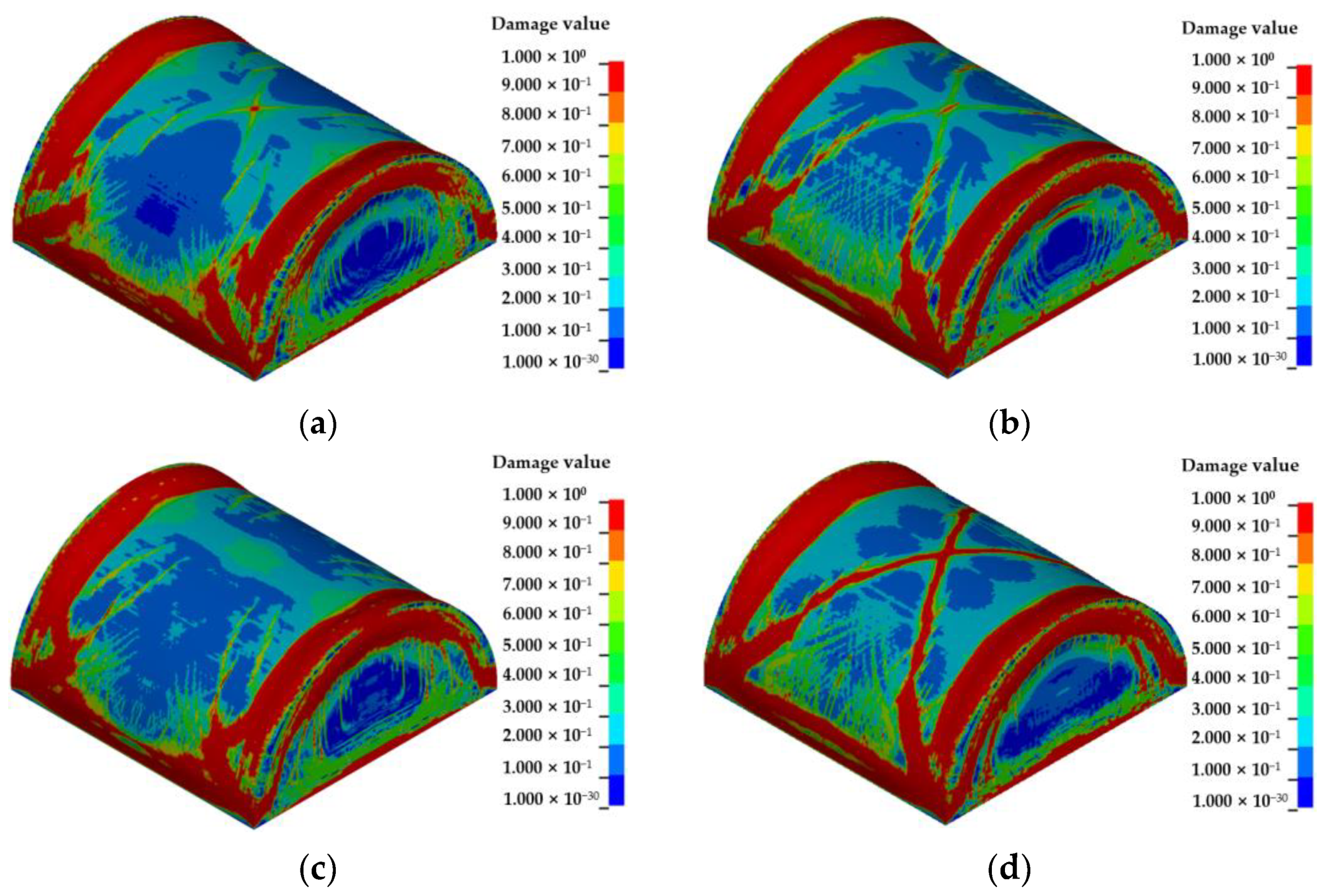
4.5. Effects of Bottom Reinforcement on the Damage Characteristics and Dynamic Response of Semi-Spherical and Semi-Cylindrical Bottom-Sitting RC Shells
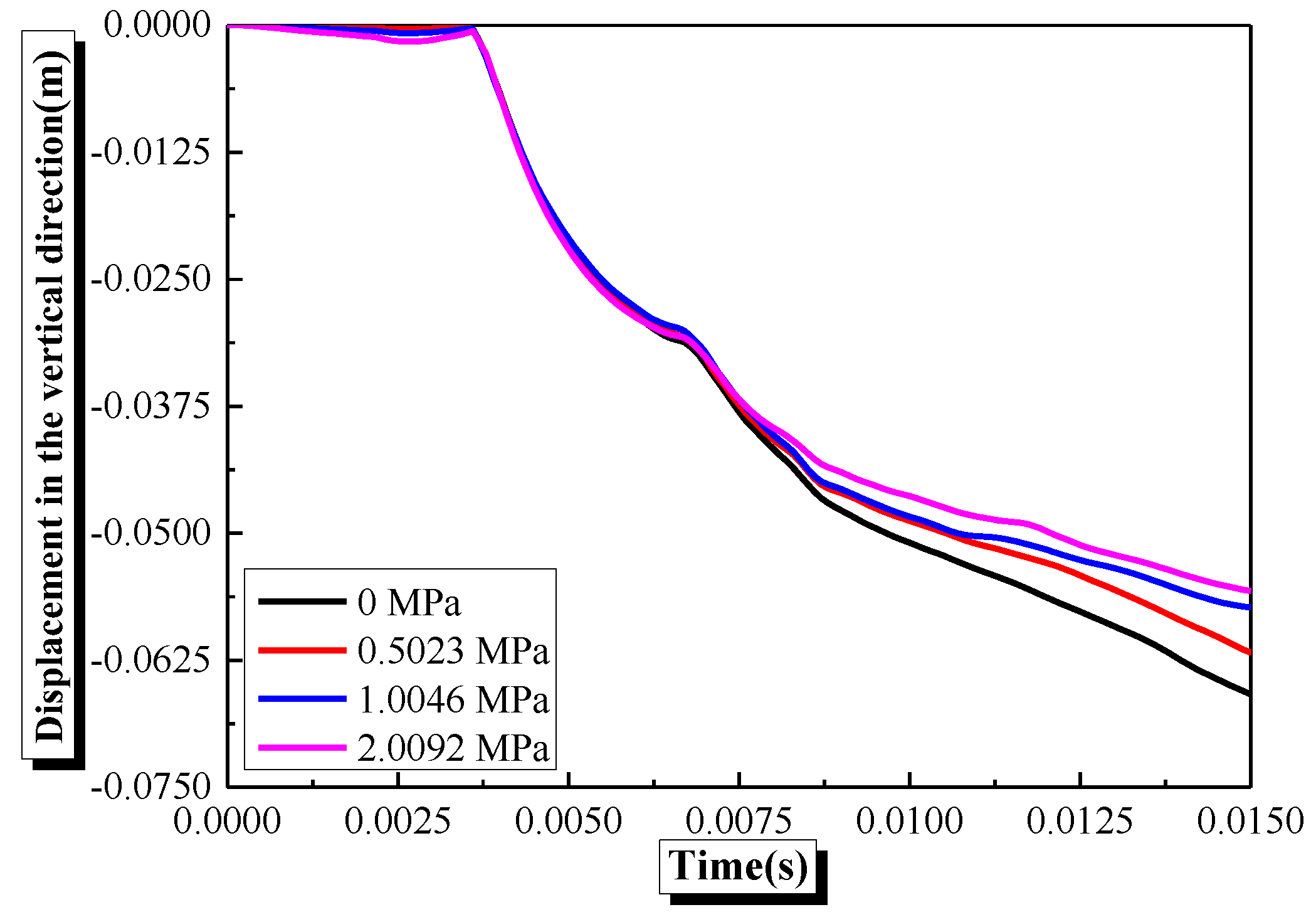
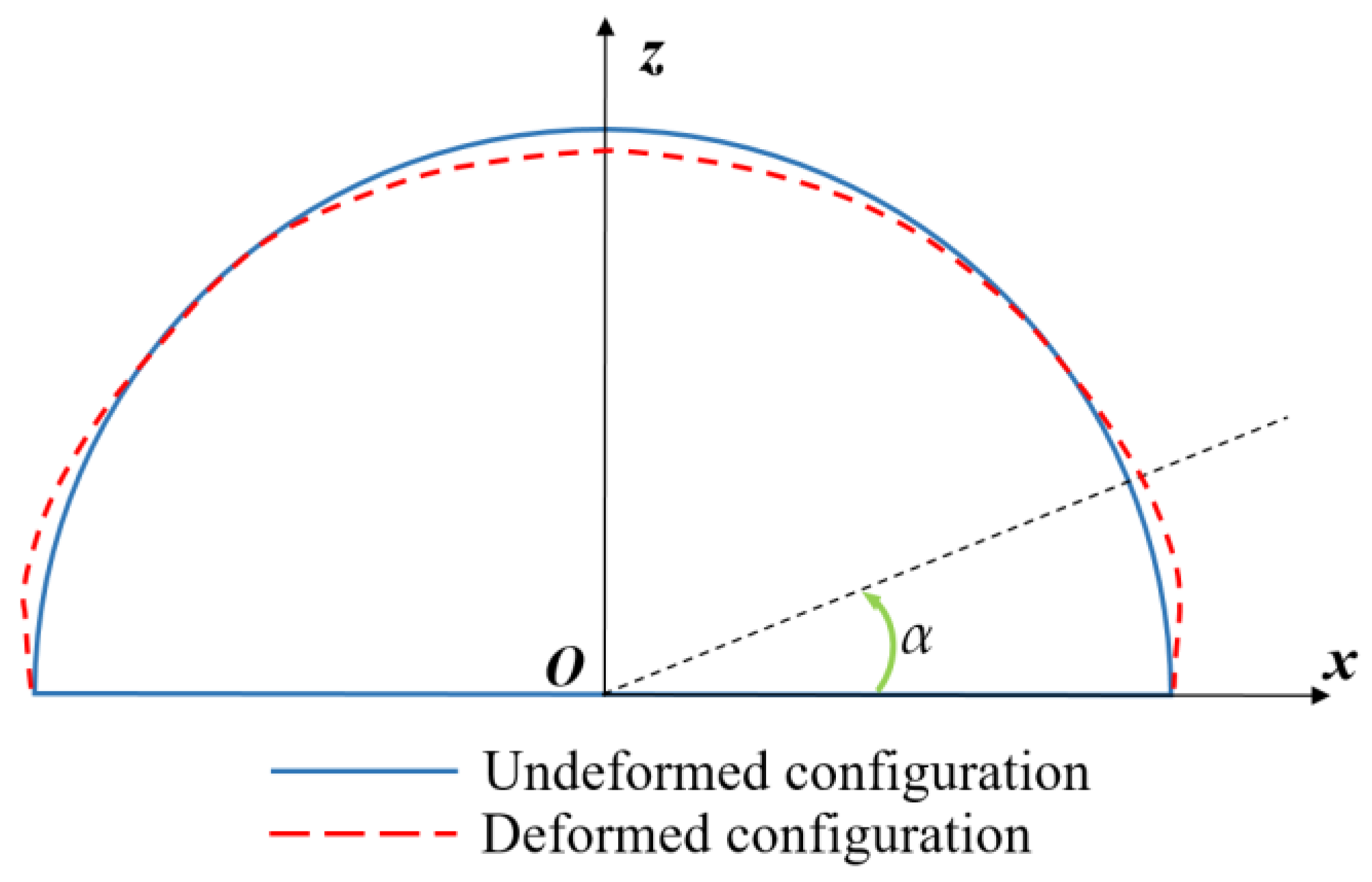
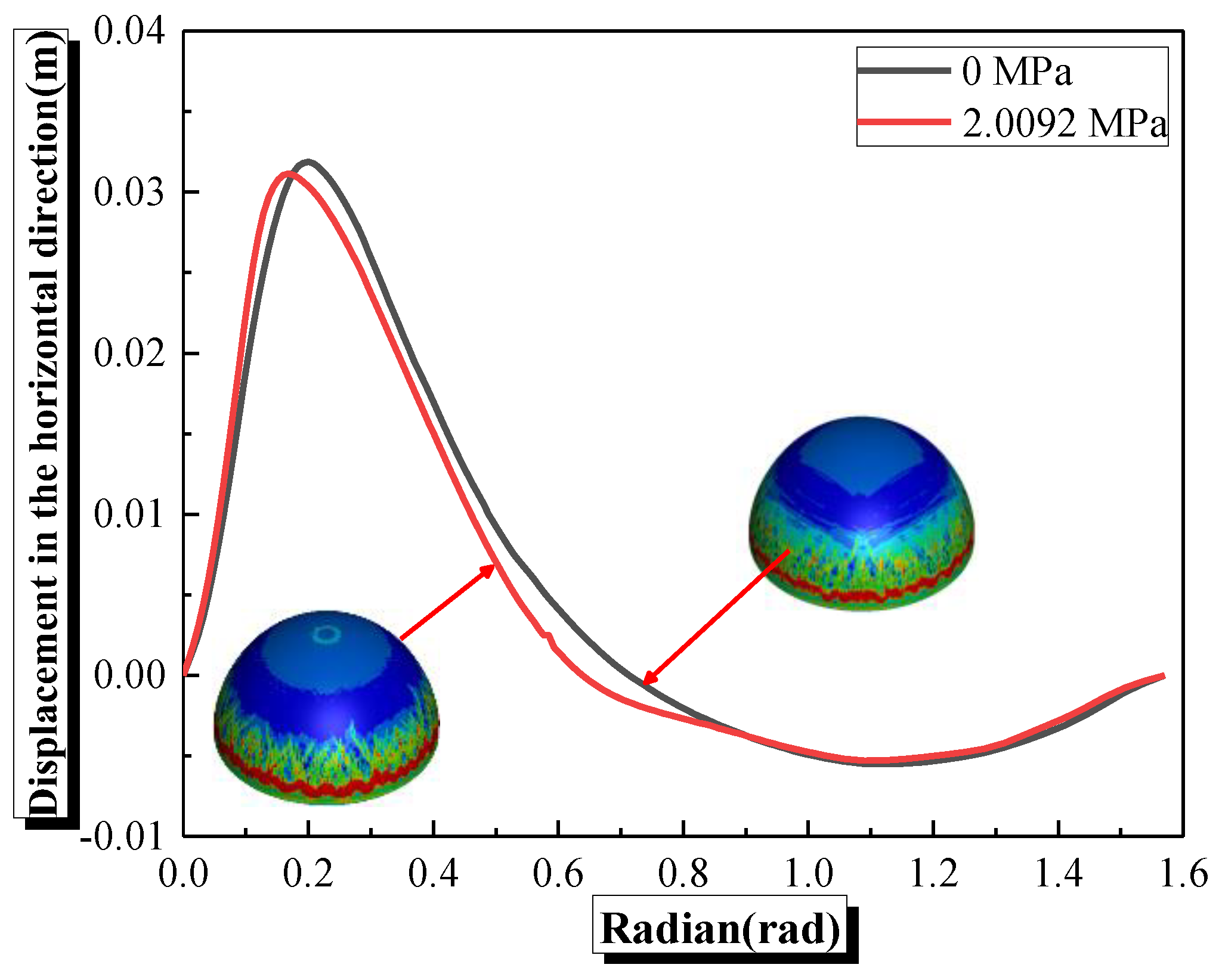
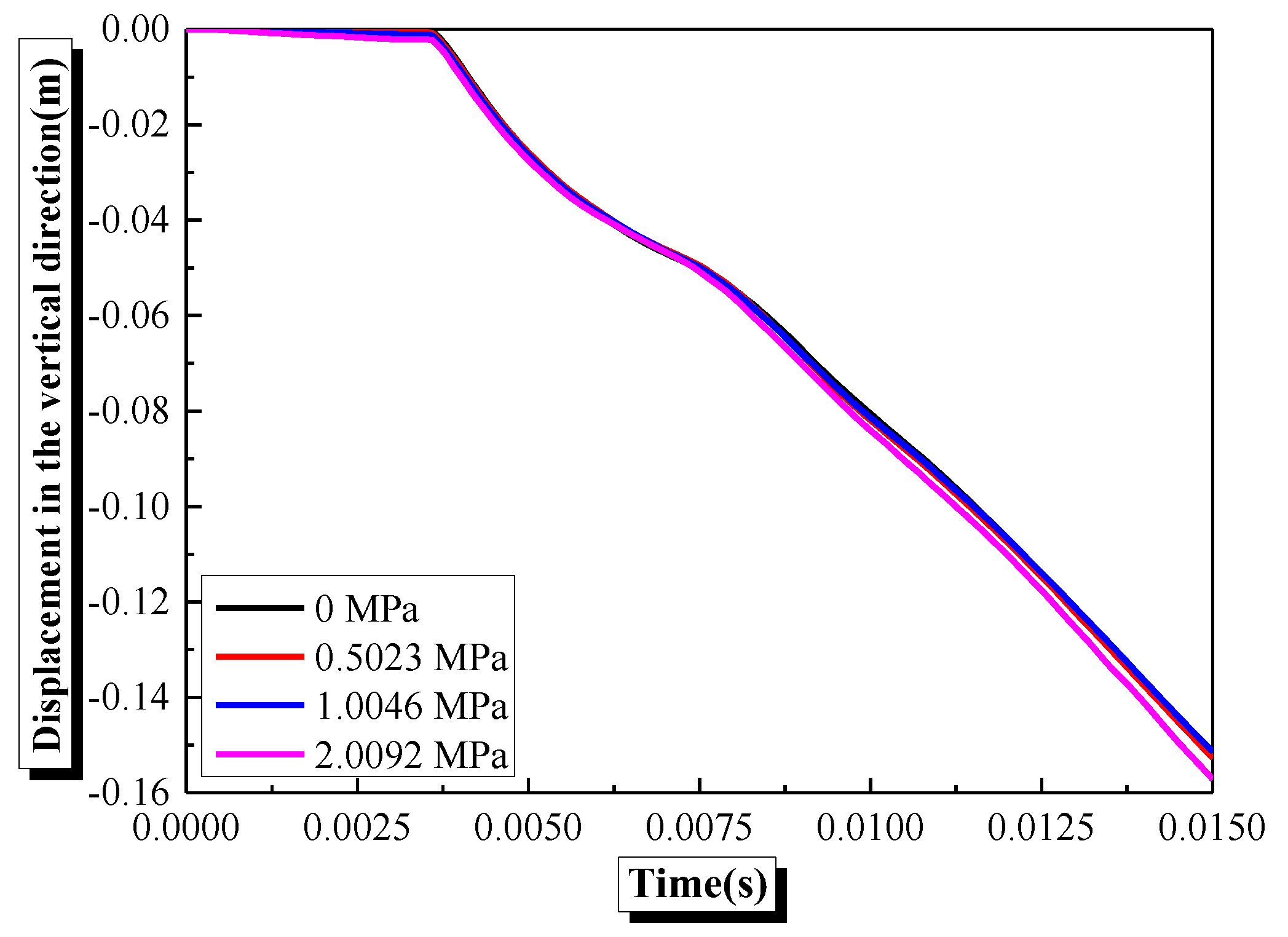
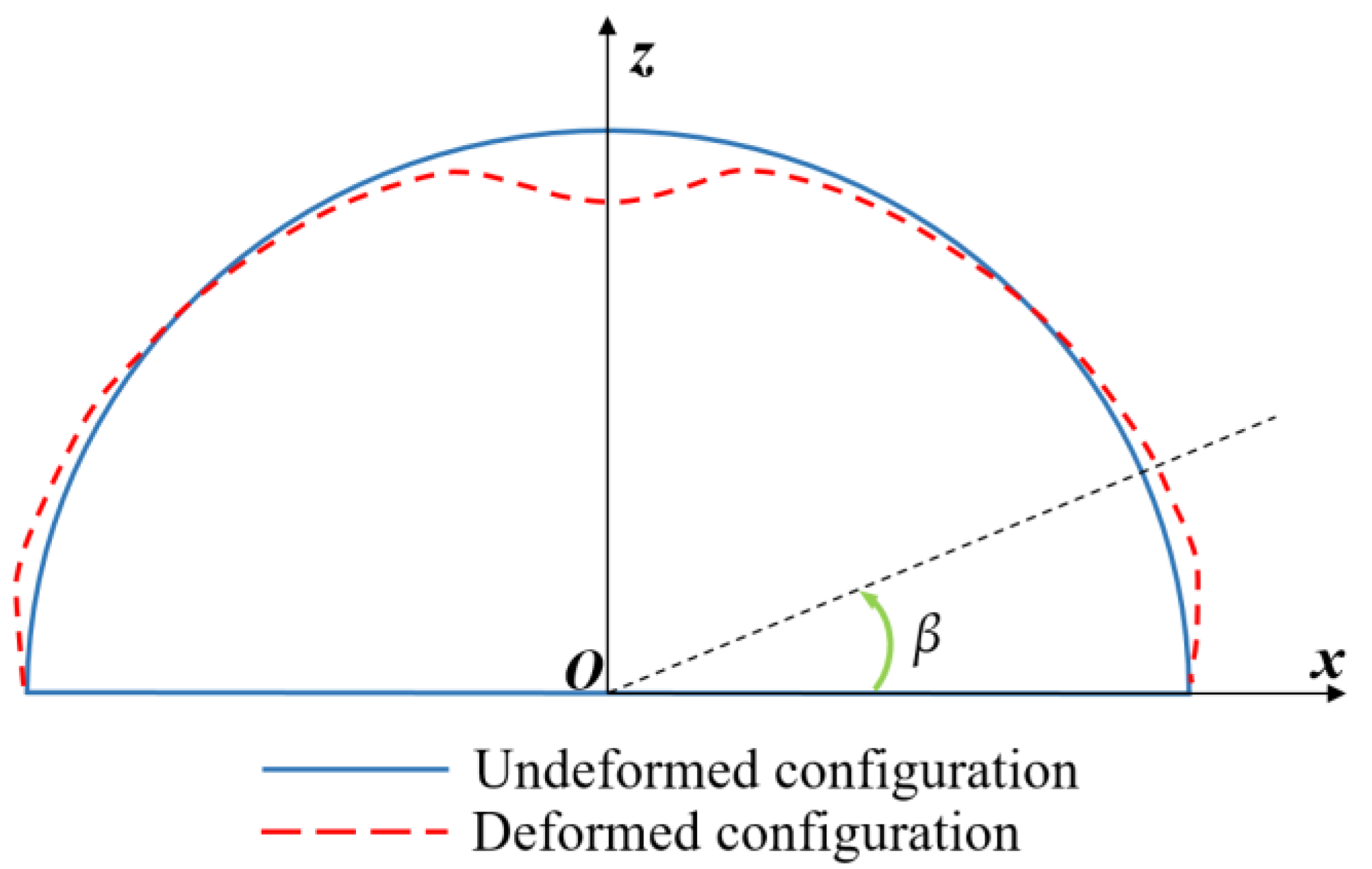
4.6. Effects of Hydrostatic Pressure on the Damage Characteristics and Dynamic Response of Semi-Spherical and Semi-Cylindrical Bottom-Sitting RC Shells
5. Discussion
6. Conclusions
- (1)
- The damage and vertical center deformation of semi-spherical and semi-cylindrical RC shells under underwater shock waves are significantly greater than those under air shock waves.
- (2)
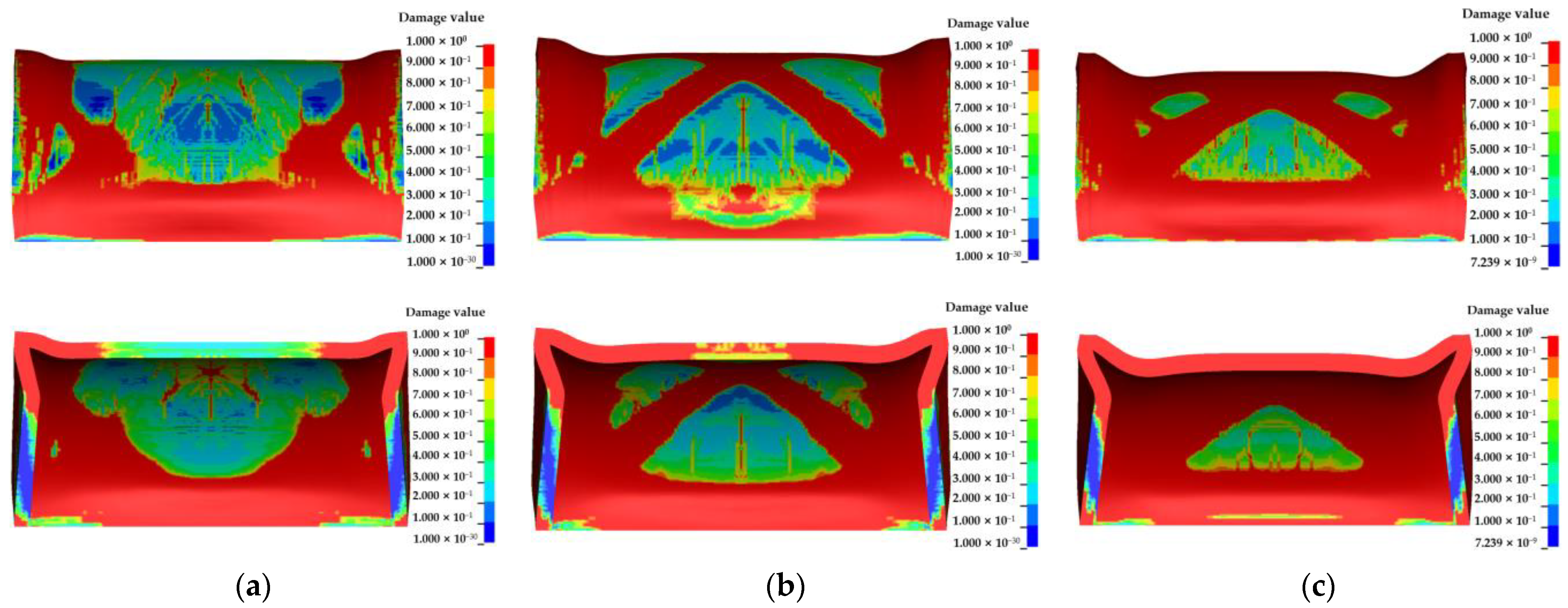
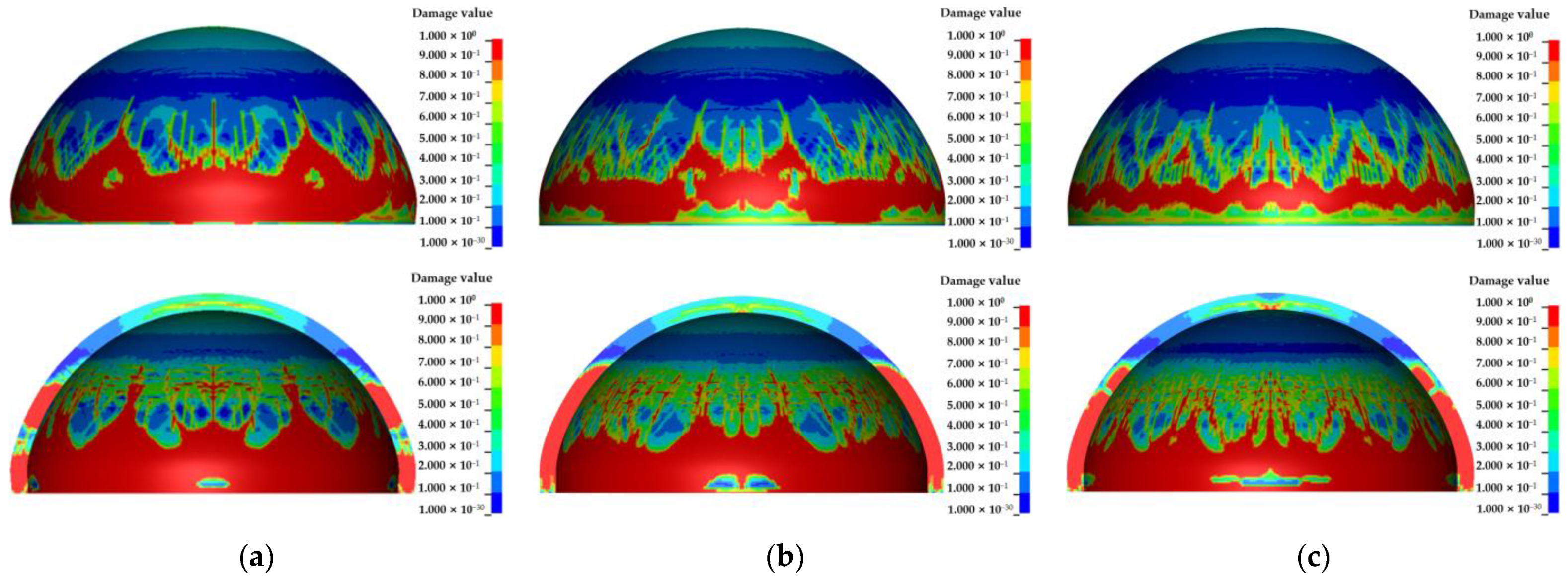
- The damage to the semi-spherical RC shell is mainly concentrated in the lower part and the center of the semi-spherical RC shell, and gradually extends from the lower part to the center of the semi-spherical RC shell with an increase in explosive equivalent. The damage to the semi-cylindrical RC shell is mainly concentrated in the junction of the semi-cylindrical RC shell and side walls at both ends, the constraint position of the semi-cylindrical RC shell, and the center of the semi-cylindrical shell. The damaged area gradually extends from the junction between the semi-cylindrical RC shell and side walls at both ends, and the restraint on both sides of the semi-cylindrical shell to the center of the semi-cylindrical shell with an increase in explosive equivalent.
- (3)
- The damage and vertical center deformation of the semi-spherical and semi-cylindrical RC shells show a gradually increasing trend with an increase in explosive equivalent or decrease in explosive distance. Meanwhile, the damage to the inner surface of the semi-spherical RC shell is more severe than the outer surface.
- (4)
- The overall damage and vertical center deformation of the semi-spherical and semi-cylindrical RC shell can be reduced by the bottom reinforcement and an increase in the diameter of the steel bar within the diameter range of 10–16 mm. However, the effect of the diameter of the steel bar on the vertical center displacement of the semi-cylindrical RC shell is lower than for the semi-spherical RC shell.
- (5)
- The ‘hoop effect’ caused by hydrostatic pressure restrains the horizontal convex deformation and slightly decreases the macroscopic damage and vertical center deformation of the semi-spherical RC shell with an increase in hydrostatic pressure within the range of 0–2.0092 MPa. The hydrostatic pressure restrains the horizontal convex deformation of the semi-cylindrical RC shell. However, the inward concave deformation of the semi-cylindrical shell center is increased by hydrostatic pressure, inducing an increase in the damage and center vertical deformation of the semi-cylindrical RC shell.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Avachat, S.; Zhou, M. Response of submerged metallic sandwich structures to underwater impulsive loads. J. Mech. Mater. Struct. 2015, 10, 17–41. [Google Scholar] [CrossRef]
- Yang, G.D.; Fan, Y.; Wang, G.H.; Gao, Q.D.; Deng, K.; Wang, F. Numerical study on dynamic response of submerged tunnel subjected to underwater explosion. Soil Dyn. Earthq. Eng. 2022, 156, 107216. [Google Scholar] [CrossRef]
- Yang, G.D.; Wang, G.H.; Fan, Y.; Wang, F.; Lu, W.B.; Zhao, J.S. Dynamic response and performance of submarine tunnel subjected to surface explosions. Mar. Struct. 2021, 80, 103091. [Google Scholar] [CrossRef]
- Yang, G.D.; Wang, G.H.; Lu, W.B.; Yan, P.; Chen, M. Damage assessment and mitigation measures of underwater tunnel subjected to blast loads. Tunn. Undergr. Space Technol. 2019, 94, 103131. [Google Scholar] [CrossRef]
- Mussa, M.H.; Mutalib, A.A.; Hamid, R.; Naidu, S.R.; Radzi, N.A.M.; Abedini, M. Assessment of damage to an underground box tunnel by a surface explosion. Tunn. Undergr. Space Technol. 2017, 66, 64–76. [Google Scholar] [CrossRef]
- Wang, Y.G.; Liao, C.C.; Wang, J.H.; Jeng, D.S. Dynamic response of pipelines with various burial depth due to underwater explosion. Ocean Eng. 2018, 164, 114–126. [Google Scholar] [CrossRef]
- Kristoffersen, M.; Minoretti, A.; Børvik, T. On the internal blast loading of submerged floating tunnels in concrete with circular and rectangular cross-sections. Eng. Fail. Anal. 2019, 103, 462–480. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, Y.L.; Ren, Y.; Guo, Z.R.; Pan, S.K. Dynamic response analysis of submerged floating tunnel subjected to underwater explosion-vehicle coupled action. Ocean Eng. 2021, 232, 109103. [Google Scholar] [CrossRef]
- Nie, B.C.; Zhang, H.Q. Hoop and axial plastic buckling modes of submerged cylindrical shells subjected to side-on underwater explosion shock wave. Mar. Struct. 2022, 84, 103200. [Google Scholar] [CrossRef]
- Brochard, K.; Sourne, H.L.; Barras, G. Extension of the string-on-foundation method to study the shock wave response of an immersed cylinder. Int. J. Impact Eng. 2018, 117, 138–152. [Google Scholar] [CrossRef]
- Huang, H. Scattering of Spherical Pressure Pulses by a Hard Cylinder. J. Acoust. Soc. Am. 1975, 58, 310–317. [Google Scholar] [CrossRef]
- Jin, Q.K.; Ding, G.Y. A finite element analysis of ship sections subjected to underwater explosion. Int. J. Impact Eng. 2011, 38, 558e566. [Google Scholar] [CrossRef]
- Hung, C.F.; Lin, B.J.; Hwang-Fuu, J.J.; Hsu, P.Y. Dynamic response of cylindrical shell structures subjected to underwater explosion. Ocean Eng. 2009, 36, 564–577. [Google Scholar] [CrossRef]
- Peng, Y.X.; Zhang, A.M.; Ming, F.R. Numerical simulation of structural damage subjected to the near-field underwater explosion based on SPH and RKPM. Ocean Eng. 2021, 222, 108576. [Google Scholar] [CrossRef]
- Nayak, S.; Lyngdoh, G.A.; Shukla, A.; Das, D.S. Predicting the near field underwater explosion response of coated composite cylinders using multiscale simulations, experiments, and machine learning. Compos. Struct. 2022, 283, 115157. [Google Scholar] [CrossRef]
- Long, N.V.; Thinh, T.I.; Bich, D.H.; Tu, T.M. Nonlinear dynamic responses of sandwich-FGM doubly curved shallow shells subjected to underwater explosions using first-order shear deformation theory. Ocean Eng. 2022, 260, 111886. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Zhou, S.; Gao, H.; Liu, H.Q. Predictions of compression capacity of randomly corroded spherical shells based on artificial neural network. Ocean Eng. 2022, 257, 111668. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, S.P.; Zhang, Z.Y. Fire Thermal Stress and Its Damage to Subsea Immersed Tunnel. In Proceedings of the 2nd International Symposium on Submerged Floating Tunnels and Underwater Tunnel Structures, Chongqing, China, 16–18 December 2016. [Google Scholar]
- MacKay, J.R.; Jiang, L.; Glas, A.H. Accuracy of nonlinear finite element collapse predictions for submarine pressure hulls with and without artificial corrosion damage. Mar. Struct. 2011, 24, 292–317. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Z.K.; Wang, F.; Zhao, T.; Zhu, Y.M. Ultimate strength of externally pressurised steel spheres containing through-thickness defects. Int. J. Press. Vessel. Pip. 2022, 199, 10470. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Tang, W.X.; Wang, W.B.; Wang, M.L. Buckling of spherical shells subjected to external pressure: A comparison of experimental and theoretical data. Thin-Walled Struct. 2017, 111, 58–64. [Google Scholar] [CrossRef]
- Ismail, M.S.; Mahmud, J.; Jailani, A. Buckling of an imperfect spherical shell subjected to external pressure. Ocean Eng. 2023, 275, 114118. [Google Scholar] [CrossRef]
- Lu, C.F.; Chen, W.Q.; Shao, J.W. Semi-analytical three-dimensional elasticity solutions for generally laminated composite plates. Eur. J. Mech. A-Solid 2008, 27, 899–917. [Google Scholar] [CrossRef]
- Wang, H.M. Dynamic electromechanical behavior of a triple-layer piezoelectric composite cylinder with imperfect interfaces. Appl. Math. Model 2011, 35, 1765–1781. [Google Scholar] [CrossRef]
- Yang, G.D.; Fan, Y.; Wang, G.H.; Cui, X.Z.; Leng, Z.D.; Lu, W.B. Blast resistance of air-backed RC slab against underwater contact explosion. Def. Technol. 2023, 28, 236–250. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhou, X.X.; Xiao, L.; Li, X.; Lin, F.T. Dynamic response and damage characteristics of special blast-resistant door structure subjected to underwater explosion. Structures 2023, 57, 105262. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. In Proceedings of the 9th International Symposium on the Effects of Munitions with Structures, Berlin-Strausberg, Germany, 3–7 May 1999. [Google Scholar]
- Zhou, Q.; Qi, L. Analysis and comparison of 5 different common anti-explosion concrete material models of LS-DYNA software. Concrete 2019, 11, 43–49. (In Chinese) [Google Scholar] [CrossRef]










| A (GPa) | B (GPa) | R1 | R2 | ω | E0 (GPa) |
|---|---|---|---|---|---|
| 373.77 | 3.747 | 4.15 | 0.9 | 0.35 | 6 |
| C (m/s) | S1 | S2 | S3 | a | γ0 | ρ (kg/m3) |
|---|---|---|---|---|---|---|
| 1647 | 1.921 | −0.096 | 0 | 0 | 0.35 | 1000 |
| ρ (kg/m3) | C0–C3, C6 | C4, C5 | E0 | V0 |
|---|---|---|---|---|
| 1.25 | 0 | 0.4 | 2.53 × 105 | 1.0 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Mass density MID (kg/m3) | 2314 | Porosity exponent NP | 3.0 |
| Initial porosity ALPHA | 1.1884 | Reference compressive strain-rate E0C | 3.0 × 10−8 |
| Crush pressure PEL (MPa) | 25.33 | Reference tensile strain rate E0T | 3.0 × 10−9 |
| Compaction pressure PCO (GPa) | 6.0 | Break compressive strain rate EC | 3.0 × 1022 |
| Hugoniot polynomial coefficient A1 (GPa) | 35.27 | Break tensile strain rate ET | 3.0 × 1022 |
| Hugoniot polynomial coefficient A2 (GPa) | 39.58 | Compressive strain rate dependence exponent BETAC | 0.0298507 |
| Hugoniot polynomial coefficient A3 (GPa) | 9.04 | Tensile strain rate dependence exponent BETAT | 0.0344828 |
| Parameter for polynomial EOS B0 | 1.22 | Volumetric plastic strain fraction in tension PTF | 0.001 |
| Parameter for polynomial EOS B1 | 1.22 | Compressive yield surface parameter GC* | 0.53 |
| Parameter for polynomial EOS T1 (GPa) | 35.27 | Tensile yield surface parameter GT* | 0.7 |
| Parameter for polynomial EOS T2 | 0 | Erosion plastic strain EPSF | 2.0 |
| Elastic shear modulus SHEAR (GPa) | 16.7 | Shear modulus reduction factor XI | 0.5 |
| Compressive strength FC (MPa) | 38 | Damage parameter D1 | 0.04 |
| Relative tensile strength FT* | 0.1 | Damage parameter D2 | 1 |
| Relative shear strength FS* | 0.18 | Minimum damaged residual strain EPM | 0.01 |
| Failure surface Parameter A | 1.6 | Residual surface parameter AF | 1.6 |
| Failure surface Parameter N | 0.61 | Residual surface parameter NF | 0.61 |
| Lode angle dependence factor Q0 | 0.6805 | Gruneisen gamma GAMMA | 0 |
| Lode angle dependence factor B | 0.0105 |
| Parameter | Value |
|---|---|
| Mass density RO (kg/m3) | 7850 |
| Young’s modulus E (GPa) | 206 |
| Poisson’s ratio PR | 0.3 |
| Yield stress SIGY (MPa) | 400 |
| Strain rate parameter C (s−1) | 35.27 |
| Strain rate parameter P | 5 |
| Tangent modulus ETAN (GPa) | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.; Zhou, X.; Zhao, J.; Xiao, L.; Tang, L.; Liu, Z.; Wang, J. Damage Characteristics and Dynamic Response of RC Shells Subjected to Underwater Shock Wave. Appl. Sci. 2024, 14, 1878. https://doi.org/10.3390/app14051878
Lin F, Zhou X, Zhao J, Xiao L, Tang L, Liu Z, Wang J. Damage Characteristics and Dynamic Response of RC Shells Subjected to Underwater Shock Wave. Applied Sciences. 2024; 14(5):1878. https://doi.org/10.3390/app14051878
Chicago/Turabian StyleLin, Fantong, Xianxiang Zhou, Jian Zhao, Lan Xiao, Lubo Tang, Ziye Liu, and Jianshuai Wang. 2024. "Damage Characteristics and Dynamic Response of RC Shells Subjected to Underwater Shock Wave" Applied Sciences 14, no. 5: 1878. https://doi.org/10.3390/app14051878
APA StyleLin, F., Zhou, X., Zhao, J., Xiao, L., Tang, L., Liu, Z., & Wang, J. (2024). Damage Characteristics and Dynamic Response of RC Shells Subjected to Underwater Shock Wave. Applied Sciences, 14(5), 1878. https://doi.org/10.3390/app14051878





